ТЕМА: КВАДРАТИЧНАЯ ФУНКЦИЯ
Т - 1 ВЫБЕРИТЕ ВЕРНЫЙ ОТВЕТ
Цель : проверка знаний учащихся:
а) проводить исследование квадратичной функции;
б) читать графики квадратичных функций;
в) решать простейшие неравенства второй степени
с одной переменной.
Проводится на уроках закрепления (в качестве устных упражнений или вместо проверки домашнего задания).
Вариант 1
Укажите область определения функции:
у = 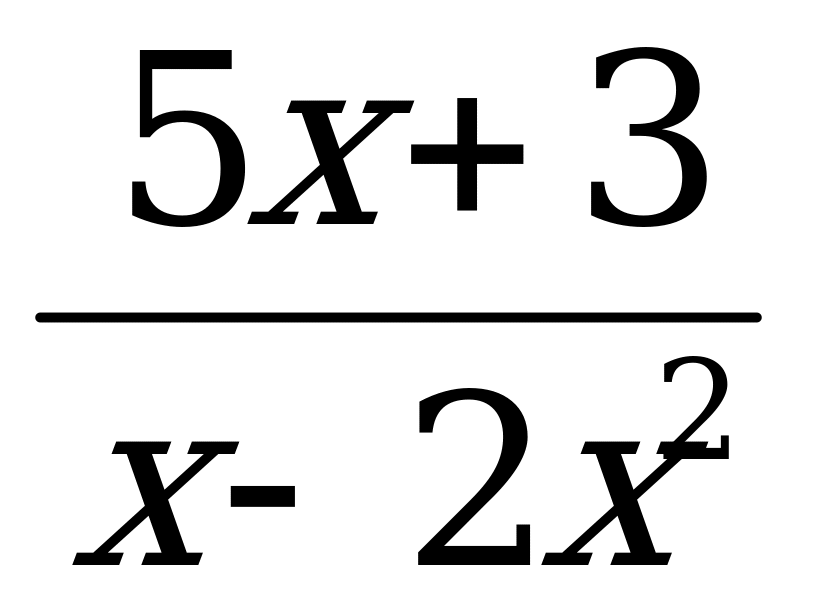
Ответы: а) D(у) = ( - ∞; 0) U (0; 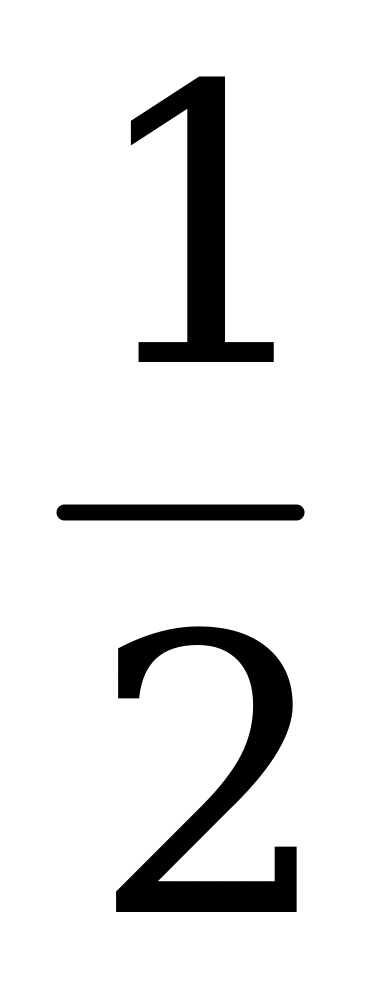 ) U (
) U (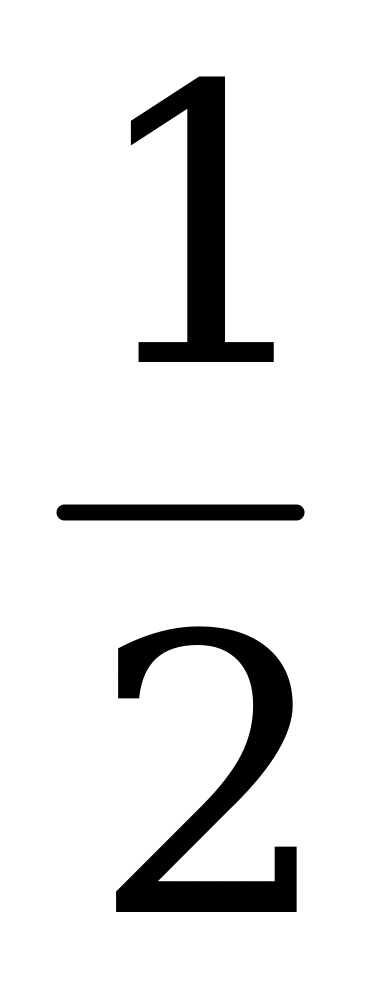 ; + ∞);
; + ∞);
б) D(у) = ( - ∞; 0) U (0; 2) U (2 ; + ∞);
в) D(у) = ( - ∞; - 2) U (- 2; 0) U (0; + ∞).
Найдите область значений функции: у = - х2 - 4х + 5
Ответы: а) Е(у) = ( - ∞; 9]; б) Е(у) = [ 9; + ∞);
в) Е(у) = (- ∞; - 9].
Разложите на множители квадратный трехчлен:
Х2 - 6 х - 7
Ответы: а)(х - 7)(х + 1); б)(х + 7)(х - 1); в)(х - 7)(х - 1).
При каких х функция у = х2 - 6х - 7 принимает положительные значения?
Ответы: а)(- ∞; 1) U (7; + ∞); б)(-1; 7); в)(1; 7).
При каких х функция у= - х2 - 4х + 5 возрастает ?
Ответы: а) (- ∞; 9]; б) (- ∞; - 2]; в) (- ∞; 2].
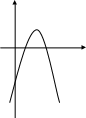
Укажите график функции у = - х2 + 4х - 3
а) б) в)
 у у
у у
у
-3 -1
0 х
0 1 3 х 3
-3
0 1 3 х
7. Укажите график функции у = (х - 3)2 + 1
а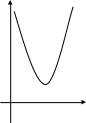
 ) б) в)
) б) в)
у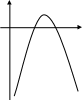 у
у
 у
у
0 1 3 х
1
1
0 3 х
3 х
-3 0 х
8. Решите неравенство: 25 – х2
Ответы: а)(- ∞; - 5) U (5; + ∞); б)(- 5; 5); в)(5; + ∞).
Укажите наименьшее целое решение неравенства:
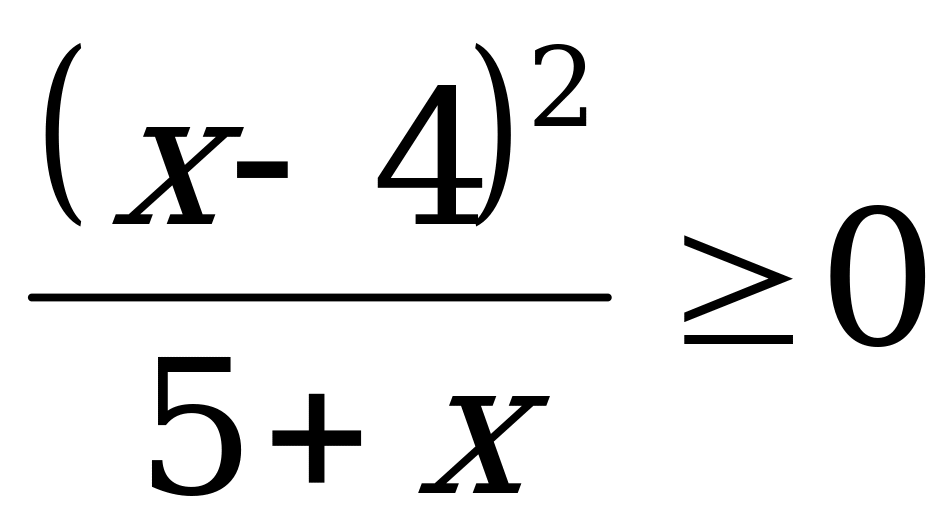
Ответы: а) - 5; б) - 4; в) 4.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| баллы | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 |
Вариант 2
Укажите область определения функции: у = 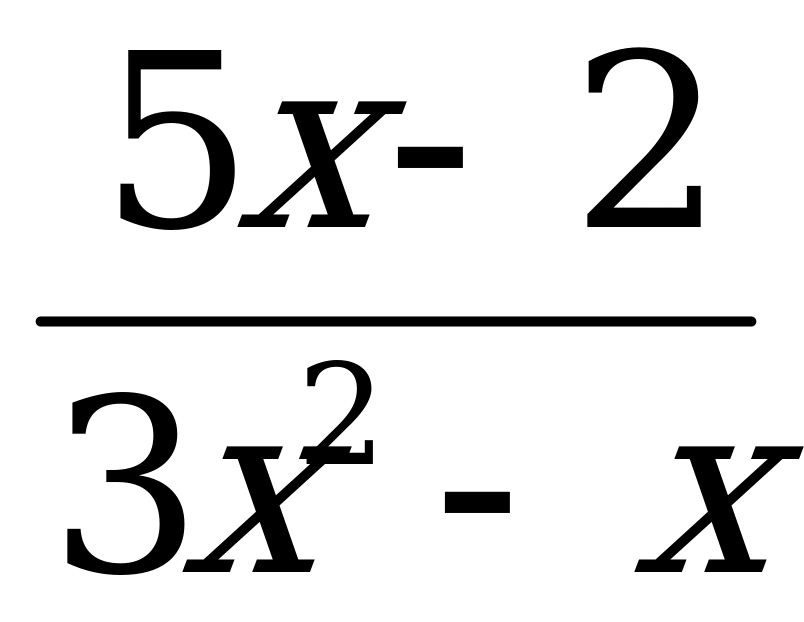
Ответы: а) D(у) = ( - ∞ ; 0)  (0;
(0; 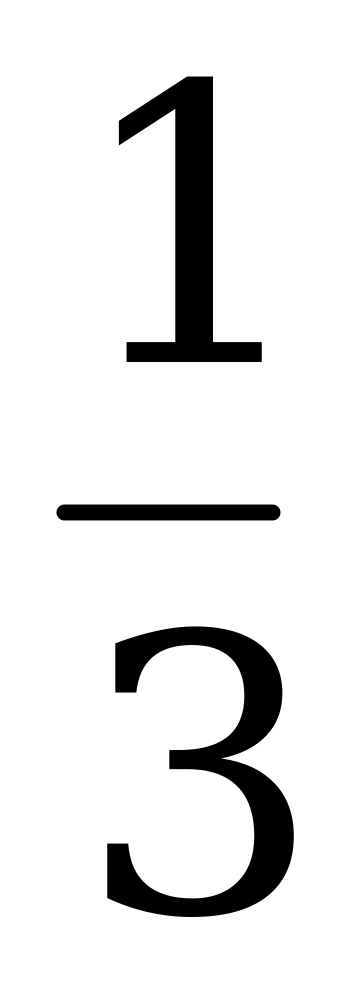 )
)  (
(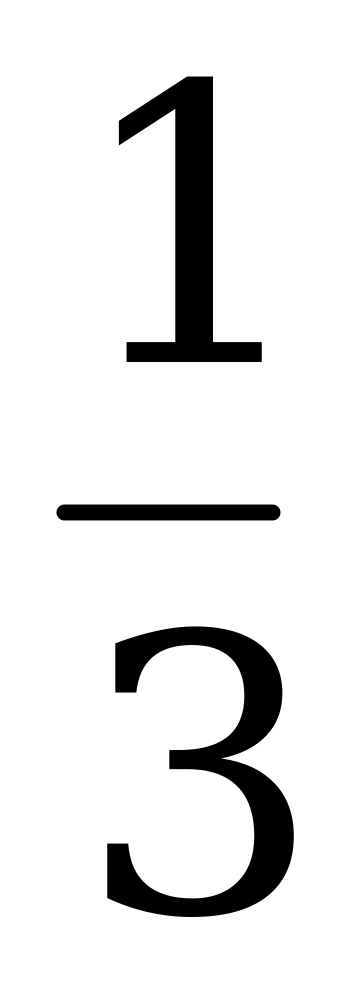 ; + ∞);
; + ∞);
б) D(у) = ( - ∞ ; - 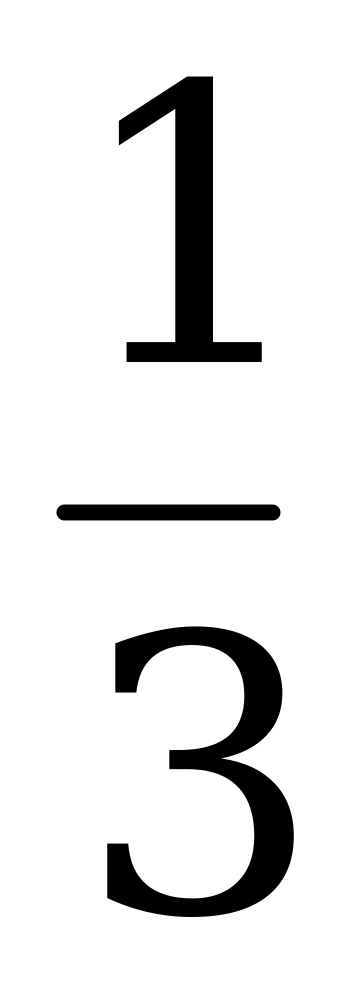 )
)  (-
(- 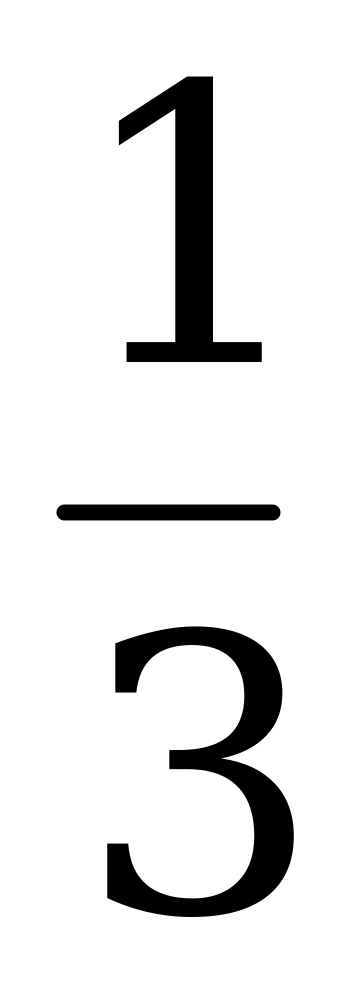 ; 0)
; 0)  (0; + ∞);
(0; + ∞);
в) D(у) = ( - ∞ ; 0)  (0; 3)
(0; 3)  (3 ; + ∞).
(3 ; + ∞).
Найдите область значений функции: у = 2х2 + 4х + 5
Ответы: а) Е (у) = ( - ∞ ; 3]; б) Е (у) = [3; + ∞);
в) Е (у) = (3; + ∞.)
Разложите на множители квадратный трехчлен:
Х2 + 4х - 5
Ответы: а) (х - 1)(х + 5); б) (х - 5)(х + 1); в) (х - 5)(х - 1).
При каких х функция у = х2 + 4х - 5 принимает положительные значения?
Ответы: а) (- 5; 1); б) (-∞ ; - 5)  (1; + ∞); в) (- 5; - 1).
(1; + ∞); в) (- 5; - 1).
При каких х функция у = 2х2 + 4х + 5 возрастает ?
Ответы: а) [3; + ∞); б) [- 1; + ∞); в) [1; + ∞).
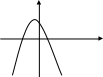
Укажите график функции у = - х2 - 2х + 2
а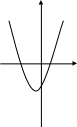 ) б) в)
) б) в)
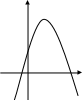
 у у у
у у у
2
-1 0 х -1 2
0 х
-2 0 1 х
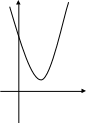
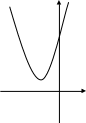
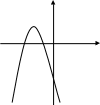
7. Укажите график функции у = (х + 2)2 + 1
а) б) в)
 у у у
у у у
1
5 5
-2 0 х
1 1
-2
0 1 2 х -2 0 х
8. Решите неравенство: - х2 + 16 0
Ответы: а)(- ∞; - 4)  (4; + ∞); б)(- 4; 4); в)(4; + ∞).
(4; + ∞); б)(- 4; 4); в)(4; + ∞).
Укажите наименьшее целое решение неравенства
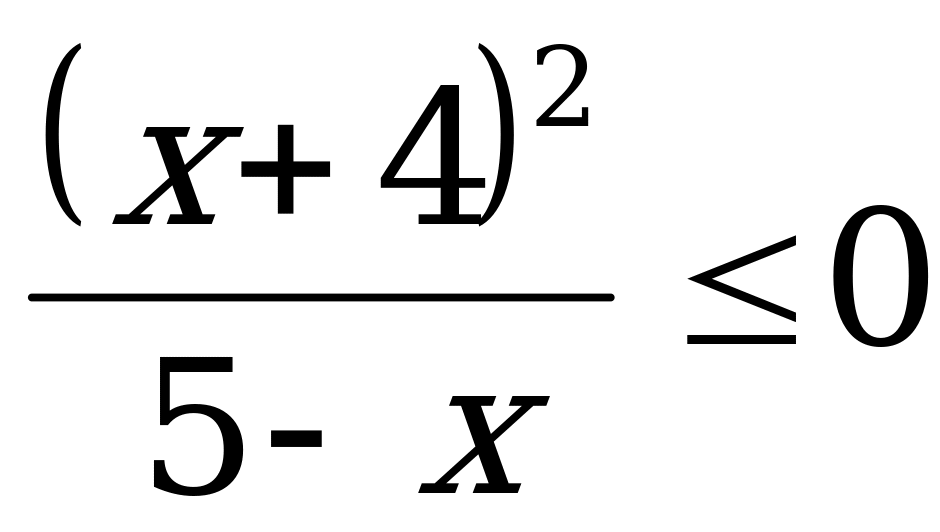
Ответы: а) 5; б) – 4; в) 4.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| баллы | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 |
ТЕМА: УРАВНЕНИЕ И СИСТЕМЫ УРАВНЕНИЙ.
Т - 1 ВЫБЕРИТЕ ВЕРНЫЙ ОТВЕТ
Цель : проверка умений учащихся:
а) решать уравнения 3-й и 4-й степени с помощью
разложения на множители и введения
вспомогательной переменной;
б) решать простейшие системы, содержащие
уравнение 2-ой степени с двумя переменными;
Проводится перед тематической контрольной работой.
Вариант 1
Какое из чисел является корнем уравнения:
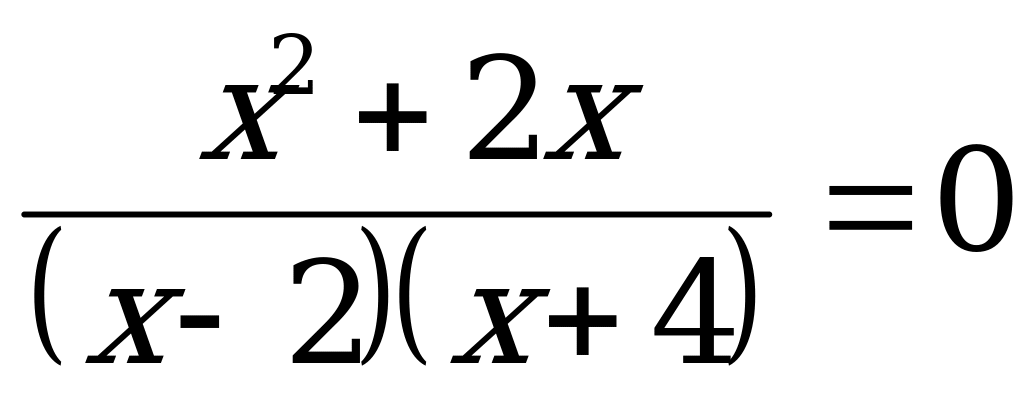
Ответы: а) 2; б) - 2; в) 4.
Решите уравнение: 4х3 + 4х2 + х = 0
Ответы: а) 0 и 2; б) - 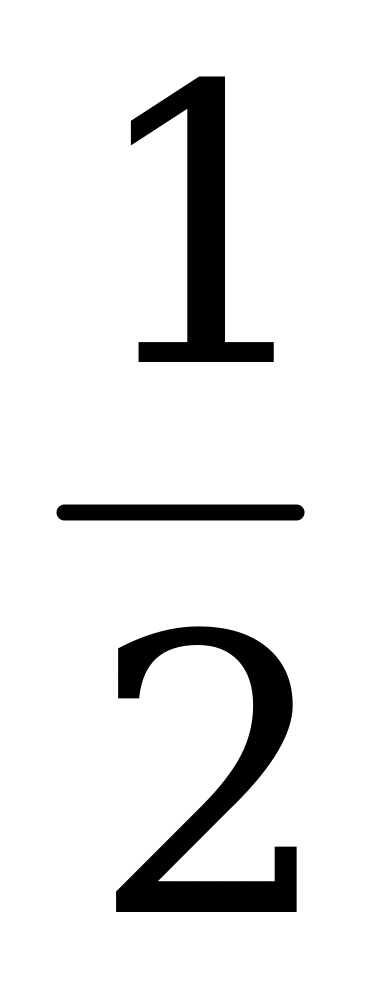 и 0; в) 0 и 0,5.
и 0; в) 0 и 0,5.
Сколько корней имеет уравнение: х4 + 8х2 - 9 = 0
Ответы: а) 4; б) 2; в) нет корней.
Найдите сумму корней уравнения:
(2х - 4)(х2 - 2х + 1) = 0
Ответы: а) 3; б) 1; в) 1,5.
Решите уравнение: (х2 + 2х)(х2 + 2х + 2) + 1 = 0
Ответы: а) - 2; - 1; б) - 1; в) - 2; 2.
Решите систему уравнений:
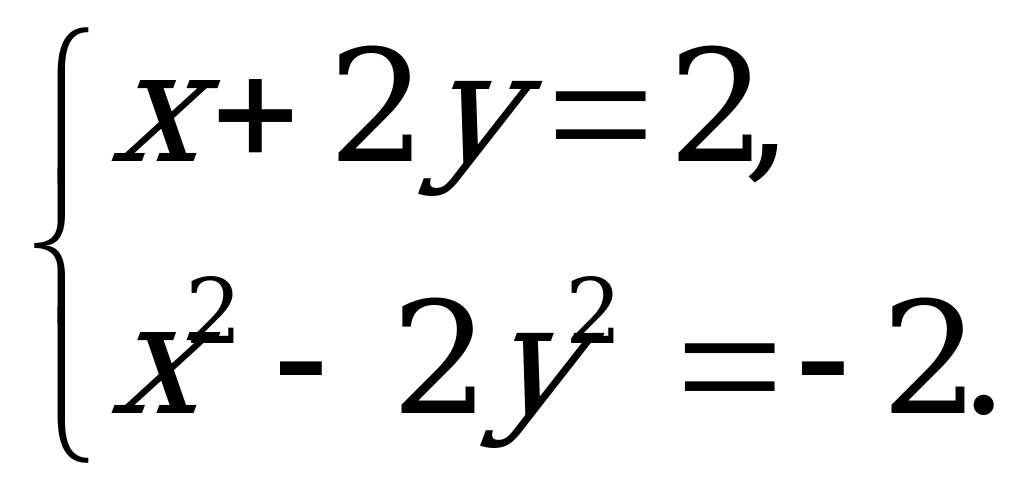
Ответы: а) (0; 1); (- 1; 3);
б) (0; - 1); (1; 3);
в) (- 1; 7); (0; 2).
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| баллы | 1 | 1 | 2 | 2 | 3 | 3 |
Вариант 2
Какое из чисел является корнем уравнения:
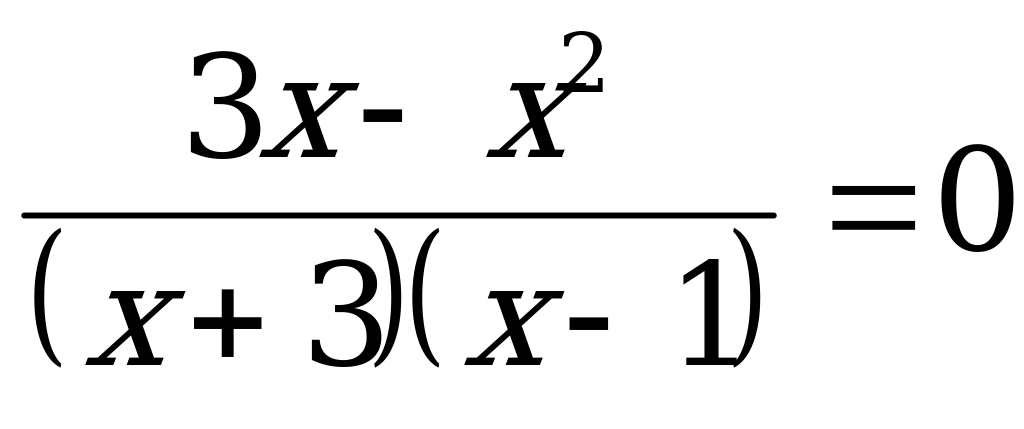
Ответы: а) - 3; б) 3; в) 1.
Решите уравнение: 9х3 - 6х2 + х = 0
Ответы: а) 0 и 3; б) - 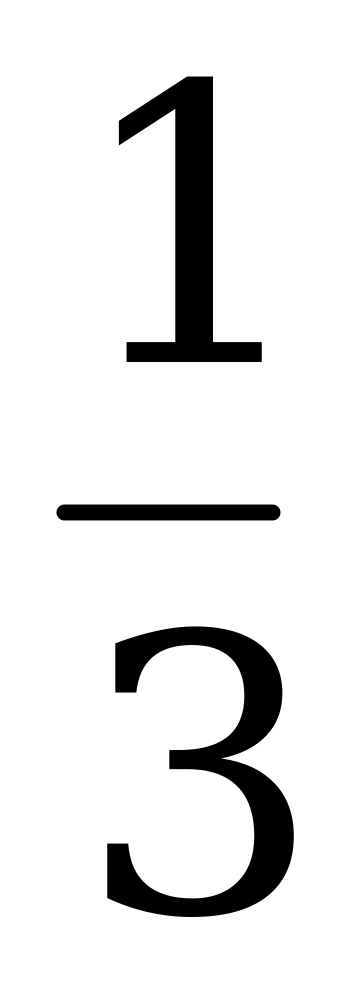 и 0; в) 0 и
и 0; в) 0 и 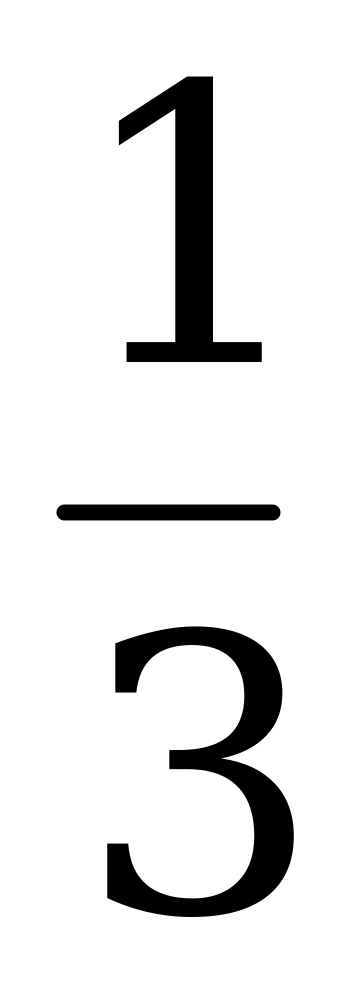 .
.
Сколько корней имеет уравнение: х4 - х2 - 6 = 0
Ответы: а) 4; б) 2; в) нет корней.
Найдите сумму корней уравнения:
(х - 3)(х2 - 4х + 4) = 0
Ответы: а) - 1; б) 5; в) 7.
Решите уравнение: (х2 + 4х)(х2 + 4х + 8) + 16 = 0
Ответы: а) - 2; - 4; б) - 2; в) - 2; 2.
Решите систему уравнений:
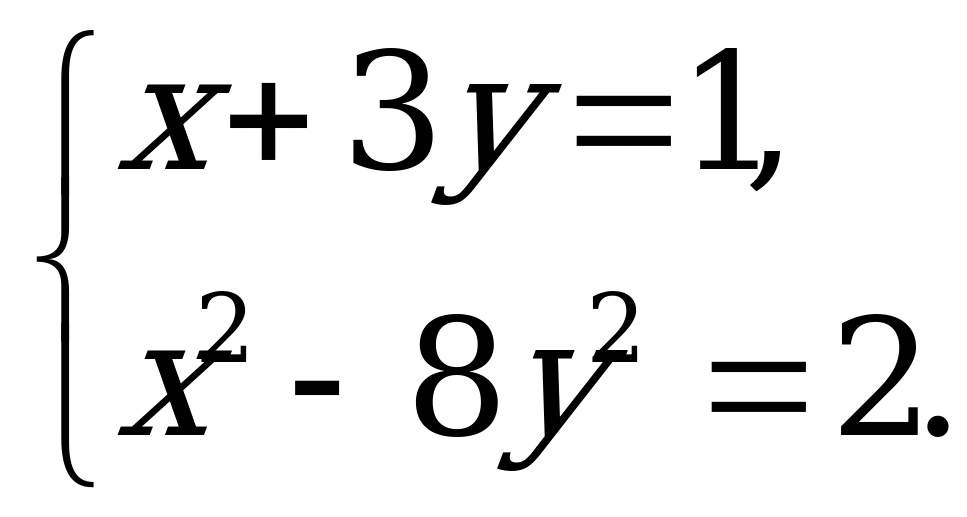
Ответы: а) (- 14; 5); (- 2; 1);
б) (16; 5); (4; 1);
в) (4; - 1); (16; - 5).
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| баллы | 1 | 1 | 2 | 2 | 3 | 3 |
ТЕМА: ПРОГРЕССИИ.
Т - 1 ВЫБЕРИТЕ ВЕРНЫЙ ОТВЕТ
Цель : проверить сформированность понятий об арифметической и геометрической прогрессиях, как числовых последовательностях особого вида.
Проводится для проверки домашнего задания.
Вариант 1
В арифметической прогрессии (an): а1 = - 2, d = 4. Найдите: а10.
Ответы: а) 38; б) 34; в) 70.
Найдите произведение а1 ∙ а10, используя данные задания № 1.
Ответы: а) - 76; б) - 68; в) - 140.
В арифметической прогрессии (аn) найдите сумму десяти первых ее членов, если аn = 3n + 4.
Ответы: а) 410; б) 205; в) 82.
Найдите знаменатель геометрической прогрессии (хn),
если х2 = 10; х10 = 160.
Ответы: а) - 4; 4; б) 4; в) - 16; 16.
В геометрической прогрессии (хn) найти сумму пяти
первых ее членов, если х1 = 4; х2 = - 12.
Ответы: а) - 240; б) 244; в) 242.
| № задания | 1 | 2 | 3 | 4 | 5 |
| баллы | 1 | 1 | 2 | 3 | 3 |
Вариант 2
В арифметической прогрессии (an): a1 = - 3, d = 2. Найдите: а11.
Ответы: а) 23; б) 17; в) 37.
Найдите произведение а1 ∙ а11, используя данные задания № 1.
Ответы: а) - 69; б) - 51; в) - 111.
В арифметической прогрессии (аn) найдите сумму десяти первых ее членов, если аn = 2n + 5.
Ответы: а) 320; б) 160; в) 66.
Найдите знаменатель геометрической прогрессии (хn),
если х2 = 2; х5 = 54.
Ответы: а) - 3; 3; б) 3; в) - 3.
В геометрической прогрессии (хn) найти сумму пяти
первых ее членов, если х1 = - 3; х2 = - 6.
Ответы: а) 31; б) - 93; в) - 33.
| № задания | 1 | 2 | 3 | 4 | 5 |
| баллы | 1 | 1 | 2 | 3 | 3 |
ТЕМА: СТЕПЕННАЯ ФУНКЦИЯ.
КОРЕНЬ n-й СТЕПЕНИ.
Т - 1 ВЫБЕРИТЕ ВЕРНЫЙ ОТВЕТ
Цель : проверить умения учащихся
а) исследовать функцию на четность;
б) выполнять несложные задания на вычисление
корней n-й степени и преобразование
выражений, содержащих корни n-й степени.
Проводится на обобщающем уроке по данной теме.
Вариант 1
Найдите значение выражения: 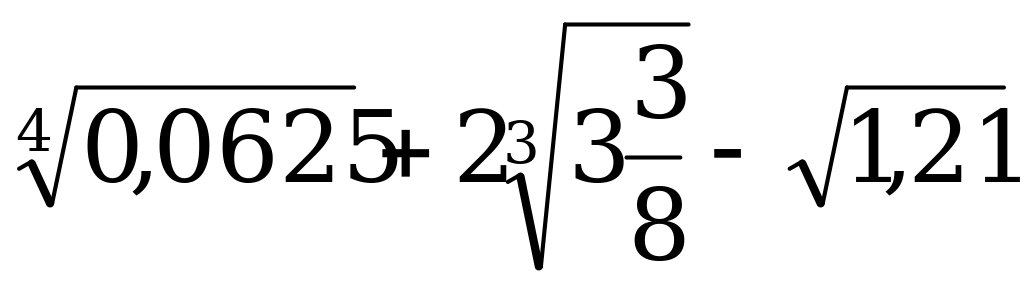
Ответы: а) 5,4; б) 2,4; в) 0,9.
Ч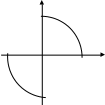 то можно сказать о функции у = f (х) ?
то можно сказать о функции у = f (х) ?
у
2
Ответы: а) четная
-2 0 2 б) нечетная
в) ни четная, ни нечетная
-2
3. Исследуйте функцию f (х) = 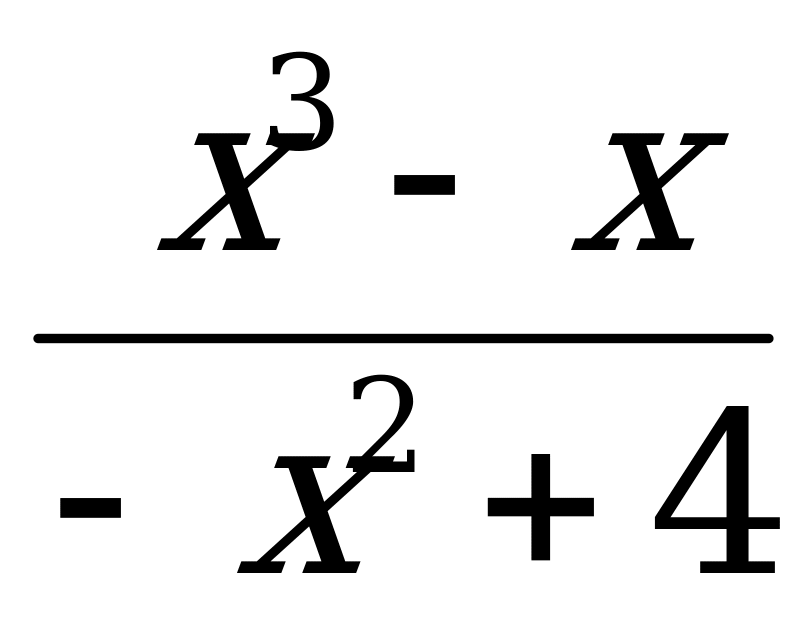 на четность.
на четность.
Ответы: а)четная; б)нечетная; в)ни четная, ни нечетная
4. Сократите дробь: 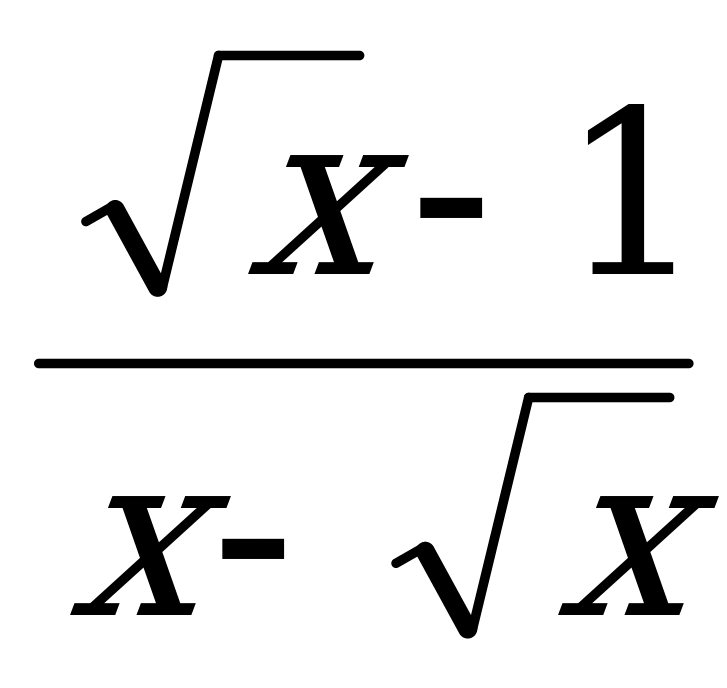
Ответы: а) 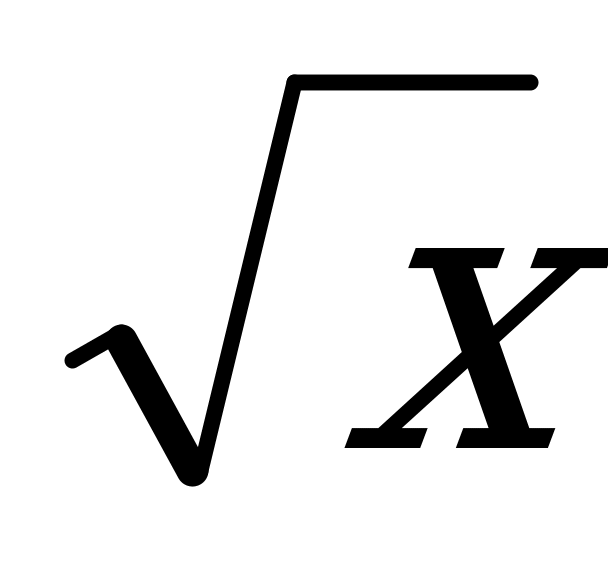 ; б)
; б) 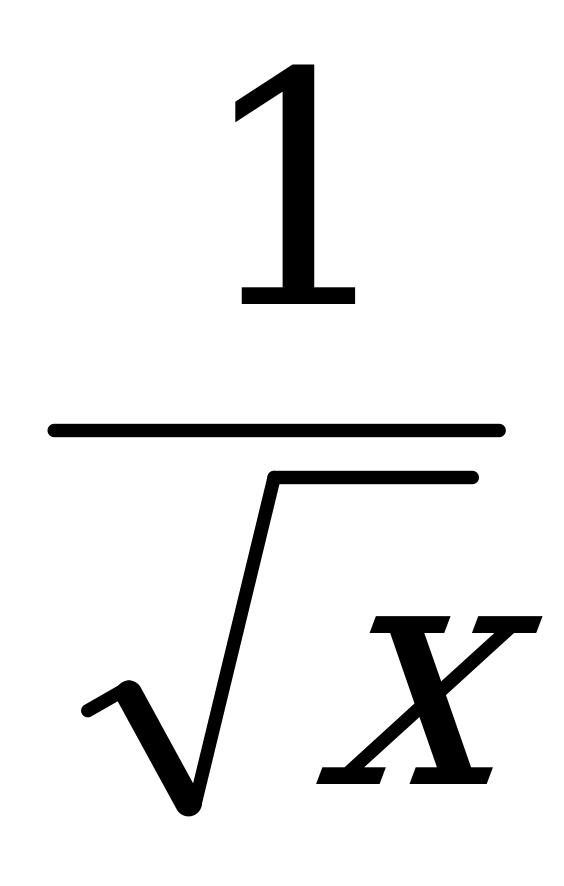 ; в)
; в) 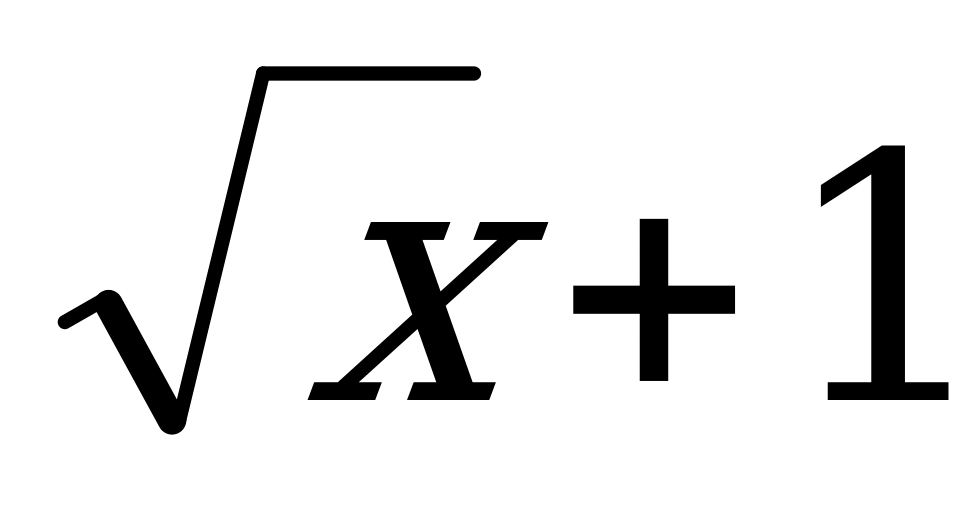 .
.
5. Упростить выражение: 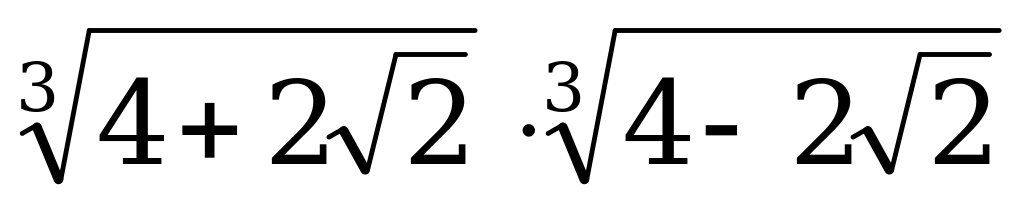
Ответы: а) 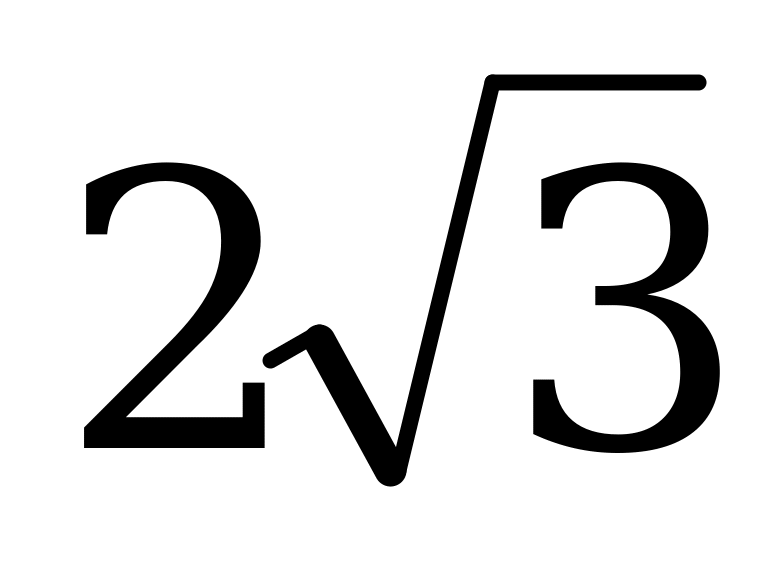 ; б) 2; в) 4.
; б) 2; в) 4.
Решить уравнение: 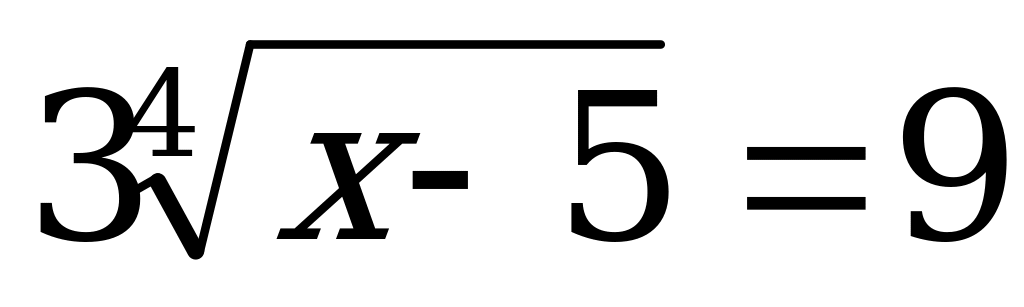
Ответы: а) 76; б) 86; в) 14.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| баллы | 1 | 1 | 2 | 2 | 3 | 3 |
Вариант 2
Найдите значение выражения: 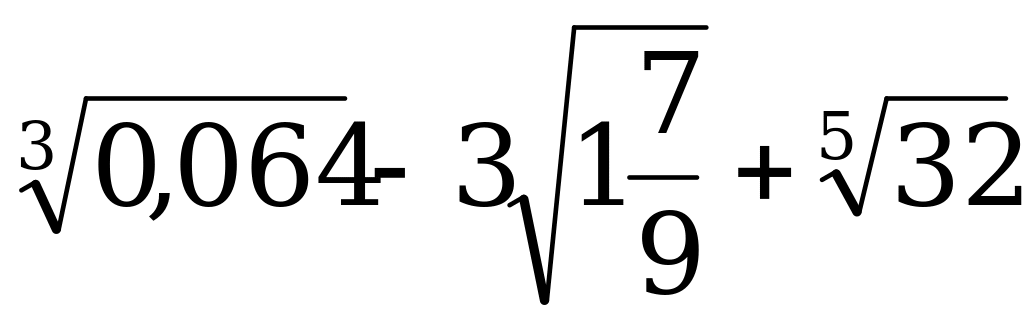
Ответы: а) 5,4; б) 1,4; в) - 0,6.
Что можно сказать о функции у = f (х) ?
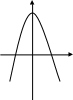 у
у
Ответы: а) четная
б) нечетная
в) ни четная, ни нечетная
-1 0 1
3. Исследуйте функцию f (х) = 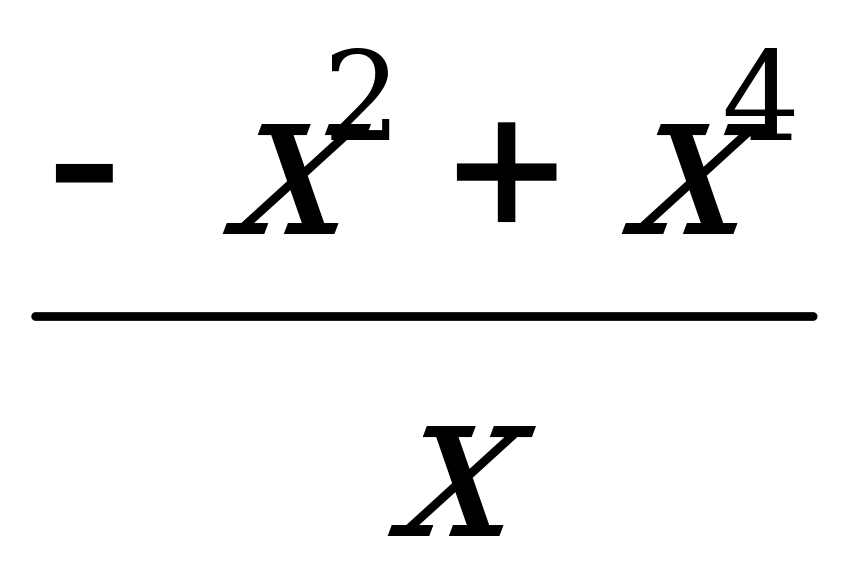 на четность.
на четность.
Ответы: а)четная; б)нечетная; в)ни четная, ни нечетная.
4. Сократите дробь: 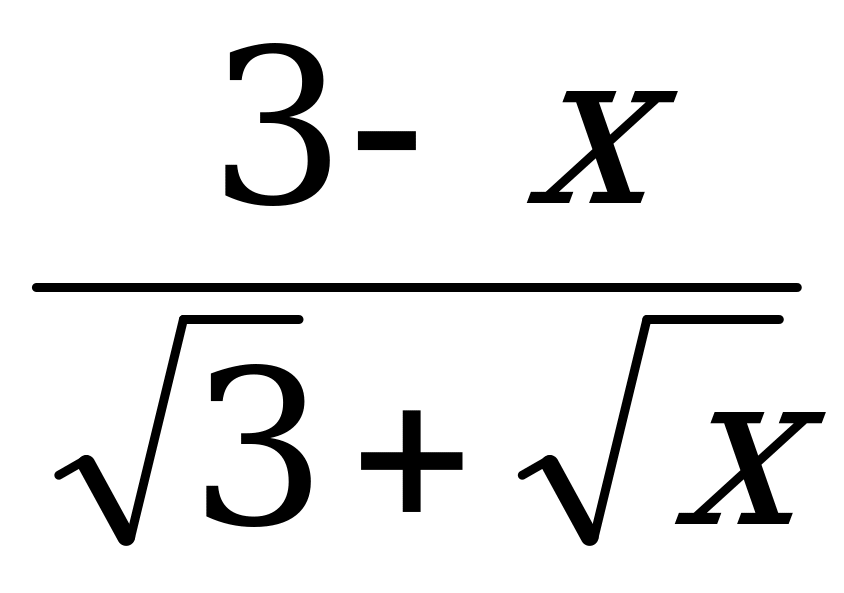
Ответы: а) 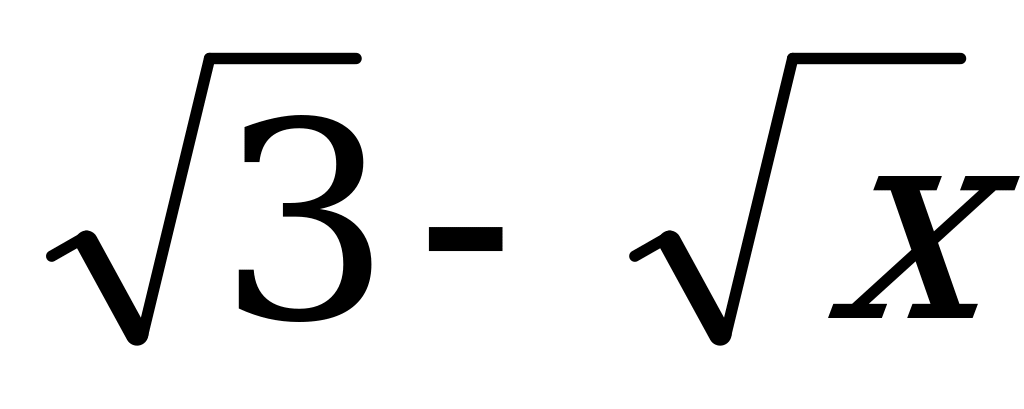 ; б)
; б) 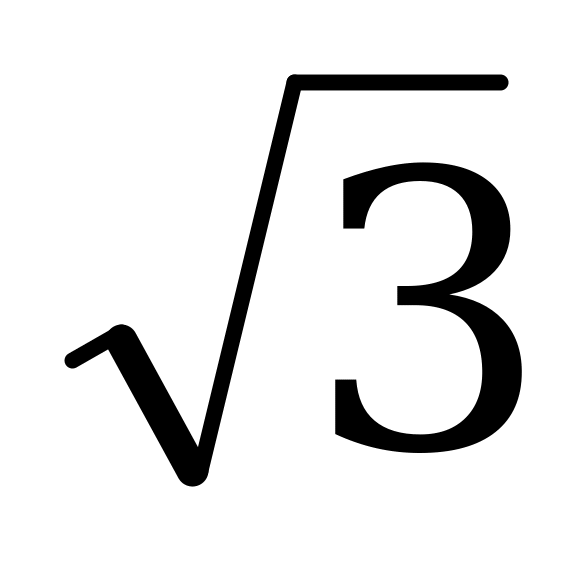 ; в)
; в) 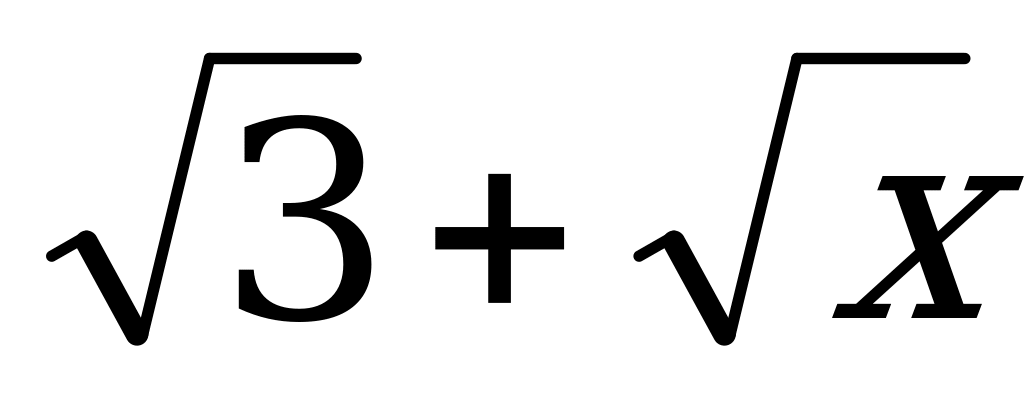 .
.
5. Упростить выражение: 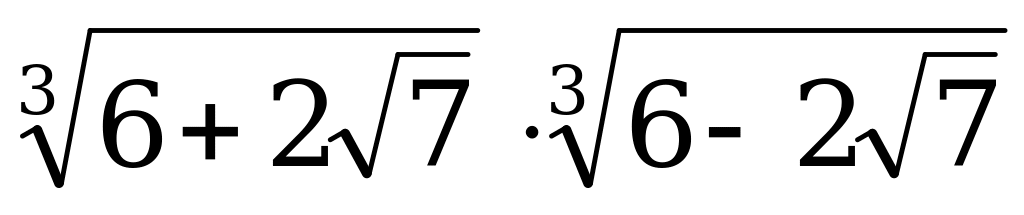
Ответы: а) 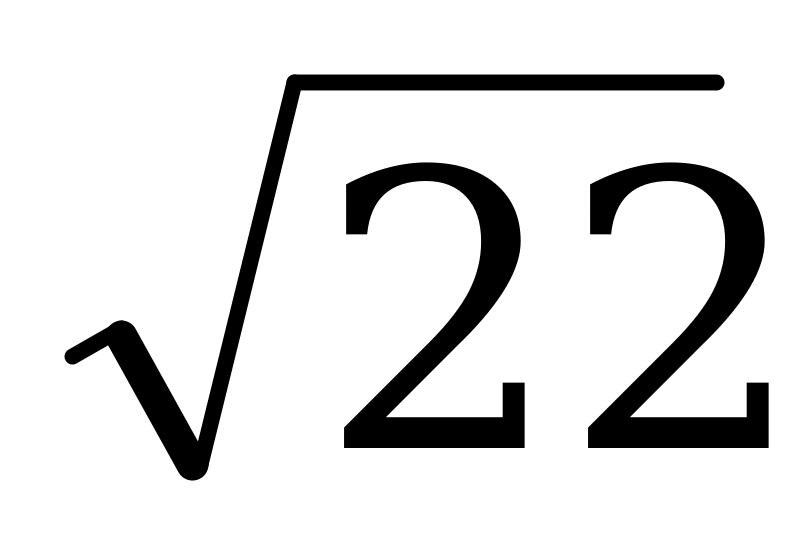 ; б) 2; в) 4.
; б) 2; в) 4.
Решить уравнение: 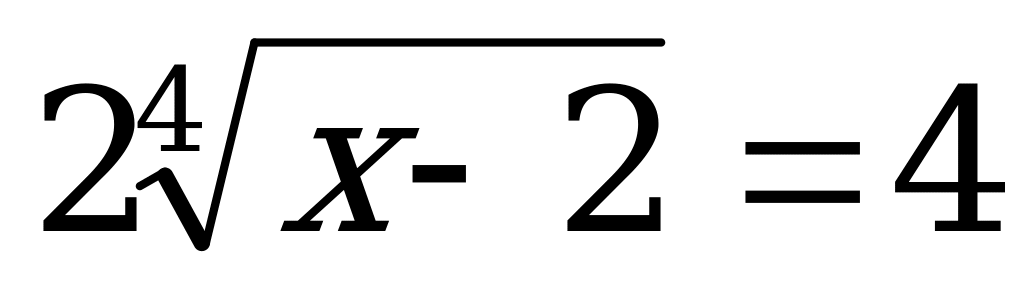
Ответы: а) 14; б) 18; в) 6.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 |
| баллы | 1 | 1 | 2 | 2 | 3 | 3 |
ТЕМА: ИТОГОВЫЙ ТЕСТ ПО АЛГЕБРЕ
ЗА ОСНОВНУЮ ШКОЛУ
Т - 1 ВЫБЕРИТЕ ВЕРНЫЙ ОТВЕТ
Цель : проверить подготовку учащихся к выпускным экзаменам по алгебре за основную школу.
Вариант 1
Решить уравнение: (10х - 4) (3х + 2) = 0
Ответы: а) - 1,5 и 0,4; б) 0,4 и - 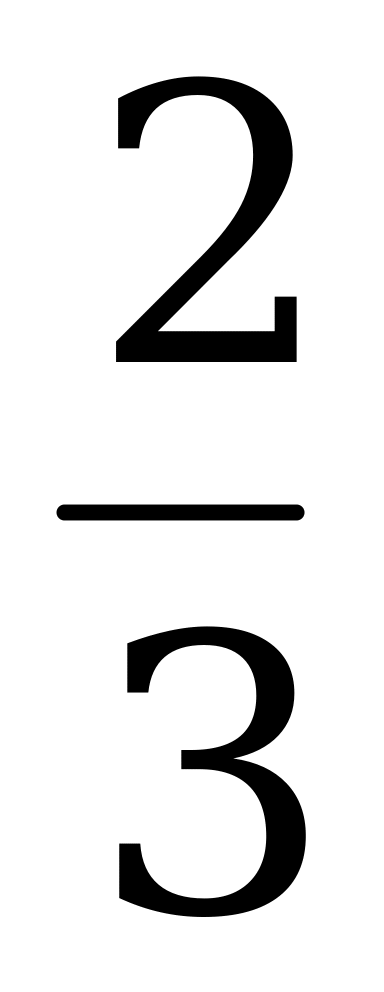 ; в) 2,5 и - 1,5.
; в) 2,5 и - 1,5.
Найти значение выражения: а + 0,5в3 при а = 20; в = - 4
Ответы: а) 52; б) - 12; в) 28.
Решите неравенство: 5х + 3 (х + 8)
Ответы: а) (17; + ∞); б) (- ∞; 17); в) (- 7; + ∞).
Найти значение выражения: 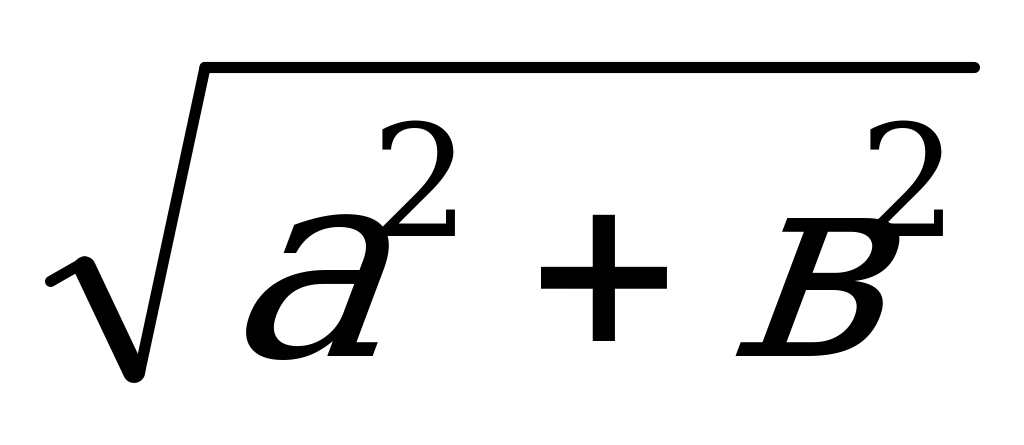 при а = 12 и в = - 5
при а = 12 и в = - 5
Ответы: а) 11; б) 13; в) 7.
Найти область определения функции у = 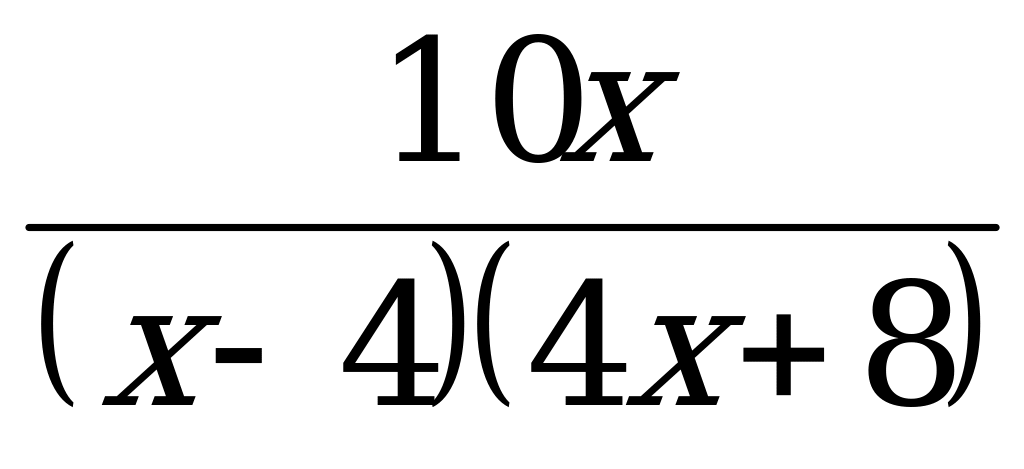
Ответы: а) D(у) = ( - ∞ ; - 2) U (- 2; 0) U (0; 4) U (4; + ∞);
б) D(у) = ( - ∞ ; - 2) U (- 2; 4) U (4; + ∞);
в) D(у) = ( - ∞ ; - 4) U (- 4; 2) U (2; + ∞).
Решите систему уравнений: 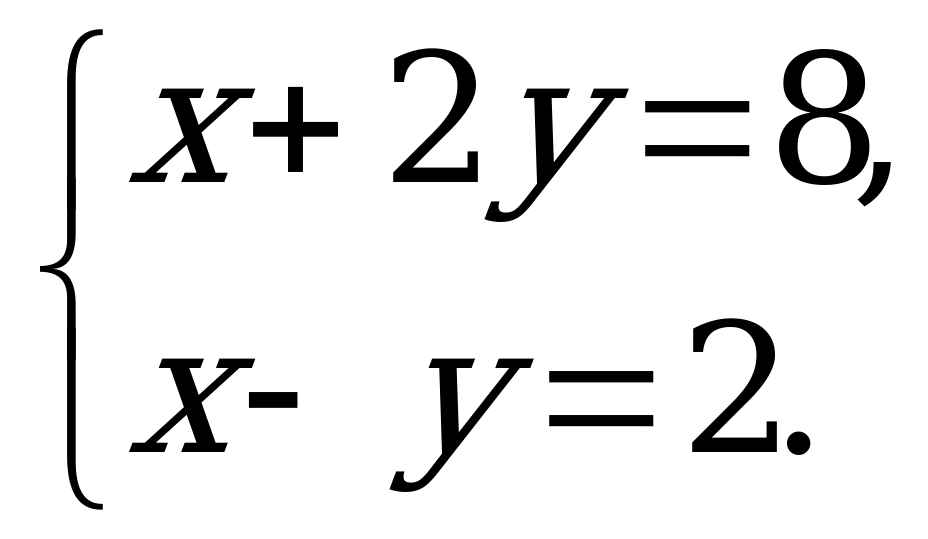
Ответы: а) (3; 4); б) (4; 2); в) (-1; 2).
Упростите выражение: 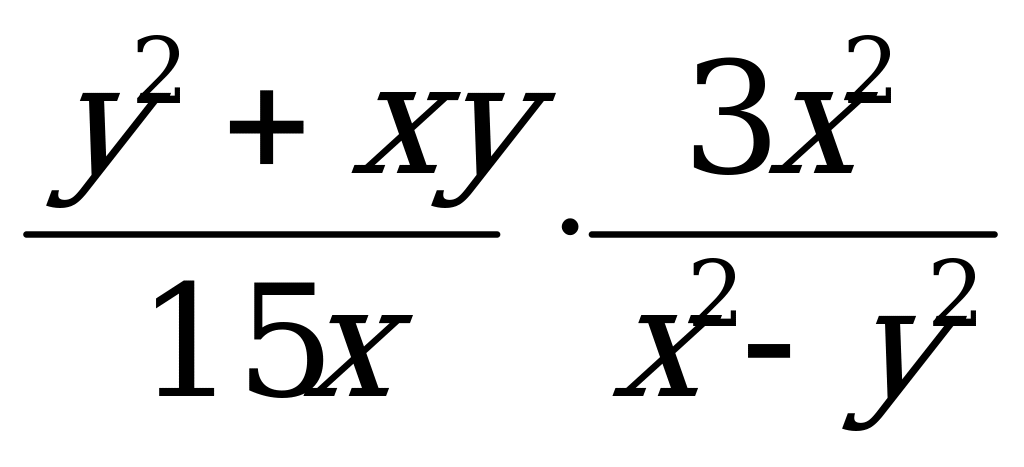
Ответы: а) 5ху(х - у); б) 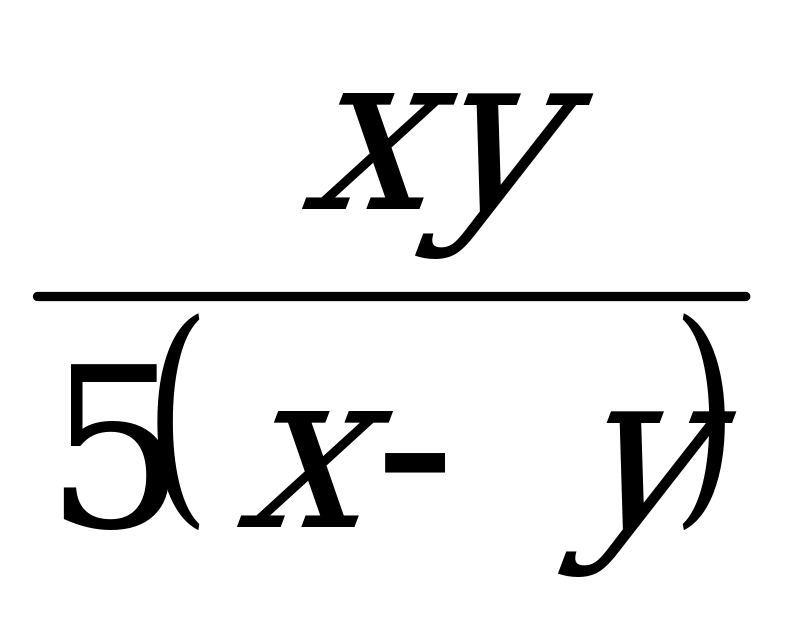 ; в)
; в) 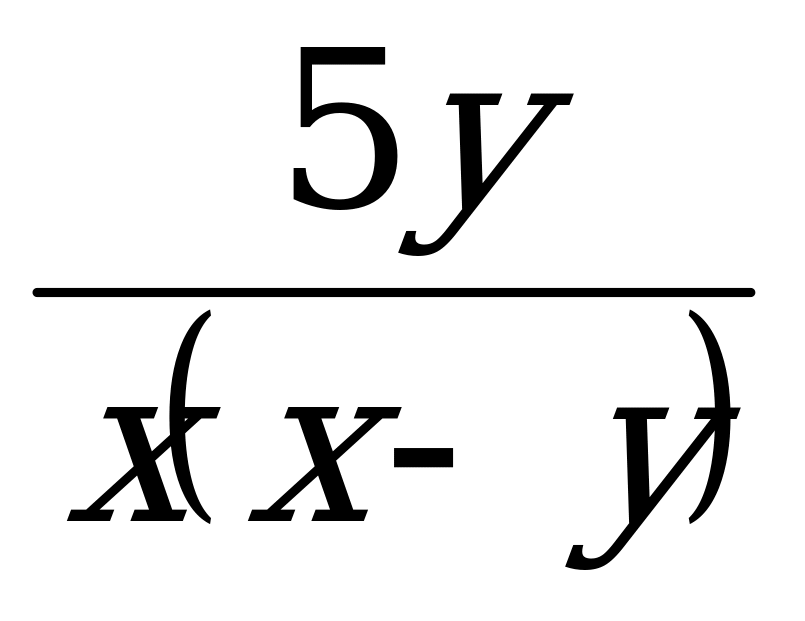 .
.
Какое из следующих уравнений имеет то же множество
решений, что и уравнение (х - 12) (х + 12) = 0 ?
1. х2 + 144 = 0,
│х │ = 12,
х = 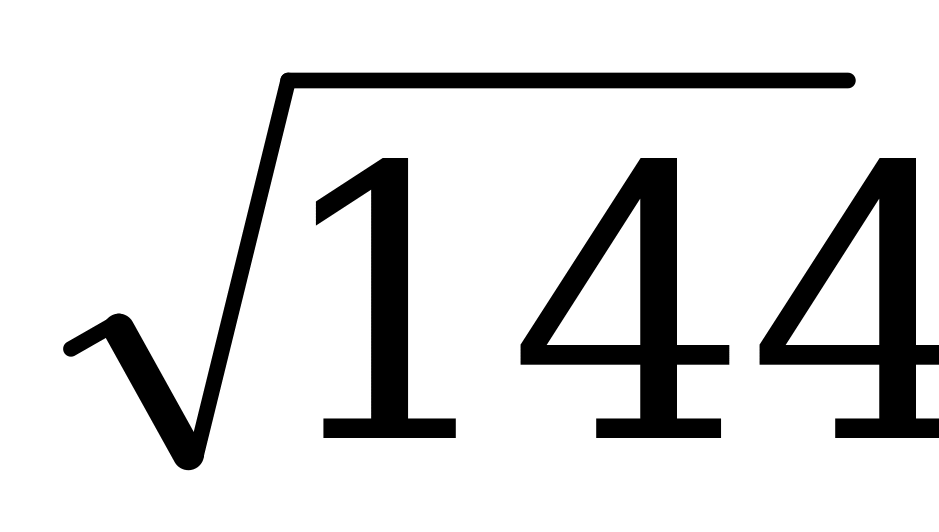 ,
,
х2 - 12х = 0.
Ответы: а) 1 и 4; б) 2; в) 2 и 3.
Упростите выражение: 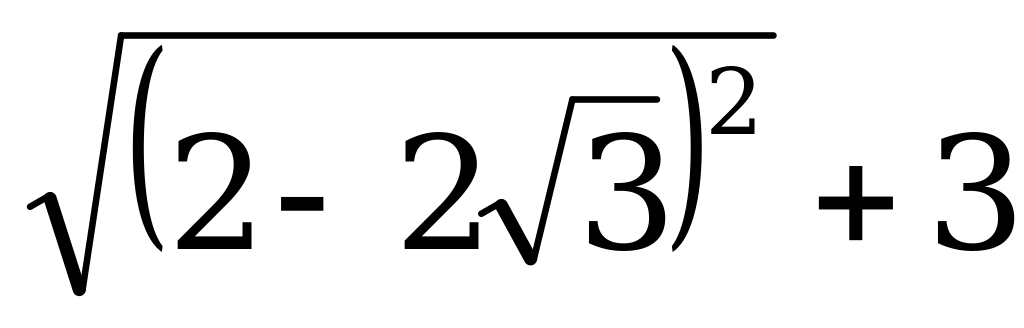
Ответы: а) 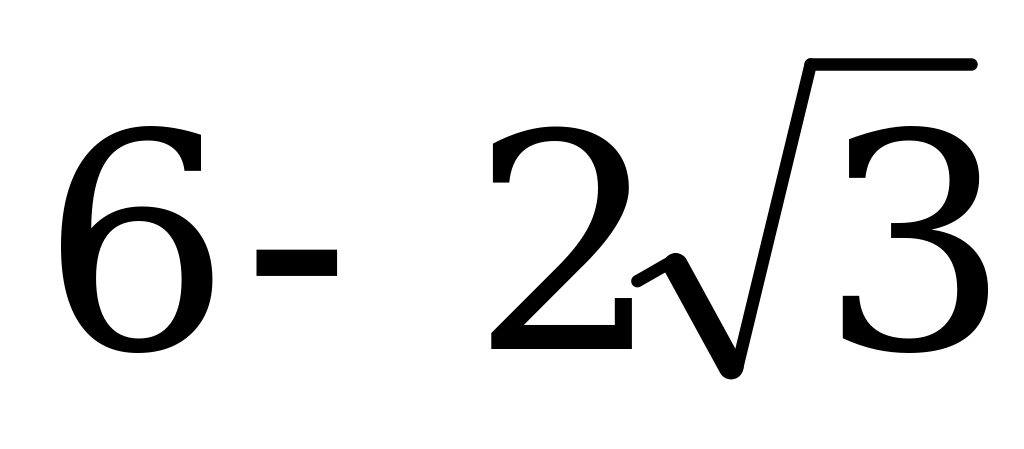 ; б)
; б) 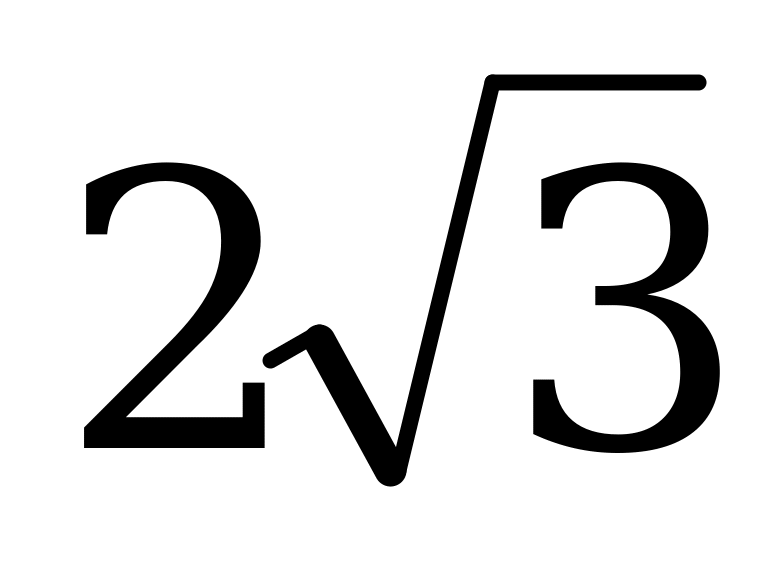 ; в)
; в) 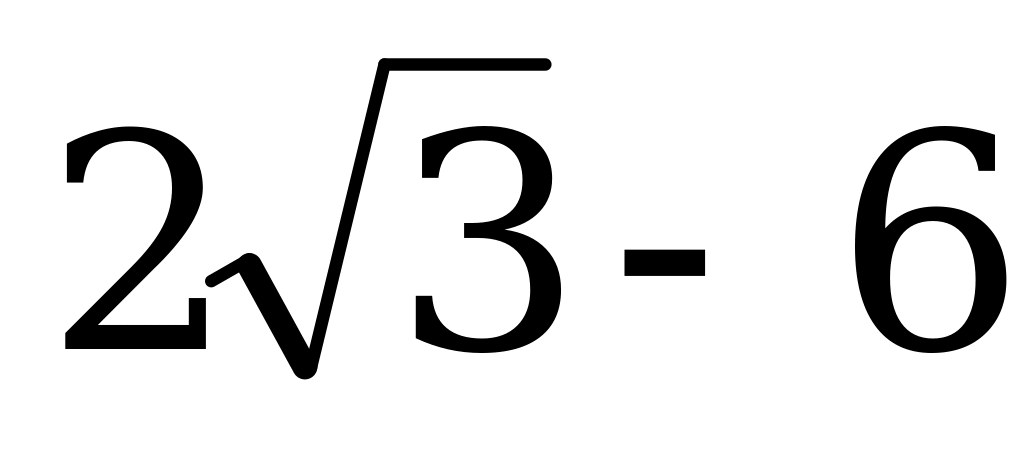 .
.
При каких значениях а функция у = 2х2 + ах + 8
принимает только положительные значения ?
Ответы: а) ( - ∞; 8); б) ( - 8; 8); в) (-∞; - 8) U (8; + ∞).
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| баллы | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |
Вариант 2
Решить уравнение: (3х + 1) (6х - 4) = 0
Ответы: а) 1,5 и 3; б) - 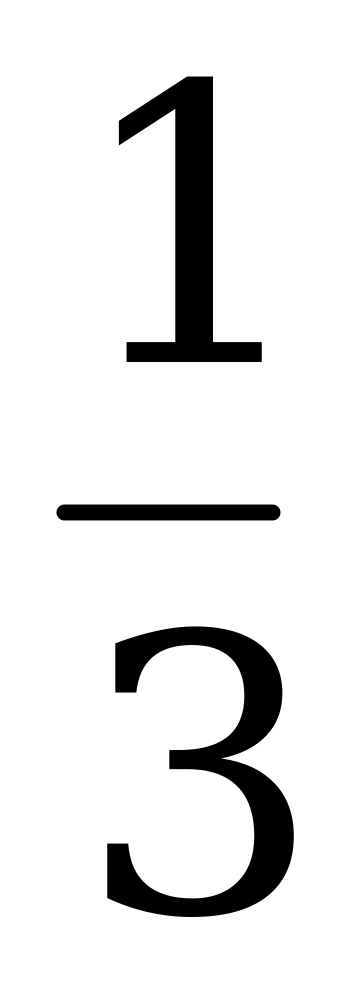 и 1,5; в) -
и 1,5; в) - 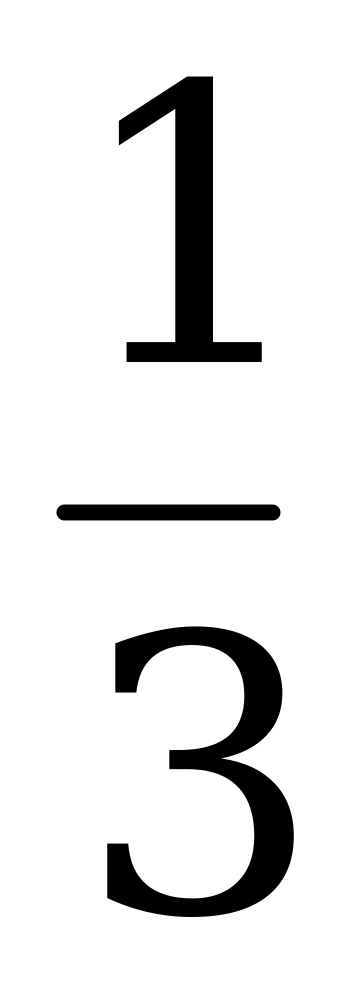 и
и 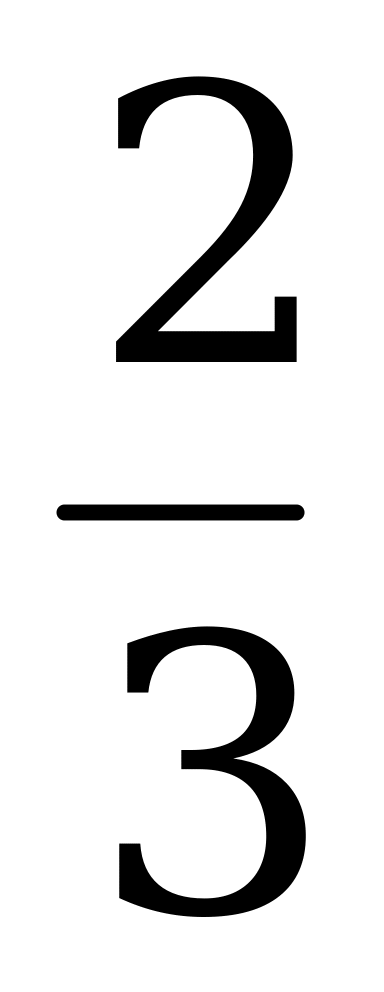 .
.
Найти значение выражения: - 0,4 х + у при х = 5; у = - 10
Ответы: а) 0; б) 40; в) - 60.
Решите неравенство: 2 (х + 3) + 3х 7 (х + 4)
Ответы: а) (- 11; + ∞); б) (-∞; - 11); в) (11; + ∞).
Найти значение выражения: х - у при х = 10 и у = - 6
Ответы: а) 2; б) 8; в) 4.
Найти область определения функции у = 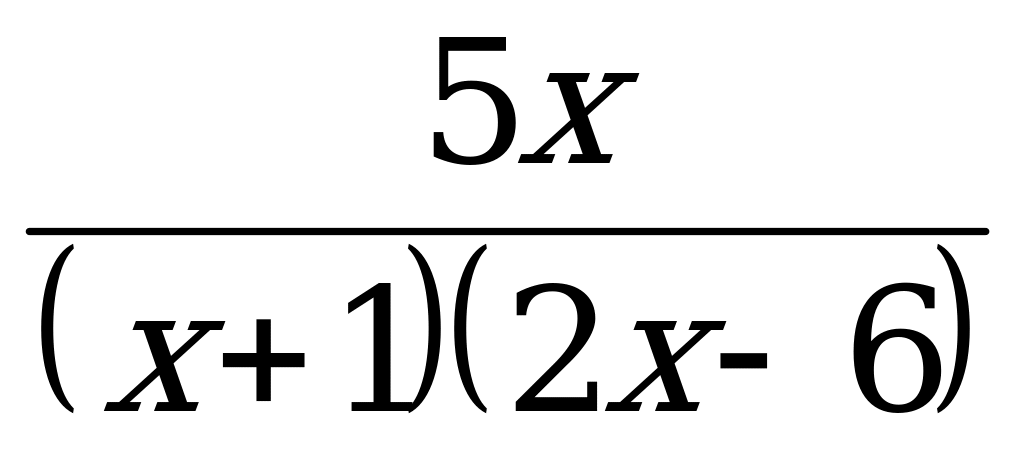
Ответы: а) D(у) = ( - ∞; - 1) U (- 1; 0) U (0; 3) U (3; + ∞ );
б) D(у) = ( - ∞; - 1) U (- 1; 3) U (3; + ∞);
в) D(у) = ( - ∞; - 3) U (- 3; 1) U (1; + ∞).
6. Решите систему уравнений: 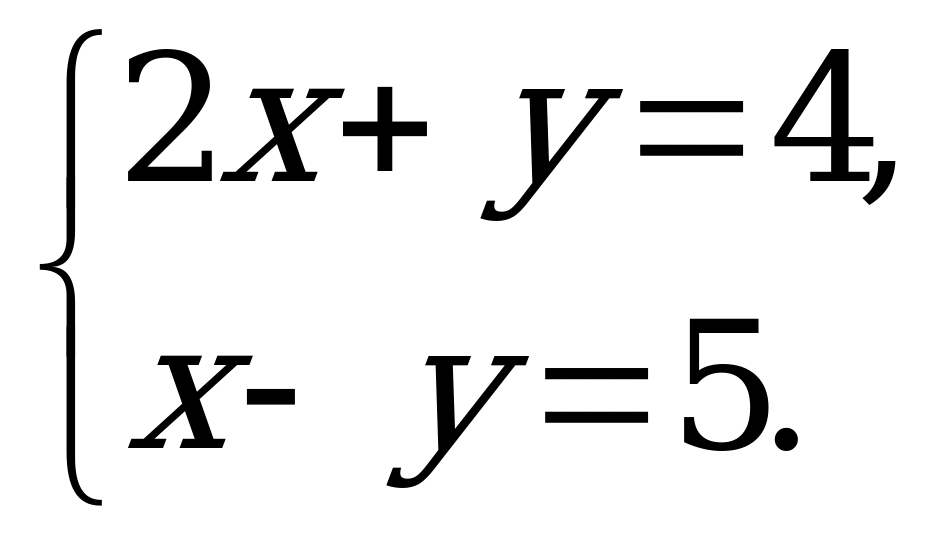
Ответы: а) (3; - 1) б) (3; - 2) в) (2; 1)
7. Упростите выражение: 
Ответы: а) 2ху (х - у);
б) 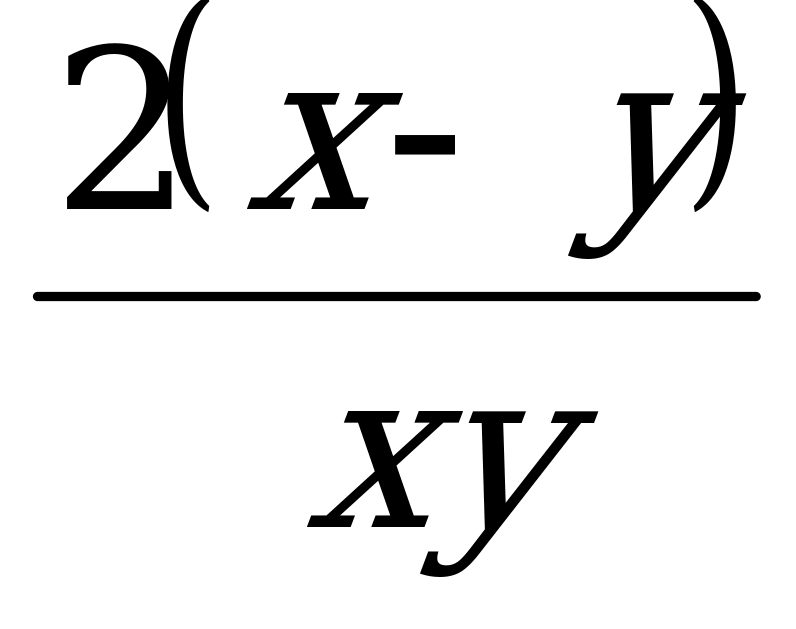 ; в)
; в) 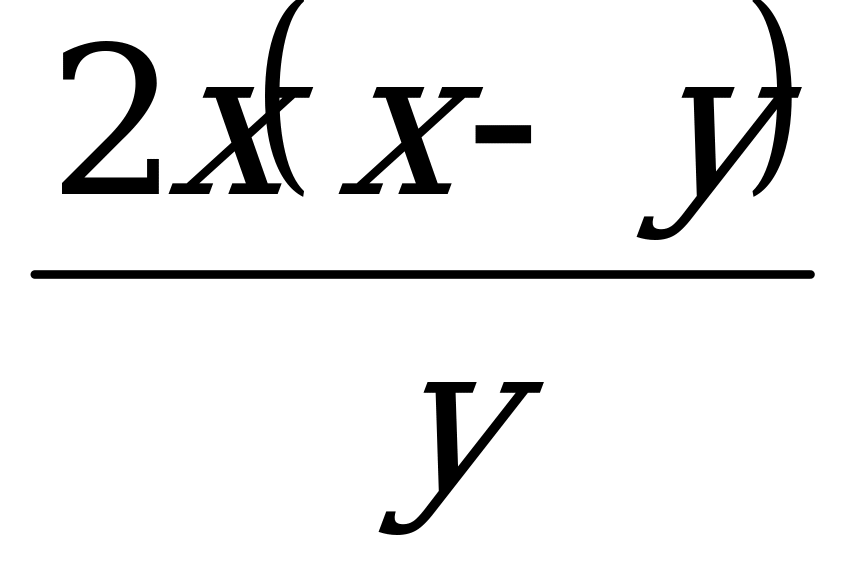 .
.
Какое из следующих уравнений имеет то же множество
решений, что и уравнение х = 10 ?
1. х2 - 10х = 0,
(х - 10) (х + 10) = 0,
х2 + 100 = 0,
х = 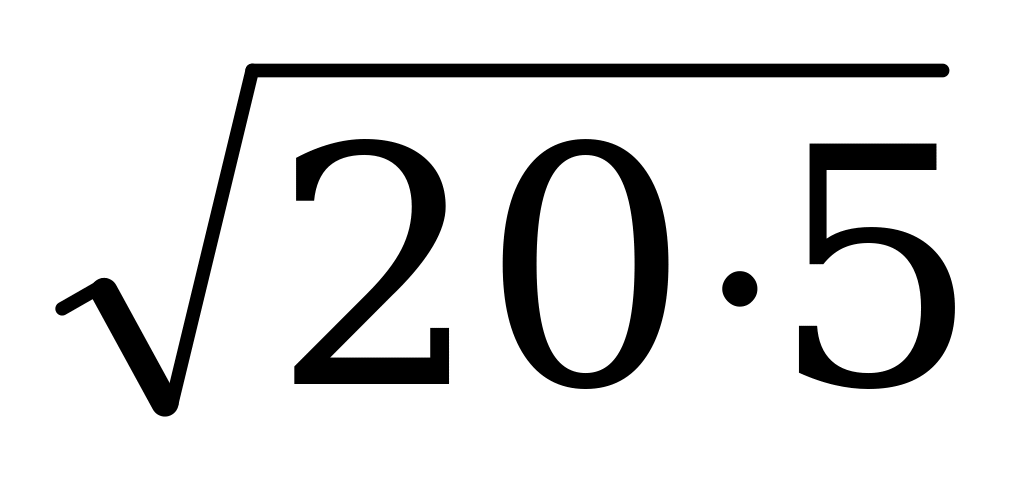 .
.
Ответы: а) 1 и 4; б) 2; в) 2 и 3.
Упростите выражение: 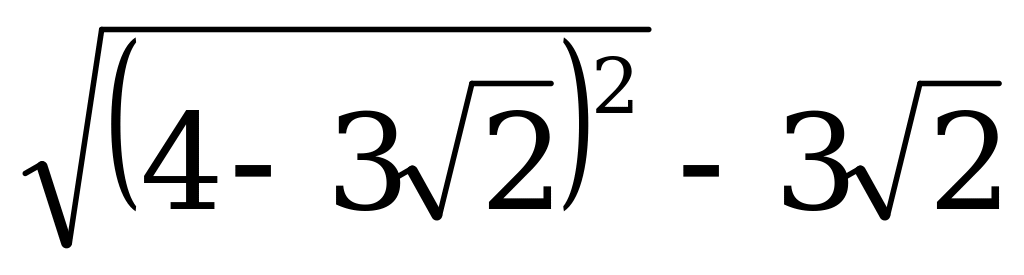
Ответы: а) 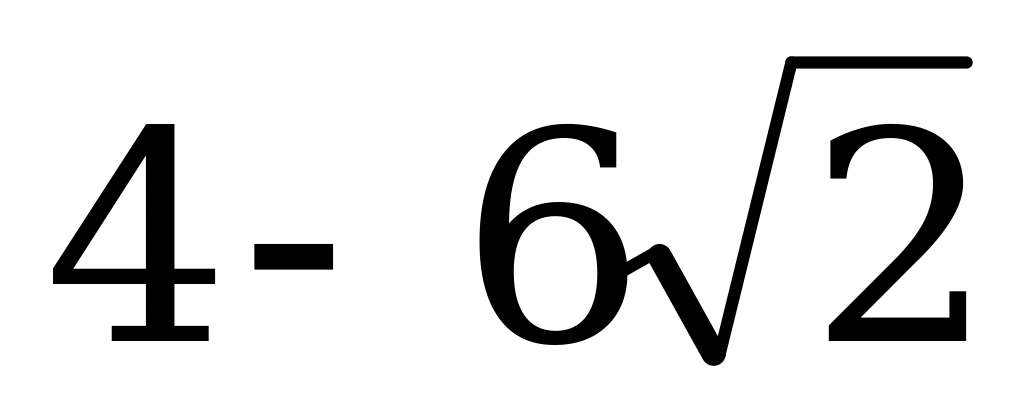 ; б) – 4; в) 4.
; б) – 4; в) 4.
При каких значениях в функция у = - х2 + вх - 9
принимает только отрицательные значения ?
Ответы: а) ( - ∞; 6); б) ( - 6; 6); в) (-∞; - 6) U (6; + ∞).
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| баллы | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 |









 у у
у у
 ) б) в)
) б) в) у
у  у
у  3 х
3 х  ) б) в)
) б) в)
 у у у
у у у

 у у у
у у у то можно сказать о функции у = f (х) ?
то можно сказать о функции у = f (х) ? у
у









