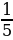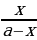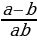| Контрольные работы 9 класс Алгебра |
КОНТРОЛЬНАЯ РАБОТА №1 «НЕРАВЕНСТВА»
Вариант 1.
Обязательная часть.
№1. Сравните числа:  и 0,143…
и 0,143…
№2. Оцените периметр прямоугольника со сторонами а см и b см, если

№3. Решите неравенство
1 – (8 + х) 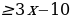
и изобразите множество его решений на координатной прямой.
Решите систему неравенств (4 – 5):
№4. 
№5. 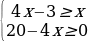
№6. Запишите промежуток
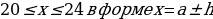 .
.
Дополнительная часть.
№7. Решите двойное неравенство
 .
.
№8. Решите систему неравенств 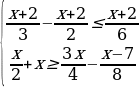
№9. При каких значениях с уравнение 2х2 – 6х + с = 0 имеет два корня?
КОНТРОЛЬНАЯ РАБОТА №1 «НЕРАВЕНСТВА»
Вариант 2.
Обязательная часть.
№1. Расположите в порядке возрастания: 
№2. Оцените площадь прямоугольника со сторонами х см и у см, если
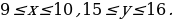
№3. Решите неравенство
2(х – 6) + 7 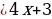
и изобразите множество его решений на координатной прямой.
Решите систему неравенств (4 – 5):
№4. 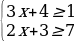 №5
№5
№6. В рулоне содержится 57 м ткани с точностью до 0,5 м. Запишите это с помощью знака 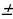 и с помощью двойного неравенства
и с помощью двойного неравенства
Дополнительная часть.
№7. Найдите все отрицательные решения неравенства
1 - 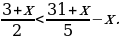
№8. Решите систему неравенств 
№9. Не пользуясь калькулятором, сравните числа: 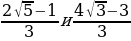
Система оценивания контрольной работы №1
Контрольная работа по математике состоит из 9 заданий. За верное выполнение каждого из заданий 1-6 выставляется по 1 баллу, за задания 7-9 по 2 балла. За неверный ответ или его отсутствие выставляется 0 баллов.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| 𝟏 𝟕 ˂ 0,143… | 1) 0,54 ˂ 0,551… ˂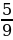 |
-
| 42 см ≤ P ≤ 46 см | 135 см2 ≤ S ≤ 160 см2 |
-
| (– ∞ ; 1,5] | (– ∞ ; – 4) |
-
| (– ∞ ; 3) | (– ∞ ; 3) |
-
| [1 ; 5] | (– 6; 3) |
-
| 22 ± 2 | 57 ± 0,5 ; 56,5 ≤ x ≤ 57,5 |
-
| (– 1 ; 6) | (– ∞ ; 0) |
-
| [1 ; + ∞) | [2 ; 3) |
-
| ( – ∞ ; 4,5) | 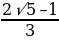 ˂ ˂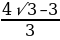
|
Максимальное количество баллов, которое может набрать ученик, правильно выполнивший 9 заданий – 12 баллов.
«2» - 0 - 3 балла;
«3» - 4 - 6 баллов;
«4» - 7 - 9 баллов;
«5» - 10 - 12 баллов.
КОНТРОЛЬНАЯ РАБОТА №2 «Квадратичная функция»
Вариант 1.
Обязательная часть.
№1. С помощью графика (рис. 2.7. учебника с. 79) ответьте на вопросы:
а) Через сколько секунд после начала полета ракета достигла максимальной высоты?
б) Какое расстояние пролетела ракета за 3 с полета?
№2. Функция задана формулой
у = 3х2 + 2х – 5.
а) Найдите значение функции при
х = 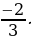
б) Найдите нули функции.
№3. а) Постройте график функции
у = -х2 + 4.
б) Укажите значение аргумента, при которых функция принимает отрицательные значения.
в) Укажите промежуток, на котором функция убывает.
№4. Решите неравенство
х2 – 3х +2 
Дополнительная часть.
№5. Запишите уравнение параболы, если известно, что она получена сдвигом параболы у = 2х2 вдоль оси Х на четыре единицы и вдоль оси У на две единицы.
№6. Найдите область определения функции у = 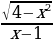 .
.
№7. При каких значениях pи q вершина параболы y = x2 + pх + q находится в точке (-1; 5)
КОНТРОЛЬНАЯ РАБОТА №2 «Квадратичная функция»
Вариант 2.
Обязательная часть.
№1. Парашютист выпрыгнул из самолета на некоторой высоте. Сначала он находился в свободном падении, а затем раскрыл парашют. На рисунке изображен график его полета. По графику ответьте на вопросы:
а) Какое расстояние пролетел парашютист за 10 с полета?
б) Через сколько секунд после прыжка раскрылся парашют?
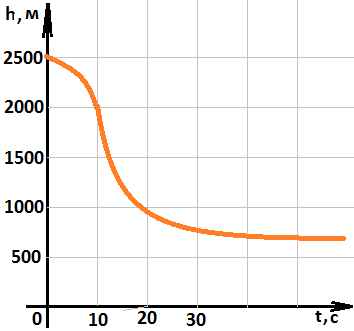
№2. С помощью графика функции (график 2 на рисунке 2.31 учебника с.102):
а) найдите значение функции
при х = 3;
б) определите значения х, при которых функция принимает значение,
равное -6.
№3. а) Постройте график функции
у = х2 + х – 6.
б) Укажите значения аргумента, при которых функция принимает положительные значения.
в) Укажите промежуток убывания функции.
№4. Решите неравенство
х2 – 6х +5 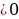 .
.
Дополнительная часть.
№5. Определите значения коэффициентов b иc, при которых вершина параболы у = х2 +bx + c находится в точке А (-1; 3)
№6. Найдите область определения функции у = 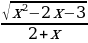 .
.
№7. Найдите все целые положительные значения m, при которых график функции
у = 4х2 + mх + 1 расположен выше оси Х.
Система оценивания контрольной работы №2
Контрольная работа по математике состоит из 7 заданий. За верное выполнение каждого из заданий 1-3,6-7, выставляется по 2 балла, за неверный ответ или его отсутствие выставляется 0 баллов, за половину верно выполненное задание выставляется 1 балл, за задания 4-5 выставляется по 1 баллу.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| а) 2 сек б) 28 км | а) 500 м б) 25 сек |
-
| а) – 5; б) −𝟏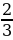 и 1 и 1 | y = 2; x = ± 3. |
-
| б) y ˂ 0 при x ˂ – 2 и x ˃ 2; в) функция убывает на [0 ; + ∞ ) | б) y ˃ 0 при x ˂ – 3 и x ˃ 2; в) функция убывает на ( – ∞; – 0,5] |
-
| 1 ˂ x ˂ 2 | 1 ˂ x ˂ 5 |
-
| y = 2(x – 4)2 – 2 | b = 4; c = 5 |
-
| [ – 2; 1) U (1; 2] | ( – ∞; – 2) U (– 2; – 1] U [3; + ∞) |
-
| p = 2; q = 6 | (– 4 ; 4) |
Максимальное количество баллов, которое может набрать ученик, правильно выполнивший 7 заданий – 12 баллов.
«2» - 0 - 4 балла;
«3» - 5 - 7 баллов;
«4» - 8 - 10 баллов;
«5» - 11 - 12 баллов.
КОНТРОЛЬНАЯ РАБОТА №3 «Рациональные выражения. Уравнения»
Вариант 1.
Обязательная часть
№1. Упростите выражение 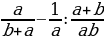 и найдите его значение при a = 0,2 и b = 0,3.
и найдите его значение при a = 0,2 и b = 0,3.
Найдите корни уравнения (2 – 3):
№2. х(2х + 3)(2 – х) = 0 №3. х + 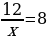 .
.
№4. Укажите значения х, при которых выражение 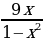 имеет смысл.
имеет смысл.
№5. Бабушка прополола 15 грядок, после чего за прополку взялся внук и прополол 14 грядок. Всего они работали 5 ч. Сколько времени работал каждый, если за 1 ч бабушка пропалывала на 2 грядки меньше внука?
Выберите уравнение, соответствующее условию задачи, если через х обозначено количество грядок, пропалываемое внуком за 1 ч.
Дополнительная часть
№6. Решите уравнение
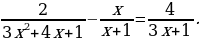
№7. Найдите область определения выражения  .
.
№8. Швея собиралась сшить 120 воротников к определенному сроку. Она посчитала, что если будет шить в час на 2 воротника больше, чем наметила первоначально, то уже за 3 часа до срока сошьет 136 воротников. Сколько воротников в час наметила шить швея первоначально?
КОНТРОЛЬНАЯ РАБОТА №3 «Рациональные выражения. Уравнения»
Вариант 2.
Обязательная часть
№1. Упростите выражение
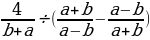 и найдите его значение при a = 0,25 и b = 0,5.
и найдите его значение при a = 0,25 и b = 0,5.
Найдите корни уравнения (2 – 3):
№2. 2х3 – 8х = 0
№3. 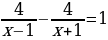 .
.
№4. Укажите значения х, при которых выражение 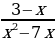 имеет смысл.
имеет смысл.
№5. Машинистка должна напечатать 300 страниц. Если она будет печатать в час на 1 страницу больше, чем обычно, то выполнит работу на 2 часа быстрее. С какой скоростью обычно печатает машинистка?
Выберите уравнение, соответствующее условию задачи, если буквой х обозначено количество страниц, которое обычно печатает машинистка за 1 ч.
| А.  | Б.  |
| В. 300(х + 1) - 300х = 2 | Г.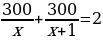 |
Дополнительная часть.
№6. Решите уравнение 3х 4 – 2х3 – 3х + 2 = 0.
№7. Найдите область определения функции 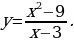
№8. Одна уборочная машина работает в 3 раза быстрее, чем другая. Начиная работу одновременно, они вместе могут заданный объем работы выполнить за 3 ч. За сколько часов каждая из машин, работая отдельно, может выполнить этот объем работы?
Система оценивания контрольной работы №3
Контрольная работа по математике состоит из 7 заданий. За верное выполнение каждого из заданий 2-5, выставляется по 1 баллу, за задания 1,6-8 выставляется по 2 балла за неверный ответ или его отсутствие выставляется 0 баллов, за половину верно выполненное задание выставляется 1 балл.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| – 0,2 | – 2 |
-
| – 1,5; 0;2 | – 2; 0; 2 |
-
| 2 и 6 | ± 3 |
-
| x ≠ ± 1 | x ≠ 0; x ≠ 7 |
-
| Б | А |
-
| – 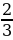 | 1 и 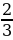 |
-
| x ≠ ± 0,5; x ≠ ± 1 | x ≠ 3; график построен в решении |
-
| 6 воротников | 12 часов и 4 часа |
Максимальное количество баллов, которое может набрать ученик,
Правильно выполнивший 8 заданий – 12 баллов.
«2» - 0 - 3 балла;
«3» - 4 – 7 баллов;
«4» - 8 - 10 баллов;
«5» - 11 - 12 баллов.
КОНТРОЛЬНАЯ РАБОТА №4 «Системы уравнений»
Вариант 1
Обязательная часть
№1. Решите систему уравнений 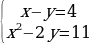 .
.
№2. Вычислите координаты точки пересечения графиков уравнений
х2 + у2 =5 и х – у = 1.
№3. Гипотенуза прямоугольного треугольника равна 15 см, а один из катетов на 3 см меньше другого. Найдите катеты треугольника.
№4. Выясните с помощью графиков, показанных на рисунке 3.22, а из учебника, сколько корней имеет уравнение
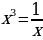 . Запишите его корни.
. Запишите его корни.
Дополнительная часть.
№5. Решите систему уравнений 
№6. Решите графически систему уравнений 
№7. Дорога между пунктами А и В состоит из двух участков: 24 км подъема и 16 км спуска. Велосипедист преодолевает этот путь от А до В за 4 ч 20 мин, а обратный путь – за 4 ч. Определите скорость велосипедиста на подъеме и спуске.
КОНТРОЛЬНАЯ РАБОТА №4 «Системы уравнений»
Вариант 2.
Обязательная часть.
№1. №1. Решите систему уравнений 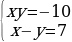 .
.
№2. Вычислите координаты точки пересечения графиков уравнений
х2 - у2 = 13 и х + у = -5.
№3. Газон прямоугольной формы обнесен бордюром, длина которого 40м. Площадь газона 96 м2. Найдите стороны газона.
№4. Выясните с помощью графиков, показанных на рисунке 3.14, а из учебника, сколько решений имеет система уравнений 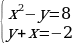 . Запишите её решения.
. Запишите её решения.
Дополнительная часть.
№5. Решите систему уравнений 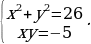
№6. Решите графически уравнение
х3 – 3х + 2 = 0.
№7. Два велосипедиста выехали одновременно навстречу друг другу из пунктов А и В, расстояние между которыми 24 км, и встретились через 1 ч 20 мин. Первый прибыл в пункт В на 36 мин раньше, чем второй в пункт А. найдите скорость каждого велосипедиста.
Система оценивания контрольной работы №4
Контрольная работа по математике состоит из 7 заданий. За верное выполнение каждого из заданий 1-4, выставляется по1 баллу, за неверный ответ или его отсутствие выставляется 0 баллов. За задания 6-7 выставляется по 2 балла, за половину верно выполненное задание выставляется 1 балл.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| (3; – 1) и (– 1; – 5) | (5; – 2) и (2; – 5) |
-
| (2; 1) и (– 1; – 2) | (– 3,8; – 1,2) |
-
| 9 см и 12 см | 8 м и 12 м |
-
| ± 1 | (– 3; 1) и (2; – 4) |
-
| (4; 6) и ( – 6; – 4) | (– 1; 5); (5; – 1); (– 5; 1); (1; – 5) |
-
| (– 2; 2) и (2,2) | – 2 и 1 |
-
| 8 км/ч – скорость на подъёме, 12 км/ч – скорость на спуске | 8 км/ч и 10 км/ч. |
Максимальное количество баллов, которое может набрать ученик, правильно выполнивший 7 заданий – 12 баллов.
«2» - 0 - 4 балла;
«3» - 5 - 7 баллов;
«4» - 8 - 10 баллов;
«5» - 11 - 12 баллов.
КОНТРОЛЬНАЯ РАБОТА №5 «Арифметическая и геометрическая прогрессии»
Вариант 1
Обязательная часть.
№1. Последовательность задана формулой n-го члена: an = n(n + 1)
а) запишите первые три члена этой последовательности и найдите а100.
б) Является ли членом этой последовательности число 132?
№2. Одна из двух данных последовательностей является арифметической прогрессией, другая – геометрической:
(хn): 12, 8, 4,… (yn): -32, -16, -8,…
а) продолжите каждую из этих прогрессий, записав следующие три члена.
б) найдите двенадцатый член геометрической прогрессии.
№3. Чтобы накопить денег на покупку велосипеда, Андрей в первую неделю отложил 10 р., а в каждую следующую откладывал на 5 р. больше, чем в предыдущую. Какая сумма будет у него через 10 недель?
Дополнительная часть.
№4. Найдите сумму всех двузначных чисел, кратных 3.
№5. Сумма первых четырех членов геометрической прогрессии равна -40, знаменатель прогрессии равен -3. Найдите сумму первых восьми членов прогрессии.
№6. Семья Петровых взяла кредит 25000 р. на покупку телевизора. Процентная ставка кредита равна 2% в месяц (проценты ежемесячно начисляются на всю сумму долга, включая начисленный в предыдущий месяц процент). Петровы выплатили весь кредит единовременно через полгода. Какую сумму они выплатили? Запишите выражение для вычисления этой суммы.
КОНТРОЛЬНАЯ РАБОТА №5 «Арифметическая и геометрическая прогрессии»
Вариант 2
Обязательная часть.
№1. Последовательность задана формулой n-го члена: xn = n(n – 1).
а) запишите первые три члена этой последовательности и найдите х120.
б) Какой номер имеет член последовательности, равный 110?
№2. Одна из двух данных последовательностей является арифметической прогрессией, другая – геометрической:
(an): 1, 2, 4,… (bn): -15, -12, -9,…
а) продолжите каждую из этих прогрессий, записав следующие три члена.
б) найдите двадцатый член арифметической прогрессии.
№3. Турист в первый день прошел 20 км, а в каждый следующий – на 2 км меньше, чем в предыдущий. Какое расстояние прошел турист за 7 дней?
Дополнительная часть.
№4. Сколько последовательных натуральных чисел, начиная с единицы, надо сложить, чтобы сумма превзошла 210?
№5. Найдите сумму первых шести членов геометрической прогрессии, если ее десятый член равен 64, а знаменатель равен 
№6. Автомобильный завод каждые два года снижает цену на определенную марку автомобиля на 20% по сравнению с ее предыдущей ценой. В первый год выпуска новая модель стоила 40000 р. Сколько будет стоить эта модель через 10 лет?
Система оценивания контрольной работы №5
Контрольная работа по математике состоит из 6 заданий. За верное выполнение задания 3 выставляется 1 балл, задания 1,2,4-6 оцениваются по 2 балла, за частично верно выполненное задание выставляется 1 балл за неверный ответ или его отсутствие выставляется 0 баллов.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| а) 2; 6; 12; 10100 б) да. | а) 0; 2; 6; 380 б) 11 |
-
| а) 0; – 4; – 8; и – 4; – 2; – 1; б)  | а) 8; 16; 32; и – 6; – 3; 0; б) 42 |
-
| 325 рублей | 98 км |
-
| 1665 | 21 |
-
| – 3280 | 64512 |
-
| 25000 · 1,026 | 400000 · 0,85 |
Максимальное количество баллов, которое может набрать ученик, правильно выполнивший 7 заданий – 12 баллов.
«2» - 0 - 4 балла;
«3» - 5 - 7 баллов;
«4» - 8 - 10 баллов;
«5» - 11 - 12 баллов.
Итоговая контрольная работа №6
Вариант 1.

Итоговая контрольная работа №6
 Вариант 2.
Вариант 2.
Система оценивания итоговой контрольной работы №6
Контрольная работа по математике состоит из 6 заданий. За верное выполнение заданий 1-7 выставляется по1 баллу, задания 8-10 оцениваются по 2 балла, за частично верно выполненное задание выставляется 1 балл за неверный ответ или его отсутствие выставляется 0 баллов.
Ключи к заданиям
| № задания | Вариант 1 | Вариант 2 |
-
| 
| 1) – 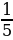 |
-
| (– 1; + ∞) | (– 2; + ∞) |
-
| 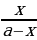
| 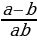
|
-
| (– ∞; – 2)∪(2; + ∞) | (– 3; 3) |
-
| 2 и 3 | 3 и – 4 |
-
| (0; – 5) и (– 2; – 7) | (– 1; 0) и (– 4; – 3) |
-
| √𝟏𝟎 ;2√𝟓 ; 5 | 2√𝟑 ; 4; √𝟏𝟕 |
-
| [– 2;0] | [0; 3,5] |
-
| 98550 | 49050 |
-
| 80 и 40 | 60 и 120 |
Максимальное количество баллов, которое может набрать ученик, правильно выполнивший 10 заданий – 13 баллов.
«2» - 0 - 5 балла;
«3» - 6 - 8 баллов;
«4» - 9 - 11 баллов;
«5» - 12 - 13 баллов.







 и 0,143…
и 0,143…
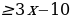

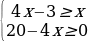
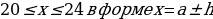 .
. .
.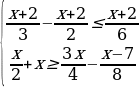

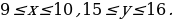
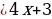
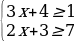 №5
№5
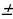 и с помощью двойного неравенства
и с помощью двойного неравенства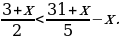

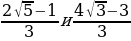
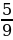
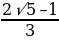 ˂
˂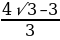
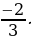

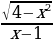 .
.
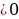 .
.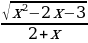 .
.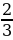 и 1
и 1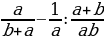 и найдите его значение при a = 0,2 и b = 0,3.
и найдите его значение при a = 0,2 и b = 0,3.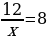 .
.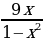 имеет смысл.
имеет смысл.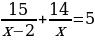
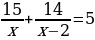
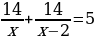

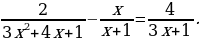
 .
.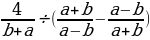 и найдите его значение при a = 0,25 и b = 0,5.
и найдите его значение при a = 0,25 и b = 0,5.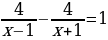 .
.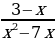 имеет смысл.
имеет смысл.

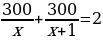
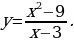
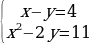 .
.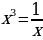 . Запишите его корни.
. Запишите его корни.

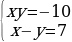 .
.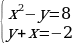 . Запишите её решения.
. Запишите её решения.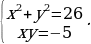



 Вариант 2.
Вариант 2.