Контрольная работа № 1 по теме «Делимость натуральных чисел»
Вариант 1
1. Из чисел 387, 756, 829, 2 148 выпишите те, которые делятся нацело:
1) на 2; 2) на 9.
2. Разложите число 756 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 24 и 54; 2) 72 и 264.
4. Найдите наименьшее общее кратное чисел:
1) 16 и 32; 2) 15 и 8; 3) 16 и 12.
5. Докажите, что числа 272 и 1 365 — взаимно простые.
6. Вместо звёздочки в записи 1 52* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Петя расставил книги поровну на 12 полках, а потом переставил их, тоже поровну, на 8 полок. Сколько книг было у Пети, если известно, что их было больше 100, но меньше 140?
Вариант 2
1. Из чисел 405, 972, 865, 2 394 выпишите те, которые делятся нацело:
1) на 5; 2) на 9.
2. Разложите число 1 176 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 27 и 36; 2) 168 и 252.
4. Найдите наименьшее общее кратное чисел:
1) 11 и 33; 2) 9 и 10; 3) 18 и 12.
5. Докажите, что числа 297 и 304 — взаимно простые.
6. Вместо звёздочки в записи 1 99* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Собранный урожай яблок фермер может разложить поровну в корзины по 12 кг или в ящики по 15 кг. Сколько килограммов яблок собрал фермер, если известно, что их было больше 150 кг, но меньше 200 кг?
Вариант 3
1. Из чисел 703, 492, 675, 3 258 выпишите те, которые делятся нацело:
1) на 2; 2) на 9.
2. Разложите число 1 848 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 32 и 56; 2) 378 и 450.
4. Найдите наименьшее общее кратное чисел:
1) 17 и 34; 2) 8 и 25; 3) 15 и 12.
5. Докажите, что числа 325 и 792 — взаимно простые.
6. Вместо звёздочки в записи 2 00* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Учеников шестых классов, которых больше 120, но меньше 150, можно отвезти на экскурсию или микроавтобусами по 12 человек, или микроавтобусами по 16 человек, при этом в обоих случаях пустых мест в микроавтобусах не будет. Сколько шестиклассников едет на экскурсию?
Вариант 4
1. Из чисел 584, 810, 729, 4 635 выпишите те, которые делятся нацело:
1) на 5; 2) на 9.
2. Разложите число 1 890 на простые множители.
3. Найдите наибольший общий делитель чисел:
1) 40 и 64; 2) 162 и 270.
4. Найдите наименьшее общее кратное чисел:
1) 18 и 36; 2) 12 и 35; 3) 16 и 24.
5. Докажите, что числа 308 и 585 — взаимно простые.
6. Вместо звёздочки в записи 1 43* поставьте цифру так, чтобы полученное число было кратным 3 (рассмотрите все возможные случаи).
7. Туристы, отправляясь в поход, планировали пройти весь маршрут за 12 дней, преодолевая ежедневно одно и то же целое число километров. Однако им удалось пройти весь маршрут за 9 дней, преодолевая ежедневно одно и то же целое число километров. Какова длина всего маршрута, если известно, что она больше 100 км, но меньше 120 км?
Контрольная работа № 2 по теме «Сравнение, сложение и вычитание дробей»
Вариант 1
1. Сократите дробь: 1) 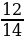 ; 2)
; 2) 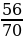 .
.
2. Сравните дроби: 1) 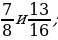 2)
2) 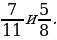
3. Вычислите:
1) 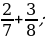 2)
2) 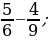 3)
3) 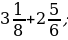 4)
4) 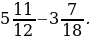
4. В первый день продали 8 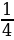 ц яблок, а во второй – на 2
ц яблок, а во второй – на 2 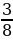 ц меньше. Сколько центнеров яблок продали за два дня?
ц меньше. Сколько центнеров яблок продали за два дня?
5. Решите уравнение: 1) 7 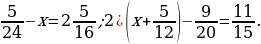
6. Миша потратил 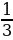 своих денег на покупку новой книги,
своих денег на покупку новой книги, 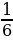 денег – на покупку тетрадей,
денег – на покупку тетрадей, 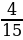 денег – на покупку карандашей, а остальные деньги – на покупку альбома. Какую часть своих денег потратил Миша на покупку альбома?
денег – на покупку карандашей, а остальные деньги – на покупку альбома. Какую часть своих денег потратил Миша на покупку альбома?
7. Найдите все натуральные значения х, при которых верно неравенство 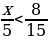 .
.
Вариант 2
1. Сократите дробь: 1) 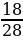 ; 2)
; 2) 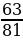 .
.
2. Сравните дроби: 1) 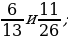 2)
2) 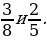
3. Вычислите:
1) 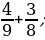 2)
2) 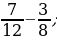 3)
3) 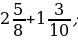 4)
4) 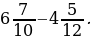
4. За первый час турист прошёл 4 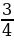 км, а за второй – на 1
км, а за второй – на 1 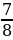 км меньше. Какой путь преодолел турист за 2 ч?
км меньше. Какой путь преодолел турист за 2 ч?
5. Решите уравнение: 1) 8 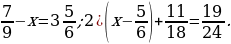
6. В магазин завезли фрукты. Яблоки составляли 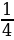 , сливы –
, сливы – 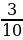 , а груши –
, а груши – 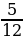 всех завезённых фруктов. Остальной завезённый товар составлял виноград. Какую часть всех фруктов составлял виноград?
всех завезённых фруктов. Остальной завезённый товар составлял виноград. Какую часть всех фруктов составлял виноград?
7. Найдите все натуральные значения х, при которых верно неравенство 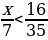 .
.
Вариант 3
1. Сократите дробь: 1) 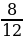 ; 2)
; 2) 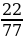 .
.
2. Сравните дроби: 1) 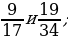 2)
2) 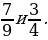
3. Вычислите:
1) 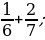 2)
2) 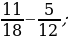 3)
3) 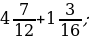 4)
4) 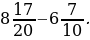
4. Груз перевозили в двух контейнерах. В первом контейнере перевезли 5 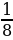 т груза, а во втором – на 2
т груза, а во втором – на 2 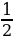 т меньше. Какова общая масса перевезённого груза?
т меньше. Какова общая масса перевезённого груза?
5. Решите уравнение: 1) 5 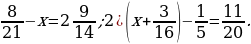
6. В туристическом походе участвовали учащиеся 5-8 классов. Восьмиклассники составляли 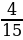 , семиклассники –
, семиклассники – 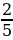 , а пятиклассники –
, а пятиклассники – 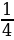 количества всех туристов. Какую часть всех туристов составляли шестиклассники?
количества всех туристов. Какую часть всех туристов составляли шестиклассники?
7. Найдите все натуральные значения х, при которых верно неравенство 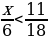
Вариант 4
1. Сократите дробь: 1) 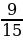 ; 2)
; 2) 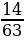
2. Сравните дроби: 1) 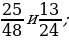 2)
2) 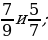
3. Вычислите:
1) 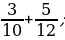 2)
2) 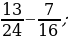 3)
3) 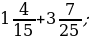 4)
4)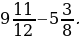
4. Сплав меди и цинка содержит 7 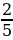 кг меди, а цинка – на 2
кг меди, а цинка – на 2 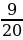 кг меньше. Какова масса сплава?
кг меньше. Какова масса сплава?
5. Решите уравнение: 1) 11 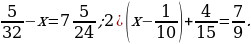
6. Четыре трактора вспахивали поле. Первый трактор вспахал 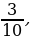 второй –
второй – 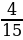 , а третий –
, а третий – 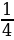 площади всего поля. Какую часть поля вспахал четвертый трактор?
площади всего поля. Какую часть поля вспахал четвертый трактор?
7. Найдите все натуральные значения х, при которых верно неравенство 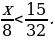
Контрольная работа № 3 по теме «Умножение дробей»
Вариант 1
1. Выполните умножение:
1) 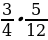 ; 2)
; 2) 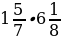 ; 3)
; 3) 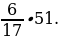
2. В магазин завезли 18 кг конфет, из них 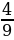 составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
3. Найдите значение выражения: 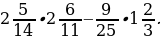
4. Ширина прямоугольного параллелепипеда равна 5 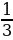 см, его длина в 7
см, его длина в 7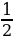 раза больше ширины, а высота составляет 30 % длины. Вычислите объем параллелепипеда.
раза больше ширины, а высота составляет 30 % длины. Вычислите объем параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
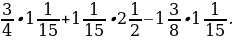
6. За первый день турист прошёл 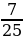 туристического маршрута, за второй –
туристического маршрута, за второй – 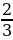 оставшейся части маршрута, а за третий – остальное. За какой день турист прошёл больше всего?
оставшейся части маршрута, а за третий – остальное. За какой день турист прошёл больше всего?
Вариант 2
1. Выполните умножение:
1) 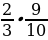 ; 2)
; 2) 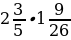 ; 3)
; 3) 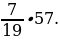
2. Туристы прошли 15 км, из них 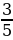 пути они шли лесом. Сколько километров прошли туристы по лесу?
пути они шли лесом. Сколько километров прошли туристы по лесу?
3. Найдите значение выражения: 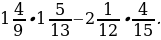
4. Высота прямоугольного параллелепипеда равна 4 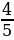 см, его длина в 3
см, его длина в 3 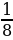 раза больше высоты, а ширина составляет 60 % длины. Вычислите объем параллелепипеда.
раза больше высоты, а ширина составляет 60 % длины. Вычислите объем параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
2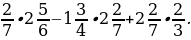
6. Первый трактор вспахал 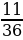 поля, второй –
поля, второй – 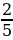 оставшейся части поля, а третий – остальное. Какой трактор вспахал больше всего?
оставшейся части поля, а третий – остальное. Какой трактор вспахал больше всего?
Вариант 3
1. Выполните умножение:
1) 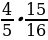 ; 2)
; 2) 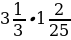 ; 3)
; 3) 
2. Фермер засеял подсолнечником 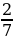 поля, площадь которого равна 14 га. Сколько гектаров поля фермер засеял подсолнечником?
поля, площадь которого равна 14 га. Сколько гектаров поля фермер засеял подсолнечником?
3. Найдите значение выражения: 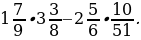
4. Ширина прямоугольного параллелепипеда равна 3 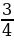 см, его длина в 5
см, его длина в 5 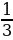 раза больше ширины, а высота составляет 80 % длины. Вычислите объем параллелепипеда.
раза больше ширины, а высота составляет 80 % длины. Вычислите объем параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
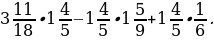
6. На первом автомобиле разместили 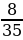 груза, на втором –
груза, на втором – 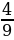 оставшейся части груза, а на третьем – остальное. На какой автомобиль положили больше всего груза?
оставшейся части груза, а на третьем – остальное. На какой автомобиль положили больше всего груза?
Вариант 4
1. Выполните умножение:
1)  ; 2)
; 2) 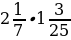 ; 3)
; 3) 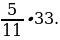
2. Возле школы растут 24 куста роз, из них 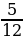 составляют кусты красных роз. Сколько кустов красных роз растет возле школы?
составляют кусты красных роз. Сколько кустов красных роз растет возле школы?
3. Найдите значение выражения: 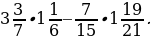
4. Высота прямоугольного параллелепипеда равна 6 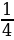 см, его длина в 3
см, его длина в 3 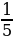 раза больше высоты, а ширина составляет 40 % длины. Вычислите объем параллелепипеда.
раза больше высоты, а ширина составляет 40 % длины. Вычислите объем параллелепипеда.
5. Вычислите значение выражения наиболее удобным способом:
2 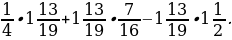
6. За первый день магазин продал 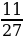 завезенной партии огурцов, за второй –
завезенной партии огурцов, за второй –  остатка, а за третий – остальные. За какой день было продано больше всего огурцов?
остатка, а за третий – остальные. За какой день было продано больше всего огурцов?
Контрольная работа № 4 по теме «Деление дробей»
Вариант 1
1. Вычислите:
1) 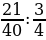 ; 2)
; 2) 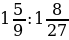 ; 3)
; 3) 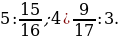
2. В бочку налили 32 л воды и заполнили 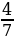 её объёма. Сколько литров составляет объём бочки?
её объёма. Сколько литров составляет объём бочки?
3. Сколько граммов девятипроцентного раствора надо взять, чтобы в нём содержалось 36 г соли?
4. Выполните действия: 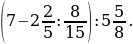
5. Преобразуйте обыкновенную дробь 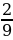 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь.
6. Из двух сёл навстречу друг другу одновременно выехали два велосипедиста. Один велосипедист ехал со скоростью 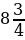 км/ч, а другой – со скоростью в
км/ч, а другой – со скоростью в 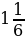 раза меньшей. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 26 км?
раза меньшей. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 26 км?
7. За первую неделю отремонтировали 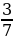 дороги, за вторую – 40 % остатка, а за третью – остальные 14,4 км. Сколько километров дороги отремонтировали за три недели?
дороги, за вторую – 40 % остатка, а за третью – остальные 14,4 км. Сколько километров дороги отремонтировали за три недели?
Вариант 2
1. Вычислите:
1) 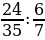 ; 2)
; 2) 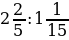 ; 3)
; 3) 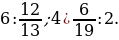
2. В саду растёт 15 вишен, что составляет 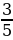 всех деревьев сада. Сколько деревьев растёт в саду?
всех деревьев сада. Сколько деревьев растёт в саду?
3. Было отремонтировано 16 км дороги, что составляет 80 % её длины. Сколько километров составляет длина всей дороги?
4. Выполните действия: 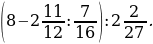
5. Преобразуйте обыкновенную дробь 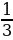 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь.
6. Из пункта А в направлении пункта В вышел турист со скоростью 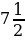 км/ч. Одновременно с этим из пункта В в том же направлении вышел второй турист, скорость которого в
км/ч. Одновременно с этим из пункта В в том же направлении вышел второй турист, скорость которого в 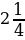 раза меньше скорости первого. Через сколько часов после начала движения первый турист догонит второго, если расстояние между пунктами А и В равно 10 км?
раза меньше скорости первого. Через сколько часов после начала движения первый турист догонит второго, если расстояние между пунктами А и В равно 10 км?
7. За первый день вспахали 30 % площади поля, за второй – 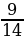 остатка, а за третий – остальные 15 га. Какова площадь поля?
остатка, а за третий – остальные 15 га. Какова площадь поля?
Вариант 3
1. Вычислите:
1) 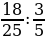 ; 2)
; 2) 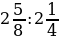 ; 3)
; 3) 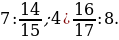
2. Туристы прошли 16 км, что составляет 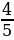 всего маршрута. Найдите длину маршрута.
всего маршрута. Найдите длину маршрута.
3. Сплав содержит 18 % меди. Сколько килограммов сплава надо взять, чтобы он содержал 54 кг меди?
4. Выполните действия: 
5. Преобразуйте обыкновенную дробь 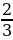 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь.
6. Из двух сёл навстречу друг другу одновременно вышли два пешехода. Первый двигался со скоростью 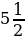 км/ч, а скорость второго была в
км/ч, а скорость второго была в 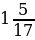 раза меньше скорости первого. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 13 км?
раза меньше скорости первого. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 13 км?
7. За первый день Коля прочёл 60 % книги, за второй – 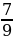 остатка, а за третий – остальные 8 страниц. Сколько страниц в книге?
остатка, а за третий – остальные 8 страниц. Сколько страниц в книге?
Вариант 4
1. Вычислите:
1) 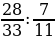 ; 2)
; 2) 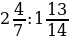 ; 3)
; 3) 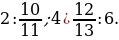
2. Зимой школьная столовая использовала 12 т овощей, что составляет 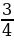 ее годового запаса. Сколько тонн овощей заготовила школьная столовая на год?
ее годового запаса. Сколько тонн овощей заготовила школьная столовая на год?
3. На стоянке было 36 автомобилей белого цвета, что составляло 40 % всех находившихся на ней автомобилей. Сколько всего автомобилей было на стоянке?
4. Выполните действия: 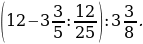
5. Преобразуйте обыкновенную дробь 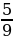 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь.
6. Из пункта А в направлении пункта В выехал велосипедист со скоростью 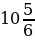 км/ч. Одновременно с этим из пункта В в том же направлении вышел турист, скорость которого в
км/ч. Одновременно с этим из пункта В в том же направлении вышел турист, скорость которого в 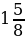 раза меньше скорости велосипедиста. Через сколько часов после начала движения велосипедист догонит туриста, если расстояние между пунктами А и В равно 5 км?
раза меньше скорости велосипедиста. Через сколько часов после начала движения велосипедист догонит туриста, если расстояние между пунктами А и В равно 5 км?
7. Яблоки разложили в 3 корзины. В первую корзину положили 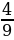 всех яблок, во вторую 70 % остатка, а в третью – остальные 9 кг. Сколько всего было килограммов яблок?
всех яблок, во вторую 70 % остатка, а в третью – остальные 9 кг. Сколько всего было килограммов яблок?
Контрольная работа № 5 по теме «Отношения и пропорции. Процентное отношение двух чисел»
Вариант 1
1. Найдите отношение 8 дм : 4 мм.
2. Замените отношение дробных чисел отношением натуральных чисел: 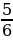 :
: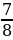 .
.
3. При изготовлении 6 одинаковых измерительных приборов израсходовали 21 г серебра. Сколько граммов серебра надо для изготовления 8 таких приборов?
4. Найдите процент содержания соли в растворе, если в 400 г раствора содержится 48 г соли.
5. Решите уравнение: 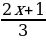 =
= 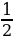 .
.
6. Цена товара повысилась с 240 р. до 252 р. На сколько процентов повысилась цена товара?
7. Число a составляет 25 % от числа b. Сколько процентов число b составляет от числа a?
Вариант 2
1. Найдите отношение 6 км : 3 м.
2. Замените отношение дробных чисел отношением натуральных чисел: 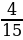 :
: 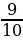 .
.
3. За 12 ч помпа перекачивает 18 м3 воды. Сколько кубических метров перекачала эта помпа за 10 ч работы?
4. Найдите процент содержания серебра в сплаве, если в 300 г сплава содержится 63 г серебра.
5. Решите уравнение: 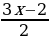 =
= 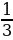 .
.
6. Цена товара снизилась со 180 р. до 153 р. На сколько процентов снизилась цена товара?
7. Число a составляет 50 % от числа b. Сколько процентов число b составляет от числа a?
Вариант 3
1. Найдите отношение 40 кг : 8 г.
2. Замените отношение дробных чисел отношением натуральных чисел: 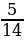 :
: 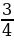 .
.
3. За 8 мин станок-автомат изготавливает 20 деталей. За какое время он изготавливает 30 деталей?
4. Найдите процент содержания хрома в чугуне, если в 600 кг чугуна содержится 42 кг хрома.
5. Решите уравнение: 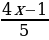 =
= 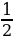 .
.
6. Цена товара повысилась с 320 р. до 368 р. На сколько процентов повысилась цена товара?
7. Число a составляет 20 % от числа b. Сколько процентов число b составляет от числа a?
Вариант 4
1. Найдите отношение 20 т : 5 кг.
2. Замените отношение дробных чисел отношением натуральных чисел: 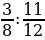 .
.
3. Оператор за 4 ч работы может набрать на компьютере 22 страницы. Сколько часов ему понадобится, чтобы набрать 55 страниц?
4. Найдите процент содержания воды в мёде, если в 500 г мёда содержится 85 г воды.
5. Решите уравнение: 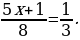
6. Цена товара снизилась с 450 р. до 315 р. На сколько процентов снизилась цена товара?
7. Число a составляет 40 % от числа b. Сколько процентов число b составляет от числа a?
Контрольная работа № 6 по теме «Прямая и обратная пропорциональные зависимости. Окружность и круг. Вероятность случайного события»
Вариант 1
1. Автомобиль проезжает некоторое расстояние за 1,8 ч. За какое время он проедет с той же скоростью расстояние в 4,5 раза большее?
2. За некоторую сумму денег можно купить 12 тонких тетрадей. Сколько можно купить за эту же сумму денег толстых тетрадей, которые в 3 раза дороже тонких?
3. Вычислите длину окружности, радиус которой равен 6,5 дм.
4. Найдите площадь круга, радиус которого равен 4 см.
5. Периметр треугольника равен 108 см, а длины его сторон относятся как 6 : 8 : 13. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 3 см, 5 см и 7 см.
7. В коробке лежат 6 красных и 8 белых шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) красным; 2) жёлтым?
8. Заполните таблицу, если величина у прямо пропорциональна величине х.
9. Заполните таблицу, если величина у обратно пропорциональна величине х.
10. Представьте число 159 в виде суммы трёх слагаемых х, у и z таких, чтобы
х : у = 5 : 6, а у : z = 9 : 10.
Вариант 2
1. Из некоторого количества свежих грибов получили 2,2 кг сухих грибов. Сколько сухих грибов можно получить, если свежих грибов взять в 3,2 раза больше?
2. За некоторую сумму денег можно купить 15 ручек. Сколько можно купить за эту же сумму денег карандашей, которые в 5 раз дешевле ручек?
3. Вычислите длину окружности, радиус которой равен 7,5 см.
4. Найдите площадь круга, радиус которого равен 8 дм.
5. Периметр треугольника равен 132 см, а длины его сторон относятся как
5 : 7 : 10. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 2 см,
5 см и 6 см.
7. В коробке лежат 6 белых и 9 синих шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) белым; 2) белым или синим?
8. Заполните таблицу, если величина у прямо пропорциональна величине х.
9. Заполните таблицу, если величина у обратно пропорциональна величине х.
10. Представьте число 175 в виде суммы трёх слагаемых х, у и z таких, чтобы х : у = 3 : 4, а у : z = 6 : 7.
Вариант 3
1. Самолёт пролетел некоторое расстояние за 1,2 ч. За какое время он пролетит с той же скоростью расстояние в 2,5 раза большее?
2. За некоторую сумму денег можно купить 28 маленьких шоколадок. Сколько можно купить за эту же сумму денег больших шоколадок, которые в 4 раза дороже маленьких?
3. Вычислите длину окружности, радиус которой равен 8,5 дм.
4. Найдите площадь круга, радиус которого равен 9 см.
5. Периметр треугольника равен 125 см, а длины его сторон относятся как
4 : 9 : 12. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 3 см,
4 см и 4 см.
7. В коробке лежат 5 голубых и 15 зелёных шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) зелёным; 2) красным?
8. Заполните таблицу, если величина у прямо пропорциональна величине х.
9. Заполните таблицу, если величина у обратно пропорциональна величине х.
10. Представьте число 86 в виде суммы трёх слагаемых х, у и z таких, чтобы х : у = 2 : 9, а у : z = 6 : 7.
Вариант 4
1. Из некоторого количества яблок получили 8,4 л сока. Сколько сока можно получить, если взять яблок в 5,5 раза больше?
2. За некоторую сумму денег можно купить 30 пирожных. Сколько можно купить за эту же сумму денег пирожков, которые в 6 раз дешевле пирожных?
3. Вычислите длину окружности, радиус которой равен 9,5 дм.
4. Найдите площадь круга, радиус которого равен 7 см.
5. Периметр треугольника равен 130 см, а длины его сторон относятся как
7 : 9 : 10. Найдите стороны треугольника.
6. С помощью циркуля и линейки постройте треугольник со сторонами 5 см,
3 см и 3 см.
7. В коробке лежат 8 белых и 12 чёрных шаров. Какова вероятность того, что выбранный наугад шар окажется: 1) чёрным; 2) белым или чёрным?
8. Заполните таблицу, если величина у прямо пропорциональна величине х.
9. Заполните таблицу, если величина у обратно пропорциональна величине х.
10. Представьте число 172 в виде суммы трёх слагаемых х, у и z таких, чтобы х : у = 3 : 8, а у : z = 12 : 5.
Контрольная работа № 7 по теме «Рациональные числа. Сравнение рациональных чисел»
Вариант 1
1. Начертите координатную прямую и отметьте на ней точки А(3), В(4), С(4,5), D( 4,5). Какие из отмеченных точек имеют противоположные координаты?
4,5). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 4;  8; 0;
8; 0; 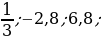
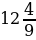 ;
;  :
:
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1)  6,9 и 1,4; 2)
6,9 и 1,4; 2)  5,7 и
5,7 и  5,9.
5,9.
4. Вычислите: 1)  3,2 +
3,2 +  1,9
1,9  2,25; 2)
2,25; 2)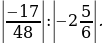
5. Найдите значение х, если:
1) –х =  12; 2) –(
12; 2) –( х) = 1,6.
х) = 1,6.
6. Решите уравнение:
1) х = 9,6; 2) х =  4.
4.
7. Найдите наименьшее целое значение х, при котором верно неравенство х  4.
4.
8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
 6,5*7
6,5*7  6,526?
6,526?
9. Найдите два числа, каждое из которых больше 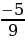 , но меньше
, но меньше 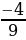 .
.
Вариант 2
1. Начертите координатную прямую и отметьте на ней точки М(2), К( 6), D(
6), D( 3,5), F(3,5). Какие из отмеченных точек имеют противоположные координаты?
3,5), F(3,5). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 5;  9;
9; 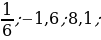
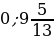 ;
; 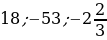 :
:
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1) 2,3 и  5,2; 2)
5,2; 2)  4,6 и
4,6 и  4,3.
4,3.
4. Вычислите: 1)  5,7 +
5,7 +  2,5
2,5  4,32; 2)
4,32; 2)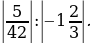
5. Найдите значение х, если:
1) –х = 17; 2) –( х) =
х) =  2,4.
2,4.
6. Решите уравнение:
1) х = 8,4; 2) х =  6.
6.
7. Найдите наибольшее целое значение х, при котором верно неравенство х  8.
8.
8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
 7,24*
7,24*  7,247?
7,247?
9. Найдите два числа, каждое из которых больше 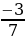 , но меньше
, но меньше 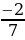 .
.
Вариант 3
1. Начертите координатную прямую и отметьте на ней точки С(5), А( 7), В(
7), В(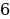 ,5), F(7). Какие из отмеченных точек имеют противоположные координаты?
,5), F(7). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 6; 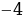 ;
; 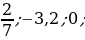
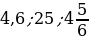 ;
; 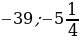 :
:
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1)  8,3 и 5,4; 2)
8,3 и 5,4; 2)  9,2 и
9,2 и  9,1.
9,1.
4. Вычислите: 1)  6,2 +
6,2 +  1,4
1,4  4,83; 2)
4,83; 2)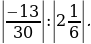
5. Найдите значение х, если:
1) –х = 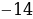 ; 2) –(
; 2) –( х) =
х) = 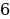 ,4.
,4.
6. Решите уравнение:
1) х = 3,2; 2) х =  2.
2.
7. Найдите наибольшее целое значение х, при котором верно неравенство х ≤  6.
6.
8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
 8,236
8,236  8,*36?
8,*36?
9. Найдите два числа, каждое из которых больше 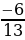 , но меньше
, но меньше 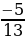 .
.
Вариант 4
1. Начертите координатную прямую и отметьте на ней точки А( 2,5), В(8), К(2,5), С(
2,5), В(8), К(2,5), С( 3). Какие из отмеченных точек имеют противоположные координаты?
3). Какие из отмеченных точек имеют противоположные координаты?
2. Выберите среди чисел 8;  5;
5;  2,2; 7,5; 0;
2,2; 7,5; 0; 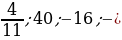 ;
; 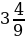 ;
; 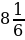 :
:
1) натуральные; 4) целые отрицательные;
2) целые; 5) дробные неотрицательные.
3) положительные;
3. Сравните числа: 1) 2,6 и  3,4; 2)
3,4; 2)  2,3 и
2,3 и  2,5.
2,5.
4. Вычислите: 1)  8,5 +
8,5 +  1,2
1,2  6,37; 2)
6,37; 2) 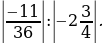
5. Найдите значение х, если:
1) –х = 16; 2) –( х) =
х) =  3,8.
3,8.
6. Решите уравнение:
1) х = 5,6; 2) х =  7.
7.
7. Найдите наименьшее целое значение х, при котором верно неравенство х  7.
7.
8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
 7,821
7,821  *,821?
*,821?
9. Найдите два числа, каждое из которых больше 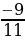 , но меньше
, но меньше 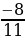 .
.
Контрольная работа № 8 по теме «Сложение и вычитание рациональных чисел»
Вариант 1
1. Выполните действия:
1) 2,9+(–6,1); 4) -6,7+ 6,7; 7) –4,2 – (–5);
2) –5,4 + 12,2; 5) 8,5 – (–4,6); 8) 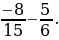
3) 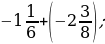 6) 3,8 – 6,3;
6) 3,8 – 6,3;
2. Решите уравнение: 1) х + 19 = 12; 2) –25 – х = -17.
3. Найдите значение выражения:
1) –34 + 67 + (–19) + (–44) + 34; 3) 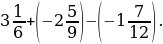
2) 6 + (–7) – (–15) – (–6) – 30;
4. Упростите выражение 6,36 + а + (–2,9) + (–4,36) + 2,9 и найдите его значение, если а = 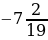 .
.
5. Не выполняя вычислений, сравните:
1) сумму чисел –5,43 и –10,58 и их разность;
2) сумму чисел –47 и 90 и сумму чисел –59 и 34.
Ответ обоснуйте.
6. Сколько целых чисел расположено на координатной прямой между числами –7 и 5? Чему равна их сумма?
7. Решите уравнение 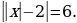
Вариант 2
1. Выполните действия:
1) 3,8 + (–4,4); 4) –9,4 + 9,4; 7) –3,8 – (–6);
2) –7,3 + 15,1; 5) 7,6 – (–3,7); 8) 
3) 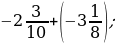 6) 5,4 – 7,2;
6) 5,4 – 7,2;
2. Решите уравнение: 1) х + 23 = 18; 2) –31 – х = –9.
3. Найдите значение выражения:
1) –42 + 54 + (–13) + (–26) + 32; 3) 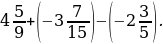
2) 8 + (–13) – (–11) – (–7) – 42;
4. Упростите выражение –9,72 + b + 7,4 + 5,72 + (–7,4) и найдите его значение, если b = 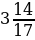 .
.
5. Не выполняя вычислений, сравните:
1) разность чисел –4,43 и –11,41 и их сумму;
2) сумму чисел 213 и –84 и сумму чисел –61 и –54.
Ответ обоснуйте.
6. Сколько целых чисел расположено на координатной прямой между числами –6 и 8? Чему равна их сумма?
7. Решите уравнение 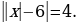
Вариант 3
1. Выполните действия:
1) 4,2 + (–7,8); 4) –8,3 + 8,3; 7) –7,6 – (–8);
2) –8,6 + 11,3; 5) 6,8 – (–5,4); 8) 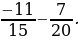
3) 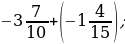 6) 4,6 – 9,4;
6) 4,6 – 9,4;
2. Решите уравнение: 1) х + 32 = 19; 2) –42 – х = –23.
3. Найдите значение выражения:
1) –54 + 82 + (–17) + (–38) + 21; 3) 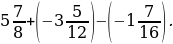
2) 4 + (–8) – (–19) – (–15) – 40;
4. Упростите выражение 5,51 + с + (–6,8) + (–8,51) + 6,8 и найдите его значение, если с = 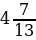 .
.
5. Не выполняя вычислений, сравните:
1) сумму чисел –8,59 и –14,73 и их разность;
2) сумму чисел 52 и –87 и разность чисел 44 и –37.
Ответ обоснуйте.
6. Сколько целых чисел расположено на координатной прямой между числами –10 и 8? Чему равна их сумма?
7. Решите уравнение 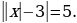
Вариант 4
1. Выполните действия:
1) 3,7 + (–8,5); 4) –4,8 + 4,8; 7) –2,8 – (–9);
2) –9,4 + 13,3; 5) 10,7 – (–7,6); 8) 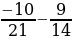 .
.
3) –2 +
+ 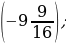 6) 2,7 – 4,8;
6) 2,7 – 4,8;
2. Решите уравнение: 1) х + 18 = 7; 2) –56 – х = –29.
3. Найдите значение выражения:
1) –68 + 83 + (–17) + (–51) + 23; 3) 5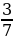 +
+ 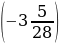 –
– 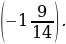
2) 12 + (–15) – (–13) – (–3) – 54;
4. Упростите выражение –10,28 + х + 4,3 + 7,28 + (–4,3) и найдите его значение, если х = 1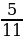 .
.
5. Не выполняя вычислений, сравните:
1) разность чисел –6,81 и –12,97 и их сумму;
2) разность чисел 31 и –72 и разность чисел –96 и –62.
Ответ обоснуйте.
6. Сколько целых чисел расположено на координатной прямой между числами –9 и 11? Чему равна их сумма?
7. Решите уравнение 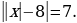
Контрольная работа № 9 по теме «Умножение и деление рациональных чисел»
Вариант 1
1. Выполните действия:
1) 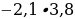 ; 2)
; 2)  ; 3) –14,16 : (–0,6); 4) –18,36 : 18.
; 3) –14,16 : (–0,6); 4) –18,36 : 18.
2. Упростите выражение:
1) 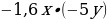 ; 3)
; 3) 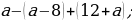
2) 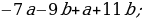 4)
4) 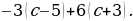
3. Найдите значение выражения:
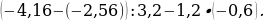
4. Упростите выражение –2(2,7х – 1) – (6 – 3,4х) + 8(0,4х – 2) и вычислите его значение при х = –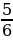 .
.
5. Чему равно значение выражения –0,8х – (0,6х – 0,7у), если 2x – y = –8?
Вариант 2
1. Выполните действия:
1) 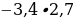 ; 2)
; 2) 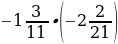 ; 3) –12,72 : (–0,4); 4) 15,45 : (–15).
; 3) –12,72 : (–0,4); 4) 15,45 : (–15).
2. Упростите выражение:
1) 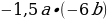 ; 3)
; 3) 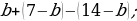
2) 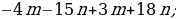 4)
4) 
3. Найдите значение выражения:
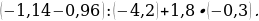
4. Упростите выражение –3(1,2х – 2) – (4 – 4,6х) + 6(0,2х – 1) и вычислите его значение при х = – 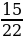 .
.
5. Чему равно значение выражения 0,9х – (0,7х + 0,6у), если 3у – х = 9?
Вариант 3
1. Выполните действия:
1) 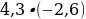 ; 2)
; 2) 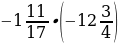 ; 3) –11,01 : (–0,3); 4) –11,44 : 11.
; 3) –11,01 : (–0,3); 4) –11,44 : 11.
2. Упростите выражение:
1) 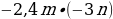 ; 3)
; 3) 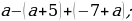
2) 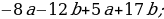 4)
4) 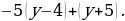
3. Найдите значение выражения:
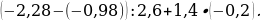
4. Упростите выражение –4(2,3х – 3) – (5 – 2,6х) + 3(0,6х – 2) и вычислите его значение при х = 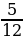 .
.
5. Чему равно значение выражения 1,2х – (–0,4х + 2,4у), если 3y – 2x = –5?
Вариант 4
1. Выполните действия:
1) 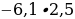 ; 3) –13,72 : (–0,7);
; 3) –13,72 : (–0,7);
2) 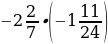 ; 4) 13,52 : (–13).
; 4) 13,52 : (–13).
2. Упростите выражение:
1) 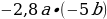 ; 3)
; 3) 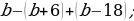
2) 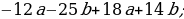 4)
4) 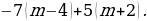
3. Найдите значение выражения:
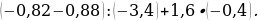
4. Упростите выражение –4(3,5х – 4) – (7 – 2,1х) + 5(0,3х – 5) и вычислите его значение при х = –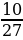 .
.
5. Чему равно значение выражения 1,7х – (0,2х + 2у), если 4у – 3х = 6?
Контрольная работа № 10 по теме
«Решение уравнений и решение задач с помощью уравнений»
Вариант 1
1. Решите уравнение 13x + 10 = 6x − 4.
2. В трёх ящиках лежит 75 кг апельсинов. Во втором ящике апельсинов в 4 раза больше, чем в первом, а в третьем — на 3 кг меньше, чем в первом. Сколько килограммов апельсинов лежит в первом ящике?
3. Найдите корень уравнения:
1) 0,4(x − 3) + 2,5 = 0,5(4 + x); 2) 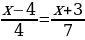 .
.
4. У Пети и Васи было поровну денег. Когда Петя потратил на покупку книг 400 р., а Вася — 200 р., то у Васи осталось денег в 5 раз больше, чем у Пети. Сколько денег было у каждого из них вначале?
5. Решите уравнение (4y + 6)(1,8 − 0,2y) = 0.
Вариант 2
1. Решите уравнение 17x − 8 = 20x + 7.
2. Три брата собрали 88 кг яблок. Старший собрал в 3 раза боль ше, чем младший, а средний — на 13 кг больше, чем младший. Сколько килограммов яблок собрал младший брат?
3. Найдите корень уравнения:
1) 0,6(x − 2) + 4,6 = 0,4(7 + x); 2) 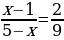 .
.
4. В двух цистернах было поровну воды. Когда из первой цистерны взяли 54 л воды, а из второй — 6 л, то в первой цистерне осталось в 4 раза меньше воды, чем во второй. Сколько литров воды было в каждой цистерне вначале?
5. Решите уравнение (3x + 42)(4,8 − 0,6x) = 0.
Вариант 3
1. Решите уравнение 7x + 30 = 19x − 6.
2. За три дня Дима решил 37 математических задач. Во второй день он решил в 2 раза больше задач, чем в первый, а в третий — на 5 задач больше, чем в первый. Сколько задач решил Дима в первый день?
3. Найдите корень уравнения:
1) 0,6(x − 6) + 14,2 = 0,8(8 − x); 2) 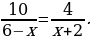
4. В двух контейнерах было поровну яблок. Когда из первого контейнера взяли 13 кг яблок, а из второго — 31 кг, то во втором контейнере осталось в 3 раза меньше яблок, чем в первом. Сколько килограммов яблок было в каждом контейнере вначале?
5. Решите уравнение (−2x − 5)(0,3x + 2,7) = 0.
Вариант 4
1. Решите уравнение 16x − 3 = 8x − 43.
2. Маша купила учебник, тетрадь и ручку, заплатив за всю покупку 385 р. Учебник стоил в 6 раз больше, чем ручка, а тетрадь — на 15 р. меньше, чем ручка. Сколько рублей стоила ручка?
3. Найдите корень уравнения:
1) −0,9(x − 4) − 3,3 = 0,6(2 − x); 2) 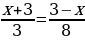 .
.
4. На двух полках стояло поровну книг. Когда с первой полки взяли 3 книги, а со второй — 14, то на первой полке осталось в 2 раза больше книг, чем на второй. Сколько книг было на каждой полке вначале?
5. Решите уравнение (7x − 2)(7x + 1,4) = 0.
Контрольная работа № 11 по теме
«Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость. Графики»
Вариант 1
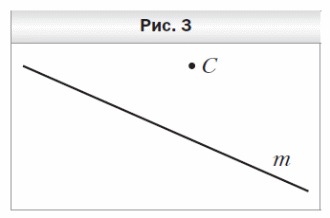
1. Перерисуйте в тетрадь рисунок 3. Проведите через точку C:
1) прямую a, параллельную прямой m;
2) прямую b, перпендикулярную прямой m.
2. Начертите произвольный треугольник ABC. Постройте фигуру, симметричную этому треугольнику относительно точки A.
3. Отметьте на координатной плоскости точки A (−1; 4) и B (−4; −2). Проведите отрезок AB.
1) Найдите координаты точки пересечения отрезка AB с осью абсцисс.
2) Постройте отрезок, симметричный отрезку AB относительно оси ординат, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол BDK, отметьте на его стороне DK точку M. Проведите через точку M прямую, перпендикулярную прямой DK, и прямую, перпендикулярную прямой DB.
5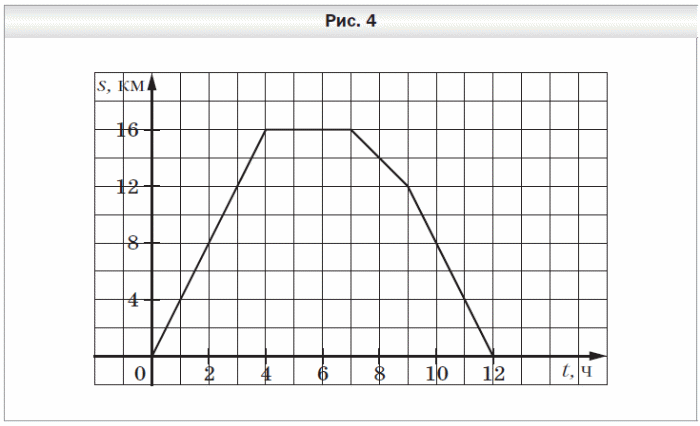 . Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 4 изображён график движения туриста.
. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 4 изображён график движения туриста.
1) На каком расстоянии от лагеря был турист через 4 ч после начала движения?
2) Сколько времени турист затратил на остановку?
3) Через сколько часов после начала движения турист был на расстоянии 12 км от лагеря?
4) С какой скоростью шёл турист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (−2; −3), B (−2; 5) и C (4; 5).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины D.
3) Найдите координаты точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (x; y) такие, что x = 2, y — произвольное число.
Вариант 2
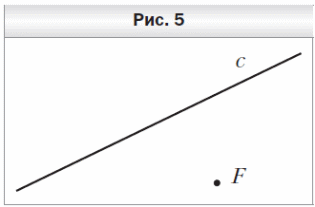
1. Перерисуйте в тетрадь рисунок 5. Проведите через точку F:
1) прямую a, параллельную прямой c;
2) прямую b, перпендикулярную прямой c.
2. Начертите произвольный треугольник DEF. Постройте фигуру, симметричную этому треугольнику относительно точки E.
3. Отметьте на координатной плоскости точки C (1; 4) и D (−1; 2). Проведите отрезок CD.
1) Найдите координаты точки пересечения отрезка CD с осью ординат.
2) Постройте отрезок, симметричный отрезку CD относительно оси абсцисс, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол OCA, отметьте на его стороне CA точку P. Проведите через точку P прямую, перпендикулярную прямой CA, и прямую, перпендикулярную прямой CO.
5. Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 6 изображён график движения велосипедиста.

1) На каком расстоянии от дома был велосипедист через 4 ч после начала движения?
2) Сколько времени велосипедист затратил на остановку?
3) Через сколько часов после начала движения велосипедист был на расстоянии 24 км от дома?
4) С какой скоростью ехал велосипедист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (−1; −3), C (5; 1) и D (5; −3).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины B.
3) Найдите координаты точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (x; y) такие, что y = −4, x — произвольное число.
Вариант 3
1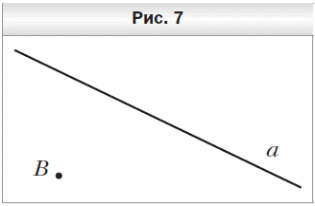 . Перерисуйте в тетрадь рисунок 7. Проведите через точку B:
. Перерисуйте в тетрадь рисунок 7. Проведите через точку B:
1) прямую b, параллельную прямой a;
2) прямую c, перпендикулярную прямой a.
2.Начертите произвольный треугольник MKP. Постройте фигуру, симметричную этому треугольнику относительно точки P.
3. Отметьте на координатной плоскости точки М (1; 2) и N (−1; 6). Проведите отрезок MN.
1) Найдите координаты точки пересечения отрезка MN с осью ординат.
2) Постройте отрезок, симметричный отрезку MN относительно оси абсцисс, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол MCK, отметьте на его стороне CM точку A. Проведите через точку A прямую, перпендикулярную прямой CM, и прямую, перпендикулярную прямой CK.
5. Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 8 изображён график движения велосипедиста.
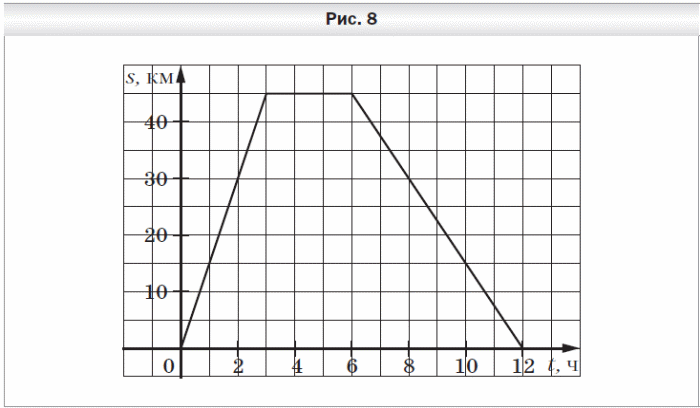
1) На каком расстоянии от дома был велосипедист через 3 ч после начала движения?
2) Сколько времени велосипедист затратил на остановку?
3) Через сколько часов после начала движения велосипедист был на расстоянии 30 км от дома?
4) С какой скоростью ехал велосипедист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: A (−2; −2), B (−2; 4) и D (6; −2).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины C.
3) Найдите координаты точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (x; y) такие, что x = −4, y — произвольное число.
Вариант 4
1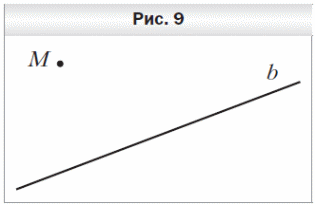 . Перерисуйте в тетрадь рисунок 9. Проведите через точку M:
. Перерисуйте в тетрадь рисунок 9. Проведите через точку M:
1) прямую a, параллельную прямой b;
2) прямую c, перпендикулярную прямой b.
2. Начертите произвольный треугольник ADK. Постройте фигуру, симметричную этому треугольнику относительно точки D.
3. Отметьте на координатной плоскости точки K (1; −1) и M (4; 2). Проведите отрезок KM.
1) Найдите координаты точки пересечения отрезка KM с осью абсцисс.
2) Постройте отрезок, симметричный отрезку KM относительно оси ординат, и найдите координаты концов полученного отрезка.
4. Начертите тупой угол APR, отметьте на его стороне PR точку E. Проведите через точку E прямую, перпендикулярную прямой PR, и прямую, перпендикулярную прямой AP.
5. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 10 изображён график движения туриста.
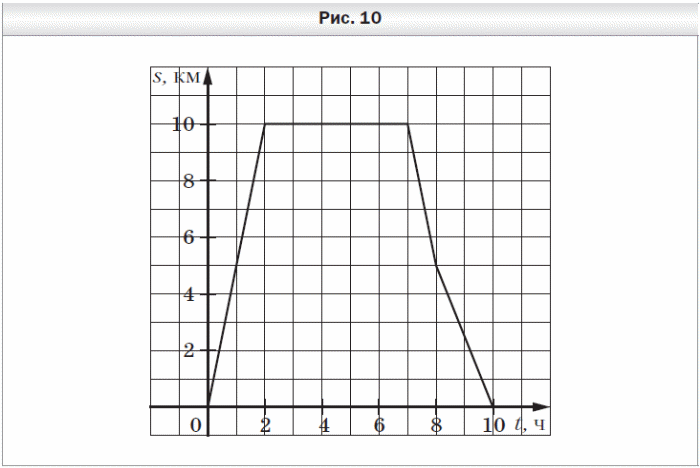
1) На каком расстоянии от лагеря был турист через 2 ч после начала движения?
2) Сколько времени турист затратил на остановку?
3) Через сколько часов после начала движения турист был на расстоянии 5 км от лагеря?
4) С какой скоростью шёл турист до остановки?
6. Даны координаты трёх вершин прямоугольника ABCD: B ( −3; 6); C (5; 6) и D (5; −2).
1) Начертите этот прямоугольник.
2) Найдите координаты вершины A.
3) Найдите координаты точки пересечения диагоналей прямоугольника.
4) Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
7. Изобразите на координатной плоскости все точки (x; y) такие, что y = 3, x — произвольное число.
Контрольная работа № 12 по теме
«Повторение и систематизация знаний учащихся»
Вариант 1
1. Найдите значение выражения:
1) 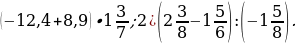
2. В 6 А классе 36 учеников. Количество учеников 6 Б класса составляет 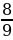 количества учеников 6 А класса и 80 % количества учеников 6 В класса. Сколько человек учится в 6 Б классе и сколько — в 6 В классе?
количества учеников 6 А класса и 80 % количества учеников 6 В класса. Сколько человек учится в 6 Б классе и сколько — в 6 В классе?
3. Отметьте на координатной плоскости точки A (−3; 1), B (0; −4) и M (2; −1). Проведите прямую AB. Через точку M проведите прямую a, параллельную прямой AB, и прямую b, перпендикулярную прямой AB.
4. В первом ящике было в 4 раза больше яблок, чем во втором. Когда из первого ящика взяли 10 кг яблок, а во второй положили ещё 8 кг, то в обоих ящиках яблок стало поровну. Сколько килограммов яблок было в каждом ящике вначале?
5. Решите уравнение: 8x − 3(2x + 1) = 2x + 4.
Вариант 2
1. Найдите значение выражения:
1) 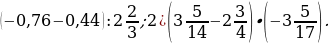
2. В саду растёт 50 яблонь. Количество груш, растущих в саду, составляет
32 % количества яблонь и 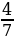 количества вишен, растущих в этом саду. Сколько груш и сколько вишен растёт в саду?
количества вишен, растущих в этом саду. Сколько груш и сколько вишен растёт в саду?
3. Отметьте на координатной плоскости точки M (3; −2), K (−1; −1) и C (0; 3). Проведите прямую MK. Через точку C проведите прямую c, параллельную прямой MK, и прямую d, перпендикулярную прямой MK.
4. В первом вагоне электропоезда ехало в 3 раза больше пассажиров, чем во втором. Когда из первого вагона вышло 28 пассажиров, а из второго — 4 пассажира, то в обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне вначале? 5. Решите уравнение: 10x − 2(4x − 5) = 2x + 10.
Вариант 3
1. Найдите значение выражения:
1) 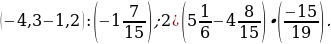
2. Провод разрезали на три части. Длина первой части была равна 240 м. Длина второй части составляла  длины первой части и 30 % длины третьей части. Найдите длины второй и третьей частей.
длины первой части и 30 % длины третьей части. Найдите длины второй и третьей частей.
3. Отметьте на координатной плоскости точки E (−2; 0), F (1; 4) и P (1; −2). Проведите прямую EF. Через точку P проведите прямую m, параллельную прямой EF, и прямую n, перпендикулярную прямой EF.
4. В первой бочке было в 5 раз больше воды, чем во второй. Когда в первую бочку долили 10 л воды, а во вторую — 58 л, то в обеих бочках воды стало поровну. Сколько литров воды было в каждой бочке вначале?
5. Решите уравнение: 19x + 4(1 − 4x) = 4 + 3x.
Вариант 4
1. Найдите значение выражения:
1) 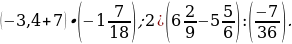
2. В автопарке 60 легковых автомобилей. Грузовые автомобили составляют 65 % количества легковых и 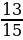 количества автобусов. Сколько грузовиков и сколько автобусов в автопарке?
количества автобусов. Сколько грузовиков и сколько автобусов в автопарке?
3. Отметьте на координатной плоскости точки C (4; 0), D (−2; 2) и A (−2; −1). Проведите прямую CD. Через точку A проведите прямую b, параллельную прямой CD, и прямую d, перпендикулярную прямой CD.
4. У Васи было в 7 раз больше марок, чем у Пети. Когда Вася подарил Пете 45 своих марок, то у обоих мальчиков марок стало поровну. Сколько марок было у каждого мальчика вначале?
5. Решите уравнение: 12x + 5(6 − 3x) = 10 − 3x.





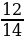 ; 2)
; 2) 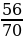 .
. 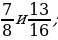 2)
2) 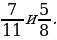
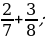 2)
2) 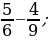 3)
3) 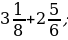 4)
4) 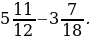
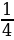 ц яблок, а во второй – на 2
ц яблок, а во второй – на 2 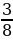 ц меньше. Сколько центнеров яблок продали за два дня?
ц меньше. Сколько центнеров яблок продали за два дня?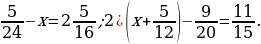
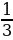 своих денег на покупку новой книги,
своих денег на покупку новой книги, 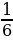 денег – на покупку тетрадей,
денег – на покупку тетрадей, 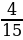 денег – на покупку карандашей, а остальные деньги – на покупку альбома. Какую часть своих денег потратил Миша на покупку альбома?
денег – на покупку карандашей, а остальные деньги – на покупку альбома. Какую часть своих денег потратил Миша на покупку альбома?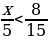 .
.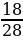 ; 2)
; 2) 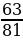 .
. 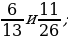 2)
2) 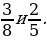
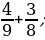 2)
2) 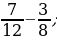 3)
3) 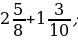 4)
4) 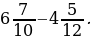
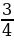 км, а за второй – на 1
км, а за второй – на 1 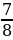 км меньше. Какой путь преодолел турист за 2 ч?
км меньше. Какой путь преодолел турист за 2 ч?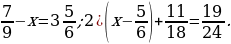
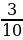 , а груши –
, а груши – 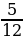 всех завезённых фруктов. Остальной завезённый товар составлял виноград. Какую часть всех фруктов составлял виноград?
всех завезённых фруктов. Остальной завезённый товар составлял виноград. Какую часть всех фруктов составлял виноград?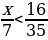 .
.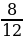 ; 2)
; 2) 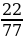 .
. 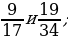 2)
2) 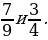
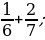 2)
2) 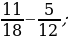 3)
3) 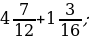 4)
4) 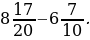
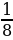 т груза, а во втором – на 2
т груза, а во втором – на 2 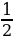 т меньше. Какова общая масса перевезённого груза?
т меньше. Какова общая масса перевезённого груза?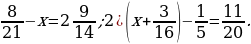
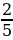 , а пятиклассники –
, а пятиклассники – 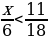
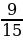 ; 2)
; 2) 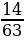
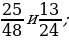 2)
2) 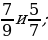
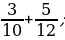 2)
2) 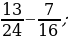 3)
3) 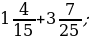 4)
4)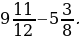
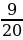 кг меньше. Какова масса сплава?
кг меньше. Какова масса сплава? 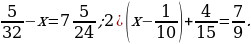
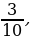 второй –
второй – 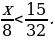
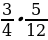 ; 2)
; 2) 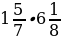 ; 3)
; 3) 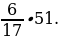
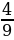 составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?
составляли шоколадные. Сколько килограммов шоколадных конфет завезли в магазин?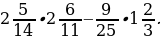
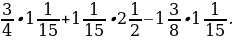
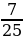 туристического маршрута, за второй –
туристического маршрута, за второй – 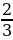 оставшейся части маршрута, а за третий – остальное. За какой день турист прошёл больше всего?
оставшейся части маршрута, а за третий – остальное. За какой день турист прошёл больше всего?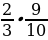 ; 2)
; 2) 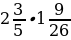 ; 3)
; 3) 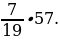
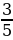 пути они шли лесом. Сколько километров прошли туристы по лесу?
пути они шли лесом. Сколько километров прошли туристы по лесу?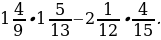
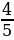 см, его длина в 3
см, его длина в 3 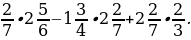
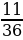 поля, второй –
поля, второй – 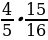 ; 2)
; 2) 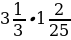 ; 3)
; 3) 
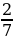 поля, площадь которого равна 14 га. Сколько гектаров поля фермер засеял подсолнечником?
поля, площадь которого равна 14 га. Сколько гектаров поля фермер засеял подсолнечником?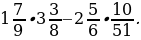
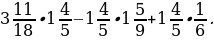
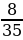 груза, на втором –
груза, на втором –  ; 2)
; 2) 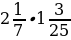 ; 3)
; 3) 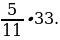
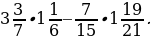
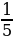 раза больше высоты, а ширина составляет 40 % длины. Вычислите объем параллелепипеда.
раза больше высоты, а ширина составляет 40 % длины. Вычислите объем параллелепипеда. 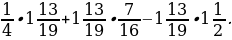
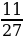 завезенной партии огурцов, за второй –
завезенной партии огурцов, за второй –  остатка, а за третий – остальные. За какой день было продано больше всего огурцов?
остатка, а за третий – остальные. За какой день было продано больше всего огурцов? 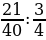 ; 2)
; 2) 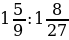 ; 3)
; 3) 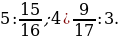
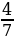 её объёма. Сколько литров составляет объём бочки?
её объёма. Сколько литров составляет объём бочки? 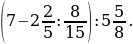
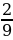 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь.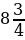 км/ч, а другой – со скоростью в
км/ч, а другой – со скоростью в 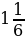 раза меньшей. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 26 км?
раза меньшей. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 26 км? 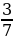 дороги, за вторую – 40 % остатка, а за третью – остальные 14,4 км. Сколько километров дороги отремонтировали за три недели?
дороги, за вторую – 40 % остатка, а за третью – остальные 14,4 км. Сколько километров дороги отремонтировали за три недели?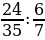 ; 2)
; 2) 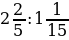 ; 3)
; 3) 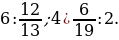
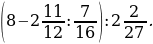
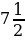 км/ч. Одновременно с этим из пункта В в том же направлении вышел второй турист, скорость которого в
км/ч. Одновременно с этим из пункта В в том же направлении вышел второй турист, скорость которого в 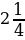 раза меньше скорости первого. Через сколько часов после начала движения первый турист догонит второго, если расстояние между пунктами А и В равно 10 км?
раза меньше скорости первого. Через сколько часов после начала движения первый турист догонит второго, если расстояние между пунктами А и В равно 10 км? 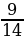 остатка, а за третий – остальные 15 га. Какова площадь поля?
остатка, а за третий – остальные 15 га. Какова площадь поля?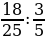 ; 2)
; 2) 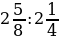 ; 3)
; 3) 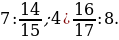

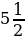 км/ч, а скорость второго была в
км/ч, а скорость второго была в 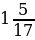 раза меньше скорости первого. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 13 км?
раза меньше скорости первого. Через сколько часов после начала движения они встретились, если расстояние между сёлами равно 13 км? 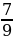 остатка, а за третий – остальные 8 страниц. Сколько страниц в книге?
остатка, а за третий – остальные 8 страниц. Сколько страниц в книге?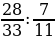 ; 2)
; 2) 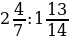 ; 3)
; 3) 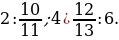
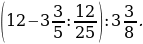
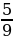 в бесконечную периодическую десятичную дробь.
в бесконечную периодическую десятичную дробь. 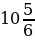 км/ч. Одновременно с этим из пункта В в том же направлении вышел турист, скорость которого в
км/ч. Одновременно с этим из пункта В в том же направлении вышел турист, скорость которого в 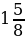 раза меньше скорости велосипедиста. Через сколько часов после начала движения велосипедист догонит туриста, если расстояние между пунктами А и В равно 5 км?
раза меньше скорости велосипедиста. Через сколько часов после начала движения велосипедист догонит туриста, если расстояние между пунктами А и В равно 5 км? 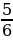 :
: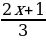 =
= 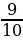 .
.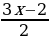 =
= 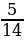 :
: 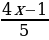 =
= 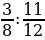 .
. 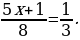
 4,5). Какие из отмеченных точек имеют противоположные координаты?
4,5). Какие из отмеченных точек имеют противоположные координаты?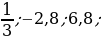
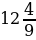 ;
;  :
: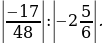
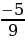 , но меньше
, но меньше 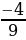 .
.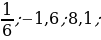
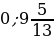 ;
; 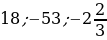 :
: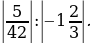
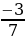 , но меньше
, но меньше 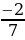 .
.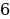 ,5), F(7). Какие из отмеченных точек имеют противоположные координаты?
,5), F(7). Какие из отмеченных точек имеют противоположные координаты?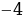 ;
; 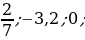
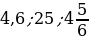 ;
; 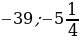 :
: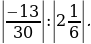
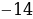 ; 2) –(
; 2) –(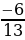 , но меньше
, но меньше 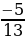 .
.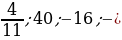 ;
; 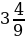 ;
; 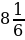 :
: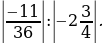
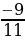 , но меньше
, но меньше 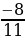 .
.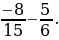
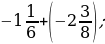 6) 3,8 – 6,3;
6) 3,8 – 6,3;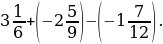
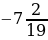 .
.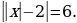

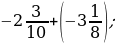 6) 5,4 – 7,2;
6) 5,4 – 7,2;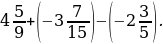
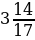 .
.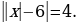
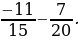
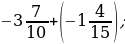 6) 4,6 – 9,4;
6) 4,6 – 9,4;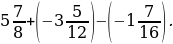
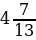 .
.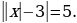
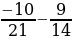 .
.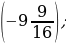 6) 2,7 – 4,8;
6) 2,7 – 4,8; 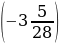 –
– 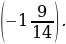
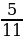 .
. 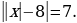
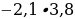 ; 2)
; 2)  ; 3) –14,16 : (–0,6); 4) –18,36 : 18.
; 3) –14,16 : (–0,6); 4) –18,36 : 18.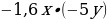 ; 3)
; 3) 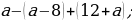
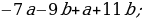 4)
4) 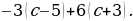
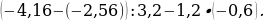
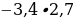 ; 2)
; 2) 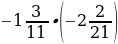 ; 3) –12,72 : (–0,4); 4) 15,45 : (–15).
; 3) –12,72 : (–0,4); 4) 15,45 : (–15).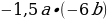 ; 3)
; 3) 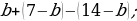
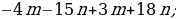 4)
4) 
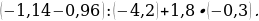
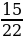 .
.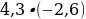 ; 2)
; 2) 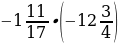 ; 3) –11,01 : (–0,3); 4) –11,44 : 11.
; 3) –11,01 : (–0,3); 4) –11,44 : 11.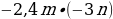 ; 3)
; 3) 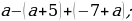
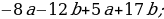 4)
4) 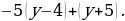
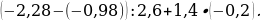
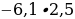 ; 3) –13,72 : (–0,7);
; 3) –13,72 : (–0,7); 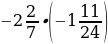 ; 4) 13,52 : (–13).
; 4) 13,52 : (–13). 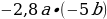 ; 3)
; 3) 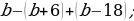
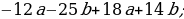 4)
4) 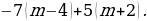
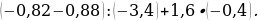
 .
. 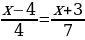 .
. 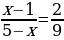 .
. 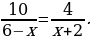
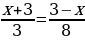 .
. 
 . Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 4 изображён график движения туриста.
. Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 4 изображён график движения туриста. 

 . Перерисуйте в тетрадь рисунок 7. Проведите через точку B:
. Перерисуйте в тетрадь рисунок 7. Проведите через точку B: 
 . Перерисуйте в тетрадь рисунок 9. Проведите через точку M:
. Перерисуйте в тетрадь рисунок 9. Проведите через точку M: 
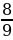 количества учеников 6 А класса и 80 % количества учеников 6 В класса. Сколько человек учится в 6 Б классе и сколько — в 6 В классе?
количества учеников 6 А класса и 80 % количества учеников 6 В класса. Сколько человек учится в 6 Б классе и сколько — в 6 В классе? 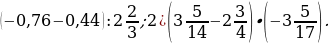
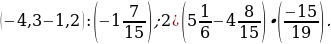
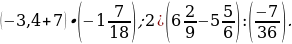
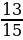 количества автобусов. Сколько грузовиков и сколько автобусов в автопарке?
количества автобусов. Сколько грузовиков и сколько автобусов в автопарке? 









