План-график проведения контрольно-оценочных мероприятий
Алгебра и начала математического анализа
| № п/п | Контролируемые разделы (темы) предмета | Наименование оценочного средства | Сроки проведения по КТП |
| план | факт |
| 1 | Множества рациональных и действительных чисел. Рациональные уравнения и неравенства | Контрольная работа №1 по теме: «Множества рациональных и действительных чисел. Рациональные уравнения и неравенства» |
|
|
| 2 | Арифметический корень n–ой степени. Иррациональные уравнения и неравенства | Контрольная работа № 2 по теме: «Арифметический корень n–ой степени. Иррациональные уравнения и неравенства» |
|
|
| 3 | Формулы тригонометрии. Тригонометрические уравнения | Контрольная работа № 3 по теме: «Формулы тригонометрии. Тригонометрические уравнения» |
|
|
| 4 | Повторение, обобщение, систематизация знаний | Контрольная работа № 4 «Итоговая» |
|
|
Геометрия
| № п/п | Контролируемые разделы (темы) предмета | Наименование оценочного средства | Сроки проведения по КТП |
| план | факт |
| 1 | Прямые и плоскости в пространстве. Параллельность прямых и плоскостей | Контрольная работа №1 по теме: «Прямые и плоскости в пространстве. Параллельность прямых и плоскостей» |
|
|
| 2 | Перпендикулярность прямых и плоскостей. Углы между прямыми и плоскостями | Контрольная работа № 2 по темам: «Перпендикулярность прямых и плоскостей» и «Углы между прямыми и плоскостями» |
|
|
| 3 | Многогранники | Контрольная работа № 3 по теме: «Многогранники» |
|
|
| 4 | Объёмы многогранников | Контрольная работа № 4 по теме: «Объёмы многогранников» |
|
|
| 5 | Повторение: сечения, расстояния и углы | Контрольная работа № 5 «Итоговая» |
|
|
Примерный перечень оценочных средств
| № п/п | Наименование оценочного средства | Краткая характеристика оценочного средства | Представление оценочного средства в фонде |
| 1 | 2 | 3 | 4 |
-
| Контрольная работа | Средство проверки умений применять полученные знания для решения задач определенного типа по теме или разделу | Комплект контрольных заданий по вариантам |
-
| Рабочая тетрадь, зачетная тетрадь, комплексная тетрадь для контроля знаний и т.п. | Дидактический комплекс, предназначенный для самостоятельной работы обучающегося и позволяющий оценивать уровень усвоения им учебного материала. | Образец тетради |
-
| Разноуровневые задачи и задания | Различают задачи и задания: а) репродуктивного уровня, позволяющие оценивать и диагностировать знание фактического материала (базовые понятия, алгоритмы, факты) и умение правильно использовать специальные термины и понятия, узнавание объектов изучения в рамках определенного раздела дисциплины; б) реконструктивного уровня, позволяющие оценивать и диагностировать умения синтезировать, анализировать, обобщать фактический и теоретический материал с формулированием конкретных выводов, установлением причинно-следственных связей; в) творческого уровня, позволяющие оценивать и диагностировать умения, интегрировать знания различных областей, аргументировать собственную точку зрения. | Комплект разноуровневых задач и заданий |
-
| Реферат | Продукт самостоятельной работы учащегося, представляющий собой краткое изложение в письменном виде полученных результатов теоретического анализа определенной научной (учебно-исследовательской) темы, где автор раскрывает суть исследуемой проблемы, приводит различные точки зрения, а также собственные взгляды на нее.
| Темы рефератов |
-
| Тест | Система стандартизированных заданий, позволяющая автоматизировать процедуру измерения уровня знаний и умений обучающегося. | Комплект тестовых заданий |
Критерии оценивания контрольных работ
Текущие контрольные работы имеют целью проверку усвоения изучаемого и проверяемого программного материала. Итоговая контрольная работа проводится в конце учебного года.
Все контрольные работы даны в двух равноценных вариантах. Каждая включает в себя как задания, соответствующие обязательному уровню, так и задания более продвинутого уровня (они отмечены знаком *). Выполнение работы рассчитано на один урок. Однако следует иметь ввиду, что работы достаточно насыщены по объему. Поэтому учителю необходимо оценить возможности своих учащихся, и если объем работы представляется чрезмерным, то ее следует уменьшить за счет исключения какого-либо из последних заданий. Возможен также и такой вариант, когда одно из заданий продвинутого уровня работы рассматривается как резервное. Тогда учащимся сообщается, что оценка «5» выставляется в том случае, если правильно выполнены все задания или все задания, кроме одного из последних.
В проверяемых работах учитель отмечает и исправляет допущенные ошибки, руководствуясь следующим:
- учитель только подчеркивает допущенную ошибку, которую исправляет сам ученик;
- подчеркивание ошибок производится учителем только красной пастой (красными чернилами, красным карандашом);
- после анализа ошибок выставляется отметка за работу.
Все контрольные работы обязательно оцениваются учителем с занесением оценок в классный журнал.
При оценке письменных работ учащихся учитель руководствуется соответствующими нормами оценки знаний умений и навыков школьников.
Оценка письменных работ учащихся по математике
Отметка «5» ставится, если:
- работа выполнена верно и полностью;
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- решение не содержит неверных математических утверждений (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
- выполнено без недочетов не менее ¾ заданий.
Отметка «3» ставится, если:
- допущены более одной ошибки или более трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме; без недочетов выполнено не менее половины работы.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере;
- правильно выполнено менее половины работы
После проверки письменных работ обучающимся дается задание по исправлению ошибок или выполнению заданий, предупреждающих повторение аналогичных ошибок. Работа над ошибками, как правило, осуществляется в тех же тетрадях, в которых выполнялись соответствующие письменные работы.
Алгебра и начала математического анализа
Контрольная работа №1
«Множества рациональных и действительных чисел. Рациональные уравнения и неравенства»
1 вариант
1. Вычислите 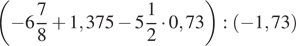 .
.
2. Решите уравнение 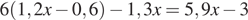 .
.
3. Решите рациональное уравнение 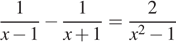 .
.
4. Решите рациональное неравенство 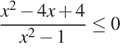 .
.
5. Решите дробно-линейное неравенство 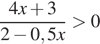 .
.
6. Решите систему или совокупность неравенств 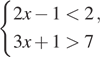 .
.
Контрольная работа №1
«Множества рациональных и действительных чисел. Рациональные уравнения и неравенства».
2 вариант
1. Вычислите 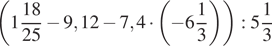 .
.
2. Решите уравнение 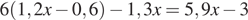 .
.
3. Решите рациональное уравнение 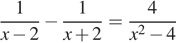 .
.
4. Решите рациональное неравенство 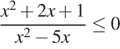 .
.
5. Решите дробно-линейное неравенство 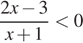 .
.
6. Решите систему или совокупность неравенств 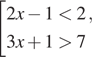 .
.
Контрольная работа №1
«Множества рациональных и действительных чисел. Рациональные уравнения и неравенства».
3 вариант
1. Вычислите 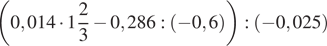 .
.
2. Решите уравнение 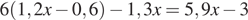 .
.
3. Решите рациональное уравнение 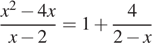 .
.
4. Решите рациональное неравенство 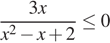
5. Решите дробно-линейное неравенство 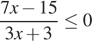 .
.
6. Решите систему или совокупность неравенств 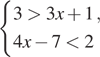 .
.
Контрольная работа №1
«Множества рациональных и действительных чисел. Рациональные уравнения и неравенства».
4 вариант
1. Вычислите 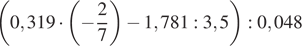 .
.
2. Решите уравнение 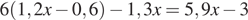 .
.
3. Решите рациональное уравнение 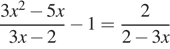 .
.
4. Решите рациональное неравенство 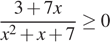 .
.
5. Решите дробно-линейное неравенство 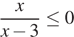 .
.
6. Решите систему или совокупность неравенств 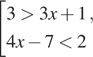 .
.
Ответы
| №п/п | 1 вариант | 2 вариант | 3 вариант | 4 вариант |
| 1 | 5,5 | 7,4 | -20 | -12,5 |
| 2 | 
| 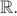
| 
| 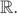
|
| 3 | 
| 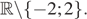
| 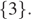
| 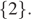
|
| 4 | 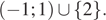
| 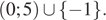
| 
| 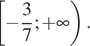
|
| 5 | 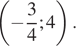
| 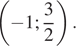
| 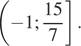
| 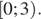
|
| 6 | 
| 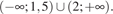
| 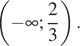
| 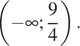
|
Контрольная работа № 2 «Арифметический корень n–ой степени. Иррациональные уравнения и неравенства»
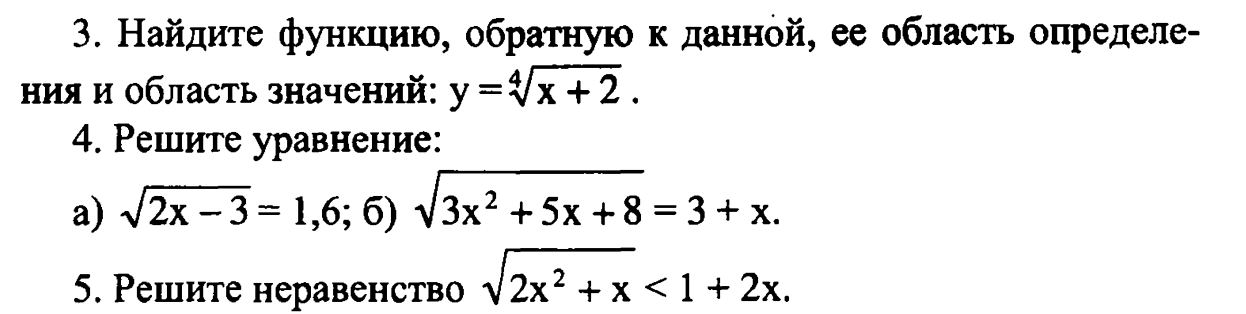

Контрольная работа № 3 «Формулы тригонометрии. Тригонометрические уравнения»

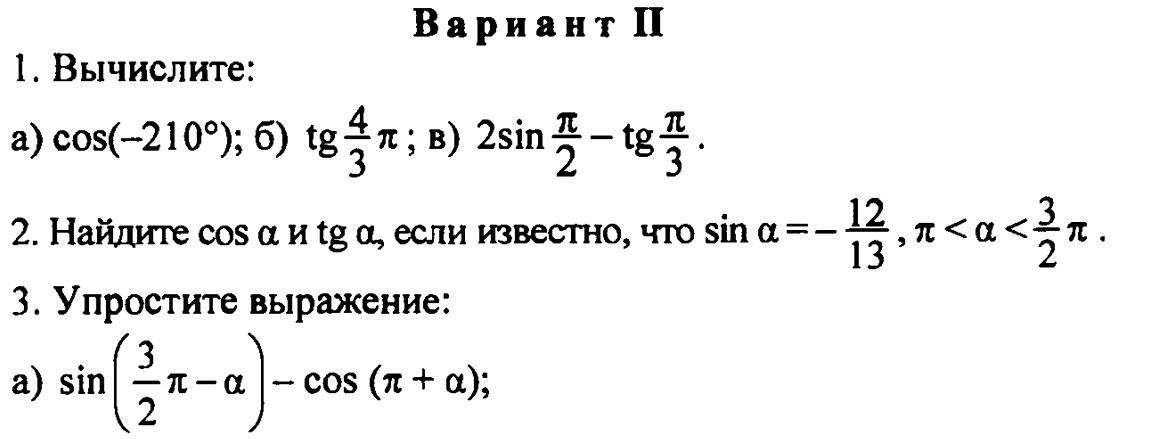
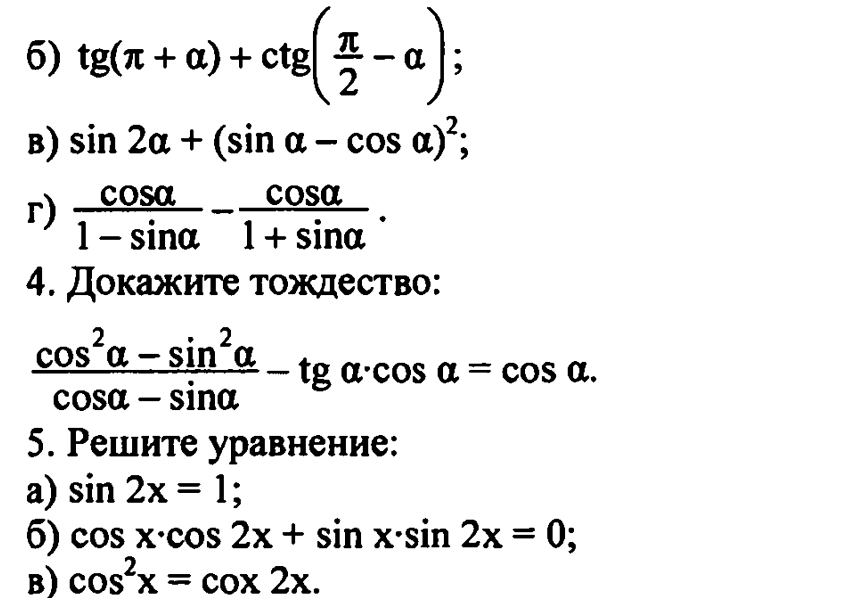
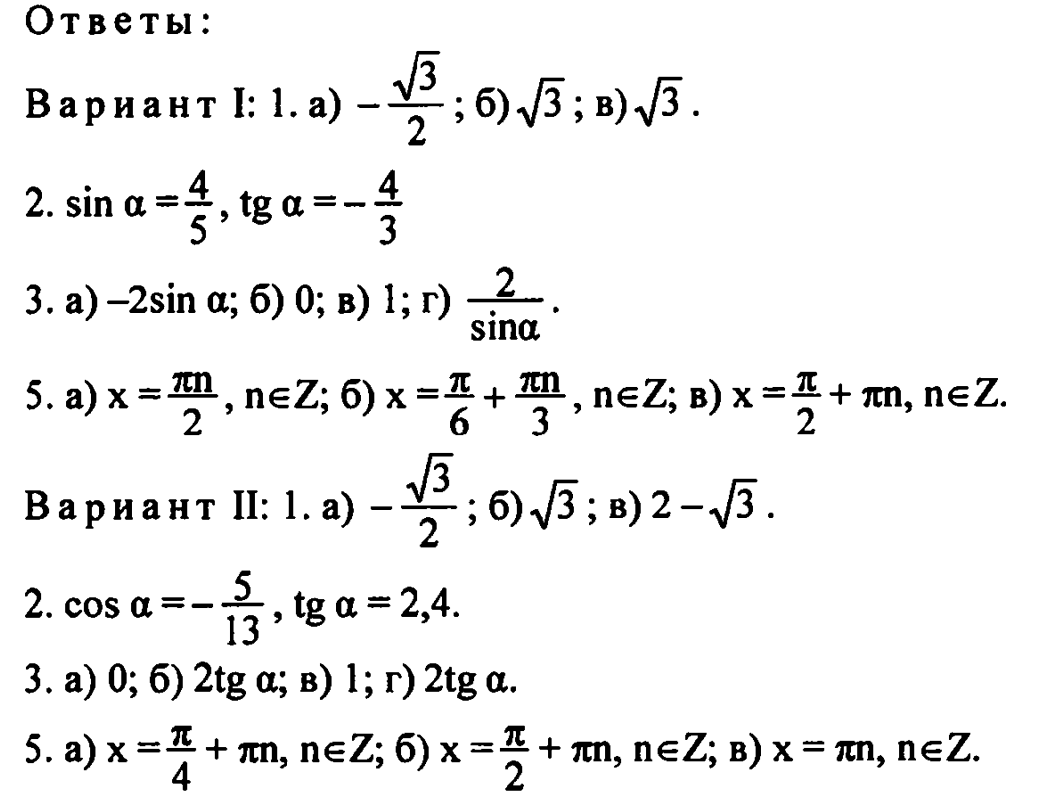
Контрольная работа № 4 «Итоговая»
ВАРИАНТ 1.
1. Найдите значение выражения:
а)  б)
б) 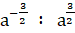 при а = 0,1 ;
при а = 0,1 ;
в) 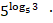
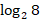 ; г) 2
; г) 2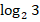 +
+ 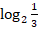 .
.
2. Найдите sin α, если cos α = - 0,6 и 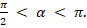
3. Вычислите: 2sin15˚۫∙cos15˚.
4. Решите уравнение:
а) 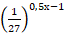 = 9 ; б)
= 9 ; б) 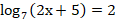 ;
;
в) 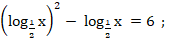 г)
г)  =
= 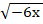 .
.
д) 2sin x - 1 = 0. Укажите наибольший отрицательный корень
в градусах.
5. Решите неравенство:
а) log3 (1 – x) 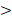 log3 (3 – 2x) ;
log3 (3 – 2x) ;
б) 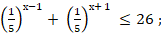
в) 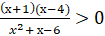 .
.
ВАРИАНТ 2.
1. Найдите значение выражения:
а) 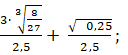 б)
б) 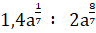 при а =
при а =  ;
;
в) 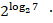
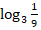 ; г)
; г) 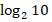 - 2
- 2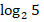 +
+ 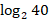 .
.
2. Найдите cos α, если sin α = 0,8 и 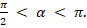
3. Вычислите: cos2 15˚ - sin2 15˚.
4. Решите уравнение:
а) 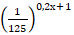 = 25 ; б)
= 25 ; б) 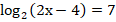 ;
;
в) 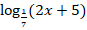
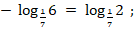 г)
г) 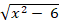 =
= 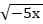 .
.
д) 2sin x + 1 = 0. Укажите ближайший к нулю корень в градусах.
5. Решите неравенство:
а) 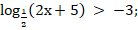
б) 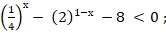
в) 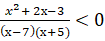 .
.
ВАРИАНТ 3.
1. Найдите значение выражения:
а) 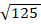 ∙
∙ 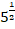 -
- 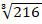 ; б)
; б) 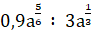 при а = 16;
при а = 16;
в) 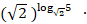
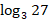 ; г)
; г) 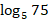 +
+ 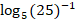 .
.
2. Найдите sin α, если cos α =  и
и 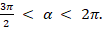
3. Вычислите: cos2 75˚ - sin2 75˚.
4. Решите уравнение:
а) 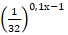 = 16 ; б)
= 16 ; б) 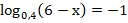 ;
;
в) 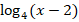 +
+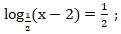 г)
г) 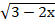 = 6 + х.
= 6 + х.
д) sin 4x = 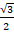 . Укажите наименьший положительный корень
. Укажите наименьший положительный корень
в градусах.
5.Решите неравенство:
а) lg2 x - 2lg x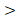 3;
3;
б) 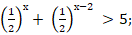
в) 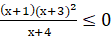 .
.
Ответы:
| № задания | Вариант 1 | Вариант 2 | Вариант 3 |
| 1а | 2 | 1 | 19 |
| 1б | 1000 | 2,1 | 1,2 |
| 1в | 9 | -14 | 8 |
| 1г | log23 | 4 | log53 |
| 2 | 0,8 | -0,6 | - 0,6 |
| 3 | 0,5 | 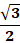
| 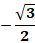
|
| 4а | 
| -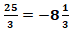 | 2 |
| 4б | 22 | 66 | 3,5 |
| 4в | 4;  | 3,5 | 2,5 |
| 4г | -1 | -6 | - 3 |
| 4д | х=(-1)n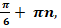 n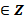 ; х=-210 ; х=-210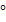 | х=(-1)n+1 + +  n n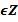 x = - 30˚ | х = (-1)n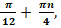 n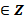 ; х=15 ; х=15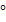 |
| 5а | х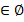 | x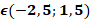 | 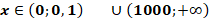
|
| 5б* | х 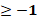 | х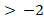 | х 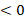 |
| 5в | х | х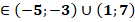 | х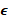 (-4; -1] (-4; -1] |
ГЕОМЕТРИЯ
Входная контрольная работа по геометрии
( 10 класс)
1 вариант
-
Один из смежных углов равен 1050. Найти другой угол.
-
В треугольнике АВС 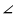 А = 420,
А = 420, 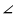 В = 890. Найти
В = 890. Найти 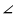 С.
С.
-
Найти площадь прямоугольного треугольника, если его катеты равны 20 см и 15 см.
-
Найти диагональ прямоугольника со сторонами 6 см и 8 см.
-
Один из углов параллелограмма равен 1050. Найти остальные углы.
-
В прямоугольном треугольнике АВС с прямым углом В катет АВ равен 8 см, а противолежащий угол С равен 300. Найти гипотенузу АС.
-
В треугольнике АВС АВ = 7 дм, ВС = 10 дм, а 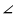 В = 450. Найти АС.
В = 450. Найти АС.
___________________________________________________
-
Смежные углы относятся как 7:2. Найти эти углы.
-
Углы треугольника АВС относятся как 3:7:8. Найти эти углы.
-
Один из углов параллелограмма в 5 раз больше другого. Найти эти углы.
Входная контрольная работа по геометрии
( 10 класс)
2 вариант
-
Один из смежных углов равен 820. Найти другой угол.
-
В треугольнике АВС 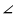 В = 510,
В = 510, 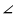 С = 790. Найти
С = 790. Найти 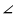 А.
А.
-
Найти площадь прямоугольного треугольника, если его катеты равны 10 см и 27 см.
-
Найти одну из сторон прямоугольника, если другая его сторона равна 6 см, а диагональ равна 10 см.
-
Один из углов параллелограмма равен 690. Найти остальные углы.
-
В прямоугольном треугольнике АВС с прямым углом С гипотенуза АВ равна 14 м, а угол В равен 300. Найти катет АС.
-
В треугольнике АВС ВС = 8 см, АС = 5 см, а 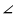 С = 300. Найти АВ.
С = 300. Найти АВ.
___________________________________________________
-
Смежные углы относятся как 3:7. Найти эти углы.
-
Углы треугольника АВС относятся как 2:5:8. Найти эти углы.
-
Один из углов параллелограмма в 8 раз больше другого. Найти эти углы.
Контрольная работа №1 по теме: «Прямые и плоскости в пространстве. Параллельность прямых и плоскостей»

Ответы:

Контрольная работа № 2 по темам: «Перпендикулярность прямых и плоскостей» и» «Углы между прямыми и плоскостями


Ответы:

Контрольная работа № 3 по теме: «Многогранники»

Ответы:

Контрольная работа № 4 по теме: «Объёмы многогранников»
Вариант 1

Вариант 2

Вариант 3

Ответы:
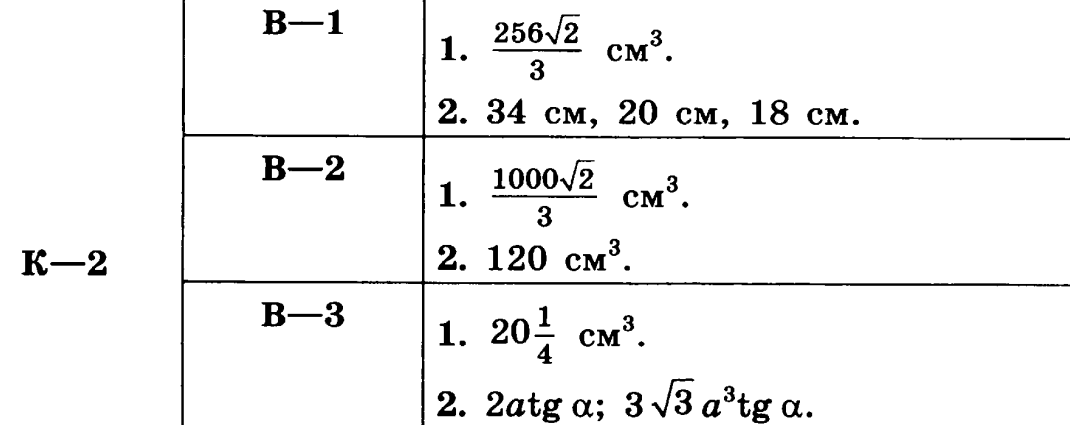
Контрольная работа № 5 «Итоговая»
Вариант 1
1. Точка M равноудалена от всех сторон квадрата со стороной 6 см и находится на расстоянии 9 см от плоскости квадрата. Найдите расстояние от точки M до сторон квадрата.
2. Точка A находится на расстоянии 9 см от плоскости α. Наклонные AB и AC образуют с плоскостью α углы 45° и 60° соответственно. Найдите расстояние между точками B и C , если угол между проекциями наклонных равен 150°.
3. Через вершину B треугольника ABC, в котором AB = BC = 34 см, AC = 32 см, проведён перпендикуляр DB к плоскости треугольника. Найдите угол между плоскостями ABC и ADC, если DB = 20 см.
4. Основание пирамиды MABCD — квадрат со стороной 6 см, боковые грани ABM и CBM перпендикулярны плоскости основания пирамиды, AM = 10 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и острым углом α. Бóльшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
Вариант 2
1. Точка F равноудалена от всех вершин прямоугольника со сторонами 12 см и 16 см и находится на расстоянии 5 см от плоскости прямоугольника. Найдите расстояние от точки F до вершин прямоугольника.
2. Точка K находится на расстоянии 4 см от плоскости α. Наклонные KA и KB образуют с плоскостью α углы 45° и 30° соответственно, а угол между наклонными равен 135°. Найдите расстояние между точками A и B.
3. Через вершину C треугольника ABC, в котором AC = BC, AC = 32 см, проведён перпендикуляр KC к плоскости треугольника. Найдите угол между плоскостями ABC и ABK, если AB = 12 см, AK = 10 см, KC = 2 см.
4. Основание пирамиды MABCD — квадрат, боковые грани ADM и CDM перпендикулярны плоскости основания пирамиды, MB = 3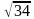 см, MA = 15 см. Найдите площадь боковой поверхности пирамиды.
см, MA = 15 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и острым углом α. Меньшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.
Вариант 3
1. Точка A равноудалена от всех сторон правильного треугольника со стороной 30 см и находится на расстоянии 5 см от плоскости треугольника. Найдите расстояние от точки A до сторон треугольника.
2. Точка B находится на расстоянии 3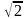 см от плоскости α. Наклонные BA и BC образуют с этой плоскостью углы 60° и 30° соответственно. Найдите расстояние между точками A и C, если угол между проекциями наклонных равен 120°.
см от плоскости α. Наклонные BA и BC образуют с этой плоскостью углы 60° и 30° соответственно. Найдите расстояние между точками A и C, если угол между проекциями наклонных равен 120°.
3. Через вершину A треугольника ABC, в котором AB = AC = 13 см, BC = 10 см, проведён перпендикуляр NA к плоскости треугольника. Найдите угол между плоскостями ABC и NBC, если NB = 15 см.
4. Основание пирамиды MABCD — квадрат, боковые грани BCM и DCM перпендикулярны плоскости основания пирамиды, MB = 13 см, MC = 12 см. Найдите площадь боковой поверхности пирамиды.
5. Основанием прямого параллелепипеда является ромб со стороной a и тупым углом α. Меньшая диагональ параллелепипеда наклонена к плоскости основания под углом β. Найдите площадь боковой поверхности параллелепипеда.







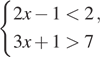 .
.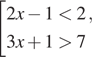 .
.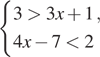 .
. .
.


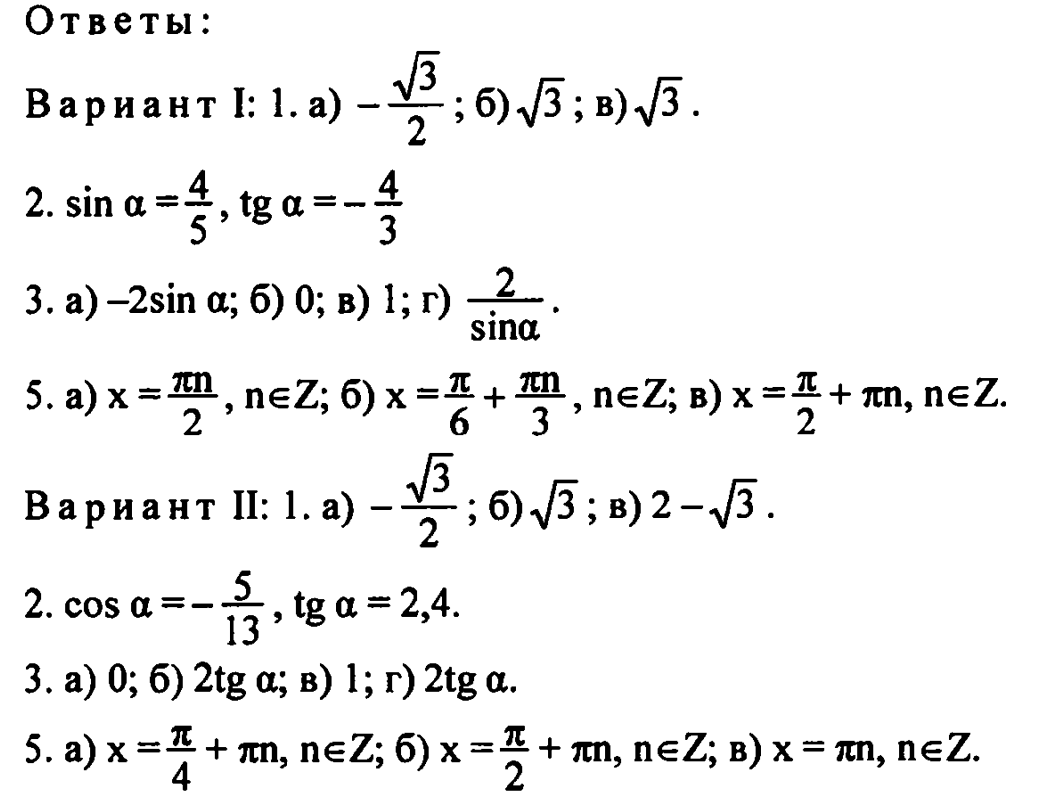
 б)
б) 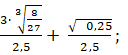 б)
б) 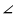 А = 420,
А = 420,