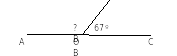Контрольные работы по геометрии в 7 классе
-
Контрольная работа за 1 триместр
-
Контрольная работа за 2 триместр
-
Контрольная работа за 3 триместр
-
Итоговая контрольная работа (итоговый тест)
Контрольная работа за 1 триместр по геометрии в 7 классе
Тема: "Начальные геометрические сведения"
Вариант I
1. На отрезке KN отмечены две точки L и M. Найдите длину отрезка LM, если известно, что KN= 12 см, MN = 3,5 см, KL = 4,6 см. Укажите, какая точка лежит на отрезке KM?
2). Сумма вертикальных углов МОЕ и DOC, образованных при пересечении прямых МС и DE, равна 204 0 . Найдите угол МОD .
3). С помощью транспортира начертите угол, равный 780 , и проведите биссектрису смежного с ним угла.
Вариант II
1. На отрезке KM отмечены две точки L и N. Найдите длину отрезка LN, если известно, что KM= 8,6 см, NM = 1,5 см, KL = 2,6 см. Укажите, какая точка лежит на отрезке KN?
2). Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 0 . Найдите угол ВОD .
3). С помощью транспортира начертите угол, равный 1320 , и проведите биссектрису одного из смежных с ним углов.
Контрольная работа за 2 триместр по геометрии в 7 классе
Тема: "Треугольник и окружность"
Вариант I
1). На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что 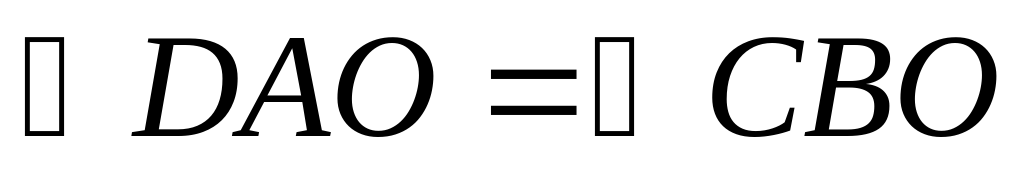 .
.
С


 А O
А O
В
D
2). Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АDВ =
АDВ =  АDС . Докажите, что АВ = АС .
АDС . Докажите, что АВ = АС .
3). В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5 : 2 . Найдите стороны треугольника.
Вариант II
1). На рисунке 1 отрезки МЕ и РК точкой D делятся пополам. Докажите, что  КМD =
КМD =  РЕD.
РЕD.


 М К
М К
D
 Р Е
Р Е
2). На сторонах угла D отмечены точки М и К так, что DМ = DК. Точка Р лежит внутри угла D и РК = РМ . Докажите, что луч DР – биссектриса угла МDК .
3). В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2 : 3 . Найдите стороны треугольника.
Контрольная работа за 3 триместр по геометрии в 7 классе
Тема: "Параллельные прямые"
Вариант I
1). Отрезки EF и PQ пересекаются в их середине М. Докажите, что РЕ // QF.
2). Отрезок DM – биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если 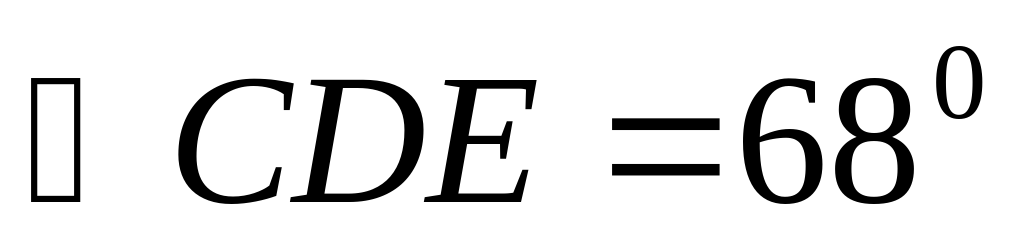 .
.
3). На рисунке АС // ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка CD.

 D
D
M

 A B
A B
C
Вариант II
1). Отрезки МN и ЕF пересекаются в их середине Р. Докажите, что ЕN // МF.
2). Отрезок AD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне FD и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если 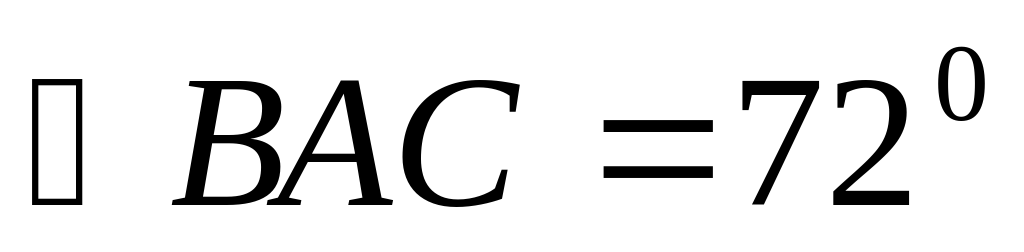 .
.
3). На рисунке AB // DC, АВ = DC. Докажите, что точка О – середина отрезков АС и ВD.
 В С
В С
Итоговая тестовая работа по геометрии 7 класс
Вариант - I
1
Найдите  АОВ.
АОВ.
1) 33º 2) 167º 3) 113º 4) 23º
В
.
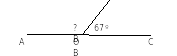
АК - биссектриса  ВАС.
ВАС.
ВК = КС.
По какому признаку равенства треугольников можно доказать, что Δ АВК = Δ АСК?
1) Первый признак 3) Третий признак
2) Второй признак 4) Ни один признак
неприменим
при
2.
3.
а
а ǀǀ b , с - секущая
 1 = 47º. Найдите:
1 = 47º. Найдите:  2,
2,  3,
3,  4,
4,  5.
5.
Ответ: 2 = ___,
2 = ___,  3 = __ ,
3 = __ ,  4 =___,
4 =___, 5 =___
5 =___
4
В
.
85º


Найдите градусную меру  А в Δ АВС.
А в Δ АВС.
1) 50º 2) 60º 3) 45º 4) 65º
?
35º
С
А

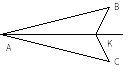
Δ АМС - прямоугольный, СК - биссектриса  С. По какому признаку равенства прямоугольных треугольников Δ МКС = Δ ЕКС?
С. По какому признаку равенства прямоугольных треугольников Δ МКС = Δ ЕКС?
1) по гипотенузе и острому углу
2) по двум катетам
3) по гипотенузе и катету
4) по катету и прилежащему углу
Е
А

5


К
. 


М
С
6. Периметр равнобедренного треугольника ΔАВС равен 35 см, одна из его сторон
относится к другой, как 1: 3. Найдите боковую сторону этого Δ АВС.
7. В прямоугольном ΔАВС катет АВ равен 3 см,  С = 15º. На катете отмечена точка D так,
С = 15º. На катете отмечена точка D так,
что  СВD = 15º. Найдите длину отрезка ВD.
СВD = 15º. Найдите длину отрезка ВD.
Вариант - II
1
К
Найдите  СОК.
СОК.
1) 34º 2) 46º 3) 44º 4) 156º
.

2
АМ - биссектриса  КАС.
КАС.
АК = АС.
По какому признаку равенства треугольников можно доказать, что Δ АКМ = Δ АСМ?
1) Первый признак 3) Третий признак
2) Второй признак 4) Ни один признак
неприменим
при
.
К

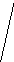
а
а ǀǀ b , с - секущая
 3 = 115º. Найдите:
3 = 115º. Найдите:  1,
1,  2,
2,  4,
4,  5.
5.
Ответ: 1 = ___,
1 = ___,  2 = ___ ,
2 = ___ ,  4 =___,
4 =___, 5 =___
5 =___
3
2
1

.

4
74º
Найдите градусную меру  F в Δ СМF.
F в Δ СМF.
1) 66º 2) 46º 3) 80º 4) 70º
М


.
36º
?
С
Е

5
В

В Δ АВС АК - биссектриса  А. По какому признаку равенства прямоугольных треугольников Δ АFК = Δ АНК?
А. По какому признаку равенства прямоугольных треугольников Δ АFК = Δ АНК?
1) по гипотенузе и катету
2) по катету и прилежащему углу
3) по гипотенузе и острому углу
4) по двум катетам
F




.


К


С
А
H

6. Периметр равнобедренного треугольника Δ МCD равен 26 см. Боковая сторона
треугольника меньше его основания на 5 см. Найдите основание этого Δ МCD .
7. В прямоугольном ΔСDE  Е = 15º. Точка К отмечена на катете DE так, что
Е = 15º. Точка К отмечена на катете DE так, что  ЕСК = 15º.
ЕСК = 15º.
Найдите длину отрезка СD, если КС = 8 см.
Критерии оценивания:
Оценка «5» − за верное решение 7 заданий;
Оценка «4» − за верное решение 6 заданий;
Оценка «3» − за верное решение 4-5 заданий;
Оценка «2» − если решено менее 4 заданий.
Ответы:
| задания | №1 | №2 | №3 | №4 | №5 | №6 | №7 |
|
В -1
| 3 | 2 | | 2 | 1 | 15 см | ВD =6см |
|
В -2
| 2 | 1 | | 4 | 3 | 12см | СD =4см |
Итоговая контрольная работа
по геометрии. 10 кл.
ВАРИАНТ 1.
-


 а Дано: а (АВС),
а Дано: а (АВС),


 М АВС – прямоугольный,
М АВС – прямоугольный,


 С= 90˚
С= 90˚


 В Доказать: МСВ -
В Доказать: МСВ -

 А прямоугольный.
А прямоугольный.
С
-
АВСDA1B1C1D1 – правильная призма. АВ = 6см, АА1= 8см.
Найти угол между прямыми АА1 и ВС; площадь полной поверхности призмы.
-
В правильной треугольной пирамиде сторона основания равна 2� �см, а высота равна 2 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах.
�см, а высота равна 2 см. Найти угол наклона бокового ребра к плоскости основания. Ответ запишите в градусах.
-
Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120˚ между ними. Наибольшая из площадей боковых граней равна 56 см2. Найти площадь полной поверхности призмы.
КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ 10 КЛАСС
УМК: Геометрия 10-11, Л.С. Атанасян, Ю.М. Колягин, «Просвещение», 2014г.
1 ПОЛУГОДИЕ
Темы: Расположение прямых в пространстве. Параллельность плоскостей в пространстве.
-
Основание АD трапеции ABCD лежит в плоскости 𝑎. Через точки В и С проведены параллельные прямые, пересекающие плоскость 𝑎 в точках E и F соответственно.
А) Каково взаимное расположение прямых EF и AB?
Б) Чему равен угол между прямыми EF и AB, если � �. Ответ обоснуйте.
�. Ответ обоснуйте.
-
Через точку О, лежащую между параллельными плоскостями � � , проведены прямые �
� , проведены прямые � �m и l. Прямая l пересекает плоскости �
�m и l. Прямая l пересекает плоскости � � в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найти длину отрезка А2 В2 если А1В1=12см, В1О:ОВ2 =3:4.
� в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найти длину отрезка А2 В2 если А1В1=12см, В1О:ОВ2 =3:4.
2 ПОЛУГОДИЕ
Темы: Многогранники. Углы между плоскостями.
-
Диагональ куба равна 6см. Найдите:
А) ребро куба
Б) косинус угла между диагональю куба и плоскостью одной из его граней.
-
Основание прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60⁰. Плоскость А D1 C1 составляет с плоскостью основания угол 60⁰. Найдите:
А) высоту ромба
Б) высоту параллелепипеда
В) площадь боковой поверхности параллелепипеда
Г)* площадь поверхности параллелепипеда.
КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ 11 КЛАСС
Темы: Цилиндр. Движения.
1 ПОЛУГОДИЕ
-
Дан куб ABCDA1B1C1D1. Найти угол между прямыми AD1 и ВМ, где М-середина ребра DD1.
-
Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь полной поверхности цилиндра.
-
При движении прямая а отображается на прямую а1, а плоскость � � на плоскость�
� на плоскость� �. Докажите, что если а║�
�. Докажите, что если а║� �, то а1║�
�, то а1║� �
�
2 ПОЛУГОДИЕ
Темы: Тела вращения и их объемы.
-
Высота конуса 6см, угол при вершине осевого сечения равен 120⁰. Найдите:
А) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 60⁰
Б) площадь боковой поверхности конуса.
-
Объем цилиндра равен 96π см3, площадь его осевого сечения равна 48см2. Найдите площадь сферы описанной около цилиндра.
КОНТРОЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ ЗА ГОД
Цель: Проверить умение применять полученные знания в курсе геометрии 11 класса на практике, при решении задач
-
Треугольник АВС – прямоугольный и равнобедренный с прямым углом С и гипотенузой 4 см. Отрезок СМ перпендикулярен плоскости треугольника и равен 2 см. найдите расстояние от точки М до прямой АВ.
-
Высота правильной четырехугольной пирамиды равна10 см и образует с боковым ребром угол 450. Найдите объем пирамиды.











 М К
М К
 D
D 
 В С
В С