Контрольная работа № 1
«Натуральные числа»
Вариант 1
Запишите цифрами число:
- пятьдесят пять миллиардов двести двадцать два миллиона девятьсот сорок одна тысяча восемьсот тридцать семь;
- семьсот два миллиона пятьдесят три тысячи одиннадцать:
- двадцать три миллиарда девять миллионов один.
Сравните числа: 1) 5 728 и 5 709; 2) 11 092 и 11 605.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 1, 5, 8, 9.
Начертите отрезок АK, длина которого равна 7 см 5 мм, отметьте на нём точку В. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка К принадлежит отрезку МЕ, МК = 19 см, отрезок КЕ на 17 см больше отрезка МК. Найдите длину отрезка МЕ.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 78*  3 784; 2) 5 8*5
3 784; 2) 5 8*5  5 872.
5 872.
Вариант 2
Запишите цифрами число:
- сорок семь миллиардов двести девяносто три миллиона восемьсот пятьдесят шесть тысяч сто двадцать четыре;
- триста семь миллионов семьдесят восемь тысяч двадцать три;
- восемьдесят пять миллиардов шесть миллионов пять.
Сравните числа: 1) 6 794 и 6 883; 2) 12 561 и 12 564.
Начертите координатный луч и отметьте на нём точки, соответствующие числам 3, 4, 6, 8.
Начертите отрезок АВ, длина которого равна 4 см 8 мм, отметьте на нём точку D. Запишите все отрезки, образовавшиеся на рисунке, и измерьте их длины.
Точка T принадлежит отрезку МN, МT = 19 см, отрезок TN на 18 см меньше отрезка МT. Найдите длину отрезка МN.
Запишите цифру, которую можно поставить вместо звёздочки, чтобы образовалось верное неравенство (рассмотрите все возможные случаи):
3 344  3 34*; 2) 2 724
3 34*; 2) 2 724  * 619.
* 619.
Контрольная работа № 2
«Сложение и вычитание натуральных чисел»
Вариант 1
Вычислите: 1) 11 225 + 196 283; 2) 28 420 455 – 12 497 653.
На одной стоянке было 53 автомобиля, что на 15 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?
Выполните сложение, выбирая удобный порядок вычислений:
(325 + 791) + 675; 2) 428 + 856 + 572 + 244.
Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎 = 249.
Вычислите:
4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.
Найдите значение выражения, выбирая удобный порядок вычислений:
(713 + 529) – 413; 2) 624 – (137 + 224).
Вариант 2
Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.
На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?
Выполните сложение, выбирая удобный порядок вычислений:
(624 + 571) + 376; 2) 212 + 497 + 788 + 803.
Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.
Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
Вычислите:
6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
Контрольная работа № 3
«Уравнение. Угол. Многоугольники»
Вариант 1
Постройте угол ABC, величина которого равна 158 . Проведите произвольно луч КM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч КM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 11 = 38 2) 135 - 𝑥 = 76.
Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.
Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.
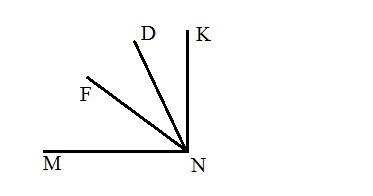
Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73 , ∠KNF = 48
, ∠KNF = 48 . Вычислите градусную меру угла DNF.
. Вычислите градусную меру угла DNF.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
64 – (𝑎 – 𝑥) = 17 было число 16?
Вариант 2
Постройте угол NMC, величина которого равна 58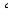 . Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
Решите уравнение: 1) 𝑥 + 53 = 97 2) 142 – 𝑥 = 76.
Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.
Решите уравнение: 1) (58 + 𝑥) – 23 = 96 2) 54 – (𝑥 – 19) = 35.
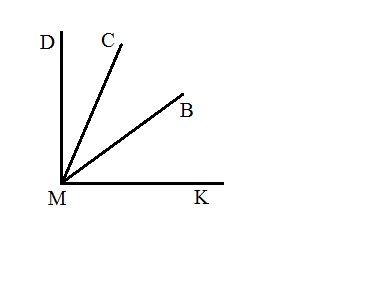
Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51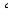 , ∠KMC = 65
, ∠KMC = 65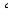 . Вычислите градусную меру угла BMC.
. Вычислите градусную меру угла BMC.
Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(𝑎 – 𝑥) – 14 = 56 было число 5?
Контрольная работа № 4
«Умножение и деление натуральных чисел. Свойства умножения»
Вариант 1
Вычислите:
15 ∙ 418; 3) 1 456 : 28;
275 ∙ 1204; 4) 177 000 : 120.
Найдите значение выражения: (326 ∙ 48 – 9 587) : 29
Решите уравнение:
𝑥 ∙ 14 = 364; 2) 324 : 𝑥 = 9; 3) 19𝑥 - 12𝑥 = 126.
В школьную столовую завезли 8 одинаковых ящиков яблок и 6 одинаковых ящиков апельсинов. Сколько килограммов апельсинов было в одном ящике, если всего было 114 кг яблок и апельсинов, а яблок в каждом ящике было 9 кг?
От одной пристани одновременно в одном направлении отплыли лодка и катер. Лодка плыла со скоростью 14 км/ч, а катер – 21 км/ч. Какое расстояние будет между ними через 5 ч после начала движения?
Вариант 2
Вычислите:
32 ∙ 1 368; 3) 1 664 : 26;
145 ∙ 306; 4) 216 800 : 160.
Найдите значение выражения: (625 ∙ 25 – 8 114) : 37.
Решите уравнение:
𝑥 ∙ 22 = 396; 2) 312 : 𝑥 = 8; 3) 19𝑥 - 7𝑥 = 144
В автомобиль погрузили 5 одинаковых мешков сахара и 3 одинаковых мешка муки. Оказалось, что общая масса груза равна 370 кг. Какова масса одного мешка муки, если масса одного мешка сахара равна 50 кг?
Из одного города одновременно в одном направлении выехали два автомобиля. Один из них двигался со скоростью 74 км/ч, а второй – 68 км/ч. Какое расстояние будет между автомобилями через 4 ч после начала движения?
Сколькими нулями оканчивается произведение всех натуральных чисел от 23 до 42 включительно?
Контрольная работа № 5
«Прямоугольник. Прямоугольный параллелепипед.
Комбинаторные задачи»
Вариант 1
Выполните деление с остатком: 478 : 15.
Найдите площадь прямоугольника, одна сторона которого равна 14 см, а вторая сторона в 3 раза больше первой.
Вычислите объем и площадь поверхности куба с ребром 3 см.
Длина прямоугольного параллелепипеда равна 18 см, ширина – в 2 раза меньше длины, а высота – на 11 см больше ширины. Вычислите объем параллелепипеда.
Поле прямоугольной формы имеет площадь 6 га. Ширина поля 150 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 5, 6 и 0 (цифры не могут повторяться).
Вариант 2
Выполните деление с остатком: 376 : 18.
Найдите площадь прямоугольника, одна сторона которого равна 21 см, а вторая сторона в 3 раза меньше первой.
Вычислите объем и площадь поверхности куба с ребром 4 дм.
Ширина прямоугольного параллелепипеда равна 6 см, длина – в 5 раз больше ширины, а высота – на 5 см меньше длины. Вычислите объем параллелепипеда.
Поле прямоугольной формы имеет площадь 3 га, его длина – 200 м. Вычислите периметр поля.
Запишите все трёхзначные числа, для записи которых используются только цифры 0, 9 и 4 (цифры не могут повторяться).
Контрольная работа № 6
«Обыкновенные дроби»
Вариант 1
Сравните числа:
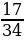 и
и 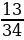 ; 2)
; 2) 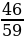 и 1; 3)
и 1; 3) 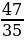 и 1.
и 1.
Выполните действия:
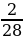 +
+ 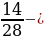
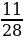 ; 3)
; 3) 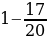 ;
;
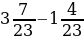 + 5
+ 5 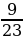 ; 4)
; 4) 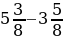 .
.
В саду растёт 72 дерева, из них 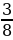 составляют яблони. Сколько яблонь растёт в саду?
составляют яблони. Сколько яблонь растёт в саду?
Кирилл прочёл 56 страниц, что составило 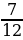 книги. Сколько страниц было в книге?
книги. Сколько страниц было в книге?
Преобразуйте в смешанное число дробь:
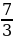 ; 2)
; 2) 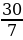 .
.
Каково наибольшее натуральное значение n, при котором верно неравенство n 
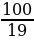 ?
?
Вариант 2
Сравните числа:
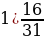 и
и 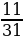 ; 2)
; 2) 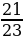 и 1; 3)
и 1; 3) 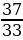 и 1.
и 1.
Выполните действия:
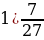 +
+ 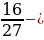
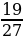 ; 3)
; 3) 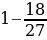 ;
;
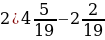 + 7
+ 7 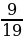 ; 4)
; 4) 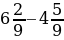 .
.
В пятых классах 64 ученика, из них 3/16 составляют отличники. Сколько отличников в пятых классах?
Ваня собрал 16 вёдер картофеля, что составляет 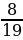 всего урожая. Сколько вёдер картофеля составляет урожай?
всего урожая. Сколько вёдер картофеля составляет урожай?
Преобразуйте в смешанное число дробь:
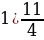 ; 2)
; 2) 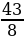
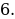 Каково наименьшее натуральное значение n, при котором верно неравенство n
Каково наименьшее натуральное значение n, при котором верно неравенство n 
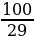 ?
?
Контрольная работа № 7
«Десятичные дроби»
Вариант 1
Сравните: 1) 14,396 и 14,3956; 2) 2,157 и 2, 6565.
Округлите: 1) 16,728 до десятых; 2) 5,1864 до тысячных.
Выполните действия: 1) 3,87 + 32,496; 2) 23,7 – 16,48; 3) 20 – 12,345.
Скорость катера по течению реки равна 24,2 км/ч, а собственная скорость катера – 22,8 км/ч. Найдите скорость катера против течения реки.
Одна сторона треугольника равна 5,6 см, что на 1,4 см больше второй стороны и на 0,7 см меньше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 5,74 и меньше 5,76.
Вариант 2
Сравните: 1) 19,497 и 17,5; 2) 0,346 и 0, 3468.
Округлите: 1) 10,86 до десятых; 2) 0,3823 до тысячных.
Выполните действия: 1) 62 + 44,289; 2) 25,3 – 15,52; 3) 40 – 14,265.
Скорость катера против течения реки равна 18,6 км/ч, а собственная скорость
катера – 19,8 км/ч. Найдите скорость катера по течению реки.
Одна сторона треугольника равна 4,5 см, что на 3,3 см меньше второй стороны и на 0,6 см больше третьей. Найдите периметр треугольника.
Напишите три числа, каждое из которых больше 3,82 и меньше 3,84.
Контрольная работа № 8
«Умножение и деление десятичных дробей»
Вариант 1
Вычислите:
2,024 ∙ 4,5; 3) 5,86 : 100; 5) 0,72 : 0,8;
2,41 ∙ 100; 4) 4 : 16; 6) 9,1 : 0,07.
Найдите значение выражения: (7 – 4,6) ∙ 4,3 + 1,08 : 1,2.
Решите уравнение: 2,4 (𝑥 + 0,98) = 4,08.
Моторная лодка плыла 1,4 ч по течению реки и 2,2 ч против течения. Какой путь преодолела лодка за всё время движения, если скорость течения равна 1,7 км/ч, а собственная скорость лодки – 19,8 км/ч?
Если в некоторой десятичной дроби перенести запятую вправо через одну цифру, то она увеличится на 14,31. Найдите эту дробь.
Вариант 2
Вычислите:
1,036 ∙ 3,5; 3) 3,68 : 1000; 5) 0,56 : 0,7;
37,53 ∙ 10; 4) 5 : 25; 6) 5,2 : 0,04.
Найдите значение выражения: (8 – 3,8) ∙ 3,4 + 1,12 : 1,6.
Решите уравнение: 0,084 : (6,2 – 𝑥) = 1,2.
Катер плыл 1,6 ч против течения реки и 2,4 ч по течению. На сколько больше проплыл катер, двигаясь по течению реки, чем против течения, если скорость течения реки равна 2,1 км/ч, а собственная скорость катера – 28,2 км/ч?
Если в некоторой десятичной дроби перенести запятую влево через одну цифру, то она уменьшится на 23,76. Найдите эту дробь.
Контрольная работа № 9
«Среднее арифметическое. Проценты»
Вариант 1
Найдите среднее арифметическое чисел: 2,8; 16,9; 22
Площадь поля равна 420 га. Рожью засеяли 15 % поля. Сколько гектаров поля засеяли рожью?
Петя купил книгу за 90 р., что составляет 30 % всех денег, которые у него были. Сколько денег было у Пети?
Катер плыл 1,5 ч со скоростью 34 км/ч и 2,5 ч со скоростью 30 км/ч. Найдите среднюю скорость катера на всём пути.
Турист прошёл за три дня 48 км. В первый день он прошёл 35 % всего маршрута. Путь пройденный в первый день, составляет 80 % расстояния , пройденного во второй день. Сколько километров прошёл турист в третий день?
В первый день Петя прочитал 40 % всей книги, во второй – 60 % остального, а в третий - оставшиеся 144 страницы. Сколько всего страниц в книге?
Вариант 2
Найдите среднее арифметическое чисел: 3,9; 6; 9,18; 15,8
Площадь парка равна 40 га. Площадь озера составляет 15 % площади парка. Найдите площадь озера.
Насос перекачал в бассейн 42 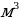 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
Черепаха ползла 2 ч со скоростью 15,3 м/ч и 3 ч со скоростью 12, 4 м/ч. Найдите среднюю скорость черепахи на всём пути.
Токарь за три дня изготовил 80 деталей. В первый день он выполнил 30 % всей работы. Известно, что количество деталей, изготовленных в первый день, составляет 60 % количества деталей , изготовленных во второй день. Сколько деталей изготовил токарь в третий день?
В первый день турист прошёл 20% всего пути, во второй – 60 % остального, а в третий – оставшиеся 24 км. Найдите длину пути, который прошёл турист за три дня.
Контрольная работа № 10
«Итоговая контрольная работа
за курс математики 5 класса»
Вариант 1
Найдите значение выражения: (134 – 15,97): 29 + 4,24∙ 35
Миша шёл из одного села в другое 0,7 ч по полю и 0,9 ч через лес, пройдя всего 5,31 км. С какой скоростью шёл Миша через лес, если по полю он двигался со скоростью 4,5 км/ч?
Решите уравнение: (46 - х) ∙ 19 = 418 16,4 – 5,4х = 14,78.
Ширина прямоугольного параллелепипеда равна 4 см, что составляет 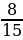 его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.
Среднее арифметическое четырёх чисел равно 1,4, а среднее арифметическое трёх других чисел – 1,75. Найдите среднее арифметическое этих семи чисел.
Вариант 2
Найдите значение выражения: (4,4 – 0,63 :1,8) ∙ 0,8
Автомобиль ехал 0,9 ч по асфальтированной дороге и 0,6 ч по грунтовой, проехав всего 93,6 км. С какой скоростью двигался автомобиль по асфальтированной дороге, если по грунтовой он ехал со скоростью 48 км/ч?
Решите уравнение: 25а – 7а – 9 = 279 7,2𝑥 – 5,4𝑥 + 0,55 = 1
Ширина прямоугольного параллелепипеда равна 4,8 см, что составляет 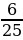 его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.
Среднее арифметическое трёх чисел равно 2,5, а среднее арифметическое двух других чисел – 1,7. Найдите среднее арифметическое этих пяти чисел.





 3 784; 2) 5 8*5
3 784; 2) 5 8*5  . Проведите произвольно луч КM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
. Проведите произвольно луч КM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.

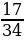 и
и 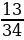 ; 2)
; 2) 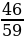 и 1; 3)
и 1; 3) 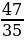 и 1.
и 1.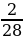 +
+ 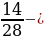
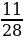 ; 3)
; 3) 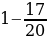 ;
;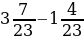 + 5
+ 5 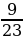 ; 4)
; 4) 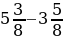 .
.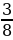 составляют яблони. Сколько яблонь растёт в саду?
составляют яблони. Сколько яблонь растёт в саду?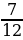 книги. Сколько страниц было в книге?
книги. Сколько страниц было в книге?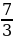 ; 2)
; 2) 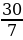 .
.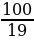 ?
?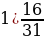 и
и 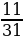 ; 2)
; 2) 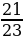 и 1; 3)
и 1; 3) 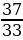 и 1.
и 1.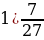 +
+ 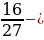
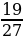 ; 3)
; 3) 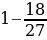 ;
;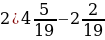 + 7
+ 7 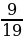 ; 4)
; 4) 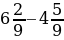 .
.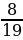 всего урожая. Сколько вёдер картофеля составляет урожай?
всего урожая. Сколько вёдер картофеля составляет урожай?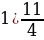 ; 2)
; 2) 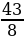
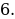 Каково наименьшее натуральное значение n, при котором верно неравенство n
Каково наименьшее натуральное значение n, при котором верно неравенство n 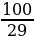 ?
?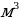 воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.
воды, что составляет 60 % объёма бассейна. Найдите объём бассейна.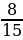 его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 40 % длины. Вычислите объем параллелепипеда.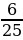 его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.
его длины, а высота составляет 45 % длины. Вычислите объем параллелепипеда.









