Конус 11 класс Геометрия

ОБЪЕМ КОНУСА

Теорема. Объем конуса равен одной третьей произведения площади его основания на высоту.

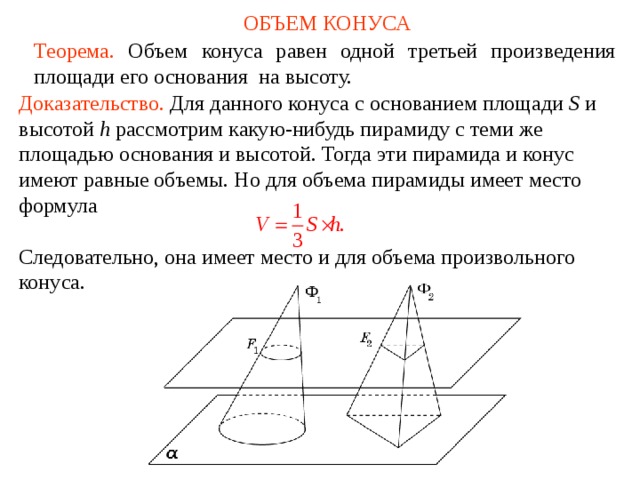
Доказательство. Для данного конуса с основанием площади S и высотой h рассмотрим какую-нибудь пирамиду с теми же площадью основания и высотой. Тогда эти пирамида и конус имеют равные объемы. Но для объема пирамиды имеет место

формула

Следовательно, она имеет место и для объема произвольного конуса.

В режиме слайдов ответы и решения появляются после кликанья мышкой

ОБЪЕМ КОНУСА

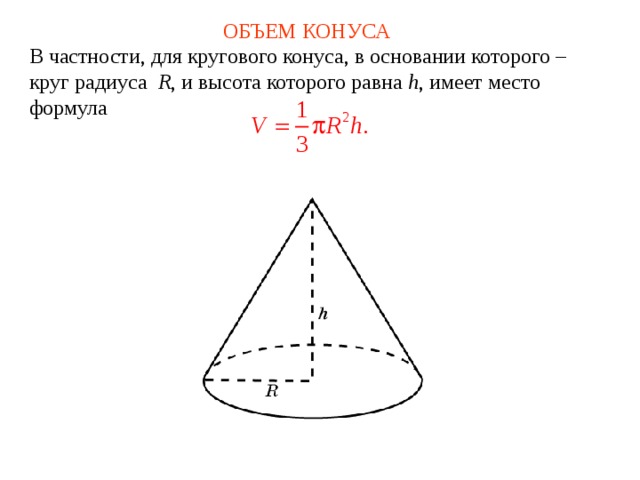
В частности, для кругового конуса, в основании которого – круг радиуса R , и высота которого равна h , имеет место формула

В режиме слайдов ответы и решения появляются после кликанья мышкой

ОБЪЕМ УСЕЧЕННОГО КОНУСА

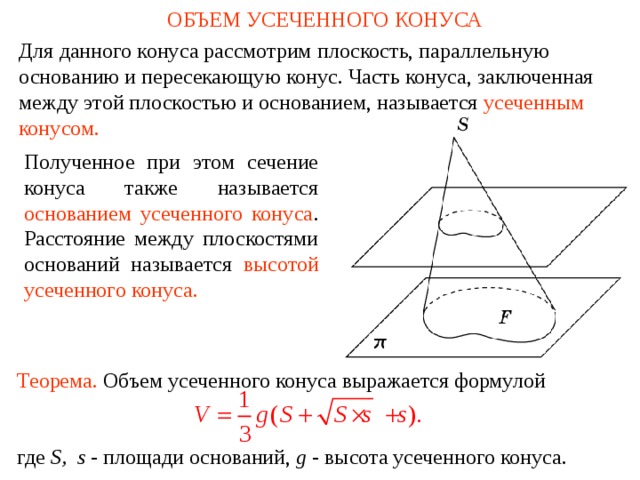
Для данного конуса рассмотрим плоскость, параллельную основанию и пересекающую конус. Часть конуса, заключенная между этой плоскостью и основанием, называется усеченным конусом.

Полученное при этом сечение конуса также называется основанием усеченного конуса . Расстояние между плоскостями оснований называется высотой усеченного конуса.

В режиме слайдов ответы и решения появляются после кликанья мышкой

Теорема. Объем усеченного конуса выражается формулой

где S , s - площади оснований, g - высота усеченного конуса.

ОБЪЕМ УСЕЧЕННОГО КОНУСА

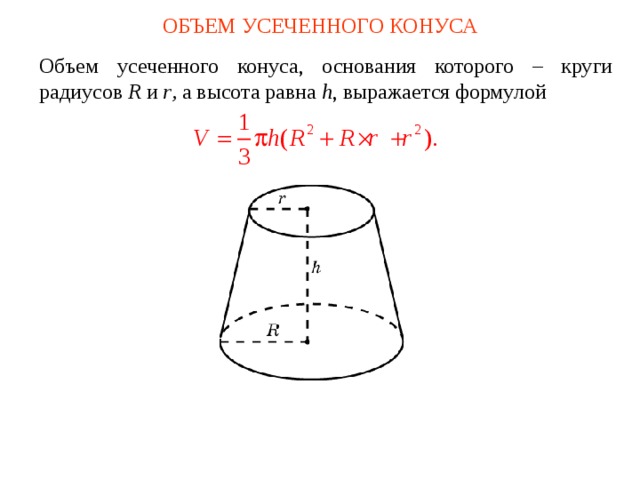
Объем усеченного конуса, основания которого – круги радиусов R и r , а высота равна h , выражается формулой

В режиме слайдов ответы и решения появляются после кликанья мышкой

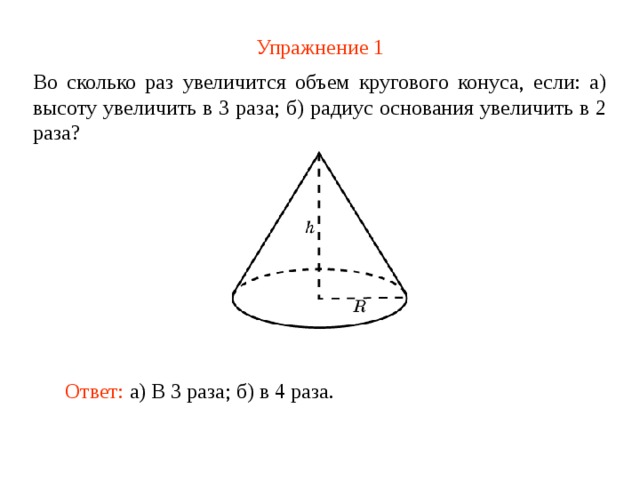
Упражнение 1

Во сколько раз увеличится объем кругового конуса, если: а) высоту увеличить в 3 раза; б) радиус основания увеличить в 2 раза?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: а) В 3 раза; б) в 4 раза.

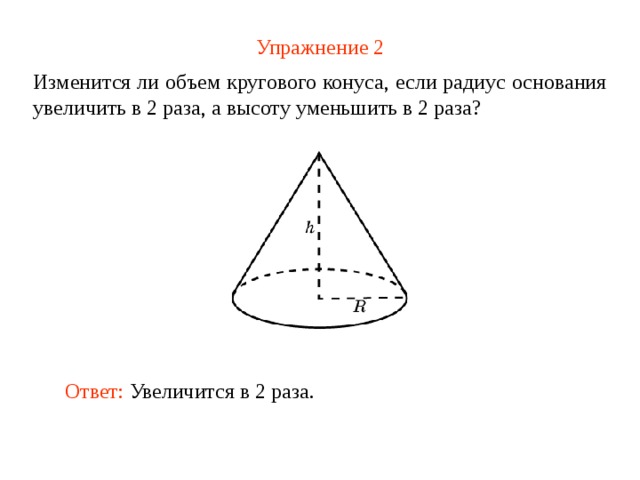
Упражнение 2

Изменится ли объем кругового конуса, если радиус основания увеличить в 2 раза, а высоту уменьшить в 2 раза?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: Увеличится в 2 раза.

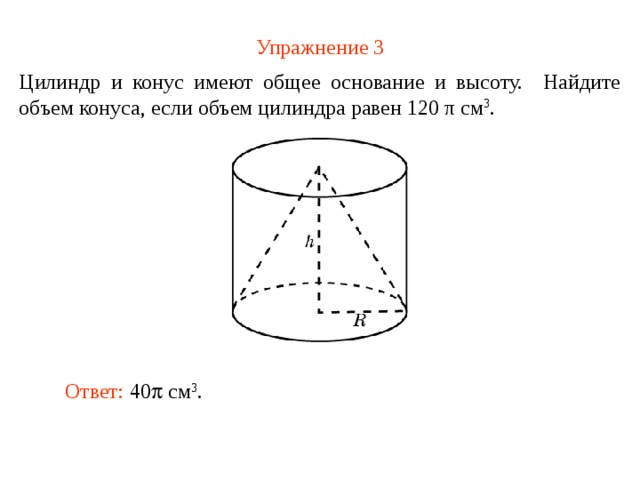
Упражнение 3

Цилиндр и конус имеют общее основание и высоту. Найдите объем конуса, если объем цилиндра равен 120 π см 3 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 40  см 3 .

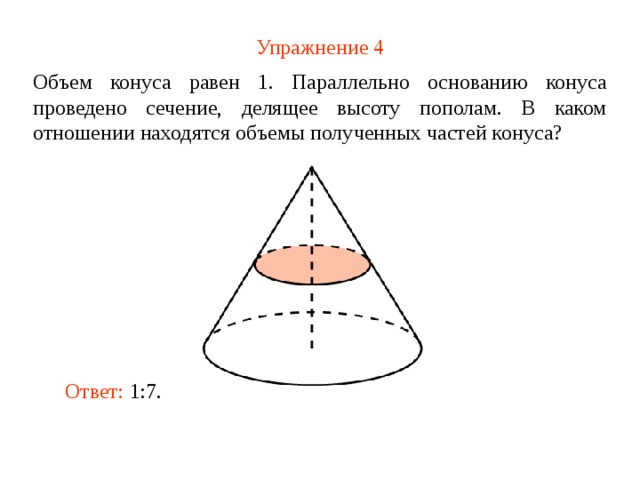
Упражнение 4

Объем конуса равен 1 . Параллельно основанию конуса проведено сечение, делящее высоту пополам. В каком отношении находятся объемы полученных частей конуса?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 1 :7 .

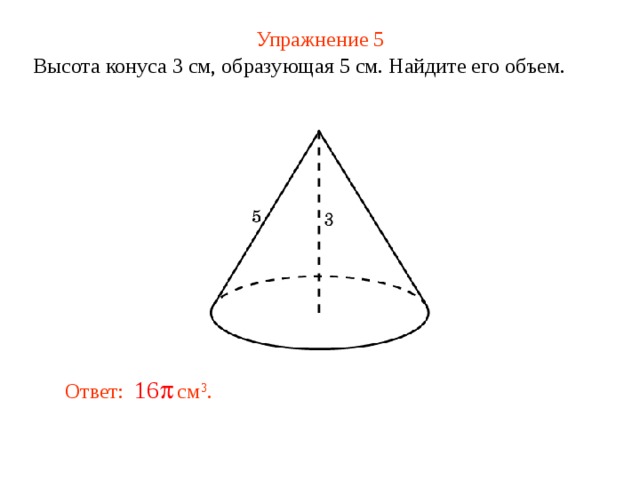
Упражнение 5

Высота конуса 3 см, образующая 5 см. Найдите его объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

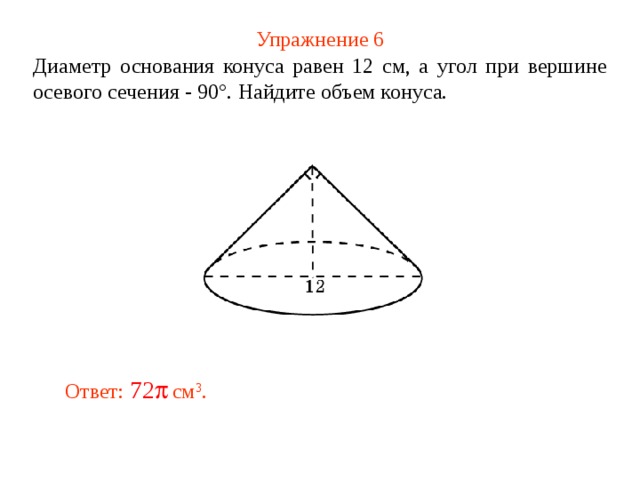
Упражнение 6

Диаметр основания конуса равен 12 см, а угол при вершине осевого сечения - 90°. Найдите объем конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

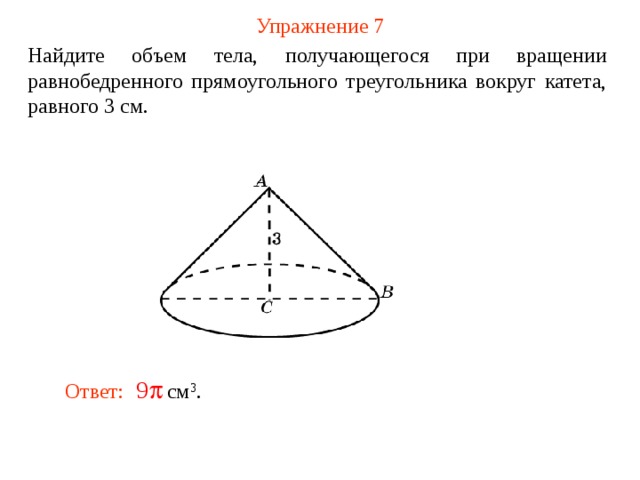
Упражнение 7

Найдите объем тела, получающегося при вращении равнобедренного прямоугольного треугольника вокруг катета, равного 3 см.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

11

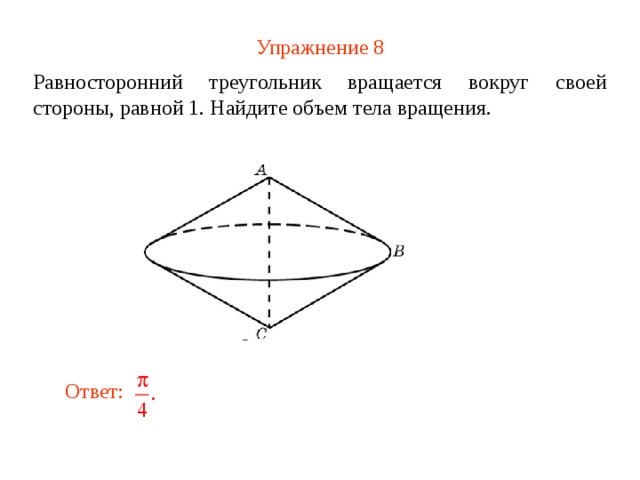
Упражнение 8

Равносторонний треугольник вращается вокруг своей стороны , равной 1 . Найдите объем тела вращения.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

12

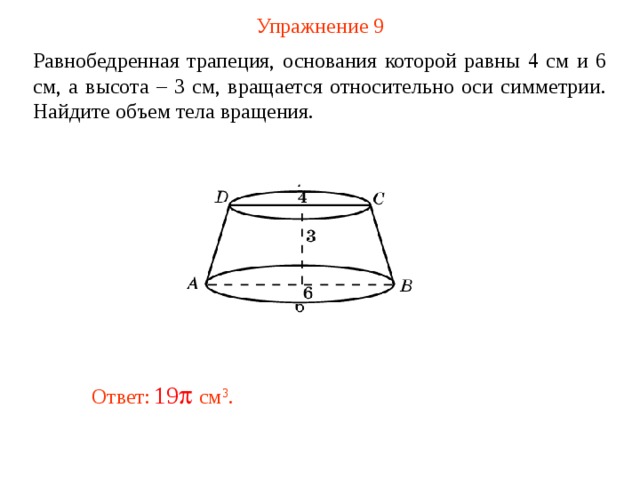
Упражнение 9

Равнобедренная трапеция, основания которой равны 4 см и 6 см, а высота – 3 см, вращается относительно оси симметрии. Найдите объем тела вращения.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

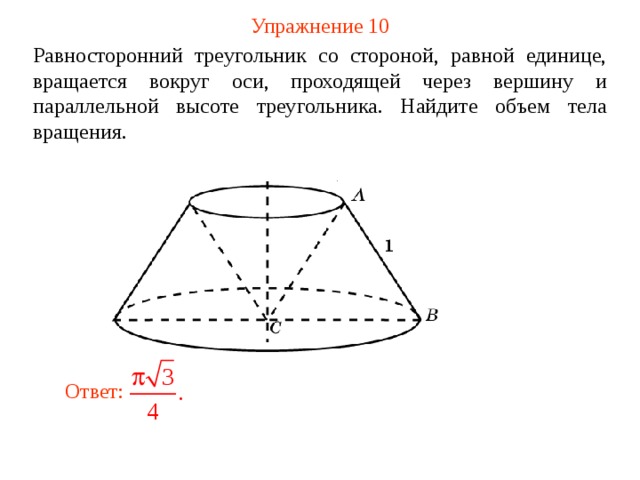
Упражнение 10

Равносторонний треугольник со стороной, равной единице, вращается вокруг оси, проходящей через вершину и параллельной высоте треугольника. Найдите объем тела вращения.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

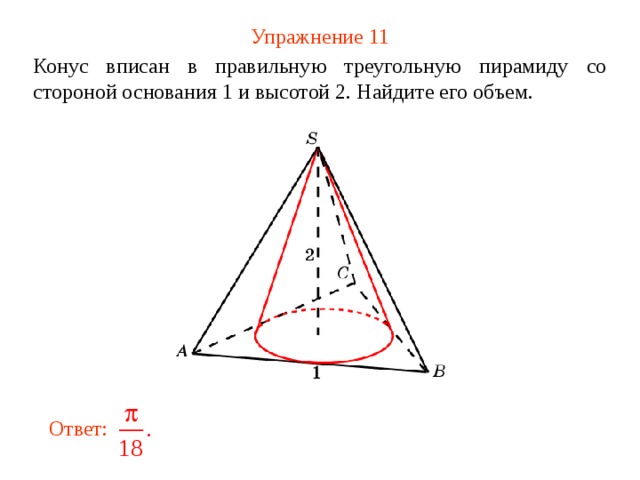
Упражнение 11

Конус вписан в правильную треугольную пирамиду со стороной основания 1 и высотой 2 . Найдите его объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

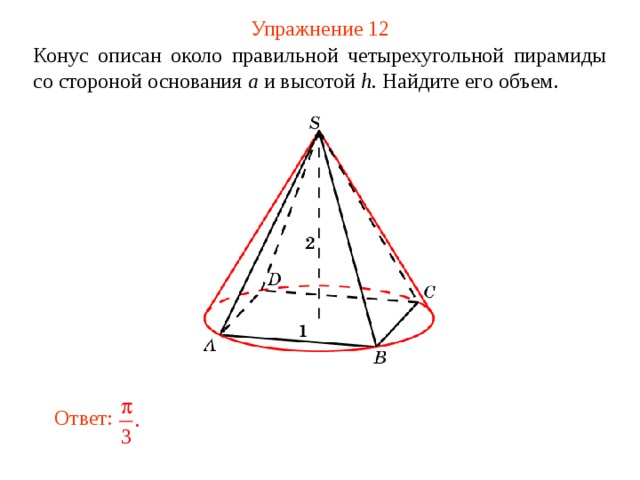
Упражнение 12

Конус описан около правильной четырехугольной пирамиды со стороной основания a и высотой h . Найдите его объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

16

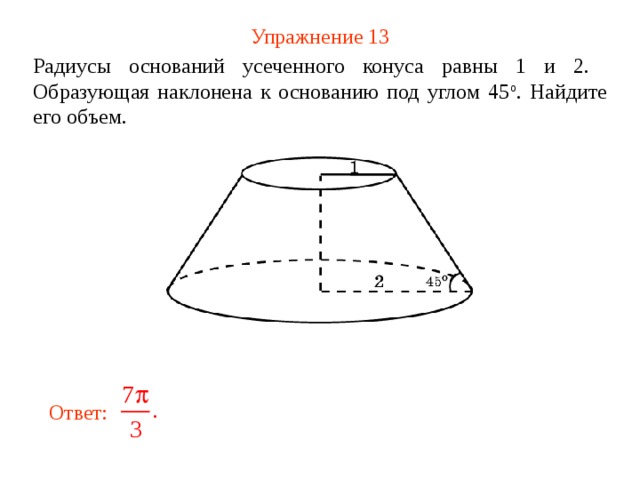
Упражнение 13

Радиусы оснований усеченного конуса равны 1 и 2 . Образующая наклонена к основанию под углом 45 о . Найдите его объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

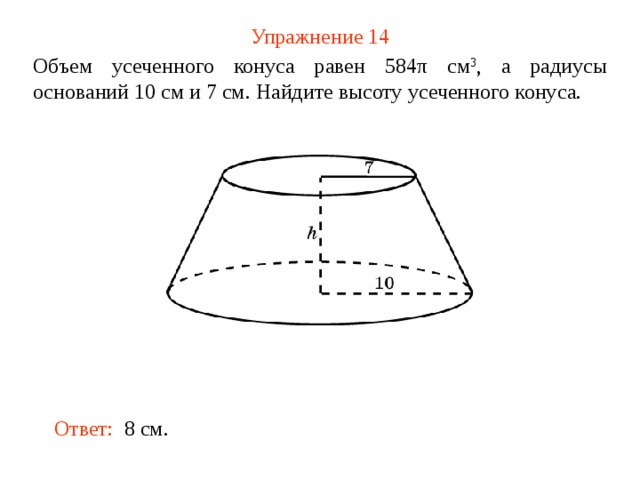
Упражнение 14

Объем усеченного конуса равен 584 π см 3 , а радиусы оснований 10 см и 7 см. Найдите высоту усеченного конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 8 см.

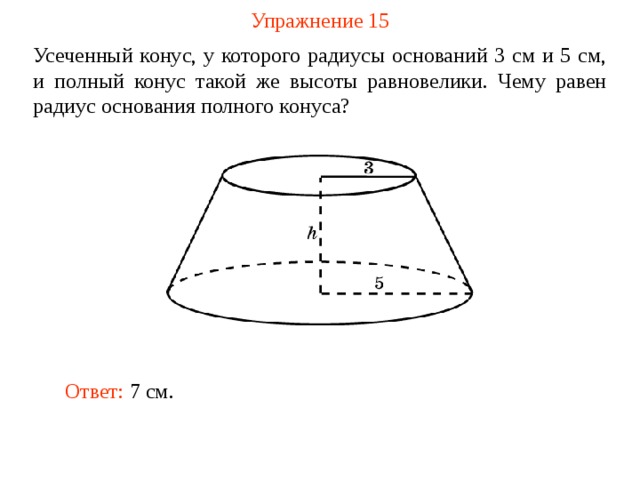
Упражнение 15

Усеченный конус, у которого радиусы оснований 3 см и 5 см, и полный конус такой же высоты равновелики. Чему равен радиус основания полного конуса?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 7 см.

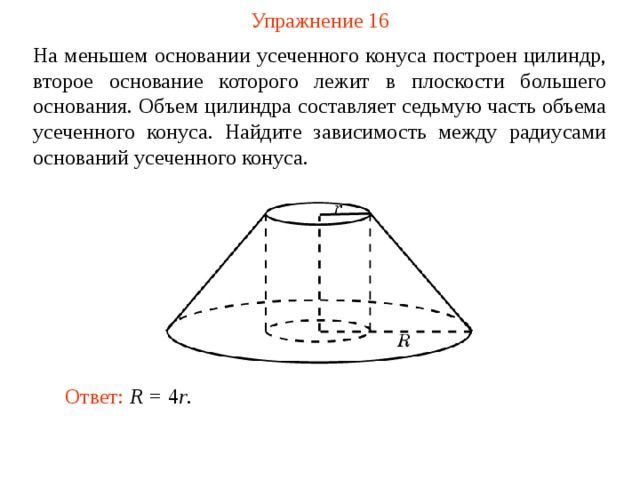
Упражнение 16

На меньшем основании усеченного конуса построен цилиндр, второе основание которого лежит в плоскости большего основания. Объем цилиндра составляет седьмую часть объема усеченного конуса. Найдите зависимость между радиусами оснований усеченного конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: R = 4 r .

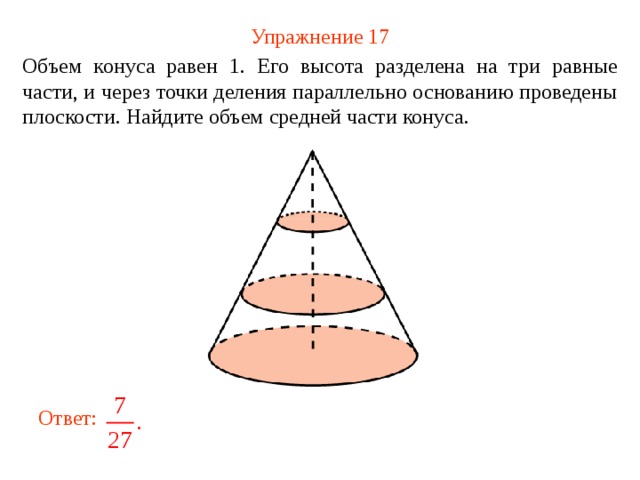
Упражнение 17

Объем конуса равен 1 . Его высота разделена на три равные части, и через точки деления параллельно основанию проведены плоскости. Найдите объем средней части конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

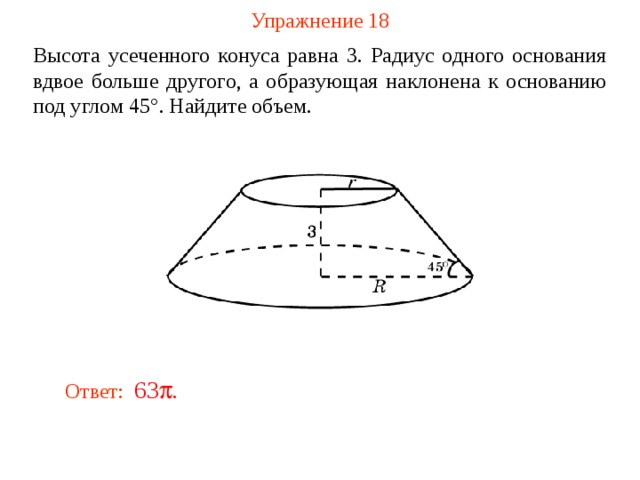
Упражнение 18

Высота усеченного конуса равна 3. Радиус одного основания вдвое больше другого, а образующая наклонена к основанию под углом 45°. Найдите объем.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

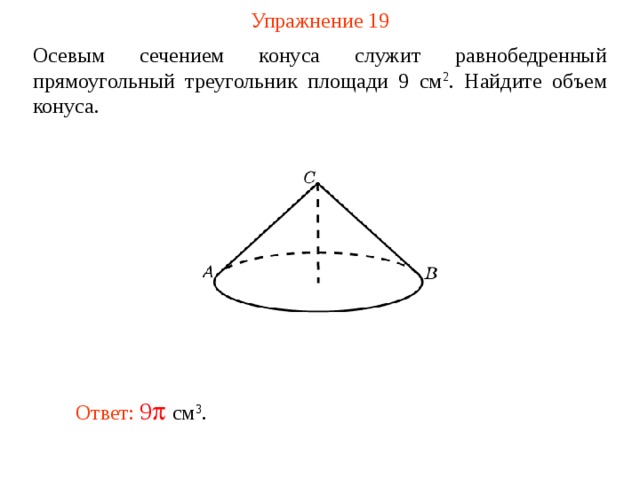
Упражнение 19

Осевым сечением конуса служит равнобедренный прямоугольный треугольник площади 9 см 2 . Найдите объем конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: см 3 .

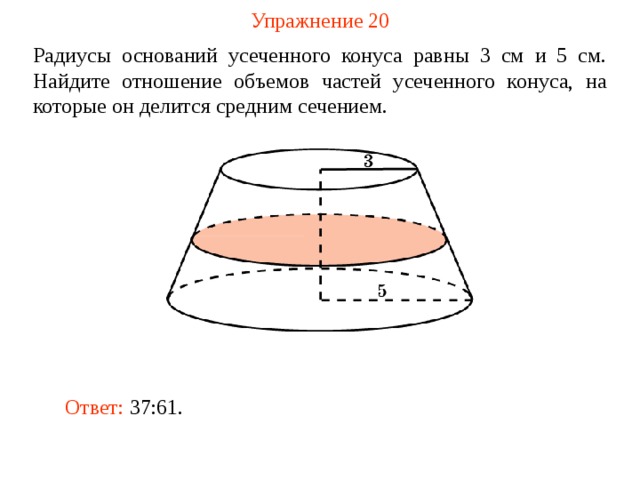
Упражнение 20

Радиусы оснований усеченного конуса равны 3 см и 5 см. Найдите отношение объемов частей усеченного конуса, на которые он делится средним сечением.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: 37:61.

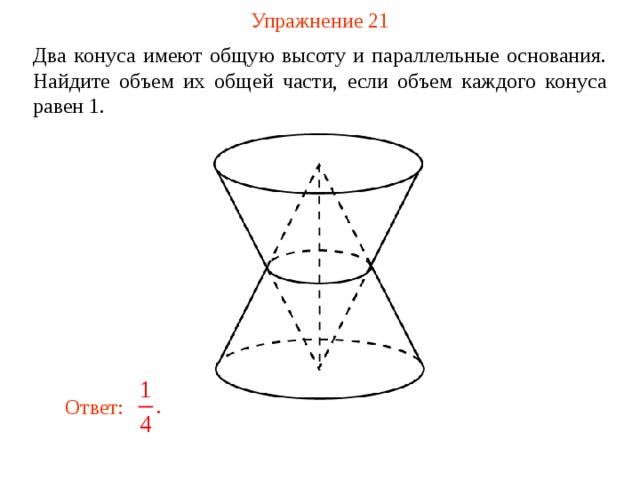
Упражнение 21

Два конуса имеют общую высоту и параллельные основания. Найдите объем их общей части, если объем каждого конуса равен 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

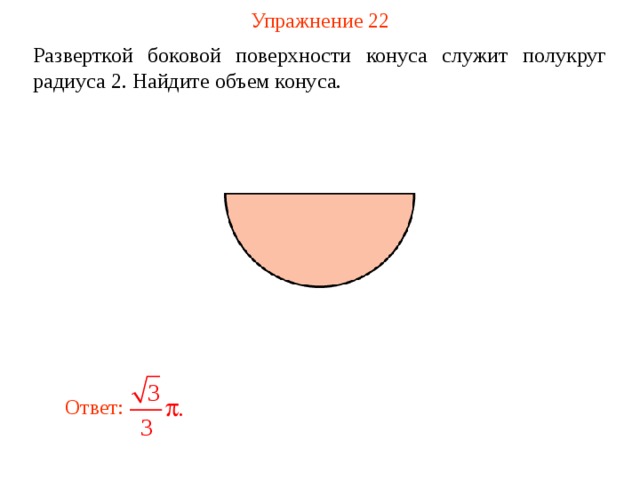
Упражнение 22

Разверткой боковой поверхности конуса служит полукруг радиуса 2. Найдите объем конуса.

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

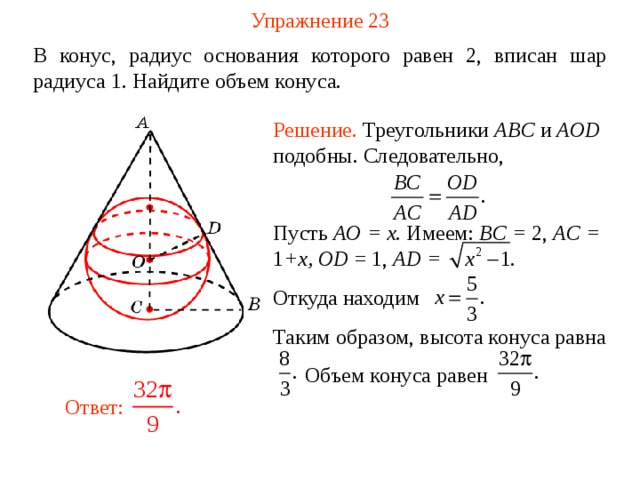
Упражнение 23

В конус, радиус основания которого равен 2, вписан шар радиуса 1. Найдите объем конуса.

Решение. Треугольники ABC и AOD подобны. Следовательно,

Пусть AO = x . Имеем: BC = 2, AC = 1 +x, OD = 1, AD =

Откуда находим

Таким образом, высота конуса равна

Объем конуса равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ:

27

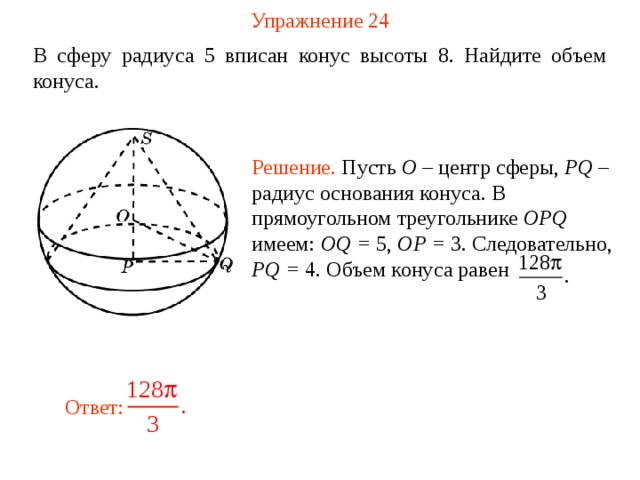
Упражнение 2 4

В сферу радиуса 5 вписан конус высоты 8. Найдите объем конуса.

Решение. Пусть O – центр сферы, PQ – радиус основания конуса. В прямоугольном треугольнике OPQ имеем: OQ = 5, OP = 3. Следовательно, PQ = 4. Объем конуса равен

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: