Координаты и конфигурации планет

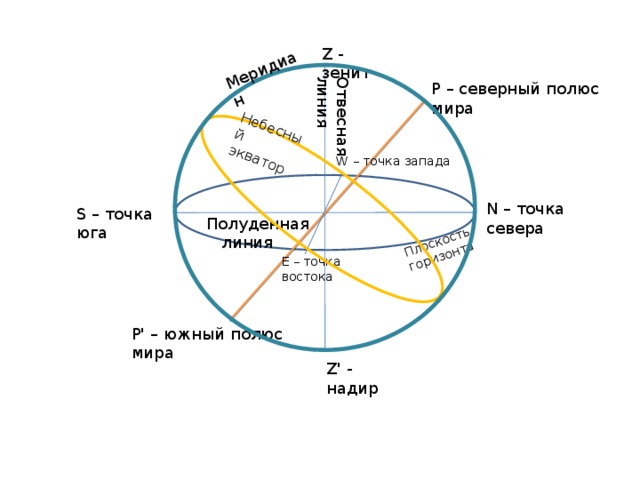
Плоскость горизонта

Отвесная линия

Меридиан

Небесный экватор

Z - зенит

Р – северный полюс мира

W – точка запада

N – точка севера

S – точка юга

Полуденная линия

E – точка востока

Р' – южный полюс мира

Z' - надир

Z

Р

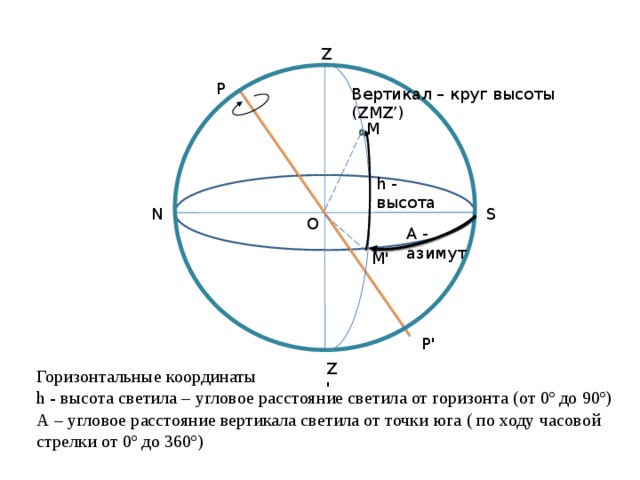
Вертикал – круг высоты (ZMZ’)

М

h - высота

N

S

О

А - азимут

М'

Р'

Z'

Горизонтальные координаты h - высота светила – угловое расстояние светила от горизонта (от 0º до 90º) А – угловое расстояние вертикала светила от точки юга ( по ходу часовой стрелки от 0º до 360º)

Q'

Р

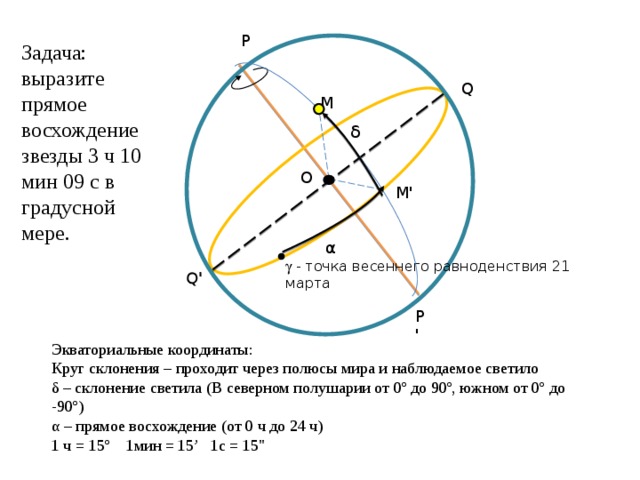
Задача: выразите прямое восхождение звезды 3 ч 10 мин 09 с в градусной мере.

Q

М

δ

О

М'

α

 - точка весеннего равноденствия 21 марта

Р'

Экваториальные координаты: Круг склонения – проходит через полюсы мира и наблюдаемое светило δ – склонение светила (В северном полушарии от 0º до 90º, южном от 0º до -90º) α – прямое восхождение (от 0 ч до 24 ч) 1 ч = 15º 1мин = 15’ 1с = 15"

Исторические линии

Гиппарх Птолемей

Гиппарх ввел сферическую карту звездного неба как систему координат, широту и долготу, поправки на сферичность, эпициклические и деферентные поправки.....составил первую полную карту неба из 850 звезд, которая стала основой астрологии и основой для Альмагеста Птолемея.

Геоцентрическая картина мира

Геоцентрическая картина мира К. Птолемея, основанная на представлении о движении небесных тел относительно Земли, находящейся в центре мира. Особенностью данной модели было движение Солнца по круговой орбите, а планет по сложным орбитам, состоящим из большого круга (деферента), по которому перемещался цент малого круга (эпицикла), по которому и двигалась сама планета.

Никола́й Копе́рник - польский астроном, математик, экономист, каноник. Наиболее известен как автор гелиоцентрической системы мира, положившей начало первой научной революции. Потеряв 9-летним ребёнком отца и оставшись на попечении дяди по матери, каноника Луки ( Lucas ) Ватценроде (Ватцельроде), Коперник в 1491 году поступил в Краковский университет, где с одинаковым усердием изучал математику, медицину и богословие, но особенно его привлекала астрономия. По окончании университета (1494) Коперник не получил никакого учёного звания, и семейный совет решил, что ему предстоит духовная карьера. Веским доводом в пользу такого выбора было то, что дядя - покровитель как раз был возведен в сан епископа. Для продолжения образования Коперник уехал в Италию (1497) и поступил в Болонский университет. Помимо богословия, права и древних языков, он имел там возможность заниматься и астрономией. Небезынтересно отметить, что одним из профессоров в Болонье был тогда Сципион дель Ферро, с открытий которого началось возрождение европейской математики. Тем временем, благодаря стараниям дяди, в Польше Коперника заочно избрали каноником в епархии Вармии. В 1500 году Коперник оставил университет, вновь не получив никакого диплома или звания, и переехал в Рим. Затем, после кратковременного пребывания на родине, уехал в Падуанский университет и продолжил изучение медицины. В 1503 году Коперник наконец завершил своё образование, сдал в Ферраре экзамены, получил диплом и учёную степень доктора канонического права. Он не спешил возвращаться и, с разрешения дяди-епископа, следующие три года занимался медициной в Падуе. В 1506 году Коперник получил известие, возможно, надуманное, о болезни дяди. Он покинул Италию и возвратился на родину. Следующие 6 лет он провёл в епископском замке Гейльсберг, занимаясь астрономическими наблюдениями и преподаванием в Кракове. Одновременно он врач, секретарь и доверенное лицо дяди Лукаса Ватценроде (Ватцельроде). Уже в 1500-е годы замысел новой астрономической системы сложился у него вполне ясно. Он начал писать книгу с описанием новой модели мира, обсуждая свои идеи с друзьями, среди которых немало его единомышленников (например, Тидеман Гизе, епископ Кульмский). В эти годы (примерно 1503—1512) Коперник распространял среди друзей рукописный конспект своей теории ( «Малый комментарий о гипотезах, относящихся к небесным движениям» ), а его ученик Ретик опубликовал ясное изложение гелиоцентрической системы в 1539 году. По-видимому, слухи о новой теории широко разошлись уже в 1520-х годах. Работа над главным трудом продолжалась почти 40 лет, Коперник постоянно вносил в неё уточнения, готовил новые астрономические расчётные таблицы.

Николай Коперник

19 февраля 1473, Торунь — 24 мая 1543, Фромборк

De revolutionibus orbium coelestium («Об обращении небесных сфер»).

Нюрнберг, 1543 год

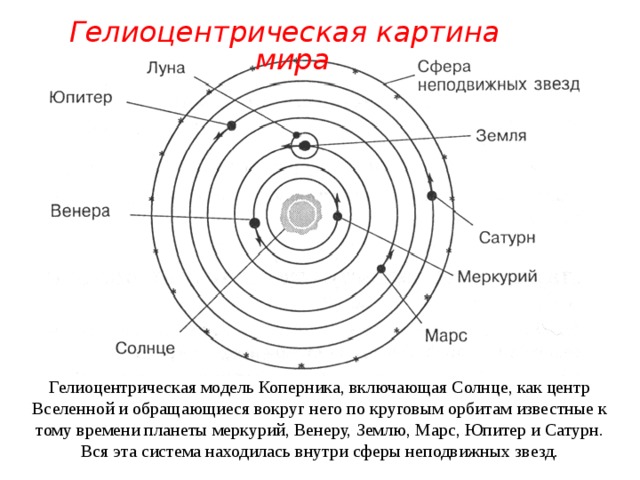
Гелиоцентрическая картина мира

Гелиоцентрическая модель Коперника, включающая Солнце, как центр Вселенной и обращающиеся вокруг него по круговым орбитам известные к тому времени планеты меркурий, Венеру, Землю, Марс, Юпитер и Сатурн. Вся эта система находилась внутри сферы неподвижных звезд.

Ти́хо Бра́ге - датский астроном, астролог и алхимик эпохи Возрождения. Первым в Европе начал проводить систематические и высокоточные астрономические наблюдения, на основании которых Кеплер вывел законы движения планет. Ураниборг  — храм астрономии. Тихо назвал свою обсерваторию « Ураниборг » («Замок Урании ») в честь музы астрономии Урании; часто это название переводят как «Небесный замок». Браге сам составил проект сооружения, прототипом которого, как полагают историки, послужила одна из работ знаменитого итальянского архитектора Андреа Палладио , с которой Браге ознакомился во время путешествия по Италии. В плане замок представлял собой квадрат со стороной около 18 метров, точно ориентированный по сторонам света.

Ти́хо Бра́ге

14 декабря 1546, Кнудструп, Дания (ныне территория Швеции) — 24 октября 1601, Прага)

23 мая 1576 года специальным указом датско-норвежского короля Фредерика II Тихо Браге был пожалован в пожизненное пользование остров Вен ( Hven ), расположенный в проливе Эресунн в 20 км от Копенгагена.

Были выделены значительные суммы на постройку обсерватории и её содержание. Это было первое в Европе здание, специально построенное для астрономических наблюдений (ландграф Вильгельм использовал в качестве обсерватории одну из башен своего замка). В личной беседе король выразил уверенность, что своими трудами Тихо Браге «прославит страну, короля и самого себя».

Система мира Тихо Браге, которую условно можно назвать гео-гелиоцентрической. «Я полагаю, что старое птолемеево расположение небесных сфер было недостаточно изящным, и что допущение такого большого количества эпициклов… следует считать излишним… В то же время я полагаю, что недавнее нововведение великого Коперника… делает это, не нарушая математических принципов. Однако тело Земли велико, медлительно и непригодно для движения… Я без всяких сомнений придерживаюсь того мнения, что Земля, которую мы заселяем, занимает центр Вселенной, что соответствует общепринятым мнениям древних астрономов и натурфилософов, что засвидетельствовано выше Священным Писанием, и не кружится в годичном обращении, как желал Коперник».

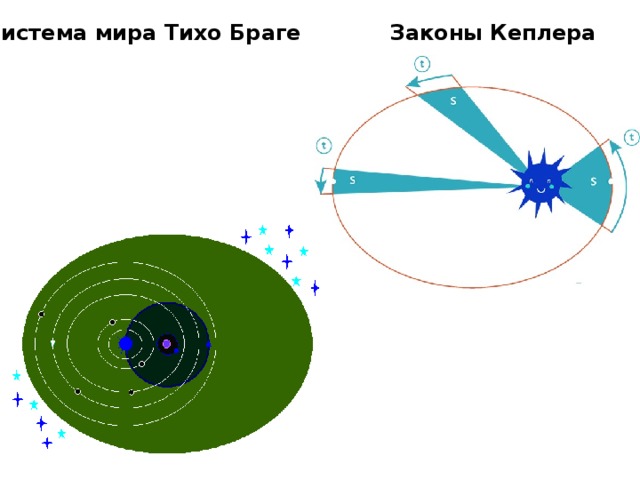
Система мира Тихо Браге

Законы Кеплера

Ио́ганн Ке́плер - немецкий математик, астроном, оптик и астролог. В 1589 году Кеплер закончил школу при монастыре Маульбронн, обнаружив выдающиеся способности. Городские власти назначили ему стипендию для помощи в дальнейшем обучении. В 1591 году поступил в университет в Тюбингене — сначала на факультет искусств, к которым тогда причисляли и математику с астрономией, затем переходит на теологический факультет. Здесь он впервые услышал об идеях Николая Коперника о гелиоцентрической системе мира и сразу стал их приверженцем. Первоначально Кеплер планировал стать протестантским священником, но благодаря незаурядным математическим способностям был приглашён в 1594 году читать лекции по математике в университете города Граца (ныне в Австрии).

Иоганн Кеплер

27 .12.1571 года, Вайль-дер-Штадт - 15 .12.1630 года, Регенсбург) 

«Любезный читатель!

В этой книжке я вознамерился доказать, что всеблагой и всемогущий Бог при сотворении нашего движущегося мира и при расположении небесных орбит избрал за основу пять правильных тел, которые со времен Пифагора и Платона и до наших дней снискали столь громкую славу, выбрал число и пропорции небесных орбит, а также отношения между движениями выбрал в соответствии с природой правильных тел.»

В Граце вышла в свет (1596) его первая книга «Тайна мира». В ней Кеплер попытался найти тайную гармонию Вселенной, для чего сопоставил орбитам пяти известных тогда планет (сферу Земли он выделял особо) различные «платоновы тела» (правильные многогранники).

В 1600 году Кеплер прибывает в Прагу. Проведённые здесь 10 лет — самый плодотворный период его жизни. В 1604 году Кеплер публикует свои наблюдения сверхновой, называемой теперь его именем.

В 1610 году Галилей сообщает Кеплеру об открытии спутников Юпитера. Кеплер встречает это сообщение недоверчиво и в полемической работе «Разговор со Звёздным вестником» приводит несколько юмористическое возражение: «непонятно, к чему быть [спутникам], если на этой планете нет никого, кто бы мог любоваться этим зрелищем»

1 и 2 законы Кеплера были сформулированы в 1609 году в книге «Новая астрономия»

(осторожности ради, он относил их только к Марсу).

В 1618 году Кеплер открывает третий закон : отношение куба среднего удаления планеты от Солнца к квадрату периода обращения её вокруг Солнца есть величина постоянная для всех планет: a³/T² = const .

Этот результат Кеплер публикует в завершающей книге «Гармония мира»,

причём применяет его уже не только к Марсу, но и ко всем прочим планетам (включая, естественно, и Землю), а также к галилеевым спутникам.

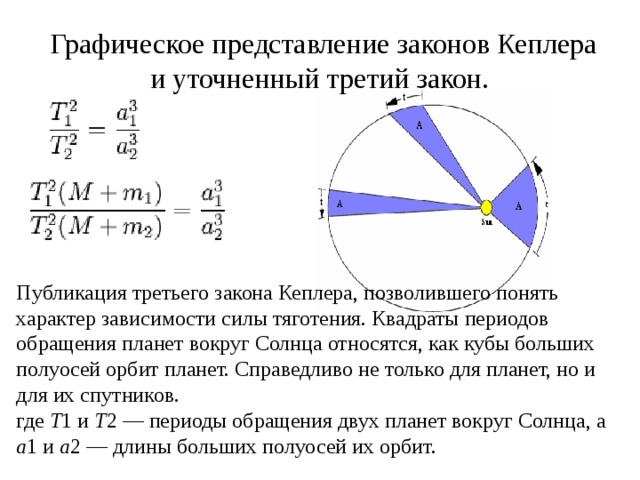
Графическое представление законов Кеплера и уточненный третий закон.

Публикация третьего закона Кеплера, позволившего понять характер зависимости силы тяготения. Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников. где T 1 и T 2 — периоды обращения двух планет вокруг Солнца, а a 1 и a 2 — длины больших полуосей их орбит.

Закон всемирного тяготения

Гравитация

В канун Рождества 1664 года на лондонских домах стали появляться красные кресты — первые метки Великой эпидемии чумы.

8 августа 1665 года занятия в Тринити-колледже были прекращены и персонал распущен до окончания эпидемии.

Но существенную часть своих научных открытий Ньютон сделал в уединении «чумных лет». Из сохранившихся заметок видно, что 23-летний Ньютон уже свободно владел базовыми методами дифференциального и интегрального исчислений, включая разложение функций в ряды и то, что впоследствии было названо формулой Ньютона-Лейбница. Проведя ряд остроумных оптических экспериментов, он доказал, что белый цвет есть смесь цветов.

Но самым значительным его открытием в эти годы стал закон всемирного тяготения .

28 апреля 1686 года первый том «Математических начал» был представлен Королевскому обществу. Выход этой книги ознаменовал переход к формированию науки современного типа.

Все три тома, после некоторой авторской правки, вышли в 1687 году. Тираж (около 300 экземпляров) был распродан за 4 года — для того времени очень быстро. На основе изложенных там интегрального и дифференциального исчислений строились все теоретические последующие модели физических явлений.

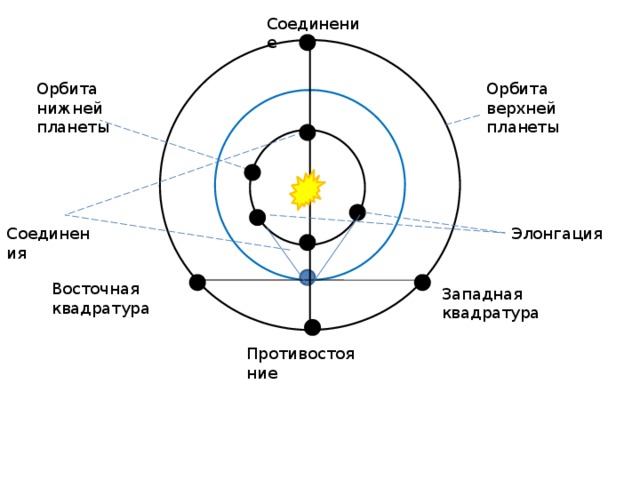
Соединение

Орбита верхней планеты

Орбита нижней планеты

Элонгация

Соединения

Восточная квадратура

Западная квадратура

Противостояние

Промежуток времени в течение которого планета совершает полный оборот вокруг Солнца по орбите называется сидерическим (звездным) периодом (Т) . Промежуток времени между двумя одинаковыми конфигурациями планеты называется синодическим периодом (S) Задача: Как часто происходят противостояния Марса, сидерический период которого 1,9 года?

Определение географической широты

Отвесная линия

Ось мира

Ось Земли

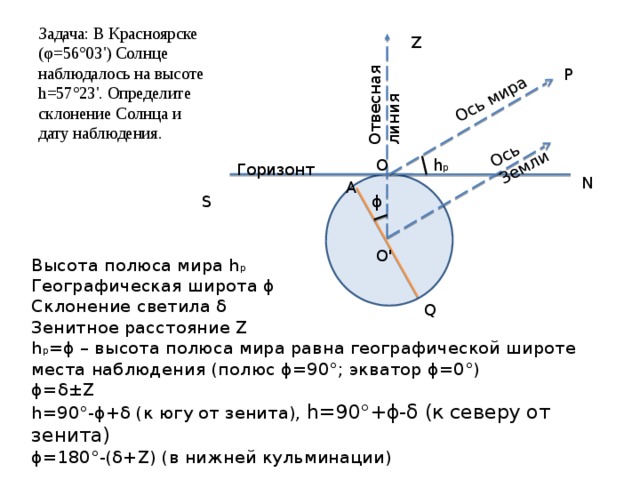
Задача: В Красноярске (φ=56°03') Солнце наблюдалось на высоте h=57°23'. Определите склонение Солнца и дату наблюдения.

Z

P

O

h p

Горизонт

N

A

ϕ

S

O'

Высота полюса мира h p Географическая широта ϕ Склонение светила δ Зенитное расстояние Z h p =ϕ – высота полюса мира равна географической широте места наблюдения (полюс ϕ=90°; экватор ϕ=0°) ϕ=δ±Z h=90°-ϕ+δ (к югу от зенита), h=90°+ϕ-δ (к северу от зенита) ϕ=180°-(δ+Z) (в нижней кульминации)

Q

Момент верхней кульминации Солнца – истинный полдень Момент нижней кульминации Солнца – истинная полночь Промежуток времени между двумя одноименными кульминациями – истинные солнечные сутки Среднее время на гринвичском меридиане (нулевой пояс) - всемирное время Т 0 Время с географической долготой λ - местное время Т λ Т λ =Т 0 +λ каждый часовой пояс n отличается на 1ч или 15° Поясное время находится: T n =T 0 +n