| № этапа | Этапы занятия, учебные вопросы, формы и методы обучения | Временная регламентация этапа |
| 1 | Организационный этап: | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подготовить обучающихся к работе на уроке. СОДЕРЖАНИЕ – взаимные приветствия, фиксация отсутствующих, проверка внешнего состояния аудитории и готовности обучающихся к занятию, организация внимания. |
|
|
| - Сообщение правил заполнения листа самоанализа: | № | Вид работы | Баллы | | 1 | Устная работа(проверка домашнего задания) |
| | 2 | Письменная работа |
| | 3 | Работа в подгруппах(парах) |
| | 4 | Самостоятельная работа |
| | ИТОГО |
|
| Критерий оценивания: | Оценка | Баллы | | 5 | 12 и более | | 4 | 7-10 | | 3 | 3-6 | | 2 | 0-2 |
|
|
| 2. | Этап проверки домашнего задания | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить правильность и осознанность выполнения домашнего задания всеми обучающимися, установить в ходе проверки обнаруженные пробелы в знаниях, совершенствую при этом знания, умения, навыки. |
|
|
| Содержание: карточки с заданиями |
|
|
| Математический диктант. Вариант 1 Сколько чисел надо указать, чтобы задать положение точки в пространстве? (три) Как называется первое из чисел, задающих положение точки в пространстве? (абсцисса) Как называется третье из чисел, задающих положение точки в пространстве? (аппликата) Запишите обозначение точки Р, если её абсцисса равна 0, а ордината 5, аппликата 0. Где лежит точка Р? (Р (0; 5; 0), на оси ординат) Чему равна ордината точки А (- 1; - 4; 1)? (- 4) Вариант 2 Как называются числа, задающие положение точки в пространстве? (абсцисса и ордината, аппликата) Сколько чисел надо указать, чтобы задать положение точки в пространстве? (три) Как называется второе из чисел, задающих положение точки на координатной плоскости? (ордината) Запишите обозначение точки С, если её абсцисса равна 6, а ордината 0, аппликата 0. Где лежит точка С? (С (6; 0; 0), на оси абсцисс) Чему равна аппликата точки М(-2; - 3; 0)? (0)
|
|
|
| | Количество правильных ответов | Баллы | | Менее 4 | 0 | | 5 | 1 | | 8 | 2 |
|
|
| 3 | Этап подготовки обучающихся к активному и сознательному усвоению материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – организовать и направить на достижение цели познавательную деятельность обучающихся, постановка целей учебной деятельности. |
|
|
| «За всю историю человечества пока не найдено лучшего способа развития интеллектуальных и творческих способностей человека , чем при помощи математики» Владимир Тихомиров, профессор МГУ. |
|
|
| Сообщение темы, цели и задач материала Какую тему созвучную с темой нашего урока Вы изучали в школе? Какое ключевое слово определяют эти две темы? (Координаты). Координаты на плоскости и в пространстве можно вводить бесконечным числом различных способов. Решая геометрическую, физическую, химическую задачу можно использовать различные координатные системы: прямоугольную, полярную, цилиндрическую, сферическую. (Показ моделей кристаллической решётки поваренной соли)В общеобразовательном курсе изучается прямоугольная система координат на плоскости и в пространстве. Иначе её называют Декартовой системой координат по имени французского ученого философа Рене Декарта (1596 – 1650) впервые введшего координаты в геометрию.) |
|
| 4 | Этап усвоения новых знаний | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – дать обучающимся конкретное представление об изучаемых фактах, явлениях, основной идее изучаемого материала; добиться от обучающихся восприятия, осознания, первичного обобщения и систематизации новых знаний, усвоения обучающимися способов, путей, средств получения знаний, оперирования ими. |
|
|
| Содержание: |
|
| 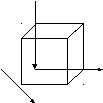
| У Декарта имелись лишь далекие намеки на возможность распространения метода координат с двумерного пространства (плоскости) на трехмерное. Потребовалось ещё почти 100 лет, чтобы идея пространственных координат была сформирована, постоянно и и широко использовалась. z - Что представляет собой система координат в Аz Ayz пространстве? Система координат в пространстве представляет Axz A собой три взаимно перпендикулярные прямые х, y, z, пересекающиеся в одной точке. О – начало отсчета, О Ау у x, y, z – координатные оси, Ax Axy xy, yz, xy – координатные плоскости. x Координатные плоскости делят все пространство на 8 октантов.
- Как определяются координаты точки А ? Через точку А проведем плоскость, параллельную плоскости yz. Она пересекает ось x в точке Аx . Координатой х точки А называется число, равное по абсолютной величине длине отрезка ОАх . Аналогично определяются и другие координаты. Таким образом, точке А в пространстве ставится в соответствие тройка чисел – её координаты. Обозначение: А(x; y; z). (Название координаты z найти самостоятельно). Рассмотрим координаты частного расположения точек в пространстве. Ах (х;0;0) Ахy (х;y;0) О (0;0;0) Где находятся данные точки? Аy (0;y;0) Аyz (0;y;z) Аz (0;0;z) Ахz (х;0;z)
|
|
| | ДИНАМИЧЕСКАЯ ПАУЗА | 5 |
|
|  | 20 |
|
| Пусть отрезок АВ имеет концы А(х1; у1) и В(х2; у2) и пусть М(х0; у0) — середина отрезка АВ (рис. 133), тогда MD — средняя линия трапеции с основаниями х1 и х2, МС — средняя линия трапеции с основаниями у1 и у2. По свойству средней линии трапеции имеем: 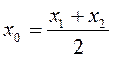 , , 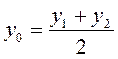 . . 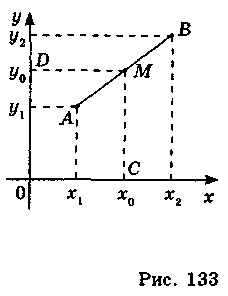 Задача на повторение. Найдите координаты середины отрезка АВ и длину отрезка АВ, если: 1 вариант – А (3;-1), В (-2;4) 2 вариант – А (3;4), В (2; -1) (Проверку работ осуществить на боковых досках).
Аналогичные формулы для координат середины отрезка применяют в пространстве. Решение: Обозначим в пространстве точки A, B и С – середину отрезка AB. Пусть А(х1; у1; z1) и В(х2; у2; z2) и пусть С(х; у; z) Координаты точки C находятся, как полусумма координат концов отрезка AB - точек A и B. Найдем координаты точки С: 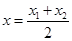 , , 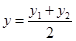 , , 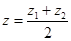 . . 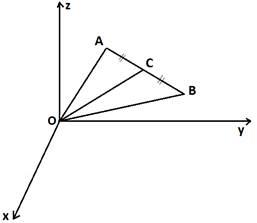
Задача №1. Дано: А (1;-1;2), В (3;1;-2) Найдите координаты середины отрезка АВ. Решение: Пусть С – середина отрезка АВ, тогда С (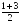 ; ; 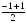 ; ; 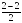 ), С (2;0;0) ), С (2;0;0) Формулы для нахождения координат конца отрезка В(х2; у2; z2) по известным координатам середины С(х; у; z) и другого конца отрезка А(х1; у1; z1): х2 =2х-х1; у2 =2у-у1; z2 =2z-z1 Задача №2. Дано: С– середина отрезка АВ, С(2; 6; -4), А(4; 2; 0). Найдите координаты точки В, длину отрезка АВ (Ответ. В(0; 10; -8)) Эти формулы вы должны научиться применять в разных задачах, связанных с серединой отрезка. Давайте вспомним, где встречается понятие “середина”. Это: 1. Медиана треугольника (делит сторону пополам) 2. Средняя линия треугольника и средняя линия трапеции (соединяет середины сторон) 3. Точка пересечения диагоналей параллелограмма (делит диагонали пополам) 4. Центр окружности (середина диаметра) Задача №3. (решаем на три варианта) В треугольнике АВС А(3;-1;1), В(-5;3;1), С(1;5;3). Найти координаты точки М, если: 1 вариант АМ1 – медиана. М1 (-2;4;2) 2 вариант ВМ2 – медиана. М2 (2;-2;2) 3 вариант СМ3 – медиана. М3 (-1;1;1) Проверка оперативная. Задача №4. Докажите, что четырехугольник АВСD является параллелограммом, если координаты вершин А(2;1;3), В(1;0;7), С(-2;1;5), D(-1;2;1) (Середина О(0;1;4)) Задача №5. В трапеции АВСD проведена средняя линия MN. Найти координаты точек А и N, если В(-6;-2; 2), С(-1;-4;2), D(13;2;4), М(-4;3;4) MN средняя линия трапеции АВСD  АМ = МВ и DN = NC АМ = МВ и DN = NC Ответ: А(-2;8;6), N(6;-1;3)
|
|
| 5 | Этап проверки понимания обучающимися материала | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить осмыслили ли обучающиеся связи и отношения фактов, содержание новых понятий, закономерностей, устранить обнаруженные пробелы. |
|
|
| Используя записи в тетради и учебник, назвать основные вопросы и формулы по данной теме |
|
|
| Критерий оценивания: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
|
|
| 6 | Этап закрепления нового материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – закрепить у обучающихся знания и умения, необходимые для самостоятельной работы по новому материалу. |
|
|
| Самостоятельная работа. 1. Найдите координаты середины отрезка АВ, если: а) А (– 6; 2;0), В (-4; 4; -8); б) А (– 5; – 4; 6), В (– 1; 2; 0). 2. Проверьте, является ли точка М (4; 2) серединой отрезка АВ, если: а) А (3; – 1, 4) В (5; 5; -6); б) А (3; 6; 7) В (– 5; – 2; 1). 3. Определите координаты центра окружности, диаметром которой является отрезок АВ, если А (4; – 2; 12), В (1; 3; -8). |
|
|
| Критерий оценивания учащихся отвечающих у доски: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
Критерий оценивания учащихся решающих на месте: (выполнив задание, учащийся поднимает руку и показывает решение примера. В соответствии с критерием оценивания получает баллы за работу.) | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 3 | | 2 | 2 | | 3 | 1 | | 4 и более | 0 |
|
|
| 7 | Рефлексия учебной деятельности | 3 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – формирование у обучающихся умения анализировать результаты своей учебной деятельности. |
|
|
| обсуждение и оценка результатов самостоятельной работы (рефлексия в письменной форме) | Что нового Вы сегодня узнали? |
| | Своей работой на уроке Вы довольны? | Доволен /не доволен | | Ваше настроение после урока | Стало лучше / стало хуже | | Материал урока Вам был | Понятен / не понятен |
|
|
| 8 | Этап информации обучающихся о домашнем задании, инструктаж по его выполнению: | 7 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подвести итоги и выставить оценки, сообщить обучающимся о домашнем задании, разъяснить методику его выполнения. |
|
|
|
|
|
|
|
|
|
|
| И если есть самостоятельная работа, то задания и форма контроля самостоятельной работы |
|
|
|
| 90 |
Преподаватель ___________________________________________________ Рахманина Э.М.
1. Найдите координаты середины отрезка АВ, если:
2. Проверьте, является ли точка М (4; 2) серединой отрезка АВ, если:
3. Определите координаты центра окружности, диаметром которой является отрезок АВ, если А (4; – 2; 12), В (1; 3; -8).
1. Найдите координаты середины отрезка АВ, если:
А (– 5; – 4; 6), В (– 1; 2; 0). ________________________________________
А (3; 6; 7) В (– 5; – 2; 1). _________________________________________
3. Определите координаты центра окружности, диаметром которой является отрезок АВ, если А (4; – 2; 12), В (1; 3; -8).
| № этапа | Этапы занятия, учебные вопросы, формы и методы обучения | Временная регламентация этапа |
| 1 | Организационный этап: | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подготовить обучающихся к работе на уроке. СОДЕРЖАНИЕ – взаимные приветствия, фиксация отсутствующих, проверка внешнего состояния аудитории и готовности обучающихся к занятию, организация внимания. |
|
|
| - Сообщение правил заполнения листа самоанализа: | № | Вид работы | Баллы | | 1 | Устная работа(проверка домашнего задания) |
| | 2 | Письменная работа |
| | 3 | Работа в подгруппах(парах) |
| | 4 | Самостоятельная работа |
| | ИТОГО |
|
| Критерий оценивания: | Оценка | Баллы | | 5 | 12 и более | | 4 | 7-10 | | 3 | 3-6 | | 2 | 0-2 |
|
|
| 2. | Этап проверки домашнего задания | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить правильность и осознанность выполнения домашнего задания всеми обучающимися, установить в ходе проверки обнаруженные пробелы в знаниях, совершенствую при этом знания, умения, навыки. |
|
|
| Содержание: карточки с заданиями |
|
|
| Математический диктант. Вариант 1 Сколько чисел надо указать, чтобы задать положение точки в пространстве? (три) Как называется первое из чисел, задающих положение точки в пространстве? (абсцисса) Как называется третье из чисел, задающих положение точки в пространстве? (аппликата) Запишите обозначение точки Р, если её абсцисса равна 0, а ордината 5, аппликата 0. Где лежит точка Р? (Р (0; 5; 0), на оси ординат) Чему равна ордината точки А (- 1; - 4; 1)? (- 4) Вариант 2 Как называются числа, задающие положение точки в пространстве? (абсцисса и ордината, аппликата) Сколько чисел надо указать, чтобы задать положение точки в пространстве? (три) Как называется второе из чисел, задающих положение точки на координатной плоскости? (ордината) Запишите обозначение точки С, если её абсцисса равна 6, а ордината 0, аппликата 0. Где лежит точка С? (С (6; 0; 0), на оси абсцисс) Чему равна аппликата точки М(-2; - 3; 0)? (0)
|
|
|
| | Количество правильных ответов | Баллы | | Менее 4 | 0 | | 5 | 1 | | 8 | 2 |
|
|
| 3 | Этап подготовки обучающихся к активному и сознательному усвоению материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – организовать и направить на достижение цели познавательную деятельность обучающихся, постановка целей учебной деятельности. |
|
|
| «За всю историю человечества пока не найдено лучшего способа развития интеллектуальных и творческих способностей человека , чем при помощи математики» Владимир Тихомиров, профессор МГУ. |
|
|
| 1.Сообщение темы, цели и задач материала Прямоугольная система координат на плоскости. Вопросы: Что называют системой координат на плоскости? Как вводится, декартова система координат? Из чего она состоит? Как определяются координаты точки на плоскости? Назовите координаты начала координат? Чему равно расстояние от начала координат до заданной точки? Назовите формулу координат середины отрезка и расстояния между точками на плоскости? |
|
| 4 | Этап усвоения новых знаний | 15 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – дать обучающимся конкретное представление об изучаемых фактах, явлениях, основной идее изучаемого материала; добиться от обучающихся восприятия, осознания, первичного обобщения и систематизации новых знаний, усвоения обучающимися способов, путей, средств получения знаний, оперирования ими. |
|
|
| Содержание: |
|
| 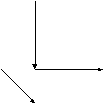
| У Декарта имелись лишь далекие намеки на возможность распространения метода координат с двумерного пространства (плоскости) на трехмерное. Потребовалось ещё почти 100 лет, чтобы идея пространственных координат была сформирована, постоянно и и широко использовалась. z - Что представляет собой система координат в Аz Ayz пространстве? Система координат в пространстве представляет Axz A собой три взаимно перпендикулярные прямые х, y, z, пересекающиеся в одной точке. О – начало отсчета, О Ау у x, y, z – координатные оси, Ax Axy xy, yz, xy – координатные плоскости. x Координатные плоскости делят все пространство на 8 октантов.
- Как определяются координаты точки А ? Через точку А проведем плоскость, параллельную плоскости yz. Она пересекает ось x в точке Аx . Координатой х точки А называется число, равное по абсолютной величине длине отрезка ОАх . Аналогично определяются и другие координаты. Таким образом, точке А в пространстве ставится в соответствие тройка чисел – её координаты. Обозначение: А(x; y; z). (Название координаты z найти самостоятельно). Рассмотрим координаты частного расположения точек в пространстве. Ах (х;0;0) Ахy (х;y;0) О (0;0;0) Где находятся данные точки? Аy (0;y;0) Аyz (0;y;z) Аz (0;0;z) Ахz (х;0;z)
|
|
| | ДИНАМИЧЕСКАЯ ПАУЗА | 5 |
|
| В результате изучения темы нужно | ЗНАТЬ: - формулу координаты середины отрезка в пространстве; - формулу расстояния между точками в пространстве | УМЕТЬ: - уметь применять формулы координат середины отрезка и расстояния между точками в пространстве к решению задач | Помни, что работать нужно по алгоритму! Не забывай проходить проверку, делать пометки на полях, заполнять рейтинговый лист темы. Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы. Будь объективен во время взаимопроверки, это поможет и тебе, и тому, кого ты проверяешь ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ № 1 1) Прочитай текст параграф 20 на стр. 66-68. 2) Запиши формулы координат середины отрезка и расстояния между | 20 |
|
| точками в пространстве в тетрадь. 3) Запиши в тетрадь: «Расстояние от точки до начала координат равно корню квадратному из суммы квадратов координат точки: 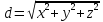 ». ».
4) Реши задачи (стр.68): № 1; № 2; № 3 (6 баллов). 5) Реши задачи (стр.68): № 5; № 6; № 7 (8 баллов).
ПРОЙДИ ПРОВЕРКУ № 1
ЗАДАНИЕ № 2 Реши задачи (стр.68): № 8; № 9 (8 баллов). 1) Найдите координаты ортогональных проекций точек A(1, 3, 4) и B(5, -6, 2) на: а) плоскость Oxy; б) плоскость Oyz; в) ось Ox; г) ось Oz. Ответ: а) (1, 3, 0), (5, -6, 0); б) (0, 3, 4), (0, -6, 2); в) (1, 0, 0), (5, 0, 0); г) (0, 0, 4), (0, 0, 2). 2) На каком расстоянии находится точка A(1, -2, 3) от координатной плоскости: а) Oxy; б) Oxz; в) Oyz? Ответ: а) 3; б) 2; в) 1 3)Найдите координаты середины отрезка: а) AB, если A(1, 2, 3) и B(-1, 0, 1); б) CD, если C(3, 3, 0) и D(3, -1, 2). Ответ: а) (1, 1, 2); б) (3, 1, 1). |
|
| 5 | Этап проверки понимания обучающимися материала | 5 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – установить осмыслили ли обучающиеся связи и отношения фактов, содержание новых понятий, закономерностей, устранить обнаруженные пробелы. |
|
|
| Используя записи в тетради и учебник, назвать основные вопросы и формулы по данной теме |
|
|
| Критерий оценивания: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
|
|
| 6 | Этап закрепления нового материала | 10 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – закрепить у обучающихся знания и умения, необходимые для самостоятельной работы по новому материалу. |
|
|
| ПРОЙДИ ПРОВЕРКУ № 2 Проверочная работа. | 1 вариант 1) На оси у найдите точку, равноудаленную от точек А(1; -3; 7) иВ(5; 7; -3). 2) Найдите длину отрезка, соединяющего точкиА(2; 0; -1) и В(3; -2; 1). 3) Докажите, что четырехугольник ABCD является параллелограммом, если A(0; 2; -3), B (-1; 1; 1), C(2; -2; -1), D(3; -1; -5). | 2 вариант 1) На оси z найдите точку, равноудаленную от точек А(4; -1; 2) иВ(0; 2; -1). 2) Найдите длину отрезка, соединяющего точкиА(6; -2; 3) и начало координат. 3) Докажите, что четырехугольник ABCD является параллелограммом, если A(2; 1; 3), B (1; 0; 7), C(-2; 1; 5), D(-1; 2; 1). |
|
|
|
| Критерий оценивания учащихся отвечающих у доски: | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 2 | | 2 | 1 | | 3 и более | 0 |
Критерий оценивания учащихся решающих на месте: (выполнив задание, учащийся поднимает руку и показывает решение примера. В соответствии с критерием оценивания получает баллы за работу.) | Количество ошибок, допущенных при решении примеров | Баллы | | 1 | 3 | | 2 | 2 | | 3 | 1 | | 4 и более | 0 |
|
|
| 7 | Рефлексия учебной деятельности | 3 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – формирование у обучающихся умения анализировать результаты своей учебной деятельности. |
|
|
| обсуждение и оценка результатов самостоятельной работы (рефлексия в письменной форме) | Что нового Вы сегодня узнали? |
| | Своей работой на уроке Вы довольны? | Доволен /не доволен | | Ваше настроение после урока | Стало лучше / стало хуже | | Материал урока Вам был | Понятен / не понятен |
|
|
| 8 | Этап информации обучающихся о домашнем задании, инструктаж по его выполнению: | 7 |
|
| ДИДАКТИЧЕСКАЯ ЗАДАЧА – подвести итоги и выставить оценки, сообщить обучающимся о домашнем задании, разъяснить методику его выполнения. |
|
|
|
|
|
|
|
|
|
|
| И если есть самостоятельная работа, то задания и форма контроля самостоятельной работы |
|
|
|
| 90 |
Преподаватель ___________________________________________________ Рахманина Э.М.









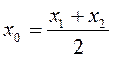 ,
, 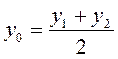 .
. 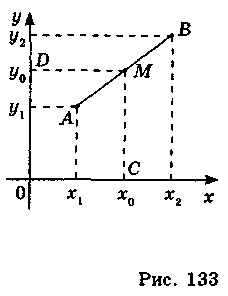

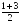 ;
; 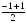 ;
; 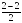 ), С (2;0;0)
), С (2;0;0)
 АМ = МВ и DN = NC
АМ = МВ и DN = NC
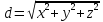 ».
».









