Урок по теме «Корень n-й степени, арифметический корень n-й степени и его свойства»
Цели урока:
Образовательная: Создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач.
Развивающая: Создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.
Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.
Ход урока
1. Организационный момент.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
- Что есть больше всего на свете? – Пространство.
- Что быстрее всего? – Ум.
- Что мудрее всего? – Время.
- Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
3.Актуализация знаний.
1. Назовите взаимообратные алгебраические операции над числами
(сложение и вычитание, умножение и деление).
2. Всегда ли можно выполнить такую алгебраическую операцию, как
деление?
(нет, делить на нуль нельзя)
3. Какую еще операцию вы можете выполнять с числами?
(возведение в степень)
4. Какая операция будет ей обратной?
(извлечение корня)
5. Корень какой степени вы можете извлекать?
(корень второй степени)
6. Какие свойства квадратного корня вы знаете?
(извлечение квадратного корня из произведения, из частного, из
корня, возведение в степень)
7. Найдите значения выражений:
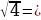 …, т.к. …2 = 4,
…, т.к. …2 = 4, 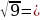 …, т.к. …2 = 9,
…, т.к. …2 = 9, 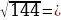 …, т.к. …2 = 144,
…, т.к. …2 = 144,
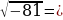 …, т.к. ……
…, т.к. …… 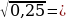 …, т.к. …2 = 0,25,
…, т.к. …2 = 0,25, 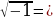 ……..
……..
Квадратным корнем из числа а называют число, квадрат которого равен а. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Запись 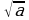 читается «квадратный корень из а», опуская при этом слово «арифметический».
читается «квадратный корень из а», опуская при этом слово «арифметический». 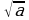 , а- подкоренное выражение, а знак
, а- подкоренное выражение, а знак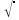 -радикал (от латинского - корень).
-радикал (от латинского - корень).
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин ( при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.
4. Изучение нового материала.
| Корнем n-й степени из числа а называется такое число b, n-я степень которого равна а, т. е. b – корень n-й степени из 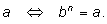 |
Очевидно, что в соответствии с основными свойствами степеней с натуральными показателями, из любого положительного числа существует два противоположных значения корня четной степени, например, числа 4 и -4 являются корнями квадратными из 16, так как (-4)2 = 42 = 16, а числа 3 и -3 являются корнями четвертой степени из 81, так как (-3)4 = З4 = 81.
Кроме того, не существует корня четной степени из отрицательного числа, поскольку четная степень любого действительного числа неотрицательна. Что же касается корня нечетной степени, то для любого действительного числа существует только один корень нечетной степени из этого числа. Например, 3 есть корень третьей степени из 27, так как З3 = 27, а -2 есть корень пятой степени из -32, так как (-2)5 = 32.
В связи с существованием двух корней четной степени из положительного числа, введем понятие арифметического корня, чтобы устранить эту двузначность корня.
Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.
Обозначение: 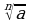 – корень n-й степени.
– корень n-й степени.
Число n называется степенью арифметического корня. Если n=2, то степень корня не указывается и пишется 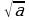 . Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.
. Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.
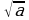 = в, в2 == а, а ≥ 0, в ≥ 0
= в, в2 == а, а ≥ 0, в ≥ 0
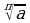 = в, вп = а
= в, вп = а
п - четное
а ≥ 0, в ≥ 0 (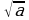 )2 = а, а ≥ 0
)2 = а, а ≥ 0
п - нечетное
а,в - любые (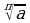 )п = а
)п = а
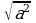
 =
= 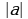
а, если а ≥ 0 - а, если а
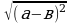 =
= 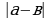
а - в. если а ≥ в в - а, если а
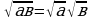 , а ≥ 0, в ≥ 0
, а ≥ 0, в ≥ 0
.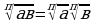 , а ≥ 0, в ≥ 0
, а ≥ 0, в ≥ 0
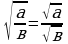 , а ≥ 0, в 0
, а ≥ 0, в 0
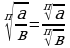 , а ≥ 0, в 0
, а ≥ 0, в 0
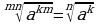 а ≥ 0
а ≥ 0
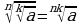 m, n, k - натуральные числа
m, n, k - натуральные числа
5. Закрепление нового материала.
Устная работа
а) Какие выражения имеют смысл?
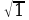 ;
; 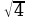 ;
; 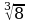 ;
; 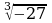 ;
;
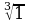 ;
; 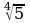 ;
; 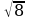 ;
; 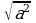 ;
;
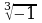 ;
; 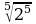 ;
; 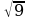 ;
; 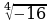 ;
;
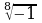 ;
; 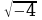 ;
; 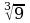 ;
; 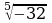 .
.
б) при каких значениях переменной а имеет смысл выражение?
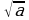
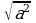
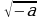
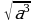
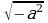
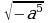
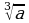
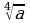
в) Вычислите:
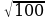 ;
; 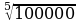 ;
; 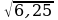 ;
; 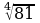 ;
; 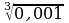 ;
; 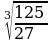 ;
; 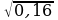 ;
; 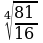 .
.
г) Верно ли равенство (устно):
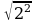 = 2;
= 2; 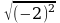 = 2; (
= 2; (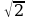 )2 = 2;
)2 = 2;
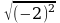 = - 2;
= - 2; 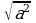 = а;
= а; 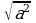 = - а;
= - а;
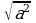 =
= 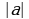 ;
; а -
а - 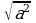 = 0; а -
= 0; а - 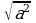 = 2а;
= 2а;
а - 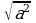 = а -
= а -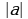 ;
; 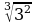 = 3;
= 3; 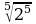 = - 2;
= - 2;
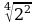 = 2;
= 2; 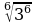 = 3;
= 3; 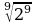 =
= 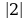 .
.
Решить № 3, 4, 7, 9, 11.
6. Физкультминутка.
Во всех делах умеренность нужна,
Пусть будет главным правилом она.
Гимнастикой займись, коль мыслил долго,
Болезни чтоб прогнать и сохранить здоровье.
Гимнастика не изнуряет тела,
Но очищает организм всецело!
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
Налево, направо, вокруг посмотрели,
Открыли глаза, и снова за дело!
7. Самостоятельная работа.
Работа в парах: с. 178.№1,2.
8. Итоги урока. Д/з. Рефлексия деятельности.
Д/з: выучить п.10(с.160-161), решить № 5, 6, 8, 12, 16(1, 2).
Достиг ли урок своей цели?
Чему вы научились?
Оцените свою деятельность на уроке в виде написания синквейна на цветных ладошках.
Спасибо всем за урок!
Примеры синквейнов:
Корень.
Квадратный, кубический.
Извлекали, возводили в степень, обобщали.
Было интересно. Я молодец.
Урок по теме «Преобразование корней»
Цели урока:
Образовательная: Создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач на преобразование корней.
Развивающая: Создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.
Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.
Ход урока
1. Организационный момент.
Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
А сердце умным будет.
2. Мотивация урока.
Мы продолжаем изучать корни степени п. Ввели понятия корня n-ой степени, изучили его свойства. Тема сегодняшнего урока “ Преобразование корней ”. Для чего, по-вашему, нужен этот материал?
– Совершенно верно. Знания свойств корней необходимы для преобразования выражений, содержащих корни n-ой степени, решения уравнений. Ведь корни находят широкое применение во многих областях: в геометрии (теорема Пифагора), а также в физике.
Например, для вычисления скорости тела, движущегося по окружности мы используем формулу 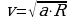 , где а – ускорение тела, R – радиус окружности.
, где а – ускорение тела, R – радиус окружности.
– Какие цели поставите вы перед собой на сегодняшний урок?
3.Актуализация знаний. Проверка д/з.
Что называется корнем n степени?
Что называется арифметическим корнем степени n?
Сформулируйте свойства арифметического корня степени n.
Восстановите записи:
а)* = ��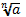
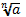 *��
*��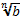
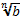
б)* = ��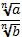
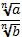
в)��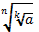
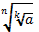 = *
= *
г) ��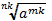
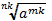 = *
= *
Вычислите:
а)��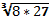
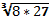
б)��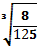
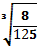
в)��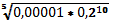
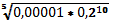
г)��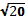
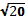 *��
*��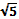
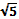
д)��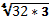
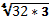 * ��
* ��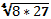
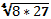
Какие из следующих записей не имеют смысла?
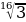 ;
; 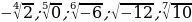 ;
; 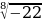 ;
; 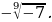
При каких значениях переменной а выражение имеет смысл?
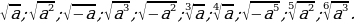
Какие из следующих записей не имеют смысла?
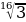 ;
; 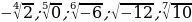 ;
; 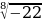 ;
; 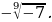
Решение упражнений на преобразование корней.
Рассмотрим различные виды преобразований корней на основе свойств корней степени п. К ним относятся преобразования корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня.
1. Корень из произведения равен произведению
корней той же степени из сомножителей, то есть
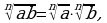 если а
если а 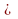 0, b
0, b  0 при четном п.
0 при четном п.
Например, 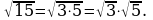
И обратно, 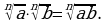
Например, 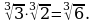
Получили правило: чтобы умножить корни с одинаковыми показателями, надо перемножить подкоренные выражения и извлечь корень данной степени из произведения.
2. Правило вынесения множителя из-под знака корня
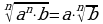
Например, 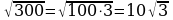 .
.
И обратно, правило внесения множителя под знак корня
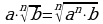
Например,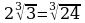
3. Корень из частного равен частному от деления корня той же степени из делимого на корень той же степени из делителя, то есть
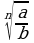 =
=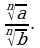
Например, 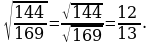
И обратно, 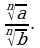 =
= 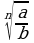 .
.
Следующая формула удобна, когда нужно избавиться от радикала в знаменателе.
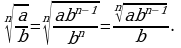
Например, 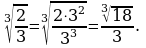
4. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное выражение, не меняя показателя корня, то есть
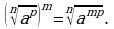
Например, 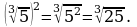
5. Чтобы извлечь корень из корня, нужно перемножить их показатели, не меняя подкоренного выражения, то есть
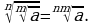
Например, 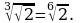
Решение уравнений.
Сколько корней имеет уравнение хn=а, если n – нечетное число? – один корень
Сколько корней имеет уравнение хn=а?
если n –четное число – зависит от а:
если а – отрицательное, то нет корней;
если а = 0, то один корень;
Физминутка.
Вытянули правую руку вперёд. Следим глазами, не поворачивая головы, за медленными движениями указательного пальца вытянутой руки влево и вправо. Вверх и вниз. Затем вытянули левую руку и повторим.
Закрепление знаний на преобразование корней.
а) Вынести множитель из-под знака корня 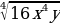 при условии, что х
при условии, что х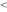 0.
0.
б) Внести множитель под знак корня 3у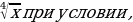 что у
что у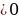 .
.
Решение. а) Так как х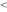 0 по условию, а у
0 по условию, а у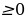 (в противном случае выражение не имеет смысла), то
(в противном случае выражение не имеет смысла), то 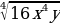 =
= 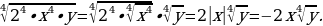
б) Так как у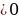 по условию, а х
по условию, а х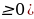 не имеет смысла выражение
не имеет смысла выражение 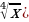 , то 3у
, то 3у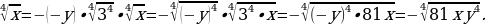
Пример . Выполнить действия: 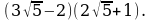
Решение. 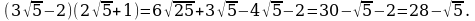
Пример . Освободиться от иррациональности в знаменателе:
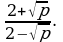
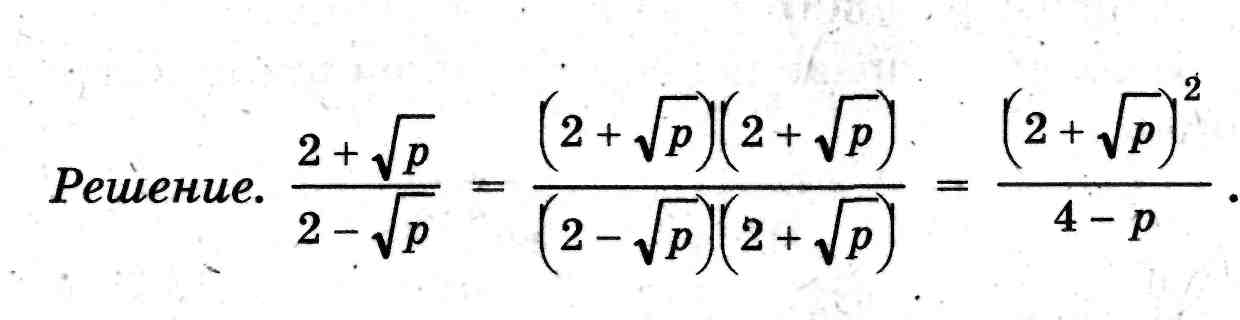
Решить из учебника №
Из истории. Начиная с XIII в. итальянские и другие европейские математики обозначали корень латинским словом «Radix» («корень») или сокращённо R. В XV в. Н. Шюке писал: R212 вместо 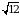 . Ныне применяемый знак корня произошёл от обозначения, которое применяли немецкие математики XV-XVI вв., называвшие алгебру «Косс», а алгебраистов «коссистами». (Математики XII-XV вв. писали свои произведения на латинском языке. Они называли неизвестное res – вещь. Итальянские математики перевели res словом cosa. Последний термин был заимствован немцами, откуда и появились «Косс» и «коссисты».) Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня
. Ныне применяемый знак корня произошёл от обозначения, которое применяли немецкие математики XV-XVI вв., называвшие алгебру «Косс», а алгебраистов «коссистами». (Математики XII-XV вв. писали свои произведения на латинском языке. Они называли неизвестное res – вещь. Итальянские математики перевели res словом cosa. Последний термин был заимствован немцами, откуда и появились «Косс» и «коссисты».) Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня 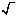 .
.
Самостоятельная работа.
Вопросы теста по теме «Корень n-й степени и его свойства».
Вычислите:
| 1) 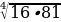 а) 5 б) 6 в) 4 г) –36.
| 4) 2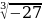 а) - 2 б) 6 в) - 6 г) 54
| 7) 5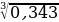 а) 5,5 б) 3 в) 0,7 г) 3,5
|
| 2) 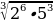 а) 15 б) 18 в) 20 г) 10
| 5) 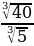 а) 8 б) 3 в) 4 г) 2
| 8) 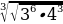 а) 12 б) 6 в) 7 г) 36
|
| 3) 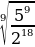 а) 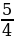 б) б) 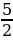 в) в) 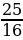 г) г) 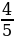
| 6) 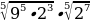 а) 18 б) 72 в) 36 г) 4
| 9) 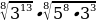 а) 15 б) 45 в) 54 г) 30
|
| 10) 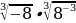 а) 1 б) 64 в) – 1 г) 38 | 11) х4= 81 а)3; б) -3; в) -3,+3; г)2 | 12) х5=32 а) -2; б) 2; в) -2; 2; г) 3
|
Итоги урока. Д/з. Рефлексия.
Вопросы и упражнения для самопроверки
Сформулируйте правило извлечения корня из произведения. Приведите пример.
Как выносить множитель за знак радикала? Приведите пример.
Сформулируйте правило извлечения корня из дроби. Приведите пример.
Как освободиться от иррациональности в знаменателе?
Как возвести корень в степень? Приведите пример.
Как извлечь корень из корня? Покажите на примере.
Выучить п. , решить №
Оцените степень вашего усвоения материала:
- усвоил полностью, могу применить;
- усвоил полностью, но затрудняюсь;
- усвоил частично;
- не усвоил, нужна консультация.
Урок по теме «Преобразование корней»
Цели урока:
Образовательная: Создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач на преобразование корней, при решении иррациональных уравнений.
Развивающая: Создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.
Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.
Ход урока
1. Организационный момент.
2. Мотивация урока.
3.Актуализация знаний. Проверка д/з.
Сформулируйте свойства арифметического корня степени n.
Сформулируйте правило извлечения корня из произведения. Приведите пример.
Как выносить множитель за знак радикала? Приведите пример.
Сформулируйте правило извлечения корня из дроби. Приведите пример.
Как освободиться от иррациональности в знаменателе?
Как возвести корень в степень? Приведите пример.
Как извлечь корень из корня? Покажите на примере.
Устная работа.
Найдите значение выражений:
а) 5 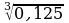 =; 0,7
=; 0,7 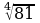 = ;
= ; 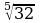 =
=
б) (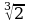 )3=; (-3
)3=; (-3 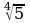 )4= ;
)4= ; 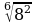 =;
=;
в) 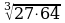 =;
=; 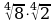 =;
=; 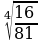 =
=
Обчисліть: 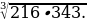 А 42 Б 21 В 14 Г 28
А 42 Б 21 В 14 Г 28
Спростіть вираз 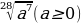 А а Б
А а Б 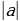 В
В 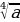 Г
Г 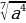
Звільніться від ірраціональності в знаменнику дробу 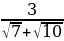 .
.
А 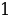 Б
Б 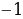 В
В 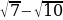 Г
Г 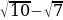
Порівняйте 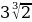 та
та 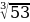 .
.
А 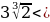
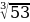 . Б
. Б 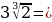
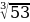 В
В 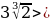
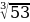 Г неможливо визначити
Г неможливо визначити
Решение упражнений на преобразование корней и иррациональных уравнений.
1 часть.
1. Вычислите: 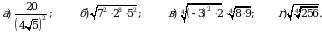
2. Упростите для отрицательного а выражение 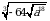 .
.
3. Упростите выражение: 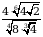 .
.
4. Упростите выражение: 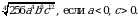
5. Найдите значение выражения 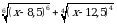 , если
, если 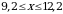 .
.
Решить № 10, 19 (1, 3)
2 часть.
Определение. Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Основные методы решения:
Метод возведения обеих частей уравнения в одну и ту же степень.
Метод введения новых переменных.
При возведении обеих частей уравнения в четную степень могут возникать посторонние корни. Поэтому при использовании указанного метода необходимо делать проверку или находить область допустимых значений и проверять все корни.
Примеры (решаются учителем, а затем учащимися на доске): №1(1, 2, 3), 2(1,2), 4(1), 5(1)
5.Физминутка. Вытянули правую руку вперёд. Следим глазами, не поворачивая головы, за медленными движениями указательного пальца вытянутой руки влево и вправо. Вверх и вниз. Затем вытянули левую руку и повторим.
6. Самостоятельная работа.
В-1
1. Вычислите: а) 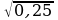 б)
б) 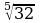 в)
в) 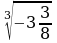 г)
г) 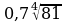 д)
д) 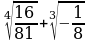
е) 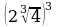 ж)
ж) 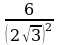 з)
з) 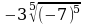
2. Решите уравнения: а) 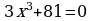 б)
б) 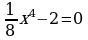 в)
в) 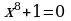 г)
г)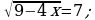
В-2
1. Вычислите: а) 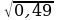 б)
б) 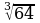 в)
в) 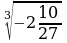 г)
г) 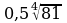
д) 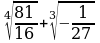 е)
е) 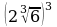 ж)
ж) 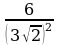 з)
з) 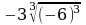
2. Решите уравнения: а)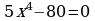 б)
б) 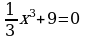 в)
в) 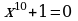 г)
г)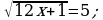
7. Итоги урока. Д/з. Рефлексия.
Выучить п.11, повторить п.10 , решить № 19(2, 4), 1(4, 5), 2(3, 4), 4(2), 5(2).
Оцените степень вашего усвоения материала:
- усвоил полностью, могу применить;
- усвоил полностью, но затрудняюсь;
- усвоил частично;
- не усвоил, нужна консультация.
Урок по теме: Действия с корнями.
Цели урока:
образовательные: закрепить знание свойств корня степени n в ходе выполнения упражнений; закрепить умение преобразовывать выражения, содержащие корни степени n;
развивающие: способствовать развитию логического мышления, математической речи учащихся, внимания, памяти;
воспитательные: воспитание интереса к математике как учебному предмету через современные технологии преподавания; способствовать развитию навыков самоконтроля.
Ход урока
1. Организационный момент.
Среди наук из всех главнейших
Важнейшая всего одна.
Учите алгебру, она глава наукам,
Для жизни очень всем нужна,
Когда достигнешь ты наук высоты,
Познаешь цену знаниям своим,
Поймешь, что алгебры красоты,
Для жизни будут кладом не плохим.
2. Мотивация урока.
3.Актуализация знаний. Проверка д/з.
Индивидуальные задания на доске:
1* 1) Вычислите:
а) 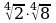 ; б)
; б) 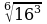 .
.
2) Вынесите множитель из-под знака корня:
а) 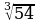 ; б)
; б) 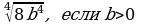 ; в)
; в) 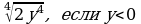 ; г)
; г) 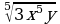 .
.
2* 1) Вычислите: 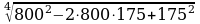 .
.
2) Избавьтесь от иррациональности в знаменателе:
а) 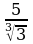 ; б)
; б) 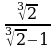 .
.
Остальные учащиеся выполняют задание в тетрадях:
1) Найдите значение выражения: а) 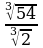 ; б)
; б) 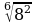 .
.
2) Вынесите множитель из-под знака корня:
а) 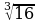 ; б)
; б) 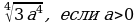 ; в)
; в) 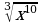
3) Представьте в виде 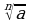 число: а)
число: а) 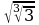 ; б)
; б) 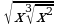 .
.
Устная работа.
Что называется корнем n степени?
Что называется арифметическим корнем степени n?
Сформулируйте свойства арифметического корня степени n.
Имеет ли смысл выражение: 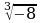 ;
; 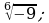
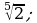
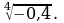
Найдите значение выражения:
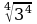 ;
; 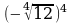 ;
; 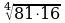 ;
; 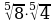 ;
; 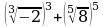 ;
; 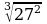 ;
; 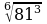 ;
; 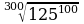 ;
; 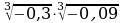 .
.
Упростите выражение:
а) 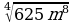 ; б)
; б) 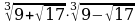 .
.
4. Действия с корнями
Выполнение упражнений (на доске с объяснением).
Упростите выражение:
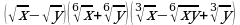 =
=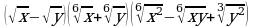 =
=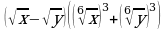 =
=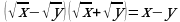 .
.
Упростите выражение:
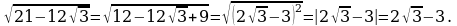
Решить №8., 10 с.178, № 4(1, 3), 5(2), 7(1) с.185.
Повторить п.п.1, понятие и запись множества, решить устно № 2, письменно №1.
Историческая пауза. Растут ли корни в огороде?
Самостоятельная работа.
I вариант.
1. Вычислите: 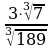 .
.
1) 1; 2) 4,5; 3) 8; 4) 21.
2. Вычислите: 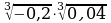 .
.
1) 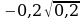 ; 2) −0,2; 3) −0,4; 4)
; 2) −0,2; 3) −0,4; 4) 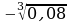 .
.
3. Упростите выражение: 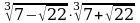 .
.
1) 3; 2) −15; 3) −3; 4) 9.
4. Упростите выражение: 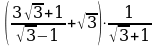 .
.
1) 2; 2) 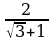 ; 3)
; 3) 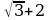 ; 4)
; 4) 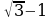 .
.
II вариант.
1. Вычислите: 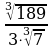 .
.
1) 1; 2) 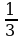 ; 3) 9; 4) 27.
; 3) 9; 4) 27.
2. Вычислите: 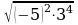 .
.
1) 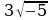 ; 2)15; 3) 45; 4) 40.
; 2)15; 3) 45; 4) 40.
3. Упростите выражение: 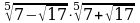 .
.
1) 2; 2) −10; 3) −3; 4) 24.
4. Упростите выражение: 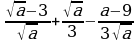 .
.
1) 0; 2)1; 3) −1; 4) 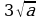 .
.
Подведение итогов урока. Рефлексия. Д/з.
Оцените степень вашего усвоения материала:
- усвоил полностью, могу применить;
- усвоил полностью, но затрудняюсь;
- усвоил частично;
- не усвоил, нужна консультация.
Повторить п.10, Решить №1 с.229, №4(2, 4), 5(1), 7(2) с.185.






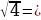 …, т.к. …2 = 4,
…, т.к. …2 = 4, 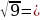 …, т.к. …2 = 9,
…, т.к. …2 = 9, 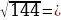 …, т.к. …2 = 144,
…, т.к. …2 = 144, 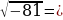 …, т.к. ……
…, т.к. …… 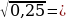 …, т.к. …2 = 0,25,
…, т.к. …2 = 0,25, 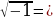 ……..
……..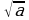 читается «квадратный корень из а», опуская при этом слово «арифметический».
читается «квадратный корень из а», опуская при этом слово «арифметический». 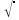 -радикал (от латинского - корень).
-радикал (от латинского - корень).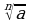 – корень n-й степени.
– корень n-й степени.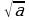 . Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.
. Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.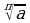 = в, вп = а
= в, вп = а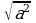
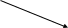
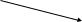 =
= 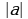
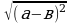 =
= 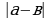
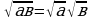 , а ≥ 0, в ≥ 0
, а ≥ 0, в ≥ 0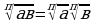 , а ≥ 0, в ≥ 0
, а ≥ 0, в ≥ 0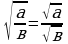 , а ≥ 0, в 0
, а ≥ 0, в 0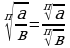 , а ≥ 0, в 0
, а ≥ 0, в 0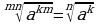 а ≥ 0
а ≥ 0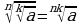 m, n, k - натуральные числа
m, n, k - натуральные числа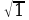 ;
; 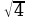 ;
; 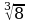 ;
; 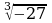 ;
; 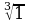 ;
; 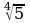 ;
; 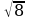 ;
; 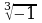 ;
; 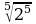 ;
; 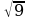 ;
; 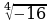 ;
; 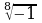 ;
; 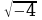 ;
; 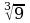 ;
; 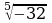 .
.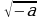
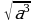
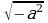
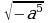
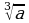
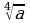
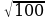 ;
; 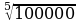 ;
; 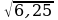 ;
; 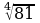 ;
; 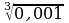 ;
; 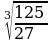 ;
; 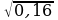 ;
; 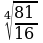 .
.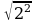 = 2;
= 2; 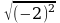 = 2; (
= 2; (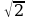 )2 = 2;
)2 = 2; 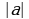 ;
; а -
а - 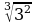 = 3;
= 3; 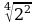 = 2;
= 2; 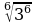 = 3;
= 3; 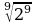 =
= 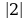 .
.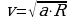 , где а – ускорение тела, R – радиус окружности.
, где а – ускорение тела, R – радиус окружности.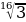 ;
; 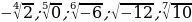 ;
; 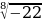 ;
; 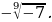
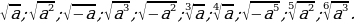
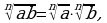 если а
если а 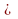 0, b
0, b 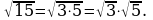
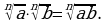
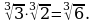
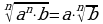
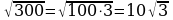 .
.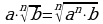
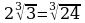
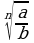 =
=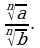
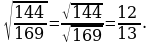
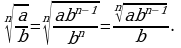
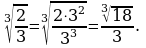
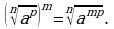
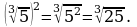
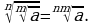
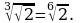
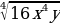 при условии, что х
при условии, что х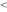 0.
0.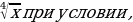 что у
что у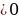 .
.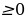 (в противном случае выражение не имеет смысла), то
(в противном случае выражение не имеет смысла), то 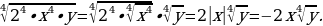
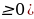 не имеет смысла выражение
не имеет смысла выражение 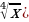 , то 3у
, то 3у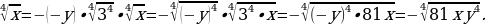
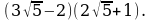
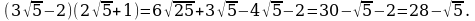
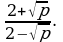
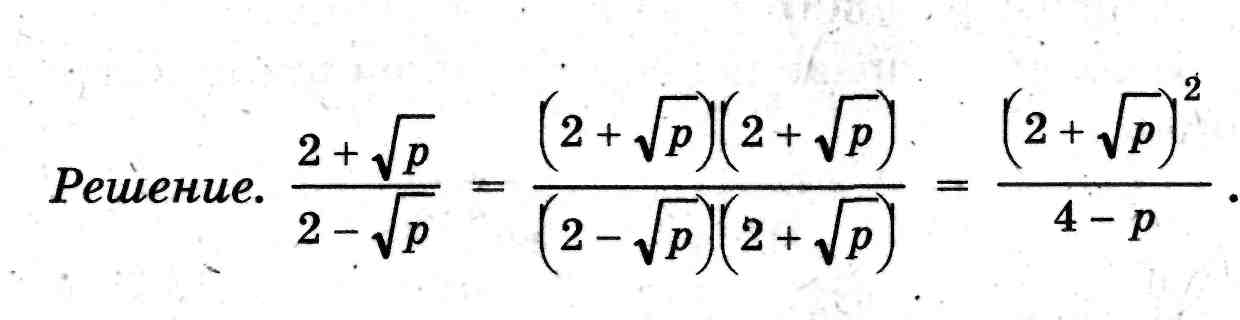
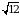 . Ныне применяемый знак корня произошёл от обозначения, которое применяли немецкие математики XV-XVI вв., называвшие алгебру «Косс», а алгебраистов «коссистами». (Математики XII-XV вв. писали свои произведения на латинском языке. Они называли неизвестное res – вещь. Итальянские математики перевели res словом cosa. Последний термин был заимствован немцами, откуда и появились «Косс» и «коссисты».) Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня
. Ныне применяемый знак корня произошёл от обозначения, которое применяли немецкие математики XV-XVI вв., называвшие алгебру «Косс», а алгебраистов «коссистами». (Математики XII-XV вв. писали свои произведения на латинском языке. Они называли неизвестное res – вещь. Итальянские математики перевели res словом cosa. Последний термин был заимствован немцами, откуда и появились «Косс» и «коссисты».) Лишь в 1637 г. Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей «Геометрии» современный знак корня 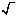 .
.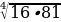
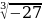
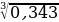
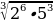
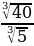
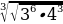
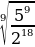
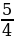 б)
б) 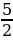 в)
в) 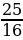 г)
г) 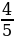
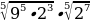
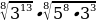
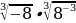
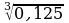 =; 0,7
=; 0,7 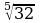 =
=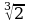 )3=; (-3
)3=; (-3 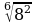 =;
=; 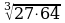 =;
=; 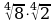 =;
=; 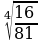 =
=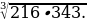 А 42 Б 21 В 14 Г 28
А 42 Б 21 В 14 Г 28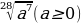 А а Б
А а Б 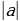 В
В 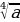 Г
Г 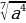
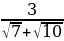 .
.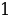 Б
Б 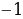 В
В 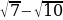 Г
Г 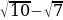
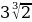 та
та 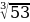 .
.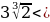
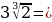
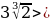
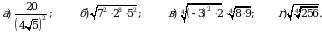
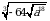 .
.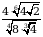 .
.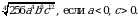
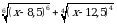 , если
, если 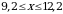 .
.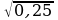 б)
б) 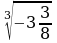 г)
г) 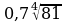 д)
д) 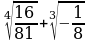
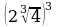 ж)
ж) 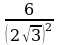 з)
з) 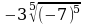
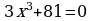 б)
б) 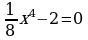 в)
в) 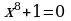 г)
г)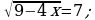
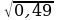 б)
б) 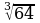 в)
в) 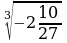 г)
г) 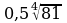
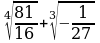 е)
е) 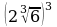 ж)
ж) 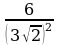 з)
з) 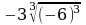
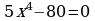 б)
б) 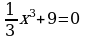 в)
в) 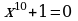 г)
г)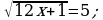
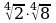 ; б)
; б) 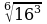 .
.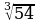 ; б)
; б) 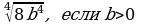 ; в)
; в) 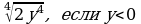 ; г)
; г) 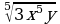 .
.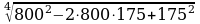 .
.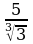 ; б)
; б) 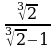 .
.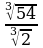 ; б)
; б) 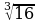 ; б)
; б) 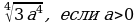 ; в)
; в) 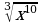
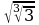 ; б)
; б) 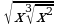 .
.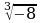 ;
; 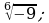
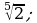
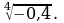
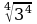 ;
; 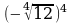 ;
; 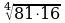 ;
; 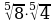 ;
; 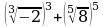 ;
; 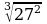 ;
; 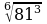 ;
; 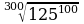 ;
; 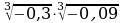 .
.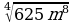 ; б)
; б) 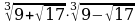 .
.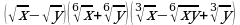 =
=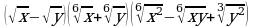 =
=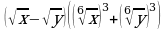 =
=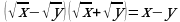 .
.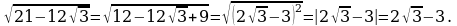
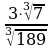 .
.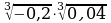 .
.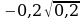 ; 2) −0,2; 3) −0,4; 4)
; 2) −0,2; 3) −0,4; 4) 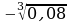 .
.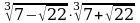 .
.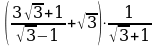 .
.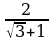 ; 3)
; 3) 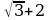 ; 4)
; 4) 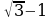 .
.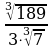 .
.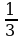 ; 3) 9; 4) 27.
; 3) 9; 4) 27.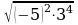 .
.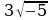 ; 2)15; 3) 45; 4) 40.
; 2)15; 3) 45; 4) 40.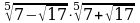 .
.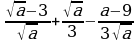 .
.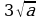 .
.









