Лекция № 21-24
Тема: Көрсөткүчтүү жана логарифмдик функциялар, алардын касиеттери.
Көрсөткүчтүү функция, касиеттери.
Логарифмдер жана алардын касиеттери.
Логарифмдик функция, касиеттери.
Көрсөткүчтүү жана логарифмдик теңдемелер, түрлөрү, аларды чыгаруунун жолдору.
Көрсөткүчтүү жана логарифмдик барабарсыздыктар, түрлөрү, аларды чыгаруунун жолдору.
Натурал, бүтүн жана рационал көрсөткүчтүү даражаларды жана алардын касиеттерин кайталоо, толуктоо жолдору.
Көрсөткүчтүү функция түшүнүгүн кийирүүнүн негизги базасы болуп – натурал, бүтүн жана рационал көрсөткүчтүү даражалар, n – даражалуу тамыр, алардын касиеттери эсептелет.
Алдын-ала  даражасын,
даражасын,  үчүн кайталап,
үчүн кайталап,  же
же  ;
;  аныктамасын эске алып, кийин касиеттерине токтолобуз.
аныктамасын эске алып, кийин касиеттерине токтолобуз.
10.  ;
;
20.  ;
;
30.  ;
;
40.  ;
;
50.  ;
;
60.  болсо, анда
болсо, анда  ;
;
70.  жана
жана  болсо, анда
болсо, анда  , айрым учурда
, айрым учурда  ;
;
80.  болсо, анда
болсо, анда  ;
;
90.  болсо,
болсо,  .
.
2. Эми натурал көрсөткүчтүү даражага окшоштуруп, анын аныктамасынан, касиеттеринен пайдаланып,  саны үчүн
саны үчүн  ,
,  - даражасын алабыз. Мында
- даражасын алабыз. Мында  эскертилет. Бул
эскертилет. Бул  учурунда да жогорудагы 10-70 касиеттердин туура болору мисалдардын жардамында көрсөтүлөт.
учурунда да жогорудагы 10-70 касиеттердин туура болору мисалдардын жардамында көрсөтүлөт.
3. Эми  болгондо
болгондо  болгондуктан,
болгондуктан,  деп белгилөөнү, себеби
деп белгилөөнү, себеби  болорун айтып, алардын жардамында
болорун айтып, алардын жардамында  болсо,
болсо,  болорун көрсөтүү жолу менен
болорун көрсөтүү жолу менен  рационал көрсөткүчтүү даражасы аныкталат
рационал көрсөткүчтүү даражасы аныкталат  ;
;  ;
;  ;
;  . Ошентип,
. Ошентип,  анык санын
анык санын  рационал көрсөткүчтүү даражага көтөрүүгө мүмкүн. Касиеттери:
рационал көрсөткүчтүү даражага көтөрүүгө мүмкүн. Касиеттери:
10.  ; 20.
; 20.  ; 30.
; 30.  ;
;
40.  ; 50.
; 50.  ; 60.
; 60.  болсо,
болсо,  ;
;
70.  болсо, анда
болсо, анда  .
.
Эми иррационал көрсөткүчтүү даража түшүнүгүнө токтолобуз.
 ,
,  ,
,  ,
,  ,
,  ,
,  ж.б. иррационал сандарын карайлы. Аларды бүтүнгө, 0,1ге, 0,01ге, 0,001ге, … чейинки тактыктагы кеми менен жана ашыгы менен алынган жакындаштырылган маанилерин карайлы. Мисалы,
ж.б. иррационал сандарын карайлы. Аларды бүтүнгө, 0,1ге, 0,01ге, 0,001ге, … чейинки тактыктагы кеми менен жана ашыгы менен алынган жакындаштырылган маанилерин карайлы. Мисалы,  үчүн алар төмөндөгүчө болот:
үчүн алар төмөндөгүчө болот:  ;
;  ;
;  ;
;  ж. б.
ж. б.
 үчүн:
үчүн:  ;
;  ;
;  ;
;  , …. Анда
, …. Анда  даражалары үчүн төмөнкүлөр алынат:
даражалары үчүн төмөнкүлөр алынат:
 ;
;  ;
;  ;
;  , …
, …
 ;
;  ;
;  ;
;  , ….
, ….
Бул берилгендерден  даражаларынындагы жакындаштырылган сан маанилерин алууга болот. Ошентип
даражаларынындагы жакындаштырылган сан маанилерин алууга болот. Ошентип  анык санын
анык санын  , анык сан көрсөткүчтүү
, анык сан көрсөткүчтүү  даражасына да көтөрүүгө болот.
даражасына да көтөрүүгө болот.
Көрсөткүчтүү функция түшүнүгүн кийирүү жана анын касиеттери.
Көрсөткүчтүү функция түшүнүгүн бир нече жолдор менен кийрүүгө болот:
Айрым, жеке мисалдарды, учурларды карап, индукция жолу менен;
Каалагандай  чыныгы сан үчүн
чыныгы сан үчүн  даражасын
даражасын  , анын касиеттери,
, анын касиеттери,  үчүн
үчүн 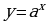 болгондой
болгондой  табыларын,
табыларын,  көз карандылыгын аткарылышын көрсөтүү менен;
көз карандылыгын аткарылышын көрсөтүү менен;
Формалдуу жол менен, б.а. шыр эле аныктаманы берүү аркылуу.
Айталы  болсун. Анда
болсун. Анда  . Эми
. Эми  анык саны үчүн
анык саны үчүн
2х даражасын карап көрөлү. Аны үчүн таблица түзүп көрөбүз.
| х | 0 | 1 | 2 | 3 | -1 | -2 | -3 | 
| 
| 
| 
| 1,4 | -0,03 | 
| 
| |
…
|
| 2х | 1 | 2 | 4 | 8 | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 2 |
… |
Ушундай эле жол менен 3х, 5х, 10х,  , 0,1х,
, 0,1х,  ж.б. даражалары үчүн да таблицаларды түзүп, даражаладын сан маанилерин табуу көрсөтүлөт. Ошентип, жогорудагы таблицадан көрүнүп тургандай, каалагандай анык х санына 2х даражасынын анык бир мааниси туура келип жатат. Анда 2х даражасы х тин функциясы болот. Ошондой эле 3х, 10х,
ж.б. даражалары үчүн да таблицаларды түзүп, даражаладын сан маанилерин табуу көрсөтүлөт. Ошентип, жогорудагы таблицадан көрүнүп тургандай, каалагандай анык х санына 2х даражасынын анык бир мааниси туура келип жатат. Анда 2х даражасы х тин функциясы болот. Ошондой эле 3х, 10х,  ж.б. даражалары да х тин
ж.б. даражалары да х тин  функциялары болушат.
функциялары болушат.
Аныктама:  жана
жана  болсун. Бардык анык сандардын көптүгүндө (сан огунда) аныкталып, мааниси
болсун. Бардык анык сандардын көптүгүндө (сан огунда) аныкталып, мааниси 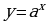 катышы менен эсептелген функция – көрсөткүчтүү функция деп аталат.
катышы менен эсептелген функция – көрсөткүчтүү функция деп аталат. 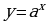 функциясында х аргументи даражанын көрсөткүчүндө берилген.
функциясында х аргументи даражанын көрсөткүчүндө берилген.
Эгерде  болсо
болсо  турактуу гана мааниге ээ болот. Эгерде
турактуу гана мааниге ээ болот. Эгерде  болсо, анда
болсо, анда  маанисинде
маанисинде  аныкталбайт, терс сандын квадрат тамыры жашабайт. Ошол себептүү
аныкталбайт, терс сандын квадрат тамыры жашабайт. Ошол себептүү  ,
,  болгон учуру гана каралат.
болгон учуру гана каралат.
Функциянын, даражанын, тамырдын касиеттеринен, 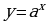 функциясынын да төмөнкүдөй касиеттери келип чыгат:
функциясынын да төмөнкүдөй касиеттери келип чыгат:
10.  функциясынын аныкталуу областы
функциясынын аныкталуу областы  бардык анык сандардын көптүгү болот.
бардык анык сандардын көптүгү болот.
20. Маанилеринин көптүгү  бардык оң анык сандардын көптүгү болот (графиги ох – огунун үстүндө жатат).
бардык оң анык сандардын көптүгү болот (графиги ох – огунун үстүндө жатат).
30. Даражанын касиети боюнча,  болгондо,
болгондо, 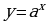 өсүүчү функция, ал эми
өсүүчү функция, ал эми  болгондо
болгондо 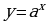 функциясы кемүүчү болот.
функциясы кемүүчү болот.
40. Каалагандай  саны үчүн
саны үчүн  болгондуктан,
болгондуктан, 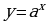 функциясынын графиги (0;1) чекити аркылуу өтөт.
функциясынын графиги (0;1) чекити аркылуу өтөт.
50.  үчүн
үчүн  болгондуктан
болгондуктан 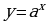 функциясы бир маанилүү функция.
функциясы бир маанилүү функция.


3
0 – касиеттен y=a
x функциясынын монотондуу болору келип чыгат. Ошентип
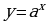
функциясы бир маанилүү, монотондуу, үзгүлтүксүз функция болот. Аны

,

,
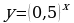
,

учурларынын графиктерин чийдирип, түшүндүрүүгө болот (45-чийме).
Көрсөткүчтүү теңдемелер жана барабарсыздыктар, аларды чыгаруунун жолдору.
Белгисизи даражанын көрсөткүчүндө болгон теңдемелер көрсөткүчтүү теңдемелер деп аталат. Эң жөнөкөй көрсөткүчтүү теңдеме  түрүндө болот. Көрсөткүчтүү теңдемелерге мисалдар келтирели.
түрүндө болот. Көрсөткүчтүү теңдемелерге мисалдар келтирели.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
 теңдемесин карап көрөлү.
теңдемесин карап көрөлү.  болсо, теңдеменин чыгарылышы жок,
болсо, теңдеменин чыгарылышы жок,  ,
,  ,
,  учурда теңдеме жалгыз чыгарылышка ээ. Көрсөткүчтүү теңдемелерди логарифм түшүнүгүнөн кийин өткөнү дурус болор эле. Себеби
учурда теңдеме жалгыз чыгарылышка ээ. Көрсөткүчтүү теңдемелерди логарифм түшүнүгүнөн кийин өткөнү дурус болор эле. Себеби  теңдемесинин чечими
теңдемесинин чечими  болот эмеспи. Бирок
болот эмеспи. Бирок  түрүнө келтирүүгө мүмкүн болгон учурларда
түрүнө келтирүүгө мүмкүн болгон учурларда  барабардыгынан
барабардыгынан  чыгарылышын логарифмсиз эле алууга болот.
чыгарылышын логарифмсиз эле алууга болот.  барабардыгынан
барабардыгынан  алынат.
алынат.
1-мисалда:  ;
;
2-мисалда:  ;
;
3-мисалда:  ;
;
4-мисалда:  белгилөөсүн пайдаланып,
белгилөөсүн пайдаланып,  ,
,  чечимдери келип чыгар эле. Негизинен көрсөткүчтүү теңде-мелерди чыгарууда 4=22; 8=23; 0,5=2-1; 0,1=10-1; 0,25=2-2;
чечимдери келип чыгар эле. Негизинен көрсөткүчтүү теңде-мелерди чыгарууда 4=22; 8=23; 0,5=2-1; 0,1=10-1; 0,25=2-2;  ;
;  ;
;  ж.у.с. теңдеш өзгөртүп түзүүлөрдү пайдалана билүү, белгисиз бир туюнтманы башка бир белгисиз менен белгилеп алып чыгаруу ж.у.с. жолдордон пайдаланууну үйрөнүү зарыл.
ж.у.с. теңдеш өзгөртүп түзүүлөрдү пайдалана билүү, белгисиз бир туюнтманы башка бир белгисиз менен белгилеп алып чыгаруу ж.у.с. жолдордон пайдаланууну үйрөнүү зарыл.
Эң жөнөкөй көрсөткүчтүү барабарсыздык  түрүндө болот. Белгисизди өз ичине алган, ар кандай көрсөткүчтүү барабарсыздыкты жогоркудай эң жөнөкөй барабар-сыздыктарга алып келүү жолу менен чыгарылат.
түрүндө болот. Белгисизди өз ичине алган, ар кандай көрсөткүчтүү барабарсыздыкты жогоркудай эң жөнөкөй барабар-сыздыктарга алып келүү жолу менен чыгарылат.
 болгондо
болгондо  барабарсыздыгы
барабарсыздыгы  , ал эми
, ал эми  болгондо
болгондо  барабарсыздыгы менен тең күчтүү болорун, мисалдардын жардамында көрсөтө билүү зарыл. Мисалдар келтирели.
барабарсыздыгы менен тең күчтүү болорун, мисалдардын жардамында көрсөтө билүү зарыл. Мисалдар келтирели.
5х -5 барабарсыздыгынын чечими жок.
10х 0,1 дин чечими х -1, б.а.  ;
;
 берилсе,
берилсе,  белгилөөсүнөн,
белгилөөсүнөн,  , мындан
, мындан  же
же  . Мындан
. Мындан  ;
;
 берилсе, анда
берилсе, анда  экендигин эске алып,
экендигин эске алып,  ди алабыз.
ди алабыз.  болгондуктан, х 1 же
болгондуктан, х 1 же  .
.
Теңдемелерди, барабарсыздыктарды чыгарганда дагы көрсөткүчтүү функциянын касиеттеринен, графиктеринен пайдалануу зарыл.
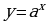 түрүндөгү көрсөткүчтүү функциясы менен катар практикада, турмушта
түрүндөгү көрсөткүчтүү функциясы менен катар практикада, турмушта  түрүндөгү функциялар көп учурайт. Мисалы,
түрүндөгү функциялар көп учурайт. Мисалы,  функциясын
функциясын  деп жазууга болот.
деп жазууга болот.
Логарифм түшүнүгүн кийирүү жана анын касиеттери.
Логарифм түшүнүгүн биринчи жолу англиялык математик Джон Непер (1550-1617) жана швецариялык математик И. Бюрги (1552-1632) математикалык эсептөөлөрдү жөнө-көйлөштүрүү жолдорун издеп олтуруп табышкан жана практикада колдонууну сунуш кылышкан.
Логарифм түшүнүгүн бир нече жолдор менен берүүгө болот:
 түрүндөгү көрсөткүчтүү теңдемелердин жардамында;
түрүндөгү көрсөткүчтүү теңдемелердин жардамында;
Өз ара тескери функциялардын жардамында, 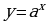 функциясына тескери болгон функцияны аныктоо жолу менен;
функциясына тескери болгон функцияны аныктоо жолу менен;
Эсептөөгө берилген жеке, айрым мисалдарды кароодон индукция жолу менен;
Даяр формада, аныктамасынан, формалдуу жолу менен.


а) 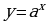 ,
,  ,
,  көрсөткүчтүү функциясын карайбыз.
көрсөткүчтүү функциясын карайбыз.
Ал үзгүлтүксүз бир маанилүү, монотондуу (өсүүчү же кемүүчү) функция. болгондо, өсүүчү, графиги 46-чийме-де көрсөтүлгөндөй болот. Эми
болгондо, өсүүчү, графиги 46-чийме-де көрсөтүлгөндөй болот. Эми  ,
,  түз сызыгын карайбыз (46-чийме).
түз сызыгын карайбыз (46-чийме). 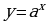 жана
жана  функцияларынын графиктеринин кесилиш чекити
функцияларынын графиктеринин кесилиш чекити  болсун. Анда
болсун. Анда  саны
саны  теңдемесинин чечими болот.
теңдемесинин чечими болот.
Аныктама: ,
,  ,
,  - негизи боюнча оң
- негизи боюнча оң  санынын логарифми деп,
санынын логарифми деп,  санын алуу үчүн
санын алуу үчүн  санын көтөрүүгө керек болгон даражанын көрсөткүчү айтылат. Ал
санын көтөрүүгө керек болгон даражанын көрсөткүчү айтылат. Ал  символу менен белги-ленет, мында
символу менен белги-ленет, мында  десек, анда
десек, анда  болот.
болот.
Мисалы, 23=8 болгондуктан  болот,
болот,  ;
;  ;
;  . Аныктамадан
. Аныктамадан  теңдештиги келип чыгат. Андан кийин логарифмдин касиеттери, аларга мисалдар иштөө үйрөтүлөт. а =10 болсо ондук логарифм деп аталат жана ал
теңдештиги келип чыгат. Андан кийин логарифмдин касиеттери, аларга мисалдар иштөө үйрөтүлөт. а =10 болсо ондук логарифм деп аталат жана ал  деп жазылат. Аларга мисалдар келтирүүгө болот. в0 болгондуктан, он сандын гана логарифми жашайт.
деп жазылат. Аларга мисалдар келтирүүгө болот. в0 болгондуктан, он сандын гана логарифми жашайт.
б) Экинчи жолду карап көрөлү.  функциясы берилсин. Мында
функциясы берилсин. Мында - аргумент,
- аргумент,  - функция.
- функция.  ти тапсак
ти тапсак  болот. Мында
болот. Мында  тин ар бир маанисинде
тин ар бир маанисинде  тин анык бир маа-ниси тиешелеш келет. Демек
тин анык бир маа-ниси тиешелеш келет. Демек  катышы да функция,
катышы да функция,  - аргумент,
- аргумент,  - функция.
- функция.  функциясы
функциясы  функциясына тескери функция болот. Айлананын узундугу
функциясына тескери функция болот. Айлананын узундугу  радиустун функциясы. Мындан
радиустун функциясы. Мындан  катышын жазсак, ал да
катышын жазсак, ал да  функциясына тескери функциясы болот. Мында
функциясына тескери функциясы болот. Мында  - аргумент,
- аргумент,  - функция. Жагы
- функция. Жагы  болгон квадраттын аянты
болгон квадраттын аянты  ,
,  тин функциясы болот. Мындан
тин функциясы болот. Мындан  , анын
, анын  катышын алсак
катышын алсак  , ал да
, ал да  функциясына тескери функция.
функциясына тескери функция.
 функциясында х чондугу у аркылуу бир маанилүү гана аныкталса, анда
функциясында х чондугу у аркылуу бир маанилүү гана аныкталса, анда  функциясына тескери функция жашайт. Мисалы, у=х2 функциясына х тин
функциясына тескери функция жашайт. Мисалы, у=х2 функциясына х тин  аралыгында тескери функциясы
аралыгында тескери функциясы  болот.
болот.
Эгерде y = f(x) функциясы бир маанилүү, монотондуу, аныкталуу областы D(f) = M көптүгү, маанилеринин көптүгү E(f) =N көптүгү болсо, анда y = f(x) функциясына тес-кери y = g(x) функциясы жашап, анын аныкталуу областы , ал эми маанилеринин көптүгү М болот. Математикада
, ал эми маанилеринин көптүгү М болот. Математикада  функциясына тескери
функциясына тескери  функциясы жашаса, андагы
функциясы жашаса, андагы  катышындагы х ти у менен, ал эми у ти х менен ал-маштырып,
катышындагы х ти у менен, ал эми у ти х менен ал-маштырып,  деп жазышат жана y = g(x) функциясы y = f(x) функциясына тескери функция деп айтылат.
деп жазышат жана y = g(x) функциясы y = f(x) функциясына тескери функция деп айтылат.
Эми болгон көрсөткүчтүү функциясын карайлы. Анын касиетте-ри боюнча
болгон көрсөткүчтүү функциясын карайлы. Анын касиетте-ри боюнча  бир маанилүү, монотондуу (өсүүчү же кемүүчү) функ-ция. Анда
бир маанилүү, монотондуу (өсүүчү же кемүүчү) функ-ция. Анда 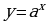 функциясына
функциясына  көптүгүндө тескери функция жашайт. Ал тес-кери
көптүгүндө тескери функция жашайт. Ал тес-кери  функциясы
функциясы  деп жазылып, ал
деп жазылып, ал  негизи боюнча x тин логарифми деп аталат. Демек,
негизи боюнча x тин логарифми деп аталат. Демек,  тен
тен  дан
дан  келип чыгат, b0.
келип чыгат, b0.
Андан кийин даражанын, көрсөткүчтүү функциянын касиеттеринен жана лога-рифмдин аныктоосунун негизинде, анын төмөнкүдөй касиеттерин келтирип чыгарууга болот:
10.  20.
20.  ; 30.
; 30.  40.
40.  (мында х 0, у0); 50.
(мында х 0, у0); 50.  ; 60.
; 60.  ; 70.
; 70.  ; 80.
; 80.  жана
жана  болсо,
болсо,  болот; 90.
болот; 90.  жана
жана  болсо,
болсо,  .
.
Аныктама:  , х(0;+) болгондо
, х(0;+) болгондо  түрүндөгү функциялар логарифмдик функция деп аталат.
түрүндөгү функциялар логарифмдик функция деп аталат.
Ал төмөнкүдөй касиеттерге ээ:
10. Аныкталуу областы  ;
;
20. Маанилеринин көптүгү  ;
;
30.  функциясынын графиги (1;0) чекити аркылуу өтөт;
функциясынын графиги (1;0) чекити аркылуу өтөт;


40. а1 болгондо  функциясы өсүүчү, ал эми
функциясы өсүүчү, ал эми  болгондо кемүүчү функция болот;
болгондо кемүүчү функция болот;
50. х1 х2 болсо,  бир маанилүү, үзгүлтүксүз функция болот.
бир маанилүү, үзгүлтүксүз функция болот.
60.  функциясынын графиги
функциясынын графиги  огунун оң жагында жайланып, аны менен кесилишпейт.
огунун оң жагында жайланып, аны менен кесилишпейт.  огун (1;0) чекитинде кесип өтөт (47-чийме).
огун (1;0) чекитинде кесип өтөт (47-чийме).
70.  функциясынын графиги у = х түз сызы-гына карата
функциясынын графиги у = х түз сызы-гына карата 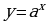 функциясынын графигине симметриялуу болот.
функциясынын графигине симметриялуу болот.
Логарифмдик теңдемелер жана барабарсыздыктар, аларды чыгаруунун жолдорун окутуу.
Белгисиз чоңдук логарифм белгисинин астында турган теңдемелер, барабарсыз-дыктар – логарифмдик теңдемелер, барабарсыздыктар деп аталат. Аларды логарифм-дин касиеттеринин негизинде, өтүлгөн материалдардан пайдаланып чыгарууга болот.
 түрүндөгү теңдемелер (
түрүндөгү теңдемелер ( ) эң жөнөкөй логарифмдик теңдеме деп аталат. Анын жалгыз гана
) эң жөнөкөй логарифмдик теңдеме деп аталат. Анын жалгыз гана  чечими бар.
чечими бар.  теңдемесинин чечими
теңдемесинин чечими  системасынын чечими болот.
системасынын чечими болот.
Ал эми  теңдемесинин чечими
теңдемесинин чечими  системасы-нан табылат. Алар потенцирлөө жолу менен чыгарылат.
системасы-нан табылат. Алар потенцирлөө жолу менен чыгарылат.
Теңдемелерди чыгарабыз: 1)  , чечими х=3; 2)
, чечими х=3; 2)  болсо, анын чечими 3 болот; 3)
болсо, анын чечими 3 болот; 3)  берилсе, чечими
берилсе, чечими  болот; 4)
болот; 4)  берилсе, анда
берилсе, анда  , мындан х=3 болот.
, мындан х=3 болот.
 түрүндөгү барабарсыздык логарифмдик барабарсыздык деп аталат. Анын чечими
түрүндөгү барабарсыздык логарифмдик барабарсыздык деп аталат. Анын чечими  же
же  системасынын чечими болот, логарифмдик барабар-сыздыктар потенцирлөө жолу менен чыгарылат. Аларды чыгарууда төмөнкү эки эрежени жетекчиликке алуу зарыл:
системасынын чечими болот, логарифмдик барабар-сыздыктар потенцирлөө жолу менен чыгарылат. Аларды чыгарууда төмөнкү эки эрежени жетекчиликке алуу зарыл:
 туюнтмасында
туюнтмасында  шартын эске алуу керек;
шартын эске алуу керек;
2) Эгерде а1 болсо, анда барабарсыздыктын белгиси өзгөрбөй сакталышын, ал эми  болсо, анда барабарсыздыктын белгисин карама-каршысына өзгөртүү керек.
болсо, анда барабарсыздыктын белгисин карама-каршысына өзгөртүү керек.
Барабарсыздыктары чыгарылсын:
 болсо, чечими
болсо, чечими  ;
;
 болсо, чечими
болсо, чечими  ;
;
 ;
;
Көрсөткүчтүү жана логарифмдик функциялардын туундуларын келтирип чыгаруу.
Алдын-ала  функциясынын туундусу түшүнүгүн, аныктамасын, формула-сын табуу эрежелерин кайталоо зарыл.
функциясынын туундусу түшүнүгүн, аныктамасын, формула-сын табуу эрежелерин кайталоо зарыл.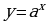 жана
жана функцияларынын үзгүлтүк-сүздүгү жана графиктери эске алынат.
функцияларынын үзгүлтүк-сүздүгү жана графиктери эске алынат.
1.  саны, анын сан мааниси бир нече жолдор менен келтирип чыгарылат.
саны, анын сан мааниси бир нече жолдор менен келтирип чыгарылат.
 сан удаалаштыгын карап көрөлү.
сан удаалаштыгын карап көрөлү.  ,
,
 өсүүчү удаалаштык,
өсүүчү удаалаштык,
 сан удаалаштыгын да
сан удаалаштыгын да  ,
,
 кемүүчү удаалаштык.
кемүүчү удаалаштык.
Ар убак  . Ошол себептүү
. Ошол себептүү  удаалаш-тыгы өсүүчү жана жогору жагынан чектелген, ал эми
удаалаш-тыгы өсүүчү жана жогору жагынан чектелген, ал эми  удаалаштыгы кемүүчү бирок төмөн жагынан чектелген. Анда Вейерштрастын монотондуу чектелген удаалаштыктары тууралуу теоремасы боюнча
удаалаштыгы кемүүчү бирок төмөн жагынан чектелген. Анда Вейерштрастын монотондуу чектелген удаалаштыктары тууралуу теоремасы боюнча  пределине ээ. Ал
пределине ээ. Ал  , б.а.
, б.а.  болгон иррационалдык сан
болгон иррационалдык сан  .
.
2. Эми 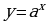 функциясын карайбыз. Анын
функциясын карайбыз. Анын  аралыгындагы орточо ылдамдыгы
аралыгындагы орточо ылдамдыгы  . Мында
. Мында  туюнтмасынын
туюнтмасынын  болгондогу предели (0;1) чекитинде
болгондогу предели (0;1) чекитинде 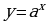 функциясына жүргүзүлгөн жаныманын бурчтук коэффициенти
функциясына жүргүзүлгөн жаныманын бурчтук коэффициенти  болот. Демек,
болот. Демек,  болгондо
болгондо  тин умтулган сан мааниси х=0 болгондогу
тин умтулган сан мааниси х=0 болгондогу 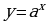 тин туундусун берер эле, б.а.
тин туундусун берер эле, б.а.  , мында
, мында  . Эми
. Эми  нын 2; 2,3; 3; 3,4 ж.б. сан маанилериндеги
нын 2; 2,3; 3; 3,4 ж.б. сан маанилериндеги  ,
,  ,
,  ,
,  , … функцияларын графиктерин чийип, х=0 болгондо аларга жүргүзүлгөн жанымалардын
, … функцияларын графиктерин чийип, х=0 болгондо аларга жүргүзүлгөн жанымалардын  огу менен түзгөн бурчу жакындаштырылган 350, 400, 480, 510, … болгон. Демек ал жанымалардын бурчтук коэффициенттери
огу менен түзгөн бурчу жакындаштырылган 350, 400, 480, 510, … болгон. Демек ал жанымалардын бурчтук коэффициенттери  ,
,  ,
,  ,
,  … болот. Мындан
… болот. Мындан  нын бир сан мааниси табылып, (0;1) чекитинде ага жүргүзүлгөн жаныманын бурчтук коэффициенти
нын бир сан мааниси табылып, (0;1) чекитинде ага жүргүзүлгөн жаныманын бурчтук коэффициенти  болот (
болот ( болот). Мындай сан 2ден чоң, 3 төн кичине сан, ал
болот). Мындай сан 2ден чоң, 3 төн кичине сан, ал  иррационалдык сан болот. Ал сан үчүн
иррационалдык сан болот. Ал сан үчүн  . Анда
. Анда  үчүн
үчүн  . Ошентип
. Ошентип  функциясынын туундусу өзүнө барабар, б.а.
функциясынын туундусу өзүнө барабар, б.а.  болот. Эгерде
болот. Эгерде  болсо, анда
болсо, анда  болот эле. Математикада көбүнчө
болот эле. Математикада көбүнчө  экспоненттик функция деп аталат.
экспоненттик функция деп аталат.
3. Негизи  саны болгон логарифмди натуралдык логарифм деп аташат, жана аны ln менен белгилешет, б.а.
саны болгон логарифмди натуралдык логарифм деп аташат, жана аны ln менен белгилешет, б.а.  .
.
Логарифмдин аныктамасынан келип чыккан биринчи теңдештик боюнча  , мындан
, мындан  . Ошол себептүү
. Ошол себептүү  болот. Анда
болот. Анда  , б.а.
, б.а.  . Мындан
. Мындан  ;
;  .
.
4. Логарифмдик функциянын туундусун: 1) өз ара тескери функциялардын туунду-сунун  формуласынан; 2) логарифмдик теңдештиктин жардамында чыгарууга да болот. Теңдештик боюнча
формуласынан; 2) логарифмдик теңдештиктин жардамында чыгарууга да болот. Теңдештик боюнча  , анда бул барабарсыздыктын эки жагын туундулап
, анда бул барабарсыздыктын эки жагын туундулап  же мындан
же мындан  ,
,  . Мындан
. Мындан  экендигин алабыз.
экендигин алабыз.  бир негизден экинчи негизге өтүү формуласынан пайдаланып
бир негизден экинчи негизге өтүү формуласынан пайдаланып 
 формулалары чыгарылат.
формулалары чыгарылат.
Логарифмдерди эсептөөлөрдү жүргүзүү.
Логарифмдердин эсептөө жумуштарында колдонулушун, таблицаларды пайдала-нууну, логарифмдерди эсептөөлөрдү карап көрөлү. Төмөнкү класстардан каалагандай оң анык санын стандарттуу түрдө  ,
,  ,
,  көрүнүшүндө жазылышы белгилүү. Мисалы, 629=6,29102; 69512= 6,9512104; 0,23=2,310-1; 0,00014=1,410-4; 3700=3,7103; 0,37=3,710-1; …. Мында
көрүнүшүндө жазылышы белгилүү. Мисалы, 629=6,29102; 69512= 6,9512104; 0,23=2,310-1; 0,00014=1,410-4; 3700=3,7103; 0,37=3,710-1; …. Мында  анык сандын тартиби деп аталат. 0,0081=8,110-3 санынын тартиби (-3), ал эми 4326=4,326103 санынын тартиби 3кө барабар. Эми
анык сандын тартиби деп аталат. 0,0081=8,110-3 санынын тартиби (-3), ал эми 4326=4,326103 санынын тартиби 3кө барабар. Эми  санынын логарифми lg α = lg a + lg 10n =lg a + n lg 10 = n+lg a болот.
санынын логарифми lg α = lg a + lg 10n =lg a + n lg 10 = n+lg a болот.  болгондуктан,
болгондуктан,  дурус ондук бөлчөк болот. Ошол себептүү
дурус ондук бөлчөк болот. Ошол себептүү  , … санына барабар. Мындагы
, … санына барабар. Мындагы  бүтүн саны анын характеристикасы, ал эми
бүтүн саны анын характеристикасы, ал эми  - дурус ондук бөлчөгүнүн үтүрдөн кийинки бөлүгү мантиссасы деп аталат. Ар кандай оң сандын тартибин (характеристикасын) аны стандарттуу формада жазып, ал эми анын мантиссасын таблицалардан (Брадистин төрт орундуу таблицасы) табууга болот.
- дурус ондук бөлчөгүнүн үтүрдөн кийинки бөлүгү мантиссасы деп аталат. Ар кандай оң сандын тартибин (характеристикасын) аны стандарттуу формада жазып, ал эми анын мантиссасын таблицалардан (Брадистин төрт орундуу таблицасы) табууга болот.
Ар кандай  он анык сандын логарифмин таблицанын антилогарифм бөлүгүнөн карап жана характеристикасын эске алып, ал сандын тартибинин жакындаштырылган маанисин алууга болот. Мисалы
он анык сандын логарифмин таблицанын антилогарифм бөлүгүнөн карап жана характеристикасын эске алып, ал сандын тартибинин жакындаштырылган маанисин алууга болот. Мисалы  санынын характеристикасы 3 болот, себеби 6871=6,871103;
санынын характеристикасы 3 болот, себеби 6871=6,871103;  санынын характеристикасы – 2 болот, себеби
санынын характеристикасы – 2 болот, себеби 
Суроолор:
Көрсөткүчтүү функциянын аныктамасы.
Көрсөткүчтүү функциянын касиеттери.
Көрсөткүчтүү функциянын мүнөздүү белгиси.
Көрсөткүчтүү функциянын графиги.
Логарифмдин аныктамасы.
Логарифмдин касиеттери.
Логарифмдик функциянын аныктамасы.
Логарифмдик функциянын касиеттери.
Логарифмдик функциянын мүнөздүү белгиси.
Көрсөткүчтүү теңдемелер, түрлөрү, аларды чыгаруунун жолдору.
Логарифмдик теңдемелер, түрлөрү, аларды чыгаруунун жолдору.
Көрсөткүчтүү барабарсыздыктар, түрлөрү, аларды чыгаруунун жолдору.
Логарифмдик барабарсыздыктар, түрлөрү, аларды чыгаруунун жолдору.
Практикалык жумуштар.
Туюнтманын сан маанисин тапкыла: а)  б)
б) 
Туюнтманы жөнөкөйлөткулө:
а) б)
б) 
Тендемени чыгаргыла: а)
 ; б)
; б)


Барабарсыздыкты чыгаргыла: а)  б)
б) 
Тендемелердин системасын чыгаргыла:
а)  б)
б) 
Барабарсыздыкты чыгаргыла: а)  б)
б) 
Тесттик тапшырмалар.
Туюнтманын сан маанисин тап: 
а) 8√2 -1; б) 0,5; в) 1. г)2.
 теңдемесин чыгар.
теңдемесин чыгар.
а)  ; б) 1; в) 7. г)1.
; б) 1; в) 7. г)1.
 барабарсыздыгын чыгар.
барабарсыздыгын чыгар.
а) (-; 0); б) (-; +); в) (0; +). г) туурасы жок.
 туюнтмасын эсепте.
туюнтмасын эсепте.
а) 0AA1; в) А=⅔ г) A=1.
 теңдемесин чыгар.
теңдемесин чыгар.
а) 4 жана –2; б) 2 жана –4; в) 1 жана –2. г) -2 жана 4.







 даражасын,
даражасын,  үчүн кайталап,
үчүн кайталап,  же
же  ;
;  аныктамасын эске алып, кийин касиеттерине токтолобуз.
аныктамасын эске алып, кийин касиеттерине токтолобуз.  ;
;  ;
;  ;
;  ;
;  ;
;  болсо, анда
болсо, анда  ;
;  жана
жана  болсо, анда
болсо, анда  , айрым учурда
, айрым учурда  ;
;  болсо, анда
болсо, анда  ;
;  .
.  саны үчүн
саны үчүн  - даражасын алабыз. Мында
- даражасын алабыз. Мында  эскертилет. Бул
эскертилет. Бул  учурунда да жогорудагы 10-70 касиеттердин туура болору мисалдардын жардамында көрсөтүлөт.
учурунда да жогорудагы 10-70 касиеттердин туура болору мисалдардын жардамында көрсөтүлөт.  болгондо
болгондо  болгондуктан,
болгондуктан,  деп белгилөөнү, себеби
деп белгилөөнү, себеби  болорун айтып, алардын жардамында
болорун айтып, алардын жардамында  болсо,
болсо,  болорун көрсөтүү жолу менен
болорун көрсөтүү жолу менен  рационал көрсөткүчтүү даражасы аныкталат
рационал көрсөткүчтүү даражасы аныкталат  ;
;  ;
;  ;
;  . Ошентип,
. Ошентип,  анык санын
анык санын  рационал көрсөткүчтүү даражага көтөрүүгө мүмкүн. Касиеттери:
рационал көрсөткүчтүү даражага көтөрүүгө мүмкүн. Касиеттери:  ; 20.
; 20.  ; 30.
; 30.  ;
;  ; 50.
; 50.  ; 60.
; 60.  болсо,
болсо,  ;
; болсо, анда
болсо, анда  .
.  ,
,  ,
,  ,
,  ,
,  ,
,  ж.б. иррационал сандарын карайлы. Аларды бүтүнгө, 0,1ге, 0,01ге, 0,001ге, … чейинки тактыктагы кеми менен жана ашыгы менен алынган жакындаштырылган маанилерин карайлы. Мисалы,
ж.б. иррационал сандарын карайлы. Аларды бүтүнгө, 0,1ге, 0,01ге, 0,001ге, … чейинки тактыктагы кеми менен жана ашыгы менен алынган жакындаштырылган маанилерин карайлы. Мисалы,  үчүн алар төмөндөгүчө болот:
үчүн алар төмөндөгүчө болот:  ;
;  ;
;  ;
;  ж. б.
ж. б.  үчүн:
үчүн:  ;
;  ;
;  ;
;  , …. Анда
, …. Анда  даражалары үчүн төмөнкүлөр алынат:
даражалары үчүн төмөнкүлөр алынат:  ;
;  ;
;  ;
;  , …
, … ;
;  ;
;  ;
;  , ….
, …. даражаларынындагы жакындаштырылган сан маанилерин алууга болот. Ошентип
даражаларынындагы жакындаштырылган сан маанилерин алууга болот. Ошентип  анык санын
анык санын  , анык сан көрсөткүчтүү
, анык сан көрсөткүчтүү  даражасына да көтөрүүгө болот.
даражасына да көтөрүүгө болот.  чыныгы сан үчүн
чыныгы сан үчүн  даражасын
даражасын  , анын касиеттери,
, анын касиеттери,  үчүн
үчүн 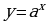 болгондой
болгондой  табыларын,
табыларын,  көз карандылыгын аткарылышын көрсөтүү менен;
көз карандылыгын аткарылышын көрсөтүү менен; болсун. Анда
болсун. Анда  . Эми
. Эми 













 , 0,1х,
, 0,1х,  ж.б. даражалары үчүн да таблицаларды түзүп, даражаладын сан маанилерин табуу көрсөтүлөт. Ошентип, жогорудагы таблицадан көрүнүп тургандай, каалагандай анык х санына 2х даражасынын анык бир мааниси туура келип жатат. Анда 2х даражасы х тин функциясы болот. Ошондой эле 3х, 10х,
ж.б. даражалары үчүн да таблицаларды түзүп, даражаладын сан маанилерин табуу көрсөтүлөт. Ошентип, жогорудагы таблицадан көрүнүп тургандай, каалагандай анык х санына 2х даражасынын анык бир мааниси туура келип жатат. Анда 2х даражасы х тин функциясы болот. Ошондой эле 3х, 10х,  функциялары болушат.
функциялары болушат.  жана
жана  болсун. Бардык анык сандардын көптүгүндө (сан огунда) аныкталып, мааниси
болсун. Бардык анык сандардын көптүгүндө (сан огунда) аныкталып, мааниси  болсо
болсо  турактуу гана мааниге ээ болот. Эгерде
турактуу гана мааниге ээ болот. Эгерде  болсо, анда
болсо, анда  маанисинде
маанисинде  аныкталбайт, терс сандын квадрат тамыры жашабайт. Ошол себептүү
аныкталбайт, терс сандын квадрат тамыры жашабайт. Ошол себептүү  функциясынын аныкталуу областы
функциясынын аныкталуу областы  бардык анык сандардын көптүгү болот.
бардык анык сандардын көптүгү болот.  бардык оң анык сандардын көптүгү болот (графиги ох – огунун үстүндө жатат).
бардык оң анык сандардын көптүгү болот (графиги ох – огунун үстүндө жатат). болгондо,
болгондо,  болгондуктан,
болгондуктан,  үчүн
үчүн  болгондуктан
болгондуктан 

 ,
,  ,
, 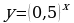 ,
,  учурларынын графиктерин чийдирип, түшүндүрүүгө болот (45-чийме).
учурларынын графиктерин чийдирип, түшүндүрүүгө болот (45-чийме).  түрүндө болот. Көрсөткүчтүү теңдемелерге мисалдар келтирели.
түрүндө болот. Көрсөткүчтүү теңдемелерге мисалдар келтирели.  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. болсо, теңдеменин чыгарылышы жок,
болсо, теңдеменин чыгарылышы жок,  ,
,  болот эмеспи. Бирок
болот эмеспи. Бирок  түрүнө келтирүүгө мүмкүн болгон учурларда
түрүнө келтирүүгө мүмкүн болгон учурларда  барабардыгынан
барабардыгынан  чыгарылышын логарифмсиз эле алууга болот.
чыгарылышын логарифмсиз эле алууга болот.  барабардыгынан
барабардыгынан  алынат.
алынат.  ;
;  ;
; ;
;  белгилөөсүн пайдаланып,
белгилөөсүн пайдаланып,  ,
,  чечимдери келип чыгар эле. Негизинен көрсөткүчтүү теңде-мелерди чыгарууда 4=22; 8=23; 0,5=2-1; 0,1=10-1; 0,25=2-2;
чечимдери келип чыгар эле. Негизинен көрсөткүчтүү теңде-мелерди чыгарууда 4=22; 8=23; 0,5=2-1; 0,1=10-1; 0,25=2-2;  ;
;  ;
;  ж.у.с. теңдеш өзгөртүп түзүүлөрдү пайдалана билүү, белгисиз бир туюнтманы башка бир белгисиз менен белгилеп алып чыгаруу ж.у.с. жолдордон пайдаланууну үйрөнүү зарыл.
ж.у.с. теңдеш өзгөртүп түзүүлөрдү пайдалана билүү, белгисиз бир туюнтманы башка бир белгисиз менен белгилеп алып чыгаруу ж.у.с. жолдордон пайдаланууну үйрөнүү зарыл.  түрүндө болот. Белгисизди өз ичине алган, ар кандай көрсөткүчтүү барабарсыздыкты жогоркудай эң жөнөкөй барабар-сыздыктарга алып келүү жолу менен чыгарылат.
түрүндө болот. Белгисизди өз ичине алган, ар кандай көрсөткүчтүү барабарсыздыкты жогоркудай эң жөнөкөй барабар-сыздыктарга алып келүү жолу менен чыгарылат.  барабарсыздыгы
барабарсыздыгы  , ал эми
, ал эми  барабарсыздыгы менен тең күчтүү болорун, мисалдардын жардамында көрсөтө билүү зарыл. Мисалдар келтирели.
барабарсыздыгы менен тең күчтүү болорун, мисалдардын жардамында көрсөтө билүү зарыл. Мисалдар келтирели. ;
; берилсе,
берилсе,  , мындан
, мындан  же
же  . Мындан
. Мындан  ;
;  берилсе, анда
берилсе, анда  экендигин эске алып,
экендигин эске алып,  ди алабыз.
ди алабыз.  болгондуктан, х 1 же
болгондуктан, х 1 же  түрүндөгү функциялар көп учурайт. Мисалы,
түрүндөгү функциялар көп учурайт. Мисалы,  функциясын
функциясын  деп жазууга болот.
деп жазууга болот. 

 ,
,  түз сызыгын карайбыз (46-чийме).
түз сызыгын карайбыз (46-чийме).  болсун. Анда
болсун. Анда  саны
саны  - негизи боюнча оң
- негизи боюнча оң  санынын логарифми деп,
санынын логарифми деп,  символу менен белги-ленет, мында
символу менен белги-ленет, мында  десек, анда
десек, анда  болот,
болот,  ;
;  ;
;  . Аныктамадан
. Аныктамадан  теңдештиги келип чыгат. Андан кийин логарифмдин касиеттери, аларга мисалдар иштөө үйрөтүлөт. а =10 болсо ондук логарифм деп аталат жана ал
теңдештиги келип чыгат. Андан кийин логарифмдин касиеттери, аларга мисалдар иштөө үйрөтүлөт. а =10 болсо ондук логарифм деп аталат жана ал  деп жазылат. Аларга мисалдар келтирүүгө болот. в0 болгондуктан, он сандын гана логарифми жашайт.
деп жазылат. Аларга мисалдар келтирүүгө болот. в0 болгондуктан, он сандын гана логарифми жашайт. функциясы берилсин. Мында
функциясы берилсин. Мында - функция.
- функция.  болот. Мында
болот. Мында  радиустун функциясы. Мындан
радиустун функциясы. Мындан  катышын жазсак, ал да
катышын жазсак, ал да  - аргумент,
- аргумент,  - функция. Жагы
- функция. Жагы  ,
,  , анын
, анын  катышын алсак
катышын алсак  , ал да
, ал да  функциясында х чондугу у аркылуу бир маанилүү гана аныкталса, анда
функциясында х чондугу у аркылуу бир маанилүү гана аныкталса, анда  аралыгында тескери функциясы
аралыгында тескери функциясы  болот.
болот. , ал эми маанилеринин көптүгү М болот. Математикада
, ал эми маанилеринин көптүгү М болот. Математикада  функциясы жашаса, андагы
функциясы жашаса, андагы  катышындагы х ти у менен, ал эми у ти х менен ал-маштырып,
катышындагы х ти у менен, ал эми у ти х менен ал-маштырып,  деп жазышат жана y = g(x) функциясы y = f(x) функциясына тескери функция деп айтылат.
деп жазышат жана y = g(x) функциясы y = f(x) функциясына тескери функция деп айтылат.  болгон көрсөткүчтүү функциясын карайлы. Анын касиетте-ри боюнча
болгон көрсөткүчтүү функциясын карайлы. Анын касиетте-ри боюнча  бир маанилүү, монотондуу (өсүүчү же кемүүчү) функ-ция. Анда
бир маанилүү, монотондуу (өсүүчү же кемүүчү) функ-ция. Анда  көптүгүндө тескери функция жашайт. Ал тес-кери
көптүгүндө тескери функция жашайт. Ал тес-кери  деп жазылып, ал
деп жазылып, ал  негизи боюнча x тин логарифми деп аталат. Демек,
негизи боюнча x тин логарифми деп аталат. Демек,  дан
дан  келип чыгат, b0.
келип чыгат, b0. 20.
20.  ; 30.
; 30.  40.
40.  (мында х 0, у0); 50.
(мында х 0, у0); 50.  ; 60.
; 60.  ; 70.
; 70.  ; 80.
; 80.  жана
жана  болсо,
болсо,  болот; 90.
болот; 90.  .
.  , х(0;+) болгондо
, х(0;+) болгондо  түрүндөгү функциялар логарифмдик функция деп аталат.
түрүндөгү функциялар логарифмдик функция деп аталат.  ;
; ;
;

 бир маанилүү, үзгүлтүксүз функция болот.
бир маанилүү, үзгүлтүксүз функция болот.  огунун оң жагында жайланып, аны менен кесилишпейт.
огунун оң жагында жайланып, аны менен кесилишпейт.  огун (1;0) чекитинде кесип өтөт (47-чийме).
огун (1;0) чекитинде кесип өтөт (47-чийме).  түрүндөгү теңдемелер (
түрүндөгү теңдемелер ( чечими бар.
чечими бар.  теңдемесинин чечими
теңдемесинин чечими  системасынын чечими болот.
системасынын чечими болот.  теңдемесинин чечими
теңдемесинин чечими  системасы-нан табылат. Алар потенцирлөө жолу менен чыгарылат.
системасы-нан табылат. Алар потенцирлөө жолу менен чыгарылат.  , чечими х=3; 2)
, чечими х=3; 2)  болсо, анын чечими 3 болот; 3)
болсо, анын чечими 3 болот; 3)  берилсе, чечими
берилсе, чечими  болот; 4)
болот; 4)  берилсе, анда
берилсе, анда  , мындан х=3 болот.
, мындан х=3 болот.  түрүндөгү барабарсыздык логарифмдик барабарсыздык деп аталат. Анын чечими
түрүндөгү барабарсыздык логарифмдик барабарсыздык деп аталат. Анын чечими  же
же  системасынын чечими болот, логарифмдик барабар-сыздыктар потенцирлөө жолу менен чыгарылат. Аларды чыгарууда төмөнкү эки эрежени жетекчиликке алуу зарыл:
системасынын чечими болот, логарифмдик барабар-сыздыктар потенцирлөө жолу менен чыгарылат. Аларды чыгарууда төмөнкү эки эрежени жетекчиликке алуу зарыл:  туюнтмасында
туюнтмасында  шартын эске алуу керек;
шартын эске алуу керек; болсо, чечими
болсо, чечими  ;
; болсо, чечими
болсо, чечими  ;
; ;
;  функциясынын туундусу түшүнүгүн, аныктамасын, формула-сын табуу эрежелерин кайталоо зарыл.
функциясынын туундусу түшүнүгүн, аныктамасын, формула-сын табуу эрежелерин кайталоо зарыл. саны, анын сан мааниси бир нече жолдор менен келтирип чыгарылат.
саны, анын сан мааниси бир нече жолдор менен келтирип чыгарылат.  сан удаалаштыгын карап көрөлү.
сан удаалаштыгын карап көрөлү.  ,
, өсүүчү удаалаштык,
өсүүчү удаалаштык, сан удаалаштыгын да
сан удаалаштыгын да  ,
, кемүүчү удаалаштык.
кемүүчү удаалаштык.  . Ошол себептүү
. Ошол себептүү  удаалаш-тыгы өсүүчү жана жогору жагынан чектелген, ал эми
удаалаш-тыгы өсүүчү жана жогору жагынан чектелген, ал эми  удаалаштыгы кемүүчү бирок төмөн жагынан чектелген. Анда Вейерштрастын монотондуу чектелген удаалаштыктары тууралуу теоремасы боюнча
удаалаштыгы кемүүчү бирок төмөн жагынан чектелген. Анда Вейерштрастын монотондуу чектелген удаалаштыктары тууралуу теоремасы боюнча  пределине ээ. Ал
пределине ээ. Ал  , б.а.
, б.а.  болгон иррационалдык сан
болгон иррационалдык сан  .
. аралыгындагы орточо ылдамдыгы
аралыгындагы орточо ылдамдыгы  . Мында
. Мында  туюнтмасынын
туюнтмасынын  болгондогу предели (0;1) чекитинде
болгондогу предели (0;1) чекитинде  болот. Демек,
болот. Демек,  тин умтулган сан мааниси х=0 болгондогу
тин умтулган сан мааниси х=0 болгондогу  , мында
, мында  . Эми
. Эми  нын 2; 2,3; 3; 3,4 ж.б. сан маанилериндеги
нын 2; 2,3; 3; 3,4 ж.б. сан маанилериндеги  ,
,  ,
,  , … функцияларын графиктерин чийип, х=0 болгондо аларга жүргүзүлгөн жанымалардын
, … функцияларын графиктерин чийип, х=0 болгондо аларга жүргүзүлгөн жанымалардын  огу менен түзгөн бурчу жакындаштырылган 350, 400, 480, 510, … болгон. Демек ал жанымалардын бурчтук коэффициенттери
огу менен түзгөн бурчу жакындаштырылган 350, 400, 480, 510, … болгон. Демек ал жанымалардын бурчтук коэффициенттери  ,
,  ,
,  ,
,  … болот. Мындан
… болот. Мындан  болот (
болот ( болот). Мындай сан 2ден чоң, 3 төн кичине сан, ал
болот). Мындай сан 2ден чоң, 3 төн кичине сан, ал  иррационалдык сан болот. Ал сан үчүн
иррационалдык сан болот. Ал сан үчүн  . Анда
. Анда  үчүн
үчүн  . Ошентип
. Ошентип  болот. Эгерде
болот. Эгерде  болсо, анда
болсо, анда  болот эле. Математикада көбүнчө
болот эле. Математикада көбүнчө  .
.  , мындан
, мындан  . Ошол себептүү
. Ошол себептүү  болот. Анда
болот. Анда  , б.а.
, б.а.  . Мындан
. Мындан  ;
;  .
.  формуласынан; 2) логарифмдик теңдештиктин жардамында чыгарууга да болот. Теңдештик боюнча
формуласынан; 2) логарифмдик теңдештиктин жардамында чыгарууга да болот. Теңдештик боюнча  , анда бул барабарсыздыктын эки жагын туундулап
, анда бул барабарсыздыктын эки жагын туундулап  же мындан
же мындан  ,
,  . Мындан
. Мындан  экендигин алабыз.
экендигин алабыз.  бир негизден экинчи негизге өтүү формуласынан пайдаланып
бир негизден экинчи негизге өтүү формуласынан пайдаланып 
 формулалары чыгарылат.
формулалары чыгарылат.  ,
,  ,
,  көрүнүшүндө жазылышы белгилүү. Мисалы, 629=6,29102; 69512= 6,9512104; 0,23=2,310-1; 0,00014=1,410-4; 3700=3,7103; 0,37=3,710-1; …. Мында
көрүнүшүндө жазылышы белгилүү. Мисалы, 629=6,29102; 69512= 6,9512104; 0,23=2,310-1; 0,00014=1,410-4; 3700=3,7103; 0,37=3,710-1; …. Мында  анык сандын тартиби деп аталат. 0,0081=8,110-3 санынын тартиби (-3), ал эми 4326=4,326103 санынын тартиби 3кө барабар. Эми
анык сандын тартиби деп аталат. 0,0081=8,110-3 санынын тартиби (-3), ал эми 4326=4,326103 санынын тартиби 3кө барабар. Эми  дурус ондук бөлчөк болот. Ошол себептүү
дурус ондук бөлчөк болот. Ошол себептүү  , … санына барабар. Мындагы
, … санына барабар. Мындагы  - дурус ондук бөлчөгүнүн үтүрдөн кийинки бөлүгү мантиссасы деп аталат. Ар кандай оң сандын тартибин (характеристикасын) аны стандарттуу формада жазып, ал эми анын мантиссасын таблицалардан (Брадистин төрт орундуу таблицасы) табууга болот.
- дурус ондук бөлчөгүнүн үтүрдөн кийинки бөлүгү мантиссасы деп аталат. Ар кандай оң сандын тартибин (характеристикасын) аны стандарттуу формада жазып, ал эми анын мантиссасын таблицалардан (Брадистин төрт орундуу таблицасы) табууга болот.  он анык сандын логарифмин таблицанын антилогарифм бөлүгүнөн карап жана характеристикасын эске алып, ал сандын тартибинин жакындаштырылган маанисин алууга болот. Мисалы
он анык сандын логарифмин таблицанын антилогарифм бөлүгүнөн карап жана характеристикасын эске алып, ал сандын тартибинин жакындаштырылган маанисин алууга болот. Мисалы  санынын характеристикасы 3 болот, себеби 6871=6,871103;
санынын характеристикасы 3 болот, себеби 6871=6,871103;  санынын характеристикасы – 2 болот, себеби
санынын характеристикасы – 2 болот, себеби 
 б)
б) 
 б)
б) 

 ; б)
; б)


 б)
б) 
 б)
б) 
 б)
б) 

 теңдемесин чыгар.
теңдемесин чыгар. ; б) 1; в) 7. г)1.
; б) 1; в) 7. г)1. барабарсыздыгын чыгар.
барабарсыздыгын чыгар. туюнтмасын эсепте.
туюнтмасын эсепте.  теңдемесин чыгар.
теңдемесин чыгар.









