Просмотр содержимого документа
«Краткий курс алгебра 7 класс»
Числовые и буквенные выражения.
При решении задач иногда только записывают действия , а выполняют их потом. Полученные записи называют числовыми выражениями.
Число, получаемое в результате выполнения всех указанных действий в числовом выражении ,называют значением этого выражения.
Выражение , содержащее буквы , называют буквенным (алгебраическим ) выражением.
Числа , которыми заменяют букву , называют значениями этой буквы.
Поскольку буквам , входящим в состав алгебраического выражения , можно придавать различные числовые значения , эти буквы называют переменными.
Если при конкретных значениях букв (переменных) алгебраическое выражение имеет числовое значение , то указанные значения переменных называют допустимыми ; если же при конкретных значениях букв (переменных) алгебраическое выражение не имеет смысла , то указанные значения переменных называют недопустимыми.
Решение задачи разбивается на 3 этапа а). Составление математической модели; б). Работа с математической моделью; в).Ответ на вопрос задачи.
Существует несколько видов моделей: Словесная модель(реальные ситуации описываются словами), алгебраическая модель (алгебраически ), геометрическая модель ( в геометрии и графики).
Линейные уравнения с одним неизвестным.
Решить линейное уравнение – это значит найти все те значения переменной , при каждом из которых уравнение обращается в верное числовое равенство. Каждое такое значение переменной называют корнем уравнения.
Линейным уравнением с одной переменной х называют уравнение вида ах+б=0 , где а и б - любые числа ( коэффициенты).
Алгоритм решения линейного уравнения ах+б=0 в случае когда а ≠ 0.
Преобразовать уравнение к виду ах= -б.
Записать корень уравнения в виде х= ( -б) : а , или, что то же самое , х= - б/а.
Алгоритм решения линейного уравнения ах+б=сх+д (а≠ с )
Перенести все члены уравнения из правой части в левую с противоположными знаками.
Получится уравнение вида кх+м=0.
Координатная прямая.
Прямую , L на которой выбрана начальная точка О ( начало отсчета ), масштаб ( единичный отрезок, т.е.отрезок , длина которого считается равной 1 ) и положительное направление, .
называют координатной прямой или координатной осью.
Числовые промежутки.
Луч-[а;∞) ---х ≥ а ; (а;б]--- х ≤ б.
Открытый луч – (а;∞)--- х › а ; (∞;б) --- х ‹ б.
Интервал – (а;б) --- а‹ х ‹ б
Отрезок - [а;б] ---- а ≤ х ≤ б
Полуинтервал - [а;в) --- а ≤ х ‹ б ; (а;б] --- а ‹ х ≤ б
Координатная плоскость.
Прямоугольной системой координат на плоскости называют две перпендикулярные координатные прямые- х и у , которые пересекаются в начале отсчета – точке О. Точка О называется началом координат.
Плоскость на которой выбрана система координат , называют координатной плоскостью.
Координатную прямую х называют осью абсцисс , а у – осью ординат.
Прямые углы , образованные осями координат , называют координатными углами.
Алгоритм отыскания координат точки М, заданной в системе координат хОу.
Провести через точку М прямую , параллельную оси У, и найти координату точки пересечения этой прямой с осью Х – это будет абсцисса точки М.
Провести через точку М прямую , параллельную оси Х, и найти координату точки пересечения этой прямой с осью У – это будет ордината точки М.
Алгоритм построения точки М(а;б) в прямоугольной системе координат хОу.
Построить прямую у=б.
Найти точку пересечения построенных прямых – это и будет точка М(а;б).
Линейное уравнение с двумя переменными.
Уравнение вида ах+ву+с=0 , где а,в,с –числа ( коэффициенты ) называют линейным уравнением с двумя переменными х и у ( или двумя неизвестными х и у ).
Решением уравнения ах+бу+с=0 называют всякую пару чисел (х;у) , которая удовлетворяет этому уравнению, т.е.обращает равенство с переменными ах+бу+с=0 в верное числовое равенство.
Графиком линейного уравнения является прямая.
Теорема №1. Если хотя бы один из коэффициентов а,б линейного уравнения ах+бу+с=0 отличен от нуля , то графиком уравнения служит прямая линия.
Алгоритм построения графика уравнения ах+бу+с=0 , где а≠0, б≠0.
Придать переменной х конкретное значение х=х₁ ( х=0 ) найти из уравнения ах₁+бу+с=0 соответствующее значение у=у₁.
Придать переменной у конкретное значение у=у₂ ( у=0 ) найти из уравнения ах+бу₂+с=0 соответствующее значение х=х₂.
Построить на координатной плоскости хОу точки (х₁;у₁) и (х₂;у₂).
Провести через эти две точки прямую – она и будет графиком уравнения ах+бу+с=0.
Линейное уравнение вида ах+бу+с=0 ( если б≠ 0) преобразованное к виду у=кх+м, где к и м коэффициенты . к= - а/б , м= - с/б будем называть линейной функцией.
У линейной функции х- независимая переменная ( или аргумент ), у – зависимая переменная ( или функция ).
Теорема 2. Графиком линейной функции у= кх +м является прямая.
Если к › 0 то функция у=кх + м возрастает.
Если к ‹ 0 то функция у=кх + м убывает.
Теорема 3. Графиком линейной функции у=кх является прямая , проходящая через начало координат.
Коэффициент К в записи у=кх называют угловым коэффициентом.
Теорема 4. Прямая ,служащая графиком линейной функции у=кх+м , параллельна прямой , служащей графиком линейной функции у=кх.
Если к › 0, то прямая у=кх+м образует с положительным направлением оси Х острый угол, а если к ‹ 0 ,- тупой угол.
Теорема 5. Пусть даны две линейные функцииу=к₁х+м₁ и у=к₂х+м₂. Прямые , служащие графиками заданных линейных функций: 1. Параллельны , если к₁=к₂, м₁≠м₂ ; 2. Совпадают , если к₁=к₂, м₁=м₂; 3. Пересекаются , если к₁≠к₂
Системы двух линейных уравнений с двумя переменными.
Если даны два линейных уравнения с двумя переменными Х и У: и поставлена задача найти такие пары значений (х;у), которые одновременно удовлетворяют и тому , и другому уравнению , то говорят, что заданные уравнения образуют систему уравнений.
Пару значений (х;у), которая одновременно является решением и первого и второго уравнений системы, называют решением системы.
Решить систему – это значит найти все её решения или установить , что их нет.
Графический метод решения системы.
Если прямые параллельны ,то система не имеет решений ( система несовместна).
Если прямые совпадают, то система имеет бесконечное множество решений ( система неопределенна)
Если прямые пересекаются , то координаты точки пересечения являются решением системы.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки.
Выразить У через Х из первого уравнения системы.
Подставить полученное на первом шаге выражение вместо У во второе уравнение системы.
Решить полученное на втором шаге уравнение относительно Х.
Подставить найденное на третьем шаге значение Х в выражение У через Х , полученное на первом шаге.
Записать ответ в виде пары значений (х;у) , которые были найдены соответственно на третьем и четвертом шаге.
Метод алгебраического сложения.
Степень с натуральным показателем.
Под аⁿ, где n=2,3,4,5,…… понимают произведение n одинаковых множителей , каждым из которых является число а. Выражение аⁿ называют степенью, число а - основанием степени, число n- показателем степени.
Степенью числа а с показателем 1 называют само это число.
1ⁿ=1, 0ⁿ=0, если n – четное число , то (-1)ⁿ=1, если n – нечетное число , то (-1)ⁿ= -1.
Теорема 1. Для любого числа а и любых натуральных чисел n и к справедливо равенство 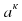 *
* =
=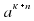 ( При умножении степеней с одинаковыми основаниями показатели складываются)
( При умножении степеней с одинаковыми основаниями показатели складываются)
Теорема 2. Для любого числа а≠0 и любых натуральных чисел n и к , таких что n › к, справедливо равенство аⁿ: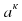 =
= 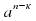 ( При делении степеней с одинаковыми основаниями из показателя делимого вычитают показатель делителя).
( При делении степеней с одинаковыми основаниями из показателя делимого вычитают показатель делителя).
Теорема 3. Для любого числа а и любых натуральных чисел n и к справедливо равенство  =
=  ( При возведении степи в степень показатели умножаются).
( При возведении степи в степень показатели умножаются).
Чтобы перемножить степени с одинаковыми показателями , достаточно перемножить основания , а показатель степени оставить неизменным.  *
* =
=
Чтобы разделить друг на друга степени с одинаковыми показателями , достаточно разделить одно основание на другое , а показатель степени оставить неизменным. 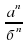 =
= , где б ≠ 0
, где б ≠ 0
Если а ≠ 0, то 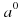 = 1.
= 1.
Одночлены . Арифметические операции над одночленами.
Одночленом называют алгебраическое выражение , которое представляет собой произведение чисел и переменных , возведенных в степень с натуральными показателями.
Числовой множитель одночлена , записанного в стандартном виде, называют коэффициентом одночлена.
Чтобы привести одночлен к стандартному виду, нужно: а) перемножить все числовые множители и поставить их произведение на первое место; б) перемножить все имеющиеся степени с одним буквенным основанием; в) перемножить все имеющиеся степени с другим буквенным основанием и т.д.
Алгоритм сложения одночленов.
Привести все одночлены к стандартному виду.
Убедиться , что все одночлены подобны; если же они не подобны , то алгоритм далее не применяется.
Найти сумму коэффициентов подобных одночленов.
Записать ответ: одночлен подобный данным , с коэффициентом , полученным на третьем шаге.
Многочлены. Арифметические операции над многочленами.
Многочленом называют сумму одночленов.
Слагаемые ( одночлены ) , из которых состоит многочлен , называют членами многочлена.
Если в многочлене все члены записаны в стандартном виде и приведены подобные члены, то говорят , что многочлен приведен к стандартному виду.
Чтобы записать алгебраическую сумму нескольких многочленов в виде многочлена стандартного вида, нужно раскрыть скобки и привести подобные члены.
Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и полученные произведения сложить.
Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена поочерёдно на каждый член другого многочлена и полученные произведения сложить.
Квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение.  =
=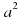 +2аб+
+2аб+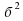
Квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение. =
=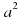 -2аб+
-2аб+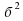
Разность квадратов двух выражений равна произведению суммы этих выражений на их разность. 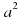 -
- 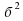 = (а- б)(а+ б).
= (а- б)(а+ б).
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы. 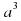 -
- 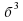 = (а- б)(
= (а- б)(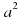 + аб+
+ аб+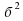 ).
).
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. 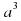 +
+ 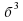 = (а + б)(
= (а + б)(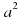 - аб+
- аб+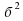 ).
).
Чтобы разделить многочлен на одночлен , нужно каждый член многочлена разделить на этот одночлен и полученные результаты сложить.
Разложение многочленов на множители.
Способ вынесения общего множителя за скобки.
Алгоритм отыскания общего множителя нескольких одночленов. а) Найти наибольший делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем ( разумеется , это относится только к случаю целочисленных коэффициентов) б) Найти переменные , которые входят в каждый член многочлена , и выбрать из них наименьший ( из имеющихся ) показатель степени. в) Произведение коэффициента , найденного на первом шаге , и степеней, найденных на втором шаге , является общим множителем , который целесообразно вывести за скобки.
Способ группировки.
Сокращение алгебраических дробей.
Алгебраической дробью называют отношение двух многочленов P и Q. При этом используют запись  , где P – числитель , Q – знаменатель алгебраической дроби.
, где P – числитель , Q – знаменатель алгебраической дроби.
Тождества.
Всякую замену одного выражения другим , тождественно равным ему, называют тождественным преобразованием выражения.
Тождество – это равенство , верное при любых допустимых значениях входящих в его состав переменных.
Функция у =  и её график.
и её график.
Графиком функции у =  является парабола.
является парабола.
Ось у , является осью симметрии параболы.
Ось симметрии разрезает параболу на две части , которые называют ветвями параболы.
Точка , в которой смыкаются обе ветви и которая лежит на оси симметрии параболы , называют вершиной параболы.







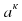 *
* =
=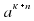 ( При умножении степеней с одинаковыми основаниями показатели складываются)
( При умножении степеней с одинаковыми основаниями показатели складываются)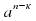 ( При делении степеней с одинаковыми основаниями из показателя делимого вычитают показатель делителя).
( При делении степеней с одинаковыми основаниями из показателя делимого вычитают показатель делителя). =
=  ( При возведении степи в степень показатели умножаются).
( При возведении степи в степень показатели умножаются). =
=
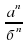 =
= , где б ≠ 0
, где б ≠ 0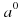 = 1.
= 1. =
=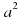 +2аб+
+2аб+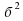
 =
=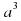 -
-  = (а- б)(
= (а- б)(

















