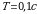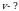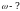Криволинейное движение. Линейная и угловая скорость
Цель урока: продолжение формирования знаний по изучению видов движения.
Задачи:
Образовательная: дать определения криволинейного движения, линейной и угловой скорости и центростремительного ускорения.
Развивающая: добиваться правильного произношения и написания, толкования и использования физических терминов, систематического пополнения их запаса.;
Воспитательная: повышение познавательной активности учащихся; формирование добросовестного отношения к учебному труду, положительной мотивации к учению.
План урока
Организационный момент
Домашнее задание
Изучение нового материала.
Закрепление материала
Подведение итогов урока
Ход урока
Организационный момент
Здравствуйте. Садитесь. Проверьте, все ли у вас готово к уроку? Итак, начнем сегодняшний урок
Домашнее задание
А теперь достаньте свои дневники и запишите домашнее задание: прочитать параграф §14,выучить все формулы и определения
Изучение нового материала
До сегодняшнего урока вы изучали прямолинейное движение. Кто мне скажет какие именно разновидности этого движения вы изучили? равномерное и равнопеременное.
Однако, в повседневной жизни, наиболее часто встречается криволинейное движение.
Давайте запишем определение криволинейного движения
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу).
Определять кинематические характеристики прямолинейного движения мы уже умеем. Теперь рассмотрим кинематику криволинейного движения, для это рассмотрим движение тела по криволинейной траектории.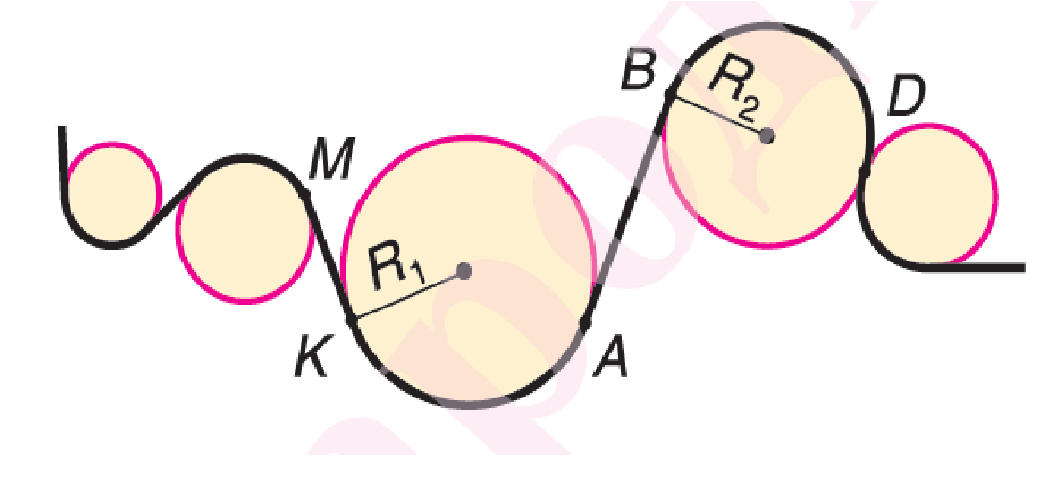
Криволинейную траекторию можно представить как состоящую из прямоугольных участков (MK, АВ) и дуг (КА, ВD) окружностей соответствующих радиусов R1 , R2.
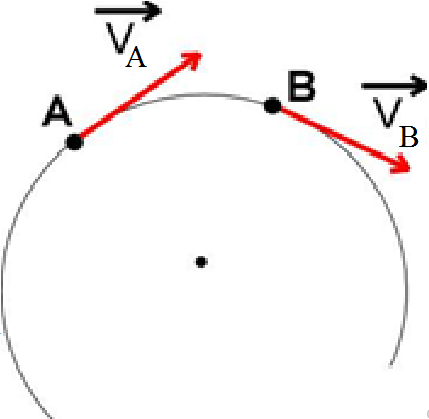 Более подробно рассмотрим тело по окружности, с учётом того, что примем его за материальную точку. Двигаясь по траектории, в каждый момент времени тело имеет мгновенную скорость, или как её называют линейной скоростью при движении по окружности(рис.2)
Более подробно рассмотрим тело по окружности, с учётом того, что примем его за материальную точку. Двигаясь по траектории, в каждый момент времени тело имеет мгновенную скорость, или как её называют линейной скоростью при движении по окружности(рис.2)
Запишем определение мгновенной скорости
Мгновенная скорость - скорость в данной точке траектории, направленная по касательной к траектории.
Теперь охарактеризуем положение движущегося тела, проведём вектор  из центра нашей окружности в точку где находится тело в момент времени t. Вектор
из центра нашей окружности в точку где находится тело в момент времени t. Вектор  называют радиус-вектором
называют радиус-вектором
Предположим, что за время  точка переместилась из точки А в точку B, тогда за это время радиус-вектор повернулся на угол
точка переместилась из точки А в точку B, тогда за это время радиус-вектор повернулся на угол 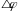
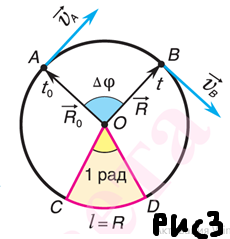 В СИ угол поворота измеряется в радианах. Запишем определение 1 рад.
В СИ угол поворота измеряется в радианах. Запишем определение 1 рад.
1 рад - это центральный угол опирающийся на дугу длина которой равна радиусу окружности.
Центральный угол – это угол образуемый двумя радиусами.
Итак, если тело прошло путь 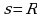 ,то это значит, что угол 1 рад, если угол будет 0,5 радиуса
,то это значит, что угол 1 рад, если угол будет 0,5 радиуса  какой это будет угол? Если дуги взять в 2 раза меньше, то на какой угол она будет опираться. А если
какой это будет угол? Если дуги взять в 2 раза меньше, то на какой угол она будет опираться. А если 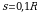 на какой угол она будет опираться? Правильно 0,1 рад. А если
на какой угол она будет опираться? Правильно 0,1 рад. А если 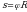 ? Правильно
? Правильно 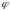 радиан.
радиан.
| 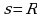
| 1 рад |
| 
| 0,5 рад
|
| 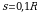
| 0,1 рад
|
| 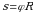
| 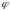 рад рад
|
Давайте перепишем эту формулу.
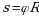 (1)
(1)
Если угол выражается в радиусах, то длину дуги легко найти, надо этот угол умножить на радиус. Из этой же формулы мы и найдём угол через дуги и радиус.
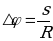 (2)
(2)
Как же связаны между собой градусы и радианы?
Например, если радиус-вектор совершил полный оборот, т.е прошёл 3600,то его путь будет равный длине окружности. Длина окружности чему будет равна? Правильно 2ПR.
Тогда 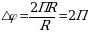 рад.
рад.
Теперь мы можем записать
3602=2П рад
1800=П рад
Тогда чтобы получить 1 рад, что необходимо сделать? Правильно, разделить левую и правую часть на 1800
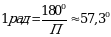 (3)
(3)
Теперь приступим к рассмотрению основных характеристик движения по окружности.
Для этого рассмотрим равномерное движение тела по окружности, тоесть за любые равные промежутки времени тело проходит одинаковые пути и модуль их скорости 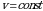 Однако по рисунку 3 видно, что направление вектора непрерывно изменяется, а это значит, что при равномерном движении по окружности линейная скорость тела не постоянная.
Однако по рисунку 3 видно, что направление вектора непрерывно изменяется, а это значит, что при равномерном движении по окружности линейная скорость тела не постоянная. 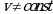 и радиус-вектор этого тела совершает равномерное вращение
и радиус-вектор этого тела совершает равномерное вращение
Быстроту вращательного движения характеризуют угловой скоростью, обозначается угловая скорость греческой буквой омега 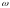
Запишем определение, физический смысл и единицу измерения угловой скорости .
При равномерном вращении угловая скорость равна отношению угла поворота радиус-вектора к промежутку времени, за который этот поворот произошёл
Формула угловой скорости: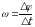 (4)
(4)
Физический смысл угловой скорости: угловая скорость показывает на какой угол повернётся радиус-вектор за единицу времени.
Единицей угловой скорости в СИ являются 1 радиан в секунду 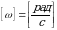
Какая же связь между линейной скоростью тела 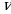 угловой скоростью
угловой скоростью 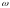 ?
?
Чтобы выяснить какая между ними связь подставим 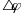 из первой формулы и получим.
из первой формулы и получим. 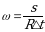 .
.
Что же в этой формуле 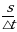 ? Правильно это скорость
? Правильно это скорость 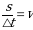 . Тогда и получим связь между линейной и угловой скоростью:
. Тогда и получим связь между линейной и угловой скоростью:
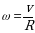 (5)
(5)
Вам с 8 класса известна величина которая представляет собой время за которое тело совершает полный оборот, как она называется? Период.
Период обращения является второй важной характеристикой движения тела по окружности. Давайте запишем определение периода обращения.
Период обращения – это времени, за которое тело (м.т) совершает один полный оборот по окружности.
Обозначается обращения буквой Т, в СИ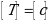
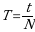 где N - число оборотов (6)
где N - число оборотов (6)
Есть ещё одна величина которая представляет число оборотов совершаемы телом за единицу времени, в 8 классе вы уже с ней встречались, как она называется? Правильно, частота вращения. Запишем определение частоты вращения.
Частота вращения тела – физическая равна числу оборотов совершаемых телом за единицу времени.
Обозначается частота буквой ню 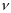 , в СИ
, в СИ 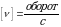 или
или 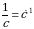
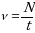 где N - число оборотов(7)
где N - число оборотов(7)
Период и частота взаимно обратные величины 
Теперь нам необходимо связать Период Т и частоту 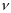 с угловой скоростью.
с угловой скоростью.
Пусть радиус-вектор за какое-то время Т делает полный оборот и поворачивается на угол 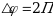 ,тогда получим, что угловая скорость согласно формуле (4) будет равна
,тогда получим, что угловая скорость согласно формуле (4) будет равна 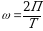 (8)
(8)
А так как частота 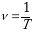 , тогда угловая скорость запишется
, тогда угловая скорость запишется
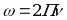 (9)
(9)
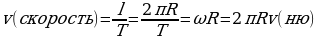
Все эти рассуждения были для движения тела по окружности, а как эти характеристики будут вести себя при движении вокруг неподвижной оси.
Пример движения по неподвижной оси есть офисный стул.
Кто мне скажет, какие точки описывают окружность, а какие покоятся при таком движении? При движении точки находящиеся на оси покоятся, а остальные лежащие в плоскости - описываю окружность. В данном случае период, частота и угловая скорость для всех точек тела-одинаковы. Из формулы (5) видно, что линейная скорость точек вращения тела прямо пропорциональна расстоянию до оси вращения.
Запишем это 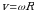 (10)
(10)
Закрепление материала
Для того, чтобы закрепить пройденную тему рассмотрим пример решения задачи.
Барабан центрифуги для вращении отжима белья вращается равномерно с частотой  . Диаметр барабана d=40 cм. Определите период и угловую скорость вращения барабана. Найдите модуль линейной скорости точек его поверхности.
. Диаметр барабана d=40 cм. Определите период и угловую скорость вращения барабана. Найдите модуль линейной скорости точек его поверхности.
| Дано 
d=40 cм. | СИ 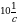
0,4м
| Решение Период вращения связанный с частотой соотношением 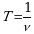
Отсюда 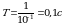 Угловая скорость вращения барабана(формула 9) 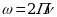
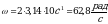
Линейная скорость на поверхности барабана(формула 10) 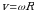
Так как радиус 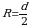 Получим Получим 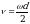
Тогда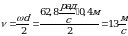 Ответ: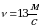 , ,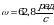 , ,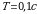 |
| Т-? 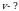
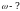
|
V. Подведение итогов урока
Теперь давайте подведём некоторые итоги, что мы сегодня узнали:
Кроме прямолинейного движения существует ещё и криволинейное движение, которое имеет свои характеристики.
Угол поворота измеряется в радианах, а не в градусах и находится он по формуле
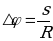
Угловая скорость обозначается буквой омега и она равна отношению угла поворота радиус-вектора к промежутку времени, за который этот поворот произошёл
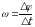
Единица угловой скорости – 1 радиан в секунду
Период обращения – одна из характеристик, показывающая время , за которое тело делает полный оборот, и измеряется в секундах
Другая характеристика тесно связанная с периодом обращения – частота вращения и она равная отношению числа оборотов совершаемых телом за единицу времени.
Модули линейный скоростей точек вращающегося тела прямо пропорциональны расстоянию до оси вращения.
Всем спасибо за урок.







 Более подробно рассмотрим тело по окружности, с учётом того, что примем его за материальную точку. Двигаясь по траектории, в каждый момент времени тело имеет мгновенную скорость, или как её называют линейной скоростью при движении по окружности(рис.2)
Более подробно рассмотрим тело по окружности, с учётом того, что примем его за материальную точку. Двигаясь по траектории, в каждый момент времени тело имеет мгновенную скорость, или как её называют линейной скоростью при движении по окружности(рис.2)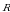 из центра нашей окружности в точку где находится тело в момент времени t. Вектор
из центра нашей окружности в точку где находится тело в момент времени t. Вектор 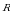 называют радиус-вектором
называют радиус-вектором 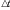 точка переместилась из точки А в точку B, тогда за это время радиус-вектор повернулся на угол
точка переместилась из точки А в точку B, тогда за это время радиус-вектор повернулся на угол 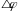
 В СИ угол поворота измеряется в радианах. Запишем определение 1 рад.
В СИ угол поворота измеряется в радианах. Запишем определение 1 рад.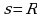 ,то это значит, что угол 1 рад, если угол будет 0,5 радиуса
,то это значит, что угол 1 рад, если угол будет 0,5 радиуса  какой это будет угол? Если дуги взять в 2 раза меньше, то на какой угол она будет опираться. А если
какой это будет угол? Если дуги взять в 2 раза меньше, то на какой угол она будет опираться. А если 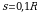 на какой угол она будет опираться? Правильно 0,1 рад. А если
на какой угол она будет опираться? Правильно 0,1 рад. А если 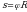 ? Правильно
? Правильно 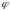 радиан.
радиан. 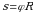
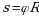 (1)
(1)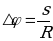 (2)
(2)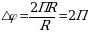 рад.
рад. 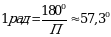 (3)
(3)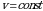 Однако по рисунку 3 видно, что направление вектора непрерывно изменяется, а это значит, что при равномерном движении по окружности линейная скорость тела не постоянная.
Однако по рисунку 3 видно, что направление вектора непрерывно изменяется, а это значит, что при равномерном движении по окружности линейная скорость тела не постоянная. 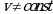 и радиус-вектор этого тела совершает равномерное вращение
и радиус-вектор этого тела совершает равномерное вращение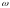
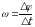 (4)
(4)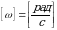
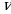 угловой скоростью
угловой скоростью 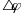 из первой формулы и получим.
из первой формулы и получим. 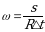 .
. 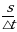 ? Правильно это скорость
? Правильно это скорость 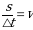 . Тогда и получим связь между линейной и угловой скоростью:
. Тогда и получим связь между линейной и угловой скоростью: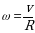 (5)
(5)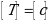
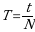 где N - число оборотов (6)
где N - число оборотов (6)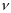 , в СИ
, в СИ 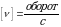 или
или 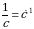
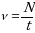 где N - число оборотов(7)
где N - число оборотов(7)
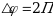 ,тогда получим, что угловая скорость согласно формуле (4) будет равна
,тогда получим, что угловая скорость согласно формуле (4) будет равна 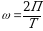 (8)
(8)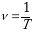 , тогда угловая скорость запишется
, тогда угловая скорость запишется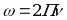 (9)
(9)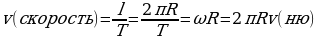
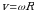 (10)
(10) . Диаметр барабана d=40 cм. Определите период и угловую скорость вращения барабана. Найдите модуль линейной скорости точек его поверхности.
. Диаметр барабана d=40 cм. Определите период и угловую скорость вращения барабана. Найдите модуль линейной скорости точек его поверхности. 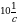
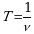
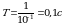
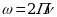
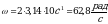
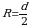 Получим
Получим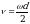
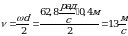
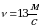 ,
,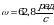 ,
,