Циклоидальные кривые

обычная
Циклоида описывается параметр ур
| Параметрические уравн | В декарт коорд |
| 
| 
|
Циклоида мб получена как решение дифф ур: 
Для провед касательной к циклоиде в произв её т A дост соед эту точку с верхней т производящ окружности. Соед A с нижней т произв окружности, получ нормаль.
Длина арки циклоиды = 8r.
Пл под каждой аркой циклоиды в 3р больше, чем п порожд круга.
Радиус кривизны у 1й арки циклоиды равен  .
.
Перевёрнутая» циклоида явл кривой скорейш спуска (брахистохр). Б того, она имеет также свво таутохронн: тяжёлое тело, поме в любую точку арки циклоиды, достиг горизо за 1 и то же время.
Период колеб м т, скользящей по перевёрн циклоиде, не зависит от ампл, этот факт б ис Гюйгенсом для созд точных механических часов.

растянутая циклоида (траектория внутр точки колеса)

Сжатая циклоида (траектория внешней точки колеса)
Внутреннее качение окружности по окружности
Гипоцикло́ида — плоская кривая, обр точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
Если радиус подвижного круга б в 2. 3 вообще в n раз меньше рад непод, то получится гипоциклоида с 2, 2, вообще с n заострениями
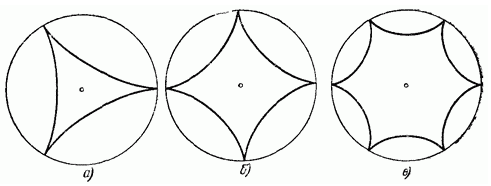 Различные гипоциклоиды.
Различные гипоциклоиды.


удлиненные гипоциклоиды укороченные гипоциклоиды
гипоциклоиду с 4заострениями наз иначе астроидой, что зн «звездообразная»
 где
где  , где R — рад непод , r — катящ окружнос
, где R — рад непод , r — катящ окружнос
Модуль вел k опр форму гипоциклоиды. При k = 2 гипоциклоида диаметр неподв окружности,
при k = 4 явл астроидой.
Пример гипоциклоид
| 
k=3 — Дельтоида | 
k=4 — Астроида | 
k=5 | 
k=6 |
| 
k=2,1 | 
k=3,8 | 
k=5,5 | 
k=7,2 |
Дельтоида (кривая Штейнера) — плоская кривая, опис фикс т окружн, катящ по внутр стороне др окружн, рад кот в 3 р больше рад 1-й. Её св--ва впер изуч Л. Эйлер в 18в и Я. Штейнер в 19в.
Уравн  , где
, где  — треть полярного угла.
— треть полярного угла.
Длина кривой  , Площадь, огр дельтоидой,
, Площадь, огр дельтоидой,  .
.
Внешнее качение окружности по окружности (эпициклоида)
Если центр неподв окружности нах в нач координат и, её радиус= R, радиус катящейся по ней окружнr, то эпициклоида опис параметрическим уравн отн  :
:
если  то
то
| Эпициклоиды при разных значениях параметра k: |
| k = 1 (кардиоида) | k = 2 (нефроида) | k = 3 | k = 4 |
| 
| 
| 
| 
|
Эволюта и эвольвента
Эволютой наз гм ц кривизны данн кривой. кривая по отн к эволюте наз эвольвентой. из опр нормаль к эвольвенте ( на кот лежит ц кривизны ) явл касательной к эволюте.. Если гибкую нерастяж нить, обтягив зад вып линию L! развёрт, сохр пост натянутой, то каждая её точка опишет эвольвенту L. Поэтому эвольвенту наз ещё развёрткой. Эта оп развёртки нити равнос качению без скольжения прямой линии по дан линии L!; Каждая то такой прямой опис эвольвенту L линии L!. Отсюда данная эволюта L! имеет беск число эвольвент L. В то же вр любая данная линия, рассм как эвольвента, имеет только 1эволюту
Эвольвенты окружности
В техн эвольвенту окружности примен для профилир зубч зацепл. Пусть бок поверхн зубьев 2 цилиндрич зубч колёс с паралл осями вращ, прохои через т O1 и O2 (рис. б), очерч по эволь-вентам, а линия контакта зубьев при нек взаим полож колёс прох через т К. Тогда в т К нормали КМ1 и КМ2 к эвольвенте Э1 и Э2 б т лежать на отр М1М2 общей касат окружн рад R1 и R2 соотв (эти окружн по отн к эвольв явл эволютами). При вращ колёс т К перемещ вдоль отр М1М2 (новое полож эвольвент пока на (рис. б) штрих лин) до тех пор, пока рассм пара зубьев не выйдет из вз зацепл. но зубч передачу профилирована так, что к этому времени возн зацепл между др парой зубьев, и линия их контакта снова перемещ вдоль отрезка М1М2
Кардиоида.
Если через точку, взятую на окружн, провести во всех направл лучи, пересек эту окр, и из каждой т пересеч отл вдоль каждого луча в обе стор отр= диаметру этой окружн, то получим т кривой, наз кардиоидой. Для постр кардиоиды возь на окруж диам d т К (фиг. 111) и пров под произ углами a1, a2 т. д. лучи K1, K2, КЗ. машиностр кардиоида примен при изготовл кулачков и др деталей.
Спираль Архимеда
Архим спираль — спираль, плоская кривая, траектория т M, кот равном движ вдоль луча OV с нач в O, в то время как сам луч OV равном вращ вокруг O. Др сл, расст ρ = OM пропорц углу поворота φ луча OV. Ур Архим спирали в полярной сме к=т ) 

где k — смещ т M по лучу r, при повороте на угол 1 рад.Повороту прямой на 2π соотв смещ a = |BM| = |MA| = 2kπ. Число a — наз шагом спирали.
исп как мех=м для передачи воды в оросит каналы из низколеж водоемов. Винт Архимеда стал прообразом шнека – у=ва, шир исп в разл машин для перемешивания жидких, сыпучих и тестообр м-лов.. Шнек — стержень со сплошной винтовой поверхностью вдоль продольн оси.его разновидность - винтовой ротор в мясорубке. самоцентрир патрон. исп в шв машинках для равном наматывания ниток. В авто технике архимедовы винты м примен вместо колес. Принцип движ шнек ороторного вездехода -. Маш оборуд 2 или б соосными с направлением движения роторами — винтами Арх. При вращ они отталкиваются от кашеобр или жидкой субст, по кот движ вездеход, и продвигают его вперед.











 Различные гипоциклоиды.
Различные гипоциклоиды.

 где
где 







 , где
, где 









