Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«СЫКТЫВКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Питирима Сорокина»
(ФГБОУ ВО «СыктГУ им. П. Сорокина»)
Институт точных наук и информационных технологий
Кафедра физико-математического и информационного образования
КУРСОВАЯ РАБОТА
Алгоритм отжига
Специальность 050201.65 «МАТЕМАТИКА» с дополнительной специальностью 050202.65 «ИНФОРМАТИКА»
Исполнитель: студентка 1515 группы Бабиева Ирина Владимировна
Научный руководитель: к. пед. н. доцент Поспелов Михаил Владимирович
Сыктывкар 2015
Оглавление
Введение…………………………………………………………………....3
1. Глобальная оптимизация………………………………………………..4
2.Алгоритм имитации отжига……………………………………………..6
3. Схемы алгоритма отжига
3.1. Больцмановский отжиг........................................................................11
3.2. Отжиг Коши (быстрый отжиг)……………………………………….11
3.3. Сверхбыстрый отжиг…………………………………………………12
3.4. Алгоритм Ксин Яо…………………………………………………….13
3.5. Метод “ тушения ”…………………………………………………….14
3.6. Естественная мотивация………………………………………………15
4. Исследуемые задачи
4.1. Задача о расстановке N ферзей……………………………………….16
4.2. Задача об «Умном муравье»………………………………………….17
4.3.Задача Коммивояжера…………………………………………………17
Заключение…………………………………………………………………19
Литература………………………………………………………………….20
Приложение к задаче о расстановке ферзей……………………………...21
Приложение к задаче Коммивояжера…………………………………….27
Введение
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим метод имитации отжига.
Название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на методе Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет вероятностных алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации.
Метод отжига – это техника оптимизации, использующая упорядоченный случайный поиск на основе аналогии с процессом образования веществом кристаллической структуры с минимальной энергией при охлаждении. История метода отжига начинается с 1953 года. В этом году Н. Метрополисом был разработан алгоритм симуляции установления равновесия в системе с множеством степеней свободы при заданной температуре. В начале 80-х у С. Киркпатрика впервые появилась идея использовать этот алгоритм не только для моделирования физических систем, но и для решения некоторых задач оптимизации.
Целью курсовой работы является изучение алгоритма отжига.
Задачи:
1. Отобрать теоретический материал по теме «Алгоритм отжига».
2. Рассмотреть различные схемы метода отжига.
3. Формировать способность практического применения алгоритма.
Алгоритмы глобальной оптимизации
Все представленные ранее методы обучения нейронных сетей являются локальными. Они ведут к одному из локальных минимумов целевой функции, лежащему в окрестности точки начала обучения. Только в ситуации, когда значение глобального минимума известно, удается оценить, находится ли найденный локальный минимум в достаточной близости от искомого решения. Если локальное решение признается неудовлетворительным, следует повторить процесс обучения при других начальных значениях весов и с другими управляющими параметрами.
При решении реальных задач в общем случае даже приблизительная оценка глобального минимума оказывается неизвестной. По этой причине возникает необходимость применения методов глобальной оптимизации. Рассмотрим метод имитации отжига.
Название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на методе Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет вероятностных алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации.
Классический алгоритм имитации отжига:
1. Запустить процесс из начальной точки w при заданной начальной температуре T=Tmax
2. Пока T0 повторить L раз следующие действия:
2.1. Выбрать новое решение w ′ из окрестности w .
2.2. Рассчитать значение целевой функции Δ = E(w′)-E(w) .
2.3. Если Δ≤0, принять w = w′ , в противном случае принять, что w = w′ с вероятностью exp(-Δ/T) путем генерации случайного числа R из интервала (0,1) с последующим его сравнением со значением exp(-Δ/T); если exp(-Δ/T)R, принять новое решение w = w′; в противном случае проигнорировать новое решение.
3. Уменьшить температуру (T← rT) с использованием коэффициента уменьшения r, выбираемого из интервала (0,1), и вернуться к п.2.
4. После снижения температуры до нулевого значения провести обучение сети любым из представленных выше детерминированных методов, вплоть до достижения минимума целевой функции.
Алгоритм имитации отжига
Алгоритм основывается на имитации физического процесса, который происходит при кристаллизации вещества из жидкого состояния в твёрдое, в том числе при отжиге металлов. Предполагается, что атомы уже выстроились в кристаллическую решётку, но ещё допустимы переходы отдельных атомов из одной ячейки в другую. Предполагается, что процесс протекает при постепенно понижающейся температуре. Переход атома из одной ячейки в другую происходит с некоторой вероятностью, причём вероятность уменьшается с понижением температуры. Устойчивая кристаллическая решётка соответствует минимуму энергии атомов, поэтому атом либо переходит в состояние с меньшим уровнем энергии, либо остаётся на месте. (Этот алгоритм также называется алгоритмом Н. Метрополиса, по имени его автора).
При помощи моделирования такого процесса ищется такая точка или множество точек, на котором достигается минимум некоторой числовой функции F(x), где x=(x1,..,xm) 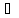 X. Вводится последовательность точек x0, x1, …, xn пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки x0, которая является начальным приближением. Алгоритм останавливается по достижении точки xn.
X. Вводится последовательность точек x0, x1, …, xn пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки x0, которая является начальным приближением. Алгоритм останавливается по достижении точки xn.
Точка xi+1 по алгоритму получается на основе текущей точки xi следующим образом. К точке xi применяется оператор Α, который случайным образом модифицирует соответствующую точку, в результате чего получается новая точка x*. Точка x*становится точкой xi+1 с вероятностью P(x*, xi+1), которая вычисляется в соответствии с распределением Гиббса:
P(x*xi+1|xi) = exp 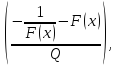
Здесь Q1 0 - элементы произвольной убывающей, сходящейся к нулю положительной последовательности, которая задаёт аналог падающей температуры в кристалле. Скорость убывания и закон убывания могут быть заданы по желанию создателя алгоритма.
Алгоритм имитации отжига похож на градиентный спуск, но за счёт случайности выбора промежуточной точки должен будет попадать в локальные минимумы реже, чем градиентный спуск. Алгоритм имитации отжига не гарантирует нахождения минимума функции, однако при правильной политике генерации случайной точки в пространстве X, как правило, происходит улучшение начального приближения.
Достоинством метода отжига является свойство избегать "ловушек" в локальных минимумах оптимизируемой функции, и продолжить поиск глобального минимума. Это достигается за счет принятия не только изменений параметров, приводящих к уменьшению значения функции, но и некоторых изменений, увеличивающих ее значение, в зависимости от температуры Т – характеристики моделируемого процесса. Чем выше температура, тем большие "ухудшающие" изменения (аналогичные случайным флуктуациям в нагретом веществе) допустимы, и больше их вероятность. Еще одним достоинством является то, что даже в условиях нехватки вычислительных ресурсов для нахождения глобального минимума, метод отжига, как правило, выдает весьма неплохое решение (один из локальных минимумов). Л. Ингбером показано, что метод отжига и его модификации являются одним из наиболее эффективных методов случайного поиска оптимального решения для большого класса задач. Им же проведен сравнительный анализ адаптивного метода отжига (Adaptive Simulated Annealing - ASA) и генетических алгоритмов, из которого следует, что на большинстве задач метод отжига не проигрывает генетическим алгоритмам, а на многих и выигрывает. К настоящему времени разработано множество различных вариантов метода отжига, как общих, так и их специализаций для решения конкретных задач.
Алгоритм имитации отжига можно представить в виде следующей структурной схемы ( рис.1).
![]()
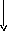
Создать начальное решение
Текущее решение
Оценить решение
![]()
Рабочее решение

![]()
Изменить решение случайным образом
Лучшее решение
Оценить новое решение
Критерий доступа
Уменьшение температуры
![]()
![]()
Рис.1. Схема алгоритма имитации отжига
Начальное решение
Для большинства проблем начальное решение будет случайным. На самом первом шаге оно помещается в текущее решение (Current solution). Другая возможность заключается в том, чтобы загрузить в качестве начального решения уже существующее, возможно, то самое, которое было найдено во время предыдущего поиска. Это предоставляет алгоритму базу, на основании которой выполняется поиск оптимального решения проблемы.
Оценка решения
Оценка решения состоит из декодировки текущего решения и выполнения нужного действия, позволяющего понять его целесообразность для решения данной проблемы. Обратите внимание, что закодированное решение может просто состоять из набора переменных. Они будут декодированы из существующего решения, а затем эффективность решения будет оценена на основании того, насколько успешно удалось решить данную задачу.
Случайный поиск решения
Поиск решения начинается c копирования текущего решения в рабочее решение (Working solution). Затем мы произвольно модифицируем рабочее решение. Как именно модифицируется рабочее решение, зависит от того, каким образом оно представляется (кодируется). Представьте себе кодировку задачи коммивояжера, в которой каждый элемент представляет собой город. Чтобы выполнить поиск по рабочему решению, мы берем два элемента и переставляем их. Это позволяет сохранить целостность решения, так как при этом не происходит повторения или пропуска города.
После выполнения поиска рабочего решения мы оцениваем решение, как было описано ранее. Поиск нового решения основан на методе Монте-Карло (то есть случайным образом).
Критерий допуска
На этом этапе алгоритма у нас имеется два решения. Первое - это наше оригинальное решение, которое называется текущим решением, а второе - найденное решение, которое именуется рабочим решением. С каждым решением связана определенная энергия, представляющая собой его эффективность (допустим, что чем ниже энергия, тем более эффективно решение).
Затем рабочее решение сравнивается с текущим решением. Если рабочее решение имеет меньшую энергию, чем текущее решение (то есть является более предпочтительным), то мы копируем рабочее решение в текущее решение.
Однако если рабочее решение хуже, чем текущее решение, мы определяем критерий допуска, чтобы выяснить, что следует сделать с текущим рабочим решением. Вероятность допуска основывается на уравнении P(δE)= exp(δE/T) (которое, в свою очередь, базируется на законе термодинамики).
При снижении температуры вероятность принятия худшего решения также снижается. При этом более высокий уровень энергии также способствует уменьшению вероятности принятия худшего решения. При высоких температурах симулированное восстановление позволяет принимать худшие решения для того, чтобы произвести более полный поиск решений. При снижении температуры диапазон поиска также уменьшается, пока не достигается равенство при температуре 0°.
Снижение температуры
После ряда итераций по алгоритму при данной температуре мы ненамного снижаем ее. Существует множество вариантов снижения температуры. В данном примере используется простая геометрическая функция T(i+1)=aTi
Константа а меньше единицы. Возможны и другие стратегии снижения температуры, включая линейные и нелинейные функции.
Повтор
При одной температуре выполняется несколько итераций. После завершения итераций температура будет понижена. Процесс продолжится, пока температура не достигнет нуля.
Общие схемы метода отжига
Больцмановский отжиг
Исторически первой схемой метода отжига является схема Больцмановского отжига. Именно эта схема использовалась Н. Метрополисом для вычисления многомерных интегралов пути в задачах статистической физики, а также с Киркпатриком для решения задачи нахождения оптимальной разводки микросхем. В Больцмановском отжиге изменения температуры задается формулой
T(k)=T0/ln(1+k),k0
Семейство распределений Q(x,T) выбирается как семейство нормальных распределений с математическим ожиданием и дисперсией, т.е. задается плотностью
g(x1,x, T) = (2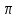 T)-D/2 exp(-|x1-x|2/(2T))
T)-D/2 exp(-|x1-x|2/(2T))
где D - размерность пространства состояний. Пространство состояний предполагается метрическим. Для Больцмановской схемы доказано, что при достаточно больших T0 и общем количестве шагов k , выбор такого семейства распределений гарантирует нахождение глобального минимума.
Отжиг Коши (быстрый отжиг)
Основным недостатком Больцмановского отжига является очень медленное убывание температуры. Например, чтобы понизить исходную температуры в 40 раз, требуется e40 ≈ 2,35 1017 итераций, что уже вряд ли приемлемо при решении каких-либо задач. Ввиду этого Цу и Хартли предложили алгоритм, который позволяет использовать для изменения температуры схему T(k)= T0/k без потери гарантии нахождения глобального минимума. Это достигается за счет использования в качестве Q распределений Коши с плотностью
g(x1,x, T)=T/ (|x1-x|2+T2)(D+1)/2
соответствующим образом нормированных. Например, в случае D = 1 приходим к плотности
g(x1,x, T)=1/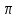 (T/ (|x1-x|2+T2)
(T/ (|x1-x|2+T2)
К сожалению, это распределение не очень удобно моделировать в пространстве размерности больше 1. Этого можно избежать, например, с помощью перемножения D одномерных распределений Коши:
g(x1,x, T)=1/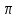 DПDi=1 (T/ (|x1-x|2+T2)
DПDi=1 (T/ (|x1-x|2+T2)
но в этом случае нахождении глобального минимума гарантируется только при законе изменения температуры не быстрее чем T(k)= T0/k
Сверхбыстрый отжиг
Недостатки двух предыдущих методов привели к тому, что в 1989 году американским исследователем Л. Ингбером был разработан метод сверхбыстрого отжига. В нем пространство S считается состоящим из D -мерных векторов (x1…xp) где x1 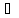 [A1, B1]. Кроме этого, температура по каждой из координат может различаться, таким образом, T также является вектором размерности D .
[A1, B1]. Кроме этого, температура по каждой из координат может различаться, таким образом, T также является вектором размерности D .
Семейство распределений сроится следующим образом. Вводится функция
В качестве y для получения плотности распределений ζ используется ∆x/Bi−Ai, таким образом, новое значение li вычисляется по формуле xl i = xi + zi(Bi − Ai) где i - случайная величина с плотностью g (i;T) на [-1;1].
При этом выходящие за границы интервала значения параметра генерируются заново или приравниваются соответствующим границам. Такую случайную величину легко промоделировать:
zi = sgn(αi – 1/2 )Ti((1 + l/Ti) (2αi−1) − 1)
где αi - независимые случайные величины, распределенные равномерно на [0;1].
Доказано, что закон изменения температуры
Ti(k) = T(i;0)exp(−cik 1/D ), ci 0
дает статистическую гарантию нахождения глобального минимума. Для вероятности принятия также используется отдельная шкала температуры, изменяющаяся по такому же закону. Как правило, при реализации этого метода ci управляется двумя параметрами:
ci = miexp(−ni / D)
Преимущество такого методы очевидны. Во-первых, экспоненциальное убывание температуры гораздо быстрее достижимого в предыдущих методах. Во-вторых, разделение размерностей может дать большой выигрыш, как и благодаря отдельным температурам, так и благодаря ускорению процесса, в случае, если не нужно менять все координаты одновременно.
Кроме того, в отличие от отжига Коши, сверхбыстрый отжиг, как было показано, допускает очень быстрое моделирование распределения ζ независимо от размерности S .
Среди недостатков этого метода можно назвать то, что ввиду большого количества параметров иногда требуется несколько месяцев, чтобы хорошо настроить его для решения конкретной задачи.
Алгоритм Ксин Яо
Алгоритм Ксин Яо был повторным применением идеи предыдущего алгоритма. В качестве g(y) выбирается
g(y)=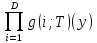 =
=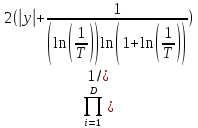
Утверждается, что при изменении температуры по закону
Ti(k) = T(i;0)exp(−exp(bik 1/D))
достигается статистическая гарантия нахождения глобального минимума.
Однако, как показано, увеличение скорости убывания температуры вовсе не означает ускорения в решении задачи. Более того, “размазанность” распределения приводит к тому, что метод генерирует огромное число “длинных” переходов, которые отвергаются в силу низкой вероятности их принятия.
Таким образом, несмотря на то. Что этот процесс итерировать до бесконечности, получая законы изменения температуры, ценность таких “улучшений” представляется сомнительной. Более того, легко видеть, что в пределе это приводит к тривиальному методу случайного поиска, которым является метод отжига при T = 0.
Это в небольшой степени применимо и к методу сверхбыстрого отжига, так что вопрос о скорости сходимости этих методов, а также о других методах, обеспечивающих не такое быстрое убывание температуры, но большую скорость сходимости, остается открытым. Вполне возможны задачи, на которых вторая итерация вышеописанного процесса может давать не плохие результаты.
Метод “ тушения ”
Далеко не всегда хватает вычислительных ресурсов на поиск глобального минимума. Кроме того, зачастую достаточно достигнуть не глобального оптимального решения задачи, а достаточно близкого к нему. Методы “тушения” не гарантируют нахождения глобального минимума, но, как правило, быстро находят близкое решение, а на практике зачастую и сам оптимум.
Основная идея этих методов заключается в том, чтобы скомбинировать семейство распределений ζ одного из предыдущих четырех методов с более быстрым законом убывания температуры.
Например, можно рассматривать нормальное распределение ζ из Больцмановского отжига, но при этом уменьшать температуру по закону Tk+1=cTk.
Как правило, в этом случае c выбирается между 0.7 и 0.99. Такой метод очень быстро сходится, и для конкретных задач может давать весьма неплохое решение, близкое к оптимальному, в условиях реального времени.
Зачастую они основаны либо на нормальном распределении, либо на распределении для сверхбыстрого отжига. Кроме того, встречаются специальные распределения, подобранные опытным путем для решения конкретных задач.
Естественная мотивация
Свойства структуры зависят от коэффициента охлаждения после того, как субстанция была нагрета до точки плавления. Если структура охлаждалась медленно, будут сформированы крупные кристаллы, что очень полезно для строения субстанции. Если субстанция охлаждается скачкообразно, образуется слабая структура.
Чтобы расплавить материал, требуется большое количество энергии. При понижении температуры уменьшается и количество энергии. Чтобы яснее представить процесс восстановления, рассмотрим следующий пример. «Взбалтывание» при высокой температуре сопровождается высокой молекулярной активностью в физической системе. Представьте себе, что вы взбалтываете емкость, в которой находится какая-то поверхность сложной формы. Внутри емкости также имеется шарик, который пытается найти точку равновесия. При высокой температуре шарик может свободно перемещаться по поверхности, а при низкой температуре «взбалтывание» становится менее интенсивным и передвижения шарика сокращаются. Задача заключается в том, чтобы найти точку минимального перемещения при сильном «взбалтывании». При снижении температуры уменьшается вероятность того, что шарик выйдет из точки равновесия. Именно в таком виде процесс поиска заимствуется из восстановления.
Исследуемые задачи
Задача о расстановке N ферзей
В качестве примера использования алгоритма отжига рассмотрим задачу о расстановке N шахматных ферзей на доске размером N*N. Ферзи должны быть расставлены так, чтобы ни один из них не бил другого. Это означает, что ни на одной вертикали, горизонтали или диагонали не могут находиться два ферзя одновременно. Иными словами, функция коллизий должна принимать минимальное значение. Пример решения задачи для размерности N = 8 показан на рисунке 2
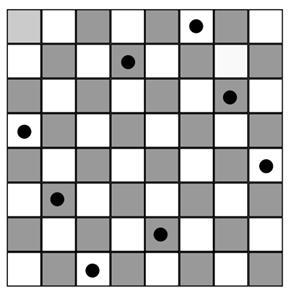
Рис.2. Ферзи на шахматной доске
Данная задача в течение многих лет решалась известными математиками, такими как Гаусс, однако оптимальное решение найдено не было. Задача может решаться непосредственно - алгоритмом полного перебора с возвратом, однако это не позволяет рассматривать данную задачу при достаточно больших N. На обычном персональном компьютере за разумное время может быть получен результат лишь для N менее 15. В то же время с помощью метода имитации отжига задача может достаточно эффективно решаться для значительно большей размерности, однако при достаточно больших N решение может содержать коллизии.
Задача об «Умном муравье»
В задаче об умном муравье рассматривается игровое поле размером 32 на 32 клеток, расположенное на поверхности тора
Некоторые клетки пусты, а на некоторых клетках находится по одному яблоку. Всего на игровом поле 89 яблок. Муравей начинает движение из левой верхней клетки и смотрит направо.
За ход муравей может выполнить следующие действия:
• повернуть налево;
• повернуть направо;
• ничего не сделать;
• сделать шаг вперед, и если на этой клетки есть яблоко, то съесть его.
Всего делается 200 шагов. Требуется построить автомат, управляющий муравьём, который съест за минимальное число ходов все яблоки
Задача Коммивояжера
В задаче коммивояжера рассматривается n городов и матрица попарых расстояний между ними. Требуется найти такой порядок посещения городов, чтобы суммарное пройденное расстояние было минимальным, каждый город посещался ровно один раз и коммивояжер вернулся в тот город, с которого начал свой маршрут. Другими словами, во взвешенном полном графе требуется найти гамильтонов цикл минимального веса (рис.3)
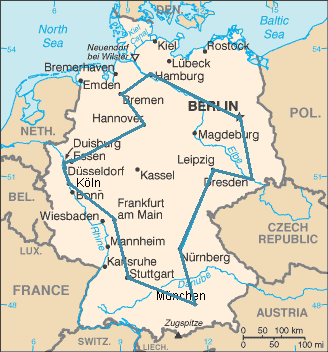
| Рис.3. Это оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600вариантов. |
Заключение
В настоящее время метод отжига применяется для решения многих оптимизационных задач – финансовых, компьютерной графики, комбинаторных, в телекоммуникационных сетях, и многих других. Зачастую метод отжига используют для обучения нейронных сетей. Несмотря на такую широкую область применения, скорость сходимости метода отжига все еще мало изучена.
Огромным преимуществом метода отжига является свойство избежать “ловушки” в локальных минимумах оптимизируемой функции, и продолжить поиск глобального минимума. Это достигается за счет принятия не только изменений параметров, приводящих к уменьшению значения функции, но и некоторых изменений, увеличивающих ее значение, в зависимости от температуры характеристики моделируемого процесса. Чем выше температура, тем больше “ухудшающие” изменения допустимы, и больше их вероятность. Еще одним преимуществом является то, что даже в условиях нехватки вычислительных ресурсов для нахождения глобального минимума, метод отжига, как правило, выдает весьма неплохое решение. Л. Ингбером показано, что метод отжига и его модификации являются одним из наиболее эффективных методов случайного поиска оптимального решения для большого класса задач. К настоящему времени разработано множество различных вариантов метода отжига, как общих так и их специализаций для конкретных задач.
Литература
1. Сигал И.Х. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы/ И.Х. Сигал, А.П.Иванова, М.: ФИЗМАЛИТ, 2003. – 240 с.
2. Акулич И.Л. Математическое программирование в примерах и задачах/ И.Л Акулич, М.: Высшая школа, 1986. — 319 с.
3. Габасов Р.П. Основы динамического программирования/ Р.П.Габасов, Ф. М. Кириллова, Мн.: Изд-во БГУ, 1975. — 262 с.
4. Елкин Д. И. Метод отжига/ Д. И. Елкин, А. C. Тяхти, M.: Мир, 2008,–46 с.
5. Beisiegel B, Simulated annealing based algorithm for the bin packing problem with impurities/ B. Beisiegel, J. Kallrath, Yu. Kochetov, Oper. Res. Proc., 2005,–113 c.
Приложение к задаче о расстановке ферзей.
program ferz;
uses crt;
type desk = array [1..8,1..8] of 0..2;
{0-пусто; 1-поле которое бьёт ферзь; 2-ферзь}
var
cur_desk : desk; {текущий статус доски}
now_f : byte; {какой ферьз ставится в данный момент}
count : byte; {количество на доске ферзей}
variants : word; {количество возможных вариантов}
fi,fj : array[1..5] of byte; {координаты ферзей}
i,j : byte; {для расстановки первого ферзя}
ferzes : desk;
{заполнить "1" столбик и строку с номером позиции ферзя ki, kj}
procedure st(ki,kj:byte);
var i:integer;
begin
for i:=1 to 8 do
begin
if cur_desk[ki,i] 2 then
cur_desk[ki,i] := 1;
if cur_desk[i,kj] 2 then
cur_desk[i,kj] := 1;
end
end;
{заполнить "1" диагонали, которые бъёт ферзь с номером позиции ki, kj}
procedure diag(ki,kj:byte);
var i,j:integer;
begin
for i:=1 to 8 do
for j:=1 to 8 do
begin
if abs(i-ki)=abs(j-kj) then
if cur_desk[i,j]2 then cur_desk[i,j]:=1;
end
end;
{проверяет бьют ли все 5 ферзей всё поле}
function filled : boolean;
var
i, j : integer;
fl : boolean;
begin
fl:=true;
for i:=1 to 8 do
for j:=1 to 8 do
if cur_desk[i,j] = 0 then fl := false;
filled := fl
end;
{выводит массив ferzes, то есть правильную расстановку}
procedure print_ar;
var
i,j:integer;
begin
for i:=1 to 8 do
begin
for j:=1 to 8 do
write(ferzes[i,j],' ');
writeln
end;
readln
end;
{рекурсивная процедура которая расставляет ферзей
after_i,after_j переменные, которые служат для исключения повторений,
то есть поиск места для след. ферзя идёт по значениям i, j которые
идут после места только что поставленного ферзя}
procedure put(after_i,after_j:byte);
var
old_desk : desk; {в ней хранится значения старой доски, чтоб при возврате из рекурсии}
{не терялись предыдущие значения}
i,j : integer;
tempk : byte;
begin
old_desk := cur_desk;
for i:=after_i to 8 do
begin
if i=after_i then tempk:=after_j
else tempk:=1; {нужно, так как after_j исп-зя один раз когда i=after_i,}
{ведь дальше j идёт с 1}
for j:=tempk to 8 do
begin
{это условие когда не могут ббить лруг друга, то есть ферзь ставится на место,}
{где никто его не "обидит" = если нужна возможность бить друг друга}
{делаем условие cur_desk[i,j] 2, тогда будет ставится в любое место, где не}
{стоит другой ферзь}
if cur_desk[i,j] = 0 then
begin
inc(now_f); {now_f = now ferz, то есть какого ферзя ставим}
inc(count); {кол-во ферзей}
fi[now_f]:=i; {запоминаем i,j позицию ферзя с номером now_f}
fj[now_f]:=j;
cur_desk[fi[now_f],fj[now_f]]:=2; {ставим его на доску}
st(fi[now_f],fj[now_f]); {2 процедуры, описанные выше}
diag(fi[now_f],fj[now_f]);
if count 5 then {если не все ферзи поставлены}
begin
put(i,j);
{восстанавливает значение, когда один из проходов закончен}
{при возврате из рекурсии}
cur_desk := old_desk;
fi[now_f]:=0;
fj[now_f]:=0;
dec(count);
dec(now_f)
end
else
begin
{ferzes - массив, которых хранит свеженайденный расклад событий на доске}
{использунтся чтобы выводить варианты}
fillchar(ferzes,sizeof(ferzes),0);
ferzes[fi[1],fj[1]] := 1;
ferzes[fi[2],fj[2]] := 1;
ferzes[fi[3],fj[3]] := 1;
ferzes[fi[4],fj[4]] := 1;
ferzes[fi[5],fj[5]] := 1;
{ставим 5-го ферзя и убираем его для дальнейшего его расставления,}
{или чтобы не была мусорна 5 переменная, когда возвращаемся на расстановку}
{4 ферзя(когда для 5 ферзя i=j=8)}
fi[now_f]:=0;
fj[now_f]:=0;
dec(count);
dec(now_f);
if filled then
begin
inc(variants);
{нашли вариант, и вывели массив если надо}
print_ar;
cur_desk:=old_desk;
end
else
begin
cur_desk:=old_desk;
end
end
end
end
end
end;
begin
{цикл по всей доске для выбора куда поставить самого 1 ферзя}
for i:=1 to 8 do
for j:=1 to 8 do
begin
{показываю инициализацию доски для 1 ферзя}
count := 0;
now_f := 0;
fillchar(cur_desk,sizeof(cur_desk),0);
fi[1]:=i;
fj[1]:=j;
cur_desk[fi[1],fj[1]]:=2;
st(fi[1],fj[1]);
diag(fi[1],fj[1]);
inc(count);
inc(now_f);
put(i,j);
end;
write('Число вариантов: ');
writeln(variants);
readln
end.
Приложение к задаче Коммивояжера
Uses CRT;
Label Out;
Const
N=8;
Var
C: array [1..N,1..N] of word; {Матрица расстояний}
Tour, P: array [1..N] of word; {Оптимальный и текущие туры}
l, s: word;
i, j, k, min, ind: byte;
All: boolean; {Признак окончания перебора}
Graph: text;
Begin
ClrScr;
{Ввод данных}
Assign(Graph,'D:\matr.in');
Reset(Graph);
TextColor(14);
Writ===========ЗАДАЧА КОММИВОЯЖЕРА (Перебор)=================');
WriteLn('Матрица смежности:');
WriteLn('=====================');
For i:=1 To N Do For j:=1 To N Do Read(Graph, C[i,j]);
For i:=1 To N Do
Begin
For j:=1 To N Do Write(C[i,j],' ');
WriteLn;
End;
{Инициализация}
All:=False; {Перебраны не все варианты}
l:=MaxInt; {Оптимальный тур неизвестен}
For i:=1 To N Do P[i]:=i; {Строим первый тур}
Repeat
{Вычисляем его длину}
s:=0;
For i:=1 To N-1 Do s:=s+C[P[i],P[i+1]];
s:=s+C[P[n],P[1]];
{Полагаем первый тур текущим}
If ls Then
Begin
Tour:=P;
l:=s;
End;
{Генерируем все (N-1)! перестановок}
For i:=N DownTo 3 do
Begin
If P[i]
Then continue;
min:=N+1;
k:=P[i-1];
{Ищем миним. число из тех, что больше k и правее}
For j:=i To N Do If (P[j]k) and (P[j]Then
Begin
min:=P[j];
ind:=j;
End;
{Рокировка min и k}
P[i-1]:=min;
P[ind]:=k;
{Элементы на местах от i до N упорядочиваем по возрастанию}
For j:=i To N-1 Do
Begin
min:=N+1;
For k:=j To N Do If min P[k] Then
Begin
min:=P[k];
ind:=k;
End;
k:=P[j];
P[j]:=min;
P[ind]:=k;
End;
GoTo out;
End;
{Проверяем перебраны ли все перестановки}
All:=true;
Out:
Until All;
{Если перебраны все перестановки, то выдаем оптимальный тур}
WriteLn('================');
Write('Минимальный тур: ');
For i:=1 To N Do Write(Tour[i],'-');
Write('1');
WriteLn(' имеет длину ',l);
WriteLn('=================');
Close(Graph);
ReadKey;
END.







 X. Вводится последовательность точек x0, x1, …, xn пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки x0, которая является начальным приближением. Алгоритм останавливается по достижении точки xn.
X. Вводится последовательность точек x0, x1, …, xn пространства X. Алгоритм последовательно находит следующую точку по предыдущей, начиная с точки x0, которая является начальным приближением. Алгоритм останавливается по достижении точки xn.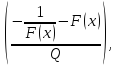

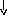
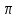 T)-D/2 exp(-|x1-x|2/(2T))
T)-D/2 exp(-|x1-x|2/(2T))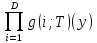 =
=