Куйбышевский филиал
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Новосибирский государственный педагогический университет»
Курсовая работа
«Методика обучения решению текстовых задач алгебраическим способом»
Выполнил студент группы 332
А.С. Сколото
Специальность 050100.62 Педагогическое образование
Профиль: Математическое образование
Научный руководитель:
доцент кафедры математики З.А. Александрова
_____ (оценка)
«____»___________ 20___г.
Куйбышев 2015
Содержание
стр.
Введение ………………………………………………………………………. 3
Глава 1. Характеристика текстовой задачи
Понятие тестовой задачи…………………………………………………. 6
1.2. Этапы процесса решения задачи………………………………………… 9
Вывод к первой главе…………………………………………………………. 15
Глава 2. Применения методики обучения решению текстовых задач алгебраическим способом
2.1. Формирование умений решать задачи алгебраическим способом…… 16
2.2. Виды алгебраических задач и примеры их решения……………………19
Выводы ко второй главе……………………………………………………… 27
Заключение…………………………………………………………………… 28
Список литературы…………………………………………………………… 30
Приложение…………………………………………………………………… 32
Введение
Далеко не все ученики основной школы осваивают алгебраический метод решения текстовых задач даже на базовом уровне. Причин тому великое множество. Одни из них носят общий характер: устоявшийся страх перед задачей, отсутствие общих представлений о рассматриваемых в задачах процессах, неумение устанавливать, что дано в задаче, что надо найти, выявлять по тексту взаимосвязи рассматриваемых в задаче величин и т.п. Другие свидетельствуют о несформированности определенных умений и навыков: незнание этапов решения задачи, непонимание содержания и цели собственной деятельности на каждом из них, неумение решать уравнения или неравенства (или их системы) определенного вида, неумение производить отбор корней уравнения или решений неравенства в соответствии с условием задачи и т.д. Недостатки в овладении необходимыми приемами рассуждений, незнание общих методов решения задач не дают возможности многим школьникам успешно работать над конкретной задачей. [13]
Следует отметить и недостатки в методике построения различных моделей обучения как на этапе текущего обучения решению текстовых задач, так и на этапе работы с задачами в процессе обобщающего повторения по отдельной теме или по целому курсу. Работая над конкретной задачей в классе, учитель дает пояснения, сущность и значимость которых понимают и запоминают в классе лишь отдельные ученики. Как правило, эти пояснения не систематизированы учителем и носят локальный характер.
К субъективным причинам можно отнести влияние индивидуальных особенностей школьников на процесс усвоения материала и формирование необходимых умений. Затрудненное восприятие, плохая память, слабое владение анализом и синтезом, отсутствие достаточного опыта в решении простейших задач оказывают несомненное влияние на освоение такими учениками алгебраического метода решения текстовых задач.
Известно, что решение сюжетной задачи алгебраическим методом состоит в последовательной реализации трех этапов:
перевод текста задачи на алгебраический язык – составление математической модели данной сюжетной задачи;
решение полученной математической задачи – внутримодельное решение;
ответ на вопрос задачи, перевод полученного результата на язык исходной ситуации – интерпретация внутримодельного решения.
Процесс обучения решению текстовых задач в контексте алгебры в основной школе построен так, что сначала школьники осваивают эту деятельность в пределах одной темы, а затем – на этапе обобщения и систематизации в пределах более крупного раздела.
Когда речь идет о решении текстовых задач в пределах одной темы, то сначала осваивается решение определенной математической задачи: решение уравнений определенного вида, системы уравнений, неравенства, системы неравенств или смешанной системы. После рассмотрения решения математической задачи определенного вида, например, решения уравнений второй степени с одной переменной ученикам предлагается решить ряд текстовых задач, решение каждой из которых сводится к только что изученной математической задаче – к уравнению второй степени с одной переменной. Таким образом, в контексте обучения решению текстовых задач в пределах определенной темы сначала ведется работа над вторым этапом – решением математической задачи, т.е. над внутримодельным решением. Это служит определенной подсказкой ученику при работе над задачей: у него есть четкий ориентир – вид модели. На этом этапе ученики довольно успешно справляются с решением текстовых задач. Значит, при обучении решению задач в пределах определенной темы акцент в работе над задачей можно и нужно перенести на первый и третий этапы: переводе задачи на математический язык и интерпретации полученного на втором этапе результата. Практика показывает, что существенные затруднения возникают у «средних» и «слабых» школьников именно на первом этапе, хотя и на этапе интерпретации тоже встречаются определенные ошибки, связанные как с невнимательностью, так и с неумением производить отбор решений. [1]
Когда же требуется перенос знаний в новую ситуацию и отсутствует предопределенность вида математической модели, учащиеся часто не справляются с решением даже совсем несложных задач, хотя при работе над темой могли решать и более сложные задачи.
Цель работы: Проанализировать методику обучения решению текстовых задач алгебраическим методом.
Задачи работы:
1. Изучить понятие текстовой задачи и этапы ее решения
2.Рассмотреть сущность алгебраического метода решения текстовых задач.
3.Изучить примеры текстовых задач решенных алгебраическим способом.
4.Проанализировать практическое применение методики обучения решению текстовых задач алгебраическим способом.
5. Разработать и апробировать конспект урока.
Объект работы: Обучение решению текстовых задач.
Предмет работы: Методика обучения решению текстовых задач алгебраическим методом.
Апробация результатов исследования проходит в МБОУ Орловской СОШ Татарского района на 5-6 классах.
Практическая ценность работы состоит в том, что её содержание можно применять в дальнейшей работе другими педагогами.
Структура работы: введение, теоретическая часть, выводы к каждой главе, заключение, приложение.
Глава 1 Характеристика текстовой задачи
Понятие текстовой задачи
В обучении математике велика роль текстовых задач.
Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, чтобы учитель имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами.
Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.
Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа. [1]
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот, вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое.
Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии. [2]
Любая текстовая задача состоит из двух частей: условия и требования.
В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними.
Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме.
Рассмотрим задачу: На тракторе «Кировец» колхозное поле можно вспахать за 10 дней, а на тракторе «Казахстан» – за 15 дней. На вспашку поставлены оба трактора. За сколько дней будет вспахано это поле?
В задаче пять неизвестных значений величин, одно из которых заключено в требовании задачи. Это значение величины называется искомым.
Иногда задачи формируются таким образом, что часть условия или всё условие включено в одно предложение с требованием задачи.
В реальной жизни довольно часто возникают самые разнообразные задачные ситуации. Сформулированные на их основе задачи могут содержать избыточную информацию, то есть, такую, которая не нужна для выполнения требования задачи.
На основе возникающих в жизни задачных ситуаций могут быть сформулированы и задачи, в которых недостаточно информации для выполнения требований. Так в задаче: «Найти длину и ширину участка прямоугольной формы, если известно, что длина больше ширины на 3 метра» – недостаточно данных для ответа на её вопрос. Чтобы выполнить эту задачу, необходимо её дополнить недостающими данными. [11]
Одна и та же задача может рассматриваться как задача с достаточным числом данных в зависимости от имеющихся и решающих значений.
Рассматривая задачу в узком смысле этого понятия, в ней можно выделить следующие составные элементы:
Словесное изложение сюжета, в котором явно или в завуалированной форме указана функциональная зависимость между величинами, числовые значения которых входят в задачу.
Числовые значения величин или числовые данные, о которых говорится в тексте задачи.
Задание, обычно сформулированное в виде вопроса, в котором предлагается узнать неизвестные значения одной или нескольких величин. Эти значения называют искомыми.
Задачи и решение их занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное развитие ребенка.
Функции задач в обучении взаимосвязаны, однако в каждом конкретном случае выделяется и реализуется ведущая функция задачи в соответствии с целевой установкой ее применения.
Умение решать задачи не находится в прямой зависимости от числа решенных задач, поэтому в психолого-дидактических и методических исследованиях отдается предпочтение приемам формирования общих подходов к задаче как объекту ее изучения, ее анализу. Понимая роль задачи и её место в обучении и воспитании ученика, учитель должен подходить к подбору задачи и выбору способов решения обоснованно и чётко знать, что должна дать ученику работа при решении данной им задачи. [6]
1.2. Этапы процесса решения задачи
Если под процессом решения задач понимать процесс, начинающийся с момента получения задачи до момента полного завершения ее решения, то очевидно, что этот процесс состоит не только из изложений уже найденного решения, а из ряда этапов, одним из которых и является изложение решения.
Из каких же этапов состоит процесс решения задачи?
Очевидно, получив задачу, первое, что нужно сделать, это разобраться в том, что это за задача, каковы ее условия, в чем состоят ее требования, т.е. провести анализ задачи. Этот анализ и составляет первый этап процесса решения задачи.
В ряде случаев этот анализ надо как-то оформить, записать. Для этого используются разного рода схематические записи задач, построение которых составляет второй этап процесса решения.
Анализ задачи и построение ее схематической записи необходимы главным образом для того, чтобы найти способ решения данной задачи. Поиск этого способа составляет третий этап процесса решения.
Когда способ решения задачи найден, его нужно осуществить, - это будет четвертый этап процесса решения – этап осуществления (изложения) решения.
После того как решение осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.
При решении многих задач, кроме проверки, необходимо еще произвести исследование задачи, а именно установить, при каких условиях задача имеет решение и притом, сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т.д. Все это составляет шестой этап процесса решения. [4]
Убедившись в правильности решения и, если нужно, произведя исследование задачи, необходимо четко сформулировать ответ задачи, - это будет седьмой этап процесса решения.
Наконец, в учебных и познавательных целях полезно также произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т.д. Все это составляет последний, конечно не обязательный, восьмой этап решения. [9]
Итак, весь процесс решения задачи можно разделить на восемь этапов:
1 этап – анализ задачи;
2 этап – схематическая запись задачи;
3 этап – поиск способа решения задачи;
4 этап – осуществление решения задачи;
5 этап – проверка решения задачи;
6 этап – исследование задачи;
7 этап – формулирование ответа задачи;
8 этап – анализ решения задачи.
Приведенная схема дает лишь общее представление о процессе решения задачи, поэтому приведем пример решения задачи.
Существуют различные методы решения текстовых задач: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей. Например при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом – строятся диаграммы ил графики. Решение задачи логическим методом начинается с составления алгоритма. Различные методы решения конкретной задачи будем называть способами решения.
Арифметический метод. Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей. [10]
Пример. Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем то одним?
Решение.
1 способ.
1) 82+32+78=192 чел. – удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192÷2=96 чел. – поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96_32=64 чел. – поют в хоре;
4) 96-78=18 чел. – занимаются танцами;
5) 96-82=14 чел. – занимаются художественной гимнастикой.
2 способ.
1) 82-32=50 чел. – на столько больше студентов поют в хоре, чем занимаются художественной гимнастикой;
2) 50+78=128 чел. – удвоенное число студентов поющих в хоре;
3) 128÷2=64 чел. – поют в хоре;
4) 78-64=14 чел. – занимаются художественной гимнастикой;
5) 82-64=18 чел. – занимаются танцами.
Ответ: 64 студента поют в хоре; 14 студентов занимаются художественной гимнастикой; 18 студентов занимаются танцами.
Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений. Одну и ту же задачу можно также решить различными алгебраическими способами, если для ее решения составлены различные уравнения или системы уравнений, в основе составления которых лежат различные соотношения меду данными и искомыми. [8]
Пример. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справиться с заданием за 2 дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?
Решение.
1 способ. Пустьx д./день – первоначальная производительность рабочего. Тогда (x+10) д./день – новая производительность, 3x д. – число деталей, которые он должен сделать. По условию получаем уравнение 3x=2(+10), решив, которое найдем x=20. Первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.
2 способ. Пусть x д. – число деталей, которое должен сделать рабочий. Тогда x/2 д./день – новая производительность, (x/2-10) д./день – первоначальная производительность рабочего. По условию получаем уравнение x=3(x/2-10), решив которое найдем x=60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.
Ответ: 20 деталей в день, 60 деталей.
Геометрический метод. Решить задачу геометрическим методом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами. Задача считается решенной различными способами, если для ее построения используются различные построения или свойства фигур.
Логический метод. Решить задачу логическим методом – это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения. Примерами таких задач могут служить задачи «на переправы», классическим представителем которых является задаче о волке, козе и капусте, или задачи «на взвешивание».
Практический метод. Решить задачу практическим методом – значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т.д.)
Т.к. тема нашей курсовой методика обучения решению текстовых задач алгебраическим способом, именно его рассмотрим более подробно.
Алгебраический метод решения задачи позволяет легко показать, что некоторые задачи, отличаются друг от друга лишь фабулой, имеют не только одни и те же соотношения между данными и искомыми величинами, но и приводят к типичным рассуждениям, посредством которых устанавливаются эти соотношения. Такие задачи дают лишь различные конкретные интерпретации одного и того математического рассуждения, одних и тех же соотношений, т.е. имеют одну и туже математическую модель. [15]
Рассмотрим классификацию задач решаемых алгебраическим способом по фабуле, из-за многообразия уравнений и неравенств.
Задачи на движение
К этой группе задач относятся задачи, в которых говорится о трех величинах: пути, скорости и времени. Как правило, в них речь идет о равномерном прямолинейном движении. В этих задачах весьма полезно делать иллюстрированный чертеж, который помогает в составлении уравнений и неравенств.
Данную группу задач, можно разбить на задачи, в которых рассматриваются движения тел: 1) навстречу друг другу, 2) в одном направлении(«вдогонку»), 3) в противоположных направлениях, 4) по замкнутой траектории, 5) по течению реки.
Задачи на работу.
К этой группе задач относятся задачи, в которых говорится о трех величинах: работе, времени, в течение которого производится работа, производительности – работе, произведенной в единицу времени. К задачам на работу относят и задачи, связанные с наполнением и опорожнением резервуаров с помощью труб, насосов и других приспособлений. В качестве произведенной работы в этом случае рассматривают объем перекачанной воды.
Задачи на работу можно отнести к группе задач на движение, т.к. в задачах такого типа можно считать, что вся работа или полный объем резервуара играют роль расстояния, а производительности объектов, совершающих работу, аналогичны скоростям движения. Однако по сюжету, фабуле эти задачи совершенно отличаются.
Задачи на смеси и проценты.
К этой группе задач относятся задачи, в которых речь идет о смешении различных веществ в определенных пропорциях, а также задачи на проценты
Мы рассмотрели некоторые классификации задач, а сейчас мы бы хотели рассмотреть более подробно решение задач с помощью математического моделирования. [12]
Вывод к первой главе
Указания учителей по решению задач быстро забываются учениками, они не приобретают навыков решения текстовых задач. Без конкретной программы деятельности учащихся, без алгоритмов, системы приемов поиска решения задачи трудно организовать процесс решения задач. Поэтому необходимы «ускорители» для приобретения навыков решения: иллюстрация, схемы, таблицы, дополнительные символы, условные знаки, стрелки, способствующие более конкретному наглядному представлению об отношениях между частями задачи, связях между величинами, порядке этих связей. Это позволяет стимулировать у учащихся развитие наглядно-действенного мышления и на основе его в дальнейшем – образного мышления. Поиск решения текстовой задачи путем составления таблицы дает возможность охватить взором отношения между элементами всей задачи. [7]
Можно выделить основные причины, вызывающие у учащихся затруднения при поиске решения:
Неумение выделить величины, о которых идет речь в задаче.
Неумение установить функциональную зависимость в математических символах.
Неумение выразить эту зависимость в математических символах.
Слабые навыки схематической и символической записи условия, способствующей анализу задачи, выражению зависимостей между величинами, входящими в задачу.
Глава 2. Применения методики обучения решению текстовых задач алгебраическим способом
2.1. Формирование умений решать задачи алгебраическим способом
Многие учителя математики, работая с текстовыми задачами, стремятся в процессе обучения как можно быстрее перейти к решению их алгебраическим способом, не понимая, что решение текстовой задачи арифметическим способом учит детей особому способу мышления – синтезу, в то время как «алгебраический» способ решения задачи учит анализу. Если учесть, что после прохождения курса математики 5-6 класса учащиеся в курсе алгебры основной школы длительное время решают текстовые задачи только алгебраическим способам, т.е. составлением уравнения, и тем самым учатся мыслить аналитически, становится ясно, что исключение или сокращение числа текстовых задач, решаемых арифметически из практики обучения в 5-6 классах не только обедняет само обучение математике, но и лишает учащихся разностороннего математического развития. Подчеркнем, что при решении текстовой задачи арифметическим способом на уровне поиска решения идет обучение детей не только синтезу, но и анализу. Для того чтобы подтвердить данную информацию был разработан конспект урока на тему «Уравнение. Понятие корня уравнения. Алгебраический способ решения задач». Данный конспект апробирован на учащихся 5 класса МБОУ Орловской СОШ. Приложение (1)
В виду методической значимости заявленной проблемы рассмотрим более подробно в данном случае взаимосвязь анализа и синтеза, которая ярко иллюстрируется при решении текстовых задач курса математики 5-6 класса. [3]
В психологии установлено, что полноценное мышление человека формируется только тогда, когда он владеет аналитико-синтетическим способом рассуждений. Всякая составная текстовая задача представляет собой логически связанную последовательность простых задач. Структура этой последовательности и определяет ход решения задачи, ведущего от условия к искомому результату. Трудность решения задачи, которая не является стандартной и состоит в обнаружении этой последовательности действий. Явно или неявно всякий человек, решающий поставленную задачу использует аналитико-синтетический способ рассуждений.
Проиллюстрируем этот метод рассуждений на примере задачи 5 класса.
Задача. «Из пунктов А и В одновременно навстречу друг другу выехали два автобуса. Первый шел со скоростью 50 км/ч, а второй – 40 км/ч. Их встреча произошла в 20 км от середины пути АВ. Найти расстояние между пунктами А и В.»
Представим условие задачи на схеме:

 2 автобус – 40 км/ч 1 автобус – 50 км/ч
2 автобус – 40 км/ч 1 автобус – 50 км/ч
20км 20км
1) Проведем рассуждения аналитически, сопровождая их схемой и записью решения.
| Чтобы узнать расстояние, пройденное автомобилем до встречи, нужно знать скорость их сближения и время сближения, скорость сближения находится действием: 50+40=90 (км/ч) Чтобы узнать время сближения, нужно узнать разницу в пройденном пути и в скоростях движения, из-за которой один путь оказался меньше другого. Оба результата находятся так: 50-40=10 (км/ч), 20+20=40 (км). Теперь нетрудно получить результат: 40÷10=4 (ч), 90×4=360 (км). | Расстояние АВ 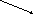  90×4=360 90×4=360
Скорость время сближения   50+40=90 40÷10=4 50+40=90 40÷10=4
разность разность скорости расстояния 20+20=40 50-40=10 |
Решение
Пусть x(км) – расстояние АВ, тогда x/2+20 (км) – расстояние, пройденное 1 автобусов до встречи, а x/2-20 (км) – расстояние, пройденное 2 автобусом до встречи.
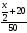 (ч) – время движения 1 автобуса, а
(ч) – время движения 1 автобуса, а 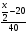 (ч) – время движения 2 автобуса.
(ч) – время движения 2 автобуса.
Составляем уравнение:
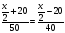
x = 360 (км).
2) Проводим рассуждения синтетически, также сопровождая их схемой и записью решения.
Анализ открывает путь решения задачи, а синтез осуществляет это решение. Поэтому анализ иногда называют методом открытия. А синтез методом обоснования. Решая любую текстовую задачу арифметическим способом, ученик обязательно намечают план решения, и уже затем формулируют первый вопрос. Решение многих текстовых задач методом уравнений, несомненно, легче, чем их решение арифметическим методом. Вместе с тем, следует помнить, что только анализ не имеет доказательной силы и поэтому всегда соседствует с синтезом. Поэтому решение задачи методом уравнений нуждается в смысловой проверке, а выкладки, полученные аналитическим путем нуждаются в синтетическом подтверждении.
При работе с текстовыми задачами, необходимо, прежде всего, помнить, что важно не столько решить задачу, сколько научить учащихся решать задачи, догадываться, рассуждать, обосновывать или опровергать свои догадки и уметь проверять полученный результат. [5]
2.2. Виды алгебраических задач и примеры их решения
Решение задач на совместное решение: начиная с 5-го класса, ученики часто встречаются с этими задачами. Еще в начальной школе учащимся дается понятие «общей скорости». В результате у них формируются не совсем правильные представления о скорости сближения и скорости удаления. Чаще всего, решая задачу, учащиеся находят сумму. Начинать решать эти задачи лучше всего с введения понятий: «скорость сближения», «скорость удаления». Для наглядности можно использовать движение рук, объясняя, что тела могут двигаться в одном направлении и в разном. После этого ученики записывают следующую таблицу:
Таблица 1 «Методы нахождения скорости сближения и скорости удаления»
|
| Движение в одном направлении V1 | Движение в разных направлениях |
| Скорость удаления | 
| 
V2  V1
|
| Скорость сближения | 
V2  V1
| 
V2  V1
|
|
| V1-V2 | V1+V2 |
При разборе задачи даются следующие вопросы.
С помощью движения рук выясняем, как двигаются тела относительно друг друга (в одном направлении, в разных).
Выясняем, каким действием находится скорость (сложением, вычитанием)
Определяем, какая это скорость (сближения, удаления). Записываем решение задачи.
Пример. Из городов А и В, расстояние между которыми 600 км, одновременно, навстречу друг другу вышли грузовая и легковая машины. Скорость легковой 100 км/ч, а грузовой – 50 км/ч. Через сколько часов они встретятся?
Учащиеся движением рук показывают, как движутся машины и делают следующие выводы:
машины движутся в разных направлениях;
скорость будет находиться сложением;
так как они движутся на встречу друг другу, то это скорость сближения.
Решение:
100+50=150 (км/ч) – скорость сближения.
600:150=4 (ч) – время движения до встречи.
Ответ: через 4 часа
Задачи решаемые с помощью таблиц: при подготовке к решению таких задач можно удачно использовать карты сигналы (см. рис. 1).
| №1 на…больше + |
| №2 в…больше Х |
| №3 на…меньше – |
| №4 в…меньше : |
Рис. 1. Карты сигналы
Устный счет следует проводить с использованием данных карт, которые должны быть у каждого учащегося, что позволяет привлечь к работе весь класс.
Пример №1. У первого мальчика на 5 марок больше, чем у второго. Как найти сколько у второго?
Учащиеся поднимают карту №1 и объясняют, что к числу первого нужно прибавить 5, так как у него на 5 больше, выделяя интонацией «на … больше».
Пример №2. У второго 30 марок, а у первого в 3 раза меньше. Сколько марок у первого?
Учащиеся должны поднять карту №4 и ответить: 10 марок, так как 30: 3 = 10. Опорные слова – «в…меньше».
Подбор задач на устный счет должен быть разнообразным, но каждый раз ученик должен давать объяснение, называя опорные слова. В таблице опорные слова лучше подчеркивать.
Пример №3. Всадник проехал 80 км за 5 часов. Сколько времени потратит на этот путь велосипедист, если его скорость на 24 км/ч больше скорости всадника?
Таблица 2 «Таблица для решения задачи»
|
| Скорость | Время | Расстояние |
| Всадник | 16 км/ч |
| 80 км |
| Велосипедист | На 24 км/ч больше |
| 80км |
При заполнении таблицы ученик должен подчеркнуть опорные слова и объяснить, что скорость всадника находится путем сложения 16 км/ч и 24 км/ч. Затем, устанавливая функциональную зависимость между величинами, учащиеся заполняют все строки и столбцы таблицы. После этого, в зависимости от поставленной задачи, ученик или отвечает на вопрос, или оформляет решение. Работая с таблицей (таблица 2), учащийся должен понимать, что при решении задачи все строки и столбцы должны быть заполнены данными задачи, и данными, которые получаются в результате использования функциональной зависимости между величинами.
Задачи на проценты: процент – это сотая часть. Наглядная иллюстрация процента может быть продемонстрирована на метровой школьной линейке с делениями по 1 см. В данном случае 1 см является сотой частью линейки, т.е. 1%. Можно дать следующие задания:
показать на линейке 25%, 40% и т.д.
назвать число процентов, которые показываются на линейке.
Затем работу можно продолжить на отрезках, задавая вопросы, например:
Как показать 1% отрезка?
Ответ: отрезок нужно разделить на 100 равных частей и взять одну часть.
Или: покажите 5% и т.д. (см. рис. 2).

Рис. 2. Метод отложения на отрезке
Условимся, что деление отрезка на 100 равных частей делаем словно. Приступая к решению задач, их нужно сравнить с задачами предыдущего пункта, что ускорит усвоение приемов решения.
Пример. В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют девочки?

Рис. 3. Графическое изображение задачи
Объяснение: Число учащихся 700 человек, что составляет 100%. Отрезок условно делим на сто равных частей. (Само выполнение чертежа подсказывает ученику первое действие).
700 / 100 = 7 (чел.) – составляют 1%.
Узнаем, сколько процентов составляют мальчики. Для этого:
357 / 7 = 51%
(Можно сказать и так: «Сколько раз в 357 содержится по 7%?»)
Работаем с чертежом. Узнаем, сколько процентов составляют девочки.
100%-51%=49%
Ответ 49%
При решении задачи чертеж должен быть постоянно в поле зрения учащихся, так как является наглядной иллюстрацией задачи.
Задачи на совместную работу: при решении этих задач нужно выяснить с учащимися, что возможны два случая:
объем выполненной работы известен;
объем выполненной работы неизвестен.
Первые задачи удобно решать, используя таблицы.
Пример. Два токаря вместе изготовили 350 деталей. Первый токарь делал в день 40 деталей и работал 5 дней, второй работал на 2 дня меньше. Сколько деталей в день делал второй токарь?
Составим таблицу (см. табл.3).
Таблица 3 «Условие задачи»
|
| Производительность | Время | Количество |
| 1т. | 40 деталей | 5 дней | 
|
| 2т. | ? | на 2 дня меньше |
Объяснение. Так как известны производительность и время работы первого токаря, найдем количество деталей, изготовленных первым токарем.
40*5 = 200 (дет.) – изготовил первый токарь.
Работая с таблицей, делаем вывод, что можно найти, сколько деталей изготовил второй токарь.
350 – 200 = 150 (дет.) – изготовил второй токарь.
Обратив внимание на опорные слова «на…меньше», делаем вывод, что можно найти, сколько дней работал второй.
5 – 2 = 3 (дня) – работал второй токарь.
Зная количество и время работы второго токаря, находим его производительность:
150 / 3 = 50 (дет.) – изготовлял второй токарь в день.
Уже при решении первых задач, нужно приучать детей к правильной терминологии.
Для решения задач второго типа, текст задачи можно проиллюстрировать чертежами, что помогает учащимся зрительно видеть задачу.
Пример № 1. Новая машина может выкопать канаву за 8 часов, а старая – за 12. Новая работала 3 часа, а старая - 5 часов. Какую часть канавы осталось выкопать?
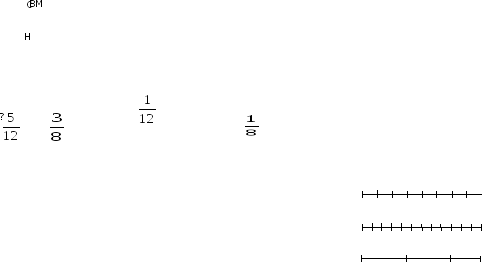
Рис.4. Графическое изображение задачи из примера №1
Дадим наглядное представление этих задач. Условимся, что объем выполненной работы неизвестен, поэтому принимаем его за 1 и изображаем в виде отрезка, но отрезков будет три, так как возможны три случая:
работает одна старая машина;
работает одна новая машина;
работают вместе обе машины.
Выясним, почему отрезки равной длины (обе машины выполняют одну и ту же работу).
Разбор задачи. На сколько равных частей делим первый отрезок? На 8, так как работа выполняется за 8 часов. Что показывает 1 часть? Какую часть работы выполняет новая машина за 1 час, т.е. какова ее производительность?
Так как новая машина работала 3 часа, то выполнила 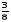 части все работы. Отмечаем на третьем отрезке -
части все работы. Отмечаем на третьем отрезке - 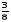 .
.
Аналогичные рассуждения проводим, рассматривая старую машину, и отмечаем на третьем отрезке - 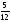 .
.
Далее рассматривается третий нижний отрезок, и по нему выясняется, как найти оставшуюся часть, т.е., отрезок, обозначенный знаком вопроса.
В связи с экономией времени деление отрезков производится «на глаз», хотя очень полезно показать, как можно разделить быстро на 4 равные части (отрезок делится пополам, а затем каждая часть еще пополам). Аналогично деление на 8 и т.д. На 6 частей – сначала пополам, а потом каждую часть - на три.
Пример №2. Два кузнеца, работая вместе, могут выполнить работу за 8 часов. За сколько часов может выполнить работу первый кузнец, если второй выполняет ее за 12 часов?
Изображая чертеж, мы проводим те же рассуждения, что и в предыдущей задаче.

Рис.5. Графическое изображение задачи из примера №2
Разбор задачи. Первый отрезок делим на 8 равных частей, так как оба выполняют работу за 8 часов. Одна часть показывает, какую часть работы они выполняют вместе за 1 час, т.е., их совместную производительность. Аналогичные рассуждения проводим для расчета производительности второго кузнеца.
Зная их совместную производительность и производительность второго, можно найти производительность первого.
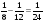
Результат показываем на чертеже.
Выясняем, сколько часов нужно первому кузнецу для выполнения работы (сколько раз в 1 содержится по  ).
).
Ответ: 24 часа.
Выводы ко второй главе
Таким образом, использование алгоритмов, таблиц, рисунков, общих приемов дает возможность ликвидировать у большей части учащихся страх перед текстовой задачей, научить распознавать типы задач и правильно выбирать прием решения.
Нередко, некоторые ученики просто списывают задачу с доски, не пытаясь вникнуть в ее смысл. Таким ученикам можно предложить творческую работы, где они должны сами составить задачу и решить ее. Составляя задачу, ученик более осознанно поймет существование зависимости между величинами, почувствует, что числа берутся не произвольно: некоторые задаются, а другие получаются на основе выбранных. При составлении задачи большое значение имеют и обратные задачи. Для активного участия в поиске решения хорошо использовать опорные карты-сигналы, которые должны быть у всех учащихся. [9]
Заключение
Таким образом, решение текстовых задач не случайно всегда волновало учителей, методистов, да и самих учащихся и их родителей.
Во-первых, нельзя решить задачу, не поняв ее содержание. Следовательно, умение решать текстовые задачи свидетельствует об одной из самых важных способностей человека - способности понимать текст. Правы те учителя, которые добиваются понимания текста не только на уроках чтения, но и на уроках математики. Критерием понимания задачи является факт решения задачи. Поэтому решение текстовых задач - это деятельность, весьма важная для общего развития. Обучая решать текстовые задачи, мы приучаем ориентироваться в ситуациях, делаем человека более компетентным. Конечно, для этого нужно резко расширить тематику задач, давать детям задачи, разнообразные по тематике, а не только «на скорость», «на работу», «на покупки». [14]
Во-вторых, решение задачи алгебраическим методом - чуть ли не единственный путь для объяснения ученикам того, чем вообще занимается математика, - объяснения метода математического моделирования. Собственная деятельность школьника в этой области протекает именно и только при решении текстовых задач алгебраическим методом. Ученик читает условия, характеризующие некоторую бытовую ситуацию, переводит эту ситуацию на математический язык (составляет уравнения) и затем решает уравнения, уже не думая о данной бытовой ситуации. Он работает с математической моделью. Наконец, он получает результат на языке этой модели и переводит его на естественный язык (осмысление и запись ответа) - получает решение бытовой задачи.
Решение текстовых задач способствует, с одной стороны, закреплению на практике приобретённых умений и навыков, с другой стороны, развитию логического мышления учащихся.
Наблюдается активизация их мыслительной деятельности. При правильной организации работы у учащихся развивается активность, наблюдательность, находчивость, сообразительность, смекалка, развивается абстрактное мышление, умение применять теорию к решению конкретных задач.
В ходе работы были решены все поставленные задачи:
1. Изучено понятие текстовой задачи и этапы ее решения
2.Рассмотрена сущность алгебраического метода решения текстовых задач.
3.Изучены примеры текстовых задач решенных алгебраическим способом.
4.Проанализировано практическое применение методики обучения решению текстовых задач алгебраическим способом.
5. Разработан и апробирован конспект урока.
Список литературы
Бобровская, А.В. Текстовые задачи курса алгебры средней школы. А.Б. Бобровская. – 3-е изд., доп. и перераб. – Шадринск: Исеть, 1999. – 64 c: ил.
Ванцян, А.Г. Эти непростые «простые задачки» А.Г. Ванцян / Практика образования. – 2007.– № 3.– C. 20-22.
Гороховцева, Л.А. Процесс решения текстовой задачи при изучении математики в средней школе. Л.А. Гороховцева / Теория и практика высш. проф. обр.– 2003. – № 9.– С. 14-21.
Демидова, Т.Е. Теория и практика решения текстовых задач: пособие для студ. высш. пед. учеб. заведений / Т.Е. Демидова, А.П. Тонких. – М.: Академия, 2002. – 288 с.
Зайцева, С.А. Организация работы над текстовой задачей на основе модели. С.А. Зайцева, И.И. Целищева / Начальное образование. – 2007. – № 4. – C. 9-15
Захарова, А.Е. Как помочь школьникам преодолеть некоторые затруднения в овладении решением текстовых задач. А. Захарова / Сборник научных трудов математического факультета МГПУ. М.: МГПУ, 2005. - С. 119-124.
Колягин, Ю.М. Задачи в обучении математике. Ю.М. Колягин. – М.: Просвещение, 1977. – 267 с.: ил.
Кузнецов, С.А. Научим учеников решать текстовые задачи по алгебре: из опыта работы учителя математики Кузнецова С. А. / С.А. Кузнецов / М-лы метод. каб. Ромодан. отд. обр.– Б.М., 2000. – 32 с.
Панкова, О.А. Текстовые задачи в учебниках Л.Г. Петерсон: учеб. пособие к курсу методики преподавания математики в нач. кл. / О.А. Панкова. – М.: СМУ, 2005. – 76 с.
Савинцева, Н.В. О текстовых задачах в современном курсе математики 5-6 класса. Н. Савинцева / Сборник научных трудов математического факультета МГПУ. М.: МГПУ, 2005. - С. 144-148.
Саранцев, Г.И. Методика обучения математике в средней школе: Учеб. пособие для студентов мат. спец. пед. вузов и ин-тов / Г.И. Саранцев. – М.: Просвещение, 2002. – 224 с.: ил.
Сафонова, Л.А. О действиях, составляющих умение решать текстовые задачи/ Л.А. Сафонова // Математика в шк. – 2000.– № 8.– С. 34-36.
Целищева, И. Как помочь каждому ученику самостоятельно решать текстовые задачи И. Целищева, С. Зайцева / Нач. шк.: еженед. прил. к газ. «Первое сентября». – 2001.– 00.05 (№ 18).– С. 2-5.
Шавернева, Л.А. Решение текстовых математических задач разными способами в системе развивающего обучения Л. В. Занкова, Л.А. Шавернева. – Самара: Федоров, 2007. – С. 268-294.
Шикова, Р.Н. Использование моделирования в процессе обучения решению текстовых задач. Р.Н. Шикова / Начальная школа: ежемес. науч.-метод. журн.– 2004.– № 12.–С. 32-41.
Приложение 1
Тема урока: «Уравнение. Понятие корня уравнения. Алгебраический способ решения задач»
Тип урока: Урок «открытия» нового знания.
УМК: Математика: 5 класс: учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков М.: Мнемозина, 2010 г
Цель урока: Сформировать способности учащихся к новому способу действий – решению задач алгебраическим способом; расширить базу понятий за счет включения в нее новых элементов: «корень уравнений», «алгебраический способ решения».
Задачи урока: образовательные (формирование познавательных УУД):
- актуализация знаний учащихся об уравнениях; определить понятие корня уравнения; изучить алгебраический способ решения задач.
развивающие (формирование регулятивных УУД) - уметь обрабатывать информацию и ранжировать ее по указанным основаниям; развить навыки самостоятельной работы; формировать умение анализировать, делать выводы, давать оценку деятельности.
воспитательные (формирование коммуникативных и личностных УУД): - формировать умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем; воспитывать ответственность и аккуратность.
Оборудование: компьютер, проектор, интерактивная доска, учебник.
Планируемые результаты: Предметные: - знать определение «уравнения», «корня уравнения»; - уметь находить неизвестные компоненты уравнения; - применять навыки решения уравнений при решении алгебраических задач. Личностные: -умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи; -инициатива, находчивость, активность при решении математических задач. Метапредметные: - умение видеть математическую задачу в контексте проблемной ситуации; - умение находить информацию, необходимую для решения математических проблем; - умение самостоятельно ставить цели и задачи, выбирать и создавать алгоритмы для решения учебных математических проблем.
Технологическая карта изучения темы
| Деятельность учителя | Деятельность учащихся | Формируемые УУД |
| 1. Мотивирование к учебной деятельности. Формулирование темы, постановка цели урока. (4-5мин) |
| Приветствие, проверка готовности учащихся к уроку. Организация внимания детей. Направляющие вопросы. Ребята, запишите, пожалуйста, в тетрадь число, классная работа. Чтобы определить тему урока, предлагаю вам выполнить следующее задание. Рассмотрите равенства (на экране записаны уравнения) x-12=48 Р; 30-x=17 Е; х – 18 =20 Ч; 40=x+26 Н; 39-х=15 И; х +25 =58 З; x+47=63 В; х – 38 = 60 Д; 55-x=30 А; x+25=45 У | 20 | 60 | 25 | 16 | 14 | 13 | 14 | 24 | 13 | |
|
|
|
|
|
|
|
|
| | 33 | 25 | 98 | 25 | 38 | 25 | |
|
|
|
|
|
| - Решите равенства и занесите в таблицу соответствующую букву. Ведет опрос получившихся ответов. - Как вы думаете, а почему именно эти слова я зашифровала в таблице? - А почему слово задача взято именно со словом уравнение? - Кто может сформулировать тему нашего урока? - Запишите тему урока в тетрадь (Уравнение. Корень уравнения. Алгебраический способ решения задач) | Включаются в деловой ритм урока. Проверяют готовность рабочего места.
Решение уравнений. Формулирование цели урока
Ответы детей. -Называют слова. - Мы будем сегодня говорить об уравнениях и задачах -Потому что мы будем говорить о задачах, которые решаются с помощью уравнения. - Решение задач с помощью уравнения. | Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества, умение выражать свои мысли.
|
| 2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии. (4-5 мин) |
| Помогает осмыслить, какие знания уже есть для решения поставленной задачи. Подводит к формулированию задач урока Вспомните: что вам уже известно об этой теме? - Давайте посмотрим, умеете ли вы решать простые уравнения? Рассмотрите уравнения (на экране записаны уравнения) 374+у=520 y-708=202 x+456=1000 511-x=308 Запишите решение на доске. Теперь внимательно посмотрите на тему и подумайте: какие учебные задачи нам нужно будет решить сегодня на уроке?
| Актуализируют знания, полученные в начальной школе. Решают простые уравнения. Исходя из темы, формулируют задачи урока. Ответы детей: Что такое уравнение. Как проверить, правильно ли решено уравнение. Как найти неизвестное. Ответы детей: (В виде вопросов записываются на доске) Что такое корень уравнения? Как его найти? | Коммуникативные: планирование учебного сотрудничества с учителем и сверстником. Познавательные: самостоятельное выделение-формулирование познавательной цели; формулирование проблемы. |
| 3. Построение проекта выхода из затруднения. (6-7мин) |
| Направляет на путь решения проблемы (учебник) -Где мы можем найти ответ на эти вопросы? 1. Работа со статьей учебника. -Прочитайте статью учебника на стр. 58-60. -Закройте учебник. Проверьте себя: что вы поняли из прочитанной статьи? - Заполните промежутки в предложениях. (На экране предложения с недостающими словами). Уравнение – равенство, содержащее букву, значение которой надо найти. Корень уравнения – значение буквы, при котором из уравнения получается верное числовое равенство. Решить уравнение – значит найти все его корни. - Продолжите предложения. Чтобы найти неизвестное слагаемое, надо. Чтобы найти неизвестное уменьшаемое, надо …. Чтобы найти неизвестное вычитаемое, надо…. Чтобы проверить, правильно ли решено уравнение, надо …… 2. Самостоятельная работа стр. 60 № 372 Акцентирует внимание на ключевых понятиях темы после решения № 372 Чему равен корень уравнения? Как называются неизвестные компоненты? Как можно найти неизвестное? | Ответы детей: В учебнике Работают со статьей учебника, отвечают на вопросы по статье учебника.
3 человека решают уравнения у доски, остальные – в тетради, отвечают на вопросы учителя. | Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: смысловое чтение, поиск информации. Личностные: самоопределение
|
| 4. Первичное закрепление с проговариванием во внешней речи. (5-6 мин) |
| Мотивирует учащихся на решение задачи. Помогает формулировать определение «алгебраический способ решения задач» 1.Коллективное решение задач при помощи составления уравнения (устно) -Ребята, умеете ли вы читать чужие мысли? А хотите? Давайте попробуем. -Я задумала число, из этого числа вычла 17 и получила 32. Какое число я задумала? -Чем является число 49 для данного уравнения? - Подумайте, а для чего нам нужно научиться решать уравнения? -Правильно. А давайте рассмотрим задачу в учебнике на стр. 60, № 373 (а). -При решении таких задач необходимо обозначать буквой то, что требуется найти. Кто может самостоятельно составить уравнение для решения этой задачи? Попробуйте. -Данный способ решения задачи называется алгебраическим. | Самостоятельно составляют уравнение, решают его и объясняют. Делают выводы. Ответы детей: -Задуманное число 49. На доске 1 ученик выполняет проверку. 49-17=32 32=32 Ответы детей: корнем уравнения. Ответы детей: Для того чтобы уметь решать жизненные проблемы, задачи. Учащиеся решают задачу в тетрадях, 1 ученик решает у доски с подробным объяснением. | Регулятивные: контроль, оценка, коррекция. Познавательные: умение структурировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: управление поведением партнера, умение выражать свои мысли. |
| 5. Самостоятельная работа с взаимопроверкой по эталону. (4-5мин) |
| Опосредованно помогает справиться со сложностями. -Попробуйте самостоятельно решить задачу с последующей взаимопроверкой по вариантам: 1 вариант – стр. 60, № 373 (б), 2 вариант – стр. 60, № 373 (г) - Что было сложно для вас, когда вы решали задачу? -Кто поможет нам разобраться с трудностями | Самостоятельно решают задачи), осуществляют взаимопроверку, формулируют вопросы, с которыми возникли сложности. Ответы детей: что нужно принять за х; как составить уравнение; решить уравнение; и т.д. Объясняет тот, кто понял. | Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения; Личностные: самоопределение
|
| 6. Включение в систему знаний и повторение. (7-8 мин) |
| Предлагает на выбор задания разного уровня сложности. Выслушивает тех, кто работает с опережением. 1. А теперь, предлагаю вам каждому выбрать для себя задание по уровню сложности. 1. Придумайте задачу на составление уравнения и выполните к ней рисунок. 2. По уравнению 27-х=10 составьте задачу и выполните рисунок. 3. У Кати было ____ конфет, а у Пети на _____ конфет было меньше. Вместе у них было ____ конфет. Составьте задачу и решите уравнение, выполните рисунок. 2. Кто выполнил раньше других, рассмотрите задание на стр 62, № 379 (устно). Будете готовы – поднимите руку. (Учитель выслушивает ответ, пока другие ребята справляются с заданием | Индивидуально работают с разноуровневыми заданиями. Те, кто закончил раньше, выполняют задание на смекалку. | Личностные: самоопределение. Познавательные: общеучебные: знаково-символические; моделирование; логические: анализировать и осмысливать текст и выбор задачи; |
| 7. Рефлексия учебной деятельности на уроке (итог). (2-3 мин) |
| Выясняет степень удовлетворенности учащихся уроком. -Напомните, какие задачи мы ставили в начале урока. - Мы их достигли? - Я заканчиваю урок в хорошем настроении, потому вы усвоили тему урока, научились решать сложные задачи, с которыми можете встретиться в жизни. А с каким настроением заканчиваете урок вы? | Соотносят поставленные цели, задачи урока с результатами. Дети показывают смайлики.
| Познавательные: оценка процесса и результатов деятельности. Коммуникативные: умение выражать свои мысли. Регулятивные: волевая саморегуляция, прогнозирование |
| 8. Домашнее задание. Выставление оценок. (1-2 мин) |
| Выставляет оценки, дает домашнее задание. -Запишите дом. задание. с.58 -п. 10, с. 65- № 397а, б, в | Выставляют в дневники оценки, записывают домашнее задание. Анализируют свое настроение |
|
21








 2 автобус – 40 км/ч 1 автобус – 50 км/ч
2 автобус – 40 км/ч 1 автобус – 50 км/ч
 90×4=360
90×4=360
 50+40=90 40÷10=4
50+40=90 40÷10=4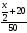 (ч) – время движения 1 автобуса, а
(ч) – время движения 1 автобуса, а 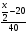 (ч) – время движения 2 автобуса.
(ч) – время движения 2 автобуса.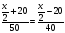









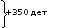
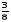 части все работы. Отмечаем на третьем отрезке -
части все работы. Отмечаем на третьем отрезке - 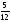 .
.