

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Курсовая работа на тему: "Формирование математической грамотности при решении текстовых задач на уроках математики в начальной школе"
Просмотр содержимого документа
«Курсовая работа на тему: "Формирование математической грамотности при решении текстовых задач на уроках математики в начальной школе"»
Министерство образования Красноярского края
КГБПОУ «Красноярский педагогический колледж № 1 им. М. Горького»
Курсовая работа
По ПМ.01 Преподавание по программам начального общего образования
МДК.01.04 Теоретические основы начального курса математики с методикой преподаваний
Тема: Формирование математической грамотности при решении текстовых задач на уроках математики в начальной школе
Выполнил: Черепанова Анастасия Владимировна
студент 21П-7 специальности:
44.02.02 Преподавание в начальных классах
Руководитель: Исаева Виктория Владимировна
Оценка: _____________________________
Красноярск, 2022
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 6
1.1 Сущность понятия «математическая грамотность» младших школьников 6
1.1.1 Понятие «математическая грамотность» как компонент функциональной грамотности 6
1.1.2 Математическая грамотность: компоненты и умения 9
1.2 Способы формирования и развития математической грамотности 14
1.2.1 Приемы умственных действий, способствующие формированию математической грамотности 14
1.2.2 Классификации заданий, способствующих формированию математической грамотности 16
1.3 Текстовые задачи в начальном курсе математики 18
1.3.1 Понятие текстовая задача в математике 18
1.3.2 Виды и методы решения текстовых задач 21
1.3.3 Текстовые задачи как способ формирования математической грамотности 23
1.3.4 Анализ текстовых задач, формирующих математическую грамотность у младших школьников 26
ЗАКЛЮЧЕНИЕ 32
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 33
ПРИЛОЖЕНИЕ 36
ВВЕДЕНИЕ
Современное общество меняет взгляд на содержание математического образования. Основное внимание направлено на развитие способности обучающихся применять полученные в школе знания и умения в жизненных ситуациях, эта способность называется математической грамотностью. Важность практического применения математических знаний подчеркивается в исследовании PISA-2021 (Programme for International Student Assessment), целью которого является проверка математической грамотности школьников по всему миру: «Способность рассуждать логически и убедительно формулировать аргументы – это навык, который приобретает все большее значение в современном мире. Математика – это наука о четко определенных объектах и понятиях, которые можно анализировать и трансформировать различными способами, используя математическое рассуждение для получения выводов» [23], [26].
Актуальность развития математической грамотности обучающихся начальной школы обусловлена некоторыми изменениями в условиях обеспечения школьного образования в России отмеченными в ФГОС НОО 2021 года [25].
Т.А. Иванова, доктор педагогических наук и О.В. Симонова, аспирант кафедры дидактики физики и математики в своей статье обозначают математическую функциональную грамотность как характеристику подготовки обучающегося, которая включает полученные знания, умения и опыт его деятельности, а также отражает смысл в отношении ученика к математике и математической деятельности, к опыту их применения для реальной жизни [19, с. 125].
Формирование математической грамотности важно и имеет большую практическую ценность в жизни, кроме того, необходимость формирования этого умения закреплена в федеральном государственном образовательном стандарте начального общего образования (далее – ФГОС НОО). Предметные результаты освоения основной образовательной программы начального общего образования по математике во ФГОС НОО должны отражать: «использование начальных математических знаний при решении учебных и практических задач и в повседневных ситуациях для описания и объяснения окружающих предметов, процессов и явлений, оценки их количественных и пространственных отношений, в том числе в сфере личных и семейных финансов», «овладение элементами математической речи: умения формулировать утверждение (вывод, правило), строить логические рассуждения (одно-двухшаговые) с использованием связок "если ..., то ...", "и", "все", "некоторые"» [1, с. 46].
В начальном обучении математике при формирование математической грамотности, велика роль текстовых задач. Решая их, учащиеся приобретают математические знания, готовятся к практической деятельности, которая будет использоваться ими в собственной жизни. Задачи способствуют развитию их логического мышления. Большое значение имеет решение текстовых задач и в воспитании личности, т.к. задачи основаны на бытовом (естественном) сюжете, поэтому учитель должен иметь глубокие представления о текстовой задаче, о её структуре, уметь решать такие задачи разными способами.
Объект исследования: формирование математической грамотности.
Предмет исследования: текстовые задачи как средство формирования математической грамотности.
Цель исследования: изучение способов формирования математической грамотности в процессе решения текстовых задач.
Задачи исследования:
определить значение основных терминов, понятий исследования;
проанализировать методы и приемы формирования математической грамотности;
выделить виды, приемы и особенности решения текстовых задач;
выявить влияние текстовых задач на формирование математической грамотности;
провести анализ задач УМК «Школа России» и УМК «Система развивающего обучения Л. В. Занкова».
Методы исследования:
анализ литературы;
сравнение.
Основные понятия:
Математическая грамотность – это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в XXI веке [23].
Текстовая задача – текстовой задачей является описание некоторой ситуации (ситуаций) на естественном языке с требованиями дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения [15, с. 60].
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В одной из своих работ А. Н. Леонтьев выделял обобщенное определение функциональной грамотности – умение решать жизненные задачи и проблемы [13, с. 2]. Позднее А. А. Леонтьев, дал корректное, но в то же время и глубокое определение функциональной грамотности – «Если формальная грамотность – это владение навыками и умениями техники чтения, то функциональная грамотность – это способность человека свободно использовать эти навыки для извлечения информации из реального текста – для его понимания, сжатия, трансформации» [16, с. 15].
Мы будем понимать функциональную грамотность как способность человека вступать в отношения с внешней средой и максимально быстро адаптироваться и функционировать в ней. В отличие от элементарной (формальной) грамотности как способности личности читать, понимать, составлять простые короткие тексты и осуществлять простейшие арифметические действия, что и упоминается в определении А. А. Леонтьева, функциональная грамотность – уровень знаний, умений и навыков, обеспечивающий нормальное функционирование личности в системе социальных отношений, который считается минимально необходимым для осуществления жизнедеятельности личности в конкретной культурной среде [13, с. 2].
Важность формирования функциональной грамотности подчеркивает в своей статье М. А. Холодная: она ссылается на требования к содержанию образования на ступени основного общего образования, одним из которых «… является достижение выпускниками уровня функциональной грамотности, необходимой в современном обществе, как по математическому и естественнонаучному, так и социально-культурному направлениям» [28].
И также выделяет основные черты функциональной грамотности:
направленность на решение бытовых проблем;
является ситуативной характеристикой личности, поскольку обнаруживает себя в конкретных социальных обстоятельствах;
связь с решением стандартных, стереотипных задач;
это всегда некоторый элементарный (базовый) уровень навыков чтения и письма;
используется в качестве оценки прежде всего взрослого населения;
имеет смысл главным образом в контексте проблемы поиска способов ускоренной ликвидации неграмотности.
Один из компонентов функциональной грамотности – это математическая грамотность, которая позволяет человеку использовать математические знания на практике и на их основе уметь описывать и объяснять явления, прогнозировать их развитие. Г. С. Ковалева выделила следующее определение математической грамотности: «Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину» [19, с. 2].
Математическая грамотность младшего школьника рассматривается как компонент функциональной грамотности и трактуется как:
понимание необходимости математических знаний для учения и повседневной жизни;
потребность и умение применять математику в повседневных (житейских) ситуациях: находить, анализировать математическую информацию об объектах окружающей действительности, рассчитывать стоимость (протяженность, массу);
способность различать математические объекты (числа, величины, фигуры), устанавливать математические отношения (длиннее-короче, быстрее-медленнее), зависимости (увеличивается, расходуется), сравнивать, классифицировать;
совокупность умений: действовать по инструкции (алгоритму), решать учебные задачи, связанные с измерением, вычислениями, упорядочиванием, формулировать суждения с использованием математических терминов, знаков [26].
Во время проведения исследования PISA-2021 (Programme for International Student Assessment), которое проверяло сформированность математической грамотности у школьников, были выведены некоторые классификации заданий, которые использовались при проверке учащихся, но о них мы поговорим в следующем пункте. Е.М. Ганичева, доцент кафедры математики и информатики ФГБОУ ВО Вологодского государственного университета, вывела критерии оценки при составление заданий на формирование функциональной грамотности [11, с. 27].
Основные критерии составления заданий для формирования и оценки функциональной грамотности:
наличие жизненной ситуации в условии задачи;
возможность перевода условий задачи, сформулированных с помощью обыденного языка, на язык математики;
новизна формулировки задачи, неопределенность в способах решения.
Если провести анализ данных критериев по оценке составления заданий и классификаций заданий, которые были использованы в исследование PISA-2021 (Programme for International Student Assessment) при проверке математической грамотности младших школьников были отобраны классификации заданий соответствуют критериям оценки составления заданий. Данный анализ основан на том, что классификации, выбранные для исследования PISA-2021 полностью направлены на наличие практического опыта, навыков жизни, соответственно подходят под критерий «наличие жизненной ситуации в условии задачи». Смотря на следующий критерий, можно сказать, что в заданиях, подобранных для исследования также упоминается про использование естественного языка, что также будет доказано далее в нашей работе. И также критерий «новизна формулировки задачи, неопределенность в способах решения», он также соответствует подобранным в исследование заданиям, т.к. хоть все задания и направленны на уже пройденные и жизненно использующиеся знания, умения и навыки. Все равно для решения заданий нужно использовать такие умственные действия, как: воспроизводить, понимать, формулировать естественным языком; применять математические знания, язык; рассуждать, устанавливать связи; интерпретировать, размышлять и рассуждать. Это также подтверждено далее в работе, в компонентах и умениях, использующихся для формирования математической грамотности.
В исследовании PISA математическая грамотность определяется как «способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в XXI веке» [23].
Для более глубокого понимания понятия «математическая грамотность» рассмотрим подробнее отдельные составляющие приведенного определения.
Умение «мыслить и формулировать ситуации математически» включает способность распознавать и выявлять возможности использовать математику, принять имеющуюся ситуацию и трансформировать ее в форму, поддающуюся математической обработке, создавать математическую модель, отражающую особенности описанной ситуации.
Умение «применять математику» рассматривается как способность применять математические понятия, факты, процедуры, рассуждения и инструменты для получения решения или выводов. Эта деятельность включает выполнение математических процедур, необходимых для получения результатов и математического решения (например, анализировать информацию на математических диаграммах и графиках, работать с геометрическими формами в пространстве, анализировать данные), работать с моделью, выявлять закономерности, определять связи между величинами и формулировать математические аргументы.
Умение «интерпретировать» подразумевает способность размышлять над математическим решением или результатами, интерпретировать и оценивать их в контексте реальной проблемы. Эта деятельность включает перевод математического решения в контекст реальной проблемы, оценивание реальности математического решения или рассуждений по отношению к контексту проблемы. Этот процесс охватывает и интерпретацию, и оценку полученного решения или определение того, что результаты разумны и имеют смысл в рамках предложенной ситуации [21, с. 64].
Каждый из этих мыслительных процессов опирается на математические рассуждения. Это означает, что учащимся потребуется продемонстрировать, как они умеют размышлять над аргументами, обоснованиями и выводами, над различными способами представления ситуации на языке математики, над рациональностью применяемого математического аппарата, над возможностями оценки и интерпретации полученных результатов с учетом особенностей предлагаемой ситуации.
Существуют принятые три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений. Эти уровни дают понять, как происходит формирование и развитие математической компетентности.
Первый уровень (уровень воспроизведения) – это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений.
Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы учащимся или выходят за рамки известного лишь в очень малой степени. Содержание задачи подсказывает, материал какого раздела математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач.
Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Задания, как правило, включают больше данных, от учащихся часто требуется найти закономерность, провести обобщение и объяснить или обосновать полученные результаты [12, с. 28].
Cравнения уровней математической компетентности и умений, составляющих понятие «математическая грамотность показывает, как математическая компетентность помогает в формировании математической грамотности. Кроме того, оно показывает, что уровни математической компетентности и три главные умения, раскрывающие понятие математической грамотности, похожи.
Умение «мыслить и формулировать ситуации математически» схоже с уровнем воспроизведения, который говорит о том, что сначала осуществляется анализ и использование в выполнении заданий известных алгоритмов.
Умение «применять математику» можно сравнить со вторым уровнем (уровнем установления связей) и рассматривать как способность применять известные знания при рассуждениях в ходе решения каких-либо задач.
Наконец, умение «интерпретировать» сравнимо с уровнем рассуждений, в которых говорится о том, что важно уметь перевести текст задачи на язык реальной жизни, на естественный язык.
Данные рассуждения можно подтвердить компонентами математической грамотности, которые выделяет доцент кафедры математического образования С. Г. Афанасьева [24].
Компонентами математической грамотности являются:
воспроизведение математических фактов, методов и выполнение вычислений;
установление связей и интеграции материала из разных математических тем, необходимых для решения поставленной задачи;
математические размышления, требующие обобщения и интуиции.
В определении «математической грамотности» основной упор сделан не на овладение предметными умениями, а на функциональную грамотность, позволяющую свободно использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов, размышлений и интуиции. Для этого важно иметь значительный объем математических знаний и умений, которые не сводятся к знанию математических фактов, терминологии, стандартных методов и умению выполнять стандартные действия и использовать определенные методы.
Можно отметить результаты обучения начальной школы, которые отражают формирование математической грамотности и также соответствуют умениям и уровням компетенций математической грамотности, в которых описывалось использование естественного языка, т.е. такого языка, который будет понятен в жизненных ситуациях [26].
Результаты обучения, отражающие отдельные позиции математической грамотности, могут быть конкретизированы, например:
выполнение письменных вычислений, связанных с бытовыми жизненными ситуациями, на основе изученных алгоритмов (сложение/вычитание многозначных чисел, умножение/деление многозначных чисел на однозначное и двузначное число);
выполнение (устно) арифметических действий над числами в пределах сотни и с большими числами в случаях, легко сводимых к действиям в пределах ста;
использование свойств арифметических действий для выполнения устных вычислений, необходимых в практической деятельности и повседневной жизни;
решение текстовых задач в 1-2 действия, связанных с бытовыми жизненными ситуациями (покупка, измерение, взвешивание и др.).
Все выше перечисленное рассматривается в математической грамотности, использование естественного языка и связь математического мира с реальным, это также указано, исходя из основного определения математической грамотности, которое мы взяли для написания данной работы PISA-2021 (Programme for International Student Assessment). Организаторы проведенного исследования составили модель математической грамотности (рисунок 1), ключевым моментом которой является связь математического мира с реальным.
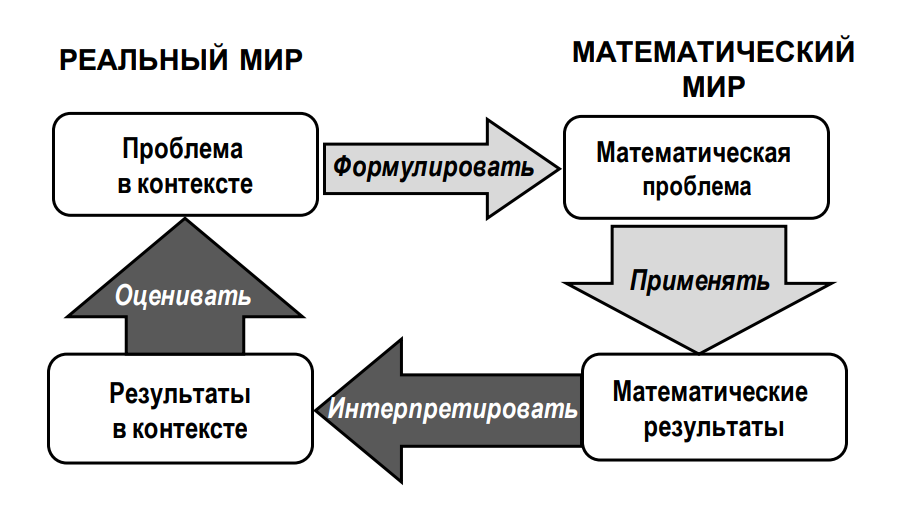
Рисунок 1 – Модель математической грамотности
Анализ модели показывает, что математическая грамотность состоит из связи реального и математического мира, в которой проблема из реального мира формулируется в математическую проблему, а позже через математически полученные результаты интерпретируется, то есть в итоге получаются результаты, сформулированные в контексте определенной проблемы реального мира. Таким образом, можем отметить важность работы с задачами, представленными на естественном языке, в формировании математической грамотности у обучающихся начальных классов [24].
1.2.1 Приемы умственных действий, способствующие формированию математической грамотности
Формирование математической грамотности – сложный, многосторонний и длительный процесс. В начальной школе идет интенсивное обучение различным видам деятельности, закладываются основы математической грамотности. Перед педагогами встает серьёзная проблема, как заложить основы этой грамотности, с помощью каких педагогических технологий, приемов, методов, и в целом – как воспитать функционально-грамотного человека.
Важнейшим видом учебной деятельности на уроках математики является решение задач. Обучающимся предлагаются не типичные учебные задачи, а близкие к реальным проблемные ситуации, представленные в некотором контексте и разрешаемые доступными обучающемуся средствами математики, что связывает решение текстовых задач с бытовым (жизненным) сюжетом и математическую грамотность. Такие задания направлены на развитие математической и естественнонаучной грамотности, которое предполагает способность учащихся использовать знания, приобретенные ими за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.
Рассмотрим приемы умственных действий, которые способствуют развитию математической грамотности.
Анализ и синтез. Это важнейшие мыслительные операции. Анализ связан с выделением элементов данного объекта, его признаков или свойств. Синтез – это соединение различных элементов, сторон объекта в единое целое. В мыслительной деятельности человека анализ и синтез дополняют друг друга, так как анализ осуществляется через синтез, синтез – через анализ.
Способность к аналитико-синтетической деятельности выражается не только в умении выделять элементы в единое целое, но и в умении включать их в новые связи, увидеть новые функции.
Формированию этих умений может способствовать: а) рассмотрение данного объекта с точки зрения различных понятий; б) постановка различных заданий к данному математическому объекту.
Сравнение. Этот прием занимает особую позицию в организации продуктивной деятельности младших школьников в процессе обучения математики. Формирование умения пользоваться этим приемом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания.
По методике Истоминой Натальи Борисовны целесообразно ориентироваться на такой этап, как выделение признаков или свойств одного объекта [10, с. 113].
Классификация. Для лучшего достижения результатов данного приема следует в обязательном порядке соблюдать этапность работы на уроке. Где каждый из этапов будет определен к решению определенных видов заданий.
Обобщение. Выделение существенных признаков математических объектов, их свойств и отношений – основная характеристика обобщения. Результат обобщения фиксируется в понятиях, суждениях, правилах. Процесс же обобщения может быть организован по-разному. В зависимости от этого говорят о двух типах обобщения – теоретическом и эмпирическом. В курсе математики в начальной школе чаще всего применяется эмпирический тип, при котором обобщение знания является результатом индуктивных рассуждений (умозаключений).
В исследование PISA-2021 (Programme for International Student Assessment) при проверке математической грамотности, содержание заданий было распределено по четырем категориям: пространство и форма, измерение и зависимости, количество, неопределенность и данные, которые охватывают основные типы проблем, возникающих при взаимодействиях с повседневными явлениями. Название каждой из этих категорий отражает обобщающую идею, которая в общем виде характеризует специфику содержания заданий, относящихся к этой области [18, с. 118].
Измерение и зависимость – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. алгебраическим материалом, а также с основами математического анализа.
Пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам, отношениям, т. е. к геометрическому материалу.
Количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относиться к курсу арифметики.
Неопределенность и данные – задания охватывают вероятные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности.
Если же сравнить приемы умственных действий, которые выделяет Н.Б. Истомина и классификации заданий, выделенных в исследование PISA-2021 (Programme for International Student Assessment), то можно выявить, что задания, которые были выбраны в исследовании и также включают в себя уровни математической компетентности, рассмотренные ранее. Что также дает связь с естественным языком, который используется в задачах, направленных на жизненные ситуации.
Так и в концепции PISA-2021 выделяется возрастание роли умения строить математические модели, которые можно было бы использовать для решения текстовых задач, в которых также используется упоминание жизненных ситуаций.
Для выполнения заданий, представленных в исследование PISA-2021 (Programme for International Student Assessment) требуется относительно небольшой объем знаний и умений, которые необходимы для математически грамотного современного человека [23].
К ним отнесены:
пространственные представления;
пространственное воображение;
свойства пространственных фигур;
умение читать и интерпретировать количественную информацию, представленную в различной форме (в форме таблиц, диаграмм, графиков реальных зависимостей), характерную для средств массовой информации;
умение работать с формулами;
знаковые и числовые последовательности;
нахождение периметра и площадей нестандартных фигур;
действия с процентами;
использование масштаба;
использование статистических показателей для характеристики реальных явлений и процессов;
умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости) и др.
Соответственно при решении задач, также можно применять полученные знания и умения на уроках по решению текстовых задач, направленных на проблемы повседневной жизни младших школьников.
Работа по формированию умения решать текстовые задачи начинается с первых дней обучения в школе. Первые шаги при решении простых задач в одно действие не вызывают у учащихся затруднений. Но самостоятельное решение составных задач вызывает трудности и учащиеся испытывают всё большие проблем с текстовыми задачами. Причина возникающих затруднений в том, что у учащихся не сформировано в значительной степени умение анализировать текст задачи, правильно выделять известное и неизвестное, устанавливать взаимосвязь между ними, которая является основой выбора действия для решения текстовой задачи.
Одним из приоритетных понятий текстовой задачи является определение Ю. М. Колягина. Текстовая задача – текстовой задачей является описание некоторой ситуации (ситуаций) на естественном языке с требованиями дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения [15, с. 60].
Особую важность также представляет определение Л. М. Фридмана:
Текстовые задачи, решаемые в школьном курсе математики, представляют собой словесные модели задач, в которых учащемуся необходимо найти значения некоторой неизвестной величины или нескольких величин;
Задачи, в которых зависимость между данными и искомыми не выражена в явной форме, а сформулирована словами, так же как и вопрос задачи, называются собственно задачами или задачами с текстом [15, с. 61].
Исходя из определений можно понять, что основными элементами текстовой задачи являются непосредственно вопрос, ситуация, текст.
И. Р. Гальперин также отмечает, что попытки некоторых теоретиков представить текст как явление безграничное бездоказательны, исходя из этого можно сделать вывод о том, что именно текст придает текстовым задачам законченную форму [2, с. 9].
У всех определений текстовой задачи по математике можно выделить особенность, заключающую в представлении условий задачи на нематематическом языке: «на естественном языке», «не математические слова», «словесные модели слов». Получается, что именно нематематическая структура представления задачи характеризует ее как текстовую.
Это можно подтвердить словами О. П. Шаровой: «…главным отличием задачи от примера является не только наличие текста, а наличие части условия или требования, выраженного на естественном (нематематическом) языке, которая требует в процессе решения перевода на математический язык» [22, с. 120].
Взаимосвязь задачи по математике и присутствия в ней нематематического языка может послужить основой предположения о том, что в текстовой задаче по математике присутствует сюжет.
Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придется работать, те инструменты, с помощью которых выполняется эта работа.
Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких основных частей они состоят, каковы инструменты, с помощью которых производится решение задач.
Любая текстовая задача состоит из двух главных частей – условия и требования (вопроса). В условии сообщаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме [15, с. 60].
Следует уделить внимание традиционно выделенным этапам решения текстовых задач, т.к. последовательность этапов обусловлена логикой условий задачи.
Этапы решения текстовой задачи:
восприятие и осмысление задачи (анализ и понимание задачи);
поиск плана решения;
выполнение плана решения;
проверка решения;
формулировка ответа на вопрос задачи (вывода о выполнении требования);
работа над задачей после решения.
Итак, в процессе решения текстовой задачи младшие школьники проходят ряд основных этапов: анализ и понимание задачи, поиск и составление плана решения, осуществление плана решения задачи, проверка решения задачи, формулировка ответа на вопрос задачи. В реальном процессе решения текстовых задач этапы не имеют четких границ. Однако, учителям следует понимать, что решение каждой отдельно взятой задачи должно содержать все указанные этапы, осмысленное прохождение которых сделает процесс усвоения материала целенаправленным, следовательно, более успешным и понятным для обучающихся. Полнота использования младшими школьниками данных этапов решения текстовых задач во многом зависит от уровня математических знаний, опыта и мыслительных умений школьников, которые также отражаются и при формирование математической грамотности [14, с. 3-5].
Также важна работа над содержанием задачи, т.е. над осмыслением ситуации изложенной в задаче, установлением зависимости между данными и искомым. Можно сказать, что перечисленные выше этапы работы с текстовой задачей, уже включают в себя работу над содержанием текста, но лучше уделить восприятию больше времени, потому что решение, которое будет происходить следующим этапов будет протекать более легко и быстро. На данном этапе восприятия текста задачи, обязательно стоит уделять время для чтения, разбора и записи условий задачи. Ведь именно этот момент даст более подробное понимание содержания условий и требований задач. Также на данном этапе стоит напомнить обучающимся, чтобы они выполняли графическую форму текста (условий и требований) задачи – модель, схема и др. Представление текста в графической форме является важным, так как именно графическая форма поможет лучше воспринять текст задачи, т.е. сделает текст более понятным для учащихся начального звена.
Подводя итог, можно сказать, что текстовая задача — это обязательный текст задачи, в котором присутствует сюжет или ситуация, вопрос (требование), и все это изложено на естественном языке. При этом обязательно должны присутствовать этапы решения, в которых можно выделить такие действия, как: восприятие; поиск плана решения; выполнение соответственно действий для решения задач; проверка; вывод и также анализ произведенного решения.
При решении текстовых задач в начальной школе в математике присутствуют различные методы их решения:
арифметический (по действиям или при помощи выражения);
алгебраический (при помощи уравнения);
геометрический;
логический;
практический;
табличный;
комбинированный (смешанный) [14, с. 1-3].
Практически каждая задача в рамках выбранного метода допускает решение с помощью модели. Используя алгебраический метод, ответ на требование в одной и той же текстовой задаче можно получить, составив и решив совершенно разные уравнения; используя логический метод – построив разные алгоритмы. В этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называют способы решения.
Арифметический метод. Помогает найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами.
Алгебраический метод. Помогает найти ответ на требование задачи, через составление и решение уравнения или системы уравнений (или неравенств). Одну и ту же задачу можно также решить различными алгебраическими способами.
Геометрический метод. Помогает найти ответ на требование задачи с помощью использования геометрического построения или свойства геометрических фигур.
Логический метод. Помогает найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.
Практический метод. Помогает найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).
Табличный метод. Позволяет видеть задачу целиком – это решение путем занесения содержания задачи в соответствующим образом организованную таблицу.
Комбинированный (смешанный) метод. Позволяет получить ответ на требование задачи более простым путем.
В курсе математики обязательно встречаются задачи разного рода, их разнообразие и вызывает затруднения у многих обучающихся. Необходимо отработать и автоматизировать эти процессы. Чтобы получить правильный ответ на задачу, необходимо понять ее суть, поэтому тренироваться необходимо начиная с простейших задач.
Умение понять и решить текстовую задачу является одним из основных и главных показателей уровня математического развития, грамотности младшего школьника. В Федеральном государственном стандарте начального общего образования указаны предметные результаты освоения основной образовательной программы, которые должны отражать: «использование начальных математических знаний при решении учебных и практических задач и в повседневных ситуациях для описания и объяснения окружающих предметов, процессов и явлений, оценки их количественных и пространственных отношений, в том числе в сфере личных и семейных финансов», «овладение элементами математической речи: умения формулировать утверждение (вывод, правило), строить логические рассуждения (одно-двухшаговые) с использованием связок "если ..., то ...", "и", "все", "некоторые"» [1, с. 46].
В начальной школе в математике также выделяется множество текстовых задач, в которых имеется одинаковая зависимость между величинами, входящими в эти задачи, при возможном различии числовых данных и ситуаций (сюжета) образуют определенный вид текстовых задач. Задачи одного вида имеют одну и ту же алгебраическую модель. Положив в основание классификации способы решения задач, можно выделить такие группы:
задачи на тройное правило;
задачи на нахождение неизвестных по результатам действий;
задачи на пропорциональное деление;
задачи на исключение одного из неизвестных;
задачи на среднее арифметическое;
задачи на проценты и части;
задачи на движение;
задачи, решаемые с конца, или «от обратного» [17, с. 4-6].
С начала и до конца обучения в начальной школе математическая задача помогает ученику глубже понимать различные стороны взаимосвязей с окружающей его жизнью, дает возможность применить изучаемую теорию на практике, т.е. в жизненных ситуациях, что позволяет устанавливать разнообразные отношения в наблюдаемых явлениях в жизни и при решение текстовых задач.
Исходя из ранее представленных пунктов о математической грамотности нашей работы, можно выявить факт того, что во время формирования математической грамотности используется связь математического мира с реальным миром, как и в текстовых задачах. Текст задач построен на сюжете, т.е. на реальном мире или более приближенном к реальному, что позволяет сделать вывод о том, что во время решения текстовых задач возможно формирование математической грамотности. Также во время анализа математических уровней и компетентностей, было указано, что производятся действия: воспроизведение и понимание текста заданий; применение при решении и установлении связей в тексте заданий; размышление и рассуждение над решением и текстом заданий. И при их сравнении с этапами решения текстовых задач, было выявлено, что при решение текстовых задач производятся все те же действия, что и в задачах на формирование математической грамотности. Соответственно, можно сказать, что текстовые задачи способствуют формированию математической грамотности.
В статье кандидатов педагогических наук Л. О. Рословой, К. А. Краснянской и Е. С. Квитко «Концептуальные основы формирования и оценки математической грамотности» из научного журнала «Отечественная и зарубежная педагогика», рассматриваются подходы к составлению заданий, предназначенные для оценки и формирования математической грамотности. Они являются необходимыми критериями, некоторыми особенностями и требованиями, которые должны учитываться при разработке заданий [20, с. 64].
Учащимся предлагаются не учебные задачи, а практические проблемные ситуации, разрешаемые средствами математики. Контекст, в рамках которого предложена проблема, должен быть действительно жизненным, а не надуманным. Ситуации должны быть характерными для повседневной учебной и внеучебной жизни учащихся (например, связаны с личными, школьными или общественными проблемами, как это понимается в концепции PISA). Поставленная проблема должна быть интересной и актуальной для учащихся того возраста, на который она рассчитана.
Для выполнения задания необходимо целостное применение математики. Это означает, что требуется осуществить весь процесс работы над проблемой: от понимания, включая формулирование проблемы на языке математики, через поиск и осуществление ее решения, до сообщения и оценки результата, а не только часть этого процесса (например, решить уравнение или упростить алгебраическое выражение).
Используется следующая структура задания: дается описание ситуации (введение в проблему), к которой предлагаются два связанных с ней вопроса.
Введение в проблему представляет собой небольшой вводный текст мотивирующего характера, который не содержит лишней информации, не связанной с заданием или непринципиальной для ответа на поставленные далее вопросы. Введение не должно содержать информацию, которая носит отвлекающий характер.
Вопрос позволяет раскрыть приведенную ситуацию с определенной стороны. Каждый самостоятельный содержательный шаг фиксируется; все основные элементы выделяются для оценивания.
В большинстве заданий не должно содержаться прямых указаний на способ, правило или алгоритм выполнения (решения), что позволяет проверить, насколько осознанно учащиеся применяют полученные знания.
В доказательство того, что данные критерии соответствуют содержанию нашей работы, можно вновь обратиться к уровням математической компетентности, умственным действиям, способствующим формированию математической грамотности и этапам решения текстовых задач. Они поясняют, что действия, производимые при формирование математической грамотности учащимися, во время решения текстовых задач и критерии, выведенные Л. О. Рословой и К. А. Краснянской соответствуют друг другу.
Исходя из данных критериев (требований), нами будет произведен отбор заданий из различных УМК.
Для понимания того, какие текстовые задачи формируют у учащихся начальной школы математическую грамотность, предлагается сравнить текстовые задачи из УМК «Школа России» и УМК «Система развивающего обучения Л. В. Занкова».
Сравнение и анализ задач будем производить по критериям, выделенным Л. О. Рословой, К. А. Краснянской и Е. С. Квитко Сформулируем эти критерии в более обобщенном виде [20, с. 64].
Ситуации, которые представлены в контексте задачи, должны быть характерны для повседневной жизни учащихся начальной школы.
Целостное применение математики (выполнены все этапы работы над текстовой задачей).
Соблюдена структура задания (проблема (текст задачи) и требование (вопрос)).
Текст задачи не содержит информацию, которая носит отвлекающий характер.
Вопрос раскрывает ситуацию (проблему).
Не должно содержаться прямых указаний на способ решения задачи.
Для сравнения будут выбраны по 2 текстовые задачи начиная с первого по 4 класс из двух УМК «Система развивающего обучения Л. В. Занкова» и УМК «Школа России». Задачи будут проанализированы по выделенным критериям и будет выполнена оценка их направленности на формирование математической грамотности.
Для начала будет представлено оценивание текстовых задач из УМК «Система развивающего обучения Л. В. Занкова» из учебников под авторством И. И. Аргинская, Е. П. Бененсон, Л. С. Итина, С. Н. Кормишина.
Задача № 1. Класс 1 [8, с. 81] (рисунок 2).

Рисунок 2 – Задача 188
Анализируя данную задачу, можно сказать, что она соответствует 1, 2, 3 и 6 критериям, т.к. соблюдается наличие: жизненной ситуации; при решении задачи будут выполняться все этапы решения текстовых задач; соблюдена структура задачи ситуация и требование; задача не содержит прямых указаний на решение. Смотря на 4 критерий и сравнивая его с задачей № 1, можно сказать, что он выполнен. Но анализ критерия 5 показал неоднозначность его выполнения. Пятый критерий предполагает, что вопрос (требование) раскрывает ситуацию (проблему), которая указана в тексте задачи, однако в данной задаче представлены сразу несколько требований. Такая ситуация является возможной для задач, но в то же время может привести к некоторым затруднениям со стороны учащихся. Так что эту задачу можно назвать усложненным заданием в учебнике.
Задача № 2. Класс 1 [9, с. 180] (рисунок 3).

Рисунок 3 – Задача 180
В данной задаче идет полное соблюдение критериев, также тут представлена схема, которая может помочь учащимся при решении задания. Задача может показаться слишком легкой для конца первого класса, но возрастные особенности полностью соблюдены. Здесь представлена схема задачи, что также поможет учащимся сформировать первичное представление о схемах и т.п.
Анализ задач, представленных в учебнике 4 класса, показал, что для большинства задач не выполняется одно из главных требований к заданиям, направленным на формирование математической грамотности, – в этих задачах нет направленности на повседневные проблемы обучающихся. Тем не менее, некоторые компоненты актуальных для обучающихся в ситуациях, которые представлены в задаче № 7.
Анализ задач с 1 по 4 класс, выявил, что большинство задач направленных на формирование математической грамотности представлено в учебниках за 1 и 2 класс, а в 3 и 4 классе идет на убывание, т.к. смысл в задачах меняется и перестает быть направленным на жизненные ситуации, которые учащихся проживает в повседневной жизни. Примеры соответствующих задач из УМК «Школа России» также указаны в Приложение № 1.
Следующими будут рассмотрены текстовые задачи из УМК «Школа России» из учебника под авторством М. И. Моро, С. И. Волкова, С. В. Степанова.
Задача № 3. Класс 1 [3, с. 69] (рисунок 4).
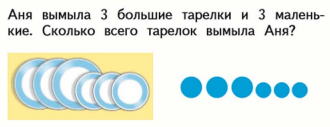
Рисунок 4 – Задача 1 класса из УМК «Школа России»
Данная задача полностью соответствует критериям, т.к. в ней предусматривается: наличие ситуации повседневной жизни; при решении применение всех этапов решения текстовой задачи; соблюдены требования к текстовой задаче (проблема и требование); не присутствует отвлекающего материала (лишнего текста задачи); вопрос направлен на решение проблемы (требования); нет прямых указаний для решения.
Задача № 4. Класс 2 [5, с. 62] (рисунок 5).

Рисунок 5 – Задача 2 класса УМК «Школа россии»
В данной задаче все критерии соблюдены, но критерий № 6 раскрывающий то, чтобы не представлялись прямые указания на решение задачи ставится под сомнение. Вопрос не ставится так прямо, потому что само условие запутано и чтобы ответить на требования в задаче предстоит выполнять некоторые действие, но однако если рассматривать требование задачи, не связывая его с условием задачи, то он будет поставлен слишком прямо для решения задачи.
После анализа двух УМК «Школа России» и УМК «Система развивающего обучения Л. В. Занкова», можно сделать вывод о том, что начиная с 1 по 4 класс количество заданий на формирование математической грамотности уменьшается. Если сравнивать 1 и 2, 3 и 4 классы, то текстовых задач способствующих формированию математической грамотности в 1 и 2 классе больше, чем в 3 и 4 классах. Примеры задач из УМК «Школа России» также указаны в Приложение № 2.
Исходя из выше представленных критериев мы попробовали составить некоторые текстовые задачи, которые будут полностью соответствовать требованиям. На примере одной из составленных задач мы покажем выполнение этапов решения текстовой задачи.
Задача № 5. 3 класс.
В актовом зале школы есть 6 окон. Чтобы их украсить ученики принесли горшки с цветами. Если поставить на каждое из окон по 3 горшка, то остается 6 горшков. Сколько горшков с цветами принести ученики?
Решение:
1) 3*6=18 (г.) – Потратили ученики на 6 окон.
2) 18+6=24 (г.) – Всего горшков с цветами принесли ученики в школу.
Проверка:
Проверку можно выполнить обратным действием.
1) 24-18=6 (г.) – Осталось после того, как было расставлено по 3 горшка на 6 окон.
Ответ: 24 горшка всего принесли ученики в школу для расстановки на 6 окон в актовом зале.
Для начала перед воспроизведением арифметических действий в задаче, происходит восприятие и осмысление текста задачи, во время которого учащиеся должны понять, что будет являться искомым, а что данным в задаче, здесь это представляет (Данное: 6 окон и на каждое из них по 3 горшка, 6 осталось после расстановки. Искомое: сколько всего горшков было?). Далее идет этап – поиск плана решения, во время которого обучающиеся начинают понимать, что им нужно будет найти (узнать), чтобы найти ответ на вопрос (требование) в задаче. 3 пункт плана, это выполнение плана решения соответственно, что было представлено под действиями 1 и 2 при решении задачи, где также учащиеся описывают, что они находят. 4 Этап – проверка решения, которая включает в себя действия уже после выполнения действий по нахождению ответа на вопрос. Здесь это представлено в виде действий для обратной задачи, также указано после нахождения выполнения арифметических действий. Остается еще два этапа это нахождение ответа на вопрос (требование) задачи и работа над задачей после ее решения. В данные два этапа входим сам заключающий ответ, который показывает, что задача решена и также некоторые вопросы учителя и ответы обучающихся по тексту задачи. В которые может входить анализ решения задачи, как хорошо справились, правильно ли выполнили действия и т.д.
Задача № 6. 1 класс.
Миша положил в рюкзак 5 учебников. Позже он взял оттуда 2 учебника. Сколько учебников осталось в рюкзаке?
Задача № 7. 2 класс.
В один школьный автобус отправившийся на экскурсию сели 36 учеников, а в другой на 18 больше. Сколько всего было учеников, которые поехали на экскурсию?
Задача №8. 4 класс.
Маша проехала на машине с родителями 144 км, им осталось проехать еще 12 км. Во сколько раз пройденный путь больше оставшегося?
В ходе работы был выполнен анализ психолого-педагогической литературы, рассмотрено несколько определений понятия «математическая грамотность» и «текстовая задача», были рассмотрены уровни математической грамотности в последствие которых было произведено сравнение с уровнями математической компетентности. Также были указаны приемы умственных действий и классификации заданий, влияющих на формирование математической грамотности, которые использовались в исследовании PISA-2021 (Programme for International Student Assessment) при проверке математической грамотности, было выполнено сравнение с видами и методами решения текстовых задач указания на их схожесть. Был выполнен анализ текстовых задач из УМК «Системы развивающего обучения Л. В. Занкова» и УМК «Школа России» по критериям Л. О. Рословой и К. А. Краснянской, также был пример составления и решения текстовой задачи самостоятельно.
В качестве исследования формирования математической грамотности были выбраны текстовые задачи, которые в итоге нашей курсовой работы указали на то, что они способствуют формированию математической грамотности у обучающихся начальной школы. Но важно, чтобы текстовые задачи, выбранные для формирования математической грамотности, соответствовали определенным критериям. Формирование математической грамотности существенно помогает учащимся начальной школы в своем повседневном опыте, развивая умения и навыки, которыми они будут пользоваться на протяжении всей жизни. Поэтому одним из важных направлений в нашем исследовании становится усиление внимания к обеспечению адаптации обучающихся к реальному миру, что помогает им обеспечить их жизнедеятельность.
В конечном итоге, данная работа определенно описывает всю важность формирования математической грамотности, что обусловлено не только использованной литературой, но документами, подтверждающими федеральную важность данной темы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОКПриказ Минпросвещения России от 31.05.2021 № 286 «Об утверждении федерального государственного образовательного стандарта начального общего образования» (Зарегистрировано в Минюсте России 05.07.2021 № 64100) – М.: Просвещение, 2021 – 46 с.
Гальперин И. Р. Текст как объект лингвистического исследования / И. Р. Гальперин. – Москва: КомКнига, 2007. – 9 с.
Моро М. И. Математика. 1 класс. Учеб. для общеобразоват. организаций. В 2 ч. Ч. 1 / М. И. Моро, С. И. Волкова, С. В. Степанова. – 6-е изд. – М. : Просвещение, 2015. – 69 с. : ил. – (Школа России).
Моро М. И. Математика. 1 класс. Учеб. для общеобразоват. организаций. В 2 ч. Ч. 2 / М. И. Моро, С. И. Волкова, С. В. Степанова. – 6-е изд. – М. : Просвещение, 2015. – 58 с. : ил. – (Школа России).
Математика. 2 класс. Учеб. для общеобразоват. организаций. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.]. – 6-е изд. – М. : Просвещение, 2015. – 62 с. : ил. – (Школа России).
Математика. 3 класс. Учеб. для общеобразоват. организаций. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.]. – 5-е изд. – М. : Просвещение, 2015. – 42 с. : ил. – (Школа России).
Математика. 4 класс. Учеб. для общеобразоват. организаций. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.]. – 4-е изд. – М. : Просвещение, 2015. – 46 с. : ил. – (Школа России).
Математика : Учебник для 1 класса : В 2 ч. Ч. 1 / Аргинская И. И. [и др.]. – 2-е изд., стер. – Самара : Издательство «Учебная литература» : Издательский дом «Федоров», 2012. – 81, 180 с.
Математика : Учебник для 1 класса : В 2 ч. Ч. 2 / Аргинская И. И. [и др.]. – 2-е изд., стер. – Самара : Издательство «Учебная литература» : Издательский дом «Федоров», 2012. – 58, 180 с.
Практикум по методике обучения математике в начальной школе. Развивающее обучение.: учебно-методическое пособие / Ассоциация XXI век; [сост. Н. Б. Истомина, Ю. С. Заяц]. – Смоленск: Ассоциация XXI век, 2009. – 113 с.
Формирование математической грамотности обучающихся: практическое пособие / Департамент образования Вологодской области, Вологодский институт развития образования; [сост. Е. М. Ганичева]. – Вологда: ВИРО, 2021. – 27 с., 77с.
Уровни математической грамотности. История языком математики: Сборник метапредметных задач. – материалы с электронного ресурса ЛитРес (1 августа 2019 г.) / [отв. ред. И. С. Куликова]. – 2019. – 28 с.
Аблеева А. А. Формирование математической грамотности у учащихся общеобразовательной школы // International scientific review. Науки об образование. 2022. № LXXXVI. – С. 2
Айвазян Н. С. Этапы, методы и способы решения текстовых задач начального курса математики // Гуадеамус. 2017. № 3-21. – С. 3-5.
Белинский С. С. Об определении понятия текстовая задача по математике // Вестник магистратуры. Языкознание и литературоведение. 2013. № 5-3. – С. 60-62.
Веряев А. А., Нечунаева М. Н., Татарникова Г. В. Функциональная грамотность учащихся: представления, критический анализ, измерение // Известия Алтайского государственного университета. Философия и педагогика. 2013. № 4. – С. 15.
Воистинова Г. Х., Рахматуллина Д. Х. Приемы обучения решению текстовых задач // StudNet. 2021. № 7-5. – С. 4-6.
Денищева Л. О., Савищева Н. В., Сафуанов И. С., Ушаков А. В., Чугунов В. А., Семеняченко Ю. А. Особенности формирования и оценки математической грамотности школьников // Science for Education Today. 2021. № 5-12. – С. 118.
Иванова Т.А., Симонова О.В. Структура математической грамотности школьников в контексте формирования их функциональной грамотности // Вестник Вятского государственного университета. Психологические науки. Науки об образование. Философия. Этика. Религиоведение. 2009. № 4. – С. 125.
Рослова Л. О., Краснянская К. А., Квитко Е. С. Концептуальные основы формирования и оценки математической грамотности // Педагогическая и зарубежная педагогика. Науки об образовании. 2019. № 5-1. – С. 67-69.
Рослова Л. О. В поиске путей развития математической грамотности учащихся // Педагогические измерения. 2017. № 4. – С. 64
Шарова О. П. Сюжетные задачи в обучении математике // Ярославский педагогический вестник. Математика. 2005. № 3. – С. 120.
Сайт федерального института оценки качества образования: https://clck.ru/SaT8h (Дата обращения: 23.09.2022).
Афанасьева С. Г. Формирование функциональной грамотности. Математическая грамотность. https://clck.ru/Vz38X (Дата обращения: 13.10.2022).
Григорьева О. Ю. Актуальность развития математической функциональной грамотности обучающихся начальной школы. https://clck.ru/32q9wS (Дата обращения: 24.09.2022)
Кочурова Е. Э. Формирование математической грамотности младшего школьника на уроках математики. https://clck.ru/32kTbA (Дата обращения: 25.09.2022)
ФГБУ «Федеральный институт оценки качества образования». Краткая информационная справка об исследование TIMSS. https://clck.ru/ZHceb (Дата обращения: 23.09.2022)
Холодная М. А. Расширенный текст доклада профессора М. А. Холодной на IVВсероссийском съезде психологов образования России «Психология и современное российское образование». https://clck.ru/32q9xt (Дата обращения: 22.11.2022)
Приложение № 1
| УМК: «Система развивающего обучения Л. В. Занкова» | ||||||
| Задание / Ссылка на библиографический список | Критерии к оценке заданий | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
|
Рисунок 6 – Задача № 9 [9, с. 58]. | + | + | + | + | + | + |
|
Рисунок 7 – Задача № 10 [8, с. 180]. | + | + | + | + | + | + |
Таблица № 1 – Сравнение задач УМК «Система развивающего обучения Л. В. Занкова» с критериями
Приложение № 2
| УМК: «Школа России» | ||||||
| Задание / Ссылка на библиографический список | Критерии к оценке заданий | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
|
Рисунок 8 – Задача № 11 [4, с. 58]. | + | + | + | + | + | + |
|
Рисунок 9 – Задача № 12 [6, с. 42]. | + | + | + | + | + | + |
|
Рисунок 10 – Задача № 13 [7, с. 46]. | + | + | + | + | + | + |
Таблица № 2 – Сравнение задач из УМК «Школа России» с критериями
Курсовая работа выполнена мной самостоятельно. Использованные в работе материалы из опубликованной научной литературы и других источников имеют ссылки на них. Проверка в системе «Антиплагиат» мною выполнена (скриншот результата проверки прилагаю). Уровень заимствований со ссылками составляет __ 83,95 __% (оригинальность не менее 50%).
Библиография:
___28___ наименований
___________________ ____Черепанова Анастасия Владимировна_____
(подпись) ФИО (Студента)
___________________ ____Исаева Виктория Владимировна____
(подпись) ФИО (Руководителя)
«____» _____________________ 2022 г.
Оценочный лист курсовой работы
Студента специальности: 44.02.02 Преподавание в начальных классах
группы: 21П - 7
ФИО: Черепанова Анастасия Владимировна
Тема: Формирование математической грамотности при решение текстовых задач на уроках математики в начальной школе
| ПК/ОК | Основные показатели оценки результатов | Отметка о сформированности | |
| ПК 4.5. Участвовать в исследовательской и проектной деятельности в области начального образования/в области музыкального образования | Обоснована актуальность исследования | (*2) | |
| Объект и предмет, цели и задачи соответствуют теме исследования | (*2) | ||
| ПК 4.3. Систематизировать и оценивать педагогический опыт и образовательные технологии в области начального общего образования/в области музыкального образования на основе изучения профессиональной литературы, самоанализа и анализа деятельности других педагогов | Научная и методическая литература подобрана в соответствии с темой, целью, задачами и типом работы | (*2) | |
| Анализ источников представлен в виде вторичного текста | (*2) | ||
| Присутствует анализ литературы | (*2) | ||
| Представлена проработанность проблемы в теории и практике | (*2) | ||
| Имеются рекомендации относительно возможностей использования материалов работы | (*2) | ||
| Оформлены адекватные выводы | (*1) | ||
| ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности | Соответствие оформления требованиям: штифт Nimes NewRoman 14 Выравнивание по ширине Грамотное оформление таблиц, схем, диаграмм, графиков | (*1) | |
| Наличие правильно оформленных ссылок Библиография составлена в соответствии с ГОСТ 7.1-2003 | (*1) | ||
| Сумма баллов |
| ||
Руководитель: Исаева Виктория Владимировна
(расшифровка подписи)
Дата _______________
Оценочный лист презентации курсовой работы
Студента специальности: 44.02.02 Преподавание в начальных классах
группы: 21П - 7
ФИО: Черепанова Анастасия Владимировна
Тема: Формирование математической грамотности при решение текстовых задач на уроках математики в начальной школе
| ПК/ОК | Основные показатели оценки результатов | Отметка о сформированности |
|
| ||
| ПК 4.5. Участвовать в исследовательской и проектной деятельности в области начального образования/в области музыкального образования | Обоснована актуальность исследования | (*1) |
|
| ||
| Объект и предмет, цели и задачи соответствуют теме исследования | (*2) |
|
| |||
| ПК 4.3. Систематизировать и оценивать педагогический опыт и образовательные технологии в области начального общего образования/в области музыкального образования на основе изучения профессиональной литературы, самоанализа и анализа деятельности других педагогов | Представлен анализ литературы в форме кратких тезисов и выводов. | (*1) |
|
| ||
| Раскрыта и представлена проработанность проблемы в теории и практике | (*2) |
|
| |||
| Описаны рекомендации относительно возможностей использования материалов работы | (*1) |
|
| |||
| Определены и представлены адекватные выводы | (*1) |
|
| |||
| ПК 4.4. Оформлять педагогические разработки в виде отчетов, выступлений.
| Соответствие выступления требованиям к публичной речи: материал изложен полно и ясно |
|
| |||
| Свободная ориентация в материале доклада (выступление без опоры на текст) | (*2) |
|
| |||
| Адекватное применение терминологии | (*2) |
|
| |||
| Демонстрация понимания сути курсовой работы при ответе на вопросы комиссии | (*2) |
|
| |||
| Рациональное использование времени презентации (10 минут). | (*1) |
|
| |||
| ОК 5. Использовать информационно- коммуникационные технологии для совершенствования профессиональной деятельности | Соответствие презентации требованиям: Содержание слайда включает формальное, структурированное изложение материала, выделение ключевых понятий. Дизайн слайдов выполняется в соответствии с темой, содержанием и местом предъявления. | (*1) |
|
| ||
| Презентация оформлена грамотно (содержание проверено на наличие ошибок). Грамотное представление данных практической части в виде таблиц, схем, диаграмм, графиков. | (*1) |
|
| |||
| Сумма баллов |
|
|
| |||
| Члены комиссии: Исаева В.В. Кондрашов А.М. Пунтус Д.А. Харитонова Т.А. |
| |||||
Дата _______________



















