МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
Государственное образовательное учреждение высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ УНИВЕРСИТЕТ (МГОУ)
Кафедра ____________________________________
(наименование кафедры)
КУРСОВАЯ РАБОТА
по __________________________________
(наименование учебной дисциплины)
тема: «Интегральные уравнения Фредгольма первого и второго рода»
|
| Выполнил студент: 41 группы 4 курса заочной формы обучения физико- математического факультета Фокина Наталья Борисовна
|
| Научный руководитель: ___________________________________ (ученая степень, ученое звание, фамилия, инициалы)
Дата защиты: «__» ____________20 __г.
Оценка: ____________________________ __________________________________ (подпись научного руководителя) |
|
|
|
Регистрационный номер ________ Дата регистрации ______________ |
Москва
2016
Содержание
Введение 3
1. Уравнение Фредгольма первого и второго рода. Основные понятия 4
1.1 Метод определителей Фредгольма 6
1.2 Пример нахождения резольвенты ядра 8
2. Рекуррентные соотношения 11
2.1 Пример нахождения резольвенты ядра с помощью рекуррентных соотношений 12
3. Метод последовательных приближений 14
3.1 Пример решения интегрального уравнения методом последовательных приближений Заключение 21
Список литературы 22
Введение
Фредгольм (Fredholm) Эрик Ивар (7.4.1866, Стокгольм, 17.8.1927, Мёрбю), шведский математик. Окончил Стокгольмский университет (1893), с 1906 профессор там же. Основные труды по интегральным уравнениям. В 1900 изложил основные свойства и теоремы теории интегральных уравнений, разработал общие методы решения некоторых их видов (т.н. уравнения Фредгольма).
В работе изложены характерные особенности интегральных уравнений и их классификация. Она является одним из разделов математического анализа.
Чтобы охарактеризовать ее место в современной математической науке, прежде всего, необходимо подчеркнуть основные понятия интегральных уравнений.
Изучая какие-либо явления, исследователь, прежде всего, создает его математическую идеализацию или, другими словами, математическую модель, т.е. пренебрегая второстепенным характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде интегральных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакциях, электрических и магнитных явлений, в электростатике, гидростатике и многих других разделов физики и математики.
Целью моей работы является рассмотрение особенностей интегральных уравнений Фредгольма и изучение применения этого метода.
1. Уравнение Фредгольма первого и второго рода. Основные понятия
Линейным интегральным уравнением Фредгольма первого рода называется уравнение вида:
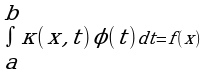 (1)
(1)
Линейным интегральным уравнением Фредгольма второго рода называется уравнение вида:
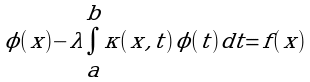 (2)
(2)
где φ(x)- неизвестная функция, k(x,t) и f(x)- известные функции, x и t действительные переменные, изменяющиеся в интервале (a,b), λ- численный множитель.
Функция k(x,t) называется ядром интегрального уравнения (2); предполагается, что ядро k(x,t) определено в квадрате Ω(a≤x≤b,a≤t≤b) на плоскости (x,t) и непрерывно в Ω, либо его разрывы таковы, что двойной интеграл:
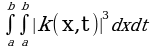
имеет конечное значение.
Если f(x)≠0, то уравнение (2) называется неоднородным; если же f(x)≡0, то уравнение (1) принимает вид:

 (3)
(3)
и называется однородным.
Пределы интегрирования в уравнениях (3) и (2) могут быть
как конечными, так и бесконечными.
Решением интегральных уравнений (3) и (2) называется любая функция φ(x), при подстановке которой в уравнения последние обращаются в тождества относительно x принадлежащий (a,b).
Пример. Показать что функция 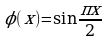 является решением интегрального уравнения Фредгольма:
является решением интегрального уравнения Фредгольма:
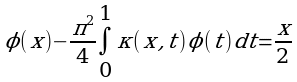 ,
,
где ядро имеет вид:

Решение. Левую часть уравнения запишем в виде:

Подставляя в полученное выражение вместо φ(x) функцию 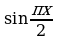 , будем иметь:
, будем иметь:
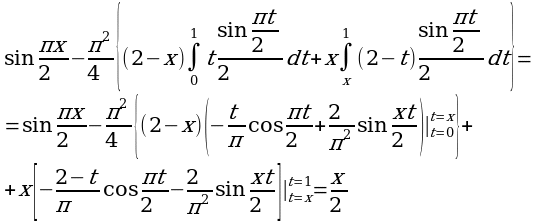
Итак, получим 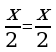 , а это означает, согласно определению, что
, а это означает, согласно определению, что 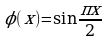 есть решение данного интегрального уравнения.
есть решение данного интегрального уравнения.
1.1 Метод определителей Фредгольма
Решение уравнения Фредгольма второго рода:
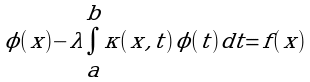 (1)
(1)
дается формулой:
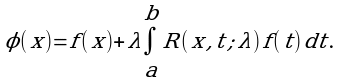 (2)
(2)
Где функция 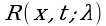 , называемая резольвентой Фредгольма уравнения (1), определяется равенством:
, называемая резольвентой Фредгольма уравнения (1), определяется равенством:
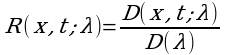 (3)
(3)
При условии что D(λ)≠0. Здесь D(x,t;λ) и D(λ)- степенные ряды по λ;
 (4)
(4)
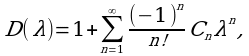 (5)
(5)
коэффициенты которых определяются формулами:
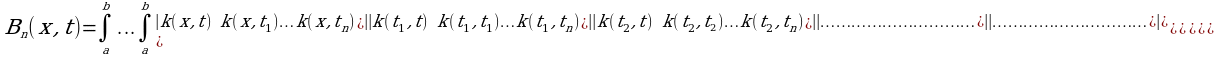 (6)
(6)
причем

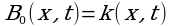
 (7)
(7)
Функция от D(x,t;λ) называется минором Фредгольма, а D(λ)- определителем Фредгольма. В случае, когда ядро k(x, t) ограничено или же интеграл
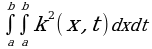
имеет конечное значение, ряды (4) и (5) сходятся для всех значений, λ и значит являются целыми аналитическими функциями от λ.
Резольвента
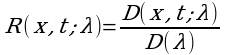
есть аналитическая функция от λ, кроме тех значений λ, которые являются нулями функции D(λ).
1.2 Пример нахождения резольвенты ядра
С помощью определителей Фредгольма найти резольвенту ядра k(x,t)=xet ; a=0 ; b=1.
Решение. Имеем B0(x,t)=xet.
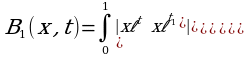
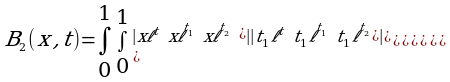
Так как определители под знаком интеграла равны нулю. Очевидно, что и все последующие Bn(x,t)=0. Находим коэффициенты Cn:
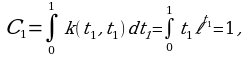
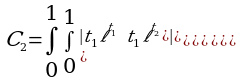
Очевидно, что и все последующие Cn=0. Согласно формулам (4) и (5) в нашем случае имеем:
D(x,t;λ)=k(x, t)= xet; D(λ)=1-λ.
Таким образом,
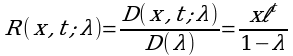
Применим полученный результат к решению интегрального уравнения:
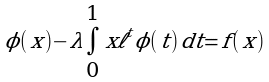 (λ≠1)
(λ≠1)
Согласно формуле (2):
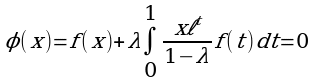
В частности, для f(x)=e-x получаем:
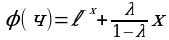
2. Рекуррентные соотношения
Вычисление по формулам (1) и (2)
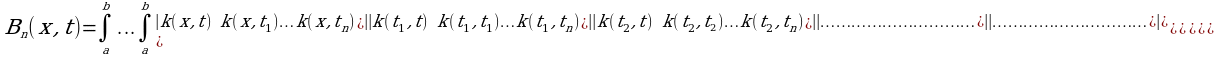 (1)
(1)
 (2)
(2)
коэффициентов Bn(x,t) и Cn практически возможно лишь в очень редких случаях, но из этих формул получаются следующие рекуррентные соотношения:
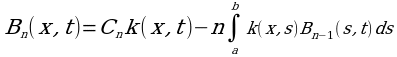 (3)
(3)

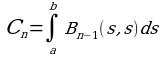 (4)
(4)
Зная, что коэффициент C0=1 и B0(x,t)=k(x,t) по формулам (3) и (4) найдем последовательно C1, B1(x,t), C2, B2(x,t), C3 и т.д.
2.1 Пример нахождения резольвенты ядра с помощью рекуррентных соотношений
Пользуясь формулами (3) и (4) найти резольвенту ядра k(x,t)=x-2t, где 0≤x≤1, 0≤t≤1.
Решение. Имеем C0=1, B0(x,t)= x-2t. Пользуясь формулой (9) найдем:
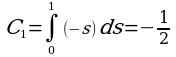
По формуле (3) получим:


Далее будем иметь:
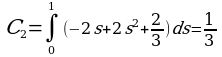
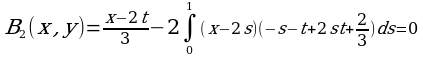
C3=C4=…=0, B3(x, t)=B4(x, t)=…=0
Следовательно,
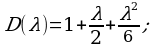
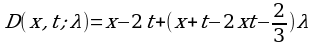
Резольвента данного ядра будет:
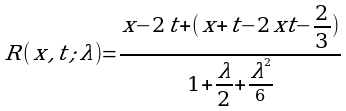
3. Метод последовательных приближений
Мы докажем существование уравнения
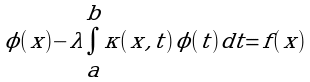 (1)
(1)
(при достаточно малых |λ|) методом последовательных приближений.
Для простоты выкладок будем предполагать, что:
ядро k(x, s) непрерывно в квадрате a≤x, s≤b; тогда оно ограничено некоторой константой А, |k|≤А.
функция f(x) непрерывна на отрезке [a, b], следовательно, она ограничена на этом отрезке некоторой константой В, |f|≤В.
Построим последовательность функций
φ 1(x),φ2(x),…,φn(x)
по следующему правилу:
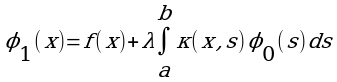
 (2)
(2)
где φ 0(s) – произвольная фиксированная непрерывная функция.
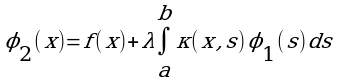 (3)
(3)
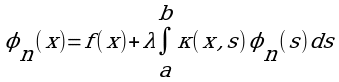 (4)
(4)
Теорема 1. Последовательность (2) – (4) функций φn(x) равномерно сходится на отрезке [a, b], к функции φ(x), являющейся решением уравнения (1) при 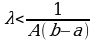 .
.
Доказательство:
Преобразуем формулы для получения φn(x). Подставляя функцию φ1(x) в φ2(x), получим:
Меняя в последнем интеграле порядок интегрирования, получим:
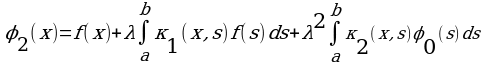
K1(x, s)=k(x, s), 
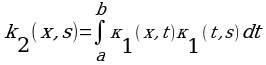
Аналогично находим:
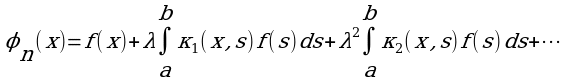
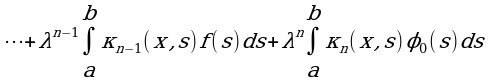
Где 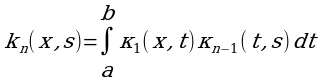
Предел функции φn(x), если он существует, равен сумме ряда:
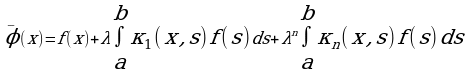 (5)
(5)
Докажем равномерную сходимость ряда. Для этого оценим интегралы:
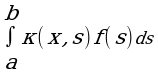
Имеем
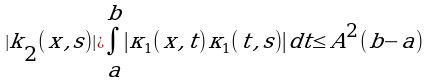
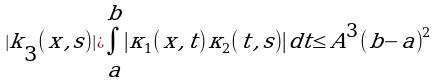
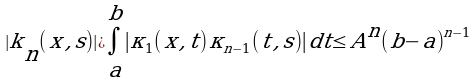
Поэтому
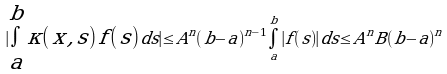
Следовательно, числовой ряд
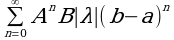 (6)
(6)
является мажорантным для ряда (5). Если 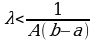 , то ряд (6) сходится. Следовательно, при таких λ ряд (6) сходится, а вместе с ним и последовательность функций φn(x) равномерно сходится к функции
, то ряд (6) сходится. Следовательно, при таких λ ряд (6) сходится, а вместе с ним и последовательность функций φn(x) равномерно сходится к функции 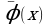 . Эта функция является решением уравнения (1.) В самом деле, переходя в формуле (4) к пределу при n→ ∞, получим
. Эта функция является решением уравнения (1.) В самом деле, переходя в формуле (4) к пределу при n→ ∞, получим
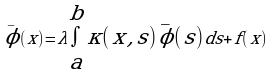
Переход к пределу под знаком интеграла здесь закончен, так как последовательность сходится равномерно.
Заметим, что предел 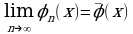 не зависит от выбора функции φ0(x)(нулевого приближения). В самом деле, если существует еще одно решение ψ(x) уравнения (1), то, полагая в процедуре построения функций (2) – (4) φ0(x)= ψ(x), получим
не зависит от выбора функции φ0(x)(нулевого приближения). В самом деле, если существует еще одно решение ψ(x) уравнения (1), то, полагая в процедуре построения функций (2) – (4) φ0(x)= ψ(x), получим
φ1(x)= ψ(x), φ2(x)= ψ(x),…, φn(x)= ψ(x)…
Эта последовательность имеет пределом функцию 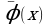 . Но вместе с тем очевидно:
. Но вместе с тем очевидно:
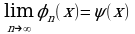
Таким образом, 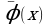 =ψ(x). Теорема доказана.
=ψ(x). Теорема доказана.
Поскольку ряд (6) сходится при 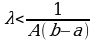 , то при таких же λ сходится и ряд:
, то при таких же λ сходится и ряд:
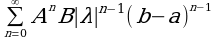
Но этот ряд является мажорантным для ряда:
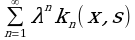 (7)
(7)
Следовательно, ряд (7) сходится равномерно. Поэтому ряд (5) можно записать в виде:
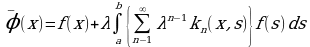
Или
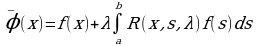 (8)
(8)
где функция
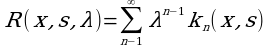
называется резольвентой уравнения (1).
3.1 Пример решения интегрального уравнения методом последовательных приближений
Решить интегральное уравнение 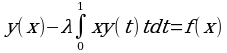 , 0≤x≤1 методом последовательных приближений. Здесь k(x, t)=xt, a=0, b=1.
, 0≤x≤1 методом последовательных приближений. Здесь k(x, t)=xt, a=0, b=1.
Решение. Последовательно найдем
K1(x, t)=xt, 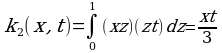
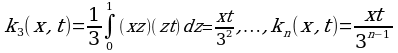
Согласно формуле
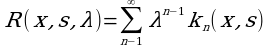
Получим
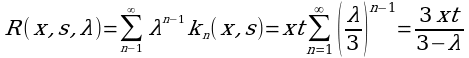 ,
,
причем |λ|и в силу формулы:
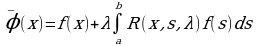
решение данного интегрального уравнения запишется в форме:
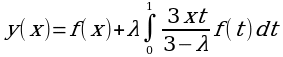 , 0≤x≤1, λ≠3
, 0≤x≤1, λ≠3
В частности, при f(x)=x получим
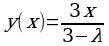 , 0≤x≤1, λ≠3
, 0≤x≤1, λ≠3
Заключение
Таким образом, мы рассмотрели с вами, какие уравнения называются линейными интегральными уравнениями Фредгольма первого и второго рода, основные понятия и методы решения этих уравнений. Проанализировали характерные особенности интегральных уравнений и их классификации.
Анализируя решения примеров, мы убедились, что, изучая какие-либо явления, исследователь, прежде всего, создает его математическую идеализацию или, другими словами, математическую модель, т.е. пренебрегая второстепенным характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. В этой работе мы рассмотрели законы, которые можно выразить в виде интегральных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакциях, электрических и магнитных явлений, в электростатике, гидростатике и многих других разделов физики и математики. Применение интегральных уравнений Фредгольма первого и второго рода очень разнообразно, что мы и увидели в этой работе.
Список литературы
М.Л. Краснов, А.И. Киселев, Г.И. Макаренко: Интегральные уравнения; Издательство Наука, Москва 1968.
Б.А. Зон: Лекции по интегральным уравнениям; Москва «Высшая школа» 2004.
Васильева А.В., Медведев Г.Н., Тихонов Н.А., Уразгильдина Т.А. Дифференциальные и интегральные уравнения, вариационное исчисление в примерах и задачах. — М.: ФИЗМАТЛИТ, 2003.
Васильева А.Б., Тихонов Н.А. Интегральные уравнения. - 2-е изд., стереот. - М.: ФИЗМАТЛИТ, 2002.
Манжиров А.В., Полянин А. Д. Методы решения интегральных уравнений: Справочник. — М.: «Факториал».
Байков В.А., Жибер А.В. Уравнения математической физики. — Москва-Ижевск: Институт компьютерных исследований, 2003.
Лизоркин П.И. Курс дифференциальных и интегральных уравнений с дополнительными главами анализа. – М.: Наука. Главная редакция физико-математической литературы, 1981.
Тер- КрикоровА.М., Шабунин А.И. Курс математического анализа, М.: Наука, 1988
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, том 2, М.: Наука, 1969
Кудрявцев Л.Д. Математический анализ т.2, М.: Высшая школа, 1981
Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1977
Данко П.Е, Попов И.Ю., Кожевникова Т.Я. Высшая математика в упражнениях. М.: Высшая школа, 1980
Блинова И.В., Попов И.Ю. Интегралы, зависящие от параметров. Методические указания. СПб. ГУ ПТМО, 2008
Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу, книга 2. М.: Высшая школа, 2000







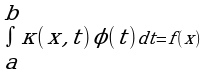 (1)
(1)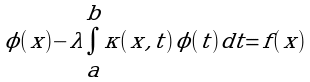 (2)
(2)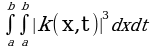

 (3)
(3)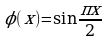 является решением интегрального уравнения Фредгольма:
является решением интегрального уравнения Фредгольма: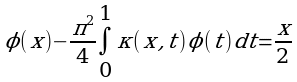 ,
,

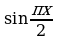 , будем иметь:
, будем иметь: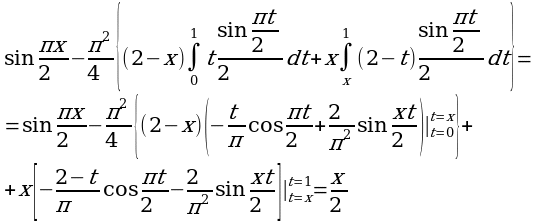
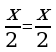 , а это означает, согласно определению, что
, а это означает, согласно определению, что 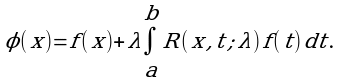 (2)
(2)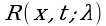 , называемая резольвентой Фредгольма уравнения (1), определяется равенством:
, называемая резольвентой Фредгольма уравнения (1), определяется равенством: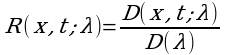 (3)
(3) (4)
(4)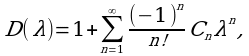 (5)
(5)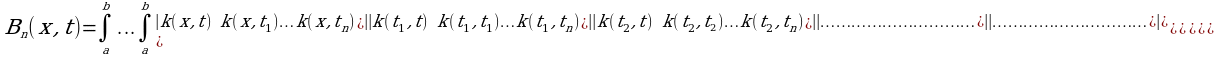 (6)
(6) 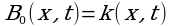
 (7)
(7)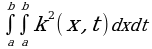
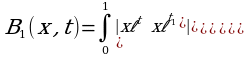
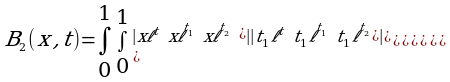
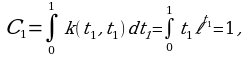
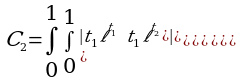
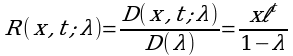
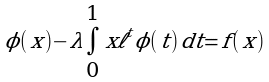 (λ≠1)
(λ≠1)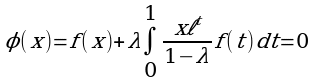
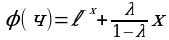
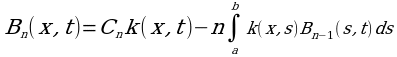 (3)
(3)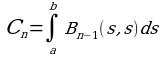 (4)
(4)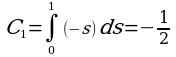

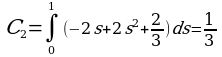
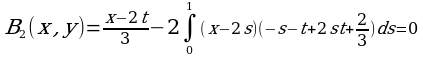
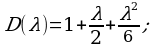
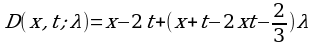
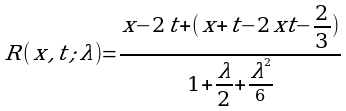
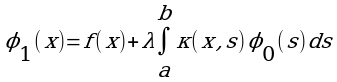
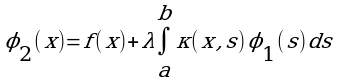 (3)
(3)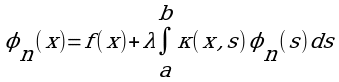 (4)
(4)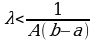 .
.
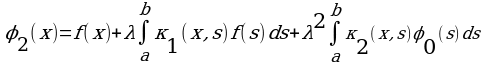
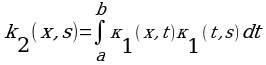
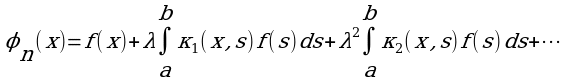
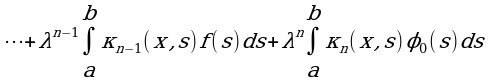
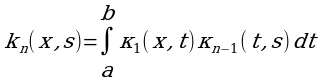
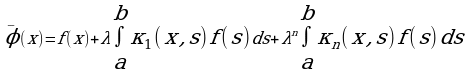 (5)
(5)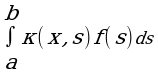
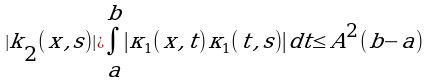
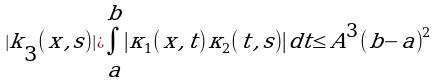
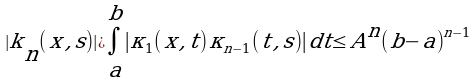
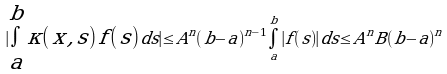
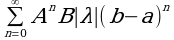 (6)
(6)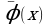 . Эта функция является решением уравнения (1.) В самом деле, переходя в формуле (4) к пределу при n→ ∞, получим
. Эта функция является решением уравнения (1.) В самом деле, переходя в формуле (4) к пределу при n→ ∞, получим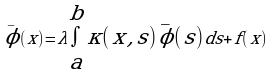
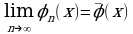 не зависит от выбора функции φ0(x)(нулевого приближения). В самом деле, если существует еще одно решение ψ(x) уравнения (1), то, полагая в процедуре построения функций (2) – (4) φ0(x)= ψ(x), получим
не зависит от выбора функции φ0(x)(нулевого приближения). В самом деле, если существует еще одно решение ψ(x) уравнения (1), то, полагая в процедуре построения функций (2) – (4) φ0(x)= ψ(x), получим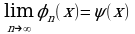
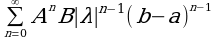
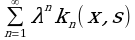 (7)
(7)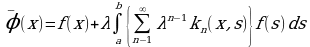
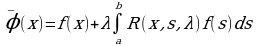 (8)
(8)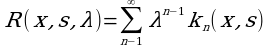
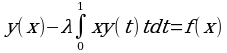 , 0≤x≤1 методом последовательных приближений. Здесь k(x, t)=xt, a=0, b=1.
, 0≤x≤1 методом последовательных приближений. Здесь k(x, t)=xt, a=0, b=1.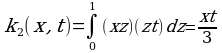
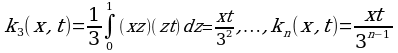
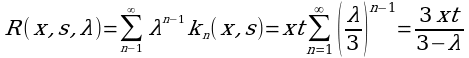 ,
,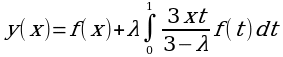 , 0≤x≤1, λ≠3
, 0≤x≤1, λ≠3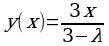 , 0≤x≤1, λ≠3
, 0≤x≤1, λ≠3









