Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
-
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
-
Квадратом называется параллелограмм, у которого все стороны и углы равны.
-
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
-
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
-
У квадрата диагонали взаимно перпендикулярны.
-
У квадрата диагонали являются биссектрисами его углов.
-
У квадрата диагонали равны.
-
У квадрата стороны являются высотами.
-
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА (I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
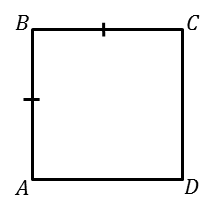
Дано:  – прямоугольник
– прямоугольник
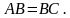
Доказать:  – квадрат.
– квадрат.
Доказательство.
Так как  – прямоугольник, то у него противолежащие стороны равны.
– прямоугольник, то у него противолежащие стороны равны.
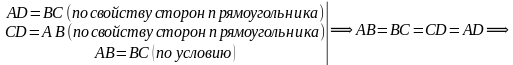
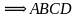 – квадрат (по определению), ч.т.д.
– квадрат (по определению), ч.т.д.
Т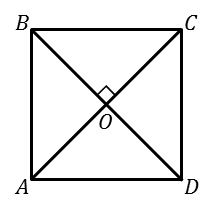 ЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
ЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Дано:  – прямоугольник
– прямоугольник
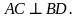
Доказать:  – квадрат.
– квадрат.
Доказательство.
Рассмотрим 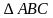 .
.
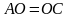 по свойству диагоналей прямоугольника, значит,
по свойству диагоналей прямоугольника, значит, 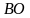 – медиана (по опред-нию).
– медиана (по опред-нию).
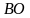 – высота
– высота 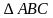 , т.к.
, т.к. 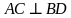 . Значит, в
. Значит, в 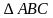
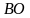 является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е.
является и медианой и высотой, поэтому этот треугольник является равнобедренным (по признаку равнобедренного треугольника), т.е. 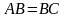 . Согласно I признаку квадрата, прямоугольник
. Согласно I признаку квадрата, прямоугольник  является квадратом, ч.т.д.
является квадратом, ч.т.д.
ТЕОРЕМА (III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
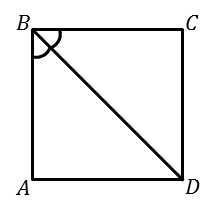
Дано:  – прямоугольник
– прямоугольник
 – диагональ
– диагональ
 – биссектриса
– биссектриса 
Доказать:  – квадрат.
– квадрат.
Доказательство.
Так как  – биссектриса
– биссектриса  , то
, то  .
.
 по свойству внутренних накрест лежащих углов при параллельных прямых. Значит,
по свойству внутренних накрест лежащих углов при параллельных прямых. Значит,  , следовательно
, следовательно  – равнобедренный, и
– равнобедренный, и  . По I признаку квадрата, прямоугольник
. По I признаку квадрата, прямоугольник  является квадратом, ч.т.д.
является квадратом, ч.т.д.
Т ЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
ЕОРЕМА (IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
Дано:  – ромб
– ромб
 - диагонали
- диагонали
Доказать:  – квадрат.
– квадрат.
Доказательство.
Рассмотрим  и
и  .
.
по III признаку равенства треугольников. Значит, все соответствующие углы у этих треугольников равны, т.е.  . Эти углы являются внутренними односторонними при параллельных прямых
. Эти углы являются внутренними односторонними при параллельных прямых  и
и  , следовательно, их сумма равна
, следовательно, их сумма равна  , т.е. , а, значит, и
, т.е. , а, значит, и  . Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по
. Так как в ромбе противолежащие углы равны, то и все остальные углы также равны по  . Значит, такой ромб является квадратом, ч.т.д.
. Значит, такой ромб является квадратом, ч.т.д.
Т ЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
ЕОРЕМА (V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Дано:  – параллелограмм
– параллелограмм

Доказать:  – квадрат.
– квадрат.
Доказательство.
Так как 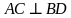 , то по II признаку ромба, параллелограмм
, то по II признаку ромба, параллелограмм  является ромбом.
является ромбом.
Так как  , то по IV признаку квадрата, ромб
, то по IV признаку квадрата, ромб  является квадратом, ч.т.д.
является квадратом, ч.т.д.
Т ЕОРЕМА (VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Дано:  – четырёхугольник
– четырёхугольник

Доказать:  – квадрат.
– квадрат.
Доказательство.
1. Так как , то четырёхугольник  является параллелограммом (по признаку параллелограмма).
является параллелограммом (по признаку параллелограмма).
2. Так как  , то параллелограмм
, то параллелограмм  является квадратом (по V признаку квадрата), ч.т.д.
является квадратом (по V признаку квадрата), ч.т.д.
Т ЕОРЕМА (VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
Дано:  – четырёхугольник
– четырёхугольник


Доказать:  – квадрат.
– квадрат.
Доказательство.
1. Так как  , то четырёхугольник
, то четырёхугольник  является ромбом (по V признаку ромба).
является ромбом (по V признаку ромба).
2. Так как  , то ромб, который по определению является параллелограммом,
, то ромб, который по определению является параллелограммом,  является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.
является прямоугольником (по III признаку прямоугольника), значит, все углы в этом четырёхугольнике прямые.
3. Итак, прямоугольник  , у которого все стороны равны, является квадратом (по определению), ч.т.д.
, у которого все стороны равны, является квадратом (по определению), ч.т.д.
Итак, признаки квадрата:
-
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
-
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
-
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
-
Если в ромбе диагонали равны, то этот ромб является квадратом.
-
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
-
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
-
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
-
Периметр квадрата  равен
равен  см. Найдите сторону квадрата
см. Найдите сторону квадрата  .
.
-
Н
а рисунке четырёхугольник  – квадрат, . Докажите, что выпуклый четырёхугольник
– квадрат, . Докажите, что выпуклый четырёхугольник  также является квадратом.
также является квадратом.
-
Н
а рисунке четырёхугольник  – прямоугольник, . Докажите, что выпуклый четырёхугольник
– прямоугольник, . Докажите, что выпуклый четырёхугольник  является квадратом.
является квадратом.
-
В треугольнике . На сторонах  и
и  взяты точки
взяты точки  и
и  , а на стороне
, а на стороне  – точки
– точки  и
и  так, что четырёхугольник
так, что четырёхугольник  является квадратом,
является квадратом,  . Найдите
. Найдите  .
.
-
В треугольнике . На сторонах  отмечены точки
отмечены точки  соответственно так, что четырёхугольник
соответственно так, что четырёхугольник  является квадратом,
является квадратом,  . Найдите
. Найдите  .
.
-
На сторонах  и
и  квадрата
квадрата  отмечены точки
отмечены точки  и
и  соответственно,
соответственно,  . Отрезки
. Отрезки  и
и  пересекаются в точке
пересекаются в точке  . Найдите
. Найдите  .
.
-
На сторонах  квадрата
квадрата  отмечены соответственно точки
отмечены соответственно точки  . Сравните отрезки
. Сравните отрезки  и
и  .
.
-
На катетах  и
и  прямоугольного треугольника
прямоугольного треугольника  построены квадраты
построены квадраты  и
и  . Докажите, что сумма расстояний от точек
. Докажите, что сумма расстояний от точек  и
и  до прямой
до прямой  равна
равна  .
.
-
На катетах  и
и  прямоугольного треугольника
прямоугольного треугольника  построены квадраты
построены квадраты  и
и  . Прямые
. Прямые  и
и  пересекаются в точке
пересекаются в точке  . Докажите, что
. Докажите, что  .
.
-
Длина проекции одной из сторон квадрата на его диагональ равна  . Найдите длину диагонали.
. Найдите длину диагонали.
-
В
четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
-
Дан квадрат . Докажите, что  – квадрат.
– квадрат.
-
Дан квадрат  . Докажите, что
. Докажите, что  – ромб.
– ромб.
-
Дан квадрат  . На стороне
. На стороне  взята точка
взята точка  такая, что
такая, что  . Докажите, что точки
. Докажите, что точки  – вершины равнобедренного треугольника.
– вершины равнобедренного треугольника.
-
Дан квадрат  . Точки
. Точки  – середины его сторон
– середины его сторон  соответственно. Докажите, что .
соответственно. Докажите, что .
-
Дан квадрат  . Точки
. Точки  и
и  делят его стороны
делят его стороны  и
и  так, что . Докажите, что .
так, что . Докажите, что .
-
К
вадраты  и
и  имеют общую вершину
имеют общую вершину  . Докажите, что медиана
. Докажите, что медиана  треугольника
треугольника  перпендикулярна отрезку
перпендикулярна отрезку  .
.
-
Внутри квадрата  взята точка
взята точка  так, что . Докажите, что треугольник
так, что . Докажите, что треугольник  равносторонний.
равносторонний.
-
Н
а рисунке  – квадрат, точка
– квадрат, точка  принадлежит
принадлежит  , точка
, точка  принадлежит
принадлежит  , точка
, точка  принадлежит
принадлежит  , прямые
, прямые  и
и  пересекаются в точке
пересекаются в точке  . Докажите, что
. Докажите, что  .
.
-
В равнобедренный прямоугольный треугольник, каждый катет которого равен  см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
-
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
-
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна  дм.
дм.
-
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна  см.
см.
-
Точка  расположена во внутренней области квадрата
расположена во внутренней области квадрата  так, что расстояния от неё до сторон
так, что расстояния от неё до сторон  и
и  пропорциональны соответственно числам
пропорциональны соответственно числам  и
и  , а расстояние от
, а расстояние от  до прямой
до прямой  равно
равно  см. Найдите периметр этого квадрата.
см. Найдите периметр этого квадрата.
-
Точка  расположена во внутренней области квадрата
расположена во внутренней области квадрата  так, что расстояния от неё до сторон
так, что расстояния от неё до сторон  и
и  пропорциональны соответственно числам
пропорциональны соответственно числам  и
и  , а расстояние от
, а расстояние от  до прямой
до прямой  равно
равно  м. Найдите периметр этого квадрата.
м. Найдите периметр этого квадрата.
-
Точка  лежит на стороне
лежит на стороне  квадрата
квадрата  . Высоты треугольников
. Высоты треугольников  и
и  , проведённые из точки
, проведённые из точки  , равны соответственно
, равны соответственно  и
и  . Найдите произведение длин диагоналей этого квадрата.
. Найдите произведение длин диагоналей этого квадрата.
-
Точка  расположена во внутренней области квадрата
расположена во внутренней области квадрата  так, что расстояния от неё до сторон
так, что расстояния от неё до сторон  и
и  пропорциональны соответственно числам
пропорциональны соответственно числам  и
и  , а расстояние от
, а расстояние от  до прямой
до прямой  равно
равно  м. Найдите периметр этого квадрата.
м. Найдите периметр этого квадрата.
-
Т
очка  лежит на стороне
лежит на стороне  квадрата
квадрата  . Высоты треугольников
. Высоты треугольников  и
и  , проведённые из точки
, проведённые из точки  , равны соответственно
, равны соответственно  и
и  . Найдите произведение длин диагоналей этого квадрата.
. Найдите произведение длин диагоналей этого квадрата.
-
На сторонах  и
и  квадрата
квадрата  отмечены точки
отмечены точки  и
и  соответственно так, что . Определите взаимное расположение прямых
соответственно так, что . Определите взаимное расположение прямых  и
и  .
.
-
В
равнобедренный прямоугольный треугольник  вписан квадрат
вписан квадрат  , имеющий с ним общий угол
, имеющий с ним общий угол  . Найдите периметр квадрата, если катет треугольника равен
. Найдите периметр квадрата, если катет треугольника равен  см.
см.
-
В
нутри квадрата отмечена такая точка  , что треугольник
, что треугольник  равносторонний. Найдите угол
равносторонний. Найдите угол  .
.
-
В равнобедренный прямоугольный треугольник вписан квадрат  , имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен
, имеющий с ним общий прямой угол. Найдите катет треугольника, если периметр квадрата равен  см.
см.
-
В
нутри квадрата отмечена такая точка  , что треугольник
, что треугольник  равносторонний. Найдите угол
равносторонний. Найдите угол  .
.
-
Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна  см.
см.
-
Через точку  – точку пересечения диагоналей квадрата
– точку пересечения диагоналей квадрата  проведена прямая, параллельная стороне
проведена прямая, параллельная стороне  и пересекающая стороны
и пересекающая стороны  и
и  в точках
в точках  и
и  соответственно. Найдите периметр квадрата, если известно, что .
соответственно. Найдите периметр квадрата, если известно, что .
-
Н
айдите периметр квадрата  по данным на рисунке.
по данным на рисунке.
4








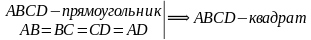

 – прямоугольник
– прямоугольник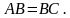
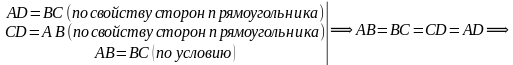
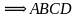 – квадрат (по определению), ч.т.д.
– квадрат (по определению), ч.т.д. ЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
ЕОРЕМА (II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.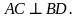
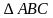 .
. 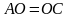 по свойству диагоналей прямоугольника, значит,
по свойству диагоналей прямоугольника, значит, 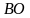 – медиана (по опред-нию).
– медиана (по опред-нию).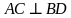 . Значит, в
. Значит, в 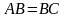 . Согласно I признаку квадрата, прямоугольник
. Согласно I признаку квадрата, прямоугольник 


















