Квадрат суммы или квадрат разности двух выражений

Квадрат суммы или квадрат разности двух выражений

Автор: Петров М.И.

Учитель информатики и ИКТ

МБОУ «Юксеевская СОШ»

Цель урока:

Познакомиться с формулами квадрата суммы и квадрата разности и их применением для разложения выражений на множители и упрощения вычислений.

Задачи урока:

1. Развивающая - познакомиться с более легким способом алгебраических вычислений, вывести формулы квадрата суммы и квадрата разности двух чисел.

2. Образовательная - приобрести навык вычисления по формулам квадрата суммы и квадрата разности двух чисел, учиться выявлять главные и определенные закономерности.

3. Воспитательная -осознать ценность и необходимость полученных знаний, сопереживать за достижения своих товарищей.

УСТНЫЙ СЧЁТ:

• Возвести в квадрат:

a; 4а; 3c; 8с²k³; 5с 4 k 6 ; 10pd 6

ОТВЕТЫ:

a 2 ; 16а 2 ; 9c 2 ; 64с 4 k 6 ; 25с 8 k 12 ; 100p 2 d 12

УСТНЫЙ СЧЁТ:

• Найдите число, которое в квадрате даст

100; 25a 2 ; 81х 2 у 4 ; 49k 6 d 10

• ОТВЕТЫ:

10; 5a ; 9ху 2 ; 7k 3 d 5

УСТНЫЙ СЧЁТ:

Найдите удвоенное произведение выражений:

a и b, 0,5c и 6,

4x и 2x², 2b и -5k

Ответы:

2ab, 3c, 8x 3 , -10 bk

Сформулируйте правило умножения многочлена на многочлен?

Рассмотрим квадрат суммы двух чисел (a+b) 2 и пользуясь правилом умножения многочлена на многочлен, получаем:

(a+b) 2 =(a+b)(a+b)= a 2 +ab+ab+b 2 = a 2 +2ab+b 2

Получаем

ФОРМУЛУ КВАДРАТА СУММЫ

(a+b) 2 =a 2 +2ab+b 2

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе и плюс квадрат второго числа.

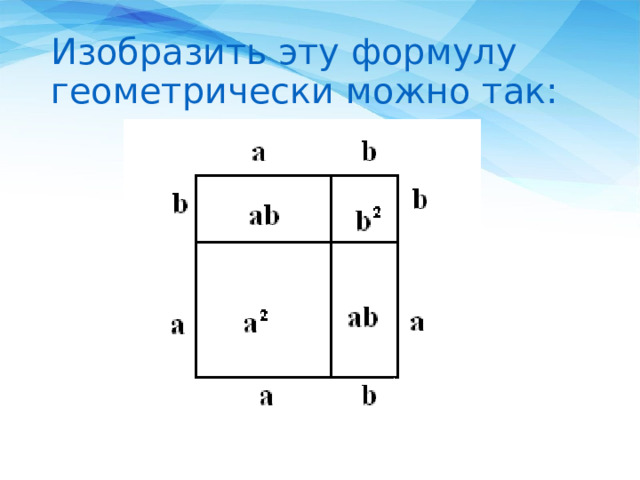
Изобразить эту формулу геометрически можно так:

ФОРМУЛА КВАДРАТА РАЗНОСТИ

(a-b) 2 =a 2 -2ab+b 2

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

ВАЖНО!

а и b в формулах могут быть любыми числами или алгебраическими выражениями

ФОРМУЛЫ СОКРАЩЁННОГО УМНОЖЕНИЯ:

(a+b) 2 =a 2 +2ab+b 2

(a-b) 2 =a 2 -2ab+b 2

Формулы сокращённого умножения применяются в некоторых случаях для упрощения вычислений.

Например:

99 2 = (100-1) 2 =10 2 -2 * 100 * 1 + 1 2 =

10 000-200+1=9801

( 5 0 +2 ) 2 =50 2 +2*50*2+2 2 =

2500+200+4=2704

Преобразуем выражение в виде многочлена:

(2m+3k)² =

(2m) 2 +2 ● 2m●3k+(3k) 2 =4m 2 +12mk+9k 2

(5a 2 -3)² =

(5a) 2- 2● 5a 2 ●3+3 2 =25a 4 -30a 2 +9

Вылечи равенство:

(a-2b) 2 = a 2 - *ab+4b 2

(2a+0,5b) 2 = 4a 2 +2ab+*b 2

9d 2 - 12dc+*c 2= (3d-2c) 2

(4k+2m) 2 = *k 2 +16km+4m 2

Представить квадрат двучлена в виде многочлена:

№ 370

1) (c+d)²

• (x-y)²
• (2+x)²

4) (x+1)²

РЕЗУЛЬТАТ:

1) ( c + d )² = c 2 +2 c d + d 2

2) ( x - y )² = x 2- 2 x y + y 2

3) ( 2 + x )² = 4 +4 x + x 2

4) ( x + 1 )² = x 2 +2 x + 1

ВЫЧИСЛИТЬ:

№ 374 №375

(90-1)² 72²

(40+1)² 57²

101² 997²

98² 1001²

РЕЗУЛЬТАТ:

№ 374 №375

7921 5184

1681 3249

10 201 994 009

9604 1 002 001

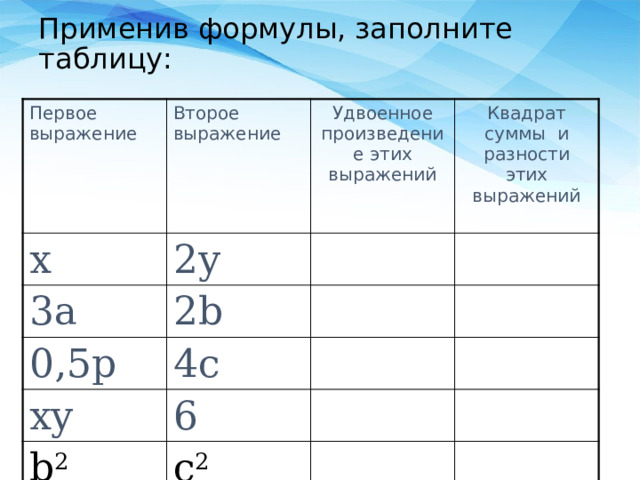
Применив формулы, заполните таблицу:

Первое выражение

Второе выражение

х

Удвоенное произведение этих выражений

2y

3a

Квадрат суммы и разности этих выражений

2b

0,5p

4c

xy

6

b 2

c 2

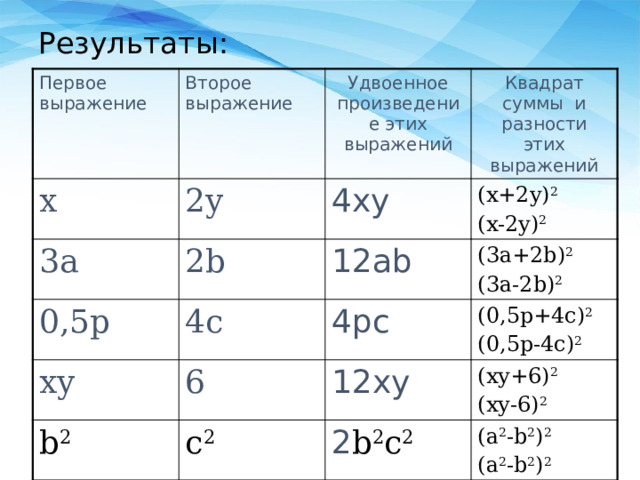
Результаты:

Первое выражение

Второе выражение

х

3a

Удвоенное произведение этих выражений

2y

2b

0,5p

Квадрат суммы и разности этих выражений

4xy

12ab

4c

(x+2y) 2

xy

(x-2y) 2

b 2

(3a+2b) 2

4pc

6

(3a-2b) 2

(0,5p+4c) 2

12xy

c 2

2 b 2 c 2

(0,5p-4c) 2

(xy+6) 2

(xy-6) 2

(a 2 -b 2 ) 2

(a 2 -b 2 ) 2

Итоги урока:

• Что нового вы узнали сегодня на уроке?
• Для чего необходимо знать изученные нами сегодня формулы?
• Как вы думаете, почему данные формулы называются формулами сокращённого умножения?