МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №13»
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОДСКОЙ ОКРУГ СИМФЕРОПОЛЬ РЕСПУБЛИКИ КРЫМ
Квадратичная функция
План-конспект урока
по алгебре в 9 классе
Разработала:
Живогляд Дарья Владимировна,
учитель математики
МБОУ СОШ № 13 г. Симферополя
Симферополь, 2018
Класс: 9 Урок № 86 Дата: 18.04.18
Тема: Квадратичная функция.
Цели:
- образовательные: обобщить и систематизировать знания, умения и навыки учащихся по теме «Квадратичная функция»; устранить пробелы в основных знаниях по теме; совершенствовать навыки построения графиков квадратичной функции и их исследование;
- развивающие: развивать у учащихся умения логически мыслить, анализировать, обобщать и делать выводы; развивать внимание и память;
- воспитательные: продолжить формирование навыка самопроверки и самоконтроля; умение работать в группах; аккуратность построения графиков; воспитывать ответственное отношение к учебе.
Тип урока: урок обобщения и систематизации знаний.
Формы работы: фронтальная, групповая.
Оборудование: интерактивная доска, презентация, раздаточный материал, учебник.
План урока
| № | Этап урока | Содержание этапа | Время (мин) |
| 1. | Организационный этап | Проверка готовности к уроку | 2 |
| 2. | Проверка домашней работы | Проверка учениками домашнего задания по решению учителя | 2 |
| 3. | Постановка цели и задач урока. Мотивация учебной деятельности | Отгадывание темы урока и совместная постановка целей урока | 5 |
| 4. | Актуализация знаний | Фронтальный опрос по теме «Квадратичная функция» | 5 |
| 5. | Обобщение и систематизация знаний | Закрепление знаний, умений и навыков в ходе решения задач | 26 |
| 6. | Подведение итогов урока. Рефлексия | Контрольные вопросы по теме «Квадратичная функция», сообщение домашнего задания. | 5 |
Ход урока
Организационный этап
Взаимное приветствие, приветствие гостей. Учащиеся рассаживаются в заранее сформированные учителем 3 группы. Учитель проводит фиксацию отсутствующих учеников. Сообщается, каким образом учащиеся сегодня работают и получают отметки.
Проверка домашней работы
Ученики обмениваются друг с другом тетрадями и с помощью слайда проверяют домашнюю работу. Учитель отвечает на возникшие вопросы, корректирует неправильно решенные задания.
Постановка цели и задач урока. Мотивация учебной деятельности
Учитель: - Чтобы узнать тему сегодняшнего урока, предлагаю вам решить кроссворд.
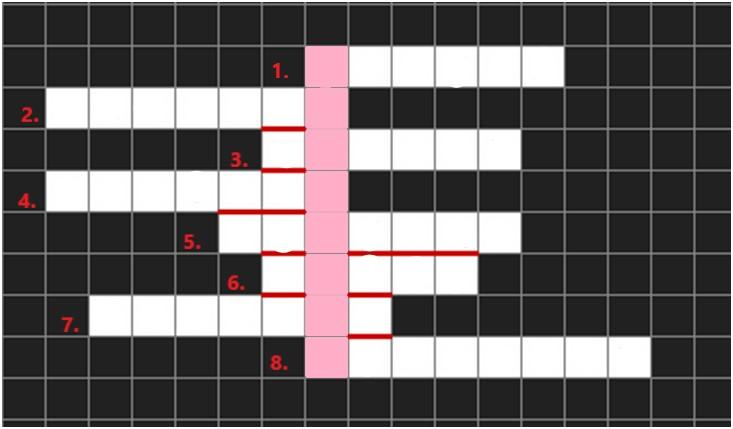
Вопросы:
Что является графиком линейной функции?
Утверждение, которое необходимо доказывать.
Геометрическое множество точек, у которых абсциссы являются допустимыми значениями аргумента, а ординаты — соответствующими значениями функции.
… линейных уравнений. Её решают способами подстановки, сложения и графическим.
Используется для нахождения координат точек функции. В неё самостоятельно задают значения независимой переменной и с помощью функции находят значения зависимой переменной.
В декартовой системе координат имеет пару координат «х» и «у».
Принятая в математике (а также физике и прикладных науках) символическая запись законченного логического суждения (определения величины, уравнения, неравенства или тождества).
Это точный набор инструкций, описывающих порядок действий для решения некоторой задачи.
Учитель: - Какое слово ключевое? Графиком какой функции является парабола?
(Парабола. Квадратичной функции.)
- Исходя из данной темы какие цели мы можем поставим перед собой?
(Ответы учеников.)
Записывают в тетрадь число и тему урока.
Актуализация знаний
Фронтальный опрос:
Какая функция называется квадратичной?
(Функция, заданная формулой y = ax2 + bx + c , где x и y - переменные, а коэффициенты a, b, c - любые числа, причем a≠0 , называется квадратичной функцией.)
Какое множество является областью определения квадратичной функции?
(Множество действительных чисел.)
Как располагается график функции в зависимости от значения коэффициента а?
(Если a 0 , то ветви параболы направлены вверх. Если a )
Какие «базовые точки» для построения графика функции у=х2 вы знаете?
( (0; 0), (1; 1), (-1; 1), (2; 4), (-2; 4).)
Как найти координаты точек пересечения квадратичной функции с осью Ох?
(необходимо решить уравнение у(х)=0, т.е. ax2 + bx + c=0.)
Какие возможные случаи расположения графика квадратичной функции с осью Ох в зависимости от значения дискриминанта?
(Если D,то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, график квадратичной функции y= ax2+bx+c не имеет точек пересечения с осью Ох.
Если D=0 ,то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, график квадратичной функции y= ax2+bx+c имеет одну точку пересечения с осью Ох.
,то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, график квадратичной функции y= ax2+bx+c имеет одну точку пересечения с осью Ох.
Если D˃0 ,то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, график квадратичной функции y= ax2+bx+c имеет две точки пересечения с осью Ох.)
,то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, график квадратичной функции y= ax2+bx+c имеет две точки пересечения с осью Ох.)
Учитель: - Внимание на слайд. Задание: к каждому графику необходимо указать знак коэффициента а и дискриминанта D.
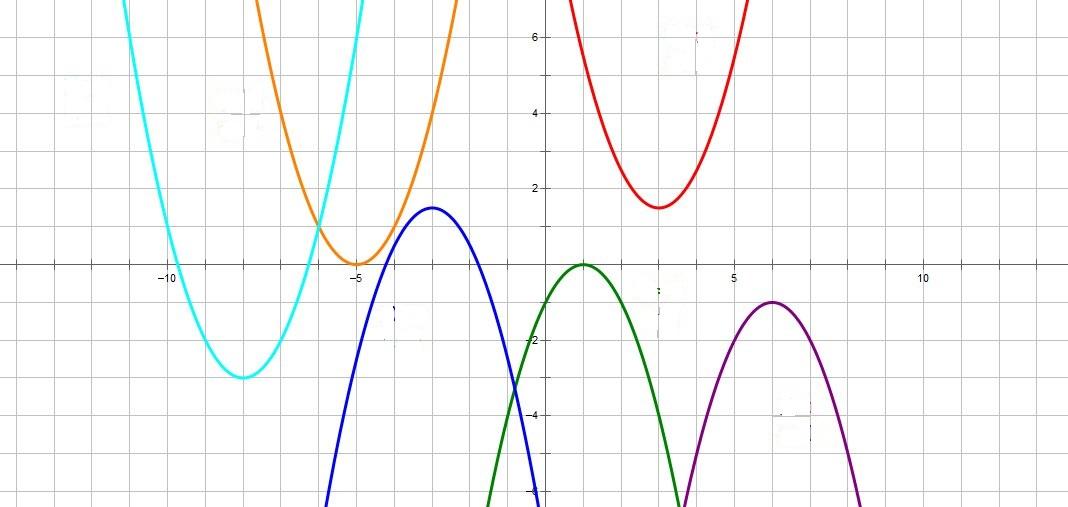
Учитель: - Молодцы, успешно справились с заданием. Следующий слайд. Повторим алгоритм построения графика квадратичной функции.
Алгоритм построения графика квадратичной функции:
Определим, куда направлены ветви соответствующей параболы.
Найти точки пересечения графика функции с осью Ох.
Найдем координаты вершины параболы:
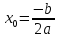 ,
, 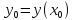 .
.
Проведем ось симметрии параболы х=х0.
Определим еще несколько точек вблизи вершины, принадлежащих параболе.
Отметить полученные точки и вершину параболы на координатной плоскости и соединить их плавной линией.
Учитель: - Вспомним при помощи каких преобразований можно получить график квадратичной функции, если исходная функция у = х2. Внимание на слайд.
(По заданной функции учащиеся дают ответы на вопросы учителя и тут же проверяют с помощью готового решения)
Обобщение и систематизация знаний
Учитель: - Повторив необходимый теоретический материал, предлагаю закрепить его на практике.
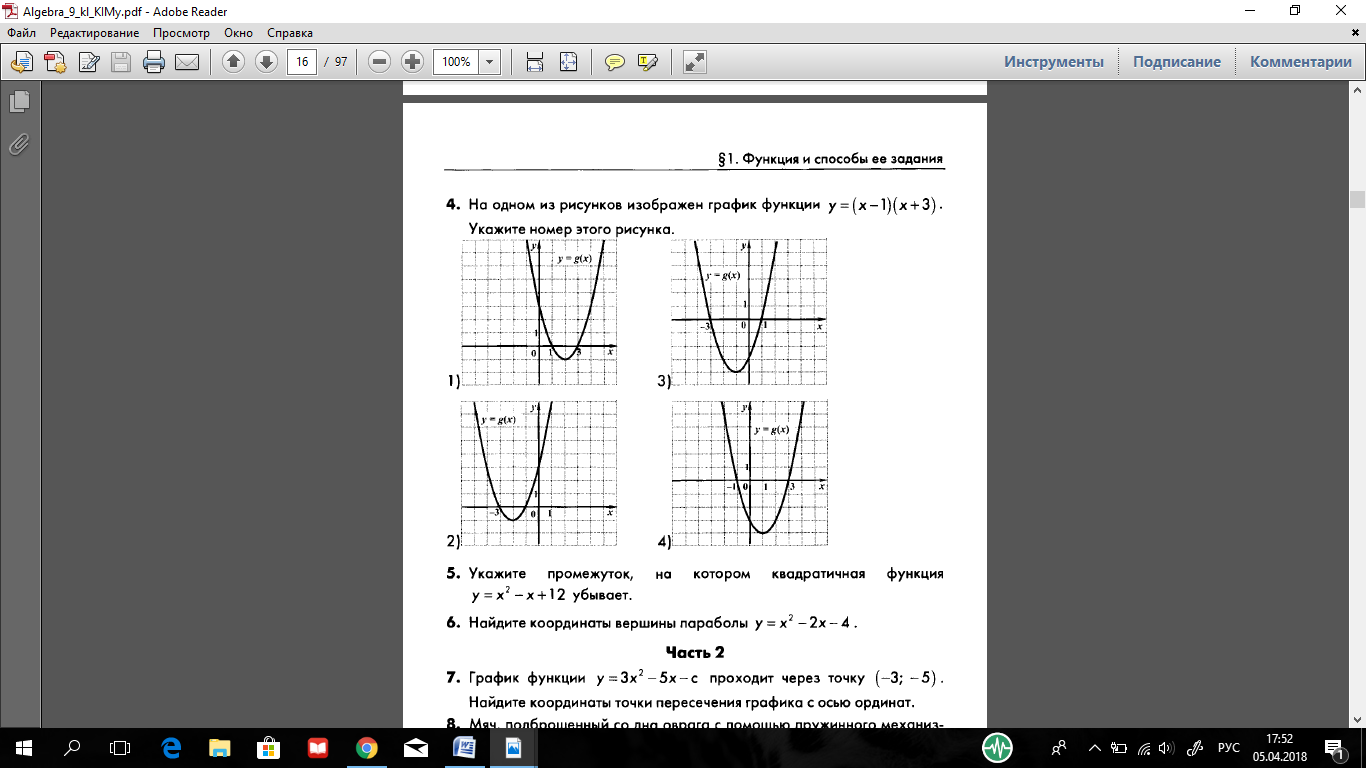
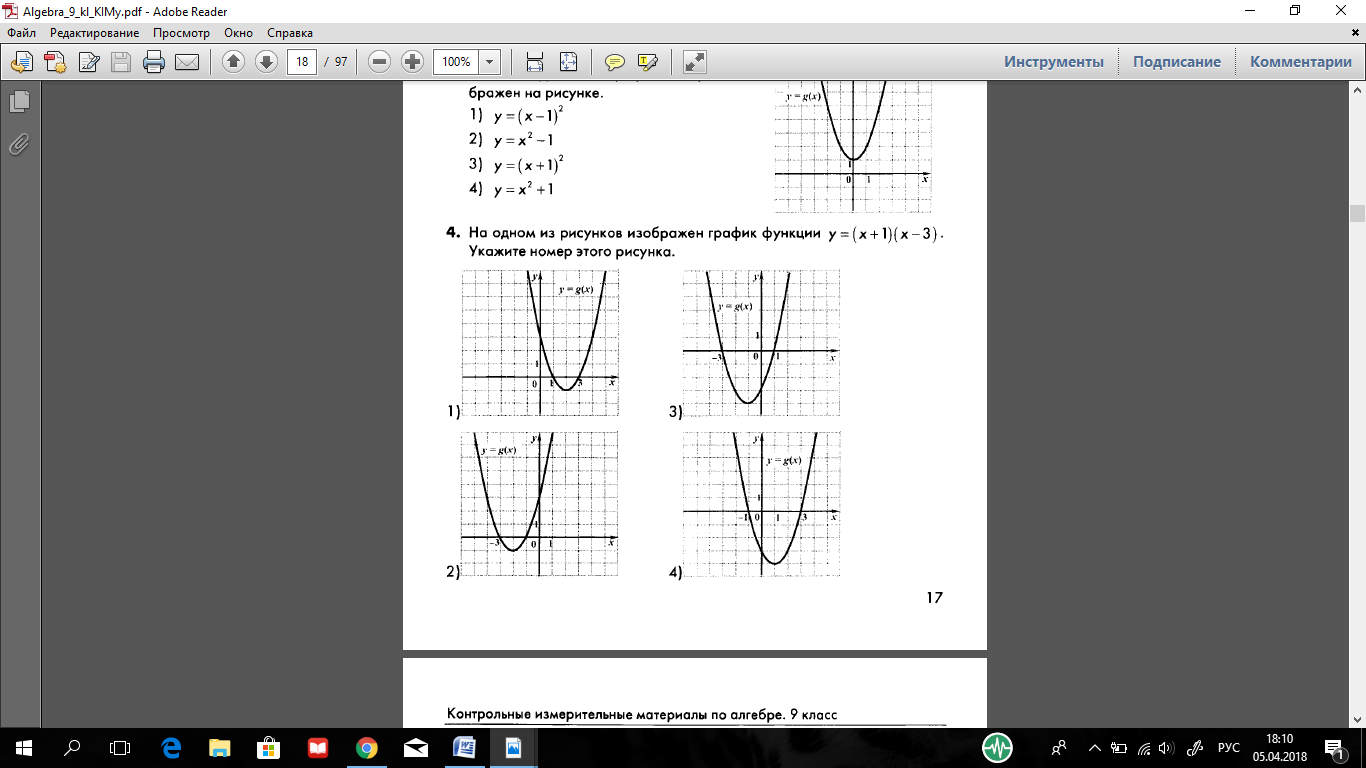
Задание №1. На одном из рисунков изображен график функции. Укажите номер рисунка.
1 группа: 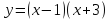 .
.
2 группа: 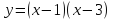 .
.
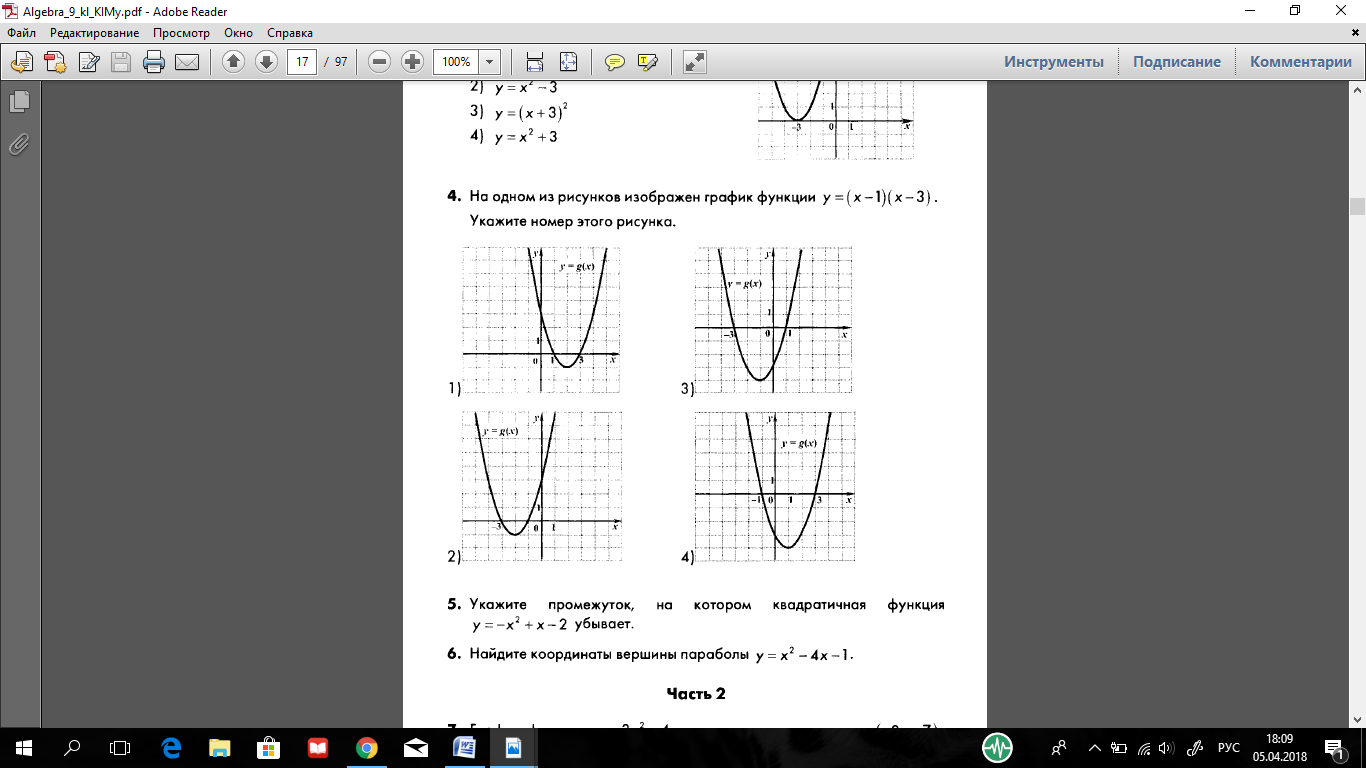
3 группа: 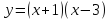 .
.
Задание №2. Найти координаты точек пересечения графиков функций:
1 группа: 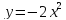 и
и 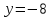 ;
;
2 группа: 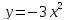 и
и  ;
;
3 группа: 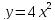 и
и 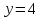 .
.
Задание №3. Построить график квадратичной функции:
1 группа: 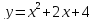 ;
;
2 группа: 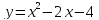 ;
;
3 группа: 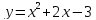 .
.
Дополнительное задание.
В задании №3 выделить полный квадрат функции и построить график квадратичной функции с помощью смещения графика у=х2 по осям Ох и Оу.
Подведение итогов урока. Рефлексия
Подведение итогов провести в виде математического теста «Да/Нет». Каждому ученику раздать листик для записи ответов. Задания указаны на слайде.
Графиком функции у=-5х+1 является парабола.
(0;0)- координаты вершины параболы у= х2+3.
Прямая х= 0- ось симметрии параболы у = х2.
Старший коэффициент функции у=-х2+4 равен 1, второй - 0, свободный член равен 4.
Функция у=х2 возрастает на множестве всех действительных чисел.
Ветви параболы у=-2х2+х+3 направлены вниз.
У функции у=5х2-х-4 есть наибольшее значение, но нет наименьшего.
Точка В(2;-40) принадлежит графику функции у=-10х2.
Квадратичная функция задается формулой вида у=ах2+вх+с, где а, в, с – любые числа.
10. График функции у=(х-1)2+2 смещен по оси Ох вправо на 1 и по оси Оу вверх на 2.
Учитель собирает листы с групповой работой и листы с ответами на математический тест, благодарит за работу.









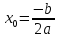 ,
, 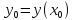 .
. 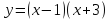 .
.
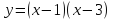 .
.
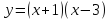 .
.
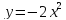 и
и 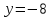 ;
;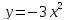 и
и  ;
;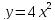 и
и 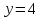 .
.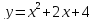 ;
;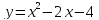 ;
;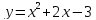 .
.









