СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

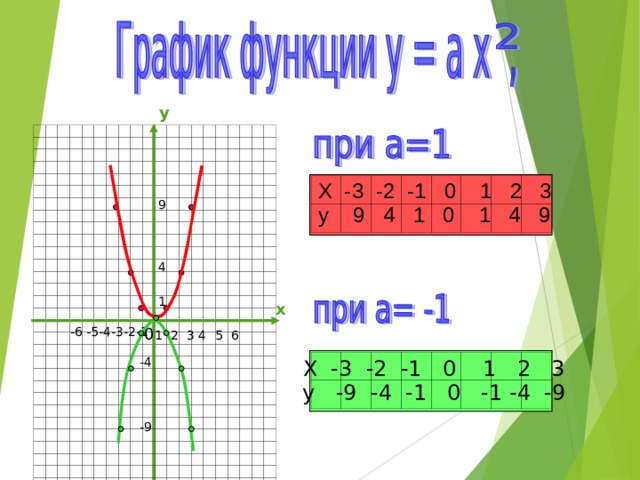
Квадратичная функция, ее график
Категория:
Алгебра
21.02.2021 22:40








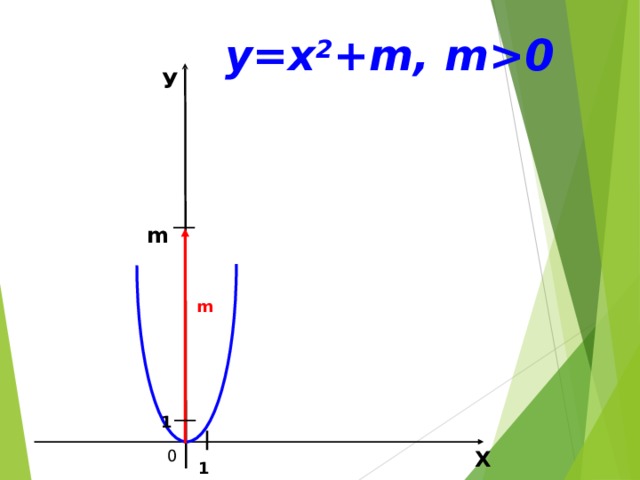 0 У m m 1 Х 0 1 " width="640"
0 У m m 1 Х 0 1 " width="640"
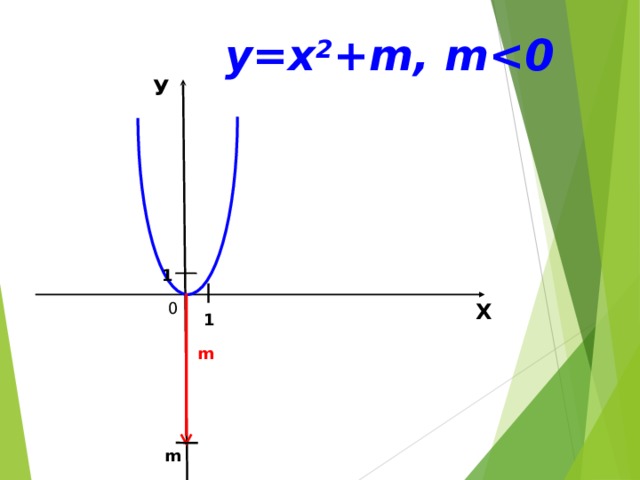


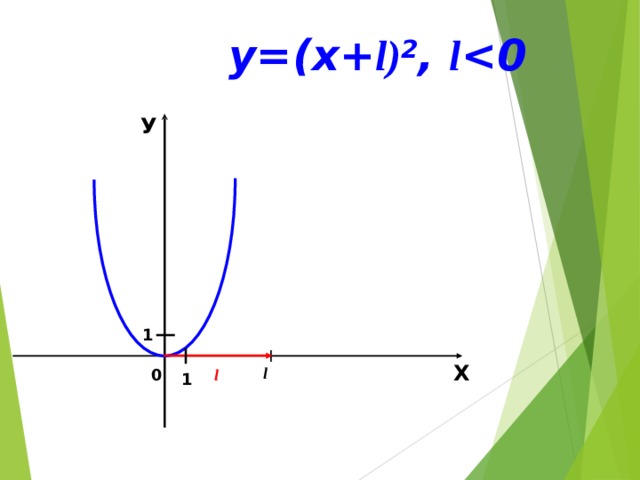
 0 У 1 Х l l 0 1 " width="640"
0 У 1 Х l l 0 1 " width="640"

 0 ) или вниз (если а у= 2 х ² +4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а 0 ). у= -7 х ² -х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а 0 ). у 0 х у 0 х " width="640"
0 ) или вниз (если а у= 2 х ² +4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а 0 ). у= -7 х ² -х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а 0 ). у 0 х у 0 х " width="640"