Предмет: Алгебра
Тема: Квадратные неравенства
Класс: 8
Тип урока: урок ознакомления с новым материалом
Методы: словесные, наглядные, контроля и оценки
Оборудование: Компьютер с установленным ПО «ActivInspire», интерактивная доска, проектор, презентация Power Point, учебники, карандаши, линейки
Цель:
Сформировать понятие квадратного неравенства с одной переменной, его свойства.
Познакомить с алгоритмом решения неравенств на основе свойств квадратичной функции, научиться решать неравенства данного вида с помощью алгоритма
Воспитывать математическую грамотность, речь, активность на уроке, последовательность в своих рассуждениях.
Структура урока.
Организационный момент
Подготовка к изучению нового материала
Объяснение нового материала
Первичное закрепление
Подведение итогов урока
Постановка домашнего задания
Ход урока.
Организационный момент
- Здравствуйте! Присаживайтесь!
Открываем тетради, записываем число и тему урока «Квадратные неравенства».
Подготовка к изучению нового материала
Для начала, следуя совету академика И.П. Павлова: «Никогда не берись за последующее, не усвоив предыдущее», мы вспомним все то, чем занимались на протяжении последних трех недель.
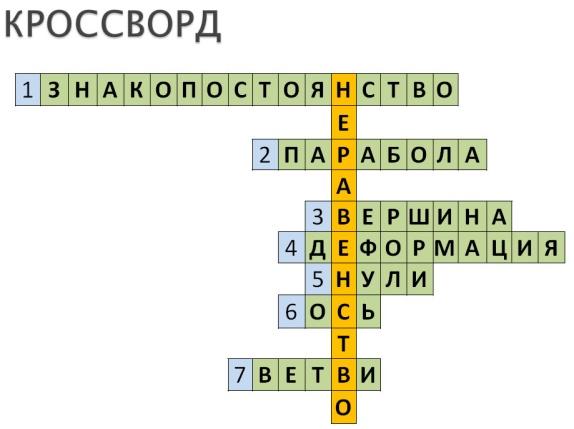
Презентация: Выполнение кроссворда.
Вопросы.
Промежутки, на которых функция принимает либо только положительные значения, либо только отрицательные значения (знакопостоянство)
Что является графиком квадратичной функции? (парабола)
Точка, координаты которой находятся по формулам xв=-b/2a, yв=axв2+bxв+c (вершина)
За что отвечает коэффициент а, если он больше или меньше единицы? (деформация)
Точки пересечения графика квадратичной функции с осями координат (нули)
Прямая, проходящая через xв и параллельно Оу (ось)
Элементы параболы, которые, в зависимости от знака коэффициента а, могут быть направлены или вверх, или вниз (ветви)
3. Объяснение нового материала
Ключевое слово этого кроссворда «НЕРАВЕНСТВО». Еще в 6 классе вы научились решать линейные неравенства и их системы, а в этом году научились решать квадратные уравнения. Теперь же мы познакомимся с понятием квадратное неравенство.
Открываем тетради. Записываем тему «КВАДРАТНЫЕ НЕРАВЕНСТВА».
Определение: Неравенства вида ax2+bx+c0 (ax2+bx+c2+bx+c≥0 (ax2+bx+c≤0), где а, в, c – действительные числа, причем а≠0, х – переменная, называются квадратными(учащиеся определение запишут дома)
Устное задание. Определить, какие из следующих неравенств являются квадратными:
x-5≥0
x2+4x-1
x2-3x≤0
-1/2x2+10≤0
x4-x2-50
x=x2
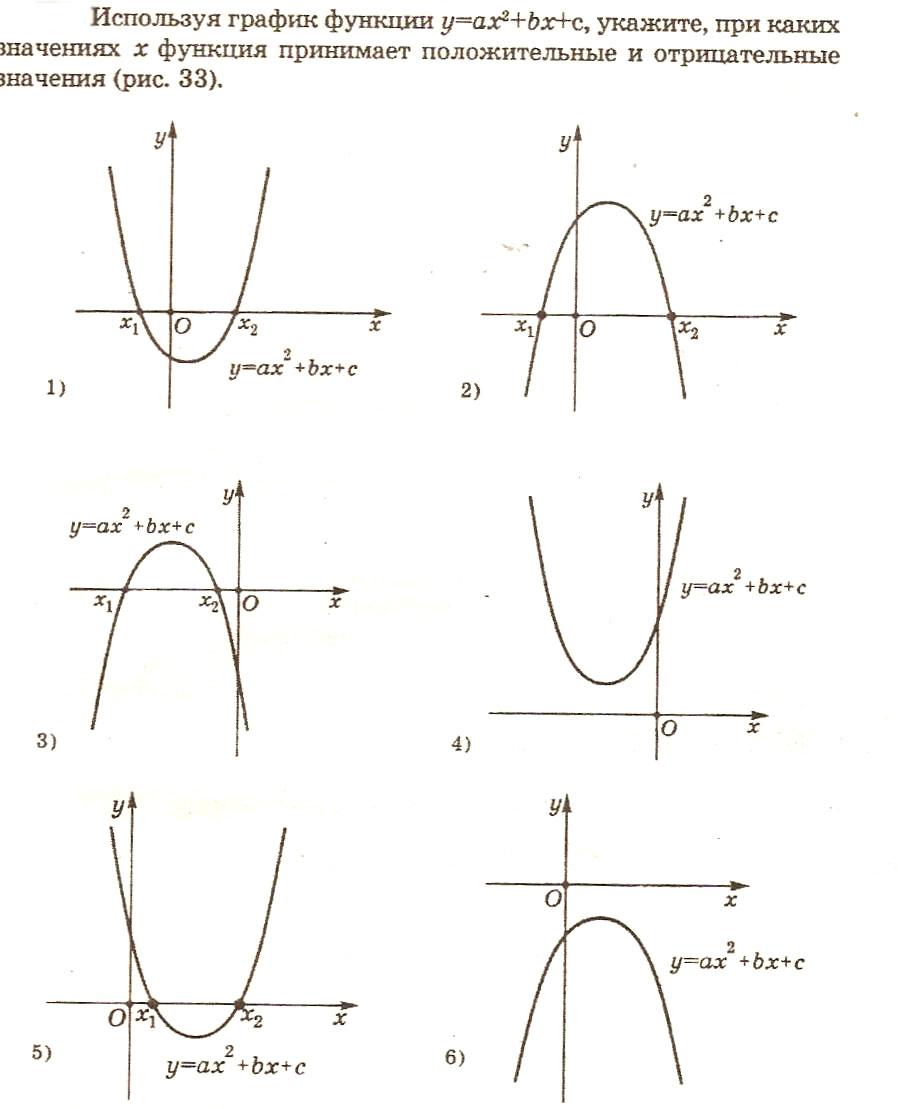
Известны два способа решения неравенств данного вида: метод параболы и метод интервалов. Сегодня мы рассмотрим методы параболы. Для этого нам необходимо знать, как изменяется знак трехчлена ax2+bx+c, когда аргумент х принимает любое действительное значение. Для наглядности и простоты мы воспользуемся графиком квадратичной функции в зависимости от коэффициента а и дискриминанта соответствующего трехчлена.
Рассмотрим случаи.
Случай I. 1) a0 и D0 (трехчлен имеет два различных корня)
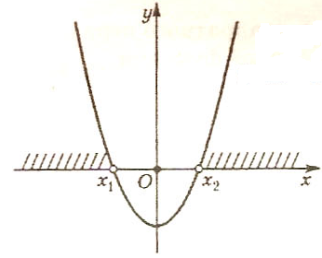
(-∞; x1) и (x2; +∞)
(x1; x2)
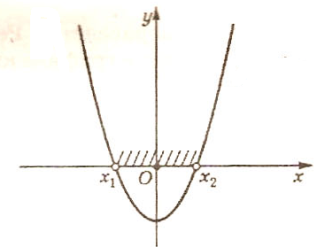
2) a0 (трехчлен имеет два различных корня)

(-∞; x1) и (x2; +∞)
(x1; x2)
Случай II. 1) a0 и D=0 (трехчлен имеет два одинаковых корня)
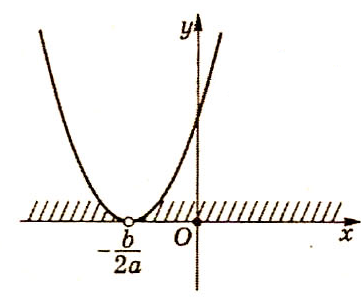
2) a(трехчлен имеет два одинаковых корня)
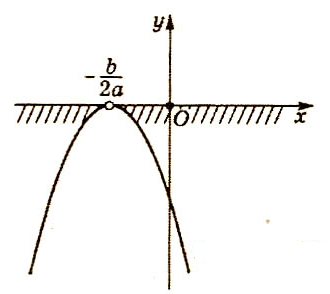
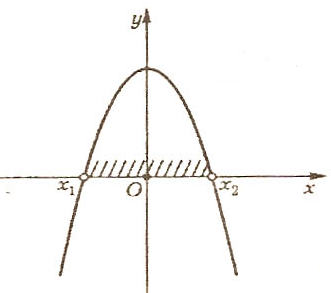
Случай III. 1) a0 и D(трехчлен не имеет действительных корней)
ax2+bx+c0 – при любом х
ax2+bx+c
2) a(трехчлен не имеет действительных корней)
![]()
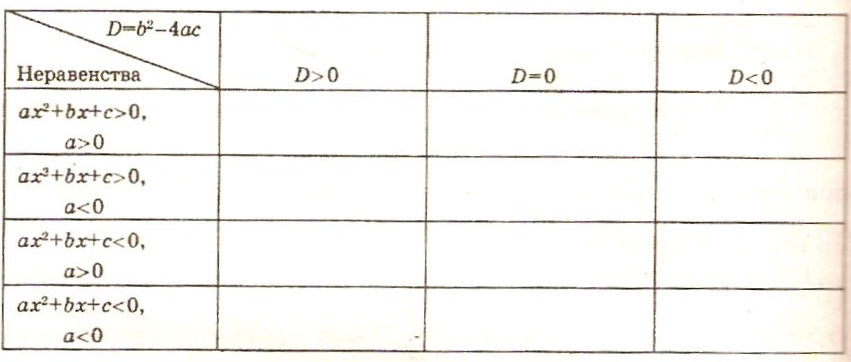
Работа в парах. Заполнить таблицу.
4. Первичное закрепление
Алгебра 8 класс, «Мектеп», 2008.
№279, 282, 284
5. Подведение итогов урока
Что нового мы узнали сегодня на уроке?
Что представляет собой квадратное неравенство?
С каким способом решения квадратного неравенства мы познакомились? В чем он заключается?
Выполнить устно задание:
6. Постановка домашнего задания


























