| Предмет алгебра Урок № Дата проведения _________________ Класс 8 Тема урока: Тема урока: Решение квадратного неравенства с помощью графика квадратичной функции. Цель урока: повторить алгоритмы построения параболы, правила решения квадратных уравнений; объяснить правило решения квадратных неравенств; формировать умение решать различные неравенства. Задачи урока: 1.Образовательная: вырабатывать навыки решения квадратных неравенств. 2.Развивающая: развитие навыков устного счета, содействовать развитию математического кругозора, мышления, речи, памяти, внимания. 3.Воспитательная: воспитание ответственности, усидчивости, самостоятельности. Формы обучения: практикум. Методы обучения: фронтальный метод. Тип урока: урок изучения и первичного закрепления новых знаний Технология: БиС, технологическая карта «Триада – Алгоритм» Задача по технологии БиС: выполнение регламента по технологической карте Планируемый результат: достижение 63% -ного качества знаний по данной теме Оборудование: ИКТ, раздаточный материал
Ход урока |
|
|
| 1 | Орг.момент Мотивация | Правила работы технологии БиС по карте «Алгоритм» Запись даты и темы урока. Норма качества знаний на 63% от количества всех учащихся на уроке (записывается на доске) (11) |
| 2 | Активизация | Вопросы учащимся: 1. Вспомните правила построения параболы и правила решения квадратных уравнений.
| 2. Для этого на доске разбирается построение графиков следующих функций: а) y = x2 – 4x + 3; б) y = –x2 + 2x + 3. Находятся точки пересечения данных графиков с осью абсцисс. |
| 3 | 1 цикл «Проба» «Актуализация субъектного опыта учащихся» | Первое объяснение по схеме ОСУД А/8/10/14 «Решение квадратных уравнений» Схемы должны быть на каждой парте. Время объяснения В1 (В1= время начало - конец) Учитель, объясняет тему по каждому элементу ОСУДА! Левая рука – указывает на нужный этап схемы, правая рука = с мелом на доске. Обязательно нужен диалог с классом. Учитель отрабатывает на доске нпс, ппс, впс №1, №2 Рассмотреть решение неравенства по данному алгоритму: x2 + 6x – 16 0 x2 + 6x – 16=0 ветви параболы направлены вверх. 4) Найдем дискриминант трехчлена x2 + 6x – 16 D = b2 – 4ac, D = 36 – 4 (–16) = 100 0 Следовательно, имеется два действительных корня трехчлена. Найдем корни этого трехчлена, решив уравнение. x2 + 6x – 16 = 0 x1 = –8, x2 = 2. | 5) Построим схематический график функции y = x2 + 6x + 16. 
|
| 8) О т в е т: x  (–∞; –8) (–∞; –8) (2; +∞). (2; +∞).
| Алгоритм решения: 
|
|
| 1) -2x2 + 3x + 9 2) -2x2 + 3x + 9 = 0 3) ветви параболы направлены вниз. 4) х1 = 3, х2 = -1,5 5) Cтроим схематически параболу. 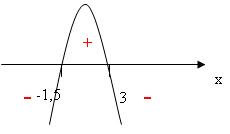 8) Ответ: (-оо; -1,5)  (3; + оо) (3; + оо) 3x2−4x−2≥0 1) 3x2−4x−2≥ 2) Запишем соответствующее квадратное уравнение: 3x2−4x−2=0 3) Найдем корни данного квадратного уравнения: D=(−4)2−4⋅3⋅(−2)=40 x1= = =  ) ) x2= = =  ) ) 4) Схематично отметим полученные корни на оси и расставим знаки:  Ответ: x∈(−∞; )]∪[ )]∪[ ); ∞) ); ∞)
|
|
| 4 | Организация восприятия | Учащиеся записывают слово «Проба», делают синхронно один хлопок и приступают к выполнению задания, №1 время работы:5 уч-ся + 30 сек. Решите уравнение: 1 вариант - 1 задания, 2 вариант - 2 задания.
| НПС | ППС | ВПС | | 1) х2 – 1 ≤ 0 2) х2 + х-12 ≤ 0 3) –х2 –х+12 › 0 4) х2 - 10х ‹ 0 5) х2 -9 ≥ 0 6) х2 + 4х -5 ≤ 0 7) х2 –х -6 › 0 8) х2 – 8х › 0 | 1) х2 – 0,49 ‹ 0 2) –х2 – 4х - 3 › 0 3) х2 +4х -4 ≤ 1 4) (х - 1)(3 - 2х) › -6 5) х2 – 0,16 › 0 6) –х2 + 3х +4 › 0 7) 3х2 – 4х ‹ -1 8) (3х +7)( 1 - х) ‹ 3 | 1) х2 ≥ 81 2) 2х2 -3х -2 › 0 3) (х - 3)2› 9 – х2 4) (х + 2)(2 - х) ≥ 3х2 – 8 5) х2 ≤ 64 6) 2 х2 + 5х – 3 › 0 7) 4 – х2 › (2 + х)2 8) 2х2 – 6 ‹ (3 - х)(х + 3)
|
| НПС | ППС | ВПС | | 1) -1≤ х ≤ 1 2) -4 ≤ х ≤ 3 3) -4 ‹ х ‹ 3 4) 0 ‹ х ‹ 10 5) х ≤ -3 , х ≥ 3 6) -5 ≤ х ≤ 1 7) х ‹ -2 , х › 3 8) х ‹ 0 , х › 8
| 1) – 0,7 ‹ х ‹ 0,7 2) -3 ‹ х ‹ -1 3) -5≤ х ≤ 1 4) -1/2 ‹ х ‹ 3 5) х ‹ -0,4 , х › 0,4 6) -1 ‹ х ‹ 4 7) 1/3 ‹ х ‹ 1 8) х ‹ -2 , х › 2/3 | 1) х ≤ - 9 , х≥ 9 2) х ‹ - ½ , х › 2 3) х ‹ 0 , х › 3 4) -√3 ≤ х ≤ √3 5) -8 ≤ х ≤ 8 6) х ‹ -3 , х › ½ 7) -2 ‹ х ‹ 0 8) - √5 ‹ х ‹ √5
|
|
| 5 | Организация осмысления. Рефлексия. | По окончании работы, звучит команда «Ручка в руках – это ошибка!». Учащиеся обмениваются тетрадями. Поэтапная проверка выполнения заданий: НПС, ППС, ВПС. Определяется качество исполнения на каждом уровне отдельно. Проводится опрос: 1.Скорость – замедленные учащиеся отражают уровень навыков и умений в классе. 2.Внимание – невнимательные дети – отражает уровень организации класса. 3.Счет – ошибки в счете отражает уровень базовых знаний. 4. Тема – происходит поиск ошибок и выписываются по порядку «хвосты» по предыдущим темам. Важно. Анализ всех проблем на этапе проба является основой плана следующего объяснения. |
| 6 | 2 цикл «Закрепление» «Актуализация субъектного опыта учащихся» | Опрашивается класс, повторное объяснение с учетом допущенных ошибок Время В2 начала и окончания объяснения записывается на доске
|
| 7 | Организация восприятия | Учащиеся записывают слово «Закрепление», делают синхронно два хлопка и приступают к выполнению задания время работы:5 уч-ся + 30 сек. Решите уравнения: |
| НПС | ППС | ВПС | | 1 вариант | –х2 –х+12 › 0
| х2 +4х -4 ≤ 1
| (х - 3)2› 9 – х2
| | 2 вариант | х2 - 10х ‹ 0
| (х - 1)(3 - 2х) › -6
| (х + 2)(2 - х) ≥ 3х2 – 8
|
|
| 8 | Организация осмысления. Рефлексия. | По окончании работы, звучит команда «Ручка в руках – это ошибка!». Учащиеся обмениваются тетрадями. Поэтапная проверка выполнения заданий: НПС, ППС, ВПС. Определяется качество исполнения на каждом уровне отдельно. |
| 9 | 3 цикл «Память» «Актуализация субъектного опыта учащихся» | Третье объяснение Опрашивается класс, повторное объяснение с учетом допущенных ошибок Время В3 начала и окончания объяснения записывается на доске
|
| НПС | ППС | ВПС | | 1 вариант | х2 -9 ≥ 0
| х2 – 0,16 › 0
| х2 ≤ 64
| | 2 вариант | х2 + 4х -5 ≤ 0
| –х2 + 3х +4 › 0
| 2 х2 + 5х – 3 › 0
|
|
| 10 | Организация восприятия | Учащиеся записывают слово «Память», делают синхронно три хлопка и приступают к выполнению задания (задания подбираются по схеме «Если-то»). время работы:5 уч-ся + 30 сек.
|
| 11 | Организация осмысления. Рефлексия. | По окончании работы, звучит команда «Ручка в руках – это ошибка!». Учащиеся обмениваются тетрадями. Поэтапная проверка выполнения заданий: НПС, ППС, ВПС. Определяется уровень усвоения материала. |
| 12 | Оценивание | «5» - выполнившим все 9 примеров правильно «4» - выполнившим 7-8 примеров правильно Оценка «3» по карте «Алгоритм» не выставляется |
| 13 | Домашнее задание. | № 283, 286, 290 (1,2) |










 =
=  )
) =
=  )
)










