Методическое пособие
по алгебре
8 класс
«Квадратные уравнения»
Материал может быть использован учителями математики при изучении нового материала и отработке практических навыков по основной теме курса алгебры 8 класса «Квадратные уравнения», а так же при закреплении в 9-11 классах. Данное пособие способствует интеграции информационных знаний с предметом «Математика», развитию личностных качеств, формирующих самооценку и самодостаточность учащихся, реализации деятельностного подхода в обучении.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема «Квадратные уравнения» - основная тема курса алгебры 8 – 11 классов. Навык решения квадратных уравнений необходим каждому ученику для итоговой аттестации за курс основной и старшей школы. Умение решать квадратные уравнения является одним из базовых умений для приобретения новых.
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит конкретным практическим целям. Большинство задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, люди находят ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д). При изучении любой темы уравнения могут быть использованы как эффективное средство закрепления, углубления, повторения и расширения теоретических знаний, для развития творческой математической деятельности учащихся.
Основная цель – выработать умения решать квадратные уравнения, простейшие рациональные и иррациональные уравнения, применять рациональные уравнения к решению задач.
Основные результаты
1. правильно употреблять и понимать термины:
• квадратное уравнение
• корни уравнения
• решить уравнение
• старший коэффициент, второй коэффициент, свободный член
• полное квадратное уравнение
• неполное квадратное уравнение
• приведенное квадратное уравнение
• корень квадратного трехчлена
• дискриминант квадратного уравнения
• рациональное уравнение
• иррациональное уравнение
• биквадратное уравнение
• параметр, уравнение с параметром
• посторонний корень
• равносильные уравнения
• равносильные и неравносильные преобразования уравнений
2. знать и уметь применять на практике алгоритмы решения
• квадратных уравнений(полных, неполных, приведенных)
• рациональных уравнений
• иррациональных уравнений
3. понимать, что уравнения – это математический аппарат решения разнообразных задач
4. в результате решать текстовые задачи с помощью составления уравнений
Тема «Квадратные уравнения» актуальна в современном мире; это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач. Также в последнее время в материалах итоговой аттестации, ЕГЭ по математике предлагаются уравнения и неравенства второй степени, другие виды уравнений, которые решаются именно с помощью формул квадратных уравнений или с помощью теоремы Виета.
Обобщение способов деятельности учащихся при решении квадратных уравнений происходит постепенно. Можно выделить следующие этапы при изучении темы «Квадратные уравнения»:
I этап – «Решение неполных квадратных уравнений».
II этап – «Решение полных квадратных уравнений».
Решение квадратных уравнений
-
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
-
x2 + 9x = 0;
-
x2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax2 + c = 0. Немного преобразуем его:
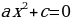
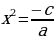

Решение неполного квадратного уравнения
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
-
Если в неполном квадратном уравнении вида ax2 + c = 0 выполнено неравенство  ≥ 0, корней будет два. Формула дана выше;
≥ 0, корней будет два. Формула дана выше;
-
Если же 
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

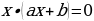

Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
-
x2 − 7x = 0;
-
5x2 + 30 = 0;
-
4x2 − 9 = 0.
x2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x1 = 0; x2 = −(−7)/1 = 7.
5x2 + 30 = 0 ⇒ 5x2 = −30 ⇒ x2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x2 − 9 = 0 ⇒ 4x2 = 9 ⇒ x2 = 9/4 ⇒ x1 = 3/2 = 1,5; x2 = −1,5.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0 , где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
-
Не имеют корней;
-
Имеют ровно один корень;
-
Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Д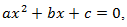 искриминант
искриминант
П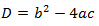 усть дано квадратное уравнение Тогда дискриминант — это просто число.
усть дано квадратное уравнение Тогда дискриминант — это просто число.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
-
Если D
-
Если D = 0, есть ровно один корень;
-
Если D 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
-
x2 − 8x + 12 = 0;
-
5x2 + 3x + 7 = 0;
-
x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a=1, b=−8, c=12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D 0, корни можно найти по формулам:
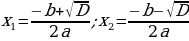
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Задача. Решить квадратные уравнения:
-
x2 − 2x − 3 = 0;
-
15 − 2x − x2 = 0;
-
x2 + 12x + 36 = 0.
Первое уравнение:
x2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)2 − 4 · 1 · (−3) = 16.
D 0 ⇒ уравнение имеет два корня. Найдем их:
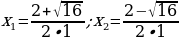
Второе уравнение:
15 − 2x − x2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)2 − 4 · (−1) · 15 = 64.
D 0 ⇒ уравнение снова имеет два корня. Найдем их

Наконец, третье уравнение:
x2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.


Решение биквадратного уравнения

Практическая часть
| 1 |
|
|
| Найдите корень уравнения. Вопрос ко всем заданиям. |
|
| 
|
|
| Ответы |
|
| 1. -0.3 2. -1.8 3. -0.1 4. -0.8 5. 1.5 6. -1.5 7. -1.2 8. -9 9. -1.8 10. -0.1 11. -0.7 12. -0.4 13. 6.75 14. 9.7 15. -10.6 16. 1.25 17. -2.7 18. 6.4 |
|
|
| 2 |
|
|
|
| 
|
|
|
| Ответы |
|
|
| 1. -1 2. 13 3. -1 4. -15 5. 8 6. -2 7. -1 8. -5 |
|
|
| 3 |
|
|
|
| 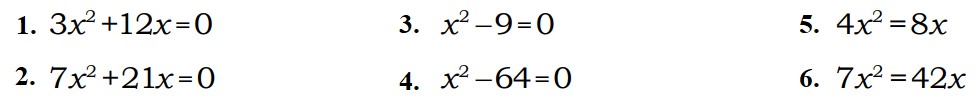
|
|
|
| Ответы |
|
|
| 1. -4 и 0 2. -3 и 0 3. -3 и 3 4. -8 и 8 5. 0 и 2 6. 0 и 6 |
|
|
| 4 |
|
|
| 
|
|
| Ответы |
|
| 1. -3 и 5 2. 1 и 7 3. -2 и 8 4. 3 и 6 5. -5 и 7 6. 2 и 3 7. -5 и 1 8. -2 и 8 9. -5 и 3 10. -1 и 8 11. -7 и 3 12. -2 и 7 13. 1 и 5 14. 3 и 6 15. 4 и 6 16. -4 и 3 17. 5 и 6 18. 2 и 5 |
|
| 5 |
|
|
|
| 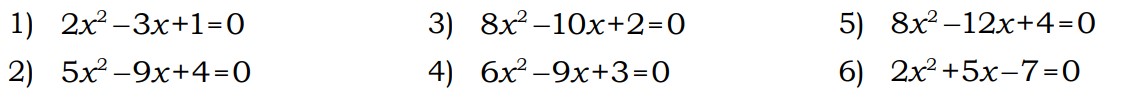
|
|
|
| Ответы |
|
|
| 1. 0.5 и 1 2. 0.8 и 1 3. 0.25 и 1 4. 0.5 и 1 5. 0.5 и 1 6. -3.5 и 1 |
|
|
| 6 |
|
|
|
|
| 
|
|
|
|
| Ответы |
|
|
|
| 1. -5 и 5 2. -3 и 3 3. -8 и 8 4. -4 и 4 5. -12 и 12 6. -7 и 7 7. -14 и 14 8. -9 и 9 |
|
|
|
| 7 |
|
|
|
| 
|
|
|
| Ответы |
|
|
| 1. -5 и -2 2. 0.5 и 3 3. -4 и -1 4. -6 и -0.4 5. 2 и 7 6. -10 и -8 |
|
|
| 8 |
|
|
|
| 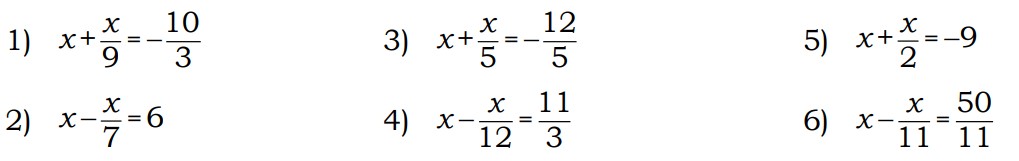
|
|
|
| Ответы |
|
|
| 1. -3 2. 7 3. -2 4. 4 5. -6 6. 5 |
|
|
| 9 |
|
|
|
|
|
|
| 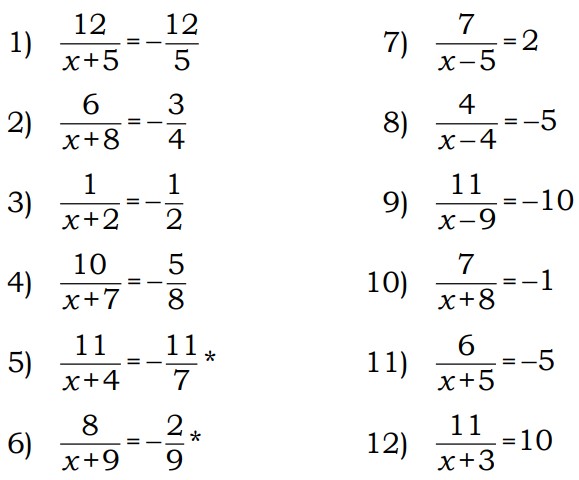
|
|
|
|
|
|
|
| Ответы |
|
|
|
|
|
| 1. -10 2. -16 3. -4 4. -23 5. -11 6. -45 7. 8.5 8. 3.2 9. 7.9 10. -15 11. -6.2 12. -1.9 |
|
|
|
|
|
| 10 |
|
|
|
|
|
| 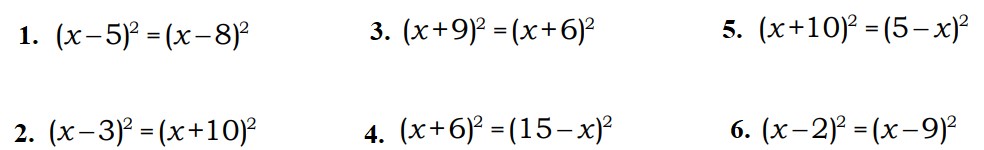
|
|
|
|
|
| Ответы |
|
|
|
|
| 1. 6.5 2. -3.5 3. -7.5 4. 4.5 5. -2.5 6. 5.5 |
|
|
|
Карточки по вариантам
| Вариант -1 1)5х2=125 2)2х2-3х+1=0 3)х2+4х+3=0 4)х4-10х2+9=0 5)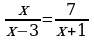
| Вариант -2 1)х2+5х=0 2)2х2+5х+2=0 3)х2-3х-10=0 4)х4-5х2+4=0 5)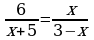
|
| Вариант -3 1)х2-3х=0 2)2х2-7х+3=0 3)х2+4х-5=0 4)х4-13х2+36=0 5)
| Вариант -4 1)9х2=1 2)4х2-11х+6=0 3)х2+6х-40=0 4)х4+3х2-4=0 5)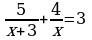
|
| Вариант -5 1)25-х2=0 2)3х2+11х+6=0 3)х2-х-2=0 4)х4-4х2-5=0 5)
| Вариант -6 1)х2-7х=0 2)2х2-7х-4=0 3)х2-5х-6=0 4)х4+х2-20=0 5)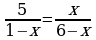
|
| Вариант -7 1)3х2-15х=0 2)3х2+2х-1=0 3)х2+3х-4=0 4)х4-9х2+20=0 5)
| Вариант -8 1)2х2-72=0 2)2х2+12х+10=0 3)х2-9х+18=0 4)х4-11х2+18=0 5)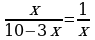
|
| Вариант -9 1) 9х2=81 2)2х2+3х+1=0 3)х2-4х-5=0 4)х4-3х2-4=0 5)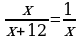
| Вариант -10 1) х2+16х=0 2)2х2+5х-3=0 3)х2+2х-15=0 4)х4-50х2+49=0 5)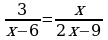
|
| Вариант -11 1) х2+11х=0 2)3х2+х-4=0 3)х2+4х-12=0 4)9х4+5х2-4=0 5)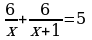
| Вариант -12 1) х2=169 2)2х2-х-1=0 3)х2-10х+16=0 4)2х4-5х2+2=0 5)
|
| Вариант -13 1)3х2-75=0 2)6х2+х-1=0 3)х2+5х+6=0 4)5х4-16х2+3=0 5)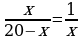
| Вариант -14 1)х2+4х=0 2)9х2-6х+1=0 3)х2+8х+7=0 4)х4-16х2-17=0 5)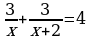
|
| Вариант -15 1)х2-11х=0 2)16х2-8х+1=0 3)х2-7х+12=0 4)2х4-х2-3=0 5)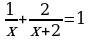
| Вариант -16 1)х2-144=0 2)6х2-5х-1=0 3)х2-8х+15=0 4)х4+х2-6=0 5)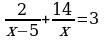
|
| Вариант -17 1)5х2=125 2)2х2-3х+1=0 3)х2+4х+3=0 4)х4-10х2+9=0 5)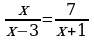
| Вариант -18 1)х2+5х=0 2)2х2+5х+2=0 3)х2-3х-10=0 4)х4-5х2+4=0 5)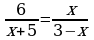
|
| Вариант -19 1)х2-3х=0 2)2х2-7х+3=0 3)х2+4х-5=0 4)х4-13х2+36=0 5)
| Вариант -20 1)9х2=1 2)4х2-11х+6=0 3)х2+6х-40=0 4)х4+3х2-4=0 5)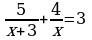
|
| Вариант -21 1)25-х2=0 2)3х2+11х+6=0 3)х2-х-2=0 4)х4-4х2-5=0 5)
| Вариант -22 1)х2-7х=0 2)2х2-7х-4=0 3)х2-5х-6=0 4)х4+х2-20=0 5)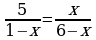
|
| Вариант -23 1)3х2-15х=0 2)3х2+2х-1=0 3)х2+3х-4=0 4)х4-9х2+20=0 5)
| Вариант -24 1)2х2-72=0 2)2х2+12х+10=0 3)х2-9х+18=0 4)х4-11х2+18=0 5)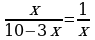
|
Ответы:
В-1. (В-17) 1)х1,2 = ±5; 2) х1 = 1; х2 = 0,5; 3) х1 =-1; х2 = -3; 4) х1,2 =± 3; х3,4 = ± 1;
5) нет решений.
В-2. (В-18) 1)х1 = 0; х2=-5; 2) х1 = -0,5; х2 = -2; 3) х1 =-2; х2 = 5; 4) х1,2 =± 2;
х3,4 = ± 1; 5) х1 = -2; х2 = -9;
В-3. (В-19) 1)х1 =0; х2 = 3;2) х1 = 3; х2 = 0,5; 3) х1 =1; х2 = -5; 4) х1,2 =± 3;
х3,4 = ± 2; 5) х1=2; х2=-6;
В-4. (В-20) 1)х1,2 = ±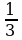 ; 2) х1 = 2; х2 = 0,75; 3) х1 =-10; х2 = 4; 4) х1,2 =± 1;
; 2) х1 = 2; х2 = 0,75; 3) х1 =-10; х2 = 4; 4) х1,2 =± 1;
5) х1,2=±2;
В-5. (В-21) 1)х1,2 = ±5; 2) х1 = -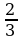 ; х2 = -3; 3) х1 =-1; х2 = 2; 4) х1,2 =±
; х2 = -3; 3) х1 =-1; х2 = 2; 4) х1,2 =±  ;
;
5) х1=1; х2=5;
В-6. (В-22) 1)х1 = 0; х2=7;2) х1 = 4; х2 = -0,5; 3) х1 =-1; х2 = 6; 4) х1,2 =± 2;
5) нет решений.
В-7. (В-23) 1)х1 = 0; х2=5;2) х1 = -1; х2 =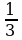 ; 3) х1 =1; х2 = -4; 4) х1,2 =± 2; х3,4 = ±
; 3) х1 =1; х2 = -4; 4) х1,2 =± 2; х3,4 = ± ; 5) нет решений.
; 5) нет решений.
В-8. (В-24) 1)х1,2 = ±6; 2) х1 = -1; х2 = -5; 3) х1 =6; х2 = 3; 4) х1,2 =± 3; х3,4 = ±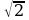 ;
;
5) х1=-5; х2=2;
В-9. (В-25) 1)х1,2 = ±3; 2) х1 = -1; х2 = -0,5; 3) х1 =-1; х2 = 5; 4) х1,2 =± 2;
5) х1=4; х2=-3;
В-10. 1)х1 = 0; х2=-16; 2) х1 = -3; х2 = 0,5; 3) х1 =-5; х2 = 3; 4) х1,2 =± 7; х3,4 = ± 1;
5) х1=9; х2=3;
В-11. 1)х1 = 0; х2=-11; 2) х1 = 1; х2 =-1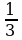 ; 3) х1 =-6; х2 = 2; 4) х1,2 =±
; 3) х1 =-6; х2 = 2; 4) х1,2 =±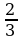 ;
;
5) х1=2; х2=-0,6;
В-12. 1)х1,2 = ±13; 2) х1 = 1; х2 = -0,5; 3) х1 =8; х2 = 2; 4) х1,2 =±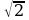 ; х3,4 = ±
; х3,4 = ±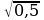 ;
;
5) нет решений.
В-13. 1)х1,2 = ±5; 2) х1 = 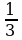 ; х2 = -0,5; 3) х1 =-2; х2 = -3; 4) х1,2 =±
; х2 = -0,5; 3) х1 =-2; х2 = -3; 4) х1,2 =± 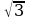 ;
;
х3,4 = ±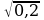 ; 5) х1=-5; х2=4;
; 5) х1=-5; х2=4;
В-14. 1)х1 = 0; х2=-4; 2) х1 = 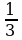 ; 3) х1 =-1; х2 = -7; 4) х1,2 =±
; 3) х1 =-1; х2 = -7; 4) х1,2 =± 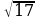 ; 5) х1=1;
; 5) х1=1;
х2=-1,5;
В-15. 1)х1 = 0; х2=11;2) х1 = 0,25; 3) х1 =3; х2 = 4; 4) х1,2 =± 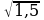 ; 5) х1=2; х2=-1;
; 5) х1=2; х2=-1;
В-16. 1)х1,2 = ±12; 2) х1 = 1; х2 = -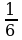 ; 3) х1 =5; х2 = 3; 4) х1,2 =±
; 3) х1 =5; х2 = 3; 4) х1,2 =± 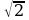 ; 5) х1=7; х2=3
; 5) х1=7; х2=3 ;
;
Заключение
Методическое пособие по разделу математики «Квадратные уравнения» можно использовать при подготовке к экзаменам, на дополнительных занятиях и при самостоятельном изучении.
В пособии даются краткие теоретические сведения, решение уравнений. Примеры подобраны с различной степенью трудности: от простых до достаточно сложных и требующих нетрадиционных методов их решения. В принципе это краткий математический справочник, который поможет ученику самостоятельно и глубоко изучить тему «Квадратные уравнения и способы их решения».
Данное пособие может не только помочь пополнить, систематизировать, углубить знания по алгебре, но и способствовать формированию умений применять приемы сравнения, выделения главного, переноса знаний в новую ситуацию; развитию творческих способностей учащихся путем решения заданий более сложного уровня.
Таким образом, собранным материалом могут воспользоваться учащиеся 8-9 классов для изучения и закрепления решения квадратных уравнений.
Список литературы:
-
Макарычев Ю.Н.. Миндюк Н.Г., Дополнительные главы к школьному учебнику. 8 класс М.,
-
Галицкий М.Л., Гольдман М., Звавич Л.И. Учебное пособие для учащихся школ и классов с углубленным изучением математики: 4-е изд.-М.: Просвещение, 1997.
-
https://www.time4math.ru/?ysclid=lr7t9raemv766862969







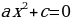
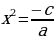

 ≥ 0, корней будет два. Формула дана выше;
≥ 0, корней будет два. Формула дана выше;
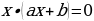

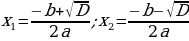
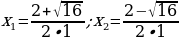







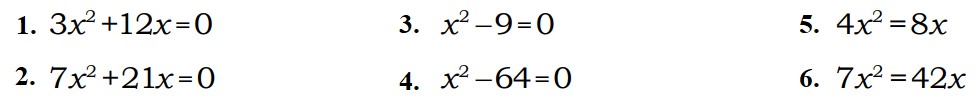

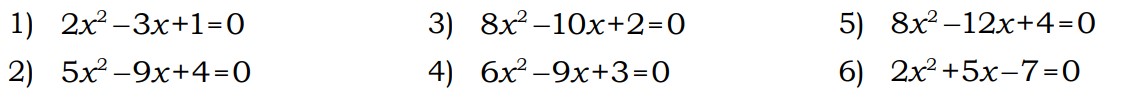


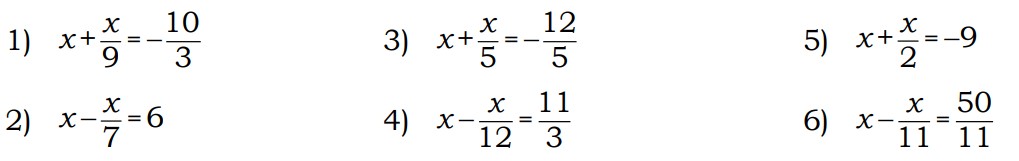
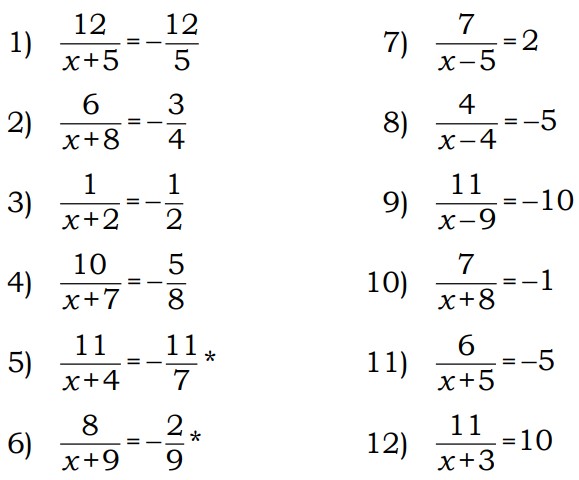
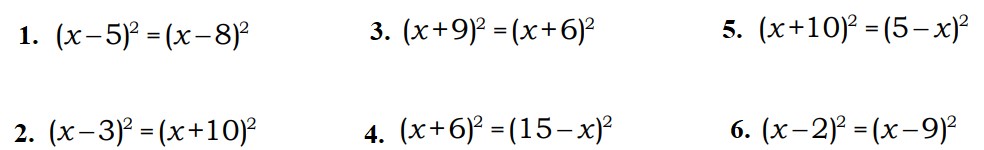
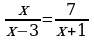
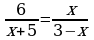

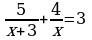

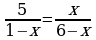

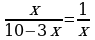
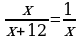
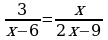
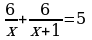

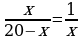
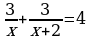
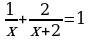
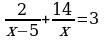
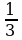 ; 2) х1 = 2; х2 = 0,75; 3) х1 =-10; х2 = 4; 4) х1,2 =± 1;
; 2) х1 = 2; х2 = 0,75; 3) х1 =-10; х2 = 4; 4) х1,2 =± 1; 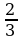 ; х2 = -3; 3) х1 =-1; х2 = 2; 4) х1,2 =±
; х2 = -3; 3) х1 =-1; х2 = 2; 4) х1,2 =±  ;
; 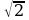 ;
; 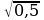 ;
; 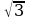 ;
; 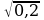 ; 5) х1=-5; х2=4;
; 5) х1=-5; х2=4;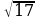 ; 5) х1=1;
; 5) х1=1; 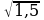 ; 5) х1=2; х2=-1;
; 5) х1=2; х2=-1; ; 3) х1 =5; х2 = 3; 4) х1,2 =±
; 3) х1 =5; х2 = 3; 4) х1,2 =± 




















