


ПЛАН УРОКА
1 . Теоретическая разминка.
2. Энциклопедия квадратных уравнений.
3. Думающий колпак.
4. Историческая справка.
5. Копилка ценных мыслей.
6. Домашнее задание.
- 1 . Теоретическая разминка. 2. Энциклопедия квадратных уравнений. 3. Думающий колпак. 4. Историческая справка. 5. Копилка ценных мыслей. 6. Домашнее задание.

Вопросы
теоретической разминки:
- Сформулируйте определение квадратного уравнения.
2. Объясните, в чём заключается смысл ограничения в определении квадратного уравнения (а ≠ 0).
3. Перечислите виды квадратных уравнений.
4. Какое квадратное уравнение называется неполным? Приведите пример.
5. Какое квадратное уравнение называется приведённым? Приведите пример.
6. Способы решения полного квадратного уравнения?
подробнее
подробнее

Специальные методы:
1. Метод выделения квадрата двучлена.
2. Метод «переброски» старшего коэффициента.
3. На основании теорем.

Общие методы:
Разложение на множители;
Введение новой переменной;
Графический метод .

ДУМАЮЩИЙ КОЛПАК
Большим и указательным пальцами мягко оттягивают назад и прижимают, массируя, раковины ушей.
УЧЕБНЫЕ ИНСТРУКЦИИ
• Держите голову прямо, чтобы подбородку было удобно. • Упражнение повторяют трижды или более раз.

Кристиан Вольф - знаменитый немецкий философ, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.
Впервые ввёл термин «квадратное уравнение» немецкий философ Кристиан Вольф.
.
http://ru.wikipedia.org/wiki/%D0%A5%D1%80%D0%B8%D1%81%D1%82%D0%B8%D0%B0%D0%BD_%D0%92%D0%BE%D0%BB%D1%8C%D1%84

Сильвестр Джеймс Джозеф – английский математик, который ввел термин «дискриминант».
http://www.persons-info.com/index.php?pid=10965

В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов произвел в 1544 году немецкий математик – Михаэль Штифель. Это было настоящее событие в математике.
http://ru.wikipedia.org/wiki/%D0%A8%D1%82%D0%B8%D1%84%D0%B5%D0%BB%D1%8C,_%D0%9C%D0%B8%D1%85%D0%B0%D1%8D%D0%BB%D1%8C

Домашнее задание
- Решите уравнение 3х 2 + 5х + 2 = 0 :
- используя формулу дискриминанта – « 3 » , двумя способами – « 4 » , тремя способами – « 5 » .
- используя формулу дискриминанта – « 3 » ,
- двумя способами – « 4 » ,
- тремя способами – « 5 » .
Дополнительно.
- Решите уравнение (х 2 -х) 2 - 14(х 2 -х) + 24 = 0 методом введения новой переменной.

Энциклопедия квадратного уравнения
подробнее
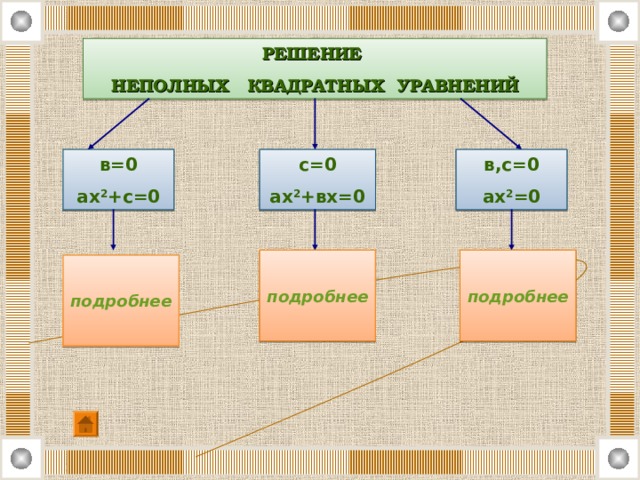
РЕШЕНИЕ
НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0
ах 2 +с=0
с=0
ах 2 +вх=0
в,с=0
ах 2 =0
подробнее
подробнее
подробнее
 0 -два решения: х 1 = и х 2 = - Если 0 - нет решений. " width="640"
0 -два решения: х 1 = и х 2 = - Если 0 - нет решений. " width="640"
Алгоритм решения
в=0
ах 2 +с=0
1.Переносим с в правую часть уравнения.
ах 2 = - с.
2.Делим обе части уравнения на а≠0.
х 2 = .
3.Если –с/а 0 -два решения:
х 1 = и х 2 = -
Если 0 - нет решений.

Алгоритм решения
с=0
ах 2 +вх=0
х (ах + в) = 0.
2. «Разбиваем» уравнение
на два:
x = 0, ах + в = 0.
3. Два решения:
х = 0 и х = (а≠0).
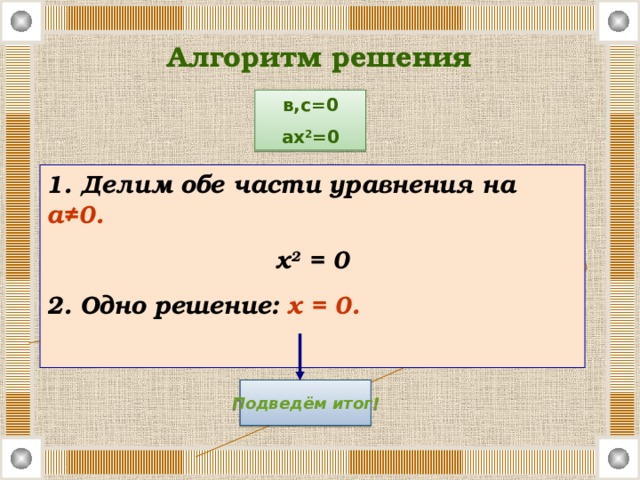
Алгоритм решения
в,с=0
ах 2 =0
1. Делим обе части уравнения на а≠0.
х 2 = 0
2. Одно решение: х = 0.
Подведём итог!
 0, то " width="640"
0, то " width="640"
Неполные квадратные уравнения:
Если корней нет.
Если 0, то
 0 Корней нет " width="640"
0 Корней нет " width="640"
D 0
D = 0
D 0
Корней нет

b = 2k ( чётное число)

Теорема Виета
x 1 и х 2 – корни уравнения
x 1 и х 2 – корни уравнения

Метод выделения квадрата двучлена.
Суть метода: привести квадратное уравнение общего вида к неполному квадратному уравнению.
Пример: х 2 - 6х + 5 = 0.
подробнее

Метод «переброски» старшего коэффициента.
Корни квадратных уравнений
и
связаны соотношениями
и
подробнее
Пример:
2х 2 - 9х – 5 = 0.

На основании теорем:
Если в квадратном уравнении a+b+c=0 , то один из корней равен 1, а
второй по теореме Виета равен
Если в квадратном уравнении a+c=b , то один из корней равен -1,
а второй по теореме Виета равен
подробнее
Примеры:
200х 2 + 210х + 10 = 0.

Метод разложения на множители
Цель:
привести квадратное уравнение общего вида к виду
А(х) · В(х)=0,
где А(х) и В(х) – многочлены относительно х.
Способы:
- Вынесение общего множителя за скобки;
- Использование формул сокращенного умножения;
- Способ группировки.
подробнее
Пример:
4х 2 + 5х + 1 = 0.

Введение новой переменной.
Удачный выбор новой переменной делает структуру уравнения более прозрачной.
подробнее
Пример:
(2х+3) 2 = 3(2х+3) – 2.

Графический метод
Для решения уравнения f(x) = g(x) необходимо построить графики функций
y = f(x), y = g(x)
и найти точки их пересечения;
абсциссы точек пересечения и будут корнями уравнения.
подробнее
Пример:
х 2 =х+2.
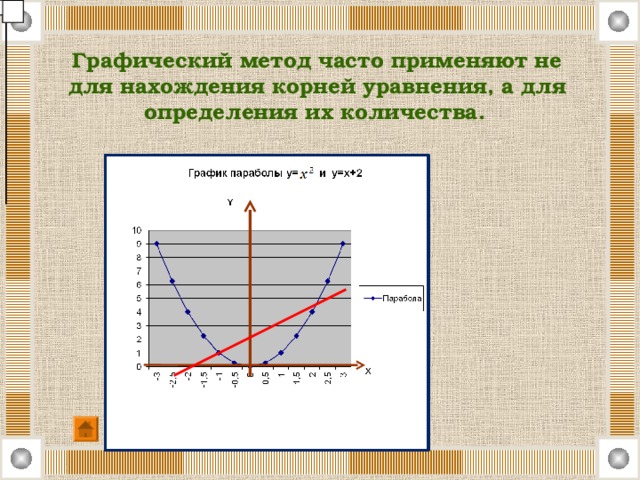
Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Метод выделения квадрата двучлена.
Решим уравнение х 2 - 6х + 5 = 0.
х 2 - 6х + 5 = 0.
(х -3) 2 – 4 = 0.
(х -3) 2 = 4.
х – 3 = 2 ; х – 3 = -2.
х = 5, х =1.
Ответ: 5; 1.
(a + b) 2 = a 2 + 2ab + b 2 ,
(a - b) 2 = a 2 - 2ab + b 2 .
 0, по теореме, обратной теореме Виета, получаем корни: -1; 10, далее возвращаемся к корням исходного уравнения: - 0,5; 5. Ответ : 5; -0,5. ax 2 + bx + c = 0 и y 2 + by + ac = 0 связаны соотношениями: " width="640"
0, по теореме, обратной теореме Виета, получаем корни: -1; 10, далее возвращаемся к корням исходного уравнения: - 0,5; 5. Ответ : 5; -0,5. ax 2 + bx + c = 0 и y 2 + by + ac = 0 связаны соотношениями: " width="640"
Метод “переброски” старшего коэффициента
Решите уравнение 2х 2 - 9х – 5 = 0.
у 2 - 9у - 10 = 0.
D0, по теореме, обратной теореме Виета, получаем корни: -1; 10,
далее возвращаемся к корням исходного уравнения: - 0,5; 5.
Ответ : 5; -0,5.
ax 2 + bx + c = 0 и y 2 + by + ac = 0
связаны соотношениями:
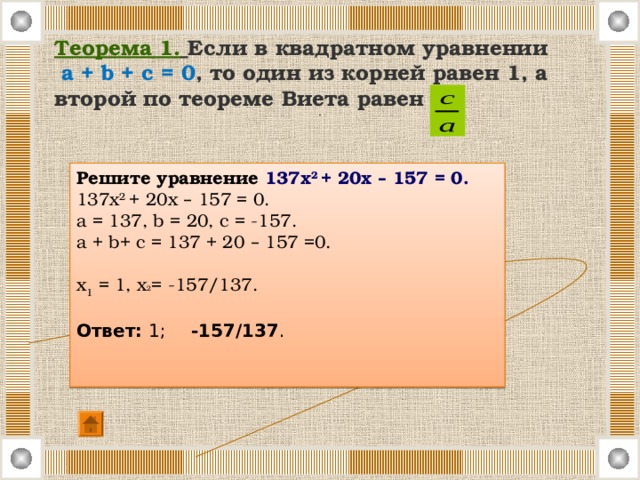
Теорема 1. Если в квадратном уравнении a + b + c = 0 , то один из корней равен 1, а второй по теореме Виета равен
.
Решите уравнение 137х 2 + 20х – 157 = 0.
137 х 2 + 20 х – 157 = 0.
a = 137, b = 20, c = -157.
a + b+ c = 137 + 20 – 157 =0.
x 1 = 1, х 2 = -157/137.
Ответ: 1; -157/137 .
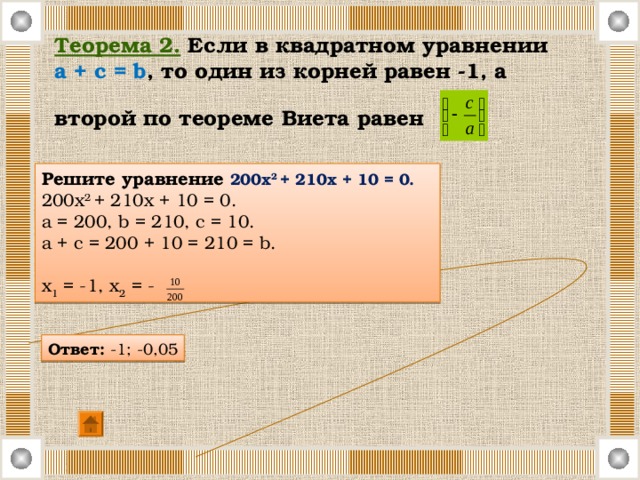
Теорема 2. Если в квадратном уравнении a + c = b , то один из корней равен -1, а второй по теореме Виета равен
Решите уравнение 200х 2 + 210х + 10 = 0.
200х 2 + 210х + 10 = 0.
a = 200, b = 210, c = 10.
a + c = 200 + 10 = 210 = b.
х 1 = -1, х 2 = -
Ответ: -1; -0,05

Метод разложения на множители.
Решите уравнение 4х 2 + 5х + 1 = 0.
4х 2 + 5х + 1 = 0.
4х 2 + 4х + х + 1 = 0.
4х(х+1) + (х+1) = 0.
4х(х + 1) = 0.
Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю.
4х = 0 и х + 1 = 0.
х = 0, х = -1.
Ответ: 0; -1.
 0. По теореме, обратной теореме Виета: t 1 = 1, t 2 = 2. Произведем обратную замену и вернемся к переменной х, получим следующие корни: -1; -0,5. Ответ: -1; -0,5. " width="640"
0. По теореме, обратной теореме Виета: t 1 = 1, t 2 = 2. Произведем обратную замену и вернемся к переменной х, получим следующие корни: -1; -0,5. Ответ: -1; -0,5. " width="640"
Метод введения новой переменной.
Решите уравнение (2х+3) 2 = 3(2х+3) – 2.
(2х+3) 2 = 3(2х+3) – 2.
Пусть: t = 2х + 3.
Произведем замену переменной: t 2 = 3 t - 2.
t 2 -3 t + 2 = 0. D 0.
По теореме, обратной теореме Виета: t 1 = 1, t 2 = 2.
Произведем обратную замену и вернемся к переменной х, получим следующие корни:
-1; -0,5.
Ответ: -1; -0,5.

1. в,с=0
4. b - нечётное
ах 2 =0
ах 2 + bx +с=0
№ уравнения
1
100x 2 + 53x – 153 = 0
2
№ метода
20 x 2 - 6x = 0
3
299x 2 + 300x + 1 = 0
4
3x 2 - 5x + 4 = 0
5
7x 2 + 8x + 2 = 0
6
35x 2 – 8 = 0
7
8
4x 2 – 4x + 3 = 0
(x – 8) 2 – (3x + 1) 2 = 0
9
4(x – 1) 2 + 0,5(x – 1) – 1 = 0
10
12x 2 = 0
2. с=0
ах 2 +вх=0
5. b - чётное
ах 2 + bx +с=0
3. в=0
ах 2 +с=0
6. Теорема Виета.
7. Метод выделения квадрата двучлена.
8. Метод «переброски» старшего коэффициента.
9. Т1 или Т2.
10. Метод разложения на множители.
11. Метод введения новой переменной.
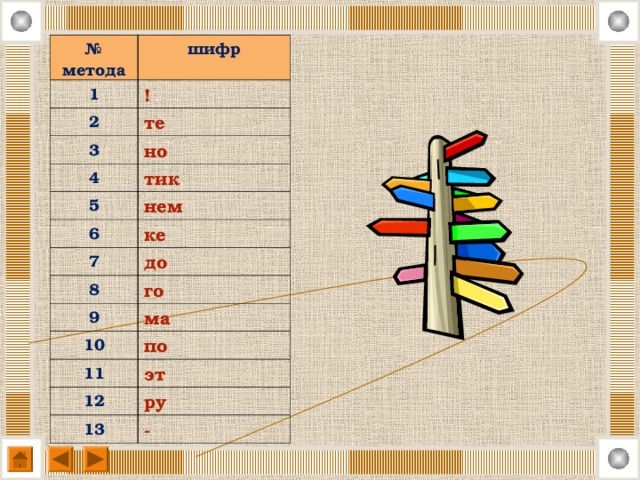
№ метода
шифр
1
!
2
те
3
но
4
тик
5
6
нем
ке
7
до
8
го
9
ма
10
11
по
эт
12
ру
13
-

№
уравнения
№
уравнения
Слог
Слог
1
1
2
2
ма
3
3
те
4
4
ма
тик
5
5
нем
6
6
7
но
7
го
8
8
по
9
9
10
эт
10
!
http://dic.academic.ru/dic.nsf/bse/158739/%D0%92%D0%B5%D0%B9%D0%B5%D1%80%D1%88%D1%82%D1%80%D0%B0%D1%81%D1%81
Математик немного поэт. Т. Вейерштрасс



















 0 -два решения: х 1 = и х 2 = - Если 0 - нет решений. " width="640"
0 -два решения: х 1 = и х 2 = - Если 0 - нет решений. " width="640"


 0, то " width="640"
0, то " width="640"
 0 Корней нет " width="640"
0 Корней нет " width="640"










 0, по теореме, обратной теореме Виета, получаем корни: -1; 10, далее возвращаемся к корням исходного уравнения: - 0,5; 5. Ответ : 5; -0,5. ax 2 + bx + c = 0 и y 2 + by + ac = 0 связаны соотношениями: " width="640"
0, по теореме, обратной теореме Виета, получаем корни: -1; 10, далее возвращаемся к корням исходного уравнения: - 0,5; 5. Ответ : 5; -0,5. ax 2 + bx + c = 0 и y 2 + by + ac = 0 связаны соотношениями: " width="640"



 0. По теореме, обратной теореме Виета: t 1 = 1, t 2 = 2. Произведем обратную замену и вернемся к переменной х, получим следующие корни: -1; -0,5. Ответ: -1; -0,5. " width="640"
0. По теореме, обратной теореме Виета: t 1 = 1, t 2 = 2. Произведем обратную замену и вернемся к переменной х, получим следующие корни: -1; -0,5. Ответ: -1; -0,5. " width="640"













