Квадратные уравнения с параметром.

Презентация на тему:

«Уравнения второй степени с параметром»

Выполнили ученицы 9 В класса:

Возиянова Светлана

Галиева Анастасия

Цели:

• Определение количества корней квадратного уравнения в зависимости от параметра;
• Решение уравнений с параметром.

Квадратное уравнение

Уравнение вида ах²+bx+с=0, где а, b, с Є R, а ≠ 0 называется квадратным уравнением. D=b²-4ac – дискриминант квадратного уравнения.

Если D0, то уравнение имеет два различных корня:

Если D=0, то уравнение имеет один корень.

Алгоритм решения квадратных уравнений с параметром

1)Если в квадратном уравнении главный коэффициент содержит параметр, то обязательно нужно выяснить, при каких значениях параметра главный коэффициент равен нулю. В этом случае квадратное уравнение превращается в линейное, которое имеет один корень.

2) Если в квадратном уравнении главный коэффициент не содержит параметра, то количество корней зависит только от значения дискриминанта.

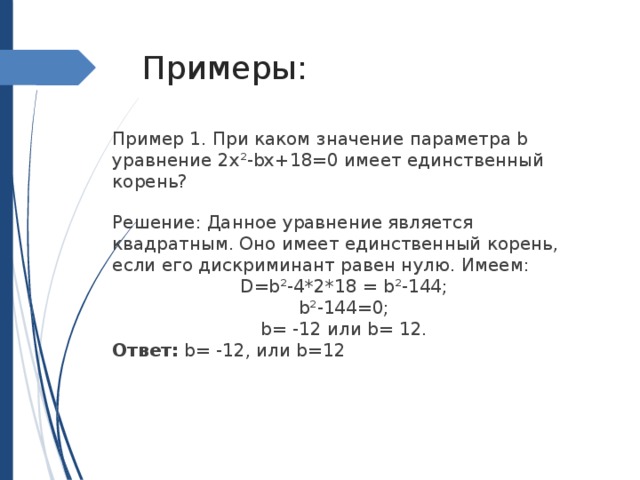
Примеры:

Пример 1. При каком значение параметра b уравнение 2х²-bx+18=0 имеет единственный корень?

Решение: Данное уравнение является квадратным. Оно имеет единственный корень, если его дискриминант равен нулю. Имеем:

D=b²-4*2*18 = b²-144;

b²-144=0;

b= -12 или b= 12.

Ответ: b= -12, или b=12

Пример 2. При каком значение параметра b уравнение (b+6)x²-(b-2)x+1=0 имеет единственный корень?

Решение: Считать такое уравнение квадратным является ошибкой. Это уравнение степени не выше второй.

При b= -6 получаем линейное уравнение 8x+1=0, имеющее один корень.

При b ≠ -6 данное уравнение является квадратным; оно имеет единственный корень, если его дискриминант равен нулю:

D=(b-2)²-4(b+6) = b²-4b+4-4b-24 = b²-8b-20

Имеем: b²-8b-20=0, отсюда b= -2 или b=10.

Ответ: b= -2, или b=10, или b= -6

0. Отсюда а-1/3. Однако промежуток (-1/3;+∞) содержит значение а=0, при котором исходное уравнение имеет единственный корень, что не удовлетворяет условию задачи.  Ответ: а= -3, или -1/30 " width="640"

Пример 3. При каких значениях параметра а уравнение a(a+3)х²+(2a+6)x-3a-9=0 имеет больше одного корня?

Решение: При а=0 получаем линейное уравнение 6х-9=0, имеющее единственный корень. 

При а=-3 получаем линейное уравнение 0х=0, имеющее бесконечно много корней. 

Если а≠0 и а≠ -3, то, разделив обе части уравнения на а+3, получим квадратное уравнение ах²+2х-3=0. Дискриминант этого уравнения равен 4(1+3а). Для выполнения условия задачи он должен быть положительным, т.е. 4(1+3а)0. Отсюда а-1/3. Однако промежуток (-1/3;+∞) содержит значение а=0, при котором исходное уравнение имеет единственный корень, что не удовлетворяет условию задачи. 

Ответ: а= -3, или -1/30

Пример 4. Решить уравнение (a²-b²)х²-2ax+1=0.

Решение: Рассмотрим три случая:

1) a=b=0. Уравнение 0x+1=0 решений не имеет.

2) a²=b²≠0. Уравнение -2ax+1=0 имеет один корень x=1/2a.

3) a²-b²≠0. Корни уравнения: x1= 1/a-b, x2= 1/a+b.

При b=0 D=b²=0, поэтому уравнение имеет один корень x=1/a (a ≠0).

Ответ: x=1/2a при a²=b²≠0; x=1/a при a ≠0, b=0; ∅ при a=0, b=0; x1= 1/a-b, x2= 1/a+b при a ² ≠ b ², b ≠0

Пример 5. Решить уравнение (4a/x²-a²)+ (x-a/x(x+a))=(1/x(x-a))

Решение: При x≠0, x≠a, x≠-a уравнение приведём к равносильному 4ax+x²-2ax+a²-x-a=0.

(x+a)²-(x+a)=0

(x+a)(x+a-1)=0

Так как x≠-a, то уравнение имеет одно решение x=1-a. Условия x≠0, x≠a влекут за собой требования a≠1, a≠1/2. Уравнение 1-a=-a решений не имеет.

Ответ: x=1-a при a≠1/2; a≠1; ∅ при a=1/2, a=1

Пример 6. При каких значениях a уравнение aх²-x+3=0 имеет единственное решение? 

Решение: Ошибочно считать данное уравнение квадратным. На самом деле это уравнение степени не выше второй. Исходя из этого соображения, рассмотрим следующие случаи: 

1)a=0. При этом уравнение принимает вид -x+3=0, откуда x=3, т.е. решение единственно. 

2) a≠0, тогда aх²-x+3=0 – квадратное уравнение, дискриминант D=1-12a. Для того, чтобы уравнение имело единственное решение, нужно, чтобы D=0, откуда a=1/12. 

Ответ: a=0 или a=1/12

Пример 7. Один из корней квадратного уравнения х²+2ах+2-3а=0 равен 1. Найдите значение параметра а и второй корень уравнения.

Решение: х1=1 подставим его в уравнение и получим верное равенство: 1²+2а*1+2-3а=0 или 3-а=0, откуда а=3. Подставим это значение параметра а в данное уравнение: х²+2*3*х²+2-3*3=0 или х²+6х-7=0.

Решим это квадратное уравнение: х1=1 и х2= -7.

Получили а=3 и х2= -7

Ответ: а=3; х2= -7

Пример 8. При каких значениях параметра а сумма квадратов корней уравнения x²+ax+a=0 равна 3?

Решение: Пусть x1 и x2 – корни данного уравнения. По условию x1² + x2²=3, т.е. (x1+x2)²-2x1x2 = 3. Применяя теорему Виета, можно записать (-a)²-2a=3; a²-2a-3=0. Отсюда a=-1 или a=3.

Казалось бы, решение завершено. Однако теорема Виета «работает» лишь для тех квадратных уравнений, у которых есть корни. А данное квадратное уравнение имеет корни не при всех значениях параметра a. Существование корней определяется условием D ≥0. Для данного уравнения D=a ²-4a. Следовательно, найденные значения a= -1 и a=3 должны удовлетворять неравенству a²-4a≥0. Легко установить, что подходит только a= -1.

Ответ: а= -1

Пример 9. При каких значениях параметра а уравнение (a+6)х²+2ax+1=0 имеет единственное решение?

Решение: По условию задачи уравнение необязательно является квадратным, поэтому рассмотрим два случая: 

1) а+6=0; а=-6 

Если а = -6, то -12х+1=0, х = 1/12. 

2) Если а ≠ -6, то квадратное уравнение имеет единственное решение, если D =0 D=4a²-4(a+6)=4(a²-a-6) a²-a-6=0 a1=3, a2=-2.

Ответ: при a ∈ {-6, -2, 3}

0. Из неравенства (2a+3)²-4(a²-a+5)0 следует, что 16a-110, откуда a11/16. Наименьшее целое значение a ∈ (11/16; +∞) равно 1. Ответ: a=1. " width="640"

Пример 10. Найти наименьшее целое a, при котором уравнение x²+(2a+3)x+a²-a+5=0 имеет два различных корня.

Решение: Уравнение имеет два различных корня, если D0. Из неравенства (2a+3)²-4(a²-a+5)0 следует, что 16a-110, откуда a11/16. Наименьшее целое значение a ∈ (11/16; +∞) равно 1.

Ответ: a=1.

Источники:

• 1) Алгебра. Углублённый уровень. 8 класс (Мерзляк А. Г., Поляков В. М.) 
• 2) Локоть В.В. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы