Лабораторная работа № 4 «Изображения пространственных фигур. Параллельное проектирование
Цель работы: научится изображать пространственные фигуры на плоскости с помощью параллельного проектирования, используя свойства параллельного проектирования
Теоретические сведения к лабораторной работе:
Параллельное проектирование
П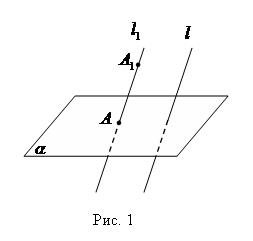 усть даны плоскость α и прямая l, пересекающая плоскость а. Возьмем произвольную точку пространства A1 и проведем через эту точку прямую l1, параллельную l. Прямая l1 пересечет плоскость α в некоторой точке A. Полученная таким образом точка A называется проекцией точки A на плоскость α при проектировании параллельно прямой l. Обычно кратко говорят, что точка A есть параллельная проекция точки A1.
усть даны плоскость α и прямая l, пересекающая плоскость а. Возьмем произвольную точку пространства A1 и проведем через эту точку прямую l1, параллельную l. Прямая l1 пересечет плоскость α в некоторой точке A. Полученная таким образом точка A называется проекцией точки A на плоскость α при проектировании параллельно прямой l. Обычно кратко говорят, что точка A есть параллельная проекция точки A1.
Параллельной проекцией пространственной фигуры Φ1 называется множество Φ параллельных проекций всех точек данной фигуры.
Свойства параллельного проектирования
1) Проекция прямой есть прямая.
2) Проекции параллельных прямых параллельны.
3) Отношение проекций двух параллельных отрезков равно отношению проектируемых отрезков.
Ортогональное проектирование
Ч астным случаем параллельного проектирования является ортогональное проектирование
астным случаем параллельного проектирования является ортогональное проектирование
Пусть даны плоскость α и прямая l, перпендикулярная α. Возьмем произвольную точку пространства A1 и проведем через нее прямую l1 параллельную l (и, следовательно, перпендикулярную плоскости α). Прямая l1 пересечет плоскость α в некоторой точке A.
Полученная точка A называется ортогональной проекцией точки A1 на плоскость α.
Ортогональной проекцией фигурыΦ1 на плоскость α называется множество Φ ортогональных проекций всех точек данной фигуры Φ1. Как частный случай параллельного проектирования, ортогональное проектирование обладает всеми свойствами параллельного проектирования.
Свойство ортогональной проекции плоского многоугольника
Площадь s ортогональной проекции плоского многоугольника на плоскость α равна площади S проектируемого многоугольника, умноженной на косинус угла γ между плоскостью многоугольника и плоскостью α:
s=S·cos(γ).
Пример1.Через сторону основания правильной треугольной призмы проведена плоскость под углом γ=300 к плоскости ее основания. Найти площадь образующегося сечения, если сторона основания равна 6 см.
Решение:
т.к. призма правильная, то ее боковые ребра перпендикулярны плоскости основания. Следовательно, плоскость основания есть проекция плоскости сечения.
Т.к. в основании правильный треугольник, то его площадь равна: 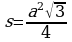 .
.
Используя свойство ортогональной проекции, имеем: 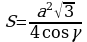 .
.
Зная, что сторона основания равна 6 см и угол γ=300, вычислим площадь:
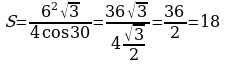 .
.
Изображение пространственных фигур на плоскости
Д 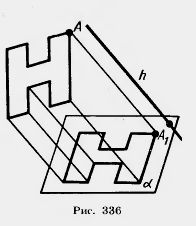 ля изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием.
ля изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием.
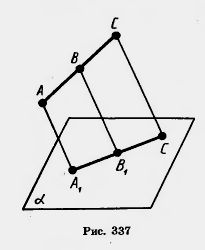
Прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками.
Действительно, все прямые, проектирующие точки отрезка АС, лежат в одной плоскости, пересекающей плоскость а по прямой А1С1. Произвольная точка В отрезка АС изображается точкой В1отрезка А1С1.
Отношение отрезков одной прямой или параллельных прямых сохраняется при параллельном проектировании:
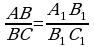 .
.
Пример 2.Дана параллельная проекция треугольника. Как построить проекции медиан этого треугольника?
Решение:
при параллельном проектировании сохраняется отношение отрезков прямой. Поэтому середина стороны треугольника проектируется в середину проекции этой стороны. Следовательно, проекции медиан треугольника будут медианами его проекции.
Задания для самостоятельного решения:
1) Каковы проекции двух прямых на плоскость, если: а) прямые пересекаются; б) прямые скрещиваются; в) прямые параллельны.
2) На модели куба ABCDA1B1C1D1 укажите проекции на плоскость грани АА1В1В отрезков C1D1, AD, C1D и DB1, треугольников C1CD и ACD, квадрата BВ1С1C.
3) Стороны треугольника равны 3,9 см, 4,1 см и 2,8 см. Найдите площадь его проекции на плоскость, составляющую с плоскостью треугольника угол 600.
4) Построить изображение правильного треугольника ABC , изображение высоты BH и биссектрисы АK.
5) Начертите параллельную проекцию ромба АBCD, имеющего угол A=600. Постройте изображение высоты этого ромба, проведенной из вершины острого угла.
Контрольные вопросы:
1. Что называется параллельной проекцией?
2. Перечислите свойства параллельного проектирования.
3. Что называется ортогональной проекцией фигуры?
4. Что является параллельной проекцией отрезка, треугольника, прямоугольника, квадрата, окружности?
5. Какие величины не изменяются при параллельном проецировании? (длина отрезка, градусная мера углов, отношения длин отрезков, отношение площадей двух фигур)?
6. Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?







 усть даны плоскость α и прямая l, пересекающая плоскость а. Возьмем произвольную точку пространства A1 и проведем через эту точку прямую l1, параллельную l. Прямая l1 пересечет плоскость α в некоторой точке A. Полученная таким образом точка A называется проекцией точки A на плоскость α при проектировании параллельно прямой l. Обычно кратко говорят, что точка A есть параллельная проекция точки A1.
усть даны плоскость α и прямая l, пересекающая плоскость а. Возьмем произвольную точку пространства A1 и проведем через эту точку прямую l1, параллельную l. Прямая l1 пересечет плоскость α в некоторой точке A. Полученная таким образом точка A называется проекцией точки A на плоскость α при проектировании параллельно прямой l. Обычно кратко говорят, что точка A есть параллельная проекция точки A1. астным случаем параллельного проектирования является ортогональное проектирование
астным случаем параллельного проектирования является ортогональное проектирование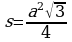 .
.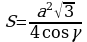 .
.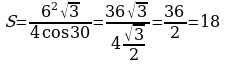 .
. ля изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием.
ля изображения пространственных фигур на плоскости обычно пользуются параллельным проектированием. 
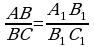 .
.

















