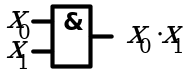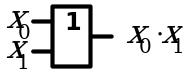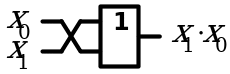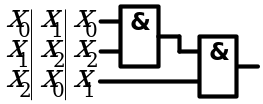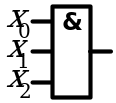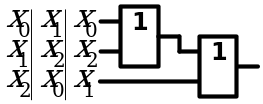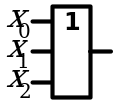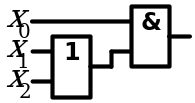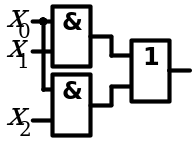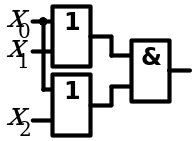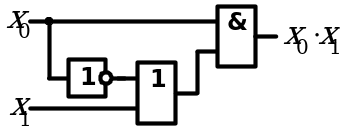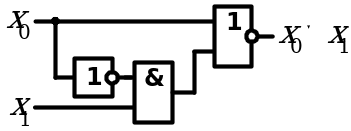Лабораторное занятие 19-20
КОМБИНАЦИОННЫЕ УЗЛЫ НА ОСНОВЕ БАЗОВЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ ДЛЯ ЭКСПЕРИМЕНТАЛЬНОГО ПОДТВЕРЖДЕНИЯ ЗАКОНОВ АЛГЕБРЫ ЛОГИКИ
Логические схемы
Целью эксперимента является составление и тестирование комбинационных узлов на основе базовых логических элементов, реализующих заданные логические функции законов алгебры логики.
Поскольку законы имеют вид равенств, в ходе эксперимента, отдельно собирают узлы, реализующие логические функции левой и правой частей равенства. Экспериментально заполняют таблицы истинности логических функций левой и правой части равенства. Сравнивая эти таблицы, убеждаются в справедливости равенства.
1. Переместительный закон
|
| Аналитическое выражение | Логическая схема |
| Левая часть равенства | Правая часть равенства |
| Конъюнкция | 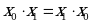
| 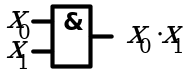
| 
|
| Дизъюнкция | 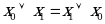
| 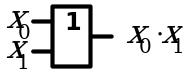
| 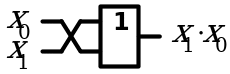
|
2. Сочетательный закон
|
| Аналитическое выражение | Логическая схема |
| Левая часть равенства | Правая часть равенства |
| Конъюнкция | 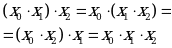
| 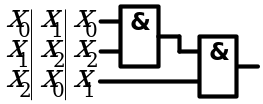
| 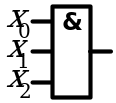
|
| Дизъюнкция | 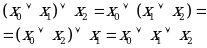
| 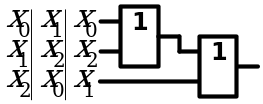
| 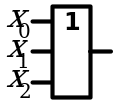
|
3. Распределительный закон
|
| Аналитическое выражение | Логическая схема |
| Левая часть равенства | Правая часть равенства |
| Конъюнкция | 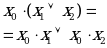
| 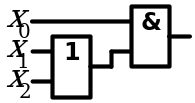
| 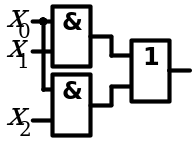
|
| Дизъюнкция | 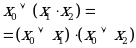
| 
| 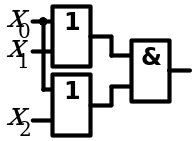
|
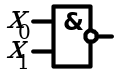
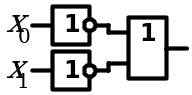
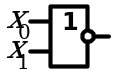
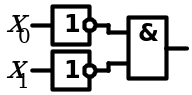
4. Закон инверсии (закон де Моргана)
|
| Аналитическое выражение | Логическая схема |
| Левая часть равенства | Правая часть равенства |
| Конъюнкция | 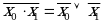
| 
| 
|
| Дизъюнкция | 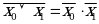
| 
| 
|
5. Закон повторения
|
| Аналитическое выражение | Логическая схема |
| Конъюнкция | 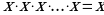 | 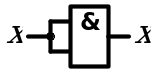 |
| Дизъюнкция | 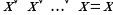 | 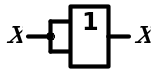 |
6. Закон двойного отрицания
| Аналитическое выражение | Логическая схема |
| 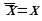 | 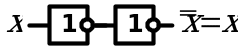 |
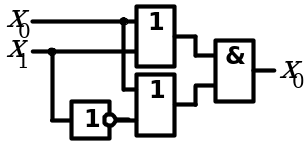
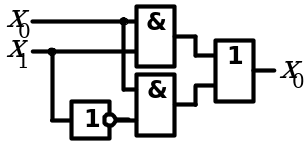
7. Закон склеивания
|
| Аналитическое выражение | Логическая схема |
| Конъюнкция | 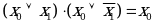
| 
|
| Дизъюнкция | 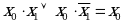
| 
|
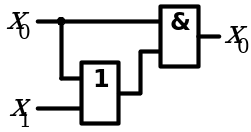
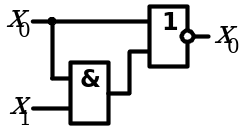
8. Законы поглощения
| Аналитическое выражение | Логическая схема |
| Левая часть равенства | Правая часть равенства |
| 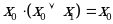
| 
|
| 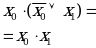
| 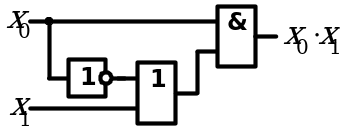
| 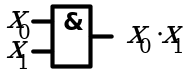
|
| 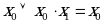
| 
|
| 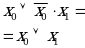
| 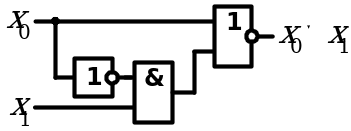
| 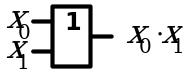
|
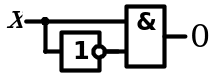
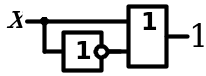
9. Соотношения с 0 и 1
|
| Аналитическое выражение | Логическая схема |
| Конъюнкция | 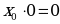
| 
|
| 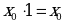
| 
|
| 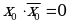
| 
|
| Дизъюнкция | 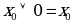
| 
|
| 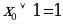
| 
|
| 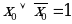
| 
|
Практическая часть:
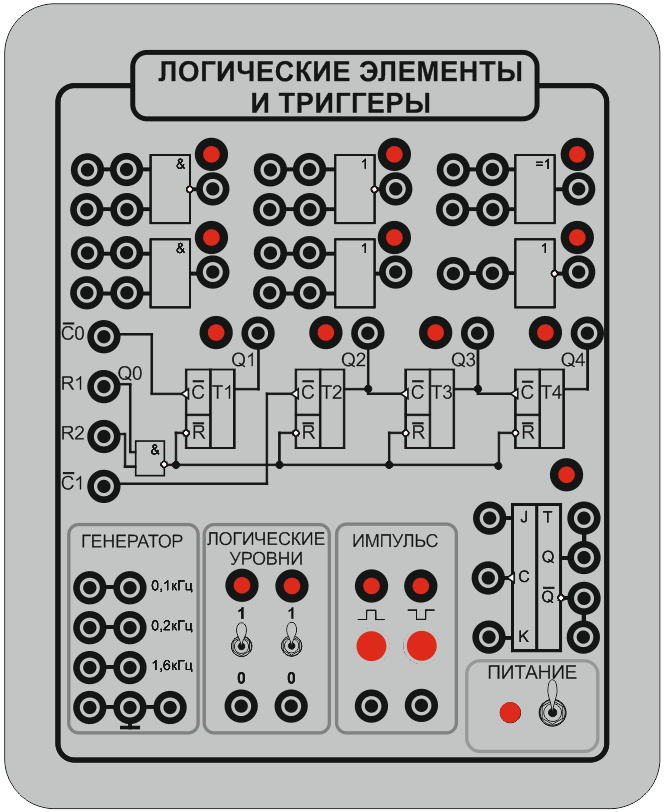
Убедитесь, что устройства, используемые в эксперименте, отключены от сети электропитания.
Соберите исследуемую логическую цепь на модуле.
Включите выключатель «СЕТЬ» блока испытания цифровых устройств А1.
Протестируйте работу логической схемы. При необходимости изменения исследуемой схемы отключите выключатель «Питание» блока испытания цифровых устройств «Логические элементы и триггеры», измените схему, включите выключатель «Питание».
По результатам тестирования заполните таблицу истинности для заданной логической функции.
По результатам тестирования заполните таблицы истинности для схем, реализующих левую и правую части проверяемого равенства.
Таблица истинности для логической функции двух переменных:
Таблица истинности для логической функции трёх переменных:
| 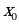
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 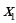
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 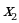
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 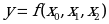
|
|
|
|
|
|
|
|
|
Таблица истинности для логической функции четырёх переменных:
| 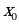
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 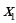
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 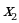
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 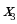
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 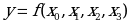
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравните таблицы истинности для левой и правой частей равенства и убедитесь в выполнении законов алгебры логики.
По завершении работы отключите выключатель «СЕТЬ» блока программируемого реле А1 и автоматический выключатель в однофазном источнике питания G1.
Контрольные вопросы:
Какие существуют виды логики?
Что такое комбинационные схемы?
Укажите разные способы записи логических уравнений.
По каким этапам происходит синтез комбинационных схем.
Перечислите основные законы преобразования логических уравнений.
Существует ли задержка в комбинационных схемах? Как влияет её наличиена работу схемы.
Типовые примеры проектных решений
1.2.1. Подобрать логический элемент для реализации функции включения лампы, соответствующей электрической схемы на рис. 1.8
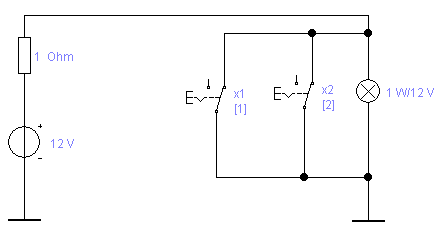
Рис. 1.8 Электрическая схема включения лампы, управляемая двумя выключателями.
Составим таблицу горения лампы (табл. 1.8) от комбинации состояния выключателей.
За разомкнутое состояние переключателя примем значение xi = 0, за замкнутое xi =1. Лампа будет загораться только при двух одновременно разомкнутых переключателях. Обозначим переменной Y = 0 состояние, когда лампочка не горит, а Y =1 состояние горящей лапочки.
Таблица 1.8
Таблица включения лампочки.
| x1 | x2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Данная таблица совпадает с булевой функцией «стрелка Пирса» и может быть реализована логическим элементом «И-НЕ».
Схема включения индикаторного светодиода (эквивалента лампочки) может быть смоделирована эквивалентной рисунку 1.8 моделируемой схемы в пакете Electronics Workbench в следующем виде рис. 1.9
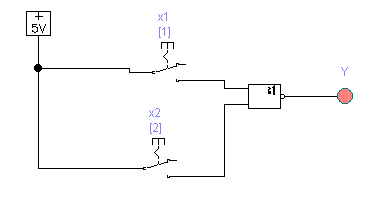
Рис. 1.9. Эквивалентная схема включения светодиода, совпадающая с логикой включения лампочки в схеме на рис. 1.8
1.3. Контрольные вопросы.
Вопросы категории 1. «Помнить».
1.3.1 Запишите выражение функции конъюнкции и приведите её таблицу истинности для трёх переменных.
1.3.2 Запишите выражение функции дизъюнкции и приведите её таблицу истинности для трёх переменных.
Вопросы категории 2. «Понимать».
1.3.3 На рис. 1.10. представлена диаграмма подачи входных сигналов x x 1 2 , на неизвестный логический элемент и диаграмма поведения выходного сигнала. Какую логическую функцию воспроизводит данный логический элемент?
Рис. 1.10 Диаграмма подачи входных сигналов на неизвестный логический элемент.
Вопросы категории 3. «Применять».
1.3.4 Постройте таблицу истинности для логического элемента ИЛИ с тремя входами. Выходной сигнал обозначим символом Y , входные сигналы соответственно x x x 1 2 3 , , .
Ответы на контрольные вопросы.
1.3.1 Таблица истинности для трёх переменных примет вид:
Таблица 1.9.
Таблица истинности для логического элемента «И» с тремя входами.
| x1 | x2 | x3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
22
1.3.3 Для решения вопроса целесообразно результаты в графическом варианте представить в виде таблицы истинности табл. 1.10.
Таблица 1.10
Таблица истинности поведения неизвестного логического элемента.
| x1 | x2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Таблица истинности 1.10. соответствует логическому элементу «ИЛИ-НЕ».
1.3.4 Таблица истинности для трёх переменных примет вид:
Таблица 1.11
Таблица истинности для логического элемента «ИЛИ» с тремя входами.
| x1 | x2 | x3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
1.4. Задачи для самостоятельного решения.
1.4.1 Записать таблицу истинности для электрической схемы рис. 1.11
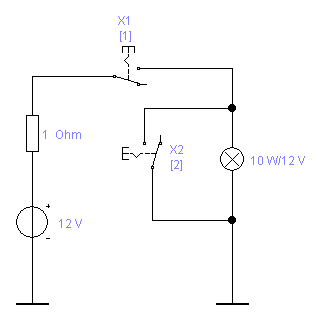
Рис. 1.11 Электрическая схема с двумя ключами.
Собрать комбинационную схему, функционирующую по полученной таблице истинности.
Решение:
Замкнутое состояние ключа X1 приведёт к протеканию тока через лампочку, если ключ X2 разомкнут. При замыкании ключа X2 лампочка окажется замкнутой накоротко и гореть не будет. При отключении ключа X1 лампочка гореть не будет и при замкнутом и при разомкнутом состоянии ключа X2. Таблица истинности получается следующей (табл.1.12).
Таблица 1.12
Таблица истинности для схемы на рис.1.11.
| x1 | x2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Горение лампочки обозначим Y =1, не горящая лампочка соответствует функции Y = 0. Таблица истинности для схемы на рис.1.11.
| x1 | x2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Горение лампочки обозначим Y =1, не горящая лампочка соответствует функции Y = 0.
По таблице истинности записывается выражение для функции Y (горение лампочки)

Этой функции соответствует следующая комбинационная схема,
реализующая булеву функцию «запрет по x2 » (рис. 1.12.)
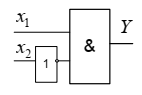
Рис. 1.12. Комбинационная схема, реализующая функцию «запрет по x2 »
1.4.2. Сформируйте электрическую схему, подобную рис. 1.11,
функционирование которой соответствует булевой функции «стрелка Пирса» («ИЛИ-НЕ»).
Решение.
Функции «стрелка Пирса» («ИЛИ-НЕ») соответствует следующая таблица истинности табл. 1.13
Таблица. 1.13
Таблица истинности функции для задания 1.4.2.
| x1 | x2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
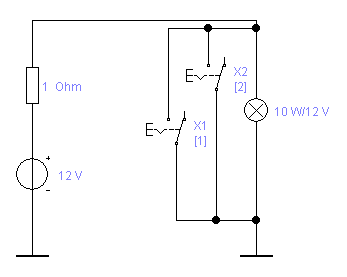
Рис. 1.13 Электрическая схема, соответствующая таблице истинности табл.1.13
Горение лампочки возможно только в случае двух разомкнутых ключей. Во всех остальных комбинациях хотя бы один ключ замыкает накоротко лампочку. 1.4.3. Сформируйте электрическую схему, подобную рис.1.11,
функционирование которой соответствует булевой функции «штрих
Шеффера» («И-НЕ»).
Решение:
Функции «штрих Шеффера» («И-НЕ») соответствует следующая таблица истинности табл. 1.13
Таблица. 1.14.
Таблица истинности функции «штрих Шеффера» («И-НЕ»).
| x1 | x2 | Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
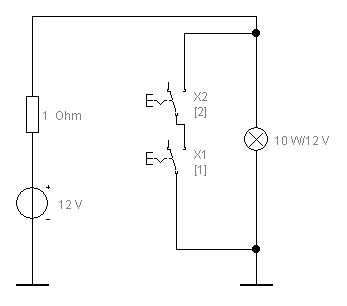
Рис. 1.14. Электрическая схема, соответствующая таблице истинности табл. 1.14.
Горение лампочки возможно только в случае двух разомкнутых ключей, либо одного из двух. Два одновременно замкнутых ключа замыкают одной цепью лампочку накоротко, лампочка не горит