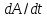Лагранжево и эйлерово описание сплошной срелы

Сплошная среда. Описание

Сплошная среда– модель вещества, в которой распределение массы, сил, импульса, энергии(и их потоков) и всех параметров(плотностей, скоростей, перемещений, температур, давлений, напряжений и т.д.), определяет состояние и движение этого вещества, определяет непрерывно дифференцируемыми функциями по пространственным координатам и времени, заданных во всех точках рассматриваемого объема и во все моменты времени из рассматриваемого интервала за исключением отдельных поверхностей, линий или точек.

под материальной точкой в механике сплошной среды понимается частица среды (вещества) вокруг нее(точки) как центра масс, частица с характерным размером порядка δr, объемом δV=O((δr)3), массой ρδV. Причем ее размер с одной стороны очень мал по сравнению с харак-терным размером исследуемого процесса или тела (δr lat), т.е. указанная частица содержит огромное число молекул

Лагранжево и эйлерово описания сплошной среды

описать сплошную среду —значит задать ее числовые характеристики. Это м сделать, по кр мере,2 способами: привязывать х-ку к частице в данный мом времени и привяз х-ку к т пр-ва, в кот в данный момент нах частица. Эти 2 способа наз, соотв, лагранжевым и эйлеровым описанием спл среды. Таким обр, в лагранжевом подходе все х-ки задаются в переменных (x, t) О W₀ × R, а в эйлеровом — в переменных (x, t) О {W_t × {t}: t О R}. Соотв, координаты (x, t) называют лагранжевыми координатами (или переменными), а (x, t) — эйлеровыми.

Эти два описания, эквивалентны. Если известна некоторая характеристика F в лагранжевом описании, то м найти ее представление в эйлеровом, и наоборот. Например, если v^L(x, t) и v^E(x, t) — лагранжево и эйлерово представления скорости, то, очевидно, v^L(x, t) = v^E(g(x, t), t),), и, наоборот, v^E(x, t) = v^L(g ^{– 1}(x, t), t).

В качестве лагранжевых координат частицы 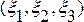 обычно используют пространственные координаты т  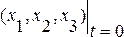, в кот эта частица находится в нач момент времени

скорость жидкости в разл точках простран­ства д б функцией 4 перем  х, у, z, t, назы­ваемых переменными Эйлера,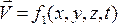, а ее дифференциал равняться

.

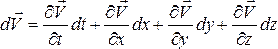Движение сплошной среды и происходящие процессы описываются полями физических величин (скорости 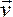 , давления  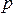, плотности  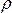, температуры  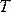и т.д.).

Лагранжев подход.Если эти величины рассматриваются как функции лагранж коорди-нат 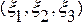 и времени  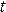, то описание называется лагранжевым  или  материальным. Т е, если  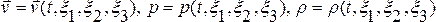и т. д., то это лагранж описание движения спл среды. При этом подходе события описываются как происходящие с индивидуальными частицами.

Основной кинематической характеристикой при лагранжевом описании является закон движения спл среды, т.е. зависимость пространственных координат от лагранжевых и времени: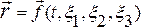 или в координатной записи  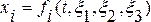, где  .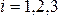

Тогда скорость и ускорение частиц сплошной среды опр соот: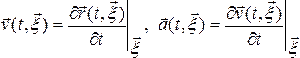 , где вектор  .

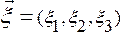скорость изменения нек величины  в индивидуальной частице сплошной среды (т. е. при фиксированных значениях лагранжевых координат) называется индивидуальной, или  матери-альной, или полной производной по времени от величины  и обозначается 

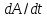
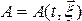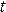
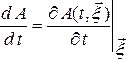При лагранжевом описании (т.е., когда  ) полная производная вел  по времени    по опред

В движущейся среде приращ dx, dy, dz не явл неза­висимыми, а соответственно равны

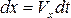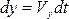, , .Поэтому справедливо равенство:

где – оператор Гамильтона (набла).Это озн, что полное ускорение индивиду жид­кой частицы, нах в момент времени t в т простр-­ва с коорди x, y, z, состоит из 2 частей: локального ускорения , обусловл изменением скорости по вре­мени в данной точке, и конвективного ускор , обусловл неоднородн поля скоростей в окрестности данной точки и связанного с этим обстоятельством конвективного переноса

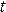Эйлеров подход.При эйлеровом описании (пространств описании) физ величина рассм как ф пространств к-т  и времени  . При этом подходе события описываются как происхо-дящие в точке пространства. Основной кинематич х=кой при эйлеровом описании является поле скорости  , где  . Вектор скор  - это скорость частицы спл среды, кот в мом 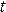  нах в т пр-ва с к=тами  .

переход от лагранжева описания к эйлеровому, н соотн, выр закон движения 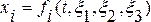 , где 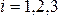 , разрешить относительно лагранжевых координат, т. е. найти функции   , где  . Тогда для любой величины  , лагранжево описание которой   изв, эйлерово описание находится как сложная функция   .

Переход от эйлерова опис к лагранжевому: ннайти реш системы обыкн дифф уравнений

 , где 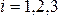 (0.1.0) с нач усл  .

Получ реш  ,  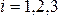и есть закон движ спл среды, а  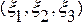- лагранжевы к-ты частиц. Тогда для любой вел  , эйлерово опис кот  изв, лагранж опис нах как сложная функция  .

Выч полной произв 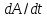  вел  по времени при эйлер опис ( т. е., когда   ):

исп:опр закона движения среды  ,  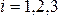,опре комп-т вектора скорости  тогда по опр полной производной имеем:

т. е.,  ,или в сокр записи   , где  - вектор градиента вел  , - вектор скорости среды.

Получ ф-ла для полной производной вел  при эйлеровом описании м так: скорость изм вел  в индивидуальной ч-це спл среды при эйлер опис= скорости изменения вел  в той точке эйлерова пр=ва, в кот в данный момент находится индивид частица ( слаг   ), плюс скорость изменения величины за счет переноса в данную т пространств изм вел  в рез макроскопического движения сплощной среды (слаг )

. Производная Лагранжа (конвективная производная), —опред изм парам данной функции в т {\displaystyle {\vec {r}}} в мом времени t при конвекции (движении среды с определённой скоростью  {\displaystyle {\vec {u}}({\vec {r}},t)} Явл одним из слаг производной Лагранжа (субстанциональной производной) и м б найд путём действия оператора {\displaystyle ({\vec {u}}\cdot \nabla )} на скалярную либо векторную функцию (тут {\displaystyle \nabla } — оператор набла).

это производная, взятая в з-ти от с-мы координат, движущейся со скоростью u и часто исп в гидроаэромеханике и классич механике. Она определена как от скалярной функции координат и времени, так и от векторной :

где — это оператор набла, а обозначает частную производную по t.

Верно следующее тождество, когда берётся производная Лагранжа от интеграла:

Док-во через п-ло диф сложных функций для частных произв. В тензорной нотации (с согл суммир Эйнштейна), можно записать:

На примере поля плотности ρ и поля скоростей  рассм некот общие характеристики полей.

Поле ρ = ρ(х_1; х₂, х₃), характеризующее данный процесс или движение, м б стационарным  dρ/dt=0 (установившим) или нестационарным dρ/dt≠0  (неустановивш). Одно и то же движение м б как установивш, так и неустановивш, все зависит от выбора системы к-т, относит кот изучается движение. Поэтому установившееся (стационарное) движение — понятие относительное.

Для любого векторного поля используют понятие векторных линий. 

Дано изменение температуры среды в эйлеровых координатах  ,

где Т₀ , k– конст; v – пост скорость; t – время.

Опр локальную производную по времени отв  ∂T/∂t= - kV

определить конвективную производную. .Отв: Vxk

Задачи Эйлерово и лагранжево описание движения спл среды

http://www.studfiles.ru/preview/3246102/

пр 0 Для нек момента времени закон движения сплошной среды задан уравн:

Опр поле перемещ в лагранжевых и эйлеровых к-тах Опр обратный закон движения 
. Перемещения ,   -радиусы-векторы текущего и начального положения. 

Пр 1. Дано эйлерово описание движения сплошной среды

Требуется найти его лагранжево описание.

Реш.Зададим материальные координаты так, что в начальный момент движения они были равны геометрическим т.е. при  . Учитывая определение скорости и начальные условия, имеем задачу Коши для системы уравнений

 , .Решим эту задачу.

Закон движения в лагранжевых переменных найден.Таким обр, чтобы перейти от эйлерова опи-сания к лагранжевому, надо составить систему  и решить ее с учетом начальных условий   . Убедимся что  и  – взаимнооднозн зав-ти, т.е. в любой момент времени в любой точке пространства находится только 1 материальная частица. Для этого надо вычислить якобиан и убедиться, что он никогда не обращается в нуль.

для любого момента времени.

След, за-ть  взаимнооднозначна. Известно что  . Отсюда следует, что обратная зависимомть также взаимнооднозначна. В этом можно убедиться непосредственно, вычислив якобиан обратного преобразования

для любого момента времени.

Найдем выражение для скорости и ускорения в лагранжевых переменных. Чтобы выразить скорость, достаточно геометрические координаты заменить на материальные, используя для этого закон движения в лагранжевых переменных. Получим

Найдем ускорение, которое вычисляется как материальная производная скорости. (при лагранжевом описании материальная производная совпадает с частной производной по времени.

Пр2 Дано лагранж описание движения тогда эйлерова описание имеет вид

Дано плоское поле скоростей

найти закон движения частиц в лагранжевых переменных.

З 4.1.2.Дан лагранжев закон движения:

Найти компоненты скорости в эйлеровом описании.

З 4.1.3.Дан лагранжев закон движения:

1)Найти якобиан перехода к эйлер переменным. 2) Найти скорость в лагранжевых переменных.

3) Найти ускорение в лагранжевых переменных. 4) Перейти к эйлерову описанию (выр через). 5) Найти якобиан перехода к лагранж перем. 6) Найти скорость и ускорение в эйлеровых переменных. 7) Зная поле скоростей в эйлеровых переменных перейти к лагранжевому описанию.

З 4.1.4.Задано поле скоростей в переменных Лагранжа:

А) б)

1) Показать, что переход к перем Эйлера возможен. Найти компоненты скорости и ускорения в перем Эйлера. 2) Рассм поле скоростей в перем Эйлера, получ в п 1, как усл задачи, перейти к перем Лагранжа и получить закон движения.

З 4.1.8.Движение среды происходит по закону

Пров, что числа для индивид частицы имеют смысл коорд,,т пр-ва, в кот она нах в мом. Найти поля скорости и ускорения в лагранж описании. Какая частица в момент временинаходится в т с коорд?

З 4.1.10.В моментрассм функции

обратные закону движения

Каков смысл их значений? Чему равны индивидуальные производные ?

З 4.1.11.Найти поля скорости и ускор в лагранжевом и эйлеровом описаниях, если движение среды происх по з-ну

а) трехосное растяжение тела:;

б) простой сдвиг:;

в) однородная деформация при одновременном вращении тела с закрепленной точкой:

.

З 4.1.12.Ввести лагранжевы координаты и найти закон движения сплошной среды, если оно происх с полем скорости

.

З 4.1.13.Ввести лагранжевы коорд и найти закон движ спл среды, если поле скорости имеет вид:

а) ,,,,;

б) ,,,;

в) ,,,,.

З 4.1.14.Задан закон движения сплошной среды

,,.

Показать, что траектории – окружности, а величины скорости постоянны. Определить связь между ии константамии.

З 4.1.15.Дано поле скоростей в лагранжевом описании

,,. Найти компоненты ускорения.

З 4.1.16.В каком случае и материальная производная нек параметрасовпадает с частной производной этого параметра по времени?

5. Задано поле скоростей v1= x1+2x2, v2=4x1– x2, v3=0. Привести его через масштабы. Найти поле ускорений в эйлеровых переменных; опр законы движения частиц в эйлеровых и лагранжевых переменных; найти поля скорости и ускорений частиц в лагранжевых переменных.

З 4.1.17.В электромагнитном континууме напряженность магнитного поля , гдеи– конст, и движение задано полем скоростей,,. Определить скорость изменения напряженности магнитного поля для частицы, расположенной в моментв точке.

З 4.1.18.Напряженность электрического поля в облпсти, занятой движущейся жидкостью, , гдеи– конст. Скорость жидкости задана к-тами,,. Найтив т.

4) Х – лагранжева координата, х – эйлерова координата

4) Индивидуальный объем в виде линейного отрезка движется со скоростью v. Температура отрезка изменяется линейно от T_o до T_к и не меняется во времени. Описать изменение температуры отрезка с позиций Эйлера и Лагранжа.

Х – лагранжева координата, х – эйлерова координата. В начальный момент времени лагранжевы и эйлеровы координаты совпадают

Описание с позиций Лагранжа Описание с позиций Эйлера 

, ,т.е. скорость с течен времени в лагражевых к-тах не меняется

Связь лагранжевых и эйлеровых координат в данной задаче , т.е. 

Подставим это выражение в уравнение для температуры в лагранжевых координатах