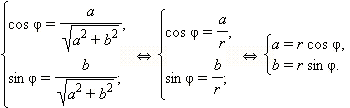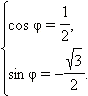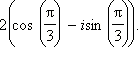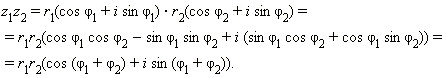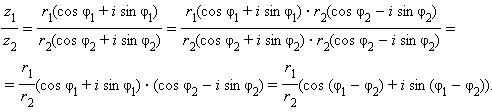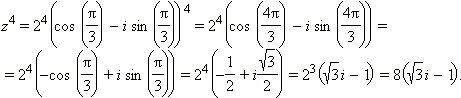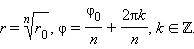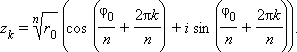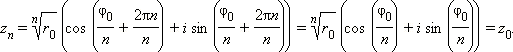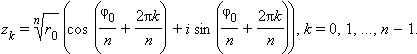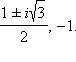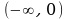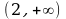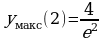СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Лекции по дисциплине ЕН.01 Математика для студентов специальности 21.02.01
|
Лекции по дисциплине ЕН.01 Математика для студентов специальности 21.02.01 |
Просмотр содержимого документа
«Лекции по дисциплине ЕН.01 Математика для студентов специальности 21.02.01»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКОГО КРАЯ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«НЕФТЕКУМСКИЙ РЕГИОНАЛЬНЫЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»
Перечень лекционных занятий
по ЕН.01 Математика
для специальности
21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений
2023 г.
| ОДОБРЕНО: на заседании МО Протокол №_1_ «30» августа 2023 г. Руководитель МО педагогов естественнонаучных и математических дисциплин _________________/ С.А.Федорченко / | Методические указания составлены в соответствии с требованиями Федерального государственного образовательного стандарта среднего профессионального образования по специальности 21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений |
| УТВЕРЖДАЮ: _________________/С.Г.Усенко /
|
Составитель: Федорченко Александр Сергеевич, преподаватель ГБПОУ НРПК
Рецензент: Федорченко Светлана Анатольевна, преподаватель ГБПОУ НРПК
Раздел 1. Элементы линейной алгебры 5
Тема 1.1. Матрицы и действия над ними. Определители, свойства и вычисления. 5
Матрицы. Действия над матрицами 5
Определители 9
Нахождение обратной матрицы 12
Тема 1.2. Системы линейных уравнений. 17
Основные понятия. Решение систем линейных уравнений 17
Раздел 2. Теория комплексных чисел 24
Тема 2.1. Комплексные числа 24
Комплексные числа. Действия над комплексными числами в алгебраической форме. Геометрическое изображение комплексных чисел. 24
Тригонометрическая форма числа. Действия с комплексными числами в тригонометрической форме. Показательная форма комплексного числа 26
Раздел 3. Математический анализ 30
Тема 3.1. Теория пределов функции 30
Предел функции в точке. Основные теоремы о пределах. Бесконечно малые и бесконечно большие функции. Некоторые замечательные пределы. Непрерывность функции и ее разрывы. 30
Тема 3.2.Дифференциальное исчисление функции одной переменной 35
Определение производной. Дифференцируемость функции. Правила дифференцирования. Производные основных функций. Производная сложной функции 35
Тема 3.3. Исследование функции с помощью производной 37
Возрастание и убывание функции. Точки экстремума. Исследование функции на экстремум с помощью производных высших порядков. Выпуклость и вогнутость кривой. Точки перегиба. Асимптоты. Общая схема исследования функций 37
Тема 3.4. Интегральное исчисление 44
Первообразная функция и неопределенный интеграл. Основные свойства и формулы неопределенных интегралов. Методы интегрирования. 44
Основные свойства определенных интегралов. Формула Ньютона-Лейбница для вычисления определенного интеграла. Геометрический и физический смысл определенного интеграла 49
Тема 3.5. Дифференциальные уравнения 54
Задачи, приводящие к дифференциальным уравнениям. Обыкновенные дифференциальные уравнения. Уравнения с разделяющимися переменными 54
Тема 3.6. Числовые и функциональные ряды 62
Числовые ряды. Признаки сходимости ряда. Функциональные ряды. Разложение функции в ряд Маклорена. 62
Раздел 4. Теория вероятностей и математическая статистика 65
Тема 4.1. Основные понятия теории вероятности 65
Понятие события и вероятности события. Достоверные и невозможные события. Теорема сложения вероятностей. Теорема умножения вероятностей. Случайная величина. Дискретная и непрерывная случайные величины. 65
Тема 4.2. Математическая статистика 70
Предмет и задачи математической статистики. Генеральная и выборочная статистические совокупности. Полигон и гистограмма. Выборочный метод. 70
Матрицы (и соответственно математический раздел - матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин "матрица" появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
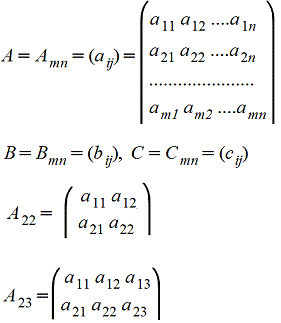
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .
Равенство матриц
A=B, если порядки матриц A и B одинаковы и aij=bij (i=1,2,...,m; j=1,2,...,n)
Действия над матрицами:
1. Сложение матриц - поэлементная операция
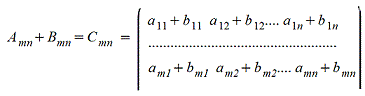
2. Вычитание матриц - поэлементная операция
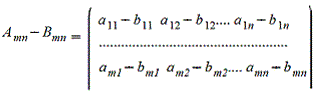
3. Произведение матрицы на число - поэлементная операция
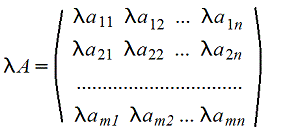
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)
Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере
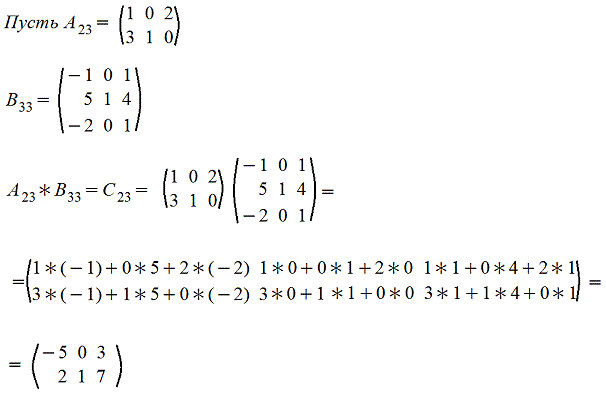
5. Возведение в степень
![]()
m1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'

Строки и столбцы поменялись местами
Пример
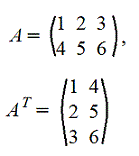
Свойства операций над матрицами:
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A')'=A
(λA)'=λ(A)'
(A+B)'=A'+B'
(AB)'=B'A'
Виды матриц
1. Прямоугольные: m и n - произвольные положительные целые числа
2. Квадратные: m=n
3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором
4. Матрица столбец: n=1. Например
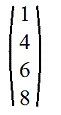
5. Диагональная матрица: m=n и aij=0, если i≠j. Например

6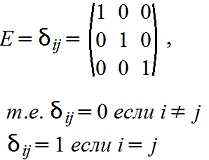 . Единичная матрица: m=n и
. Единичная матрица: m=n и
7. Нулевая матрица: aij=0, i=1,2,...,m
j=1,2,...,n
![]()
8. Треугольная матрица: все элементы ниже главной диагонали равны 0.
Пример.
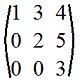
9. Симметрическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательноA'=A
Например,
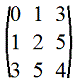
Контрольные вопросы:
Что называют матрицей?
Что такое главная диагональ матрицы?
Какие матрицы называются равными?
Как выполнить сложение матриц?
Как выполнить вычитание матриц?
Как выполнить умножение матрицы на число?
Как выполнить произведение матриц?
Какая матрица называется транспонированной?
Какие свойства операций над матрицами вам известны?
Какие виды матриц вы знаете?
Квадратной матрице 
![]() -го порядка ставиться в соответствие число
-го порядка ставиться в соответствие число , называемое определителем матрицы или детерминантом.
, называемое определителем матрицы или детерминантом.
Вычисление определителей первого порядка.
Матрица размера ![]() это просто число. Определителем такой матрицы является само это число.
это просто число. Определителем такой матрицы является само это число.
Пример:
![]()
Вычисление определителей второго порядка.
Определитель второго порядка (матрицы размера 2 на 2) вычисляется по правилу:
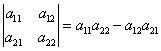
Запомнить просто: произведение элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной.
Пример:
![]() .
.
Вычисление определителей третьего порядка.
Определитель третьего порядка вычисляется по правилу:
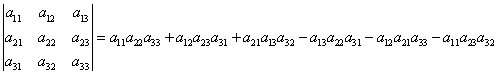
Запомнить порядок сомножителей, конечно же, очень трудно, если не знать визуального представления этого правила, которое называется правило треугольников:
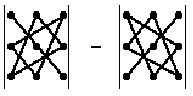
Здесь схематично показано, какие сомножители соседствуют в слагаемых.
Пример:
Вычислить определитель:
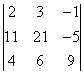 ….
….
Ответ: 108
Решить определитель 3 порядка можно, раскрыв его по любой строке или по любому столбцу. Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.
Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения
Свойства определителей:
(Замечание. Все что будет сказано относительно строк, будет относиться и к столбцам.)
1° При транспонировании квадратной матрицы её определитель не меняется: ![]()
Пример
Известно, что определитель матрицы ![]() равен 3. Тогда определитель матрицы
равен 3. Тогда определитель матрицы ![]() , которая равна
, которая равна ![]() , также равен 3.
, также равен 3.
2° Общий множитель в строке можно выносить за знак определителя.
Пример
![]()
3° ![]()
То есть, если квадратная матрица ![]()
![]() -го порядка умножается на некоторое ненулевое число
-го порядка умножается на некоторое ненулевое число ![]() , то определитель полученной матрицы равен произведению определителя исходной матрицы
, то определитель полученной матрицы равен произведению определителя исходной матрицы ![]() на число
на число ![]() в степени, равной порядку матриц.
в степени, равной порядку матриц.
Пример
Задание. Пусть определитель матрицы ![]() третьего порядка равен 3, вычислить определитель матрицы
третьего порядка равен 3, вычислить определитель матрицы ![]() .
.
Решение. По свойству ![]()
Ответ. ![]()
4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.
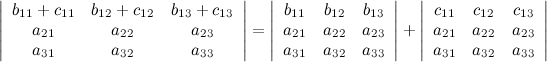
5° Если две строки определителя поменять местами, то определитель поменяет знак.
Пример
![]()
6° Определитель с двумя равными строками равен нулю.
Пример

7° Определитель с двумя пропорциональными строками равен нулю.
Пример
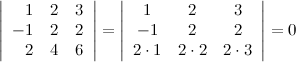
8° Определитель, содержащий нулевую строку, равен нулю.
Пример
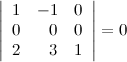
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.
Пример
Пусть задан определитель третьего порядка  . Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:
. Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:
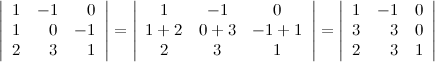
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Пример
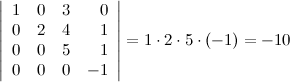
11° Определитель произведения матриц равен произведению определителей: ![]()
Контрольные вопросы:
Что называют определителем матрицы?
Как вычислить определитель первого порядка?
Как вычислить определитель второго порядка?
Как вычислить определитель третьего порядка?
Какими свойствами обладают определители?
Нахождение обратной матрицы - задача, которая чаще решается двумя методами:
методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Существуют еще способы, но мы рассмотрим 2.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица ![]() , произведение на которую матрицы А справа является единичной матрицей, т.е,
, произведение на которую матрицы А справа является единичной матрицей, т.е, ![]() . (1)
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Теорема. Для каждой невырожденной квадратной матрицы можно найти обратную матрицу, и притом только одну. Для вырожденной квадратной матрицы обратная матрица не существует.
Квадратная матрица называется невырожденной, если её определитель не равен нулю, и вырожденной, если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и bравно единице: ab = 1. Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для невырожденной квадратной матрицы А обратной является матрица
![]() , (2)
, (2)
где ![]() - определитель матрицы А, а
- определитель матрицы А, а ![]() - матрица, союзная с матрицей А.
- матрица, союзная с матрицей А.
Союзной с квадратной матрицей A называется матрица ![]() того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы ![]() , транспонированной относительно матрицы A. Таким образом, если
, транспонированной относительно матрицы A. Таким образом, если
 то
то  и
и 
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
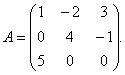
Пример 1. Для матрицы найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
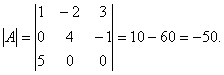
Следовательно, матрица А –невырожденная и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу ![]() , транспонированную относительно матрицы A:
, транспонированную относительно матрицы A:
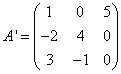
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Следовательно, матрица ![]() , союзная с матрицей A, имеет вид
, союзная с матрицей A, имеет вид
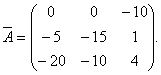
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
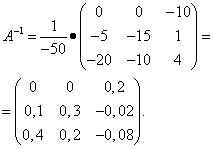
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса - приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы получим сдвоенную матрицу ![]() . Умножим обе части этой матрицы на
. Умножим обе части этой матрицы на ![]() , тогда получим
, тогда получим
![]() ,
,
но
![]() и
и ![]() .
.
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы 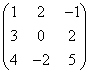 найти обратную матрицу.
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу

и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
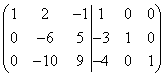 .
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
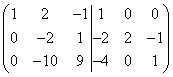 .
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
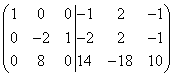 .
.
Разделим третью строку на 8, тогда
 .
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
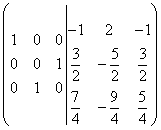 .
.
Переставим местами вторую и третью строку, тогда окончательно получим:
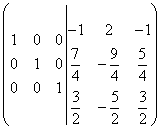 .
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица ![]() . Таким образом:
. Таким образом:
 .
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
![]() .
.
В результате должна получиться обратная матрица.
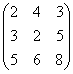
Пример 3. Для матрицы найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
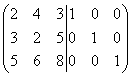 и будем её преобразовывать.
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
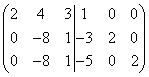 .
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
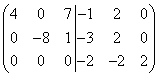 .
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Контрольные вопросы:
Какая матрица называется обратной для данной?
Как найти обратную матрицу методом алгебраических дополнений?
Как найти обратную матрицу методом исключения неизвестных Гаусса?
В курсе высшей математики системы линейных уравнений требуется решать как в виде отдельных заданий, так и в ходе решения остальных задач. С системами линейных уравнений приходится иметь дело практически во всех разделах высшей математики.
Что в данном случае обозначает математическое слово «линейных»? Это значит, что в уравнения системы все переменные входят в первой степени: ![]()
Решить систему уравнений – это значит найти множество её решений или доказать, что их нет
1. Решение системы линейных уравнений способом подстановки
![]()
Рассмотрим пример
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
![]()
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:
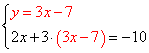
3) Решаем полученное второе уравнение:
![]()
4) Полученное решение подставляем в первое уравнение системы:
![]()
Система уравнений имеет единственное решение: пару чисел x = 1, y = - 4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй - y.
2. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на "3".
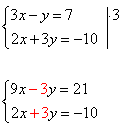
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
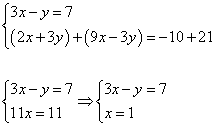
3) Полученное решение подставляем в первое уравнение системы:

3. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2![]() ) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы
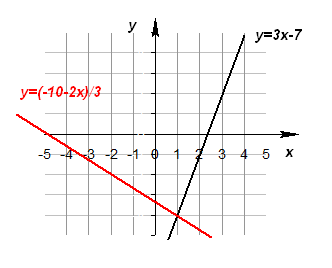
Ответ: (1; -4).
4.Решение системы по формулам Крамера
Рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. 

На первом шаге вычислим определитель , его называют главным определителем системы.
Если ![]() , то система имеет бесконечно много решений или несовместна (не имеет решений).
, то система имеет бесконечно много решений или несовместна (не имеет решений).
Если ![]() , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
, то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
 и
и 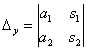
Корни уравнения находим по формулам:
 ,
, 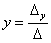
Пример. Решить систему линейных уравнений
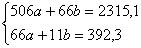
Решение:
 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.
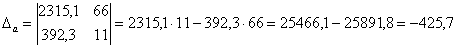 ;
;

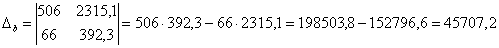 ;
;
![]()
Ответ: ![]() ,
, ![]()
Пример. Решить систему по формулам Крамера. Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
![]()
Пример. Решить систему по формулам Крамера.

Ответ: ![]() .
.
5. Метод Гаусса (последовательного исключения неизвестных).
![]() решим систему методом Гаусса.
решим систему методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы:
 .
.
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: ![]() . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:  . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 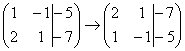
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
Элементарные преобразования не меняют решение системы уравнений
Цель элементарных преобразований – привести матрицу к ступенчатому виду: 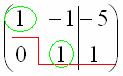 . треугольный вид.
. треугольный вид.
Ответ: ![]()
Пример 1
Решить методом Гаусса систему уравнений:
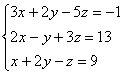
Ответ: ![]()
6. Решение системы с помощью обратной матрицы
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом

Решение: Запишем систему в матричной форме:
![]() , где
, где 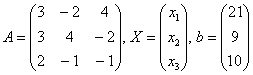
если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице ![]() нужно было бы поставить нули.
нужно было бы поставить нули.
Согласно формуле нам нужно найти обратную матрицу ![]() и выполнить матричное умножение
и выполнить матричное умножение ![]() .
.
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.
Внимание! Если ![]() , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).
, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров 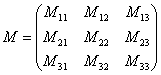
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
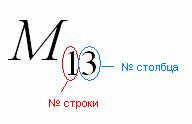 То есть, двойной подстрочный индекс указывает, что элемент
То есть, двойной подстрочный индекс указывает, что элемент ![]() находится в первой строке, третьем столбце, а, например, элемент
находится в первой строке, третьем столбце, а, например, элемент ![]() находится в 3 строке, 2 столбце
находится в 3 строке, 2 столбце
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом:
 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
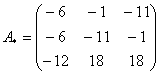 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
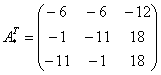 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
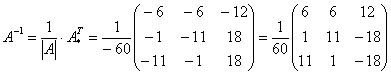
Ни в коем случае не вносим ![]() в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Ответ: ![]()
Контрольные вопросы:
Какие уравнения называются линейными?
Что значит решить систему линейных уравнений?
Как решить систему линейных уравнений способом подстановки?
Как решить систему линейных уравнений способом сложения?
Как решить систему линейных уравнений графическим способом?
Как решить систему линейных уравнений по формулам Крамера?
Как решить систему линейных уравнений методом Гаусса (последовательного исключения неизвестных)?
Как решить систему линейных уравнений с помощью обратной матрицы?
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1.
Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.
Если b = 0, то вместо a + 0i пишут просто a.
Действительные числа — это частный случай комплексных чисел.
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга.
Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1).
Примеры.
Число ![]() = a – bi называется комплексно-сопряженным к z = a + bi.
= a – bi называется комплексно-сопряженным к z = a + bi.
Примеры.
Равенство z · ![]() = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
= a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
![]() .
.
(Например, ![]() .)
.)
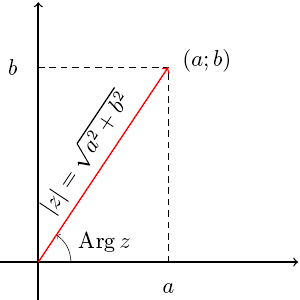
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами).
Примеры.
При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма).
По теореме Пифагора длина вектора с координатами (a; b) равна ![]() . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|.
. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|.
Примеры.
Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z.
Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ).
Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)).
Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки.
Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются).
Отсюда следуют формулы Муавра: zn = |z|n · (cos(n · (Arg z)) + i sin(n · (Arg z))).
С помощью этих формул легко научиться извлекать корни любой степени ![]() из комплексных чисел.
из комплексных чисел.
Корень n-й степени из числа z — это такое комплексное число w, что wn = z.
Видно, что ![]() , а
, а ![]() , где k может принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
, где k может принимать любое значение из множества {0, 1, ..., n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
Контрольные вопросы:
Что такое комплексное число? Мнимая единица?
Как выполняются арифметические действия с комплексными числами? Привести примеры.
Какое число называют комплексно-сопряженным?
Как изображают комплексные числа на плоскости?
Что называют модулем комплексного числа?
Что называют аргументом комплексного числа?
Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть ![]() и φ = arg z. Тогда по определению аргумента имеем:
и φ = arg z. Тогда по определению аргумента имеем:
|
|
Отсюда получается
| z = a + bi = r(cos φ + i sin φ). |
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Пример 1
Записать число ![]() в тригонометрической форме.
в тригонометрической форме.
Решение
| Найдём модуль этого числа:
Значит, один из аргументов числа
Ответ. |
Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z1 = r1(cos φ1 + i sin φ1) и z2 = r2(cos φ2 + i sin φ2). Имеем:
|
|
|
|
Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ1, φ2, ..., φn – аргументы чисел z1, z2, ..., zn, то
|
|
|
|
В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.
|
Первая формула Муавра:
|
Пример 2
Вычислить ![]() если
если ![]()
| Решение
|
Число z называется корнем степени ![]() из комплексного числа w, если
из комплексного числа w, если ![]() Корень степени
Корень степени ![]() обозначается
обозначается ![]() Пусть теперь число w фиксировано. Найдём z из уравнения
Пусть теперь число w фиксировано. Найдём z из уравнения ![]()
Если w = 0, то у уравнения ![]() существует единственное решение z = 0.
существует единственное решение z = 0.
Если w ≠ 0, то положим, что нам известно тригонометрическое представление числа w = r0(cos φ0 + i sin φ0), и будем искать число z также в тригонометрической форме: z = r(cos φ + i sin φ). Из определения аргумента и геометрической интерпретации комплексных чисел следует, что два комплексных числа, записанных в тригонометрической форме, равны тогда и только тогда, когда равны их модули, а аргументы отличаются на угол, кратный 2π. Имеем:
|
|
откуда получается:
|
|
Итак, все решения уравнения ![]() задаются формулой
задаются формулой
|
|
Заметим, что если в эту формулу подставлять натуральные числа k, то при k = 0, 1, ..., n мы будем получать разные комплексные числа, а при k = n имеем:
|
|
Значит, и в дальнейшем значения корней будут повторяться. Следовательно, существует ровно n корней уравнения ![]() и все они задаются одной формулой.
и все они задаются одной формулой.
|
Вторая формула Муавра:
|
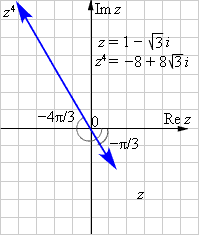
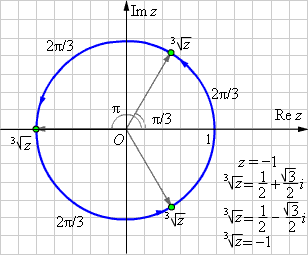
Пример 3
Найти ![]()
Решение
Представим число –1 в тригонометрической форме:
По второй формуле Муавра получаем:
Получаем последовательно:
Ответ. |
Контрольные вопросы:
Как выглядит тригонометрическая форма комплексно числа?
Как выполнить арифметические действия над комплексными числами, записанными в тригонометрической форме?
Пусть функция y =f(x) определена в некоторойокрестностиx0,кроме, может быть, самой точки x0.
Определение. ЧислоA называется пределом функцииy =f(x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε 0найдетсятакоечисло δ 0, что для всех х ¹x0, удовлетворяющих неравенству
│ х –x0│f(x) –А│
Или кратко: ![]() ε 0
ε 0 ![]() δ 0,
δ 0, ![]() x:│ х –x0│х ¹x0= │f(x) –А│
x:│ х –x0│х ¹x0= │f(x) –А│
![]()
Геометрический смысл предела функции заключается в следующем: число ![]() , если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А.
, если для любой ε – окрестности точки A найдется такая δ – окрестность точки x0, что для всех х ¹x0 из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А.
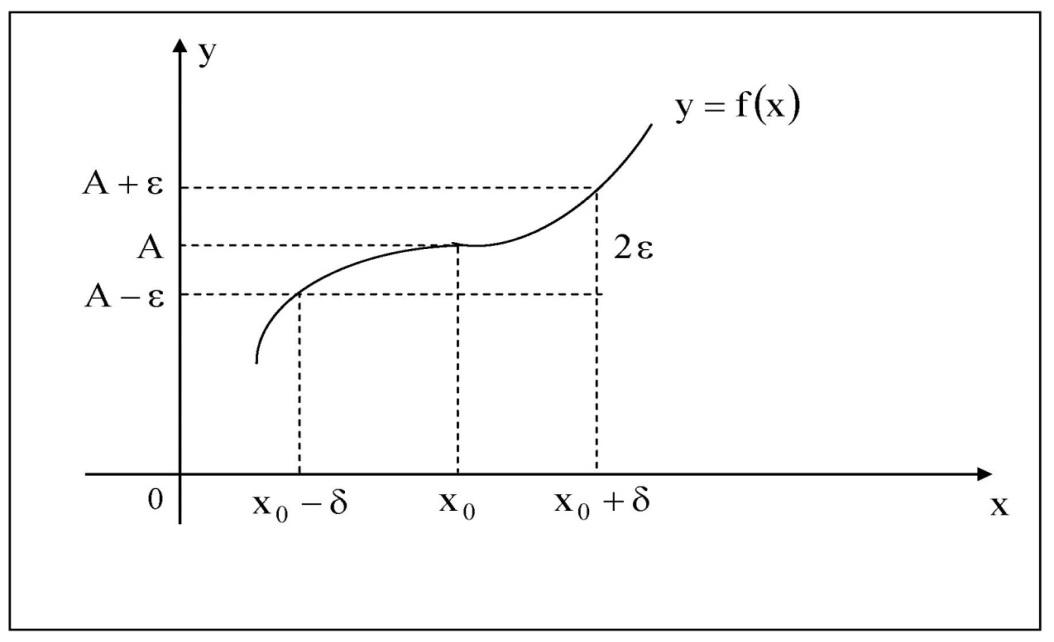
Рис. 1
Пример: Доказать, что ![]()
Решение. Возьмем произвольное ![]() и найдем
и найдем ![]() такое, что для всехx, удовлетворяющих неравенству,
такое, что для всехx, удовлетворяющих неравенству, ![]() , выполняется неравенство
, выполняется неравенство![]() , то есть
, то есть![]() .
.
Взяв ![]() , видим, что для всехx, удовлетворяющих неравенству,
, видим, что для всехx, удовлетворяющих неравенству, ![]() , выполняется неравенство
, выполняется неравенство![]() , следовательно,
, следовательно,
![]()
Пусть функция y =f(x) определена в промежутке (–![]() ; +
; +![]() ).
).
Определение. Число A называется пределом функции f(x) при х ![]()
![]() , если для любого числа ε 0 существует такоечисло M = M (ε) 0, что для всех значений x, удовлетворяющих неравенству │x│M,выполняется неравенство │f(x) – А│ ε. В этом случае пишут
, если для любого числа ε 0 существует такоечисло M = M (ε) 0, что для всех значений x, удовлетворяющих неравенству │x│M,выполняется неравенство │f(x) – А│ ε. В этом случае пишут ![]() f(x) = А.
f(x) = А.
Или кратко: ![]() ε 0
ε 0 ![]() M 0, │x│ M= │f(x) –А│
M 0, │x│ M= │f(x) –А│
![]() f(x) = А.
f(x) = А.
Бесконечно малые и бесконечно большие функции.
Определение 1. Функция f(x) называется бесконечно большой функцией при х →x0, если ![]() f(x) =
f(x) = ![]() .
.
Определение 2. Функция f(x) называется бесконечно малой функцией при х →x0, если ![]() f(x) = 0.
f(x) = 0.
Основные теоремы о пределах функций.
Теорема 1. Предел постоянной величины равен самой постоянной: ![]() c = c.
c = c.
Теорема 2. Предел суммы (разности) двух функций равен сумме (разности) их пределов: ![]()
![]() =
= ![]() f(x)
f(x)![]()
![]() φ(x).
φ(x).
Теорема 3.Предел произведения двух функций равен произведению их пределов:
![]()
![]() =
= ![]() f(x)
f(x)![]()
![]() φ(x).
φ(x).
Теорема 4. Предел дроби равен пределу числителя, деленному на передел знаменателя, если предел знаменателя не равен нулю:
![]()
![]() ,
, ![]()
![]() 0.¹
0.¹
Теорема 5. (О пределе промежуточной функции) Если в окрестности точки x0 выполняются неравенства: ![]() и
и![]()
![]() =
=![]()
![]() =А, то
=А, то ![]() .
.
Первый замечательный предел ![]() .
.
Второй замечательный предел.
Функция ![]() при
при![]() и
и![]() (где х в отличие от натурального n «пробегает» все значения числовой оси) имеет предел, равный числу е:
(где х в отличие от натурального n «пробегает» все значения числовой оси) имеет предел, равный числу е:
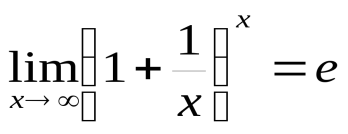 .
.
Эквивалентные бесконечно малые функции используются при вычислении пределов отношений двух бесконечно малых для раскрытия неопределенностей вида ![]() .
.
Запишем следствия из 1-го и 2-го замечательных пределов в виде таблицы эквивалентных бесконечно малых. При ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J Пример 13.2. 1) Найти ![]() .
.
При ![]()
![]() и, значит,
и, значит,![]() . Заменяя знаменатель на эквивалентную бесконечно малую, получаем
. Заменяя знаменатель на эквивалентную бесконечно малую, получаем![]() .
.
2) Найти ![]() .
.
![]() .
.
3) Найти ![]() .
.
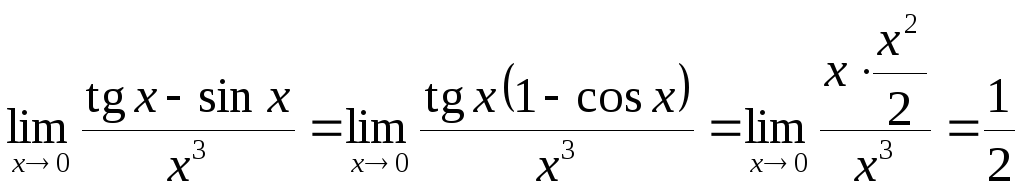
Определение 1. Функция  , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки  , называется непрерывной в точке
, называется непрерывной в точке  , если
, если 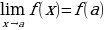 .
.
Необходимо обратить внимание учащихся на то, что согласно данному определению непрерывность функции  в точке
в точке  означает одновременную выполняемость следующих условий:
означает одновременную выполняемость следующих условий:
1. Функция  должна быть определена в точке
должна быть определена в точке  .
.
2. У функции  должен существовать предел в точке
должен существовать предел в точке  . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов в точке
. Как отмечалось выше, это подразумевает существование и равенство односторонних пределов в точке  .
.
3. Предел функции  в точке
в точке  совпадает со значением функции в этой точке.
совпадает со значением функции в этой точке.
Определение 2. Функция называется непрерывной в точке  , если бесконечно малому приращению аргумента
, если бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 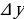 , то есть
, то есть  .
.
Определение 3. Если функция  определена на полуинтервале
определена на полуинтервале  и
и 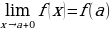 , т.е.
, т.е. 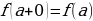 , то эта функция называется непрерывной справа в точке
, то эта функция называется непрерывной справа в точке  .
.
Определение 4. Если функция  определена на полуинтервале
определена на полуинтервале  и
и 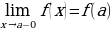 , т.е.
, т.е. 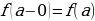 , то эта функция называется непрерывной слева в точке
, то эта функция называется непрерывной слева в точке  .
.
Для непрерывности функции в точке необходимо и достаточно её непрерывности в этой точке слева и справа.
Определение 5. Если функция непрерывна в каждой точке интервала  , то она называется непрерывной на этом интервале.
, то она называется непрерывной на этом интервале.
Определение 6. Функция называется непрерывной на отрезке 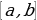 , если она непрерывна на интервале
, если она непрерывна на интервале  и, кроме того, непрерывна справа в точке
и, кроме того, непрерывна справа в точке  и непрерывна слева в точке
и непрерывна слева в точке 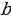 .
.
Определение 7. Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если эта функция либо не определена в точке
, если эта функция либо не определена в точке  , либо определена, но не является непрерывной в точке
, либо определена, но не является непрерывной в точке  .
.
При этом следует отметить, что в точке разрыва нарушается одно из трех условий непрерывности. В зависимости от того, какое условие нарушается, выделяют точки разрыва первого рода (точки устранимого разрыва, точки разрыва с конечным скачком функции) и точки разрыва второго рода. У каждого типа разрыва есть свои характерные особенности, на которые нужно обратить внимание.
Определение. Точка х0 называется точкой разрыва 1 - го рода, если в этой точке функция ![]() имеет конечные, но не равные друг другу левый и правый пределы.
имеет конечные, но не равные друг другу левый и правый пределы. ![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке ![]() , достаточно того, что она определена слева и справа от нее.
, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 - го рода функция может иметь только конечный скачок.
Определение. Точка х0 называется точкой разрыва 2 - го рода, если в этой точке функция ![]() не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) - немецкий математик, член-корреспондент Петербургской АН 1837г)
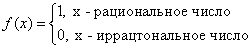
не является непрерывной в любой точке ![]() .
.
Пример. Функция ![]() имеет в точке
имеет в точке ![]() точку разрыва 2 - го рода, т.к.
точку разрыва 2 - го рода, т.к. ![]() .
.
Основные свойства функции, непрерывной в точке:
1. Ограниченность в некоторой окрестности точки  непрерывной в точке
непрерывной в точке  функции.
функции.
2. Знак функции, непрерывной в точке  , в некоторой окрестности этой точки.
, в некоторой окрестности этой точки.
3. Непрерывность в точке суммы, произведения и частного непрерывных в точке функций.
4. Непрерывность сложной функции.
8. Формулировка основных свойств функций, непрерывных на отрезке
1. Теорема о нулях непрерывной на отрезке функции.
Если функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 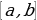 и принимает на его концах значения разных знаков, т.е.
и принимает на его концах значения разных знаков, т.е. 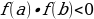 , то на интервале
, то на интервале  имеется по крайней мере один корень функции, т.е.
имеется по крайней мере один корень функции, т.е. 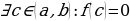 .
.
2. Теорема о промежуточных значениях непрерывной на отрезке функции.
Если функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 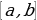 и принимает на его концах различные значения
и принимает на его концах различные значения  , то для любого числа C, лежащего между A и B, на интервале
, то для любого числа C, лежащего между A и B, на интервале  найдется такая точка с, что
найдется такая точка с, что  .
.
3. Теорема об ограниченности непрерывной на отрезке функции.
Если функция  непрерывна на отрезке
непрерывна на отрезке 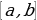 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
4. Теорема о достижимости своего наименьшего и наибольшего значений функции, непрерывной на отрезке.
Если функция  непрерывна на отрезке
непрерывна на отрезке 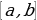 ,то она достигает на этом отрезке своего наибольшего и наименьшего значений.
,то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Контрольные вопросы:
Что называется пределом функции в точке?
В чем геометрический смысл предела функции?
Какая функция называется бесконечно большой? Бесконечно малой?
Какие замечательные пределы вы знаете?
Какая функция называется непрерывной в точке? Непрерывной справа? Непрерывной слева? Непрерывной на интервале? Непрерывной на отрезке?
Какая точка называется точкой разрыва?
Какая точка называется точкой разрыва 1-го рода? 2-го рода?
Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Производная обозначается  (x0).
(x0).
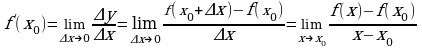
Е
сли  (x0) существует, то говорят, что функция f (x) дифференцируема в точке x0.
(x0) существует, то говорят, что функция f (x) дифференцируема в точке x0.
Теорема. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке.
Замечание. Если в точке x0 функция f (x) непрерывна, то в этой точке функция может и не иметь производной.
Угловой коэффициент касательной к графику y = f (x) в точке с абсциссой x0 равен производной функции f(x) в точке x0:  (x0) = k = tg
(x0) = k = tg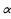
В этом состоит геометрический смысл производной. Очевидно, что уравнение касательной M0K имеет вид: y – f (x0) =  (x0)(x – x0).
(x0)(x – x0).
Производная от пути S = f(t) в момент времени t0 есть скорость в момент времени t0. Производная от скорости есть ускорение. В этом состоит физический смысл производной.
Основные правила дифференцирования
Теорема 1. Если функции u (x), v (x) дифференцируемы в точке x, то их сумма дифференцируема в этой точке, причем
(u(x) + v(x))' = u'(x)+v'(x).
Теорема 2. Если функции u(x), v(x) дифференцируемы в точке x, то их произведение дифференцируемо в этой точке, причем
(u(x)v(x))' = u'(x)v(x) + u(x)v'(x).
Следствие. Постоянный множитель можно выносить за знак производной.
Теорема 3. Если функции u(x), v(x) дифференцируемы в точке x и v(x) 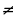 0, то их частное дифференцируемо в этой точке, причем:
0, то их частное дифференцируемо в этой точке, причем:
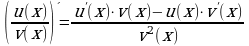
Таблица производных:
Сложная функция: Элементарная функция:
1)  1)
1) ![]()
2) ![]() 2)
2) ![]()
3) ![]() 3)
3) ![]()
4) ![]() 4)
4) ![]()
5![]() 5
5 ![]()
6 ![]() 6
6 ![]()
![]()
7 ![]() 7
7 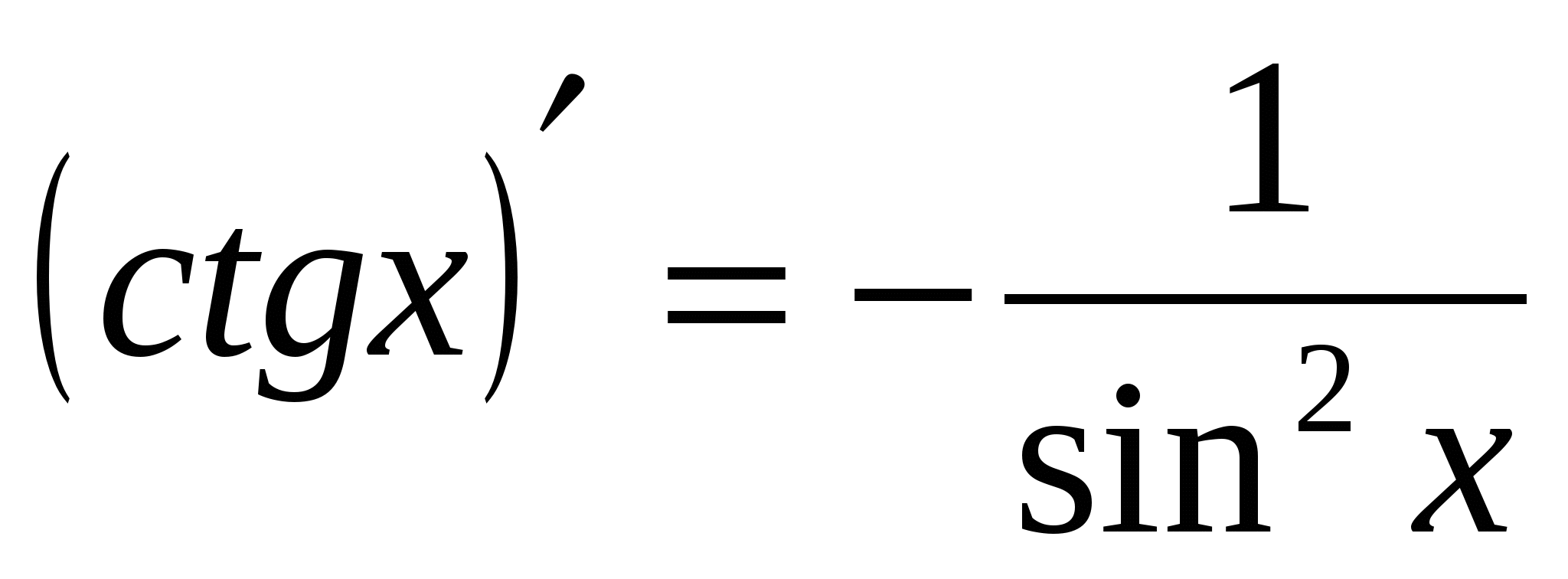
8 ![]() 8
8 ![]()
9 ![]() 9
9 ![]()
10 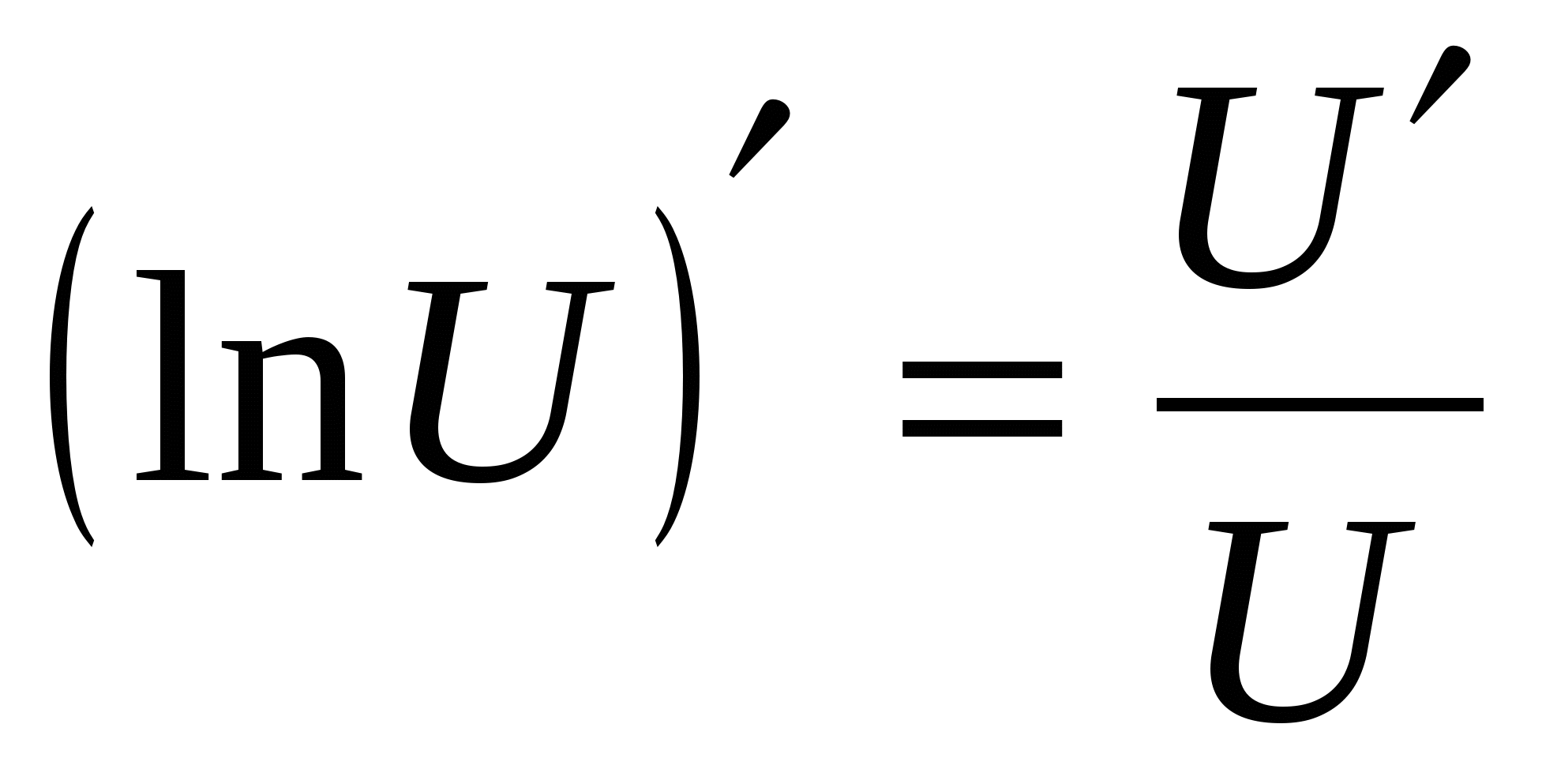 10
10 ![]()
11 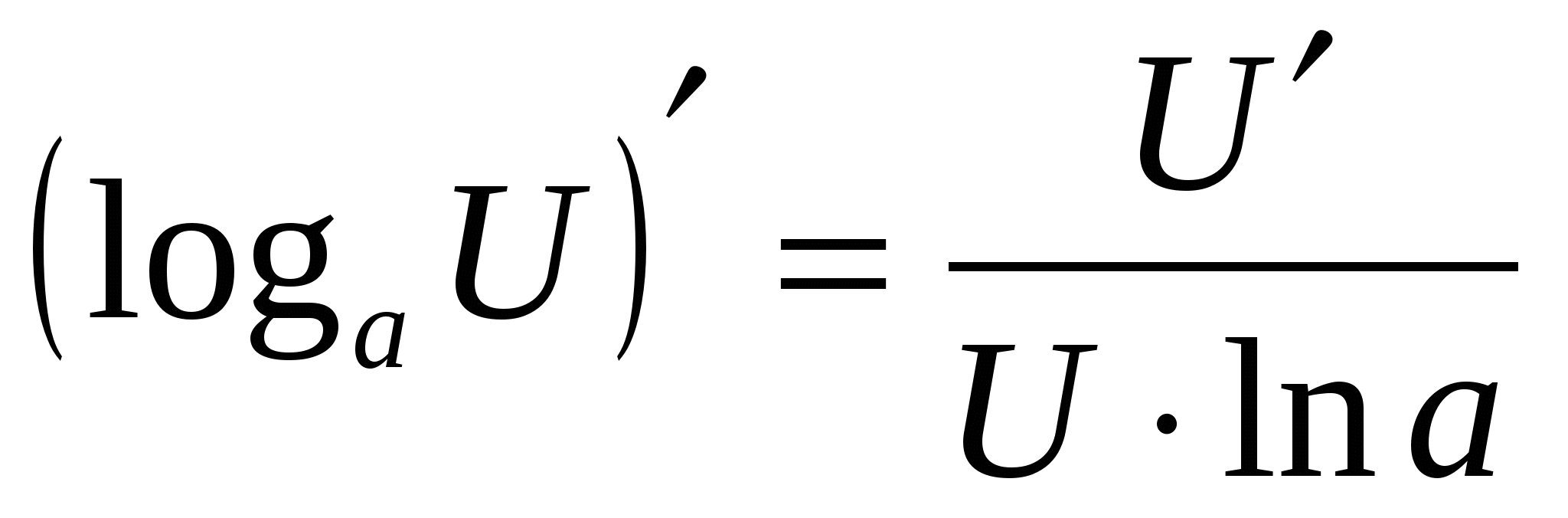 11
11![]()
![]()
![]()
Теорема 4 Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
Контрольные вопросы:
Что такое производная функции в точке?
В чем геометрический смысл производной?
В чем физический смысл производной?
Каковы основные правила дифференцирования?
Как найти производную сложной функции?
Тема 3.3. Исследование функции с помощью производной
Теорема 1. (Достаточное условие возрастания функции)
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), причем  (x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
(x) 0 для любого x(a, b), то эта функция возрастает на отрезке [a, b].
Теорема 2. (Необходимое условие возрастания функции)
Если функция f(x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то  (x 0 для) любого x из интервала (a, b).
(x 0 для) любого x из интервала (a, b).
Сформулируйте и докажите достаточное условие и необходимое условие для убывания функции.
П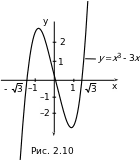
ример. Исследовать на монотонность (т.е. возрастание и убывание) функцию:
f (x) = x3 – 3x.
Решение.  (x) = 3x2 – 3 = 3(x2 – 1).
(x) = 3x2 – 3 = 3(x2 – 1).
Неравенство  (x) 0, т.е. 3(x2 – 1) 0, справедливо для x x 1. Следовательно, функция f(x, –1)) возрастает на интервалах (– и ). Поскольку неравенство(1, +
(x) 0, т.е. 3(x2 – 1) 0, справедливо для x x 1. Следовательно, функция f(x, –1)) возрастает на интервалах (– и ). Поскольку неравенство(1, +  (x) x2 – 1) x(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
(x) x2 – 1) x(–1, 1), то на интервале (–1, 1) функция f(x) убывает.
Построим график функции y = x3 – 3x (рис. 2.10), используя ее значения в точках:
x1 = –1, x2 = 1, x3 = 0, x4 = –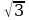 , x5 =
, x5 =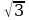 :
:
f(–1) = 2, f(1) = –2, f(0) = 0, f(–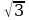 ) = 0, f(
) = 0, f(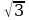 ) = 0.
) = 0.
Заметим, что в точке x1 = –1 значение f(–1) больше, чем значение f(x) в соседних с x1 точках. Говорят, что в точке x1 функция имеет максимум (локальный максимум). Аналогично, f(x2) f(x) для x, близких к x2. В этом случае говорят, что в точках x2 функция имеет минимум (локальный минимум).
Экстремумы функции
Говорят, что в точке x0 функция f(x) имеет максимум, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) f(x0).
Точка x0 называется точкой минимума, если существует такая окрестность точки x0, что для любого x из этой окрестности f(x) f(x0).
Точки максимума и минимума называются точками экстремума.
Замечание. Точки экстремума всегда являются внутренними точками промежутка, т.е. не могут быть его концом.
Теорема 1. (Необходимое условие экстремума)
Если функция f(x) дифференцируема в точке x0 и некоторой ее окрестности и x0 – точка экстремума, то  (x0) = 0.
(x0) = 0.
Следствие. Если x0 – точка экстремума, то  (x0) = 0 или
(x0) = 0 или  (x0) не существует.
(x0) не существует.
Если f'(x0) = 0 или f'(x0) не существует, то точку x0 будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.
Теорема 2. (Первое достаточное условие экстремума)
Пусть функция f (x) определена и непрерывна в точке x0 и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, может быть, точки x0, и x0 – критическая точка для функции f (x) (т.е.  (x0) = 0 или
(x0) = 0 или  (x0) не существует). Тогда: 1) если при x x0 производная
(x0) не существует). Тогда: 1) если при x x0 производная  (x) 0, а для x x0:
(x) 0, а для x x0:  (x) x0 – точка максимума; 2) если при x x0:
(x) x0 – точка максимума; 2) если при x x0:  (x) x x0:
(x) x x0:  (x) 0, то x0 – точка минимума.
(x) 0, то x0 – точка минимума.
Теорема 3. (Второе достаточное условие экстремума).
Пусть функция f (x) дважды дифференцируема в точке x0 и некоторой ее окрестности и пусть  (x0) = 0. Если
(x0) = 0. Если 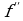 (x0) 0, то x0 – точка минимума. Если
(x0) 0, то x0 – точка минимума. Если 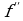 (x0) x0 – точка максимума.
(x0) x0 – точка максимума.
Пример 1. Исследовать на монотонность и экстремумы функцию
f(x) = x2e–x. Построить ее график.
Решение. Эта функция определена и непрерывна на всей ). Найдем производную:, числовой оси (–  (x) = 2xe–x – x2e–x = xe–x(2 – x). Тогда
(x) = 2xe–x – x2e–x = xe–x(2 – x). Тогда  (x) = 0 при x1 = 0 и x2 = 2, где x1, x2 – критические точки. ; 0), (0; 2), (2;Эти точки разбивают всю числовую ось на три интервала: (– ). Составим таблицу, в первой строке которой поместим указанные точки и+ интервалы, во второй строчке – сведения о производной
(x) = 0 при x1 = 0 и x2 = 2, где x1, x2 – критические точки. ; 0), (0; 2), (2;Эти точки разбивают всю числовую ось на три интервала: (– ). Составим таблицу, в первой строке которой поместим указанные точки и+ интервалы, во второй строчке – сведения о производной  (x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
(x) в точках и на интервалах, а в третьей – поведение данной функции f(x):
| x |
| x1 = 0 | (0, 2) | x2 = 0 |
|
|
|
| 0 |
| 0 |
|
| f(x) | убывает |
| возрастает |
| убывает |
Определим знак  (x) на каждом из интервалов: если x, 0),(– то
(x) на каждом из интервалов: если x, 0),(– то  (x) x(0, 2), то
(x) x(0, 2), то  (x)0; если x), то(2, +
(x)0; если x), то(2, +  (x) f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) =
(x) f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x1 = 0 является точкой минимума, yмин(0) = 0, а x2 = 2 – точка максимума, yмакс(2) =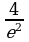 0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и
0,54. Для построения графика заметим, что f (x) 0 для всех x, отличных от нуля, и
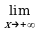
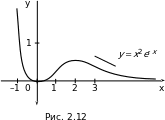
x2e–x = 0,
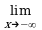 x2e–x ,= f(–1) = e 2,7.
x2e–x ,= f(–1) = e 2,7.
График этой функции изображен на рис. 2.12.
Отметим, что дальнейшее исследование этой функции (см. следующий раздел) позволит уточнить ее график.
Пример 2. Исследовать на экстремум функцию f (x) = x + 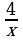 .
.
Решение(0,, 0). Область определения функции (- ), в каждом из этих интервалов функция непрерывна. Найдем+ f'(x) и f''`(x): f `(x) = 1 – 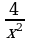 , f''(x) =
, f''(x) =  . Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
. Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
1 – 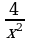 = 0, отсюда x1 = –2, x2 = +2 – критические точки. Используем теорему 3 для исследования критических точек, для этого вычислим f''(x) в точках x1 и x2. Так как
= 0, отсюда x1 = –2, x2 = +2 – критические точки. Используем теорему 3 для исследования критических точек, для этого вычислим f''(x) в точках x1 и x2. Так как
f''(–2) = 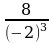 = –1x1 = –2 является точкой максимума fмакс(–2) = –2 –
= –1x1 = –2 является точкой максимума fмакс(–2) = –2 – 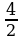 = –4. Для x2: f''(2) =
= –4. Для x2: f''(2) =  = 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 +
= 1 0, поэтому x2 = 2 – точка минимума, fмин(2) = 2 + 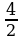 = 4.
= 4.
Т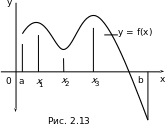
аким образом, функция f(x) = x + 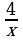 имеет максимум при x1 = –2, f(–2) = –4 и имеет минимум при x2 = 2, f(2) = 4.
имеет максимум при x1 = –2, f(–2) = –4 и имеет минимум при x2 = 2, f(2) = 4.
Известно, что если функция непрерывна на отрезке, то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения (см. гл. 1). Иногда требуется найти наименьшее или наибольшее значение такой функции.
Если на отрезке [a, b] есть точки минимума и максимума функции f(x) (рис. 2.13), то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка [a, b]. Аналогично для наибольшего значения.
Алгоритм нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке:
найти критические точки x1, x2, ..., xn функции f(x), принадлежащие отрезку 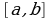 ;
;
вычислить значения функции f (x) в критических точках и на концах отрезка;
из этих значений выбрать самое большое и самое малое, эти числа и будут наибольшим и наименьшим значениями f(x) на отрезке [a, b].
Пример 3. Найти наименьшее и наибольшее значения функции:
f(x) = x4 – 2x2 + 5 на отрезке [–2, 2].
Решение. Найдем критические точки для данной функции:
 (x) = 4x3 – 4x = 4x(x2 – 1);
(x) = 4x3 – 4x = 4x(x2 – 1);
 (x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
(x) = 0 при x1 = 0, x2 = –1, x3 = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:
f(–2) = (–2)4 (–2)– 22 + 5 = 16 – 8 + 5 = 13, f(–1) = 1 – 2 + 5 = 4,
f(0) = 5, f(1) = 4, f(2) =13.
Из найденных значений самое малое число 4, а самое большое число 13.
Итак, наименьшее значение функции равно 4, наибольшее значение равно 13.
Выпуклость, вогнутость графика функции,
точки перегиба
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x).
Кривая, заданная функцией y = f(x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.
Точка кривой M0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции).
Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f''(x) y = f(x) на этом интервале выпукла.
Если во всех точках интервала (a, b): 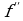 (x) 0, то кривая y = f(x) на этом интервале вогнута. (правило дождя)
(x) 0, то кривая y = f(x) на этом интервале вогнута. (правило дождя)
Теорема 2 (достаточное условие точки перегиба)
Пусть кривая является графиком функции y = f(x). Если 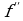 (x0) = 0 или
(x0) = 0 или 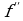 (x0) не существует и при переходе через x0 вторая производная
(x0) не существует и при переходе через x0 вторая производная 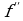 (x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
(x) меняет свой знак, то точка M0(x0, f(x0)) этой кривой является точкой перегиба.
Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
А
симптотой графика функции y = f(x) называется такая прямая, что расстояние от переменной точки M на графике до этой прямой стремится к нулю при удалении точки M в бесконечность (рис. 2.17, 2.18).
С примерами асимптот мы встречались при изучении пределов функции (глава 1). Напомним, что если 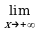 f (x) = b, то прямая y = b является асимптотой графика
f (x) = b, то прямая y = b является асимптотой графика
y = f(x) (при x ), эта асимптота параллельна оси Ox и называется горизонтальной асимптотой (см. рис. 2.18). Аналогично, прямая y = b является асимптотой графика
y = f(x) при x , если 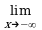 f (x) = b (рис. 2.17).Рассмотрим асимптоты, параллельные оси Oy. Они называются вертикальными асимптотами.
f (x) = b (рис. 2.17).Рассмотрим асимптоты, параллельные оси Oy. Они называются вертикальными асимптотами.
Пусть для функции f (x): 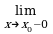 f(x или) =
f(x или) =  f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая x = x0 является асимптотой, то хотя бы один из пределов,
f(x, тогда из определения асимптоты) = следует, что прямая x = x0 асимптота. Очевидно и обратное, если прямая x = x0 является асимптотой, то хотя бы один из пределов, 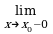 f(x),
f(x),  f(x), является бесконечным (см. рис. 2.19, 2.20).
f(x), является бесконечным (см. рис. 2.19, 2.20).
С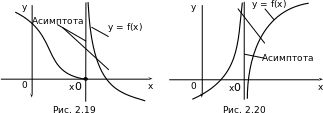
ледовательно, для отыскания вертикальных асимптот нужно найти такие значения x0, односторонние пределы в которых равны бесконечности.
Пример 1. Найти вертикальные асимптоты для графика функции y =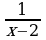 .
.
Решение. Функция f(x) = 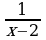 определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
определена и непрерывна во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
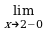
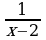 ,= –
,= – 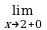
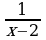 . Следовательно, прямая= + x = 2 является вертикальной асимптотой для графика y =
. Следовательно, прямая= + x = 2 является вертикальной асимптотой для графика y =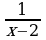 . Кроме того,
. Кроме того, 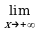
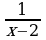 = 0 и
= 0 и 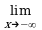
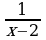 = 0, следовательно, прямая y = 0 является горизонтальной асимптотой при x и при x (см. рис. 2.21).
= 0, следовательно, прямая y = 0 является горизонтальной асимптотой при x и при x (см. рис. 2.21).
Рассмотрим асимптоты, которые не параллельны оси Oy, будем называть их наклонными асимптотами. Пусть график функции y = f(x) имеет наклонную асимптоту при x , тогда ее уравнение имеет вид y = kx + b. Определим числа k и b.
Опустим из точки M(x, f(x)) графика функции перпендикуляр MN на асимптоту (см. рис. 2.22). Из определения асимптоты следует, что при x длина MN 0 (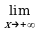 MN = 0). Из MNK имеем MK =
MN = 0). Из MNK имеем MK = , где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит,
, где – угол наклона асимптоты к оси Ox, поэтому cos –постоянная величина. Значит, 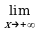 MK = 0. Так как MK = |AK – AM|,
MK = 0. Так как MK = |AK – AM|,
AK = kx + b, то MK = |kx + b – f(x)|, следовательно,
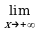 (f(x) – kx – b) = 0. (2.31)
(f(x) – kx – b) = 0. (2.31)
Итак, если прямая y = kx + b является асимптотой графика функции y = f (x), то выполняется равенство (2.31) и наоборот, если при постоянных числах k, b выполняется равенство (2.31), то прямая y = kx + b является асимптотой. Из равенства (2.31), разделив бесконечно малую функцию (f(x) – kx – b) на x (а x ), получим:
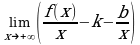 = 0, (2.32)
= 0, (2.32)
о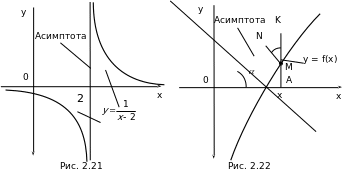
тсюда угловой коэффициент асимптоты:
 . (2.33)
. (2.33)
Определим коэффициент b из равенства (2.31), подставив в это равенство значение k:
b = 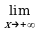 (f(x) – kx). (2.34)
(f(x) – kx). (2.34)
Итак, если прямая y = kx + b является асимптотой графика y = f(x), то k, b находятся по формулам (2.33), (2.34). Обратно, если существуют пределы (2.33), (2.34), то прямая y = kx + b есть асимптота. Если хотя бы один из пределов (2.33), (2.34) не существует, то при x кривая не имеет асимптоты.
Аналогично решается вопрос об асимптотах при x . Заметим, что отдельно находить горизонтальные асимптоты нет надобности, они будут найдены при нахождении наклонных асимптот (при k = 0).
Пример 2. Найти асимптоты линии y = ex – x.
Решение. Функция f (x) = ex – x определена, непрерывна на бесконечном интервале ), поэтому вертикальных асимптот нет., +(–
Найдем наклонные асимптоты, для этого вычислим пределы (2.33), (2.34) при
x , x :
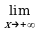
 =
= 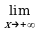 (
(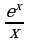 ,– 1) =
,– 1) =
так как 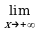
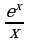 (проверьте= это по правилу Лопиталя). Отсюда следует, что при
(проверьте= это по правилу Лопиталя). Отсюда следует, что при
x наклонных асимптот нет:
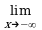
 =
= 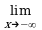 (
(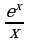 – 1) = –1, так как
– 1) = –1, так как 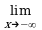
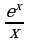 = 0,
= 0,
отсюда k = –1. Далее, 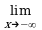 (f(x) – kx) =
(f(x) – kx) = 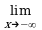 (ex – x + x) =
(ex – x + x) = 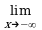 ex = 0, значит, b = 0.
ex = 0, значит, b = 0.
Итак, прямая y = –x есть наклонная асимптота при x для графика функции y = ex – x.
Контрольные вопросы:
Каково достаточное условие возрастания / убывания функции?
Каково необходимое условие возрастания / убывания функции?
Какие точки называются точками экстремума?
Как найти наибольшее и наименьшее значения функции на отрезке?
Когда кривая называется выпуклой / вогнутой на отрезке?
Какая точка называется точкой перегиба?
Что называется асимптотой графика? Какие бывают асимптоты?
Неопределенный интеграл
ОПР. Пусть задана функция ![]() . Функция
. Функция ![]() называется первообразной функции
называется первообразной функции ![]() на
на ![]() , если
, если ![]() .
.
У функции ![]() может существовать много первообразных . Например, функции
может существовать много первообразных . Например, функции
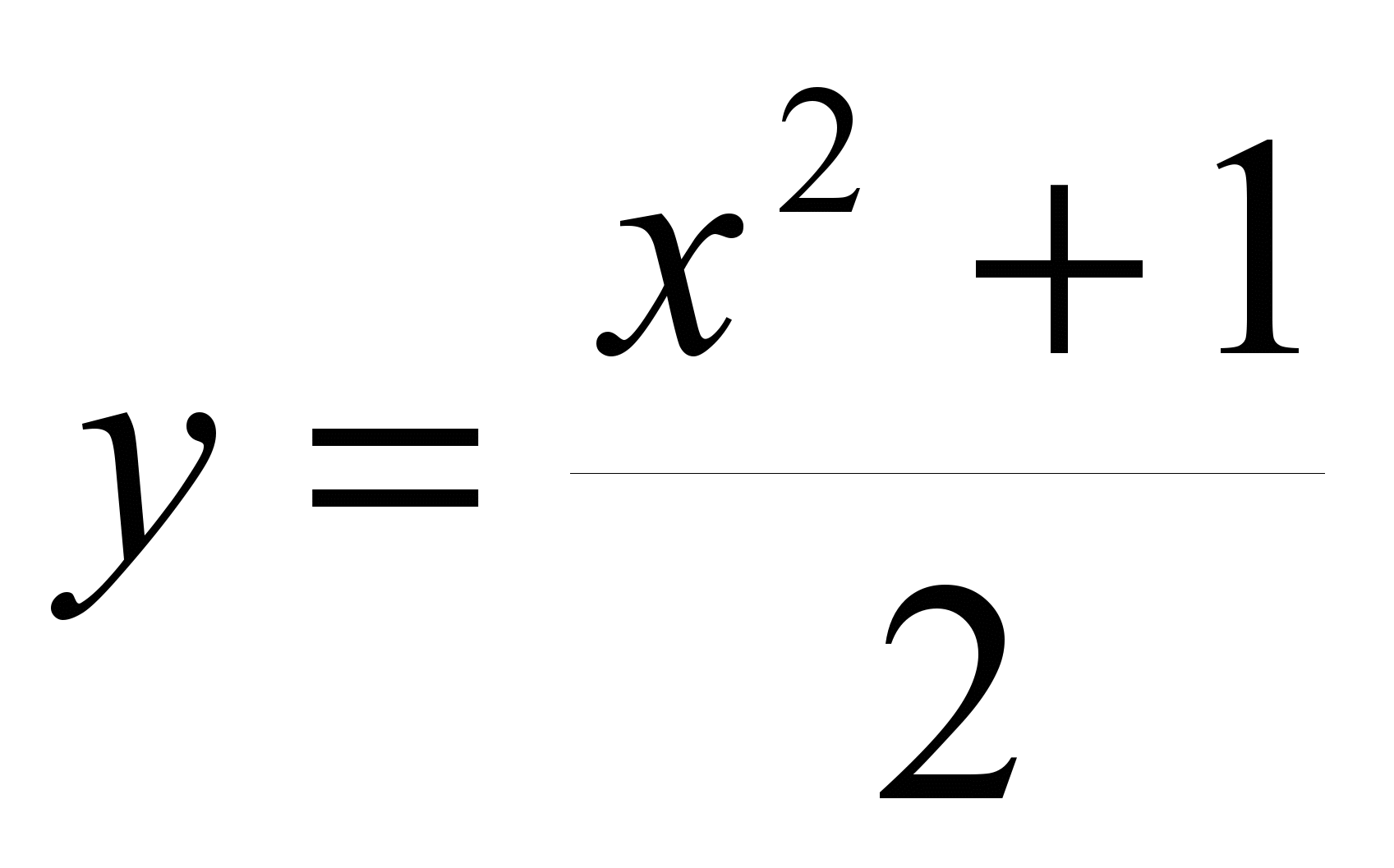 и
и 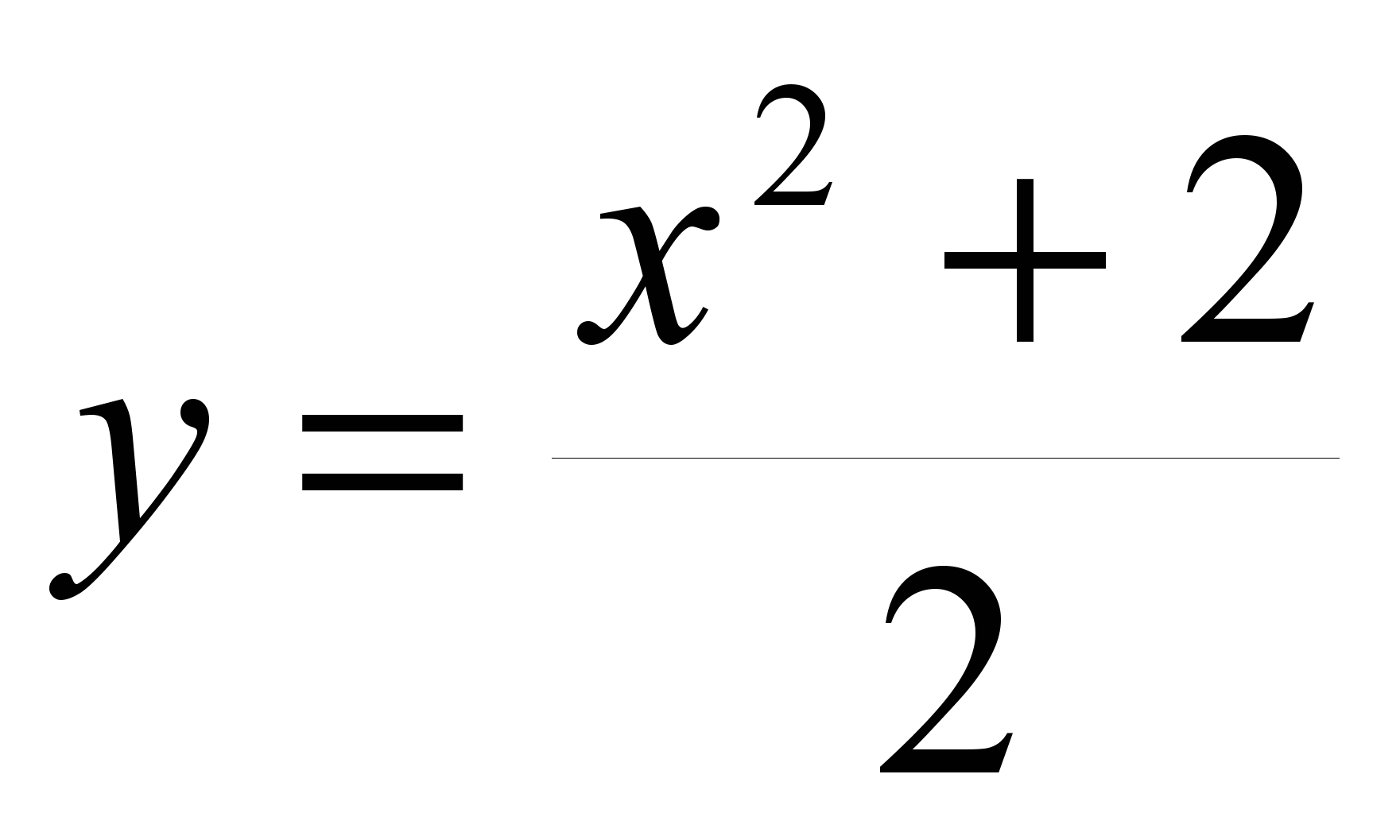 являются первообразными функции
являются первообразными функции ![]() .
.
ТЕОРЕМА 1 (о структуре множества первообразных)
Пусть ![]() и
и ![]() две первообразные функции
две первообразные функции ![]() на
на ![]() . Тогда
. Тогда ![]() .
.
ДОК. Предположим противное : ![]() . Тогда на
. Тогда на
отрезке ![]() для функции
для функции ![]() справедлива теорема Лагранжа :
справедлива теорема Лагранжа :
![]() . Последнее противоречит условию того, что
. Последнее противоречит условию того, что
![]() и
и ![]() две первообразные функции
две первообразные функции ![]() на
на ![]() , поскольку
, поскольку
![]() на
на ![]() .
.
ОПР. Неопределенным интегралом функции ![]() на
на ![]() называется множество всех
называется множество всех
первообразных функции ![]() на
на ![]() . Обозначение
. Обозначение ![]() .
.
Операции дифференцирования и интегрирования обратные в том смысле, что ![]() и
и ![]()
Доказательство этих формул находится на уровне определений понятий дифференциала функции и неопределенного интеграла (самостоятельно). Таким образом, значки d и ![]() стоящие рядом друг друга уничтожают.
стоящие рядом друг друга уничтожают.
В качестве простейших свойств интеграла, вытекающий из его определения, следует отметить его линейность : ![]() .
.
Техника неопределенного интегрирования
А. Замена переменной.
ТЕОРЕМА 2.( о замене переменной в неопределенном интеграле)
Пусть функция ![]() имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке ![]() и
и ![]() ,а функция
,а функция ![]() непрерывна на
непрерывна на ![]() . Рассмотрим две первообразных
. Рассмотрим две первообразных ![]() и
и ![]() .Тогда справедлива формула
.Тогда справедлива формула ![]() .
.
ДОК. ![]() . Тогда
. Тогда
![]() .
.
Пример. Найти интеграл ![]() .
.
РЕШЕНИЕ. Делаем замену ![]() . Тогда
. Тогда  и , по доказанному,
и , по доказанному,
![]() =
=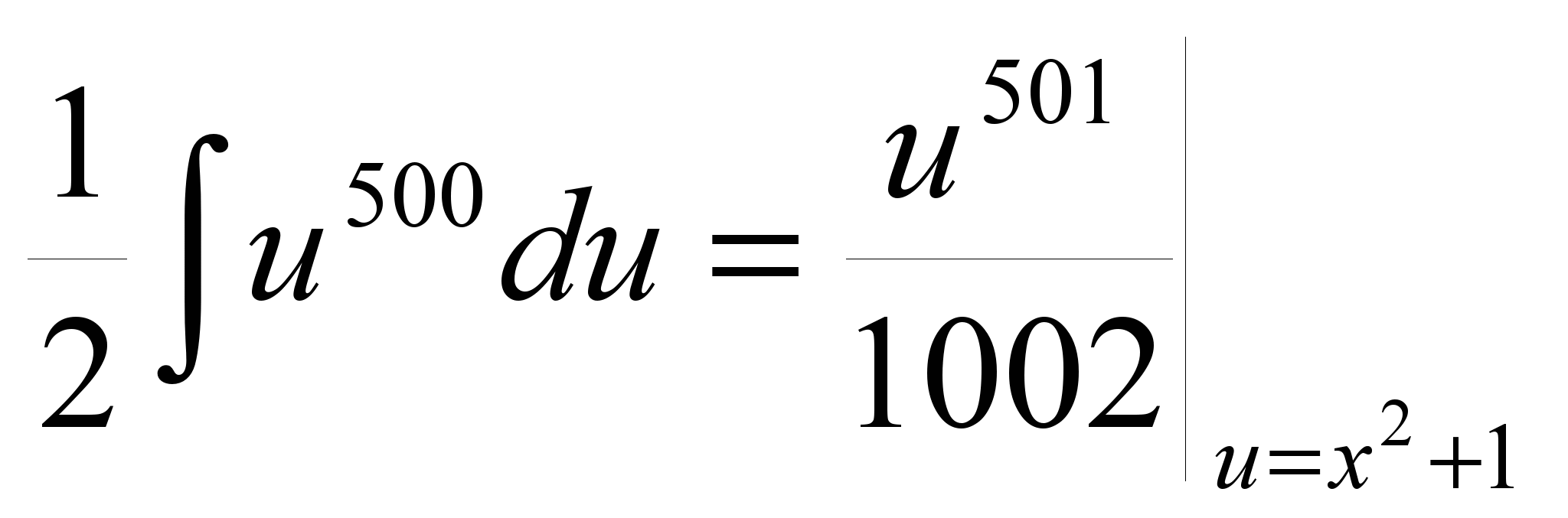
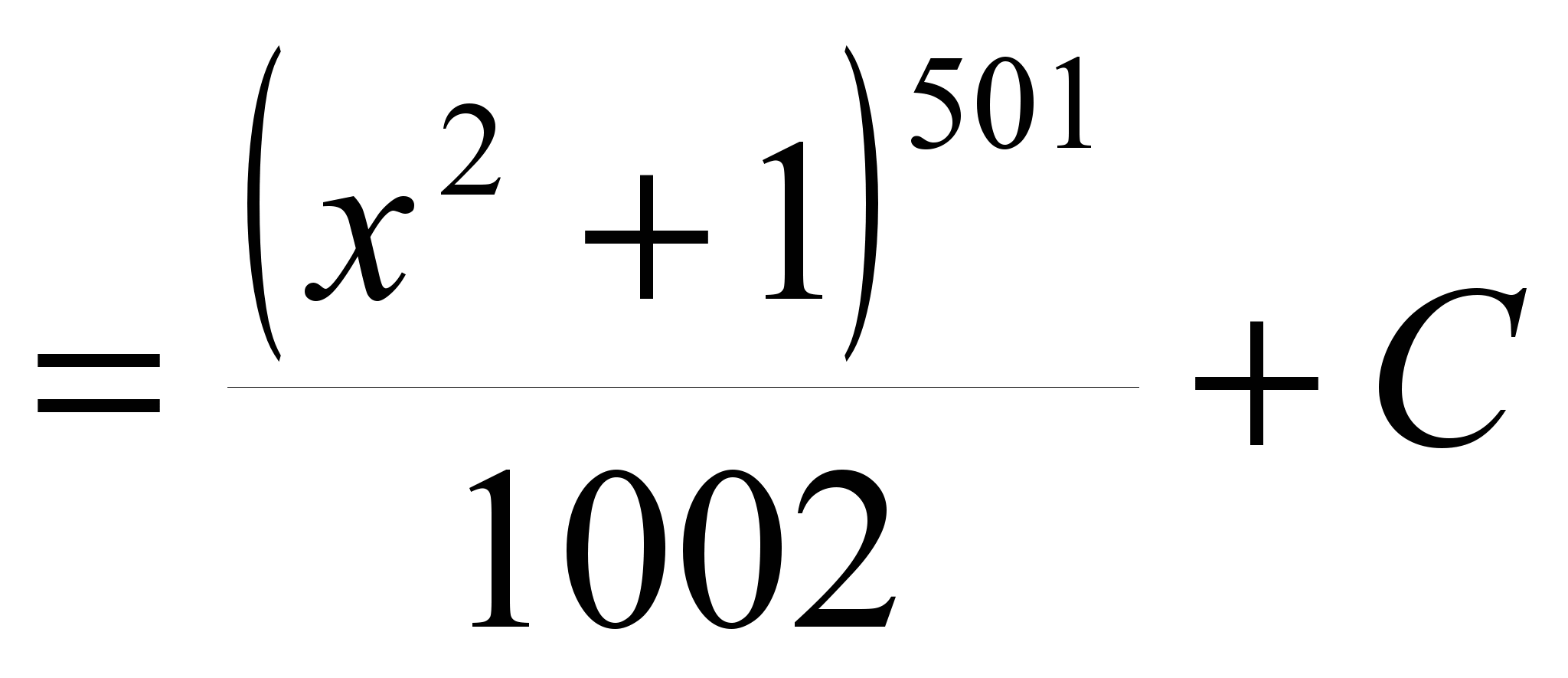 .
.
Б. Интегрирование по частям.
ТЕОРЕМА 3. ( формула интегрирования по частям)
Для любых двух функций ![]() , имеющих непрерывные производные
, имеющих непрерывные производные
на ![]() , справедлива формула
, справедлива формула ![]() .
.
ДОК. ![]()
![]()
![]()
![]() +
+![]() .
.
Формулу интегрирования по частям записывают обычно в дифференциальной форме :
![]()
ПРИМЕР. Вычислить интеграл ![]() .
.
РЕШЕНИЕ. ![]()
![]()
![]() .
.
ПРИМЕР. Вычислить интеграл ![]() .
.
РЕШЕНИЕ. ![]() .
.
П.3 Таблица первообразных элементарных функций.
Следующая таблица является обращением таблицы производных элементарных функций.
Каждый результат проверяется дифференцированием.
1. ![]()
9. 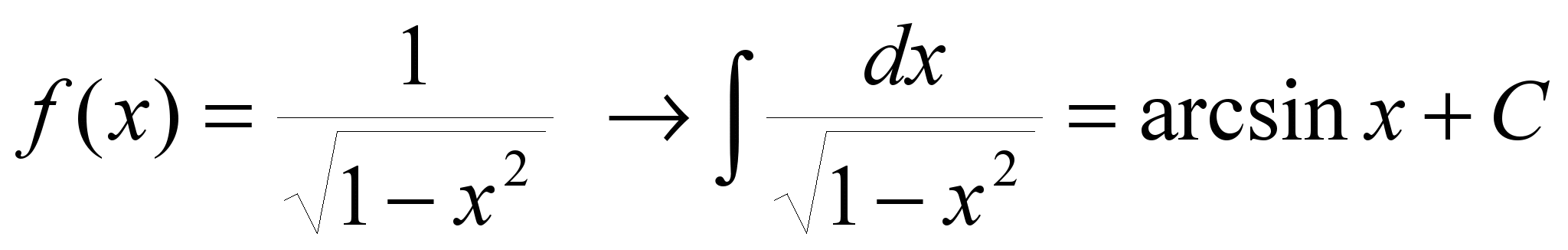
2. 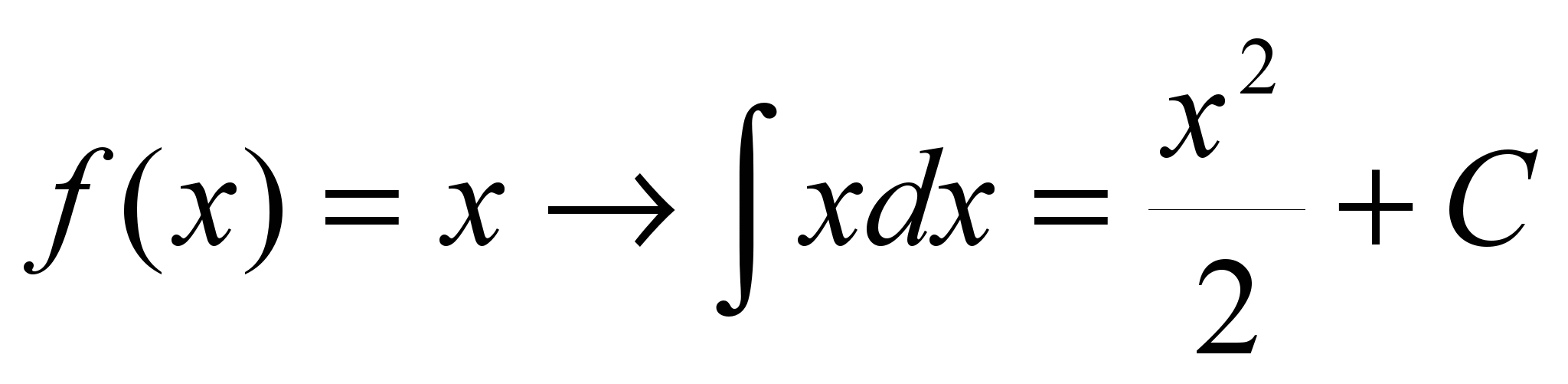
10. ![]()
3. 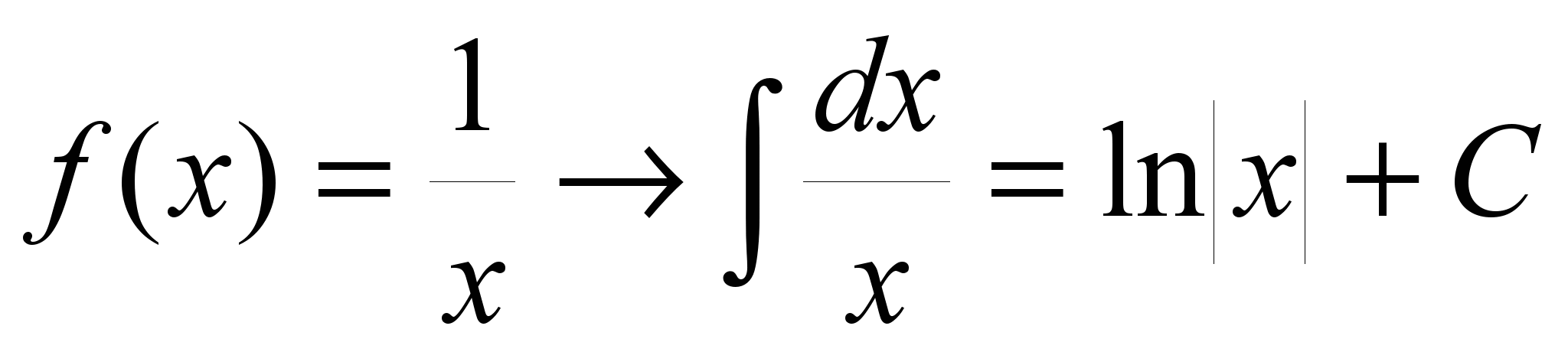
11. ![]()
4. 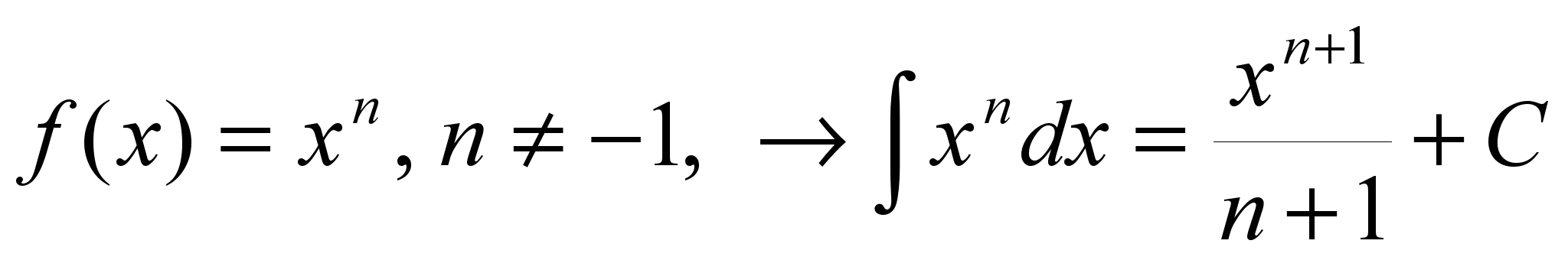
12. ![]()
5. ![]()
13. ![]()
6. 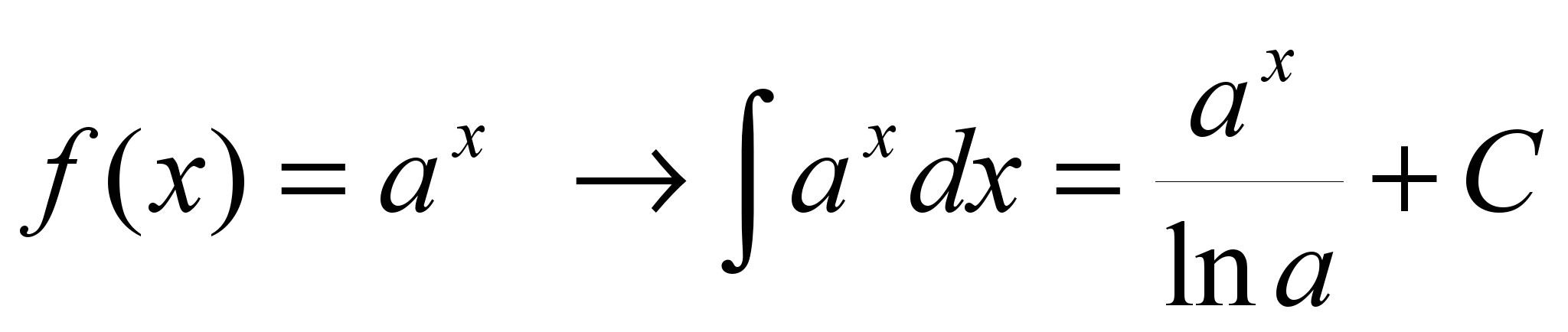
14. 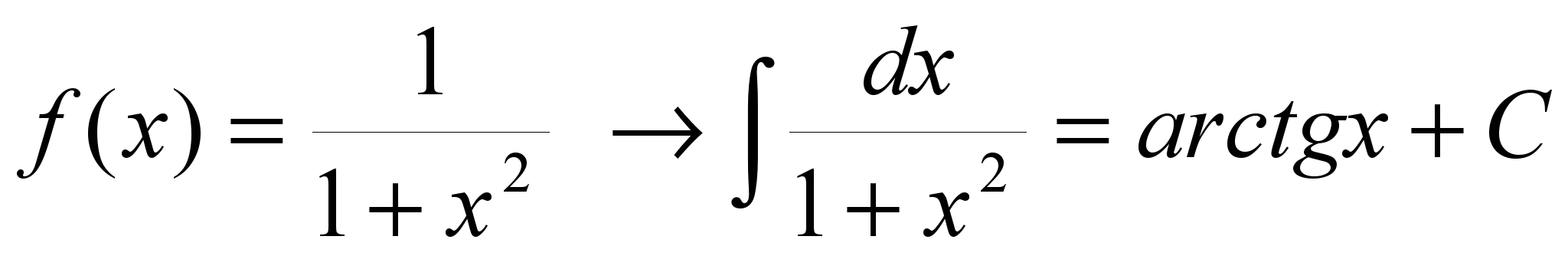
7. ![]()
15. 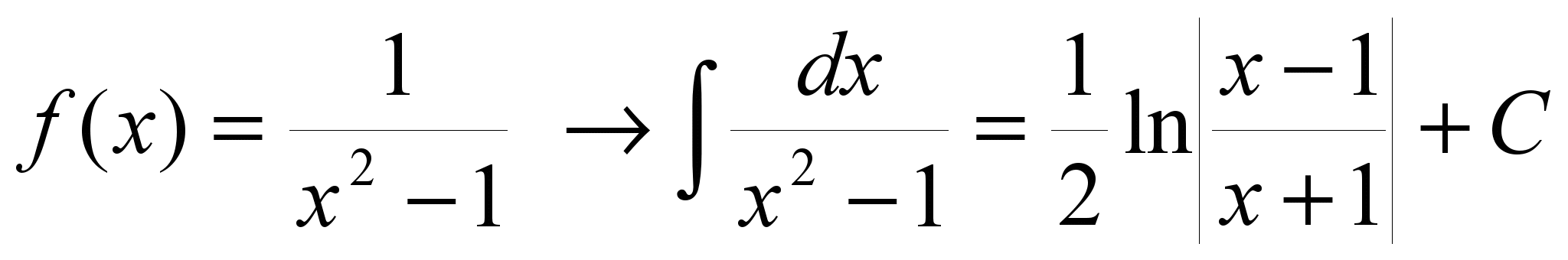
8. 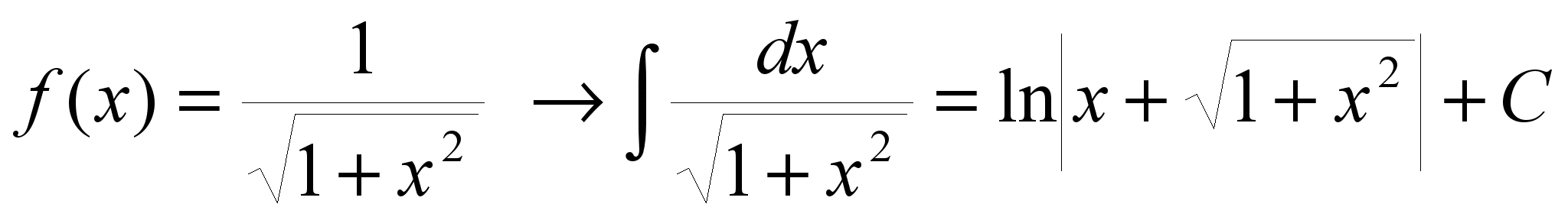
16. 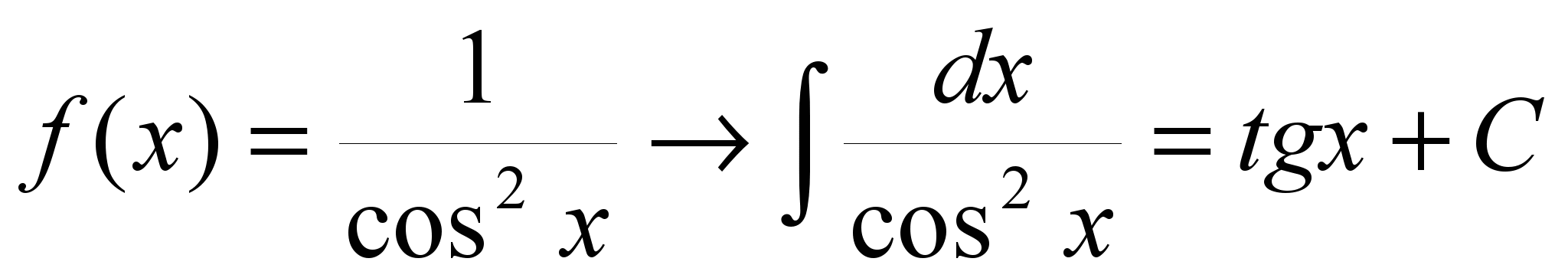
17. 
18. 
19. 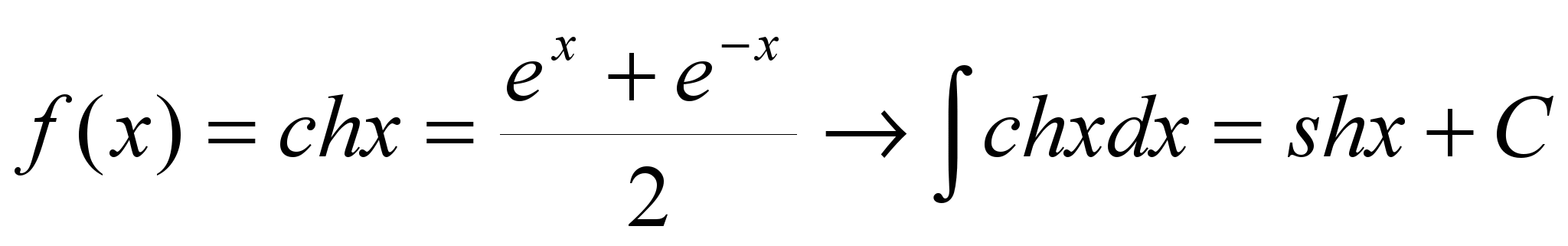
20. 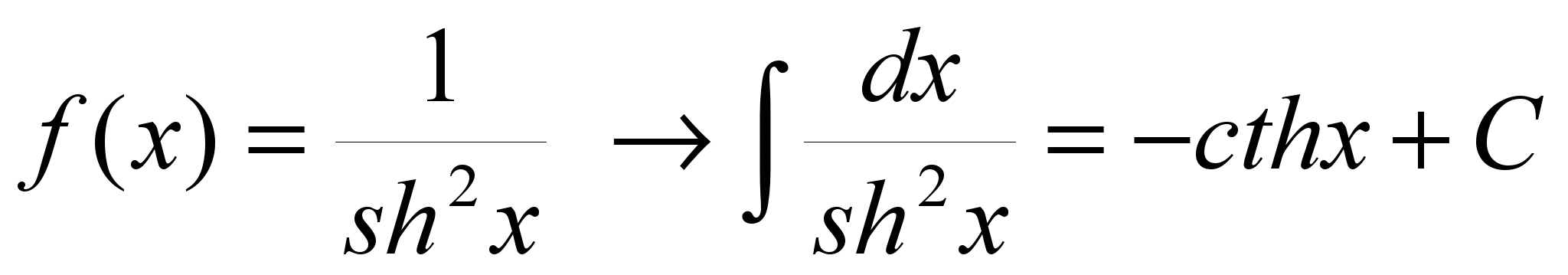
21. 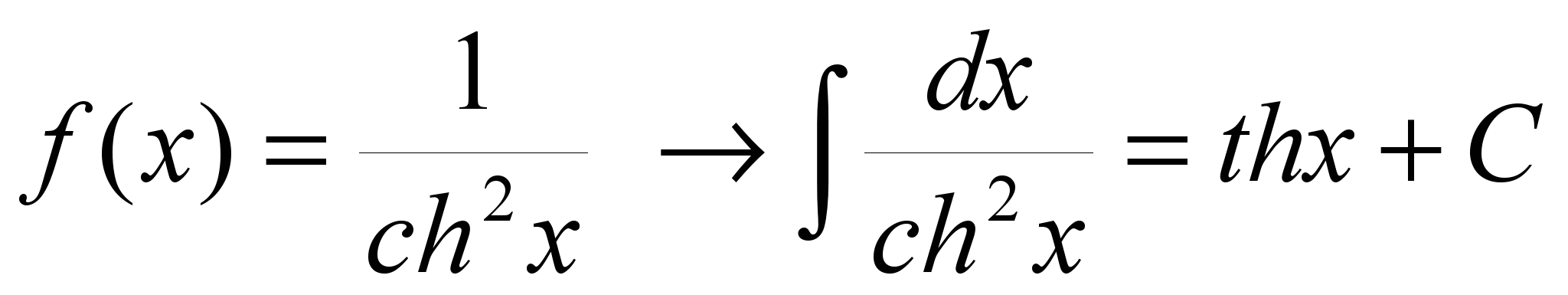 .
.
Контрольные вопросы:
Какая функция называется первообразной функции f(x)?
Что называют неопределенным интегралом функции?
Какие техники интегрирования вам известны? Приведите примеры
Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы (суммы Римана) при стремлении максимальной длины частичного интервала к нулю.
Свойства определенных интегралов:
Определенный интеграл от единицы равен длине интервала интегрирования:
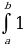 dx=b−a
dx=b−a
Постоянный множитель можно выносить за знак определенного интеграла:
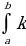 f(x)dx=k
f(x)dx=k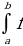 (x)dx
(x)dx
Определенный интеграл от суммы функций равен сумме интегралов от этих функций:
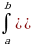 f(x)+g(x)]dx=
f(x)+g(x)]dx=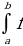 (x)dx+
(x)dx+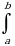 g(x)dx
g(x)dx
Определенный интеграл от разности функций равен разности интегралов от этих функций:
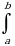 [f(x)−g(x)]dx=
[f(x)−g(x)]dx=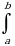 f(x)dx−
f(x)dx−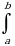 g(x)dx
g(x)dx
Если верхний предел равен нижнему, то определенный интеграл равен нулю:
 f(x)dx=0
f(x)dx=0
При перестановке пределов интегрирования определенный интеграл изменяет знак на противоположный:
 f(x)dx=−
f(x)dx=−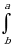 f(x)dx
f(x)dx
Пусть точка c принадлежит отрезку [a,b]. Тогда определенный интеграл от функции f(x) на отрезке [a,b] равен сумме интегралов на частичных промежутках [a,c] и [c,b]:
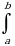 f(x)dx=
f(x)dx= f(x)dx+
f(x)dx+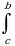 f(x)dx
f(x)dx
Определенный интеграл от неотрицательной функции всегда больше или равен нулю:
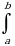 f(x)dx≥0, если f(x)≥0 на [a,b].
f(x)dx≥0, если f(x)≥0 на [a,b].
Определенный интеграл от неположительной функции всегда меньше или равен нулю:
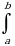 f(x)dx≤0, если f(x)≤0 на [a,b].
f(x)dx≤0, если f(x)≤0 на [a,b].
Формула Ньютона-Лейбница
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедлива формула Ньютона-Лейбница: 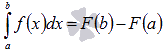 .
.
Формулу Ньютона-Лейбница называют основной формулой интегрального исчисления.
Для доказательства формулы Ньютона-Лейбница нам потребуется понятие интеграла с переменным верхним пределом.
Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента ![]() интеграл вида
интеграл вида  является функцией верхнего предела. Обозначим эту функцию
является функцией верхнего предела. Обозначим эту функцию  , причем эта функция непрерывная и справедливо равенство
, причем эта функция непрерывная и справедливо равенство  .
.
Действительно, запишем приращение функции ![]() , соответствующее приращению аргумента
, соответствующее приращению аргумента ![]() и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
и воспользуемся пятым свойством определенного интеграла и следствием из десятого свойства:
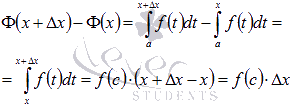
где ![]() .
.
Перепишем это равенство в виде ![]() . Если вспомнить определение производной функции и перейти к пределу при
. Если вспомнить определение производной функции и перейти к пределу при ![]() , то получим
, то получим ![]() . То есть,
. То есть, ![]() - это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как
- это одна из первообразных функции y = f(x) на отрезке [a; b]. Таким образом, множество всех первообразных F(x) можно записать как  , где С – произвольная постоянная.
, где С – произвольная постоянная.
Вычислим F(a), используя первое свойство определенного интеграла: 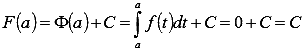 , следовательно,
, следовательно, ![]() . Воспользуемся этим результатом при вычислении F(b):
. Воспользуемся этим результатом при вычислении F(b): 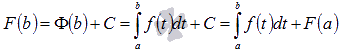 , то есть
, то есть 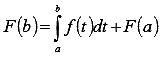 . Это равенство дает доказываемую формулу Ньютона-Лейбница
. Это равенство дает доказываемую формулу Ньютона-Лейбница 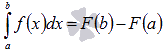 .
.
Приращение функции принято обозначать как ![]() . Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид
. Пользуясь этим обозначением, формула Ньютона-Лейбница примет вид  .
.
Для применения формулы Ньютона-Лейбница нам достаточно знать одну из первообразных y=F(x) подынтегральной функции y=f(x) на отрезке [a; b] и вычислить приращение этой первообразной на этом отрезке. В статье методы интегрирования разобраны основные способы нахождения первообразной. Приведем несколько примеров вычисления определенных интегралов по формуле Ньютона-Лейбница для разъяснения.
Пример.Вычислить значение определенного интеграла ![]() по формуле Ньютона-Лейбница.
по формуле Ньютона-Лейбница.
Решение.
Для начала отметим, что подынтегральная функция ![]() непрерывна на отрезке [1;3], следовательно, интегрируема на нем. (Об интегрируемых функциях мы говорили в разделе функции, для которых существует определенный интеграл).
непрерывна на отрезке [1;3], следовательно, интегрируема на нем. (Об интегрируемых функциях мы говорили в разделе функции, для которых существует определенный интеграл).
Из таблицы неопределенных интегралов видно, что для функции ![]() множество первообразных для всех действительных значений аргумента (следовательно, и для
множество первообразных для всех действительных значений аргумента (следовательно, и для ![]() ) записывается как
) записывается как ![]() . Возьмем первообразную при C = 0:
. Возьмем первообразную при C = 0: ![]() .
.
Теперь осталось воспользоваться формулой Ньютона-Лейбница для вычисления определенного интеграла:  .
.
Геометрический и физический смысл определенного интеграла
Площадь криволинейной трапеции
Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.
Д ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
ля этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х01n) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).
Умножим значением функции ƒ(ci) на длину ∆xi=xi-xi-1соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений
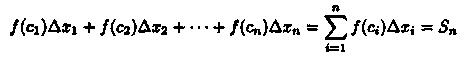
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:
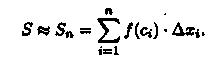
С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0:
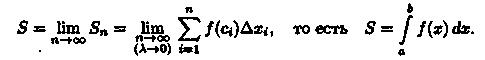
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
В этом состоит геометрический смысл определенного интеграла.
Работа переменной силы
Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.
Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а 0, х1, ..., b = хn (х0 1 n) разобьем на n частичных отрезков [х0; x1], [x1; x2],..., [xn-1; xn]. Сила, действующая на отрезке [xi-1; xi], меняется от точки к точке. Но если длина отрезка Δхi = хi-xi-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = ci Î [xi-1; xi]. Поэтому работа, совершенная этой силой на отрезке [xi-1;xi], равна произведению F(ci)•Δхi (Как работа постоянной силы F(ci) на участке [xi-1; xi].)
Приближенное значение работы А силы F на всем отрезке [а; b] есть

Это приближенное равенство тем точнее, чем меньше длина Δхi Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю: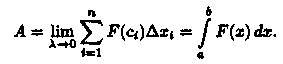 Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].
Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].
В этом состоит физический смысл определенного интеграла.
Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от

t=а до t=b, равен определенному интегралу от скорости v(t):
м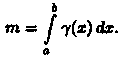 асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от
асса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от
плотности g(х):
Контрольные вопросы:
Что называется определенным интегралом от функции?
Какими свойствами обладают определенные интегралы?
Как выглядит формула Ньютона-Лейбница?
В чем геометрический смысл определенного интеграла?
В чем состоит физический смысл определенного интеграла?







Контрольные вопросы:
Какое уравнение называется дифференциальным?
Что называют порядком дифференциального уравнения?
Что называют решением дифференциального уравнения?
Что называют общим решением дифференциального уравнения? Частным решением дифференциального уравнения?
Какой схемы нужно придерживаться при решении дифференциальных уравнений с разделяющимися переменными?
Дифференциальные уравнения второго порядка
с постоянными коэффициентами





Контрольные вопросы:
Как записывается в общем виде дифференциальное уравнение второго порядка?
Что называется общим решением дифференциального уравнения второго порядка?
Что называется частным решением дифференциального уравнения второго порядка?
Какое уравнение называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами?
Какой определитель называется определителем Вронского?
Выражение  (1)
(1)
называется числовым рядом, числа 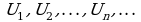 - членами ряда,
- членами ряда, 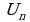 - общим членом ряда.
- общим членом ряда.
Сумма n первых членов ряда 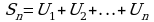 называется частичной суммой этого ряда.
называется частичной суммой этого ряда.
Ряд 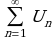 называется сходящимся, если последовательность его частичных сумм имеет конечный предел:
называется сходящимся, если последовательность его частичных сумм имеет конечный предел: 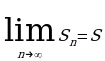 Значение S называется суммой ряда.
Значение S называется суммой ряда.
Если ряд не сходиться, то он называется расходящимся.
Признаки сходимости рядов
Необходимый признак сходимости ряда.
Если ряд (1) сходится, то  . (3)
. (3)
Этот признак сходимости является необходимым, но не достаточным.
Достаточный признак расходимости.
Если для ряда (1) предел 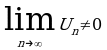 или не существует, то ряд расходится.
или не существует, то ряд расходится.
Признак Даламбера. Если для ряда (1)существует 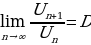 (4)
(4)
то при D1 ряд расходится, при DD=1 вопрос остается нерешенным.
Признак Коши. Если для ряда (1) существует  (5)
(5)
то при C 1 ряд расходится, при C = 1 вопрос остается нерешенным.
Пример1 Исследовать на сходимость ряд 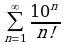 .
.
Решение:
Применим признак Даламбера; имеем 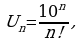
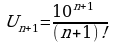 ,
,

Так как D
Пример2. Исследовать на сходимость ряд 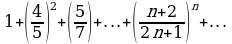
Решение:
Признак Коши для этого ряда дает: 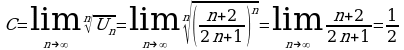 .
.
Так как C
Алгоритм исследования на сходимость знакопеременных рядов
Исследовать на сходимость ряд, составленный из модулей членов данного ряда, используя
какой-либо признак сравнения.
Сделать вывод об абсолютной или условной сходимости этого ряда.
Выяснить, сходится ли данный знакочередующийся ряд, применяя признак Лейбница.
Для этого:
- Проверить, выполняется ли равенство для абсолютных величин членов ряда
- Найти предел общего члена ряда
- Сделать вывод о сходимости данного исходного ряда


Контрольные вопросы:
Что называют числовым рядом?
Какой ряд называется сходящимся / расходящимся?
Какие признаки сходимости рядов вам известны? Сформулировать их.
Как исследовать на сходимость знакопеременные ряды?
Какой ряд называется функциональным?
Что нужно сделать для определения области сходимости функционального ряда?
Как разложить функцию в ряд Маклорена?
Теория вероятностей –математическая наука, изучающая закономерности случайных явлений и событий, способных многократно повторяться при воспроизведении определенного комплекса условий.
Испытание – неопределяемое понятие, понимается как наблюдение того или иного явления. Событие – возможный исход того или иного испытания.
Определение1:Результат наблюдения или эксперимента, который при данном испытании может произойти, а может и не произойти, называется случайным событием.
Определение2:Событие, которое обязательно наступает при каждом испытании, называется достоверным.
Определение3:Событие, которое заведомо не может произойти, называется невозможным.
Определение4:Два события называются равносильными, если при каждом испытании они либо оба наступают, либо оба не наступают.
Определение5:События, которые не могут произойти одновременно в результате испытания, называются несовместными.
Определение6: Под множеством элементарных событий задачи понимают полное множество взаимоисключающих исходов эксперимента.
Пример: 1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки».
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, выпадание двойки, тройки и т.д…
Определение7 (классическое определение вероятности): Вероятностью события называется число, равное отношению числа исходов испытания, благоприятствующих событию (m) к числу всевозможных исходов испытания (n).
Обозначается: P(A)= ![]() , P – вероятность случайного события, A – само событие.
, P – вероятность случайного события, A – само событие.
Примеры:
1) Пусть эксперимент состоит в подбрасывании монеты. Два элементарных события: «выпадание орла» и «выпадание решки», значит n=2. Тогда вероятность события-«выпадание орла» равна P(A)= ![]() , где m=1.
, где m=1.
2) Пусть эксперимент состоит в подбрасывании кости. Шесть элементарных событий: выпадание единицы на верхней грани кости, и т.д… Вероятность события «выпадание шести очков на грани кости» равна P(A)= ![]() , где m=1.
, где m=1.
Определение 8. Событие (А и B), т. е. событие, состоящее в наступлении обоих событий А и B, называется произведением событий А и B и обозначается через АB
Определение 9. Событие (А или B), т. е. событие, состоящее в наступлении хотя бы одного из событий А и B, называется суммой событий А и B и обозначается через А+B
Теорема сложения вероятностей (для попарно несовместимых событий): вероятность того, что произойдет хотя бы одно из попарно несовместимых событий, равна сумме вероятностей этих событий P(A+B+ C) = P(A) + P(B) + P(C).
Теорема произведения вероятностей (для попарно независимых событий): вероятность того, что произойдут одновременно независимые события, равна произведению вероятностей P(A•B) = P(A) • P(B).
Задача 1.В двух коробках лежат карандаши.В первой коробке – 4 синих и 3 красных карандаша. Во второй коробке – 2 синих, 2 красных. Одновременно из двух коробок извлекают по одному карандашу. Найти вероятность того, что оба карандаша окажутся красными.
Решение: Пусть А- событие, что вынут красный карандаш из первой коробки. По классическому определению вероятности P(A)= 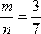 , где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)=
, где m=3, так как благоприятных исхода 3- в первой коробке 3 красных карандаша, а всего карандашей 7, значит n=7. Пусть В – событие, что вынут красный карандаш из второй коробки. Аналогично, P(В)= ![]() . Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) =
. Тогда по теореме произведения вероятностей, так как события происходят одновременно P(A•B) = P(A) • P(B) = ![]() .
.
Случайная величина - величина, которая при каждом испытании принимает то или иное числовое значение (наперед неизвестно, какое именно), зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины обозначают заглавными буквами латинского алфавита, а возможные значения случайной величины – малыми. Так, при бросании игрального кубика происходит событие, связанное с числом x , где x – выпавшее число очков. Число очков – случайная величина, а числа 1, 2, 3, 4, 5, 6 – возможные значения этой величины. Расстояние, которое пролетит снаряд при выстреле из орудия – тоже случайная величина (зависит от установки прицела, силы и направления ветра, температуры и других факторов), а возможные значения этой величины принадлежат некоторому промежутку (a; b).
Дискретная случайная величина – случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины – бесконечно.
Например, число выпавших очков при бросании кубика, балльная оценка за контрольную работу – дискретные случайные величины; расстояние, которое пролетает снаряд при стрельбе из орудия, погрешность измерений показателя времени усвоения учебного материала, рост и вес человека – непрерывные случайные величины.
Раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненным тем или иным условиям, можно составить из заданных объектов называется комбинаторикой.
Правило суммы: если элемент ![]() можно выбрать
можно выбрать ![]() различными способами и независимо от него элемент
различными способами и независимо от него элемент ![]() можно выбрать
можно выбрать ![]() различными способами, то выбрать все различные комбинации элементов «
различными способами, то выбрать все различные комбинации элементов «![]() или
или ![]() » можно сделать
» можно сделать ![]() способами.
способами.
Правило произведения: если элемент ![]() можно выбрать
можно выбрать ![]() различными способами и независимо от него элемент
различными способами и независимо от него элемент ![]() можно выбрать
можно выбрать ![]() различными способами, то все различные комбинации элементов «
различными способами, то все различные комбинации элементов «![]() и
и ![]() » можно выбрать
» можно выбрать ![]() способами.
способами.
Правила суммы и произведения естественным образом обобщаются и на случай комбинаций многих элементов, а именно, если первый элемент совокупности из ![]() различных элементов можно выбрать
различных элементов можно выбрать ![]() способами, второй —
способами, второй — ![]() способами и так далее,
способами и так далее, ![]() -й элемент —
-й элемент — ![]() способами, то всевозможных комбинаций соответственно
способами, то всевозможных комбинаций соответственно ![]() и
и ![]() .
.
Произведение ![]() первых натуральных чисел называется n-факториал и обозначается n!; По определению:
первых натуральных чисел называется n-факториал и обозначается n!; По определению: ![]() .
.

Перестановки без повторений

Перестановки в ряд
Перестановкой из ![]() элементов (или
элементов (или ![]() -перестановкой) называется
-перестановкой) называется ![]() -элементное упорядоченное множество, составленное из элементов
-элементное упорядоченное множество, составленное из элементов ![]() -элементного множества.
-элементного множества.
Иначе: Перестановкой из ![]() элементов (или
элементов (или ![]() -перестановкой) называется размещение из
-перестановкой) называется размещение из ![]() элементов по
элементов по ![]() без повторений.
без повторений.
Число перестановок из ![]() элементов без повторений обозначается
элементов без повторений обозначается ![]() от французского словаperturbation.
от французского словаperturbation.
Теорема: число способов расположить в ряд ![]() различных объектов есть
различных объектов есть
![]()
Замечание: Рекуррентная формула: ![]() .
.
Перестановки симметричных объектов
![]() различных предметов можно расположить по кругу
различных предметов можно расположить по кругу ![]() способами, а если их можно еще и переворачивать, то
способами, а если их можно еще и переворачивать, то ![]() различными способами.
различными способами.

Размещения без повторений

Подсчитаем количество способов расположить ![]() различных элементов по
различных элементов по ![]() различным позициям (
различным позициям (![]() ). Такие расположения называются размещениями, а их количество, от французского слова arrangement обозначается
). Такие расположения называются размещениями, а их количество, от французского слова arrangement обозначается ![]() . В случае, если
. В случае, если ![]() количество предметов совпадает с количеством имеющихся мест, и это уже изученная задача о числе перестановок.
количество предметов совпадает с количеством имеющихся мест, и это уже изученная задача о числе перестановок.
Если из ![]() объектов выбирают
объектов выбирают ![]() штук, то число выборов последнего объекта есть
штук, то число выборов последнего объекта есть ![]() невыбранных объектов, что означает наличие
невыбранных объектов, что означает наличие ![]() возможности выбора последнего выбранного объекта. То же, другими словами: после выбора первых
возможности выбора последнего выбранного объекта. То же, другими словами: после выбора первых ![]() элемента остается выбрать
элемента остается выбрать ![]() элемент.
элемент.
Теорема: число размещений ![]() различных элементов по
различных элементов по ![]() различным позициям есть
различным позициям есть
![]() ,
,
или, в терминах факториалов,
![]() .
.
Примечание: заметим, что в случае, когда число мест, по которым размещают предметы, совпадает с количеством самих предметов, т. е. когда ![]() , рассматриваемая задача становится задачей о числе перестановок. В нашем случае при этом мы получаем в знаменателе дроби ноль факториал, и для того, что бы разные формулы, соответствующие одной и той же задаче, приводили к одинаковым результатам, полагают, что
, рассматриваемая задача становится задачей о числе перестановок. В нашем случае при этом мы получаем в знаменателе дроби ноль факториал, и для того, что бы разные формулы, соответствующие одной и той же задаче, приводили к одинаковым результатам, полагают, что ![]() .
.

Сочетания

Подсчитаем количество способов, которыми можно выбрать ![]() из
из ![]() различных предметов. Такие выборки называются сочетаниями, а их количество обозначается
различных предметов. Такие выборки называются сочетаниями, а их количество обозначается ![]() .
.
При ![]() , выбрать k предметов из n можно
, выбрать k предметов из n можно ![]() способами, переставляя их
способами, переставляя их ![]() способами:
способами:
![]() .
.
Рекуррентная формула: ![]() .
.
Свойства сочетаний: ![]() ;
;![]() .
.

Перестановки с повторениями

Пусть даны ![]() элементов первого типа,
элементов первого типа, ![]() — второго типа, ...,
— второго типа, ..., ![]() —
— ![]() -го типа, всего
-го типа, всего ![]() элементов. Способы разместить их по
элементов. Способы разместить их по ![]() различным местам называются перестановками с повторениями. Их количество обозначается
различным местам называются перестановками с повторениями. Их количество обозначается ![]() .
.
Теорема: число перестановок с повторениями есть
![]() .
.

Размещения с повторениями

Пусть даны ![]() различных видов предметов, которые можно разместить по
различных видов предметов, которые можно разместить по ![]() различным местам, причем выбирать предметы можно с повторениями (т.е. можно выбрать несколько предметов одного вида). Такие выборки называются размещениями с повторениями, а их количество вычисляется по формуле:
различным местам, причем выбирать предметы можно с повторениями (т.е. можно выбрать несколько предметов одного вида). Такие выборки называются размещениями с повторениями, а их количество вычисляется по формуле: ![]() .
.

Сочетания с повторениями

Пусть имеются предметы ![]() различных видов предметов, и из них составляются наборы, содержащие
различных видов предметов, и из них составляются наборы, содержащие ![]() элементов. Такие выборки называются сочетаниями с повторением. Их число обозначается
элементов. Такие выборки называются сочетаниями с повторением. Их число обозначается ![]() .
.
Теорема: число сочетаний с повторениями может быть вычислено по формулам:
![]() .
.
Контрольные вопросы:
Что изучает теория вероятностей?
Что такое испытание? Событие?
Какое событие называется случайным? Достоверным? Невозможным?
Какие события называются равносильными? Несовместными?
Как звучит классическое определение вероятности события?
Какие теоремы вероятностей вам известны? Сф1ормулируйте их
Какая величина называется случайной? Дискретной? Непрерывной?
Что изучает комбинаторика?
Что такое перестановка? Размещение? Сочетание? (без повторений)
Как найти число перестановок/ размещений/ сочетаний с повторениями?
Математической статистикой называется наука, занимающаяся методами обработки экспериментальных данных, полученных в результате наблюдений над случайными явлениями.
Первая задача математической статистики: указать способы сбора и группировки статистических данных, полученных в результате экспериментов.
Вторая задача математической статистики: разработать методы анализа статистических данных.
Ко второй задаче относятся:
Оценка неизвестных параметров (вероятности события, функции распределения и её параметров и т.д.) с построением доверительных интервалов (методы оценивания).
Проверка статистических гипотез о виде неизвестного распределения и параметров распределения (методы проверки гипотез).
При этом решаются следующие в порядке сложности и важности задачи:
Описание явлений, то есть, упорядочение поступившего статистического материала, представление его в наиболее удобном для обозрения и анализа виде (таблицы, графики).
Анализ и прогноз, то есть приближённая оценка характеристик на основании статистических данных. Например, приближённая оценка математического ожидания и дисперсии наблюдаемой случайной величины и определение погрешностей этих оценок.
Выработка оптимальных решений. Например, определение числа опытов n, достаточного для того, чтобы ошибка от замены теоретических числовых характеристик их экспериментальными оценками не превышала заданного значения. В связи с этим возникает задача проверки правдоподобия гипотез о параметрах распределения и о законах распределения случайной величины, решением которой является возможность сделать один из выводов:
– отбросить гипотезу, как противоречащую опытным данным;
– принять гипотезу, считать ее приемлемой.
Математическая статистика помогает экспериментатору лучше разобраться в опытных данных, полученных в результате наблюдений над случайными явлениями; оценить, значимы или не значимы наблюдаемые факты; принять или отбросить те или иные гипотезы о природе случайных явлений.
Генеральной совокупностью называют полный набор всех возможных N значений дискретной случайной величины Х. Практически сложно получить полную информацию о случайной величине. Поэтому случайным образом отбирают объекты, которые называется выборкой, при этом число – n называется объемом выборки. Выборку делают либо из ранее полученных результатов, либо планируют эксперимент. По результатам выборки строят простой статистический ряд в виде таблицы, состоящей из двух строк, в первой – порядковый номер измерения, во второй – его результат xi. Затем производят группировку данных. Вначале xi располагают в порядке возрастания, интервал наблюдаемых значений случайной величины разбивают на последовательные непересекающиеся частичные интервалы, далее подсчитывают количество значений xi, попавших в каждый интервал, т.е. ni. Таким образом, получается группированный статистический ряд или статистическое распределение выборки. Статистическим распределением выборки или статистическим рядом называют перечень вариант и соответствующих им частот или относительных частот.
Пример 1. После группировки данных в выборке статистический ряд задан таблицей 6.1 (где объем выборки n = 15).
Таблица 6.1
| i | 1 | 2 | 3 | 4 |
| xi | 2 | 3 | 5 | 10 |
| ni | 5 | 5 | 3 | 2 |
В таблице 6.1 значения xi называют вариантами. Последовательность вариант, записанных в возрастающем порядке (вся строка xi) называется вариационным рядом. Число наблюдений ni называют частотами, i – номер варианты.
Учитывая, что ![]() – это объем выборки, можно найти относительную частоту pi=ni/n, наблюдаемого значения xi – варианты, k – количество вариант.
– это объем выборки, можно найти относительную частоту pi=ni/n, наблюдаемого значения xi – варианты, k – количество вариант.
Тогда таблица 6.1 будет иметь вид:
Таблица 6.2
| i | 1 | 2 | 3 | 4 |
| xi | 2 | 3 | 5 | 10 |
| ni/n | 0,33 | 0,33 | 0,2 | 0,14 |
Табличные данные могут быть представлены графически в виде полигона или гистограммы. Если выборка задана в виде отдельных точек, а не интервалов, тогда строят полигон частот. Полигоном частот называется ломанная, отрезки которой соединяют точки (x;; ni/n). На рис.6.1 изображен полигон относительных частот, приведённых в таблице 6.2.

Рис. 6.1. Полигон
Пример 2. В этом примере наблюдаемые значения случайной величины после группировки данных в выборке разбиты на последовательные непересекающиеся частичные интервалы. В результате получается статистический ряд, который задан таблицей 6.3.
Таблица 6.3
| i | 1 | 2 | 3 | 4 |
| xi | 0-2 | 2-4 | 4-6 | 6-8 |
| ni | 5 | 10 | 12 | 3 |
Данную таблицу можно представить через относительную частоту pi =ni/n (где объем выборки n = 30).
Таблица 6.4
| i | 1 | 2 | 3 | 4 |
| xi | 0-2 | 2-4 | 4-6 | 6-8 |
| рi=ni/n | 0,17 | 0,33 | 0,4 | 0,1 |
При этом частоты рi удовлетворяют условию ![]() =1. Если выборка задана в виде интервалов, тогда строят гистограмму.
=1. Если выборка задана в виде интервалов, тогда строят гистограмму.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы xi, их высоты равны рi =ni/n (плотности относительной частоты). На рис. 6.2 изображена гистограмма относительных частот, приведённых в таблице 6.4.

Рис. 6.2. Гистограмма
Контрольные вопросы:
Чем занимается математическая статистика?
Что называется генеральной совокупностью?
Что такое выборка? Объем выборки?
Что такое вариационный ряд? Частоты?
Что называют полигоном частот? Гистограммой частот?
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
Н.В. Богомолов. Математика: учебник для среднего профессионального образования – М: Дрофа, 2019.
Н.В. Богомолов. Сборник задач по математике: учебное пособие для ссузов. – М: Дрофа, 2019.
И.И. Баврин. Высшая математика. - М: Академия, 2018.
В.П. Григорьев, Ю. А. Дубинский. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования. – М.: Издательский центр «Академия», 2018.
В. П. Григорьев, Т. Н. Сабурова. Сборник задач по высшей математике: учебное пособие для студ. учреждений сред. проф. образования.- М.: Издательский центр «Академия», 2018.
С. В. Григорьев, С.В, Иволгина. Математика: учебник для студ. образоват. учреждений сред. проф. образования. – М.: Издательский центр «Академия», 2017.
И. Д. Пехлецкий. Математика : учебник для студ. учреждений сред. проф. образования. – М.: Издательский центр «Академия», 2017.
М. С. Спирина, П. А. Спирин. Теория вероятностей и математическая статистика: учебник для студ. учреждений сред. проф. образования. – М.: Издательский центр «Академия», 2017.
Дополнительные источники:
М.Я.Выготский. Справочник по высшей математике. – М.:Росткнига, 2018
В.Е.Гмурман. Руководство по решению задач по теории вероятностей и математической статистики. – М.: Высшее образование, 2017
А.А.Дадаян. Математика. – М.: ФОРУМ: ИНФРА, 2017
А.А.Дадаян. Сборник задач по математике. – М.: ФОРУМ: ИНФРА, 2017
И.Л.Зайцев. Элементы высшей математики для техникумов. – М.: Наука, 2017
В.А.Подольский, А.М.Суходольский, Е.С.Мироненко. Сборник задач по математике. – М.: Высшая школа, 2017
Интернет-ресурсы и электронные носители:


© 2024, Федорченко Александр Сергеевич 59 0
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Полезное для учителя