
к.п.н., преподаватель высшей категории Никитин М.Е. Раменское, 2018

Множества. Основные определения.
Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.
Объекты, из которых состоит множество, называют его элементами .
Множество, не содержащее ни одного элемента, называют пустым и обозначают .

Множества, элементами которых являются числа, называют числовыми . Примерами числовых множеств являются:
множество натуральных чисел;
N
Z
множество целых чисел;
множество рациональных чисел;
Q
R
множество действительных чисел.

В дальнейшем для сокращения записей будем использовать некоторые логические символы:
означает «для любого», «для всякого», «каждый»;
означает «существует», «найдется»;
: «имеет место», «такое, что»;
и
равносильны»;
«предложения
следует
«из предложения
предложение
» .

Числовые промежутки. Окрестность точки.
Пусть
и
действительные числа, причем
Числовыми промежутками (интервалами) называются подмножества всех действительных чисел, имеющих следующий вид
отрезок;
интервал;
полуинтервал;
полуинтервал.

называются соответственно левым и правым концами промежутков .
Числа и
Пусть
любое действительное число (точка на числовой оси).
Окрестностью точки
называется любой интервал
содержащий точку
В частности, интервал
, где
называется
окрестностью точки
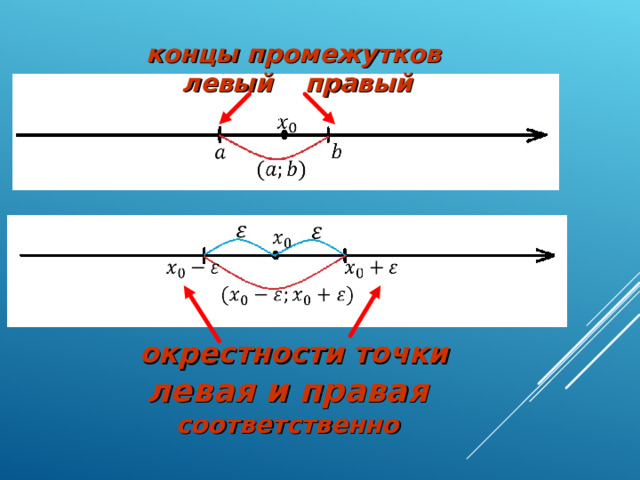
концы промежутков
левый и правый
окрестности точки
левая и правая
соответственно

Понятие функции. Способы задания функций.
и
Пусть даны два непустых множества
Правило
по которому каждому элементу
поставлен в соответствие один и только один элемент
называется функцией и записывается
или
называется областью
При этом множество
определения функции и обозначается
множеством
а множество
или
значений функции

Существуют следующие способы задания функций:
1) графический: задается график функции;
2) табличный: функция задается таблицей ряда значений аргумента и соответствующих значений функции;
3) аналитический: функция задается в виде одной или нескольких формул или уравнений.
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию

Основные характеристики функции
1) Функция
определенная на множестве
называется четной , если и
и
выполняются условия:
2) нечетной , если
выполняются условия:
и
График четной функции симметричен относительно оси
а нечетной относительно точки С (0;0), т.е. начала координат.

3) Функция
называется возрастающей
на интервале
если
выполняется условие
4) Функция
называется убывающей
на интервале
если
выполняется условие
Возрастающие и убывающие функции называются строго монотонными .
Интервалы, на которых функции монотонны, называются интервалами монотонности.

Числовая последовательность. Предел числовой последовательности .
Функция, областью определения которой является
N натуральных чисел, называется
множество
числовой последовательностью и обозначается
или
или
При этом
называется n -ым членом
последовательности.
Пример : Формула
задает последовательность:
Геометрически каждому члену последовательности соответствует точка на числовой оси

последовательно
Пусть функция
принимает значения:
т.е.пробегает последовательность
Важным случаем такого изменения функции является тот, при котором по мере возрастания номера
соответствующие значения
неограниченно приближаются (стремятся)
к некоторому постоянному значению
в этом случае говорят, что
стремится к пределу
последовательность
Но выражения «неограниченно приближаются», «стремятся» неопределенные и поэтому не годятся для точного математического понятия предела.

Для точного определения понятия « предел » введем произвольное малое положительное число
поскольку оно произвольно, его по желанию можно задавать равным 0,01, и 0,001, и вообще
Факт неограниченного сближения последовательности
можно охарактеризовать так:
с постоянной
каково бы ни было малое положительное число
в процессе изменения последовательности рано или поздно должен наступить такой момент, начиная с которого все ее дальнейшие значения
будут отличаться от
по абсолютному значению меньше , чем на это произвольное малое положительное число

Определение. Число называется пределом
последовательности если для любого
положительного числа найдется такое
натуральное число что для всех номеров будет выполняться неравенство
Кратко определение предела можно записать так:

Геометрический смысл определения предела последовательности:
Неравенство
равносильно неравенствам
или
т.е.
Поэтому определение предела последовательности можно сформулировать так:
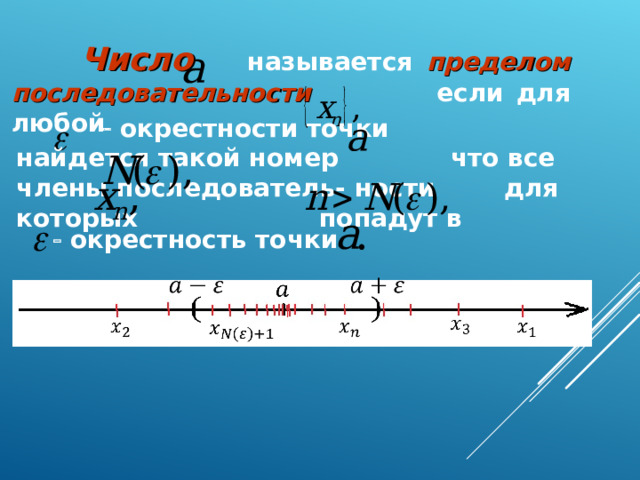
Число называется пределом последовательности если для любой
окрестности точки найдется такой номер что все члены последователь- ности для которых попадут в
окрестность точки

Предел функции в точке. Бесконечно большая и бесконечно малая функция.
Рассмотрим функцию
непрерывно изменяющегося аргумента
и предположим, что аргумент
стремится к
некоторому числу
Может случиться, что при неограниченном приближении аргумента к числу
соответствующие значения функции
неограниченно приближаются к некоторому числу
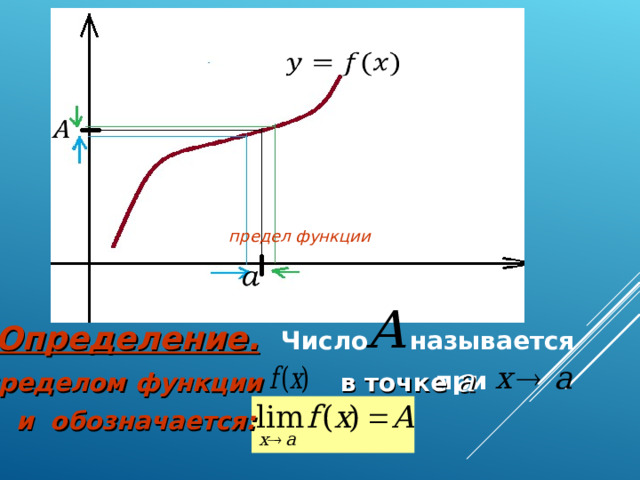
предел функции
Определение. Число
называется
пределом функции в точке а
при
и обозначается:

Бесконечно большая функция (б.б.ф)
называется
Определение. Функция
бесконечно большой функцией
при
если для любого числа
найдется такое положительное число
что для всех
зависящее от выбора
удовлетворяющих условию
будет выполняться:
и обозначается:

Бесконечно малая функция (б.м.ф.).
Связь между б.м.ф. и б.б.ф.
Определение. Функция
называется
бесконечно малой функцией
если для любого числа
при
зависящее от
найдется такое положительное число
выбора
что для всех
удовлетворяющих условию
будет выполняться:
и обозначается:

Теорема: 1) Если
б.м.ф. в
то
т.е.
б.б.ф. в
обозначается:
2) Если
б.б.ф. в
то
б.м.ф. в
т.е.
обозначается:

Символически это утверждение можно записать как:
и
и
следует понимать как
где символы
неограниченно близкое приближение к нулю и к бесконечности соответственно.

Вычисление пределов
Практическое вычисление пределов основывается на связи между б.м.ф. и б.б.ф. и на следующей теореме :
Теорема:
Если
и
то:
1)
2)
3)
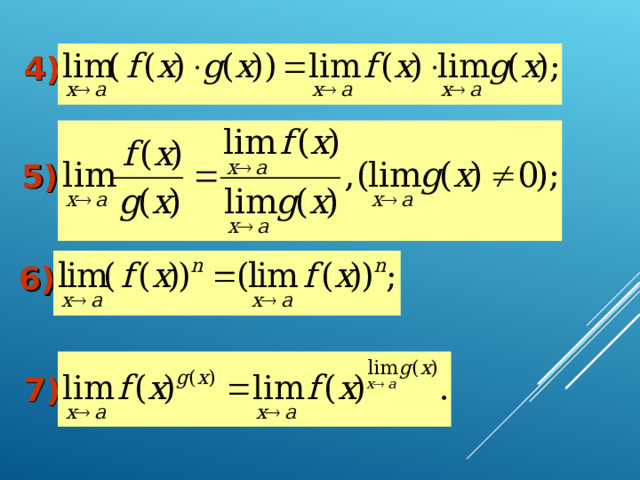
4)
5)
6)
7)

А если условия этой теоремы не выполнены, то могут возникнуть неопределенности вида :
которые в простейших случаях раскрываются с помощью алгебраических преобразований данного выражения и отыскание предела в таких случаях называют раскрытием неопределенностей .

Кроме того, будем пользоваться тем фактом, что для всех основных элементарных функций в любой точке их области определения имеет место равенство:
Последнее равенство можно понимать так: вычисление любого предела нужно начинать с непосредственной подстановки предельного значения , и, если нет неопределенностей , то сразу записать ответ .

Также при нахождении пределов полезно иметь в виду следующие свойства показательной функции:

Примеры:
1)
2)

3)
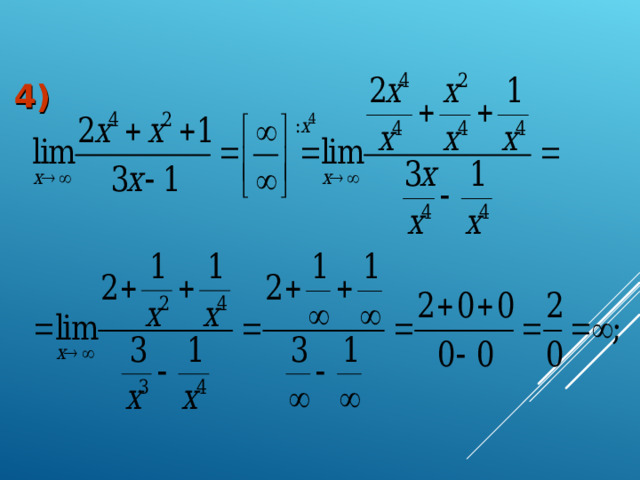
4)

5)
Примечание:
где
и
корни соответствующего квадратного уравнения.

ПРОИЗВОДНАЯ ФУНКЦИИ
- Определение производной
- Геометрический смысл производной
- Связь между непрерывностью и дифференцируемостью
- Производные основных элементарных функций
- Правила дифференцирования
- Производная сложной функции
- Применение производной

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть функция y = f(x) определена в некотором интервале ( a; b) .
Аргументу x придадим некоторое приращение :
Найдем соответствующее приращение функции:
y
f(x+ Δ x )
Если существует предел
f(x )
то его называют производной функции y = f(x) и обозначают одним из символов:
х
0
х
x +Δ x

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Возьмем на непрерывной кривой L две точки М и М 1 :
Через точки М и М 1 проведем секущую и обозначим через φ угол наклона секущей.
y
М 1
f(x+ Δ x )
М
f(x )
φ
0
х
х
x +Δ x
При в силу непрерывности функции также стремится к нулю, поэтому точка М 1 неограниченно приближается по кривой к точке М, а секущая ММ 1 переходит в касательную.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Производная f’(x) равна угловому коэффициенту касательной к графику функции y = f(x) в точке, абсцисса которой равна x .
Если точка касания М имеет координаты ( x 0 ; y 0 ) , угловой коэффициент касательной есть k = f ’(x 0 ) .
Уравнение прямой с угловым коэффициентом:
Уравнение касательной
Уравнение нормали
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.

СВЯЗЬ МЕЖДУ НЕПРЕРЫВНОСТЬЮ И ДИФФЕРЕНЦИРУЕМОСТЬЮ ФУНКЦИИ
Теорема
Если функция f(x) дифференцируема в некоторой точке , то она непрерывна в ней.
Доказательство:
Пусть функция y = f(x) дифференцируема в некоторой точке х , следовательно существует предел:
при
где
По теореме о связи функции, ее предела и бесконечно малой функции
Функция y = f(x) – непрерывна.
Обратное утверждение не верно: непрерывная функция может не иметь производной.

Нахождение производной называют дифференцированием

ТАБЛИЦА ПРОИЗВОДНЫХ
f (x)
f ′(x)
C
f (x)
kx + b
0
f ′(x)
√ x
K
x 2
1/(2 √ x)
e x
2x
x n
1/x
nx n–1
e x
a x
tg x
a x lna
– 1/x 2
sin x
cos x
ctg x
cos x
1/cos 2 x
ln x
– sin x
– 1/sin 2 x
log a x
1/x
1/(x lna)

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале ( a; b) функции, С – постоянная.

ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ
1. Если функции u(x) и v(x) имеют в точке х производные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем
( u + v )′ = u′ + v′
2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С ∙ u(x) также имеет в этой точке производную, причем
(С u )′ = С∙ u′

ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ
3 . Если функции u(x) и v(x) имеют в точке х производные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем
( u ∙ v )′ = u′∙v + u∙v′
4. Если функция v(x) имеет в точке х производную и v(x) ≠ 0 , то функция также имеет в этой точке производную, причем
1
v(x)
′
( )
v′
1
= –
v
v 2
42

ПРАВИЛА НАХОЖДЕНИЯ ПРОИЗВОДНОЙ
5 . Если функции u(x) и v(x) имеют в точке х производные и v(x) ≠ 0 , то функция также имеет в этой точке производную, причем
u(x)
v(x)
u
( )
u′v – uv′
′
=
v
v 2
6. Производная сложной функции
(f(g(x)))′ = f′(g(x))∙g′(x)
43

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная функция с промежуточным аргументом u и независимым аргументом x .
Теорема
Если функция u = φ(x) имеет производную в точке x а функция y = f(u) имеет производную в соответствующей точке u , то сложная функция имеет производную , которая находится по формуле:
Это правило остается в силе, если промежуточных аргументов несколько:

ПРИМЕР
Вычислить производную функции

ПРИМЕР:
Вычислить производную функции:
Данную функцию можно представить следующим образом:
Коротко:
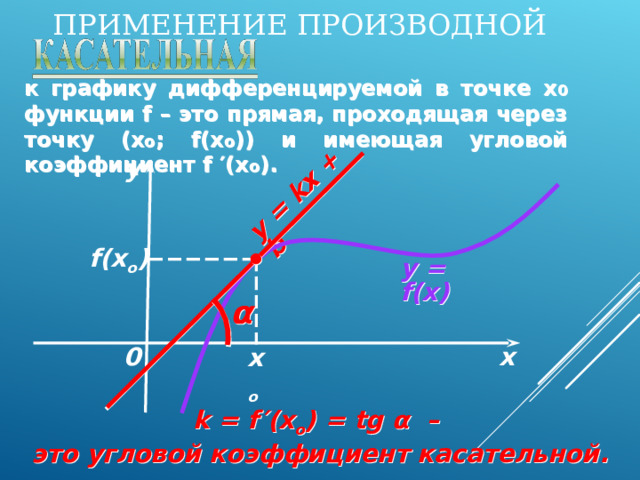
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
y = kx + b
к графику дифференцируемой в точке х 0 функции f – это прямая, проходящая через точку (х о ; f(x о )) и имеющая угловой коэффициент f ′ (х о ).
у
f(x o )
y = f(x)
α
х о
х
0
k = f ′(x o ) = tg α –
это угловой коэффициент касательной.

y = f ′(x o )(x – x o ) + f(x o )
1 о Находим значение функции в точке х о : f(x o ) .
2 о Дифференцируем функцию: f′(x) .
3 о Находим значение производной в точке х о : f′(x o ) .
4 о Подставляем эти данные в общее уравнения
касательной: y = f′(x o )(x – x o ) + f(x o ) .
 0 в каждой точке интервала I , то функция f возрастает на I . Признак убывания функции: Если f´(x) 0 в каждой точке интервала I , то функция f убывает на I . " width="640"
0 в каждой точке интервала I , то функция f возрастает на I . Признак убывания функции: Если f´(x) 0 в каждой точке интервала I , то функция f убывает на I . " width="640"
Одна из основных задач исследования функции – это нахождение промежутков её возрастания и убывания.
Признак возрастания функции:
Если f´ ( x ) 0 в каждой точке интервала I , то функция f возрастает на I .
Признак убывания функции:
Если f´(x) 0 в каждой точке интервала I , то функция f убывает на I .

АЛГОРИТМ РЕШЕНИЯ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ:
Выделить функцию y=f(x) .
- Найти область определения функции D ( f) . Указать промежутки непрерывности.
- Найти нули функции , решив уравнение f(x)=0 .
- Определить знак функции между
её нулями в области определения.

Решите неравенство:
1. 2x+5≠0 , х ≠-2,5
2. f(x)=0 , если
x 1 = 8 , x 2 = -2
3.
Ответ:
-2
X
8
-2,5

АЛГОРИТМ НАХОЖДЕНИЯ ПРОМЕЖУТКОВ ВОЗРАСТАНИЯ (УБЫВАНИЯ) ФУНКЦИИ y=f(x) :
- Найти производную функции f ´ (x) .
- Решить уравнение f´ (x) =0 .
- Найти знак производной на каждом интервале.
- Согласно признаку возрастания (убывания) функции, найти промежутки возрастания и убывания.

Найдите промежутки возрастания и убывания функции:
1.
2. f´(x)=0 , если
3.
Ответ:
f´(x)
f (x)
0
1
X
 f(x o ) . Если в точке х о производная функции f(x) меняет знак с «–» на «+» , то х о – точка локального минимума функции f(x). min – + f′(x) x x o f(x) f (x о ) – минимум функции " width="640"
f(x o ) . Если в точке х о производная функции f(x) меняет знак с «–» на «+» , то х о – точка локального минимума функции f(x). min – + f′(x) x x o f(x) f (x о ) – минимум функции " width="640"
Точка х о называется точкой минимума функции f(x) , если существует такая окрестность точки х о , что для всех х ≠ х о из этой окрестности выполняется неравенство f(x) f(x o ) .
Если в точке х о производная функции f(x) меняет знак с «–» на «+» , то х о – точка локального минимума функции f(x).
min
–
+
f′(x)
x
x o
f(x)
f (x о ) – минимум функции
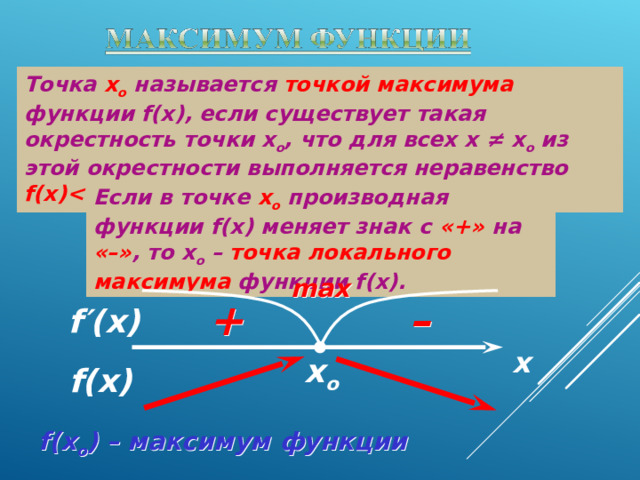
Точка х о называется точкой максимума функции f(x) , если существует такая окрестность точки х о , что для всех х ≠ х о из этой окрестности выполняется неравенство f(x) o ) .
Если в точке х о производная функции f(x) меняет знак с «+» на «–» , то х о – точка локального максимума функции f(x).
max
–
+
f′(x)
x
x o
f(x)
f (x о ) – максимум функции
 0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ] . б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞) . " width="640"
0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ] . б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞) . " width="640"
1 о Дифференцируем функцию: f′(x) .
2 о Находим критические точки из уравнения: f′(x) = 0 .
3 о Решаем неравенства: f′(x) 0 и f′(x) .
4 о Полученные данные изображаем на схеме:
f′(x)
+
–
+
–
x
x 1
x 3
x 2
f(x)
5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ] .
б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞) .
 0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума. б) f(x 1 ) ; f(x 3 ) – максимумы функции; f(x 2 ) – минимум функции. " width="640"
0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума. б) f(x 1 ) ; f(x 3 ) – максимумы функции; f(x 2 ) – минимум функции. " width="640"
1 о Дифференцируем функцию: f′(x) .
2 о Находим критические точки из уравнения: f′(x) = 0 .
3 о Решаем неравенства: f′(x) 0 и f′(x) .
4 о Полученные данные изображаем на схеме:
f′(x)
+
–
+
–
x
x 1
x 3
x 2
f(x)
5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума.
б) f(x 1 ) ; f(x 3 ) – максимумы функции;
f(x 2 ) – минимум функции.

ПРИМЕРЫ


+
+
+
–
–































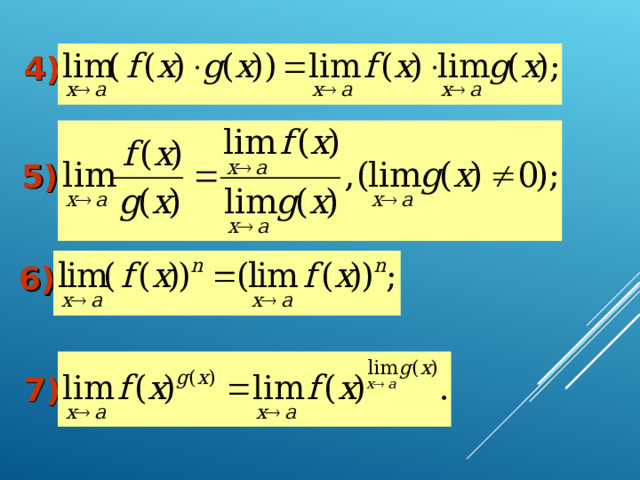





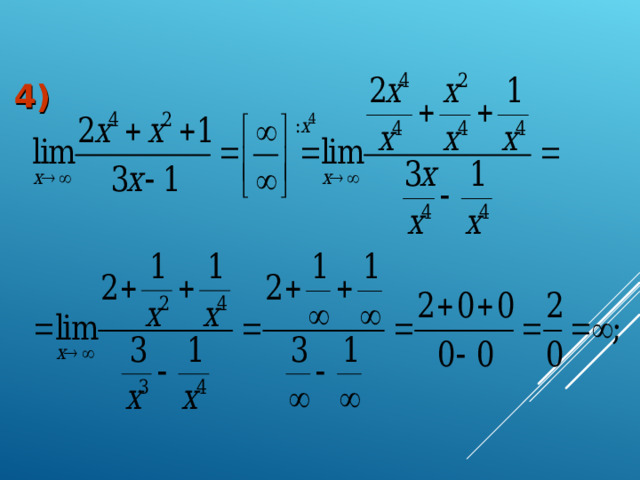

















 0 в каждой точке интервала I , то функция f возрастает на I . Признак убывания функции: Если f´(x) 0 в каждой точке интервала I , то функция f убывает на I . " width="640"
0 в каждой точке интервала I , то функция f возрастает на I . Признак убывания функции: Если f´(x) 0 в каждой точке интервала I , то функция f убывает на I . " width="640"




 f(x o ) . Если в точке х о производная функции f(x) меняет знак с «–» на «+» , то х о – точка локального минимума функции f(x). min – + f′(x) x x o f(x) f (x о ) – минимум функции " width="640"
f(x o ) . Если в точке х о производная функции f(x) меняет знак с «–» на «+» , то х о – точка локального минимума функции f(x). min – + f′(x) x x o f(x) f (x о ) – минимум функции " width="640"

 0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ] . б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞) . " width="640"
0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) Промежутки возрастания: (– ∞; х 1 ] ; [x 2 ; x 3 ] . б) Промежутки убывания: [x 1 ; x 2 ] ; [x 3 ; + ∞) . " width="640"
 0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума. б) f(x 1 ) ; f(x 3 ) – максимумы функции; f(x 2 ) – минимум функции. " width="640"
0 и f′(x) . 4 о Полученные данные изображаем на схеме: f′(x) + – + – x x 1 x 3 x 2 f(x) 5 o a) х 1 ; x 3 – точки максимума; x 2 – точка минимума. б) f(x 1 ) ; f(x 3 ) – максимумы функции; f(x 2 ) – минимум функции. " width="640"













