14.05.2020
Лекция для группы Т11, Са11 по теме
Подобие тел. Отношение площадей поверхностей и объемов подобных тел.
ЗАПИСАТЬ ЛЕКЦИЮ, прочитав ее и выписав самое главное.
ОПРЕДЕЛЕНИЕ: Два тела подобны, если одно из них может быть получено из другого путём увеличения (или уменьшения) всех его линейных размеров в одном и том же отношении. Пример 1: Автомобиль и его модель – подобные тела. Два тела (фигуры) зеркально подобны, если одно из них подобно зеркальному отражению другого.
Пример 2: Картина и её фотонегатив зеркально подобны друг другу.
В подобных и зеркально подобных фигурах все соответственные углы ( линейные и двугранные ) равны.
В подобных телах многогранные и телесные углы равны; в зеркально подобных телах они зеркально равны.
Если два тетраэдра (две треугольные пирамиды) имеют соответственно пропорциональные рёбра (или соответственно подобные грани), то они подобны или зеркально подобны. Пример 3: Если грани первой пирамиды вдвое больше, чем у второй, то высоты, апофемы, радиус описанного круга первой пирамиды также вдвое больше, чем у второй.
Эта теорема не имеет места для многогранников с большим числом граней. Предположим, что мы соединили все рёбра куба в его вершинах посредством шарниров; тогда мы можем изменить форму этой фигуры, не растягивая её стержни, и получить из начального куба параллелепипед.
Пример 4: Две правильные призмы или пирамиды с одинаковым числом граней подобны, если радиусы их оснований пропорциональны их высотам. Два круглых цилиндра или конуса подобны, если радиусы их оснований пропорциональны их высотам.
УТВЕРЖДЕНИЕ 1: Если два и более тел подобны, то площади всех соответствующих плоских и кривых поверхностей этих тел пропорциональны квадратам любых соответствующих отрезков.
УТВЕРЖДЕНИЕ2:Если два и более тел подобны, то их объёмы, а также объёмы любых их соответствующих частей, пропорциональны кубам любых соответствующих отрезков.
П р и м е р 5: Чашка диаметром 8 см и высотой 10 см вмещает 0.5 литра воды. Каких размеров должна быть подобная чашка, вмещающая 4 литра воды ?
| Решение: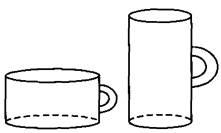 | Поскольку чашки – подобные цилиндры, то отношение их объёмов равно отношению кубов соответствующих отрезков ( в нашем случае – высот и диаметров чашек). Следовательно, высота h новой чашки находится из отношения: ( h / 10 ) 3 = 4 / 0.5, то есть h 3 = 8 · 10 3, откуда h = 20 см; аналогично, для диаметра d получим: ( d / 8 ) 3 = 4 / 0.5 , то есть d 3 = 8 · 8 3, откуда d = 16 см . |
Объемы подобных тел пропорциональны кубам соответствующих линейных размеров.
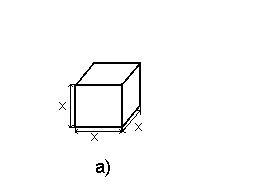
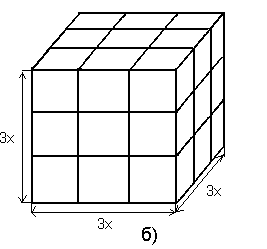
Пример 6: На рисунке выше показаны два куба, сторона одного из которых в 3 раза больше стороны другого.
Объем тела с рисунка а) V=x*x*x=x3
Объем тела с рисунка б) V=3x*3x*3x=27x3
Следовательно, тело на рис. б) имеет объем объем 33, т.е. его объем в 27 раз больше объема тела на рис. а).
Пример 7: Определение массы тела, подобного данному.
Масса автомобиля 1050 кг. Изготовлена модель автомобиля в масштабе 1:60. Определить массу модели автомобиля, если она сделана из того же материала, что и сам автомобиль.
Решение:
(Объем модели)/(объем автомобиля)=(1/60)3, поскольку объемы подобных тел пропорциональны кубам соостветствующих линейных размеров.
Масса =плотность*объем, а так как автомобиль и модель сделаны из одного материала, значит:
(Масса модели)/(Масса автомобиля)=(1/60)3
Следовательно,
Масса модели = (Масса автомашины) *(1/60)3=(10050)/(603)=0,0049 кг=4,9г.


















