21.05. 2020 год
Лекция для групп Св11 по теме
«ИНТЕГРАЛЬНАЯ ФОРМУЛА ОБЪЕМА»
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности вращения и многое другое. Представьте некоторую плоскую фигуру на координатной плоскости. Представили? ... Интересно, кто что представил… =))) Её площадь мы уже находили. Также находили и объем, посмотрите свои лекции за январь, именно тогда мы записывали формулы площади и объема через интеграл. Там же в лекциях есть решение таких задач. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс ОХ;
– вокруг оси ординат ОУ.
Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ОХ
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями  ,
,  вокруг оси
вокруг оси  .
.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости  необходимо построить фигуру, ограниченную линиями
необходимо построить фигуру, ограниченную линиями  ,
,  , при этом не забываем, что уравнение
, при этом не забываем, что уравнение  задаёт ось. Чертёж здесь довольно прост:
задаёт ось. Чертёж здесь довольно прост:
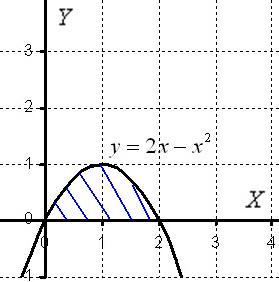
Искомая плоская фигура заштрихована , именно она и вращается вокруг оси ОХ. В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси  .
.
Объем тела вращения можно вычислить по формуле:

В формуле перед интегралом обязательно присутствует число  . Так повелось – всё, что в жизни крутится, связано с этой константой.
. Так повелось – всё, что в жизни крутится, связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция  … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы
… что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы  сверху. Это и есть та функция, которая подразумевается в формуле.
сверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси  . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:
. Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:  , таким образом интеграл всегда неотрицателен, что весьма логично.
, таким образом интеграл всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:

Ответ: 
В ответе нужно обязательно указать размерность – кубические единицы  . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т. д
. То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т. д
Пример 2
Найти объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями 2х-у=0, у=0, х=3
Это пример для самостоятельного решения.
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями  ,
,  ,
,  и
и 
Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями  ,
,  ,
,  ,
,  , не забывая при этом, что уравнение
, не забывая при этом, что уравнение  задает ось
задает ось  :
:
Искомая фигура заштрихована. При её вращении вокруг оси  получается такой бублик с четырьмя углами.
получается такой бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая опирается ось ОХ отрезком от 0 до 1.Это большая верхняя трапеция. При её вращении вокруг оси  получается усеченный конус. Обозначим объем этого усеченного конуса через
получается усеченный конус. Обозначим объем этого усеченного конуса через  .
.
Рассмотрим фигуру, которая также опирается на ось ОХ отрезком от 0 до 1. Это маленькая нижняя трапеция, которая при вращении образует дырку в так называемом бублике. Если вращать данную фигуру вокруг оси  , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через
, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через  .
.
И, очевидно, разность объемов  – в точности объем нашего «бублика».
– в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:

1) Фигура, ограничена сверху прямой  , поэтому:
, поэтому:
2) Фигура, ограничена сверху прямой  , поэтому:
, поэтому:
3) Объем искомого тела вращения: 
Ответ: 
Итак, чтобы найти объем тела вращения, необходимо применить интегральную формулу объема:

СОСТАВИТЬ КРАТКИЙ КОНСПЕКТ ПО ТЕМЕ И РЕШИТЬ ПРИМЕР 2



















