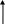ТЕМА 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
4.1 Уравнения прямой на плоскости
Пусть на плоскости задана система координат. Рассмотрим уравнение вида
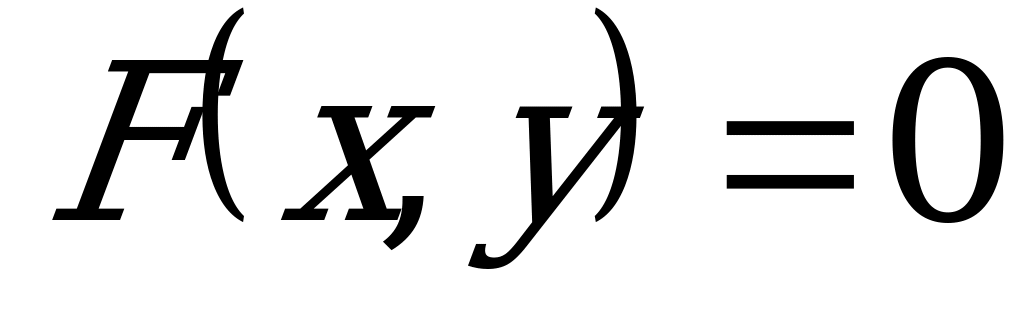 . (4.1)
. (4.1)
Это равенство, если оно выполняется не для всех пар чисел 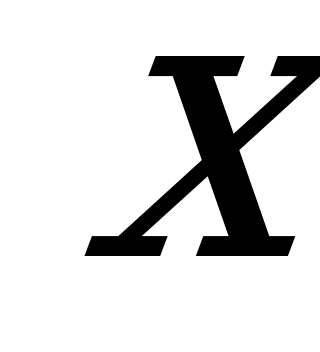 и
и  , называется уравнением некоторой линии
, называется уравнением некоторой линии  в заданной системе координат
в заданной системе координат  . Уравнение (4.1) определяет или задает линию
. Уравнение (4.1) определяет или задает линию  .
.
Известно, что любое линейное уравнение с двумя переменными определяет прямую линию на плоскости.
Чтобы написать уравнение прямой  , ее надо задать. Существуют разные способы задания прямой, что приводит к различным по форме уравнениям, которые равносильны между собой, так как имеют одно и то же множество решений – координаты точек прямой
, ее надо задать. Существуют разные способы задания прямой, что приводит к различным по форме уравнениям, которые равносильны между собой, так как имеют одно и то же множество решений – координаты точек прямой  .
.
Зададим прямую  при помощи точки
при помощи точки  , принадлежащей данной прямой, и ненулевого вектора
, принадлежащей данной прямой, и ненулевого вектора 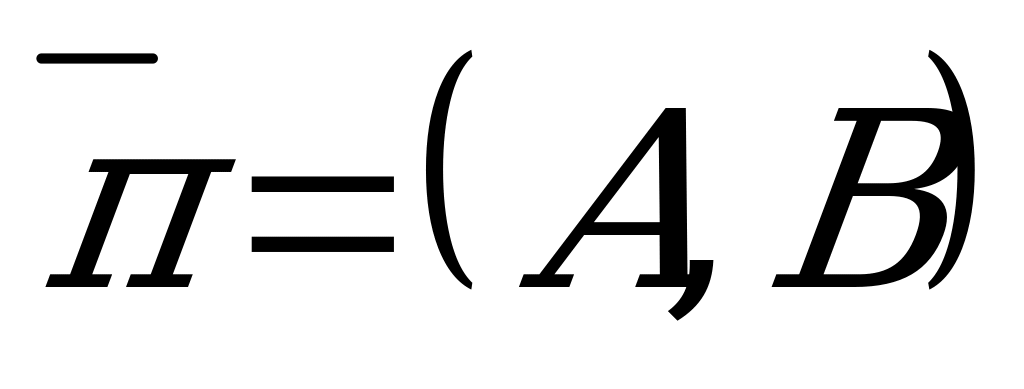 , перпендикулярного этой прямой (рис. 4.1).
, перпендикулярного этой прямой (рис. 4.1).
|

    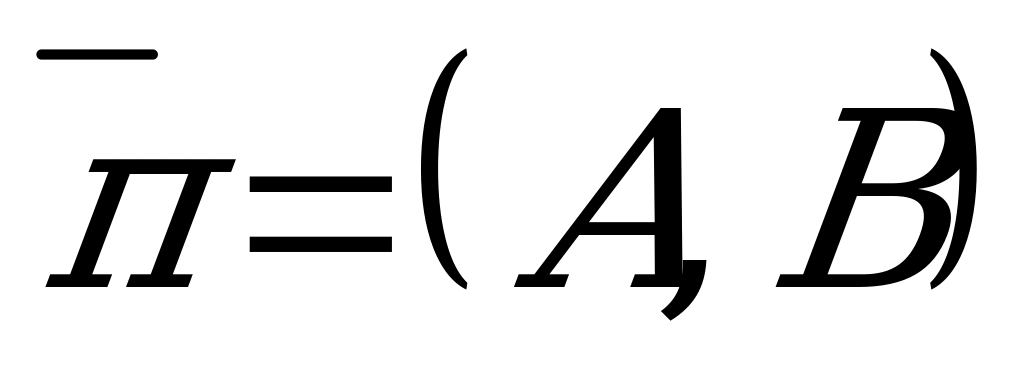
 
О 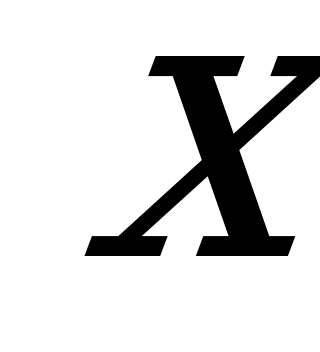 Рис. 4.1 |
Эти условия однозначно определяют прямую, так как через точку перпендикулярно вектору можно провести только одну прямую. Пусть 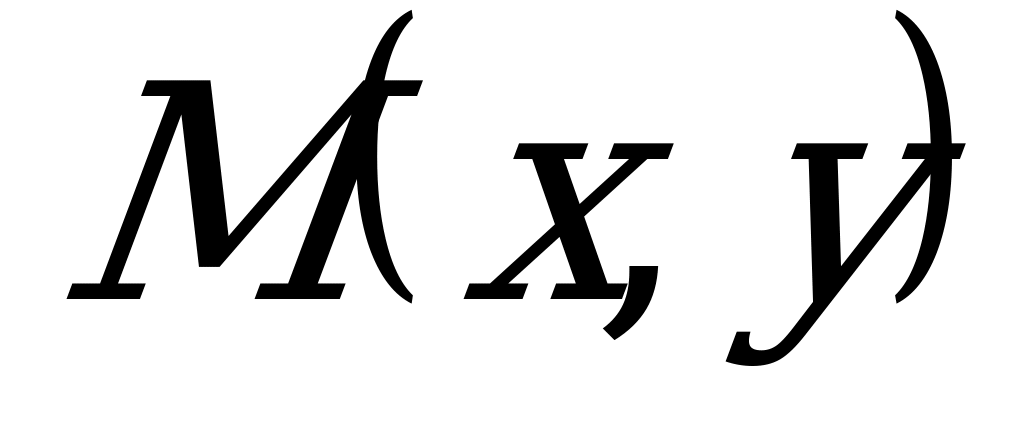 - произвольная точка прямой - произвольная точка прямой  . Так как . Так как 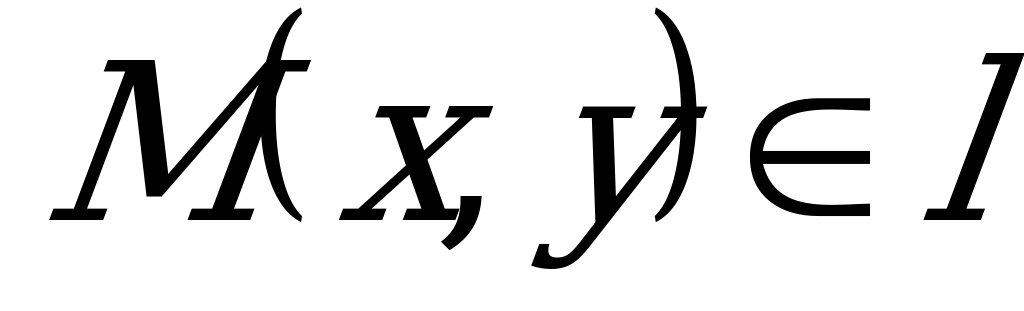 , то , то 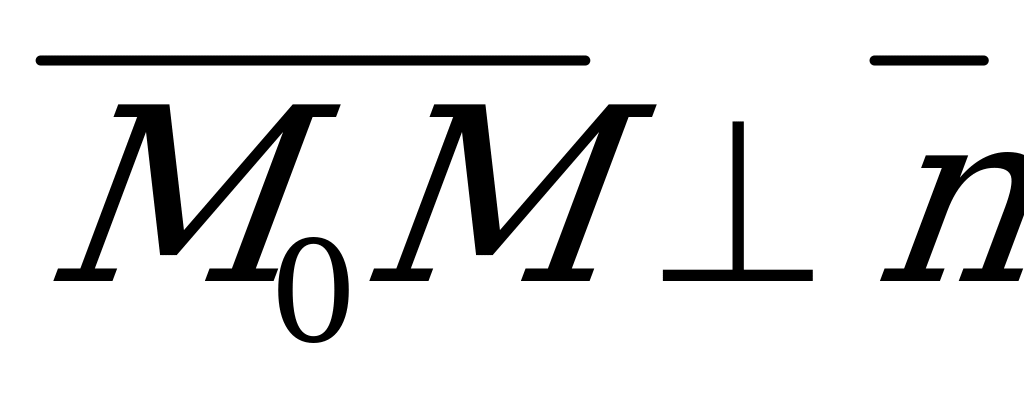 и и 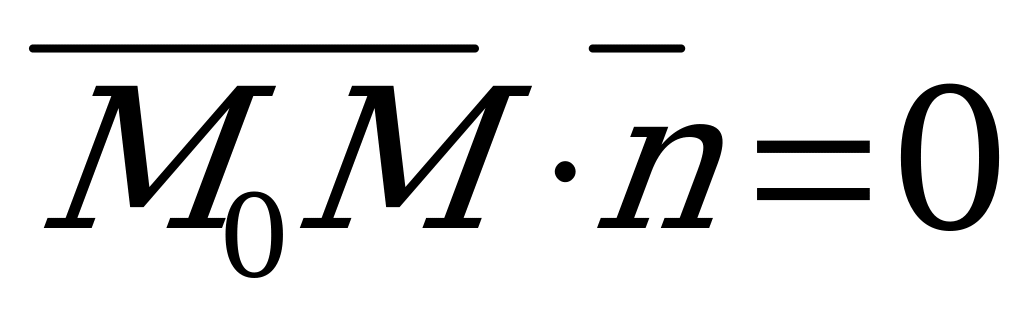 , т.е. , т.е.
|
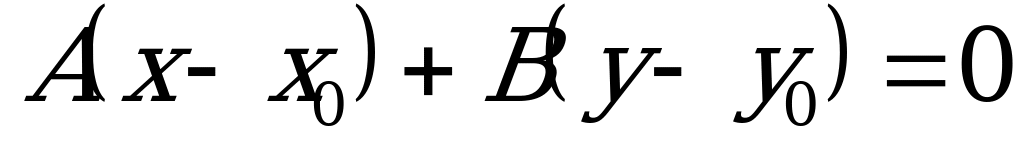 . (4.2)
. (4.2)
Каждый ненулевой вектор 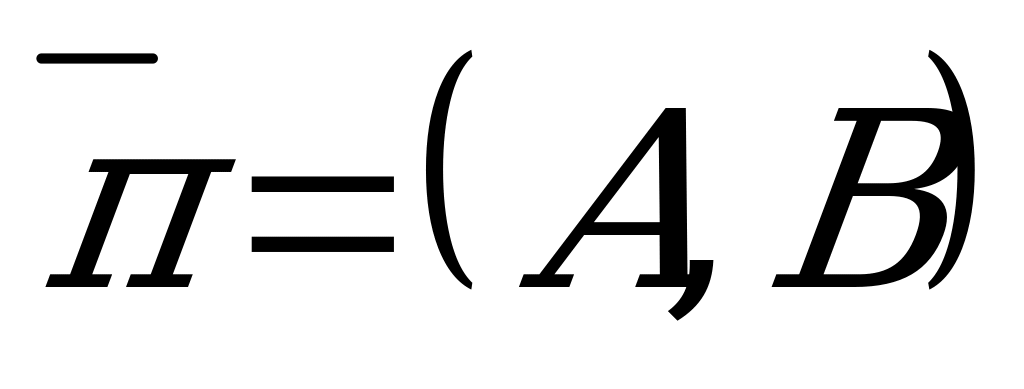 , перпендикулярный данной прямой, называется ее нормальным вектором.
, перпендикулярный данной прямой, называется ее нормальным вектором.
Уравнение (1.2) называется уравнением прямой, заданной с помощью нормального вектора и точки.
Зададим прямую  при помощи двух точек
при помощи двух точек 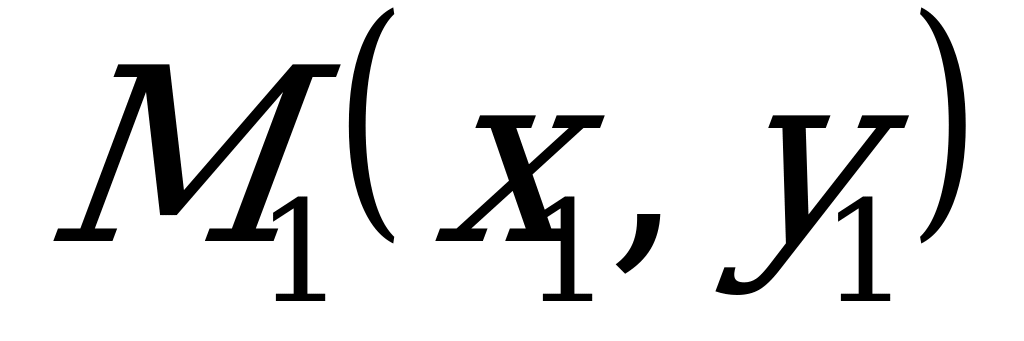 и
и 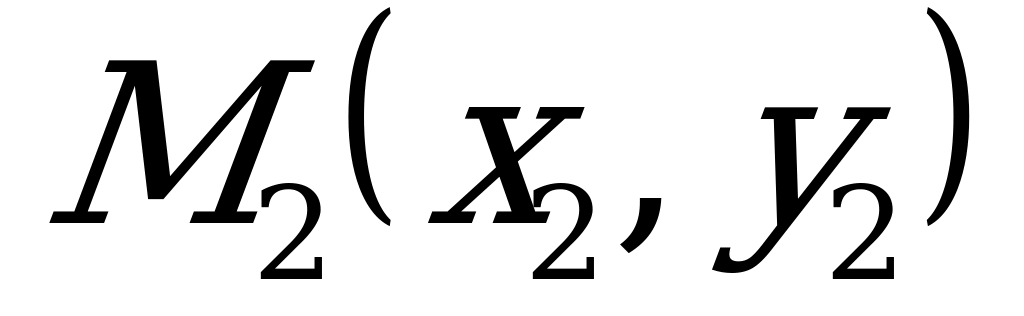 , принадлежащих этой прямой.
, принадлежащих этой прямой.
Эти условия однозначно определяют прямую, так как через две заданные точки можно провести только одну прямую.
| 

 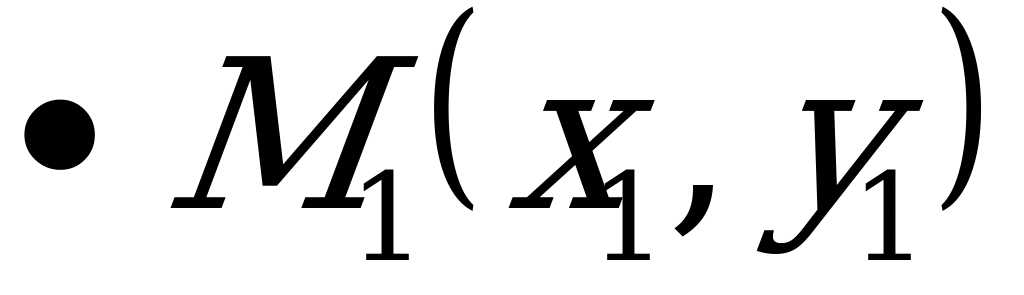 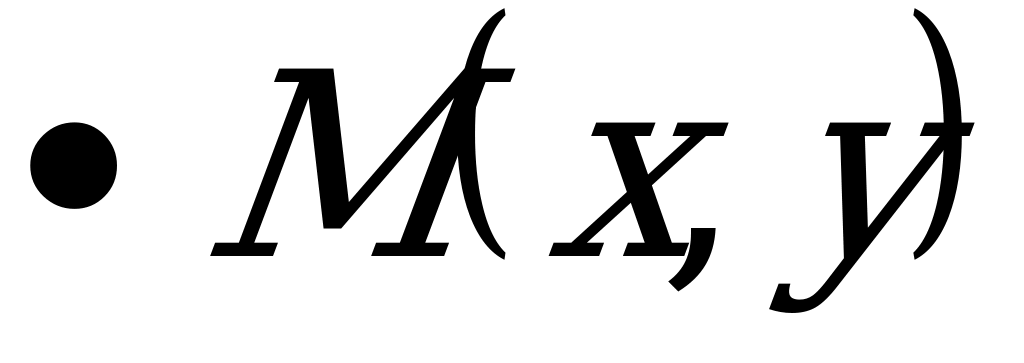  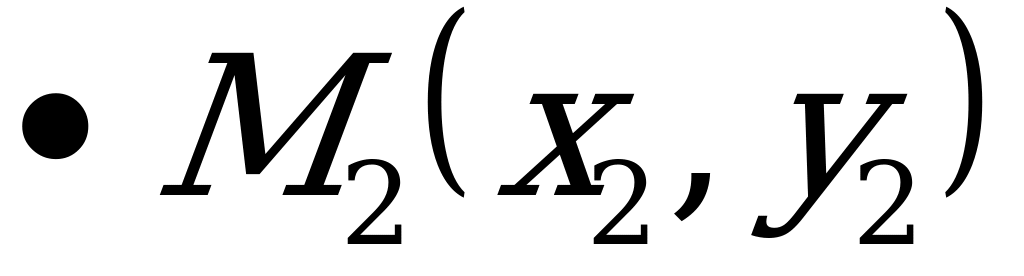 
О 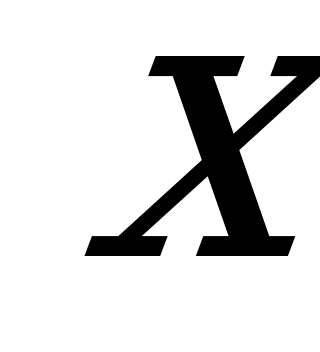 Рис. 4.2. | Пусть 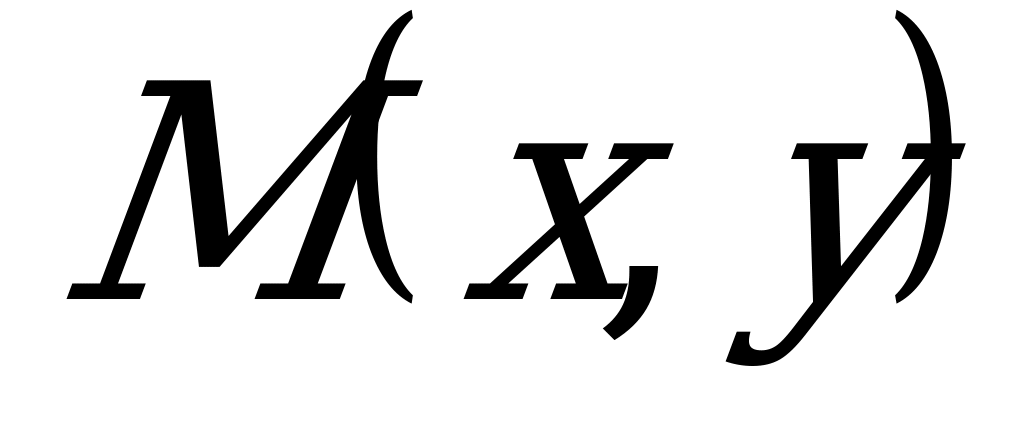 - произвольная точка прямой - произвольная точка прямой  . . Так как 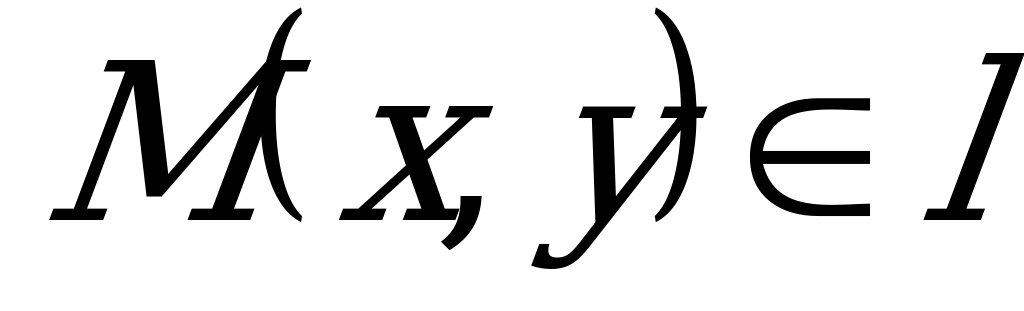 , то , то 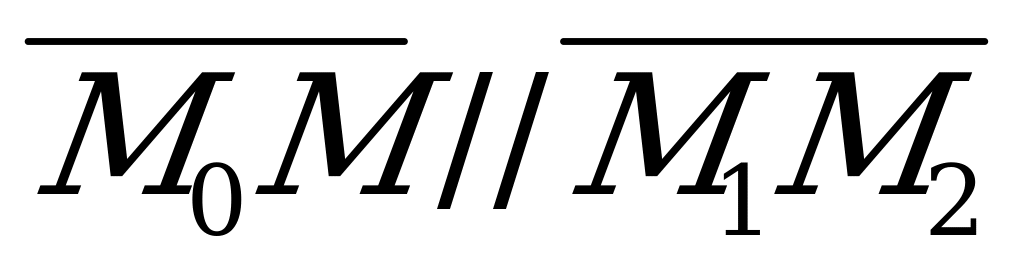 и и 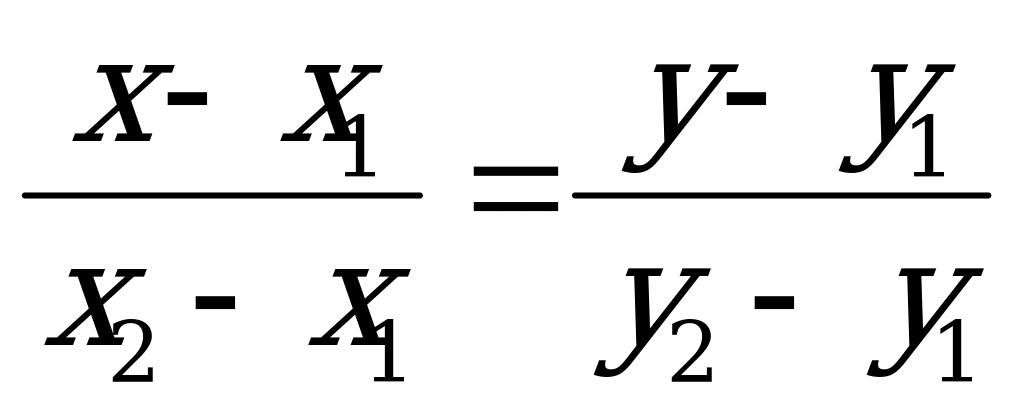 (4.3) (4.3)
|
Уравнение (4.3) называется уравнением прямой, проходящей через две заданные точки.
Уравнения (4.2) и (4.3) с помощью тождественных преобразований приводятся к равносильному виду
 . (4.4)
. (4.4)
Уравнение (4.4) называется общим уравнением прямой линии. Здесь  - какие-либо числа. Некоторые коэффициенты могут равняться нулю, однако хотя бы одно из чисел
- какие-либо числа. Некоторые коэффициенты могут равняться нулю, однако хотя бы одно из чисел  или
или  должно быть отлично от нуля, иначе в уравнении исчезнут обе текущие координаты
должно быть отлично от нуля, иначе в уравнении исчезнут обе текущие координаты 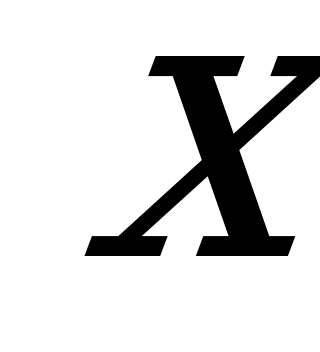 и
и  .
.
Если в (4.4) какой-либо из коэффициентов равен нулю, то:
1) при 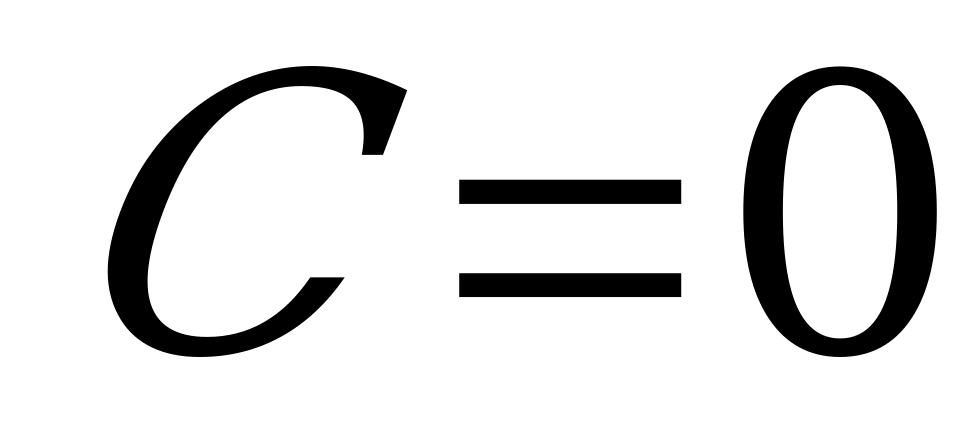 :
: 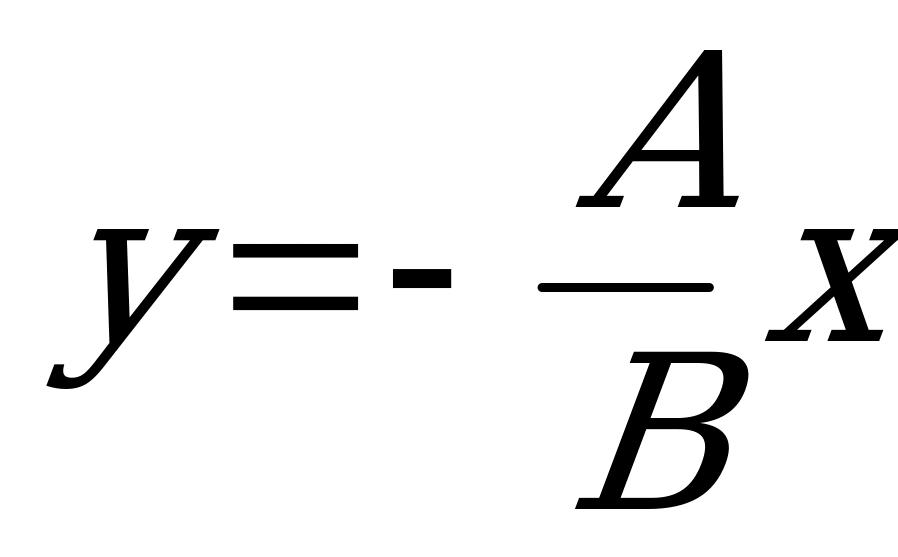 - прямая проходит через начало координат;
- прямая проходит через начало координат;
2) при 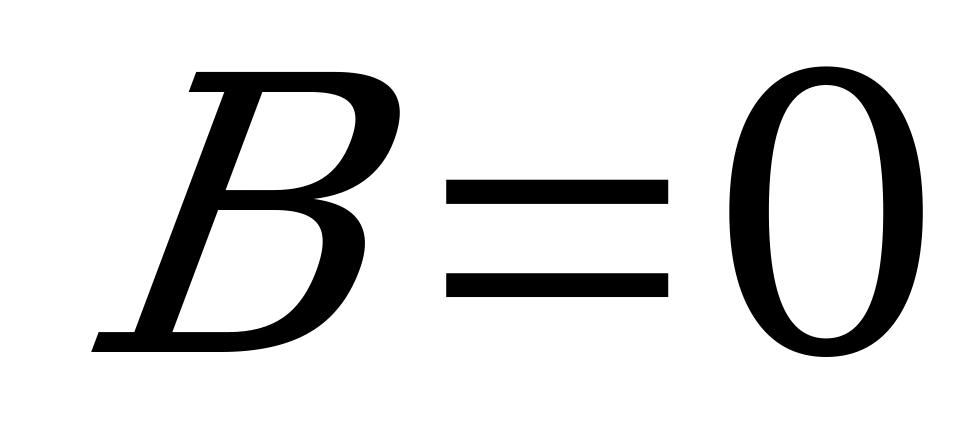 (
(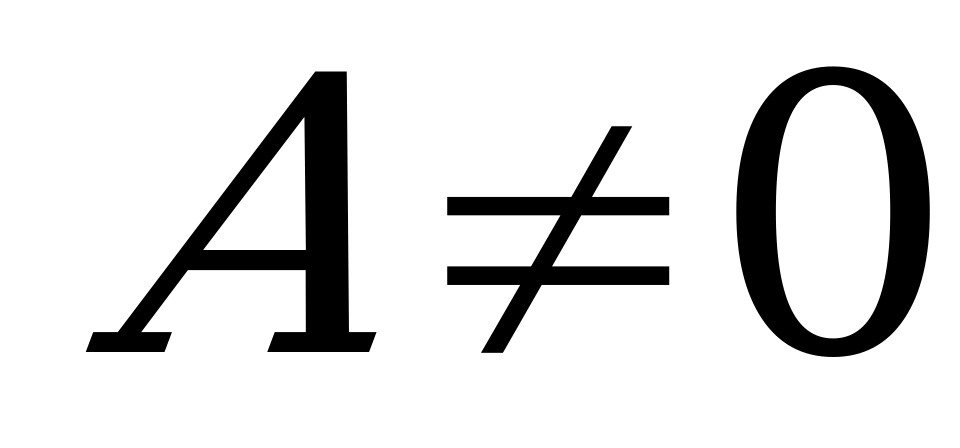 ):
): 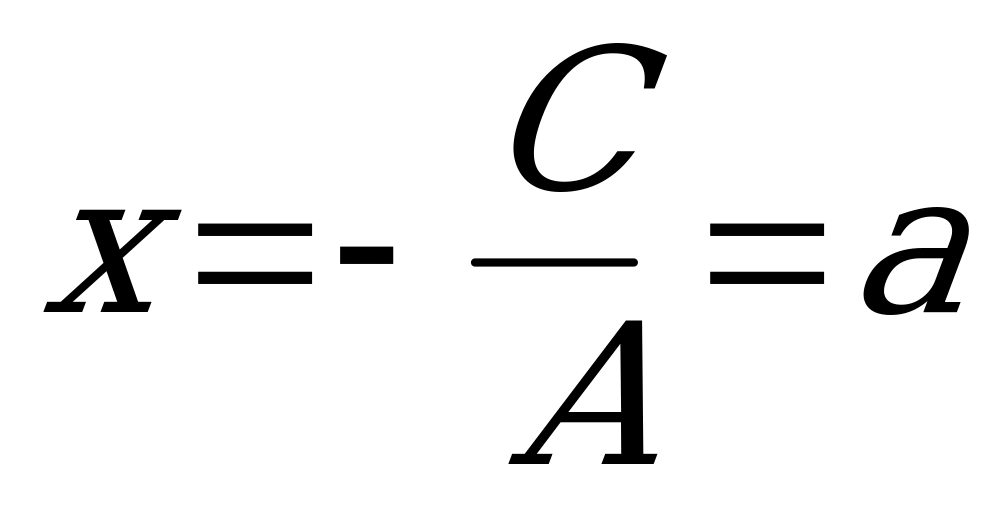 - прямая, параллельная оси
- прямая, параллельная оси  ;
;
3) при 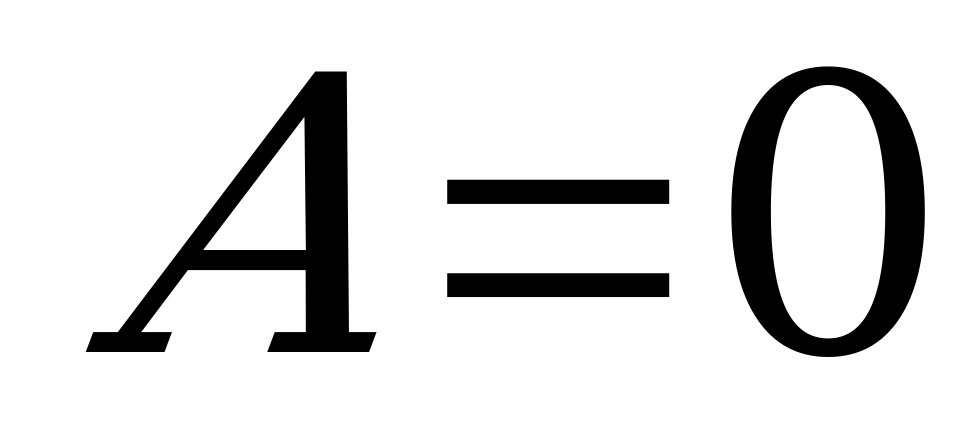 (
(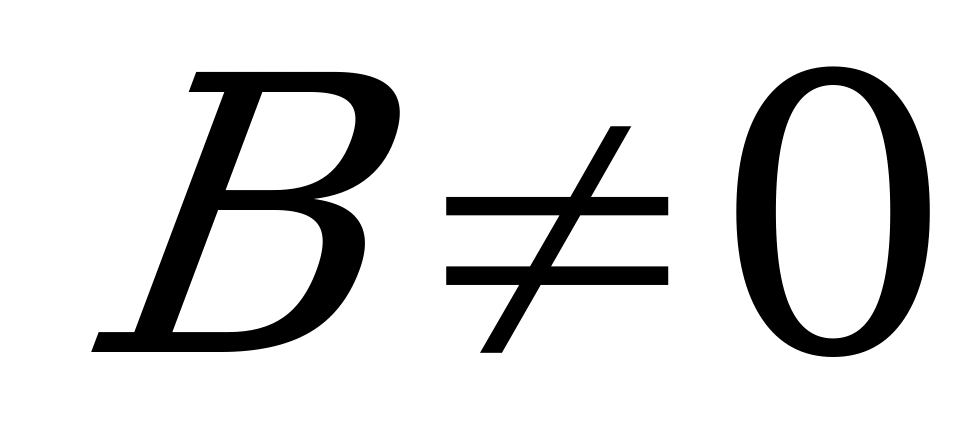 ):
):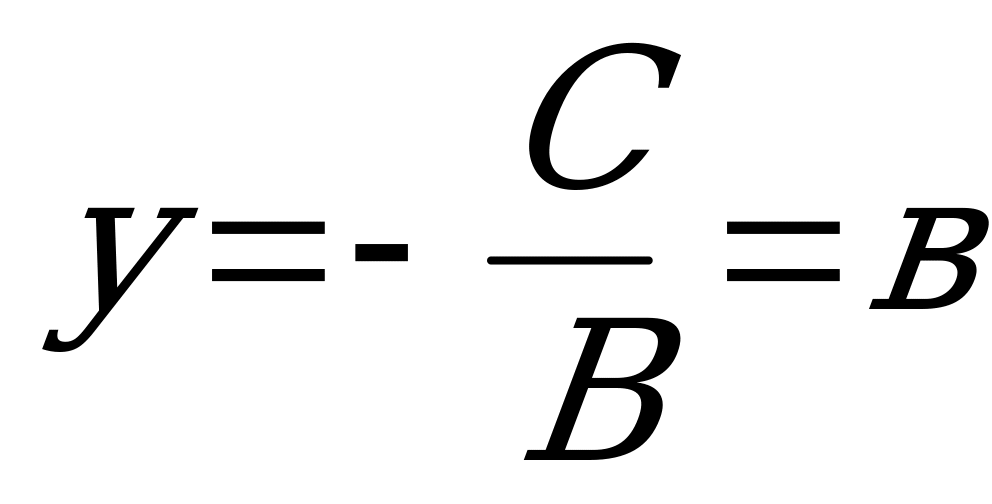 - прямая, параллельная оси
- прямая, параллельная оси  ;
;
4) при 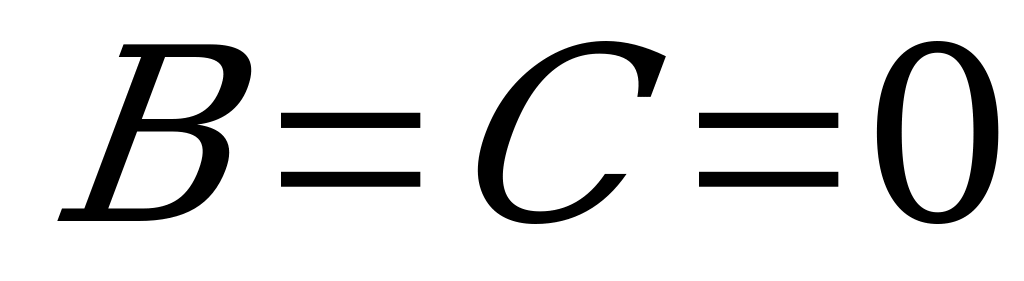 :
:  - ось
- ось  ;
;
5) при 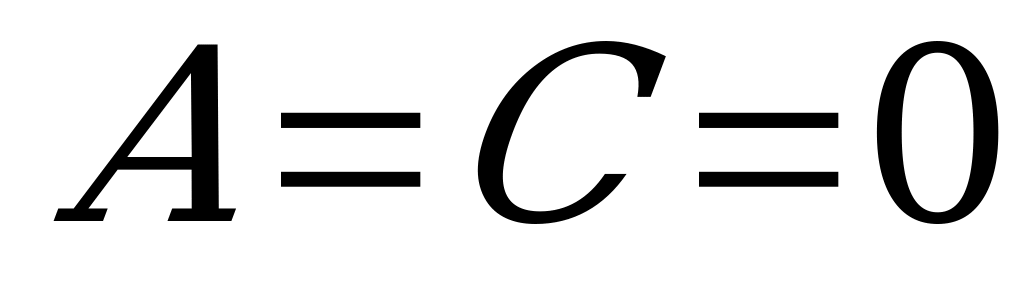 :
: 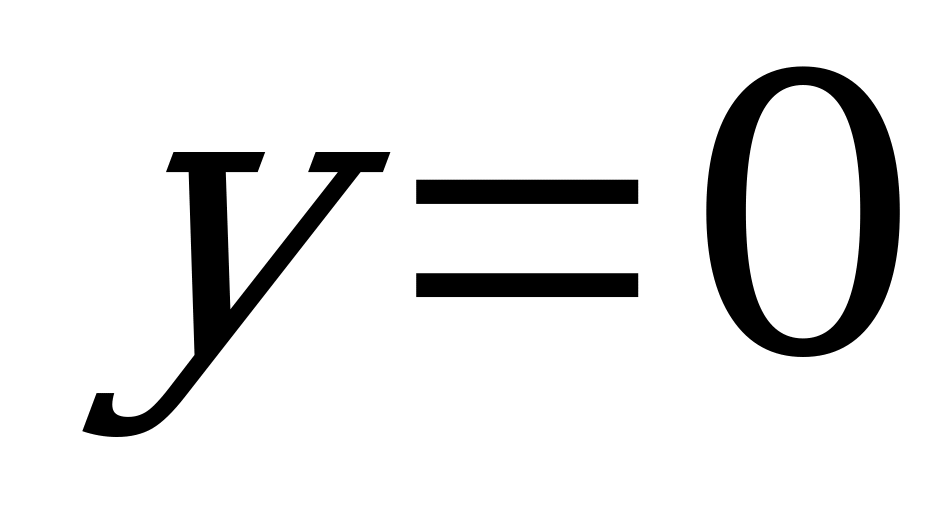 - ось
- ось  .
.
| 

 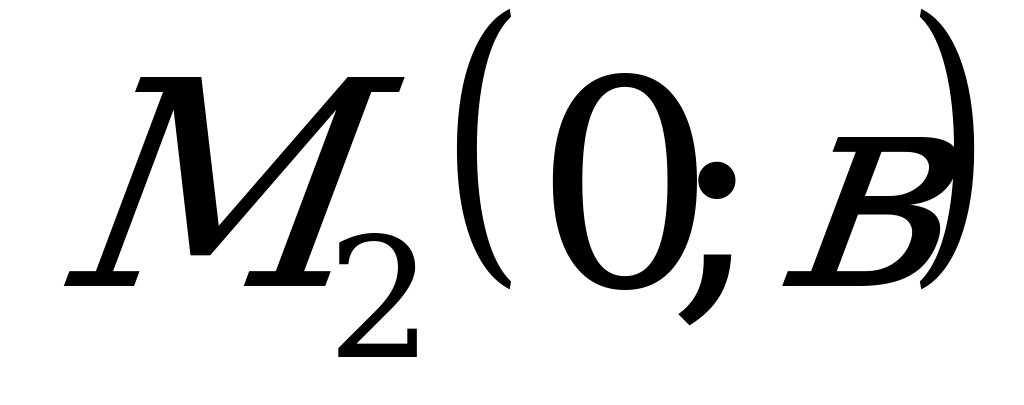   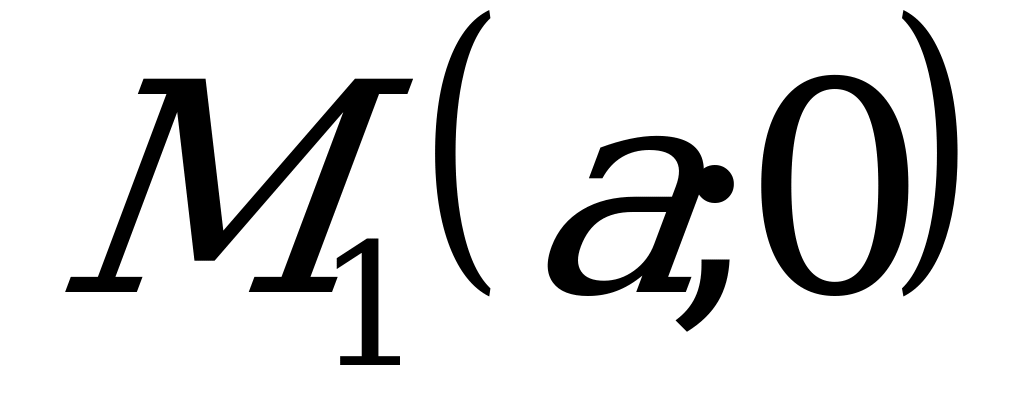 О   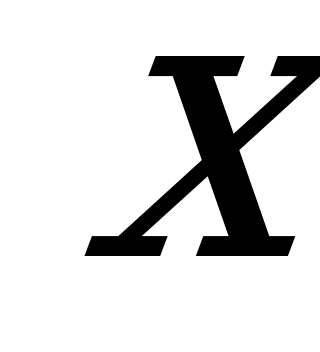 Рис. 4.3 | Если ни один из коэффициентов уравнения (4.4) не равен нулю, то его можно преобразовать к виду: 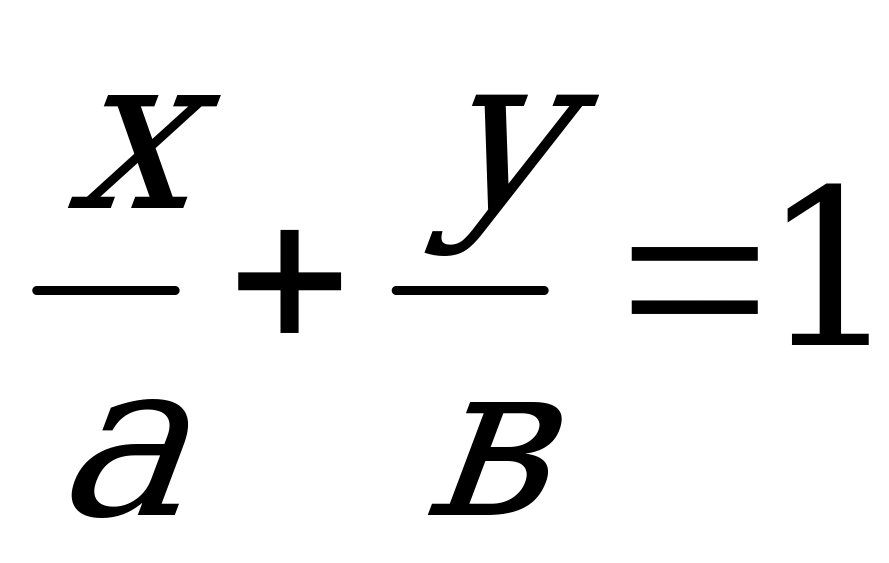 , (4.5) , (4.5) где 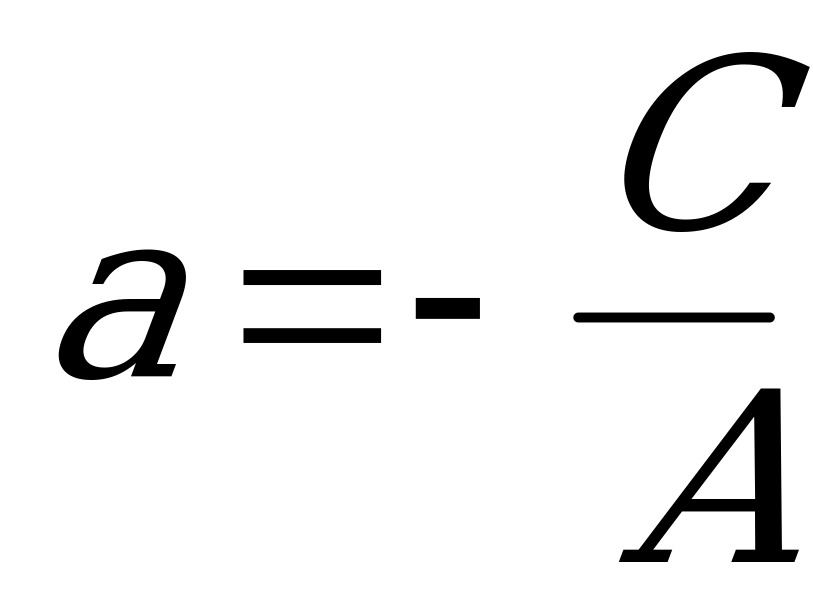 и и 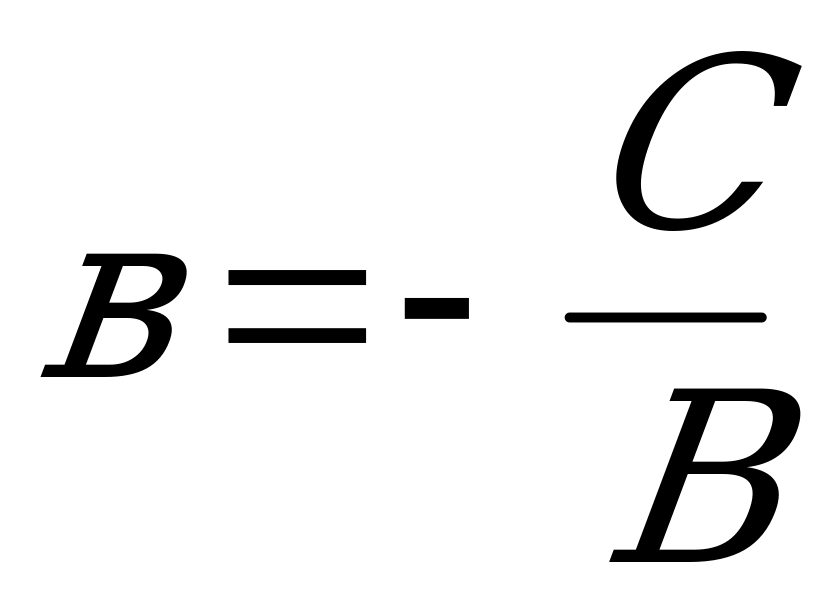 - величины направленных отрезков, которые отсекает прямая на осях координат (рис. 4.3). - величины направленных отрезков, которые отсекает прямая на осях координат (рис. 4.3). |
Уравнение (4.5) называется уравнением прямой «в отрезках».
Из уравнения (4.4) можно выразить переменную  как функцию от аргумента
как функцию от аргумента 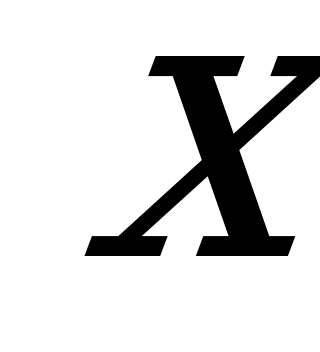 при
при 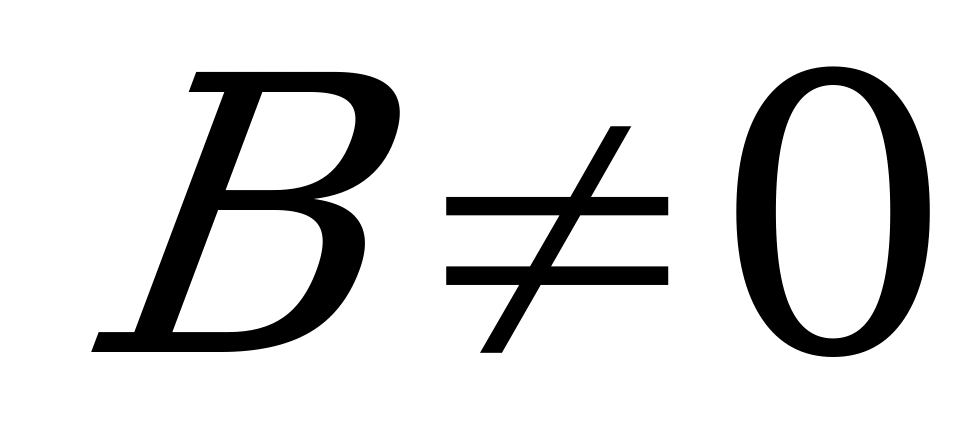 :
:
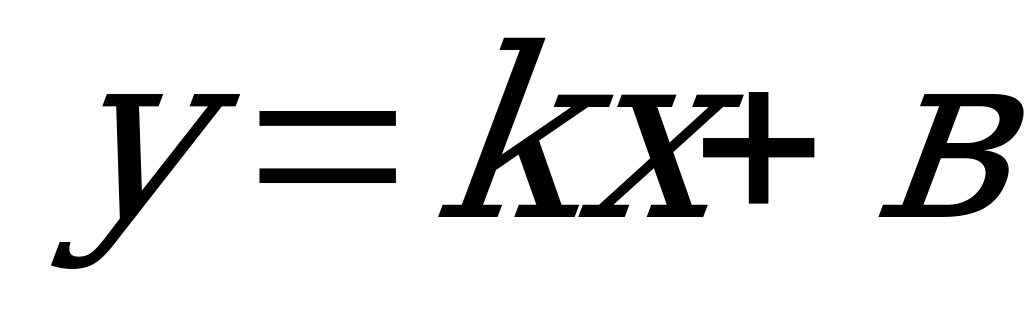 . (4.6)
. (4.6)
Уравнение (4.6) известно из элементарной математики, его называют уравнением с угловым коэффициентом.
Угловой коэффициент 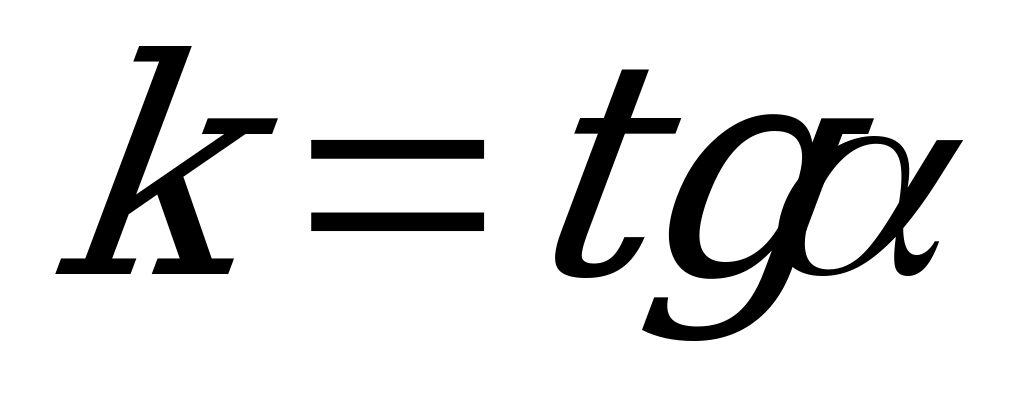 , где
, где  - меньший из неотрицательных углов, образуемых прямой
- меньший из неотрицательных углов, образуемых прямой  с положительным направлением оси
с положительным направлением оси 
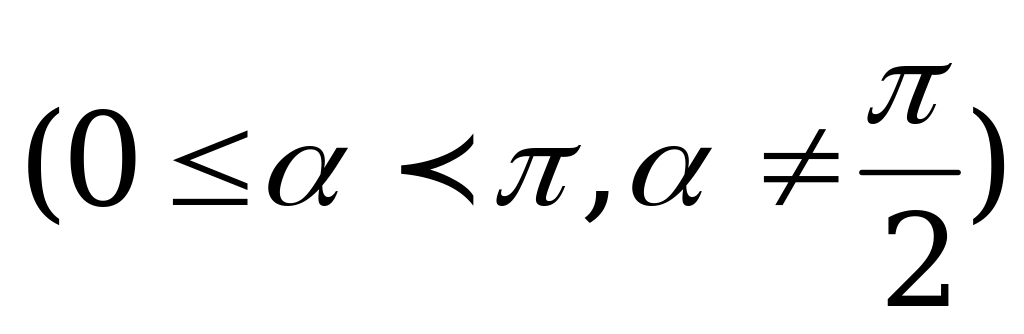 . Ордината точки пересечения прямой с осью
. Ордината точки пересечения прямой с осью  равна
равна  (рис. 4.4).
(рис. 4.4).
Приведем еще некоторые сведения справочного характера.
Если известны угловые коэффициенты 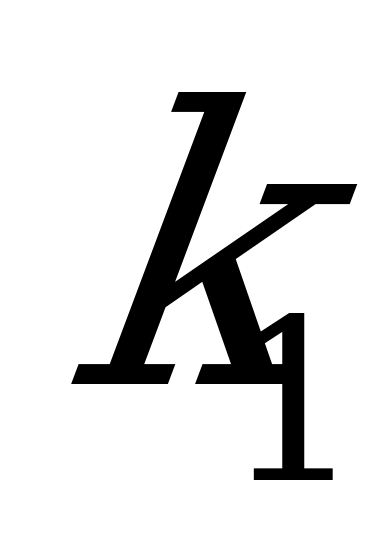 и
и 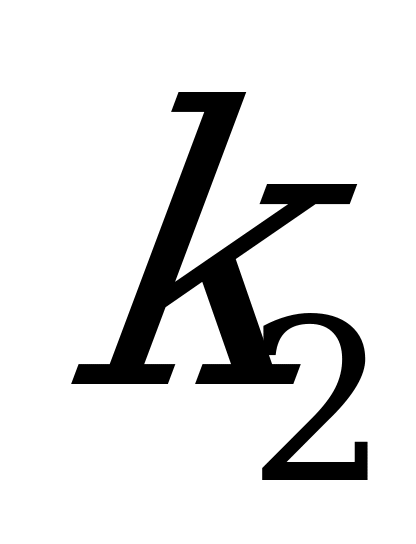 двух прямых (рис. 4.5.), то один из углов
двух прямых (рис. 4.5.), то один из углов 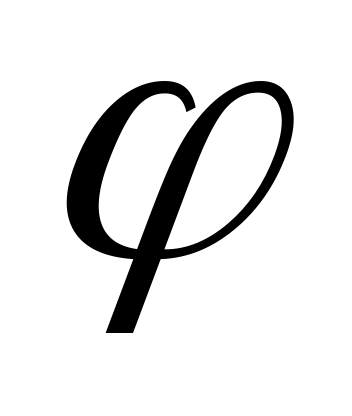 между этими прямыми определяется по формуле
между этими прямыми определяется по формуле
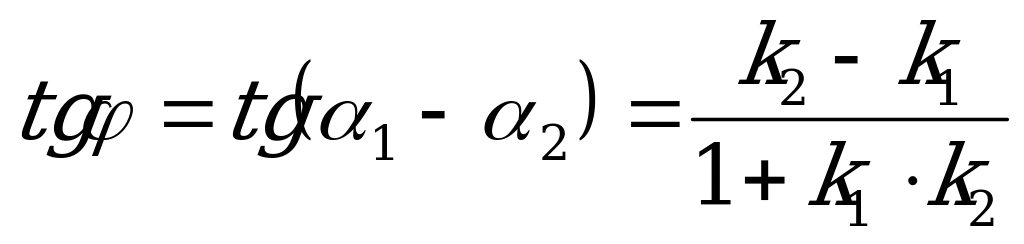 . (4.7)
. (4.7)
Второй угол равен 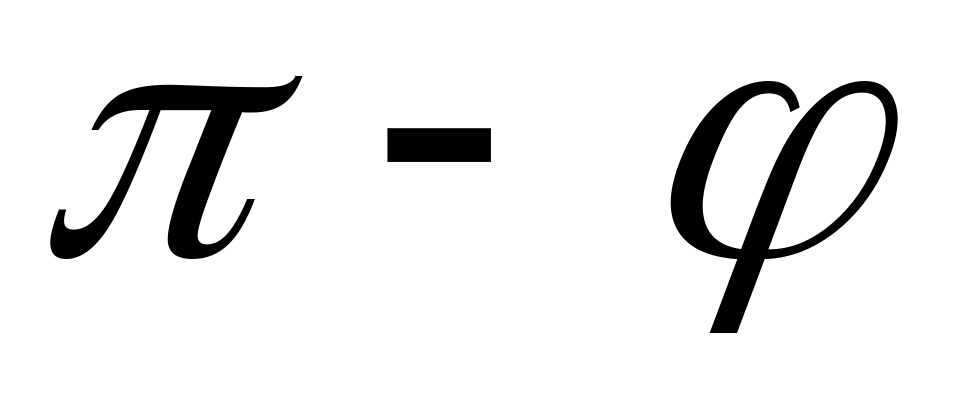 .
.
Условие параллельности двух прямых:
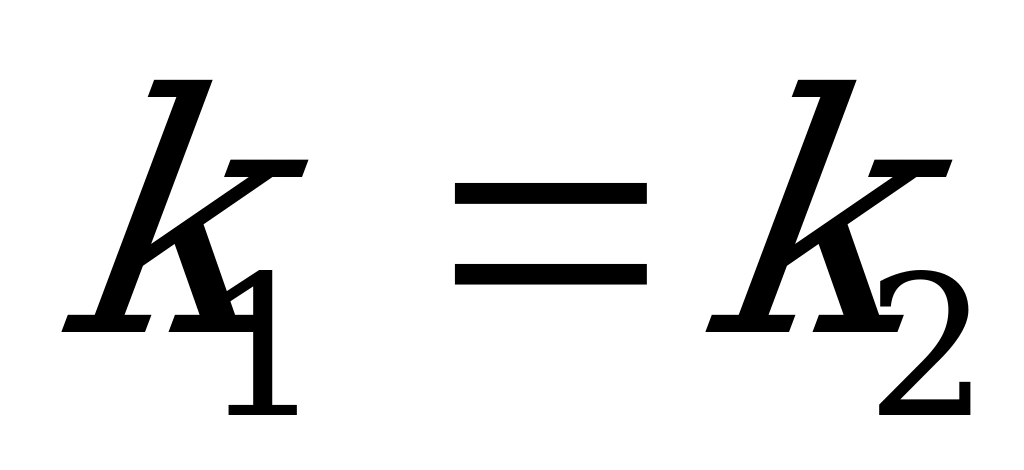 . (4.8)
. (4.8)
Условие перпендикулярности двух прямых:
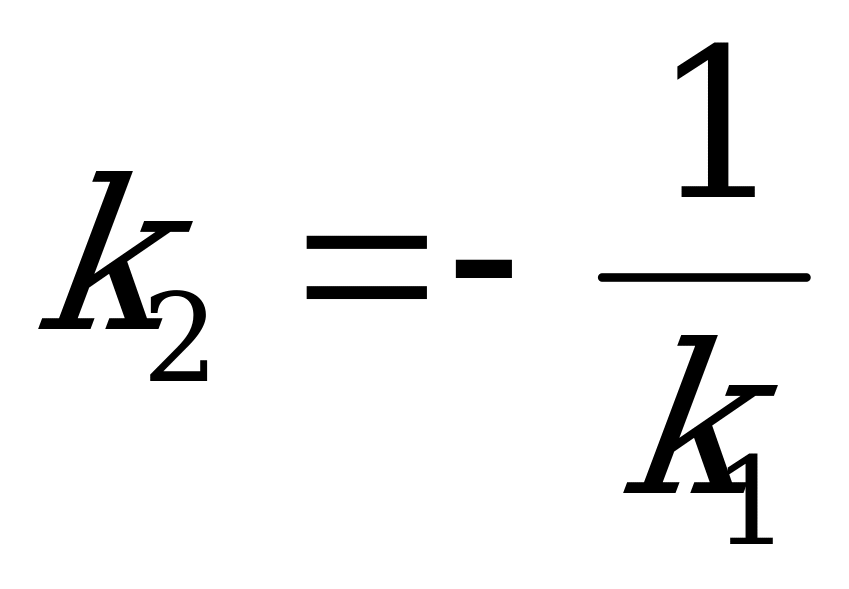 . (4.9)
. (4.9)
Точка пересечения прямых  и
и 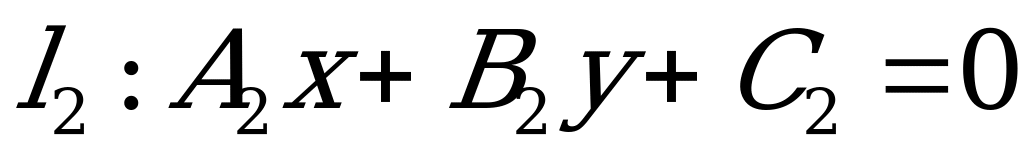 определяется как решение системы:
определяется как решение системы:
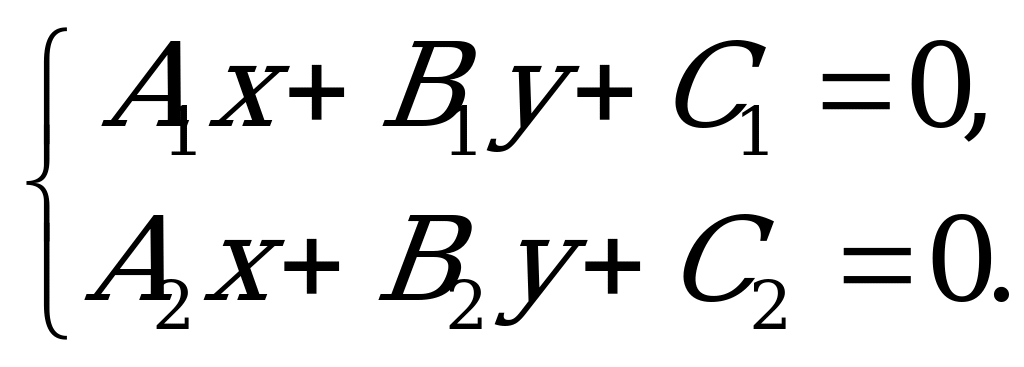 (4.10)
(4.10)
Расстоянием  от точки
от точки 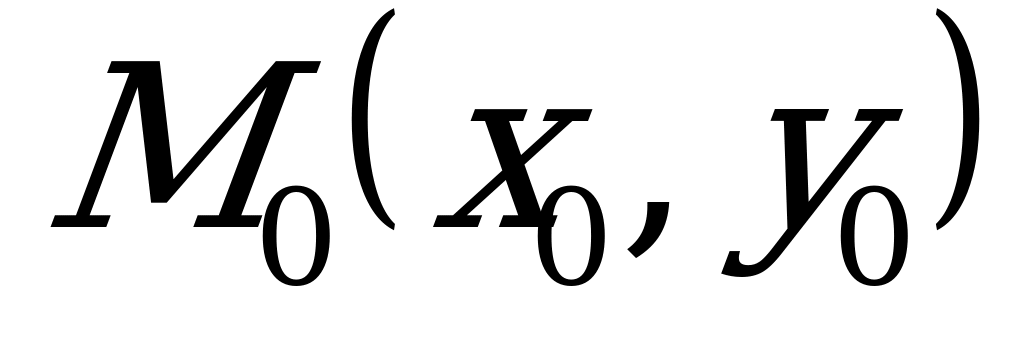 до прямой
до прямой  называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние
называется длина перпендикуляра, опущенного из этой точки на прямую. Расстояние  определяется по формуле
определяется по формуле
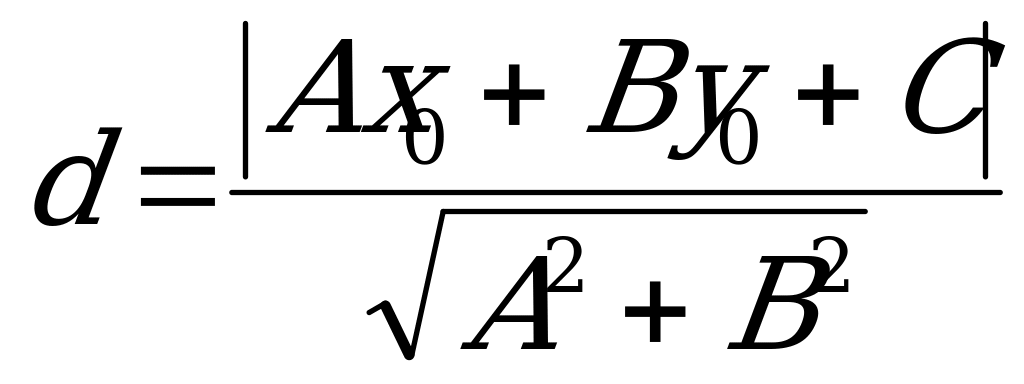 . (4.11)
. (4.11)
4.2 Кривые второго порядка
Любое линейное уравнение  задает на плоскости прямую. Линии, задаваемые уравнениями вида
задает на плоскости прямую. Линии, задаваемые уравнениями вида
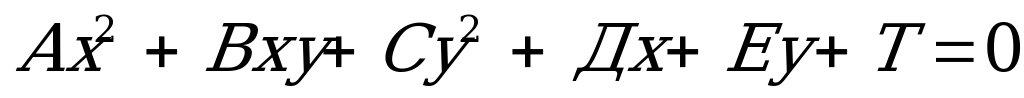 , (4.12)
, (4.12)
называются кривыми второго порядка. За исключением вырожденных случаев имеется всего 3 кривых второго порядка: эллипс (частный случай - окружность), гипербола и парабола, они имеют следующие канонические уравнения и вид.
Окружность
Окружностью радиуса 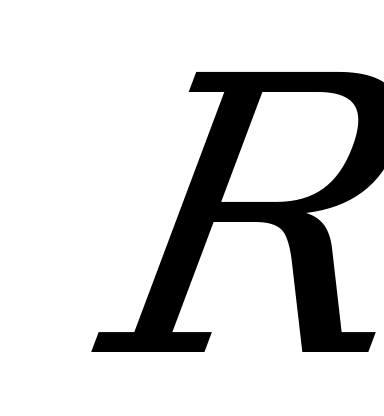 с центром в точке
с центром в точке  называется множество точек плоскости удаленных от точки
называется множество точек плоскости удаленных от точки  на расстоянии
на расстоянии 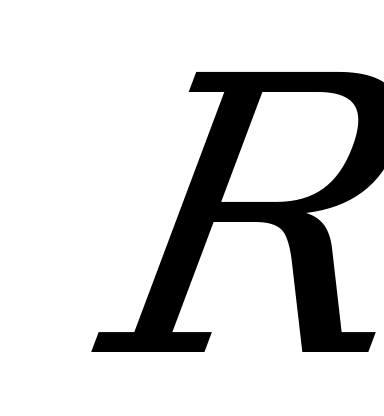 .
.
Уравнение окружности имеет вид: 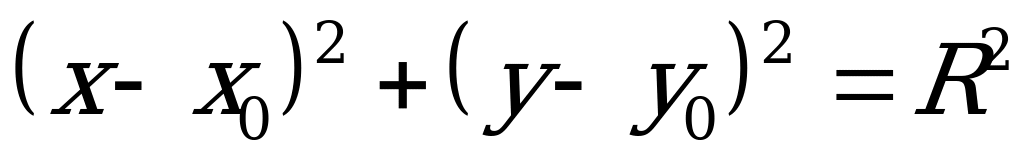 . (4.13)
. (4.13)
В частности, полагая, 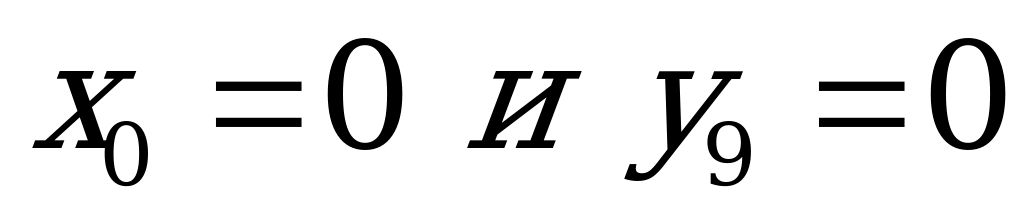 получим уравнение окружности с центром в начале координат
получим уравнение окружности с центром в начале координат  .
.
Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Каноническое уравнение эллипса имеет вид: 
Здесь  - полуоси эллипса; О (0; 0) – центр эллипса.
- полуоси эллипса; О (0; 0) – центр эллипса.  - половина расстояния между фокусами. Вершины эллипса
- половина расстояния между фокусами. Вершины эллипса 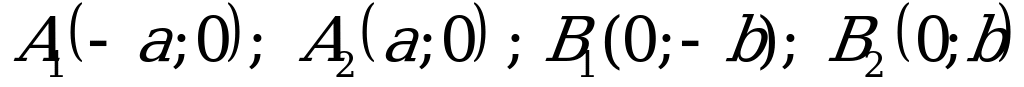 .
.
Фокусы 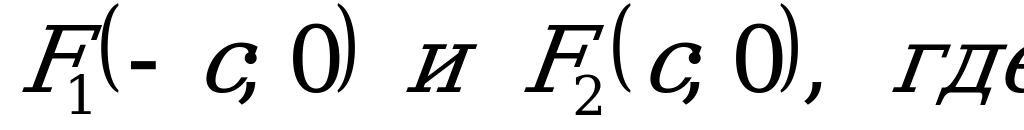
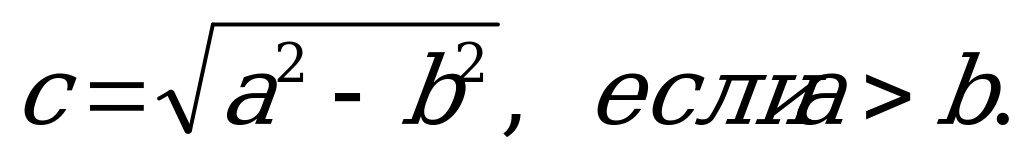 -
-
Прямые 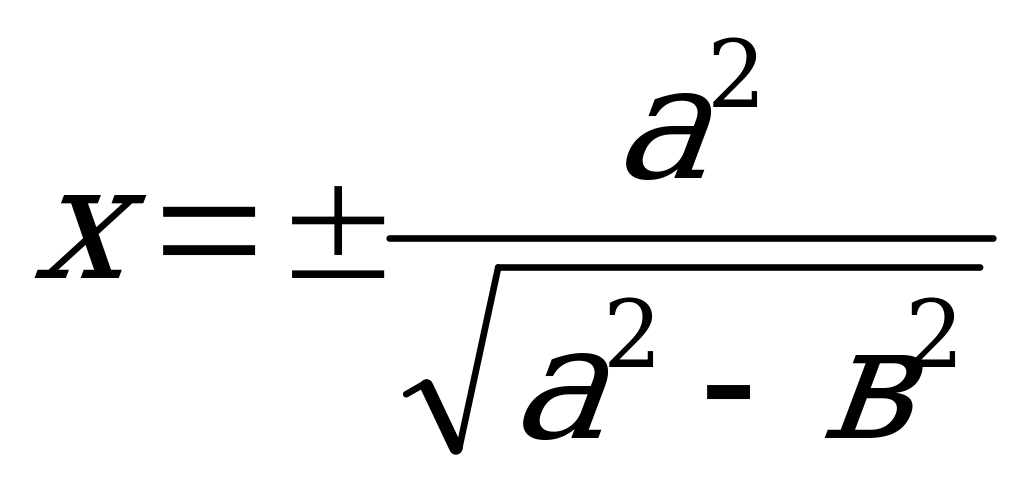 называются директрисами эллипса.
называются директрисами эллипса.
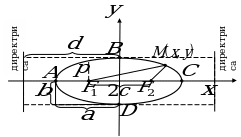
Рис. 4.6
Форму эллипса характеризует отношение 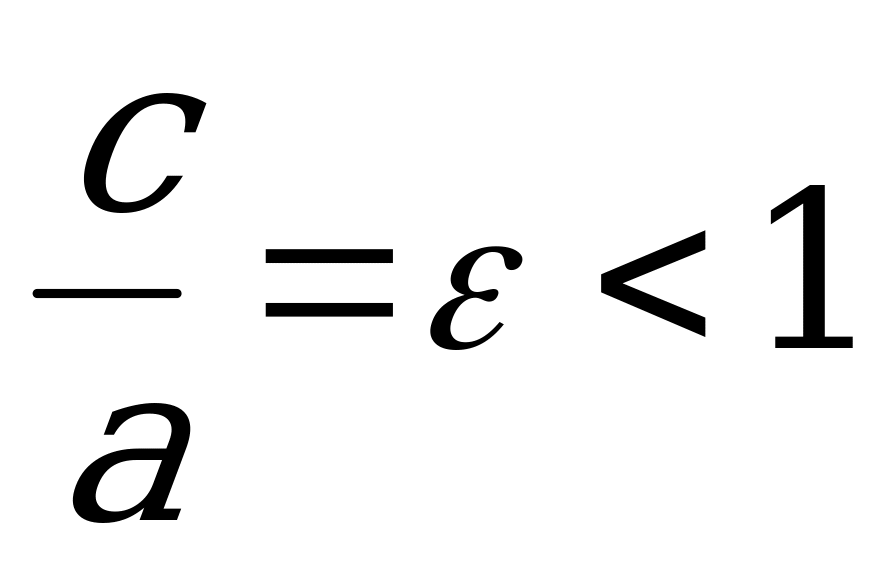 , называемое эксцентриситетом эллипса. Чем меньше эксцентриситет, тем меньше вытянут эллипс вдоль фокальной оси, т.е. оси на которой лежат фокусы.
, называемое эксцентриситетом эллипса. Чем меньше эксцентриситет, тем меньше вытянут эллипс вдоль фокальной оси, т.е. оси на которой лежат фокусы.
В предельном случае при 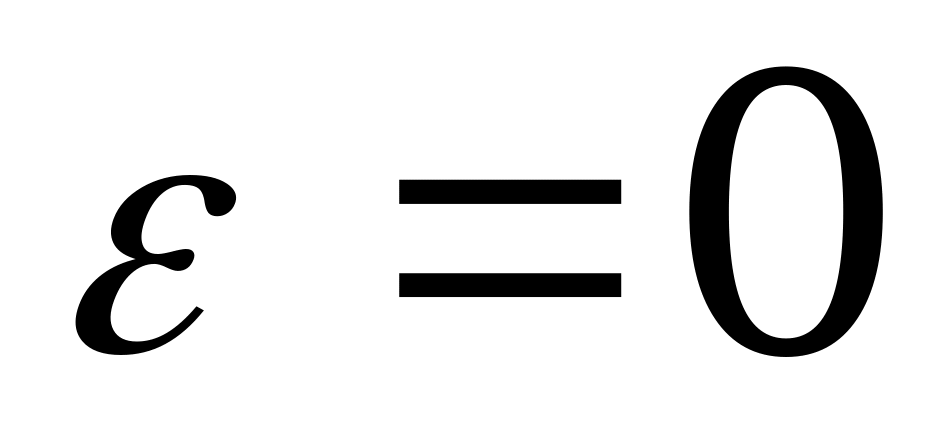 эллипс переходит в окружность.
эллипс переходит в окружность.
Если в каноническом уравнении эллипса 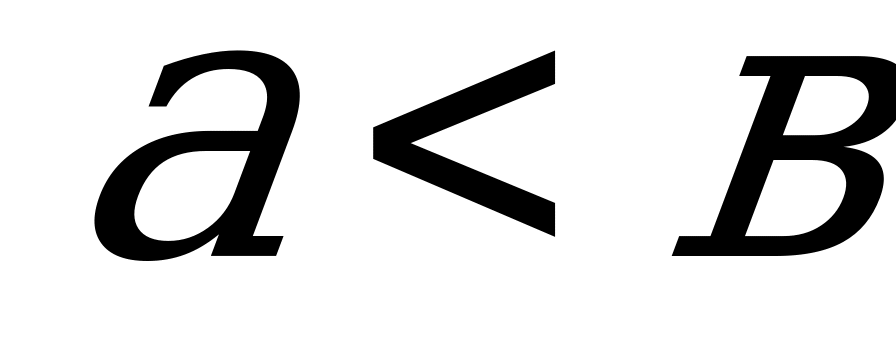 , то фокусы располагаются на оси ОУ и имеют координаты
, то фокусы располагаются на оси ОУ и имеют координаты 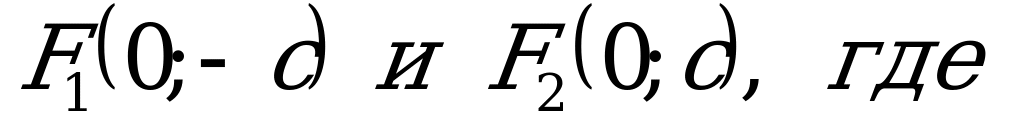

Гипербола
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид: 
Здесь 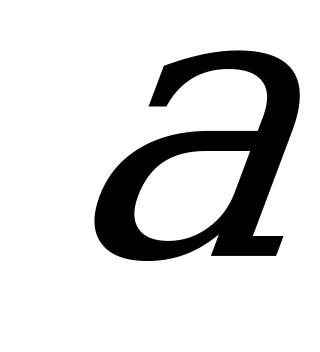 - действительная полуось гиперболы,
- действительная полуось гиперболы, 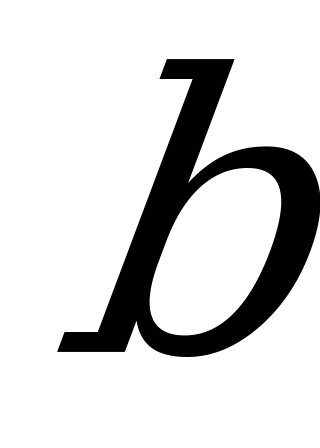 - мнимая полуось гиперболы.
- мнимая полуось гиперболы.
Точки 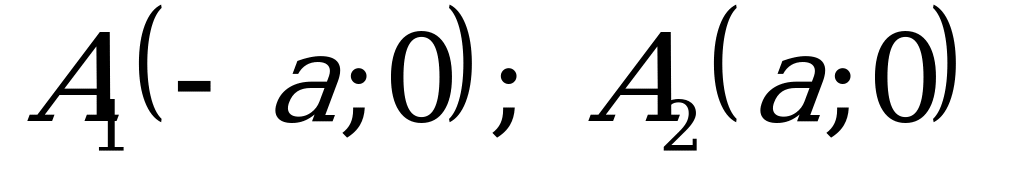 - вершины гиперболы.
- вершины гиперболы.
Фокусы гиперболы 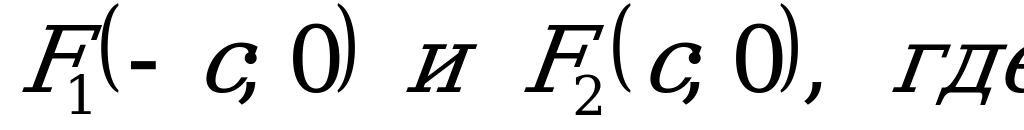
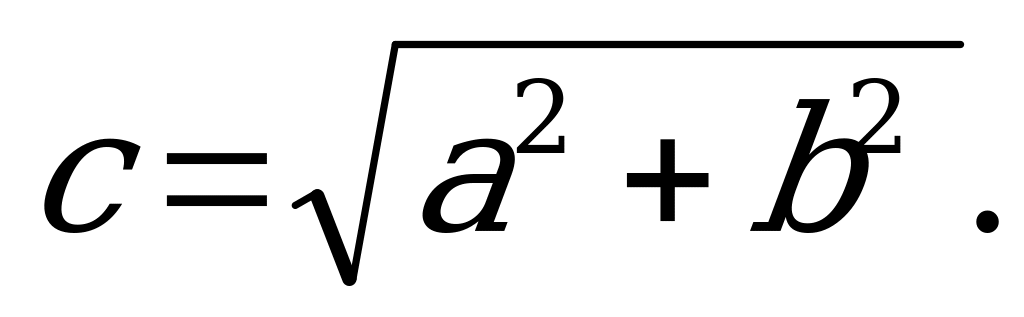
Гипербола имеет две асимптоты 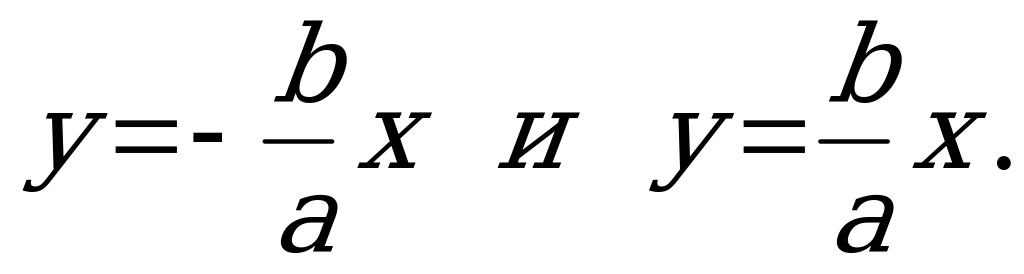
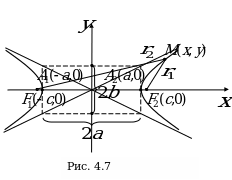
Для построения гиперболы сначала строят основной прямоугольник, ограниченный прямыми 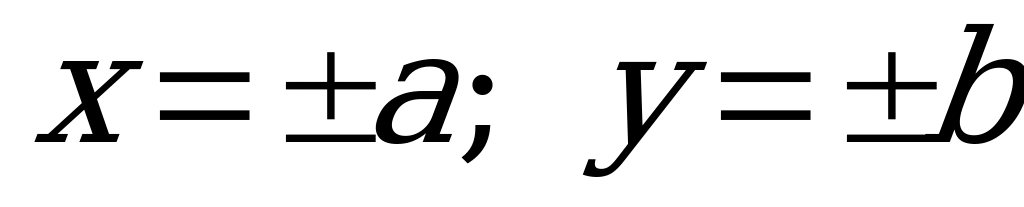 , затем проводят его диагонали, которые совпадают с асимптотами гиперболы.
, затем проводят его диагонали, которые совпадают с асимптотами гиперболы.
Форму гиперболы характеризует эксцентриситет 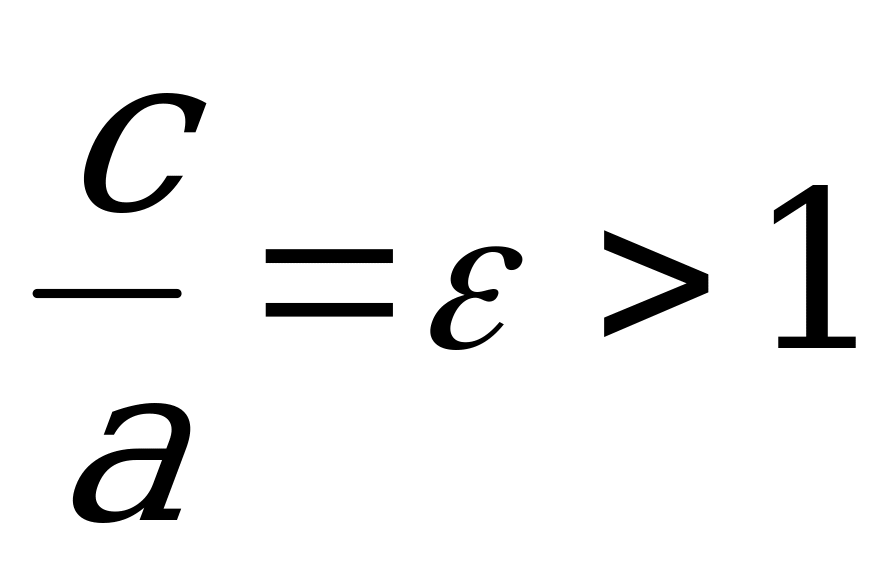 . Чем меньше эксцентриситет, тем более вытянут её основной в направлении фокальной оси.
. Чем меньше эксцентриситет, тем более вытянут её основной в направлении фокальной оси.
Гипербола 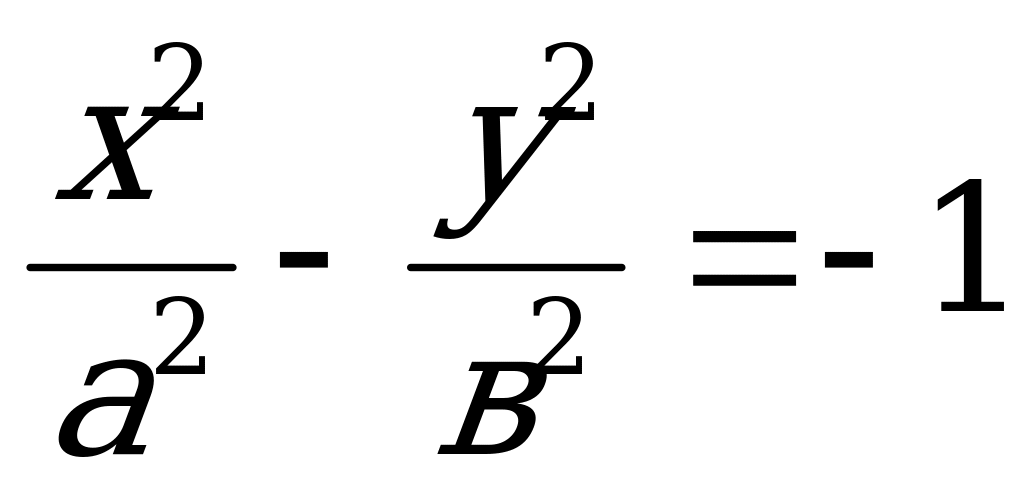 называется сопряженной к гиперболе (4.15).
называется сопряженной к гиперболе (4.15).
Здесь 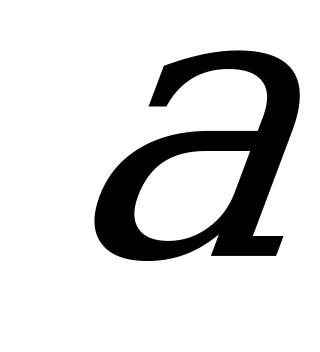 - мнимая полуось гиперболы,
- мнимая полуось гиперболы, 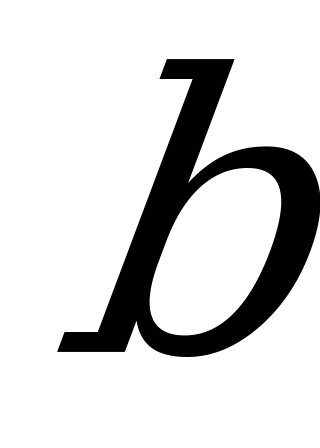 - действительная полуось гиперболы Вершины сопряженной гиперболы
- действительная полуось гиперболы Вершины сопряженной гиперболы 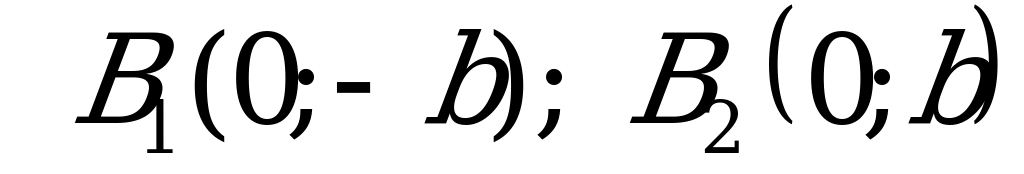 и фокусы
и фокусы  лежат на оси ОY.
лежат на оси ОY.
Парабола
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от фиксированной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса 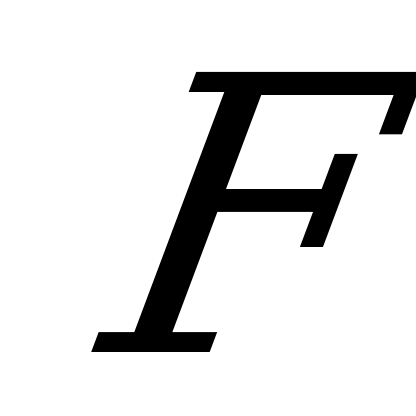 до директрисы, называется параметром параболы и обозначается через
до директрисы, называется параметром параболы и обозначается через 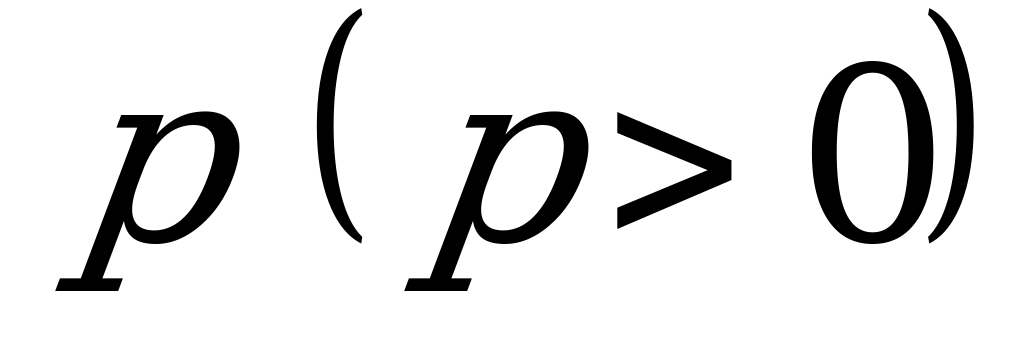 .
.
Каноническое уравнение параболы имеет вид: 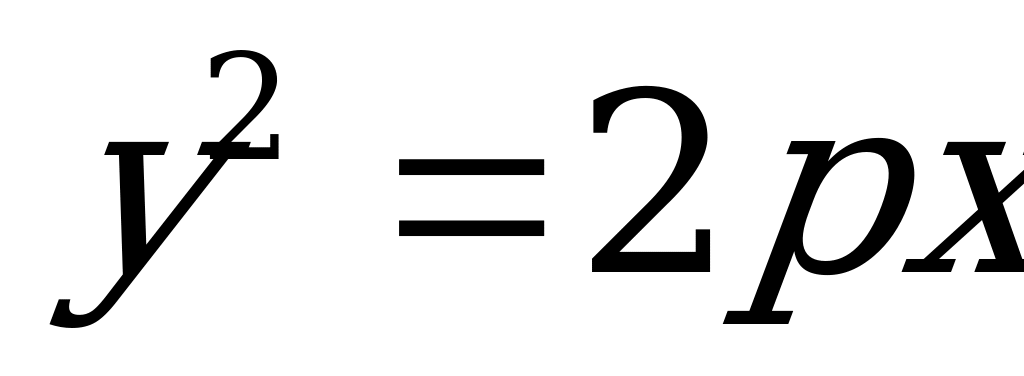 , где
, где 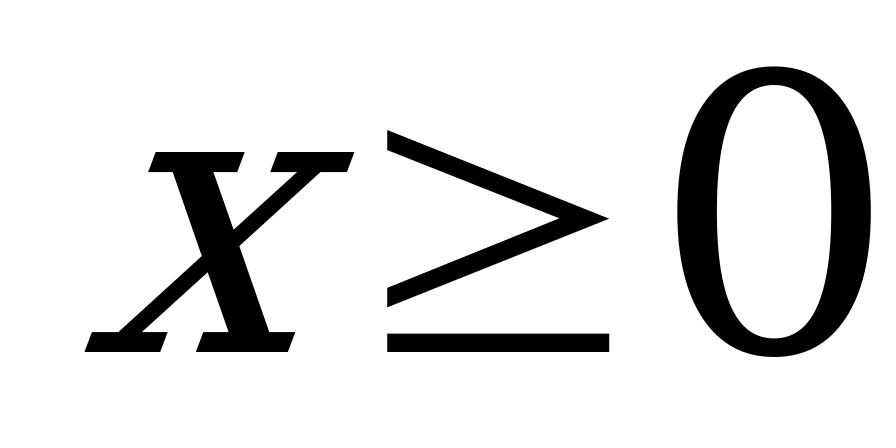 . (4.16)
. (4.16)
Точка 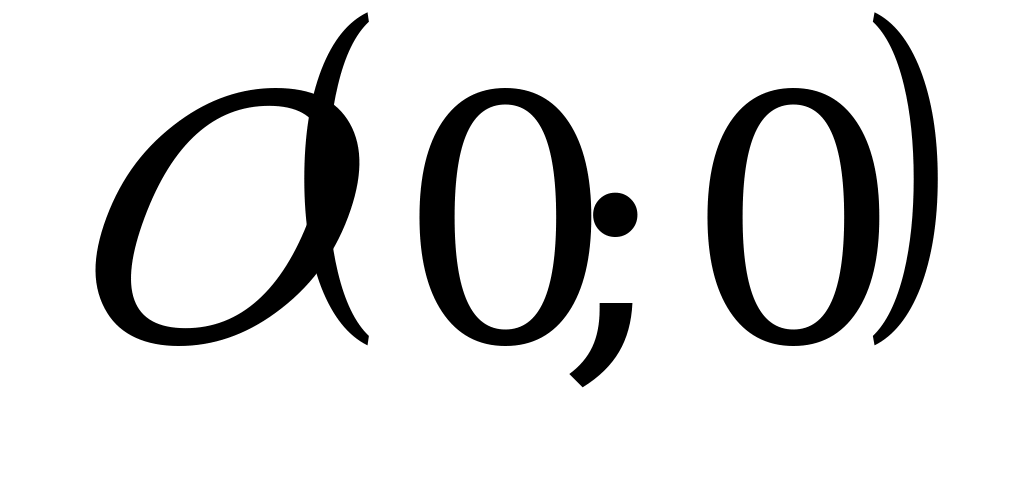 - вершина параболы, ось
- вершина параболы, ось 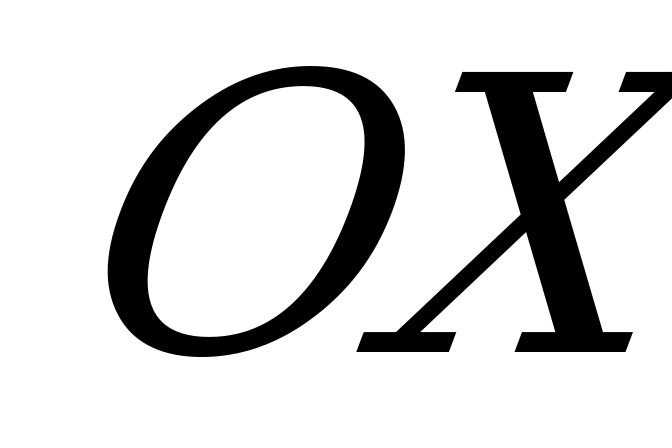 - ось симметрии параболы.
- ось симметрии параболы.
Фокус 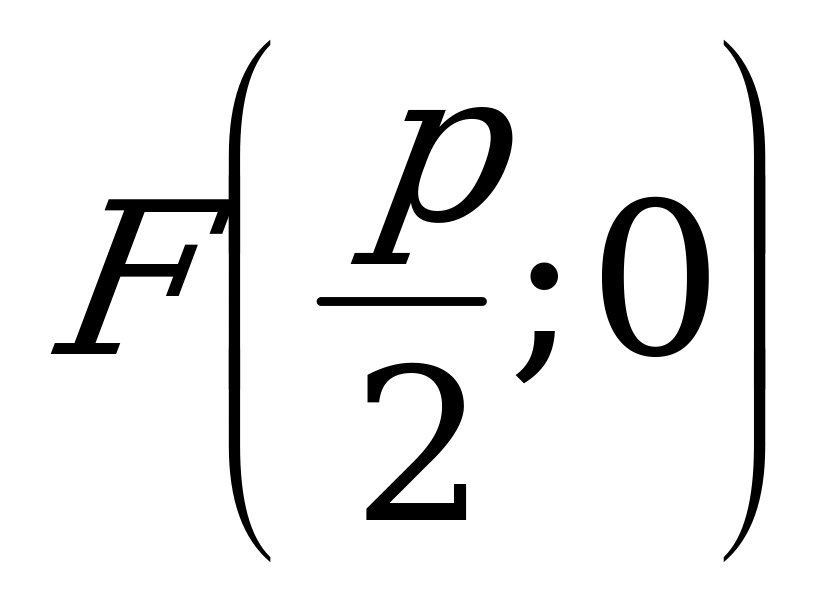 и уравнение директрисы
и уравнение директрисы 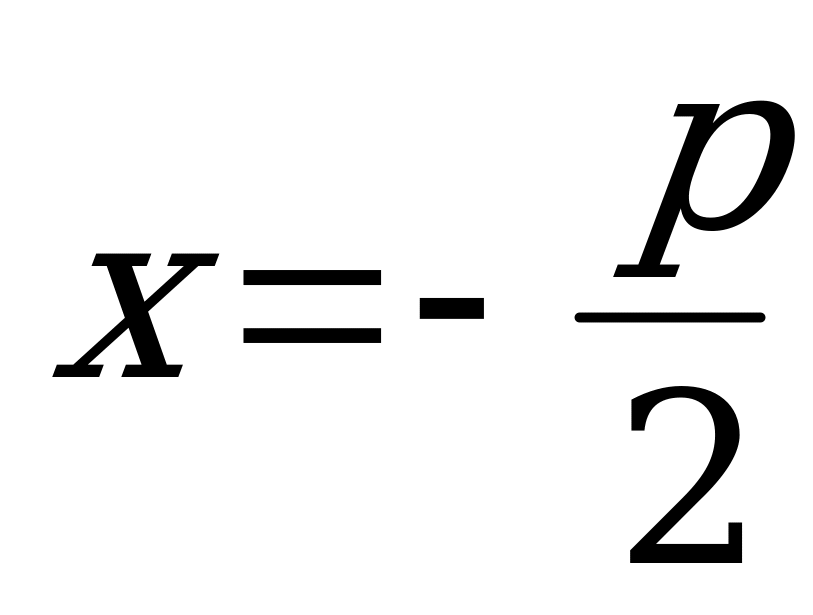 .
.

Парабола  располагается симметрично относительно оси
располагается симметрично относительно оси 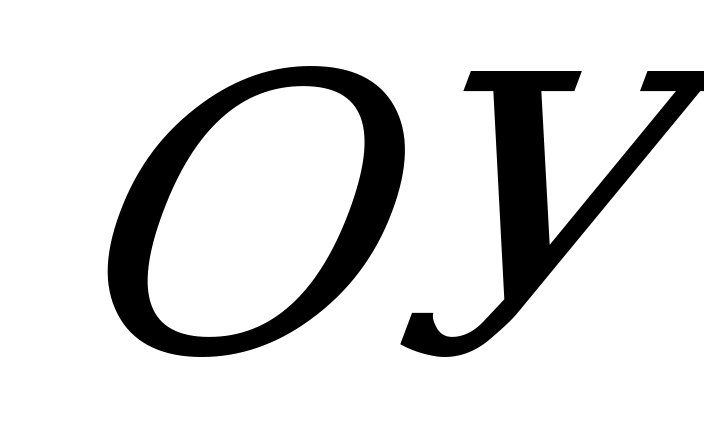 .
.
Уравнение кривых второго порядка с осями симметрии параллельными осям координат
Если в уравнении (4.12) кривой второго порядка 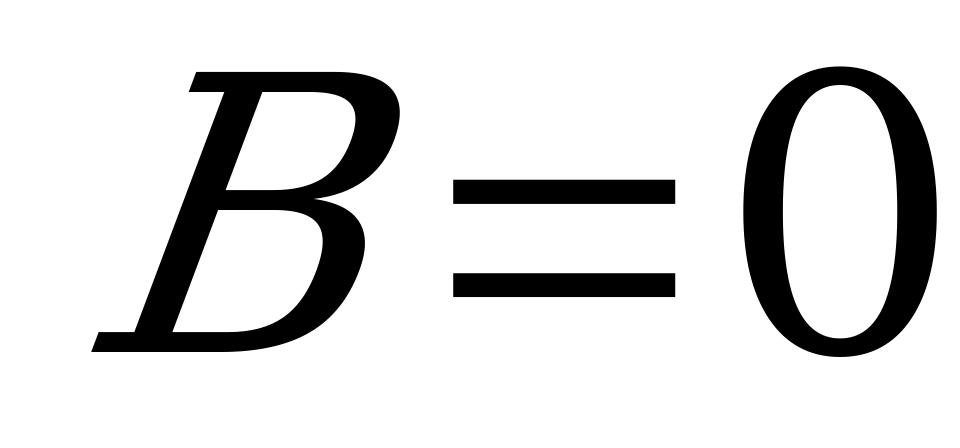 , то каноническое уравнение можно получить с помощью параллельного переноса системы координат, при котором начало
, то каноническое уравнение можно получить с помощью параллельного переноса системы координат, при котором начало  новой системы
новой системы 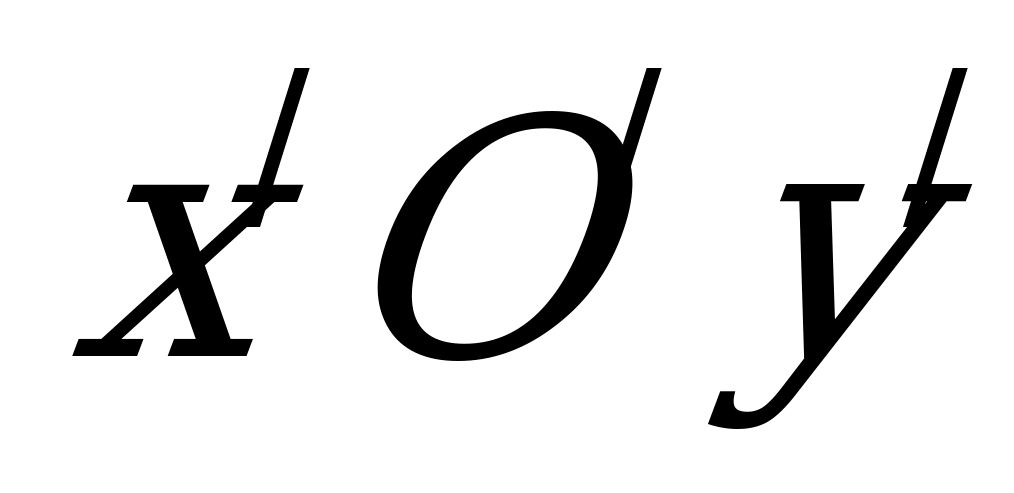 помещается в точку
помещается в точку 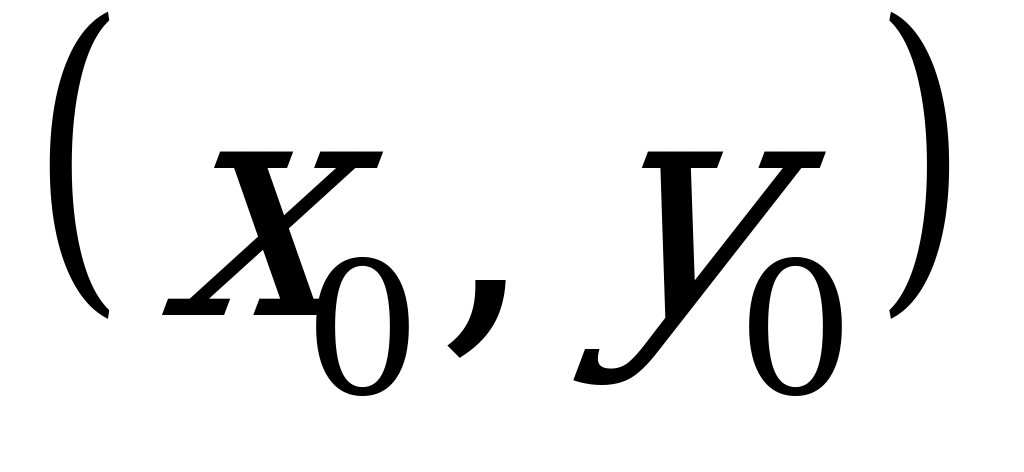 , а «старые» и «новые» координаты связаны формулами:
, а «старые» и «новые» координаты связаны формулами:
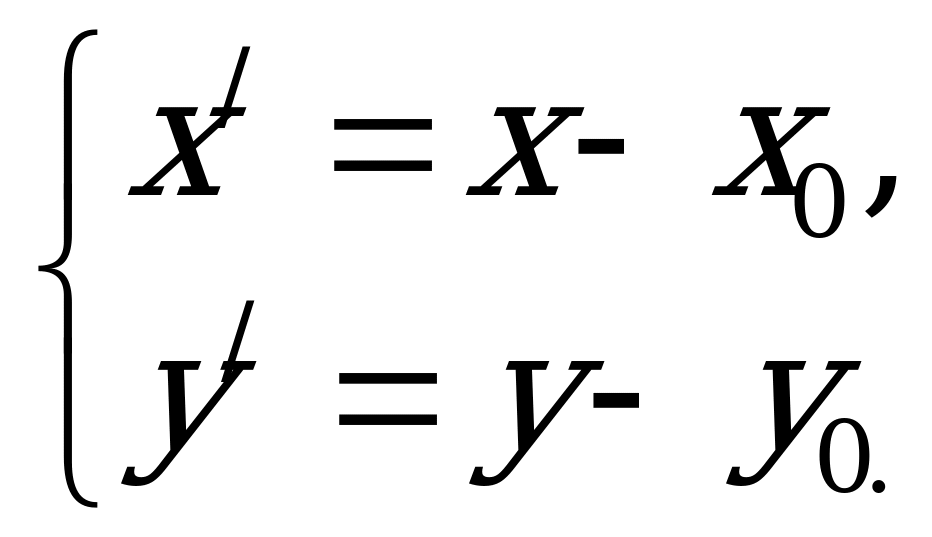 (4.17)
(4.17)
Уравнение эллипса с центром 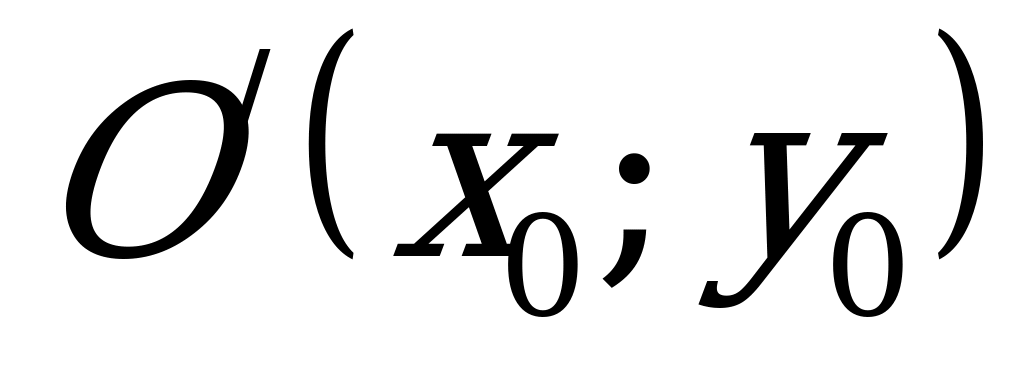 имеет вид:
имеет вид:
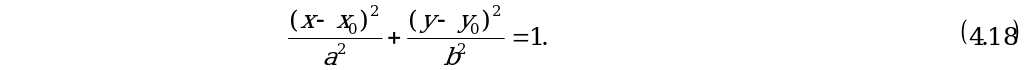 Если
Если 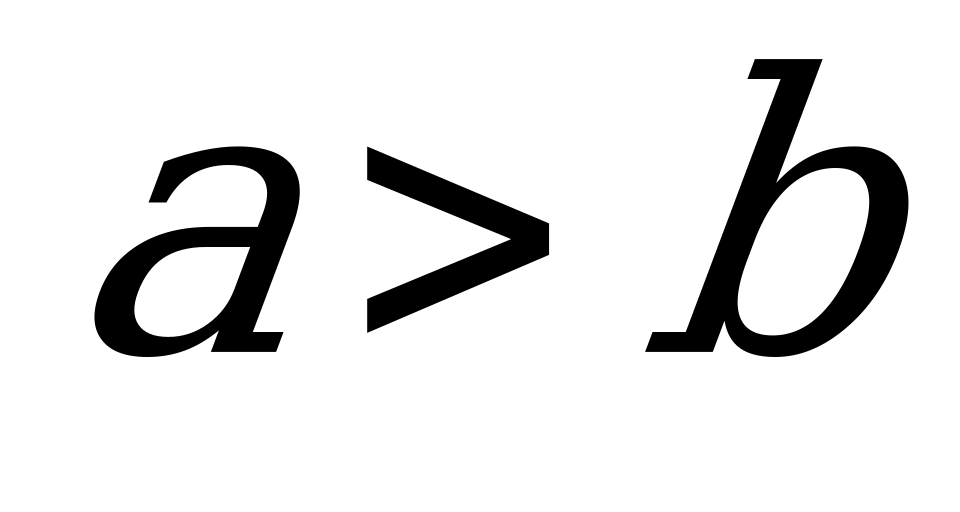 ,
,
то вершины эллипса 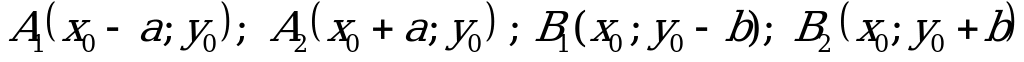 , а фокусы
, а фокусы 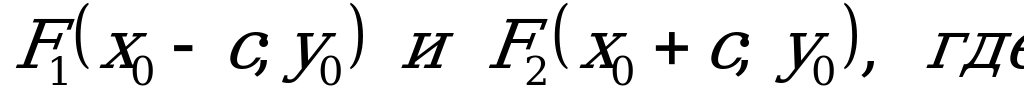
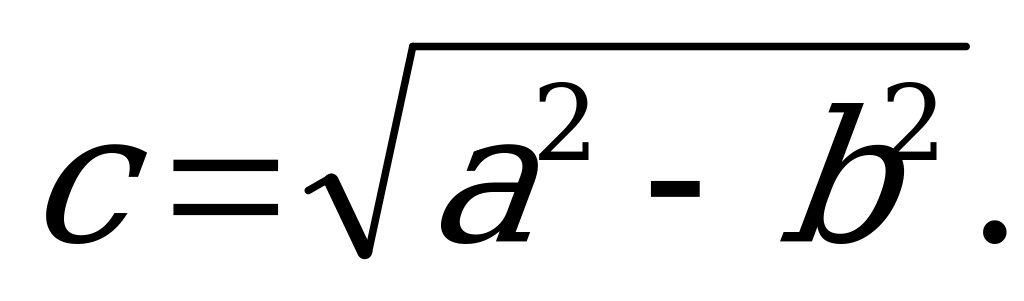
Если 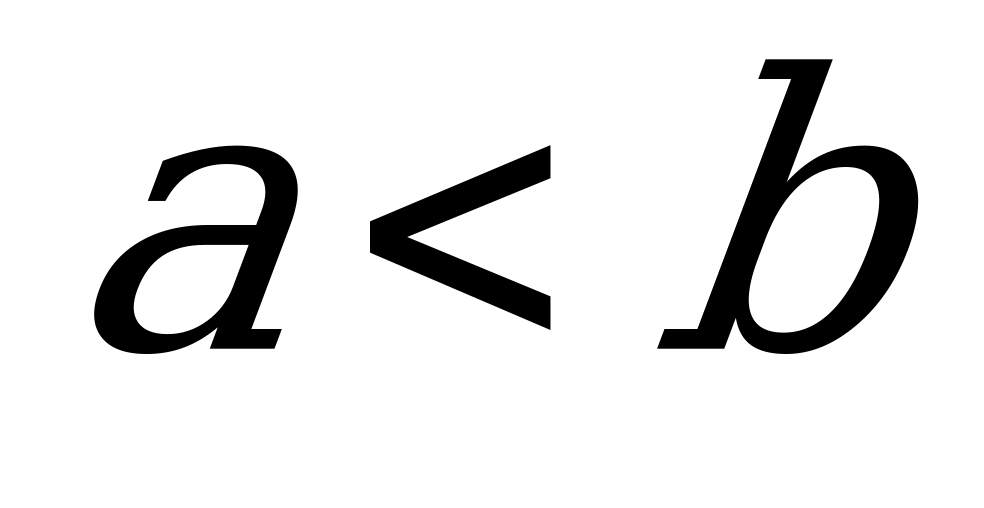 ,
,
то вершины эллипса 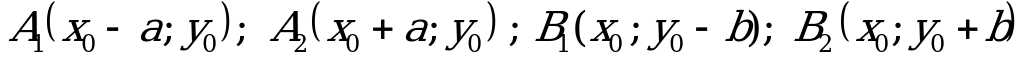 , а фокусы
, а фокусы
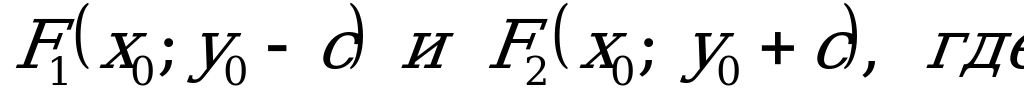
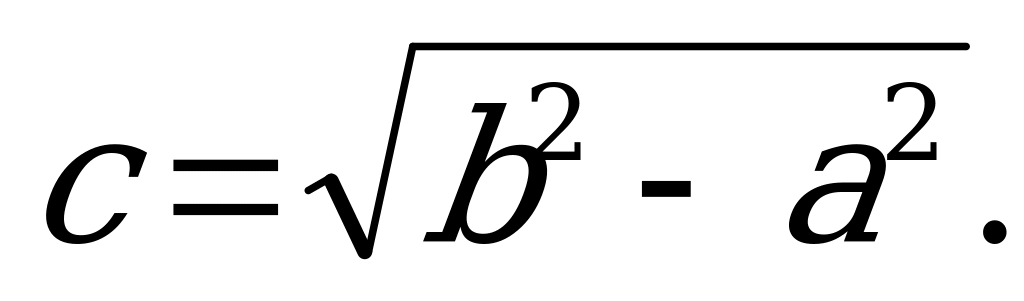
Уравнение гиперболы с центром 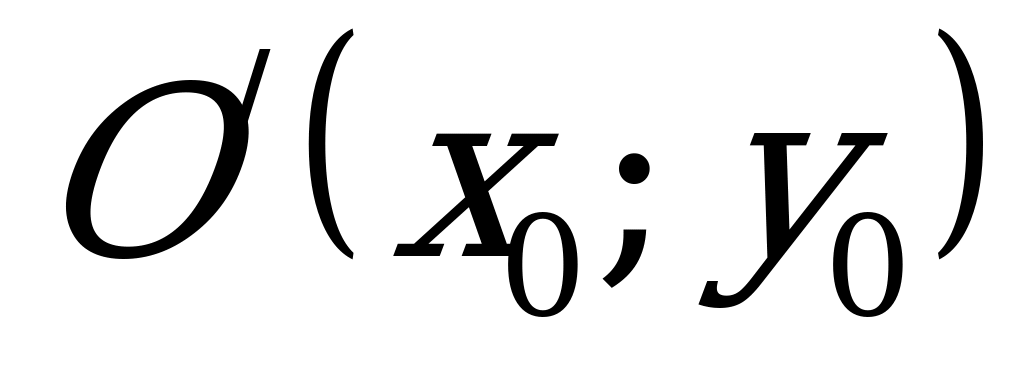 имеет вид:
имеет вид:

Вершины гиперболы 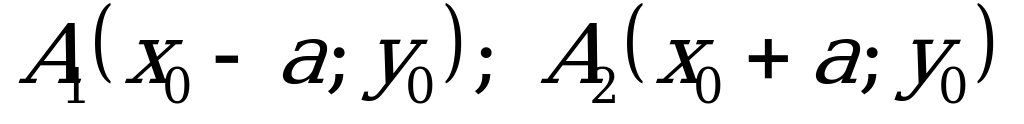 , а фокусы
, а фокусы

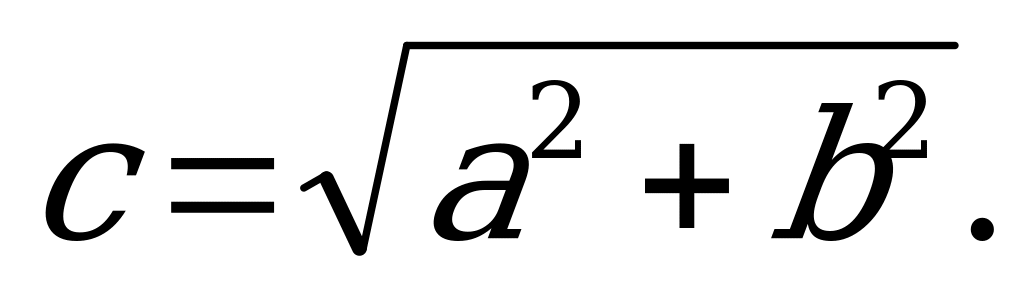
Уравнение сопряженной гиперболы с центром 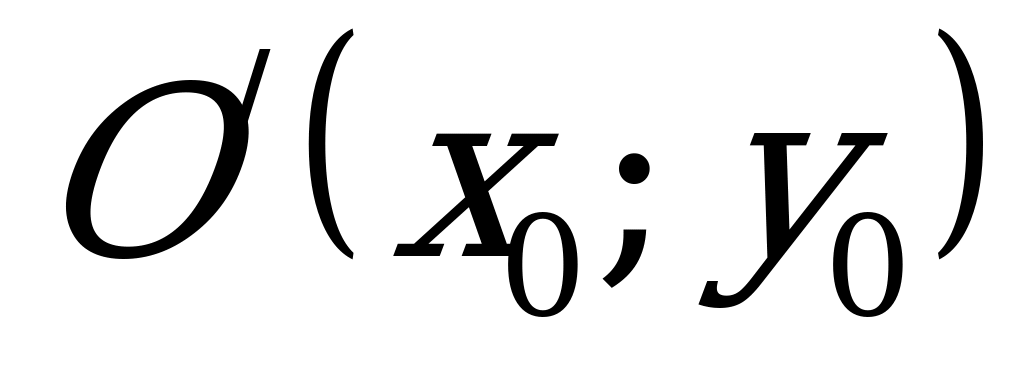 имеет вид:
имеет вид:
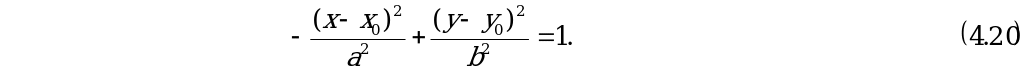 Вершины гиперболы
Вершины гиперболы 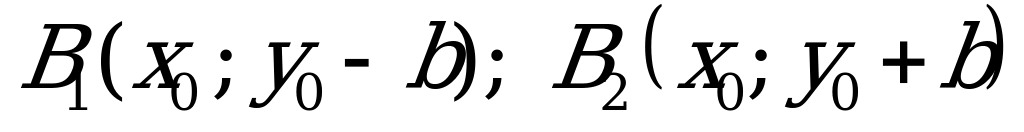 а фокусы
а фокусы
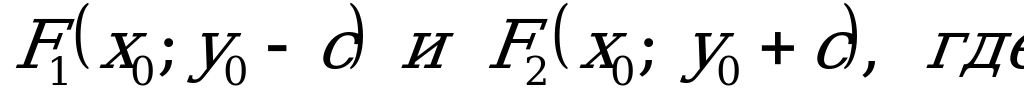
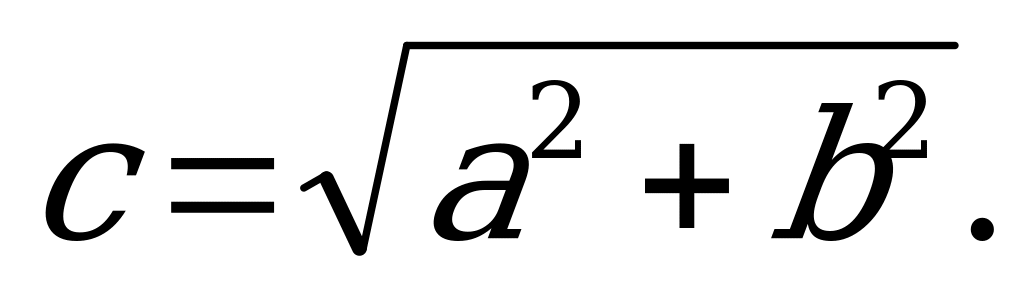
Уравнение параболы с вершиной 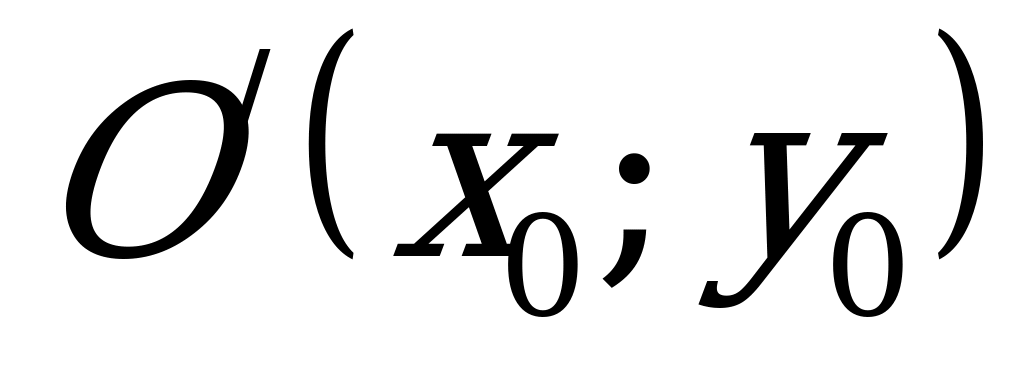 с осью симметрии параллельной оси OX :
с осью симметрии параллельной оси OX :
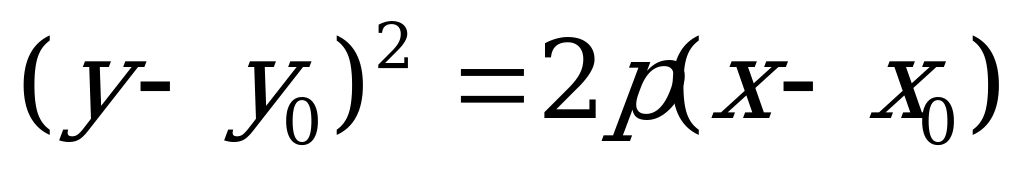 (4.21)
(4.21)
или
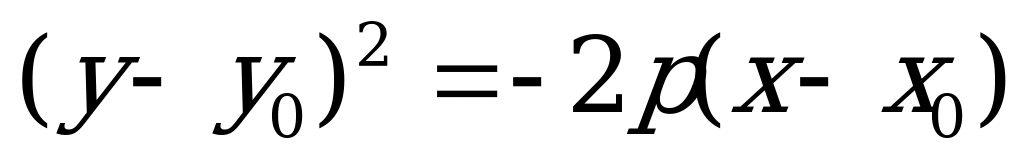 (4.22)
(4.22)
Уравнение параболы с вершиной 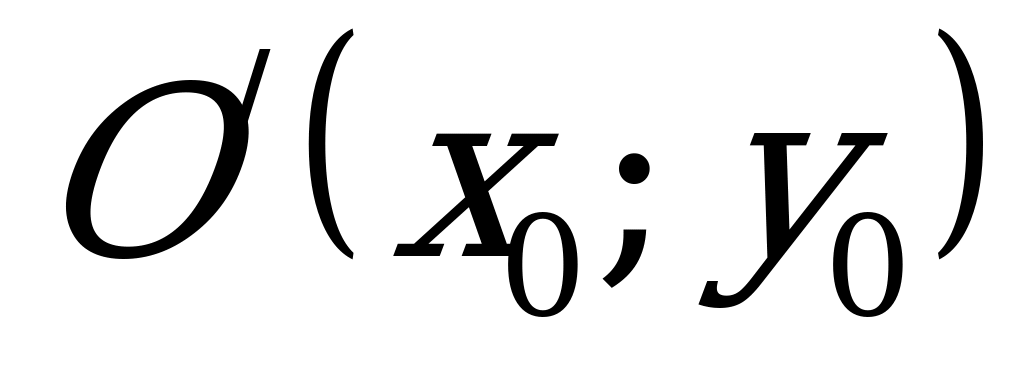 с осью симметрии параллельной оси OY :
с осью симметрии параллельной оси OY :
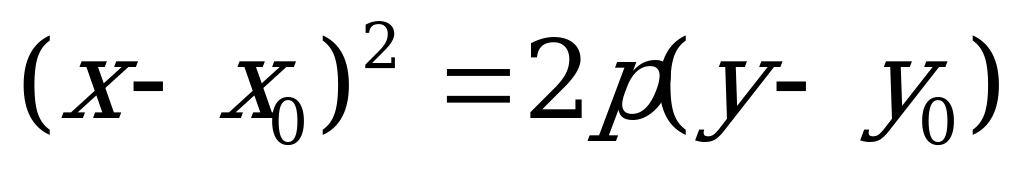 (4.23)
(4.23)
или
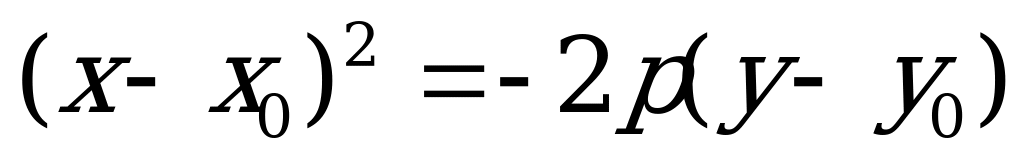 (4.24)
(4.24)
Пример. Используя параллельный перенос системы координат привести уравнение кривой 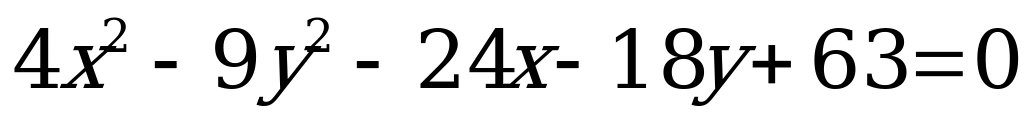 к каноническому виду и построить кривую.
к каноническому виду и построить кривую.
Решение. Преобразуем уравнение линии, группируя члены с 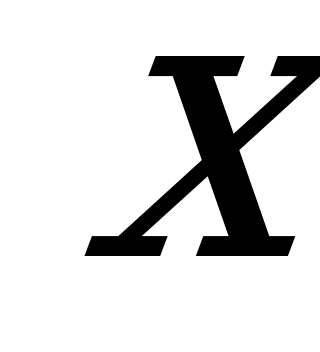 и члены с
и члены с  , и вынося за скобки коэффициенты при квадратах:
, и вынося за скобки коэффициенты при квадратах:
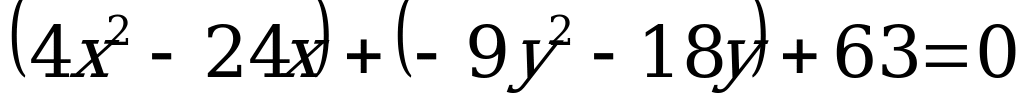 ,
,
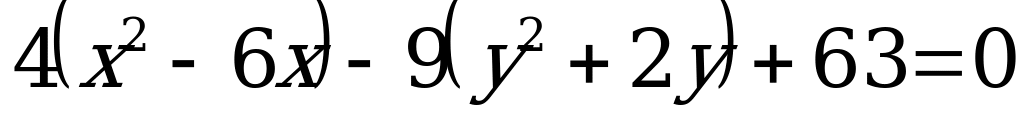 ;
;
выделим в скобках полные квадраты:
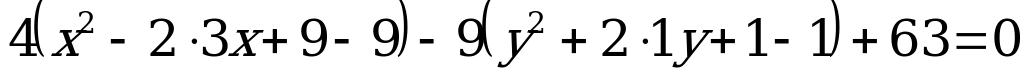 ,
,
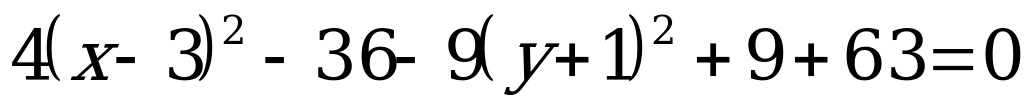 ,
,
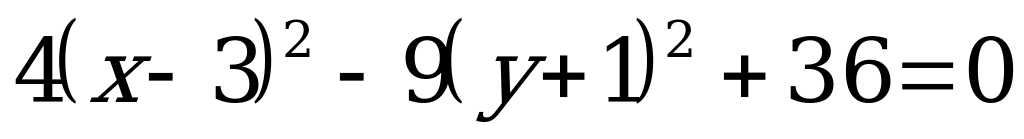 ,
,
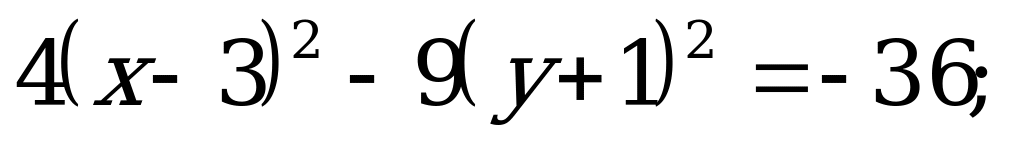
разделим обе части уравнения на (-36):
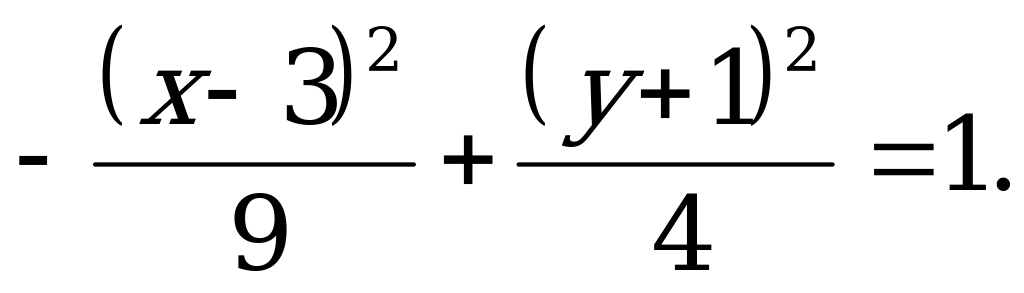
Получили уравнение сопряженной гиперболы (4.20) с центром в точке 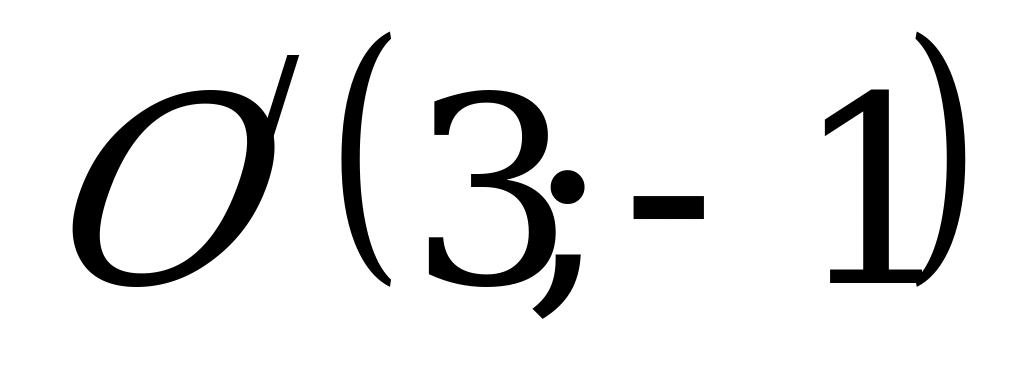 .
.
Выполним параллельный перенос
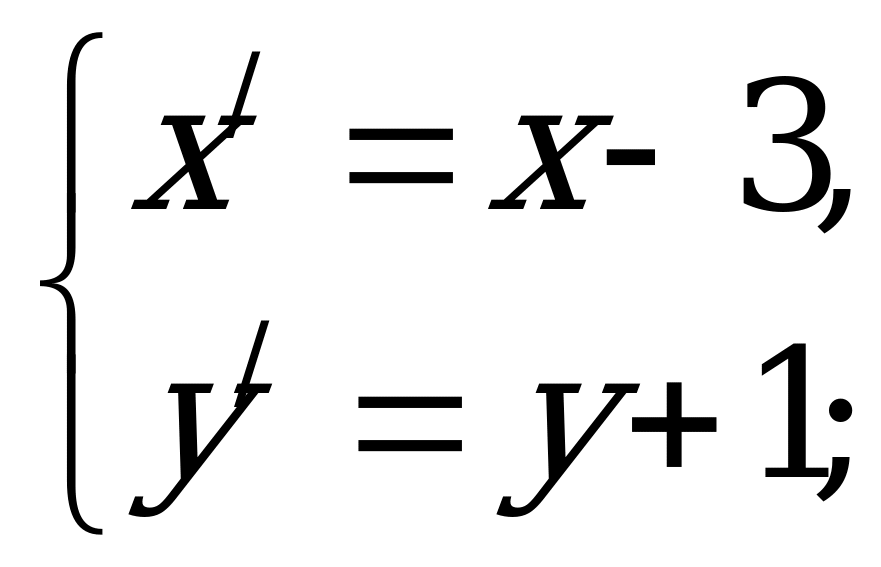
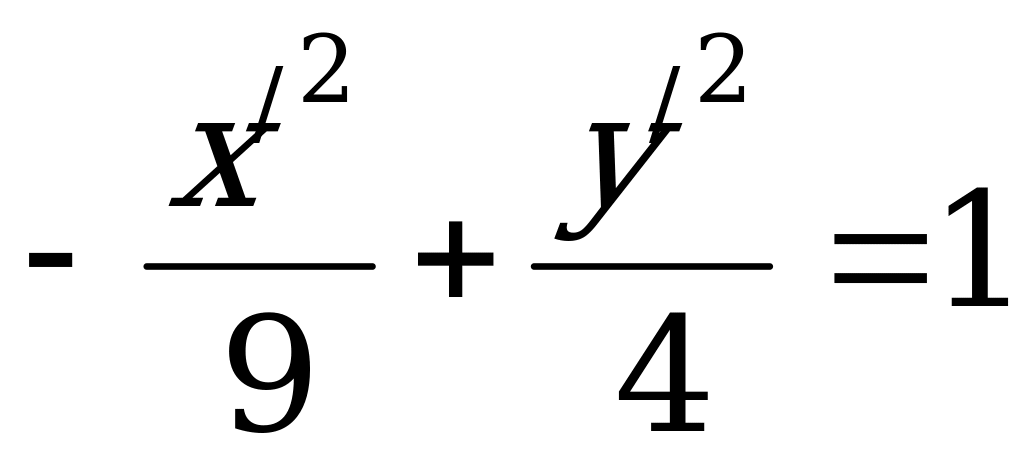 ,
,
получили каноническое уравнение гиперболы в системе 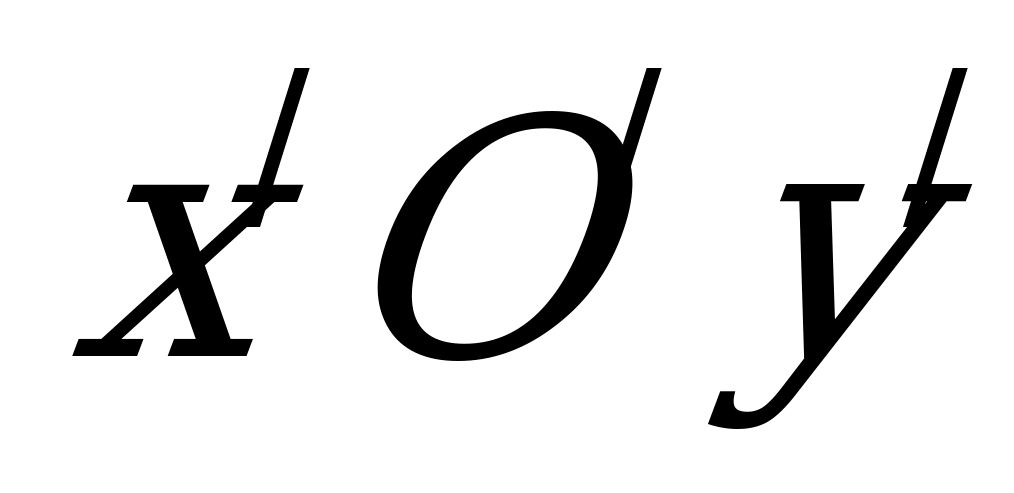 , где
, где 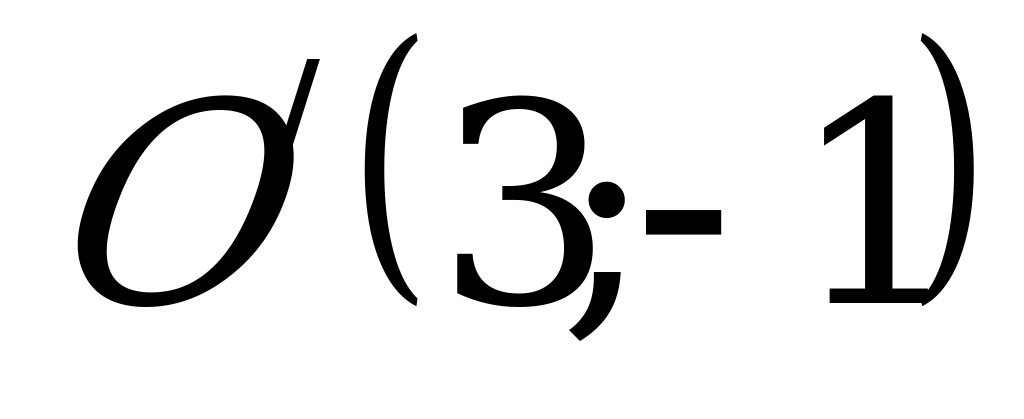 - новое начало.
- новое начало.
Полярная система координат
Полярная система координат на плоскости определяется заданием некоторой точки О, называемой полюсом, луча  , исходящего из этой точки и называемого полярной осью, и единицы масштаба
, исходящего из этой точки и называемого полярной осью, и единицы масштаба  (рис. 4.10).
(рис. 4.10).
Пусть М – произвольная точка плоскости. Обозначим 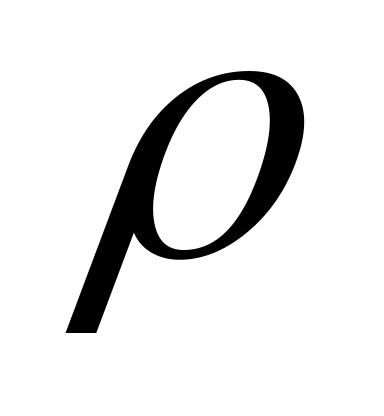 = ОМ – расстояние точки М от полюса,
= ОМ – расстояние точки М от полюса, 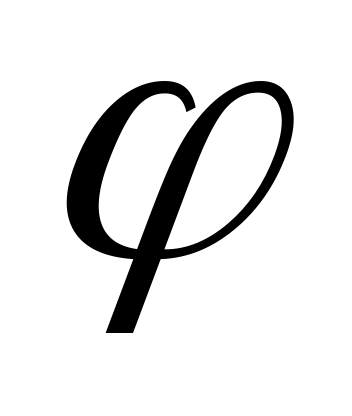 – угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ.
– угол, отсчитываемый от полярной оси против часовой стрелки до направления ОМ.
Числа 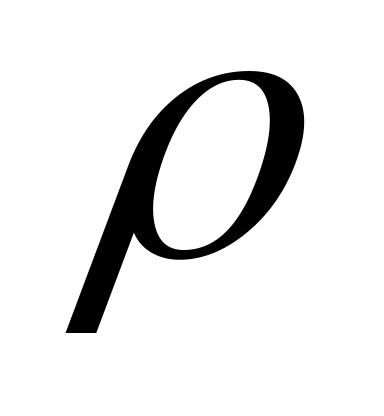 и
и 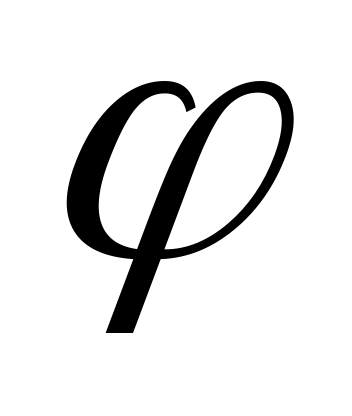 называются полярными координатами точки М,
называются полярными координатами точки М, 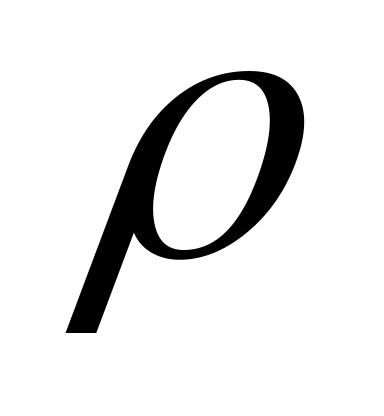 – полярный радиус,
– полярный радиус, 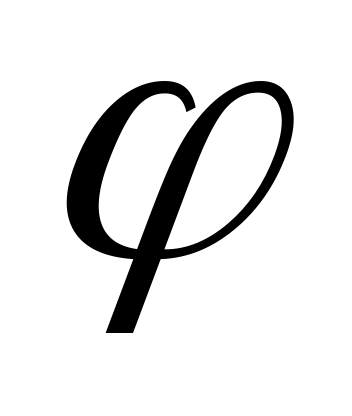 – полярный угол точки М.
– полярный угол точки М.
Задание пары чисел (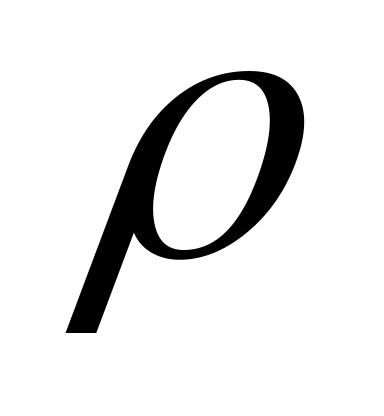 ,
, 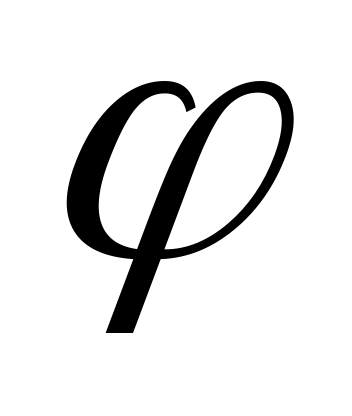 ) однозначно определяет точку М на плоскости. Если ограничить изменение
) однозначно определяет точку М на плоскости. Если ограничить изменение 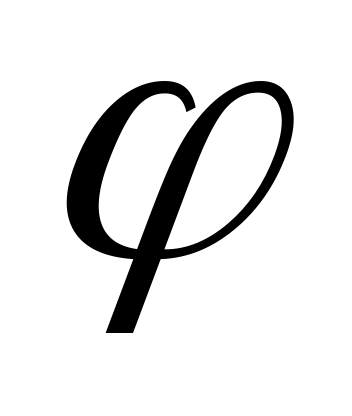 пределами
пределами 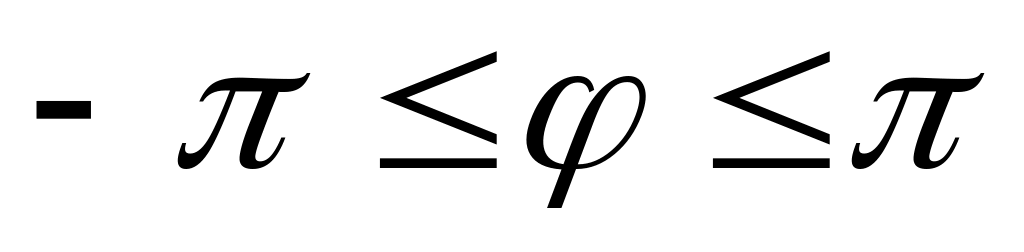 (или
(или 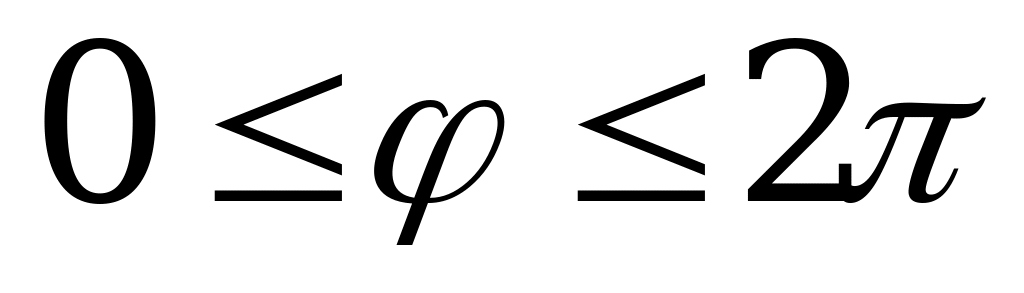 ), то каждой точке плоскости также будет однозначно соответствовать пара чисел (
), то каждой точке плоскости также будет однозначно соответствовать пара чисел (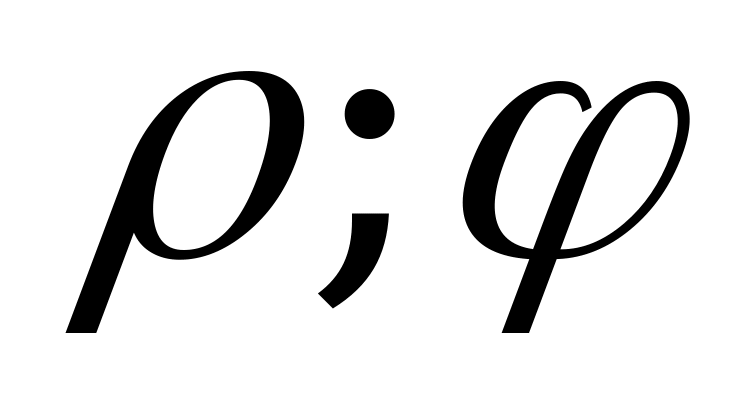 ).
).
Исключение составляет полюс, для которого 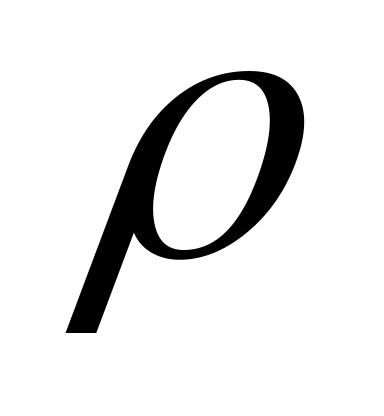 = 0, а угол
= 0, а угол 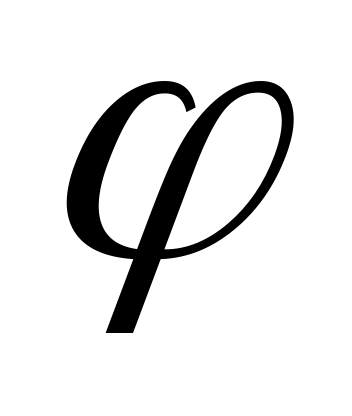 не определен.
не определен.
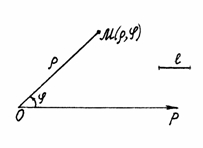
Рис. 4.10
Часто оказывается полезным рассматривать на плоскости полярную систему координат (ПСК) вместе с декартовой системой координат (ДСК). Выберем ДСК так, чтобы ее начало 0 совпадало с полюсом, а ось ОХ была направлена по полярной оси  (рис.4.11). Тогда полярные координаты (
(рис.4.11). Тогда полярные координаты (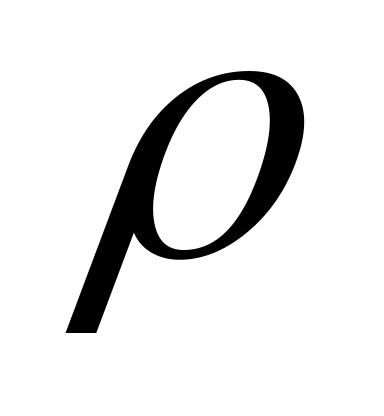 ,
,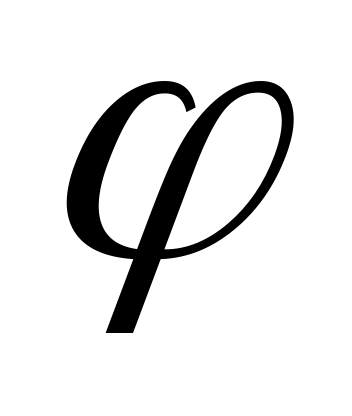 ) и декартовы координаты (
) и декартовы координаты (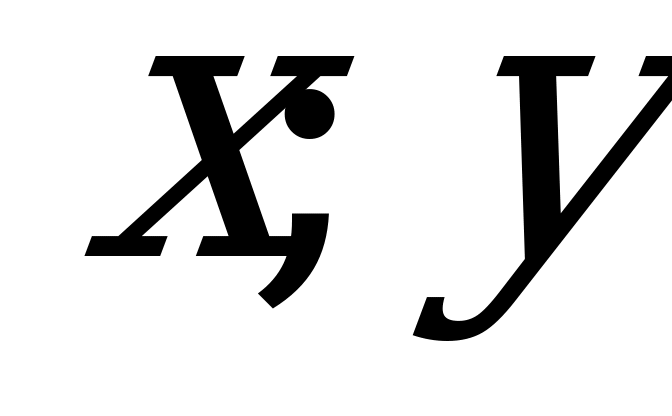 ) точки М связаны соотношениями:
) точки М связаны соотношениями:
 (4.27)
(4.27)
Из этих формул следует:
| 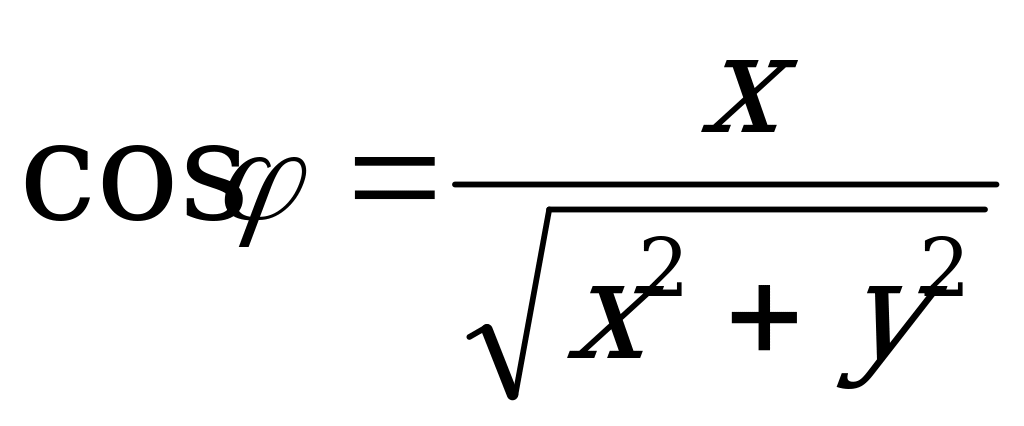 ; ; 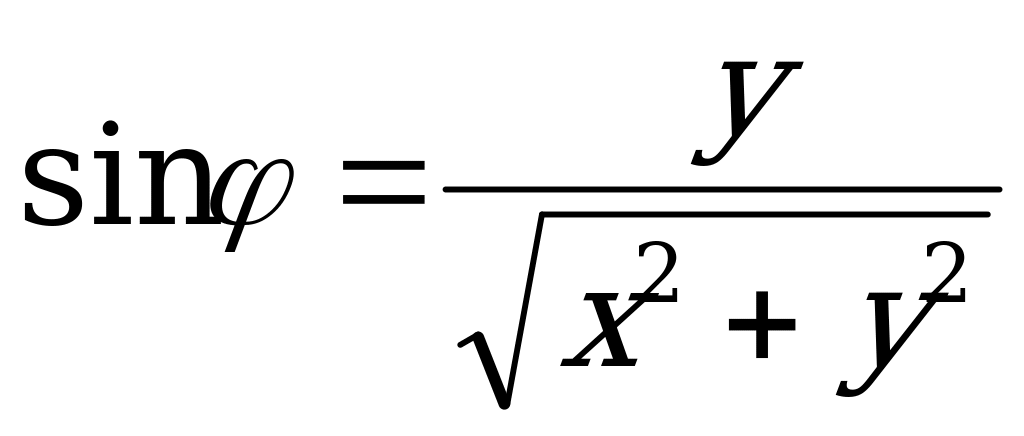
| (4.28) |

Рис. 4.11
Формула для  определяет два угла
определяет два угла 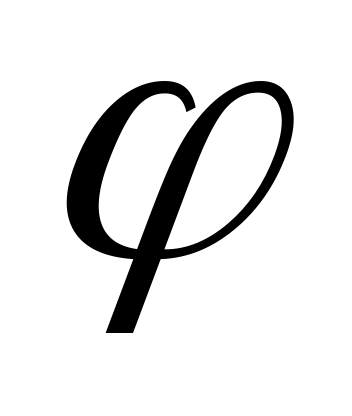 и
и 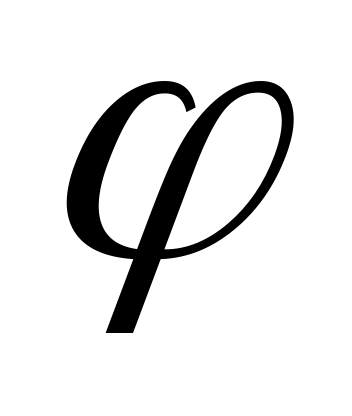 +
+  в промежутке [0; 2
в промежутке [0; 2 ). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (4.28).
). Чтобы уточнить, какой из углов выбрать, нужно учесть четверть, в которой находится точка М, или воспользоваться формулами (4.28).
Чтобы перейти от уравнения линии в декартовых координатах к ее полярному уравнению, нужно вместо ( ), подставить в уравнение их выражения из формул (4.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью формул (4.26), (4.28).
), подставить в уравнение их выражения из формул (4.25). Обратный переход от полярного уравнения к уравнению в декартовых координатах осуществляется с помощью формул (4.26), (4.28).
Пример . Построить в полярной системе координат точки :
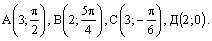
Решение. Построение точек показано на рис. 4.12.
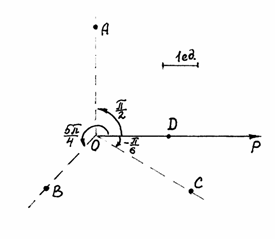
Рис. 4.12
Тема 5. Аналитическая геометрия в пространстве
Уравнение 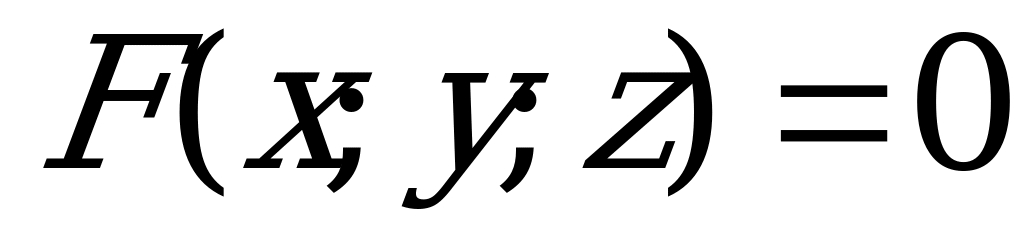 , связывающее три переменные
, связывающее три переменные 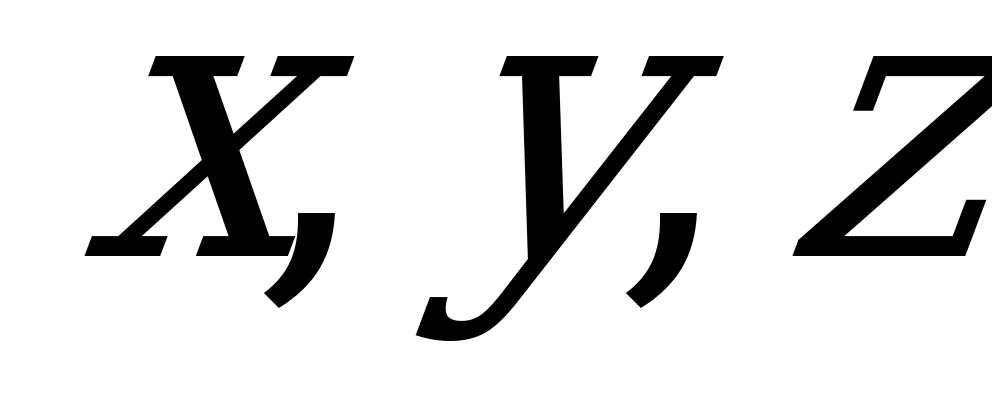 , задает в пространстве некоторую поверхность
, задает в пространстве некоторую поверхность  .
.
Основная задача: на основании некоторой информации о данной поверхности  (обычно геометрического смысла) составить уравнение, которому удовлетворяют координаты любой точки поверхности
(обычно геометрического смысла) составить уравнение, которому удовлетворяют координаты любой точки поверхности  и только они.
и только они.
Рассмотрим простейшую поверхность – плоскость.
5.1 Плоскость в пространстве
Плоскость в пространстве можно задать различными способами; соответственно получим различные виды уравнений плоскости.
1) Уравнение плоскости, проходящей через точку 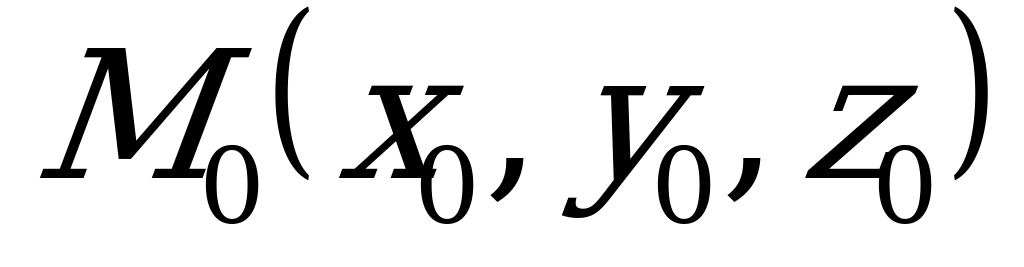 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 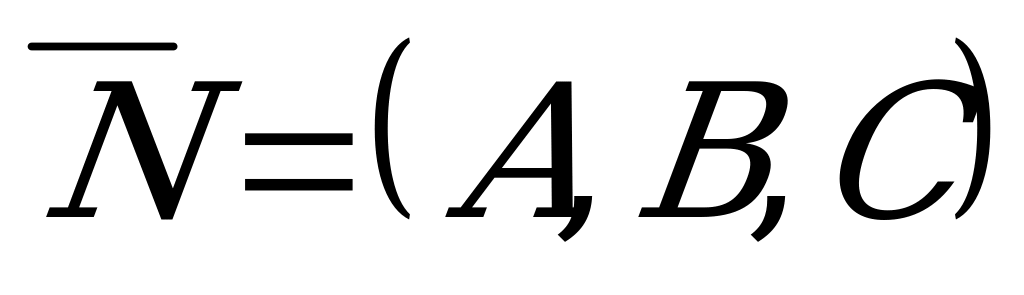 :
:
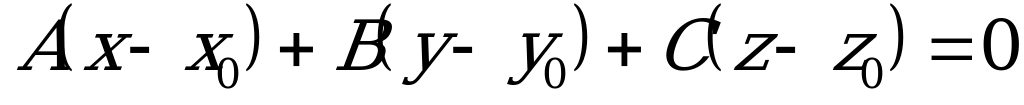 , (5.1)
, (5.1)
где 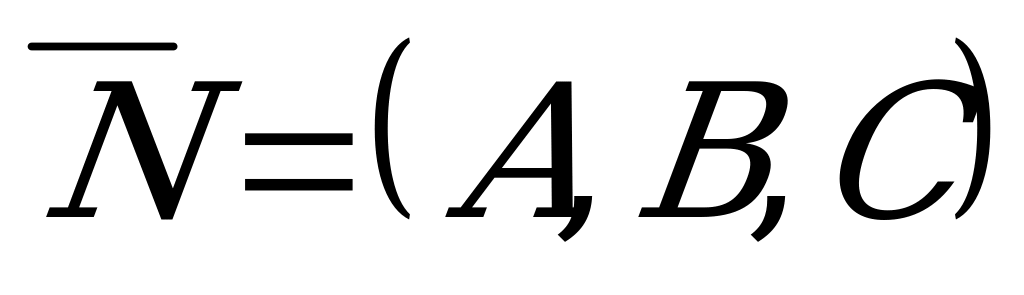 - нормаль.
- нормаль.
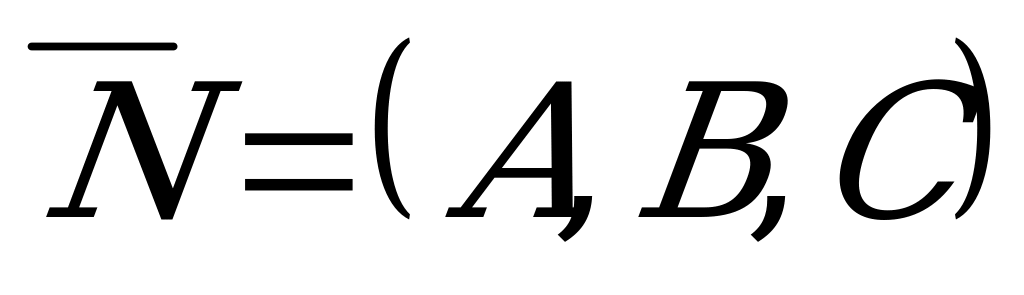
| 
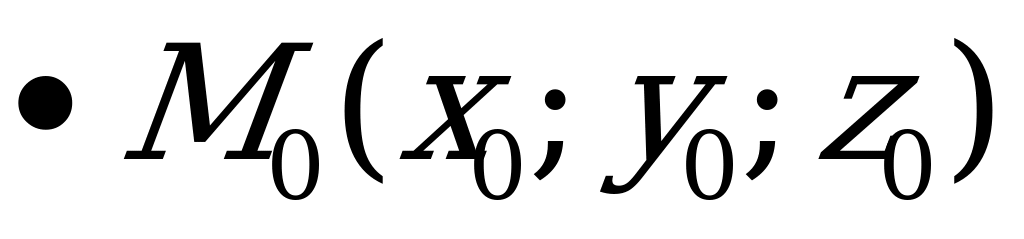

Рис. 5.1 | Уравнение (5.1) получено из следующих соображений. Если 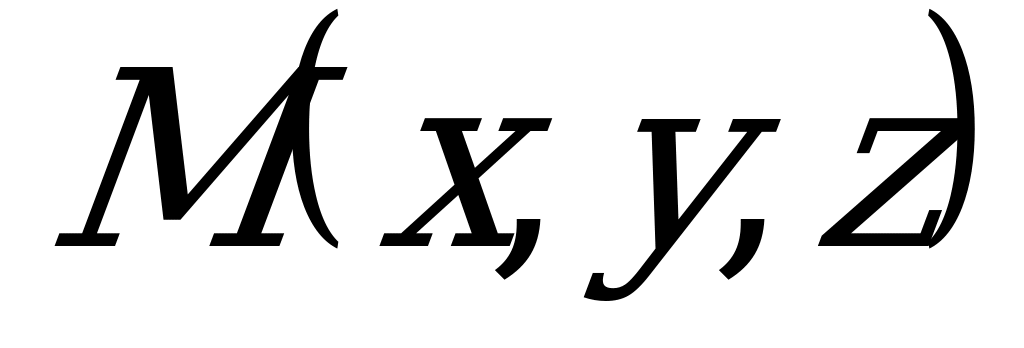 - произвольная точка плоскости - произвольная точка плоскости  , то вектор , то вектор 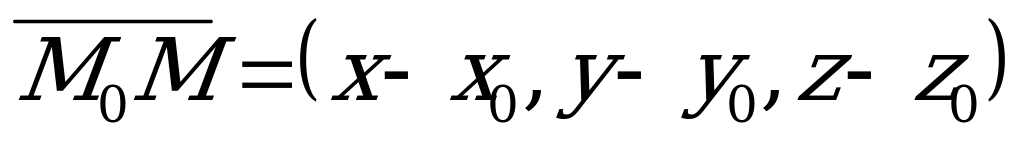 перпендикулярен нормали перпендикулярен нормали  , т.е. , т.е. 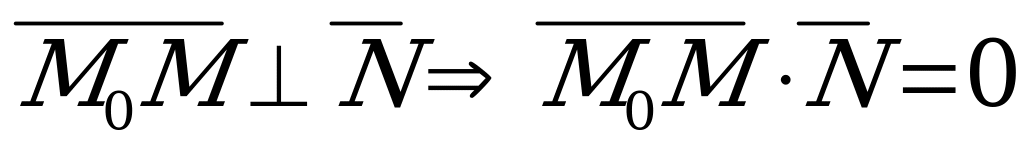 , откуда следует, что , откуда следует, что 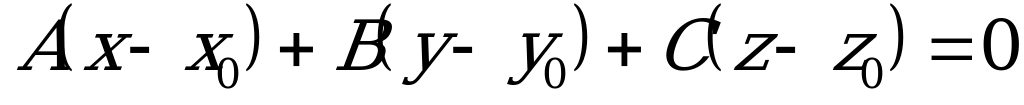 . .
|
2) Общее уравнение плоскости
 , (5.2)
, (5.2)
где коэффициенты  ,
,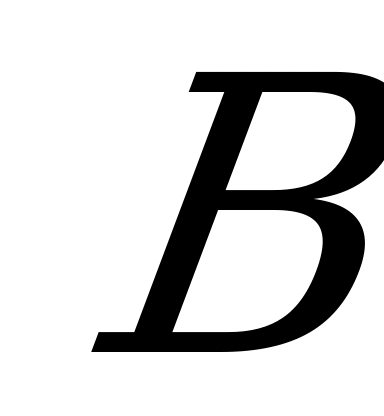 ,
, - координаты нормального вектора
- координаты нормального вектора  .
.
Уравнение (5.2) следует из уравнения (5.1), если в нем раскрыть скобки и число 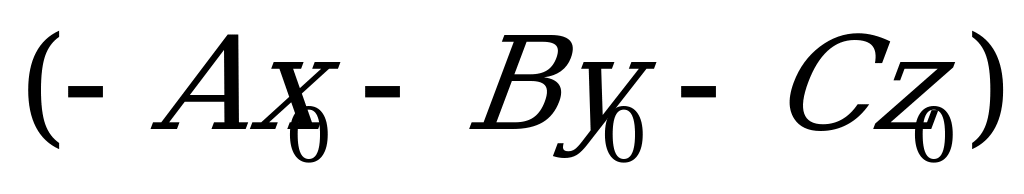 обозначить за
обозначить за 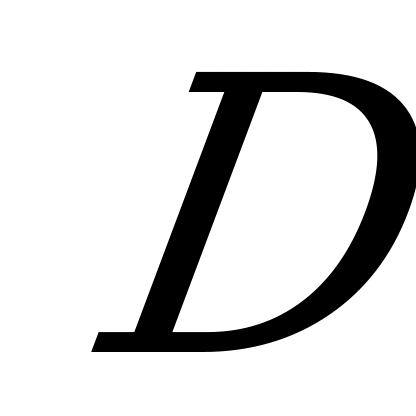 . Таким образом, плоскость задается уравнением первой степени относительно
. Таким образом, плоскость задается уравнением первой степени относительно 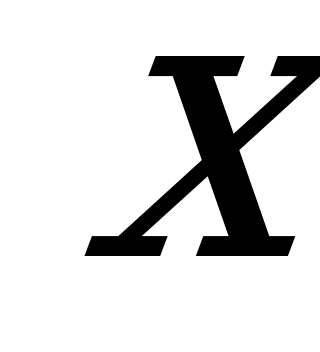 ,
,  и
и  .
.
Верно и обратное утверждение: всякое уравнение первой степени вида (5.2) определяет в заданной прямоугольной системе координат плоскость.
3) Уравнение плоскости «в отрезках»
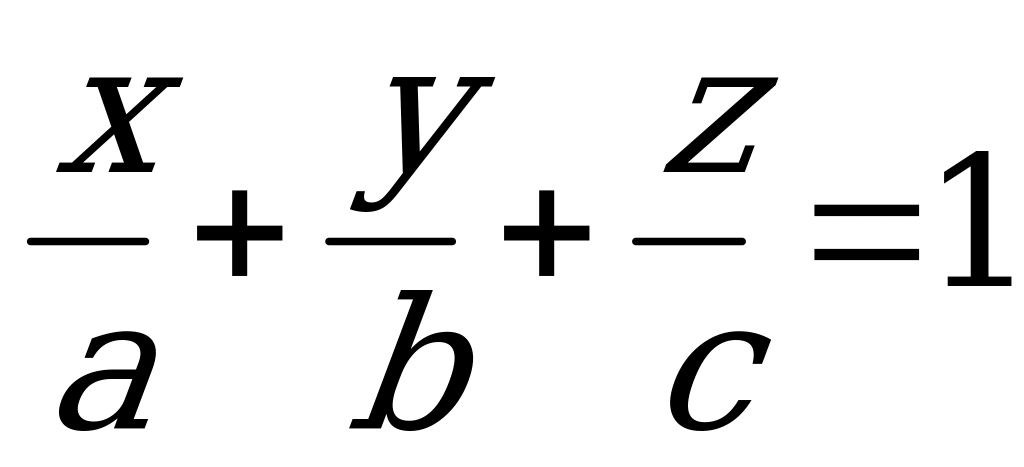 (5.3)
(5.3)
4) Уравнение плоскости, проходящей через три точки 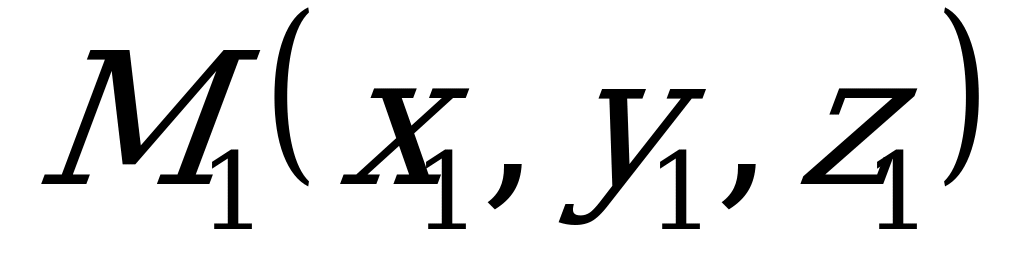 ,
, 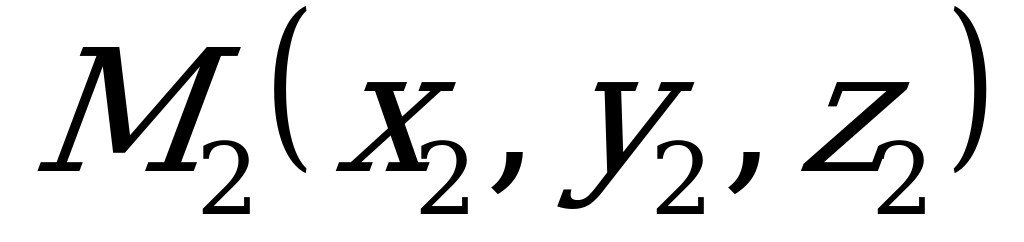 и
и 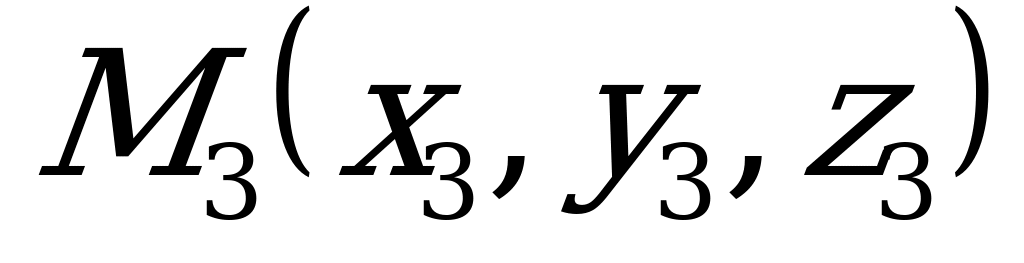 , не лежащие на одной прямой, может быть записано в виде:
, не лежащие на одной прямой, может быть записано в виде:
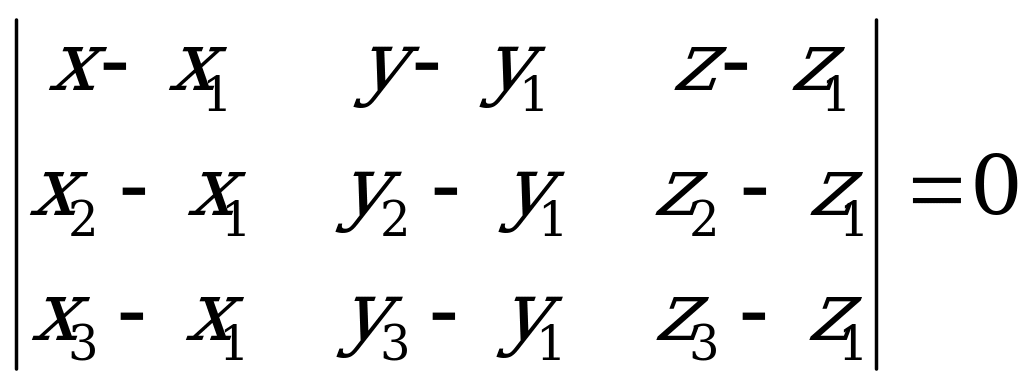 . (5.4)
. (5.4)
|




Рис. 5.3 
| Уравнение вида (5.4) получено из следующих соображений. Если 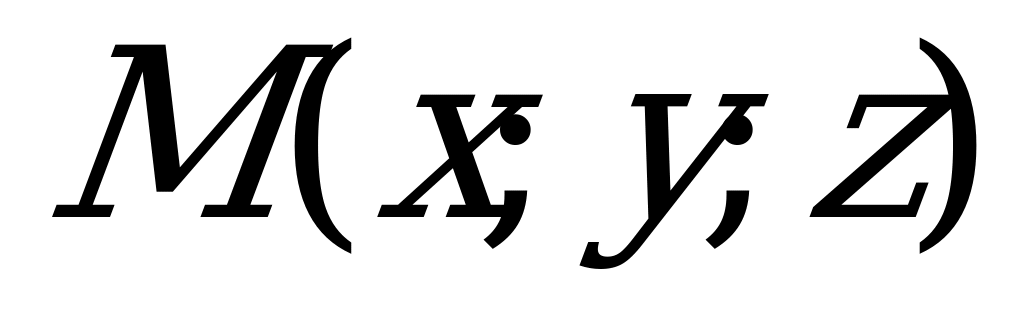 - произвольная точка плоскости - произвольная точка плоскости  , то три вектора , то три вектора  , ,  , , 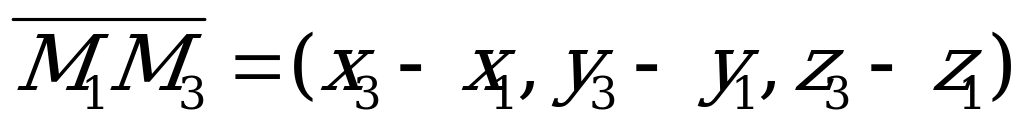
|
лежащие на плоскости  , компланарны, а следовательно, их смешанное произведение равно нулю, т.е.
, компланарны, а следовательно, их смешанное произведение равно нулю, т.е. 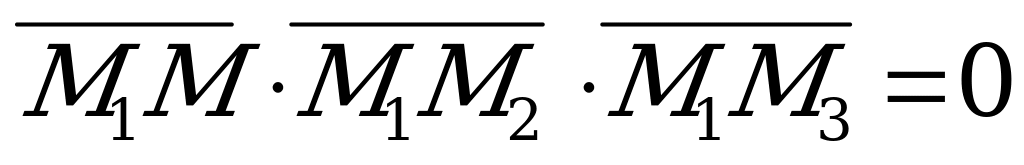 . Используя выражение смешанного произведения в координатной форме, получим уравнение (5.4).
. Используя выражение смешанного произведения в координатной форме, получим уравнение (5.4).
Если в уравнении (5.4) раскрыть определитель (лучше всего разложением по первой строке) и привести подобные члены, то получим уравнение вида (5.2).
5) Расстояние от точки 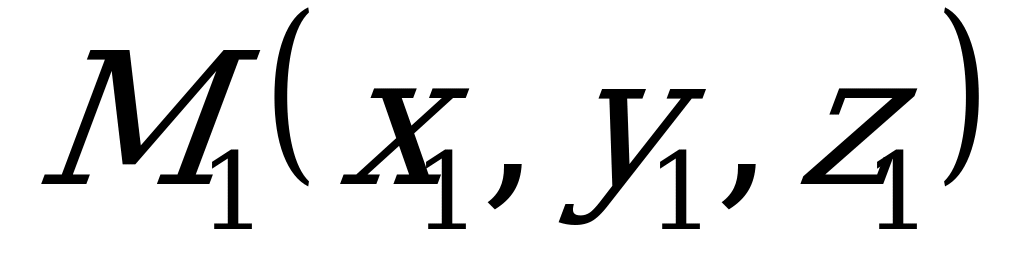 до плоскости
до плоскости  , заданной общим уравнением
, заданной общим уравнением  вычисляется по формуле:
вычисляется по формуле:
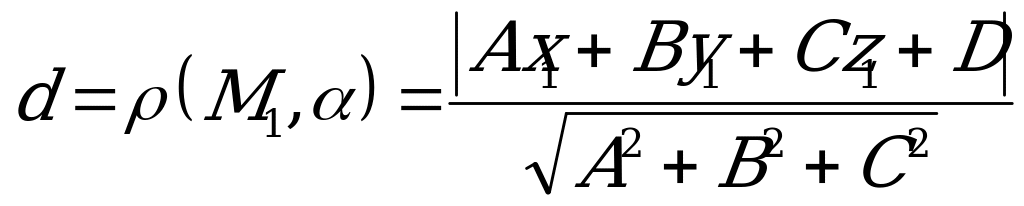 . (5.5)
. (5.5)
6) Угол между двумя плоскостями.
Пусть даны две плоскости:
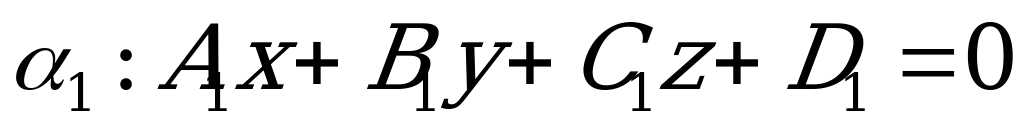 с нормалью
с нормалью  и
и
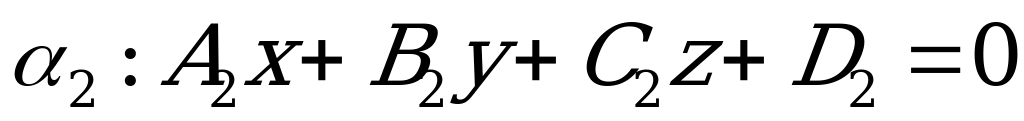 с нормалью
с нормалью 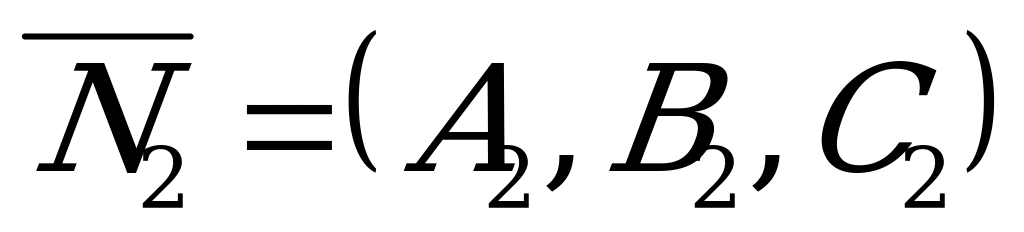 .
.
В качестве угла 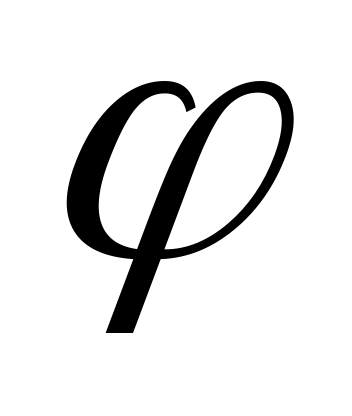 между плоскостями
между плоскостями  и
и 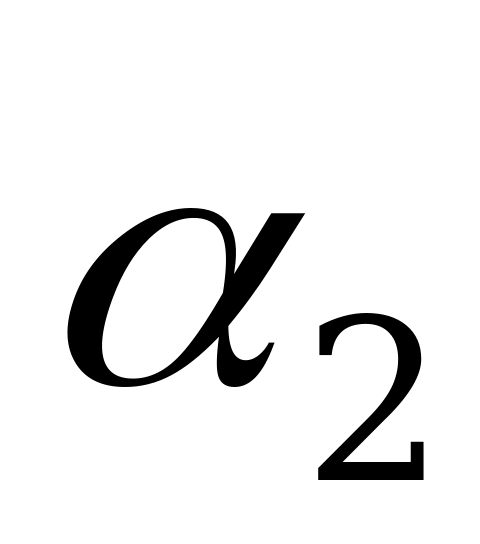 принимается угол между их нормалями:
принимается угол между их нормалями: 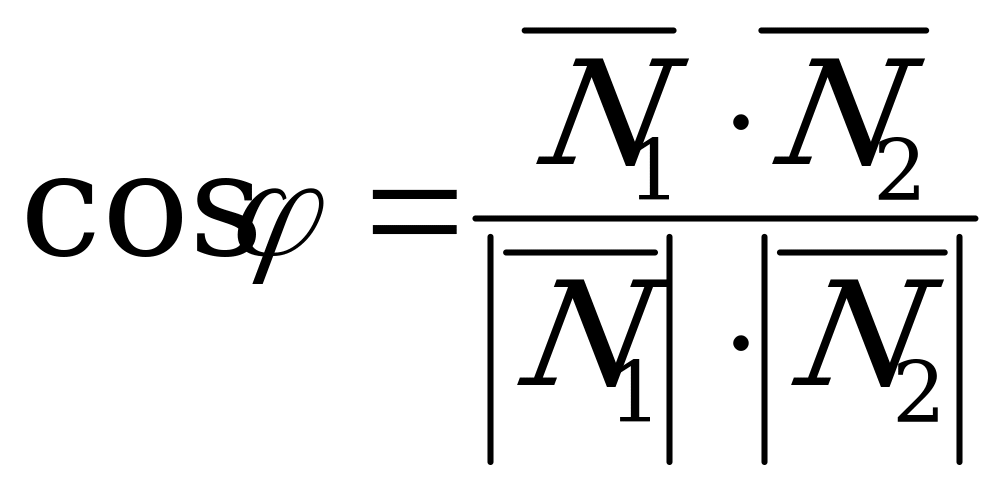 или в координатной форме
или в координатной форме
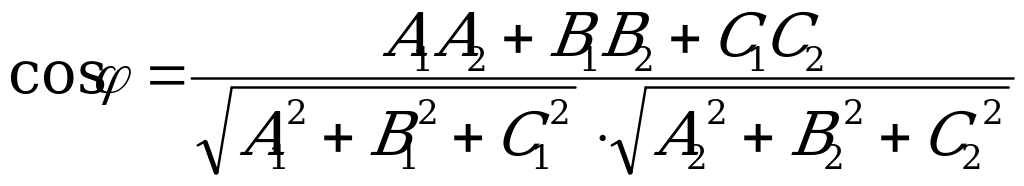 . (5.6)
. (5.6)
7) Условие параллельности двух плоскостей 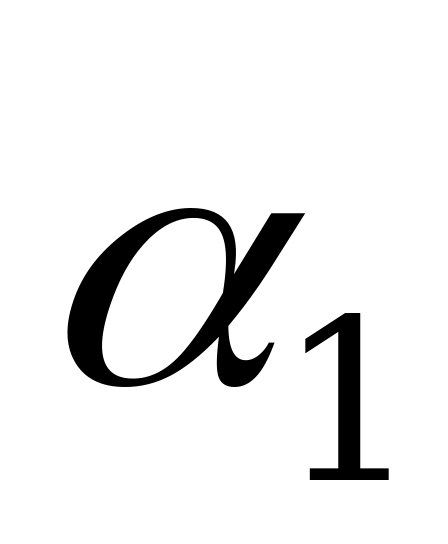 и
и  :
:
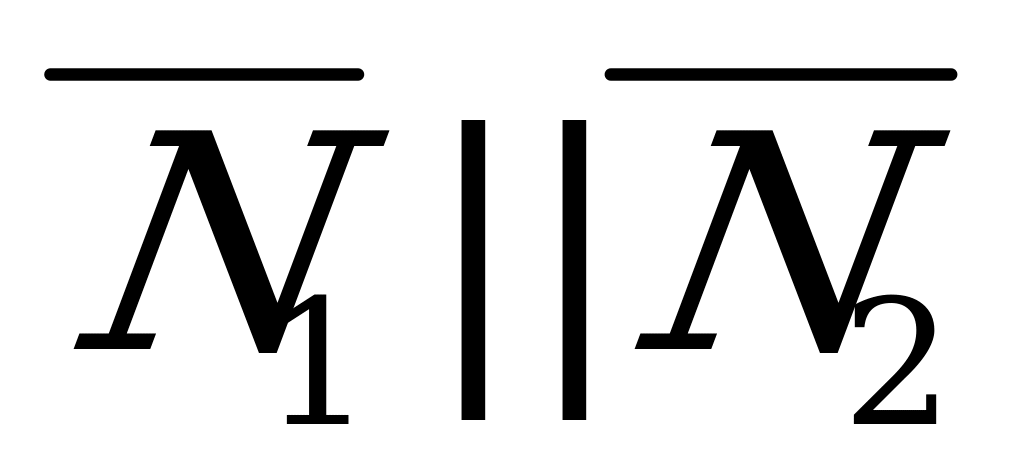 или в координатной форме
или в координатной форме
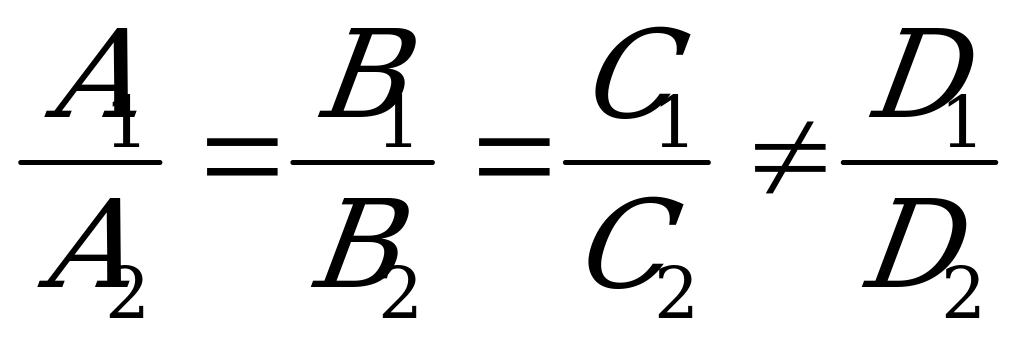 . (5.7)
. (5.7)
Если 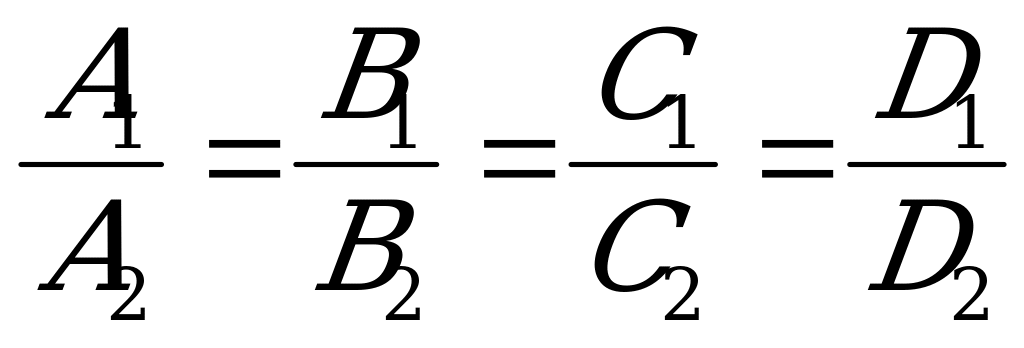 , то обе плоскости
, то обе плоскости 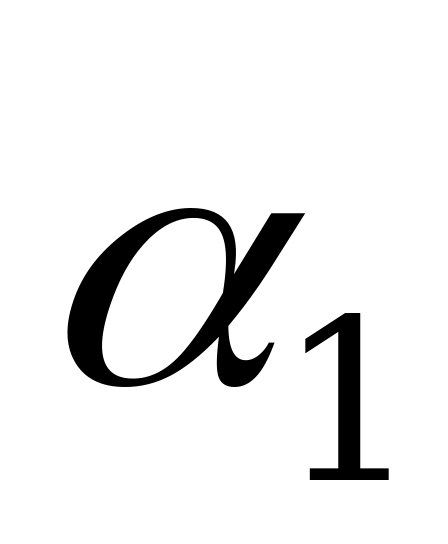 и
и 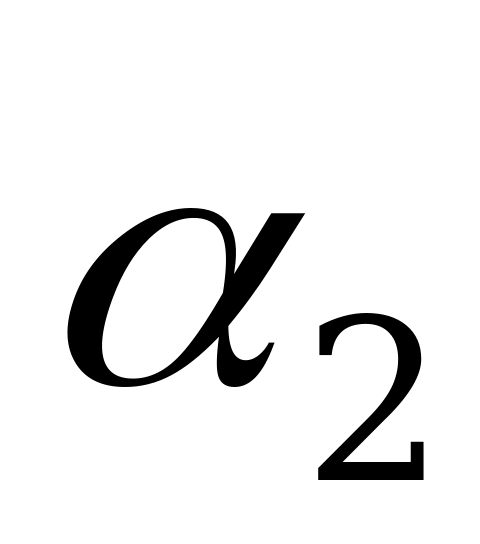 совпадают.
совпадают.
8) Условие перпендикулярности двух плоскостей 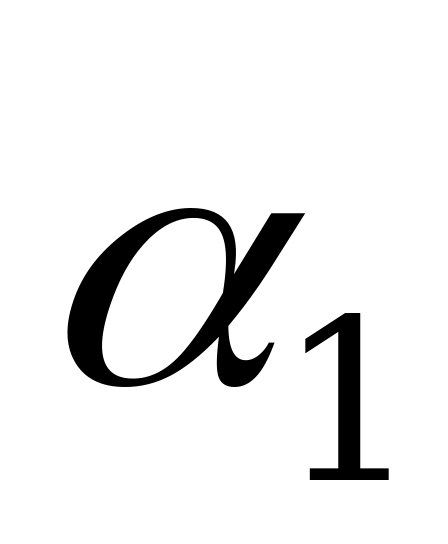 и
и 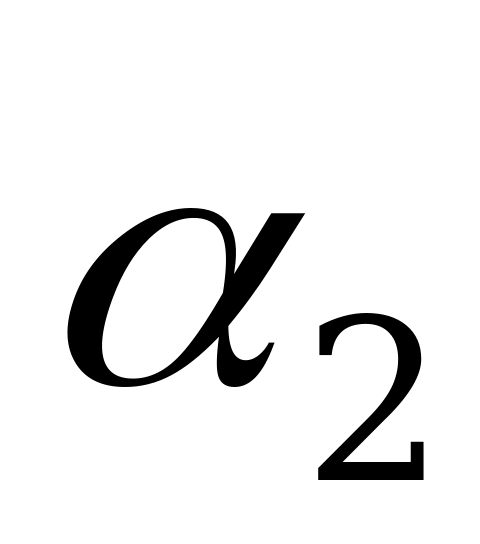 :
:
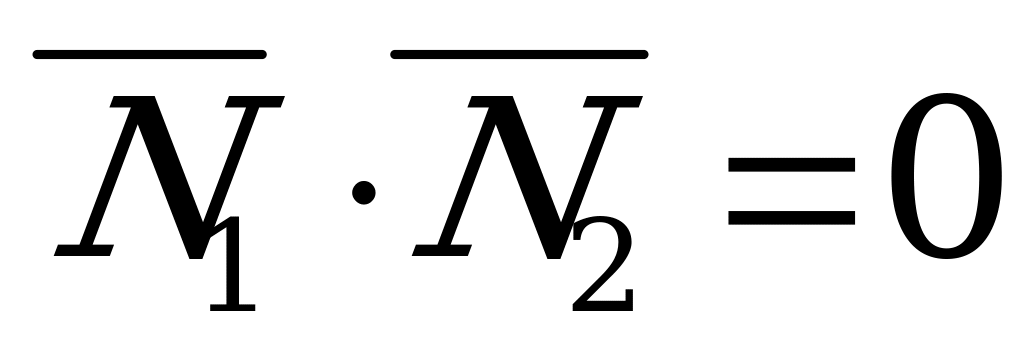 или в координатной форме
или в координатной форме
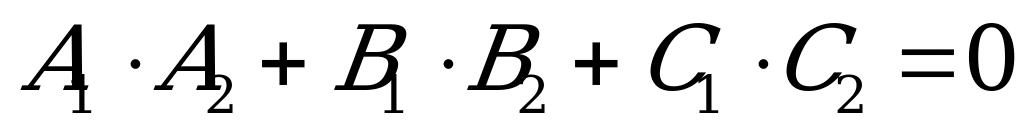 . (5.8)
. (5.8)
9) Неполные уравнения плоскости.
Общее уравнение плоскости  называется полным, если все его коэффициенты
называется полным, если все его коэффициенты  ,
,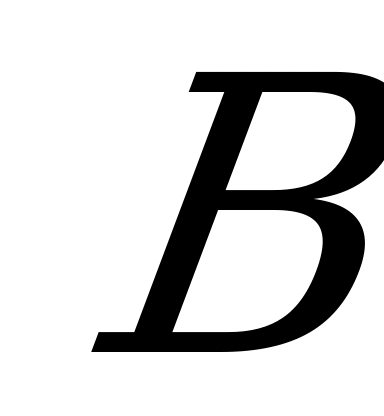 ,
, и
и 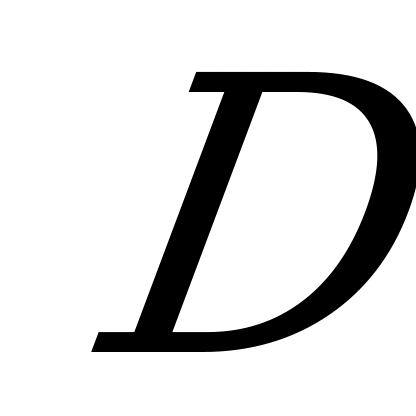 отличны от нуля. Если хотя бы один из коэффициентов равнее нулю, то уравнение (5.2) называется неполным.
отличны от нуля. Если хотя бы один из коэффициентов равнее нулю, то уравнение (5.2) называется неполным.
Рассмотрим различные виды неполных уравнений.
а) Если 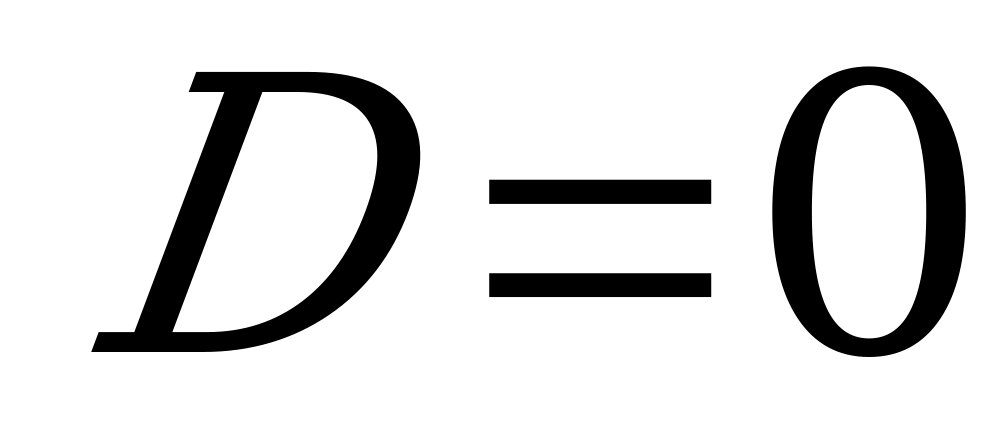 , то плоскость
, то плоскость 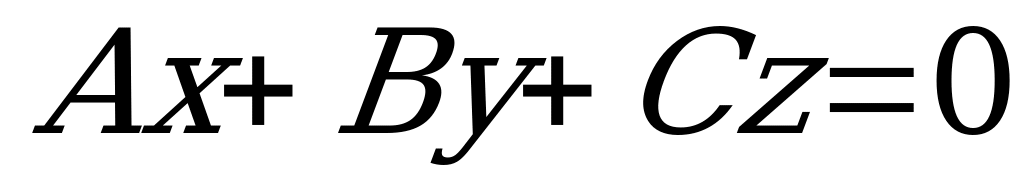 проходит через начало координат (поскольку координаты
проходит через начало координат (поскольку координаты 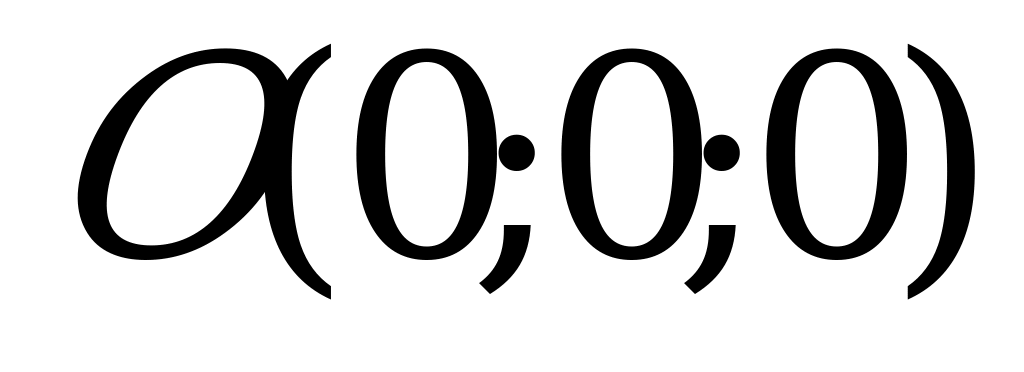 удовлетворяют этому уравнению);
удовлетворяют этому уравнению);
б) Если 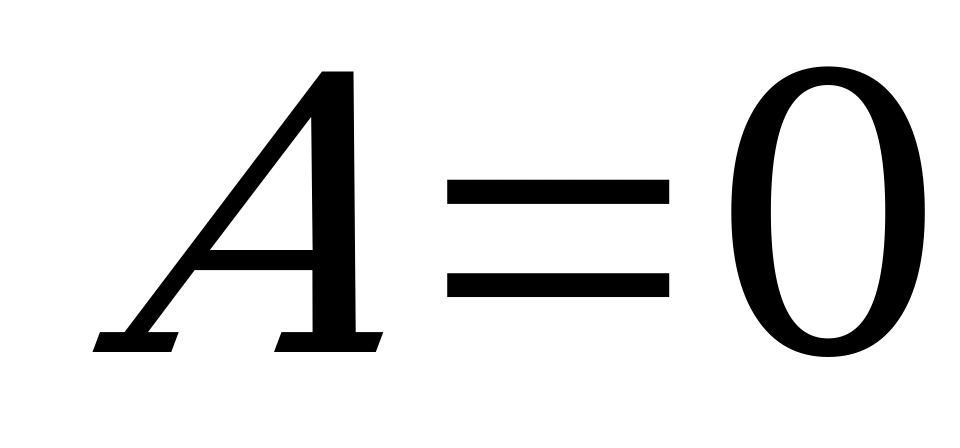 , то плоскость
, то плоскость 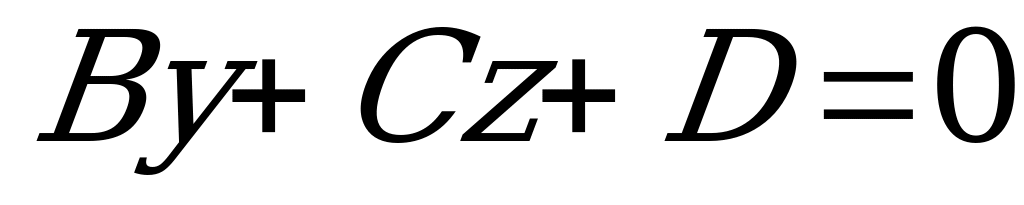 параллельна оси
параллельна оси  ;
;
в) Если 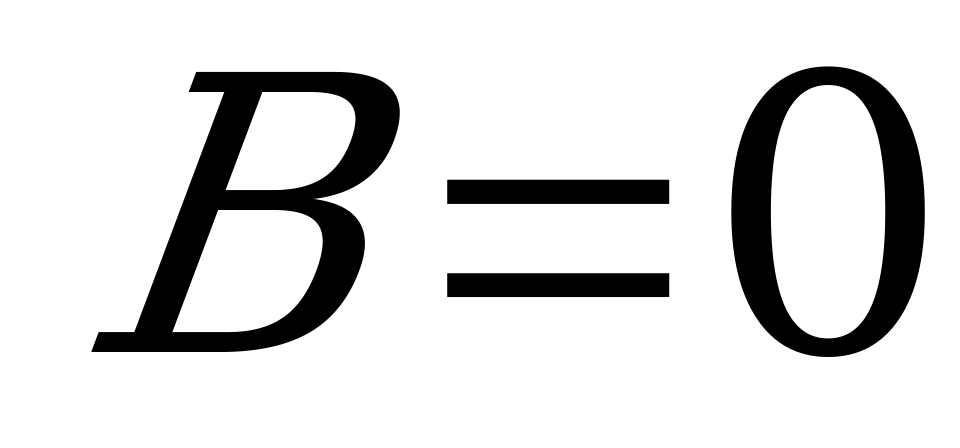 , то плоскость
, то плоскость 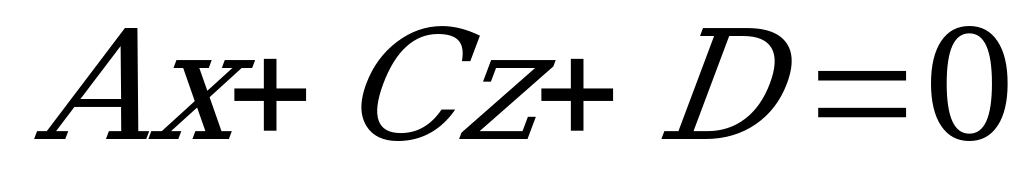 параллельна оси
параллельна оси  ;
;
г) Если 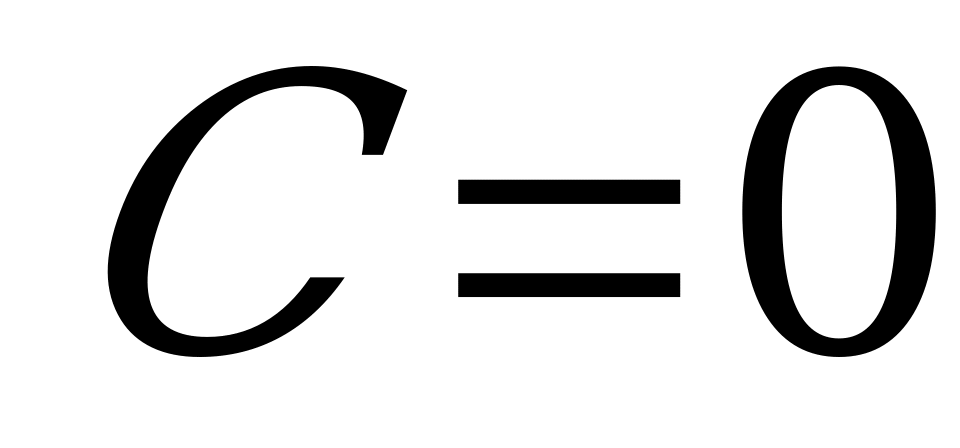 , то плоскость
, то плоскость  параллельна оси
параллельна оси  .
.
Признак параллельности плоскости координатной оси:
- если в уравнении нет переменной 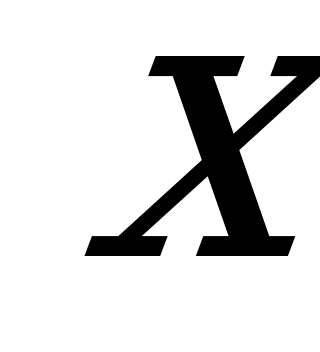 , то плоскость параллельна оси
, то плоскость параллельна оси  ;
;
- если в уравнении нет переменной  , то плоскость параллельна оси
, то плоскость параллельна оси  ;
;
- если в уравнении нет переменной  , то плоскость параллельна оси
, то плоскость параллельна оси  ,
,
т.е. плоскость параллельна той координатной оси, наименование которой отсутствует в уравнении плоскости.
д) Если 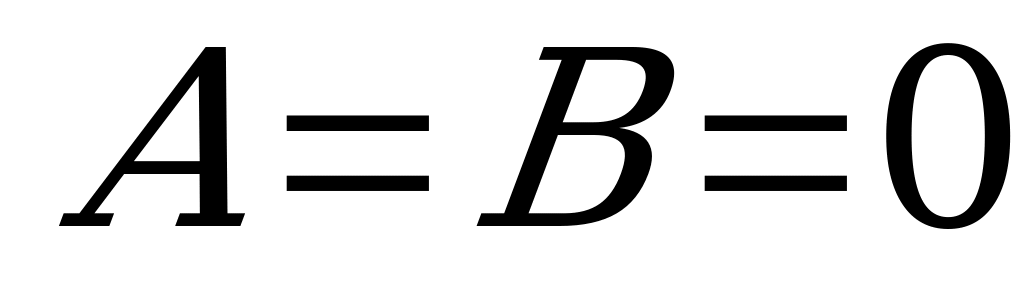 , то плоскость
, то плоскость  параллельна координатной плоскости
параллельна координатной плоскости 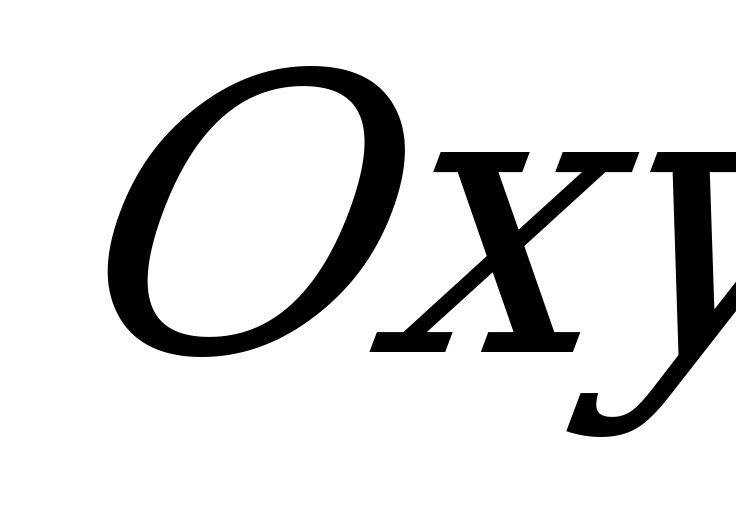 (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси  и оси
и оси  );
);
е) Если 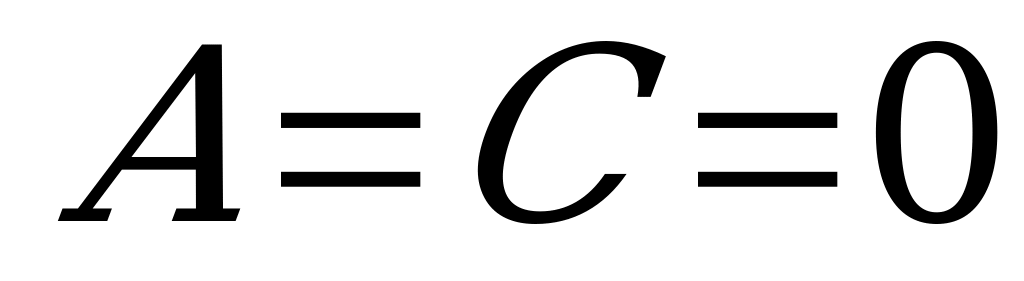 , то плоскость
, то плоскость 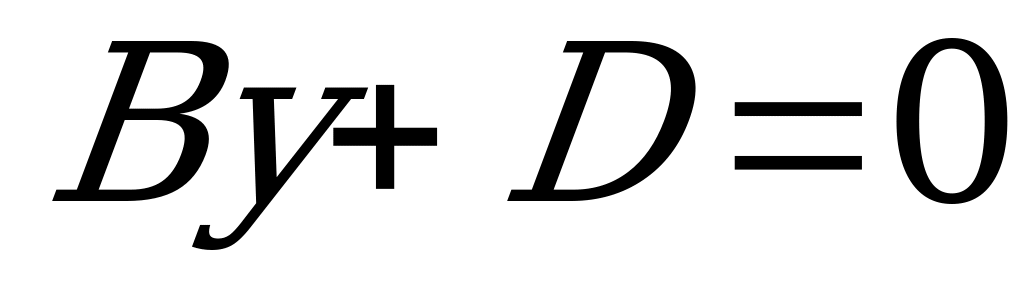 параллельна координатной плоскости
параллельна координатной плоскости 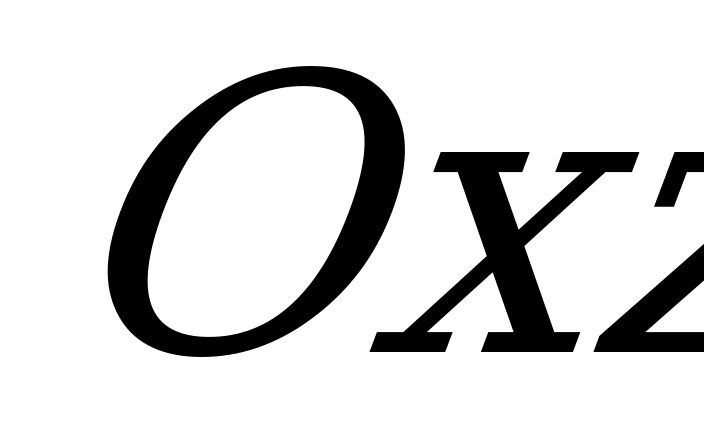 (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси  и оси
и оси  );
);
ж) Если 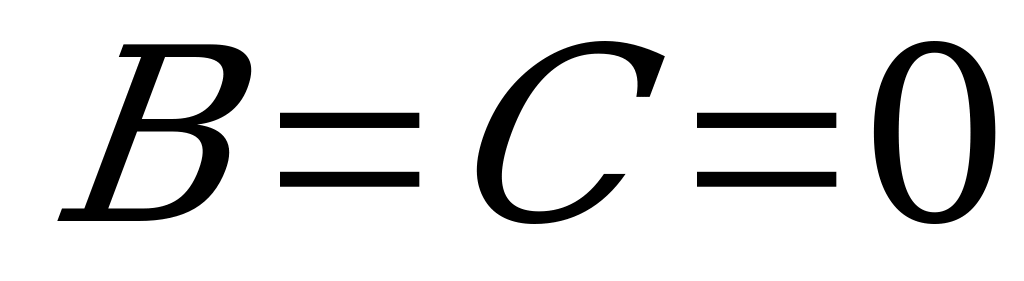 , то плоскость
, то плоскость 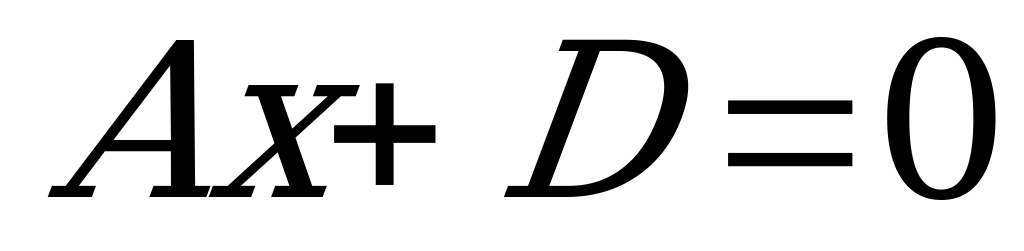 параллельна координатной плоскости
параллельна координатной плоскости  (так как эта плоскость одновременно параллельна оси
(так как эта плоскость одновременно параллельна оси  и оси
и оси  );
);
з) Если 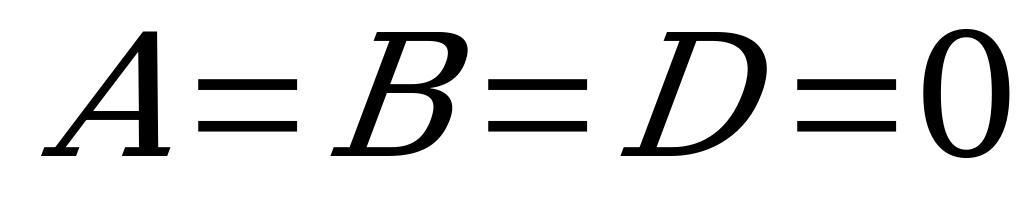 , то уравнение
, то уравнение 
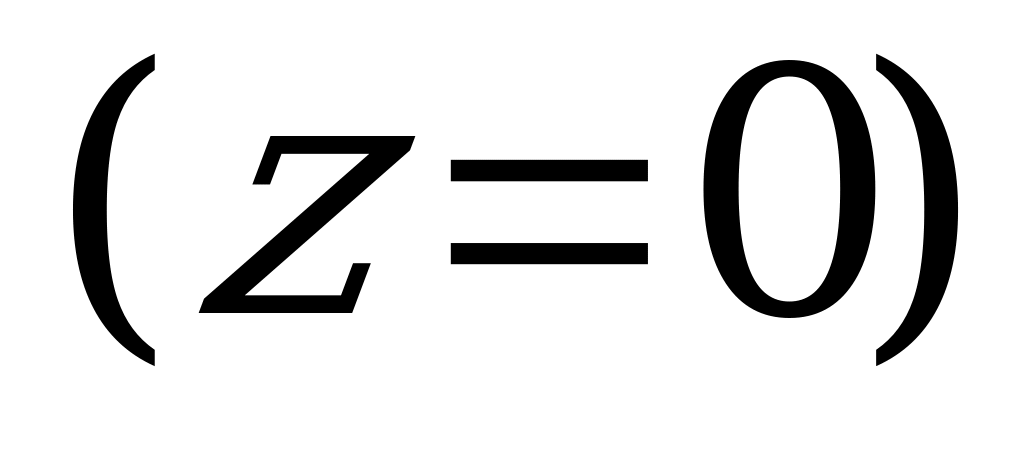 задает координатную плоскость
задает координатную плоскость  (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости  и проходит через начало координат);
и проходит через начало координат);
и) Если 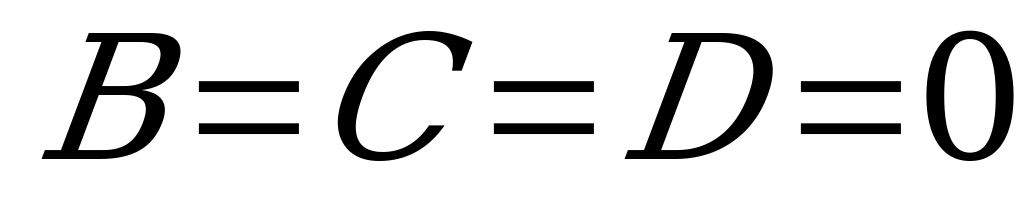 , то уравнение
, то уравнение 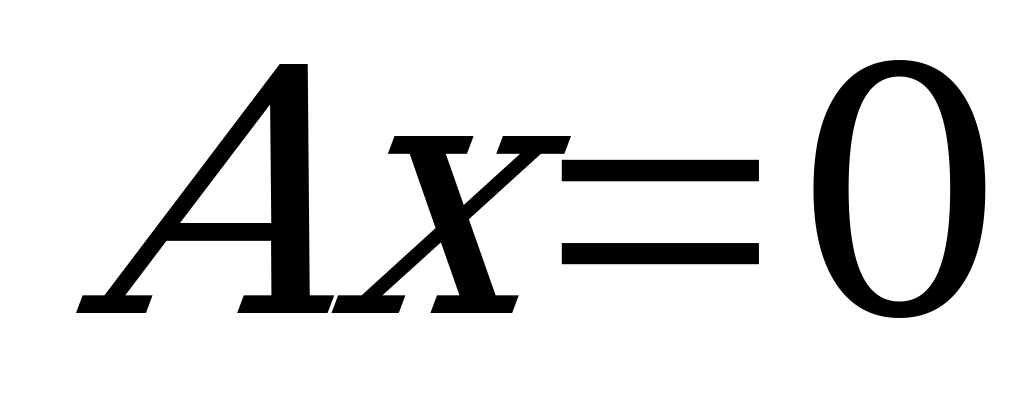
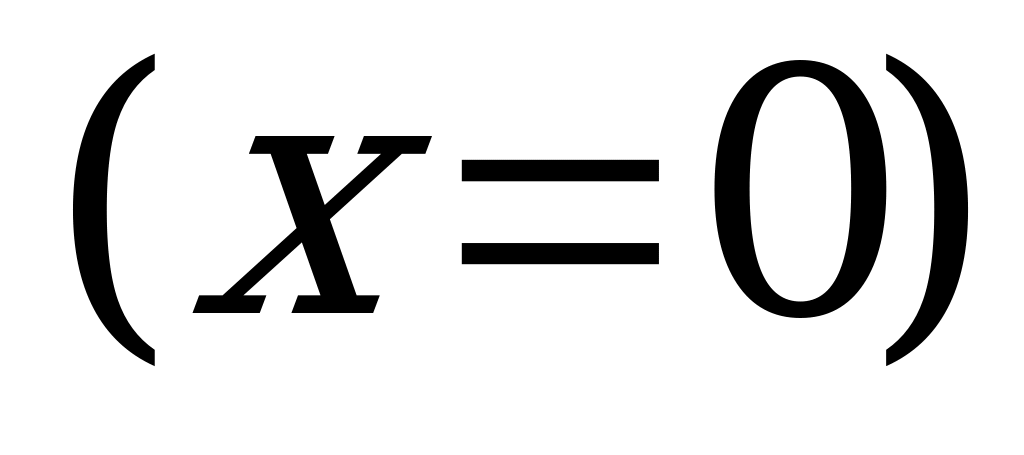 задает координатную плоскость
задает координатную плоскость  (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости  и проходит через начало координат);
и проходит через начало координат);
к) Если 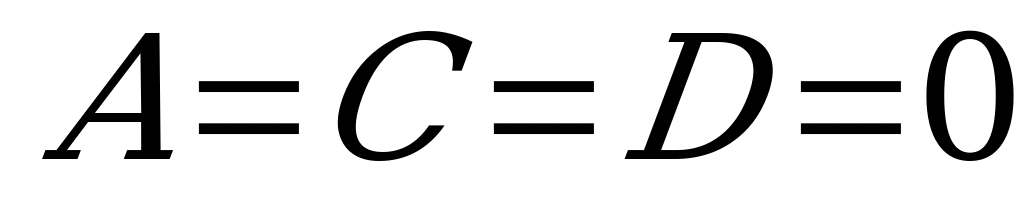 , то уравнение
, то уравнение 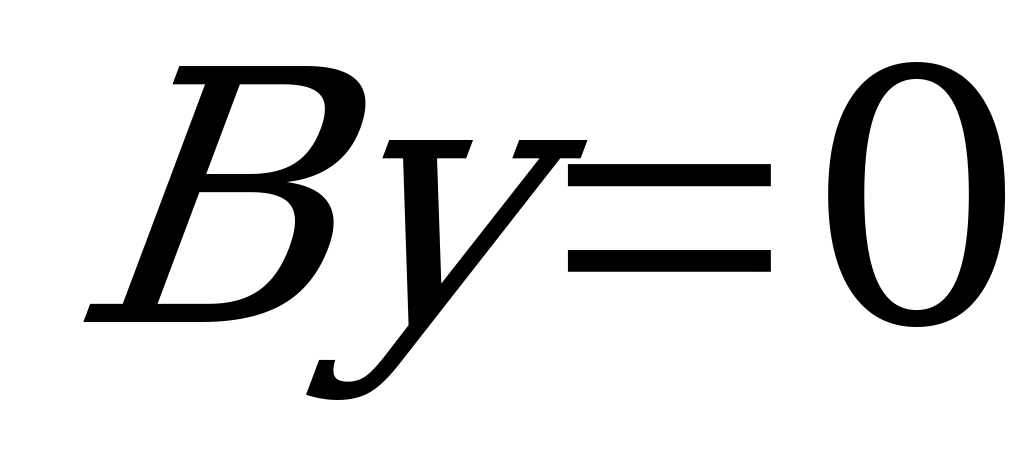
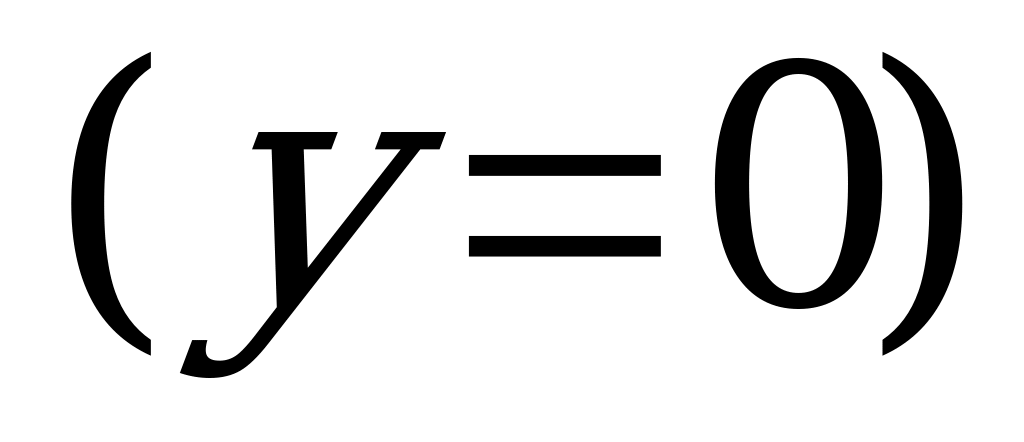 задает координатную плоскость
задает координатную плоскость  (так как плоскость параллельна плоскости
(так как плоскость параллельна плоскости 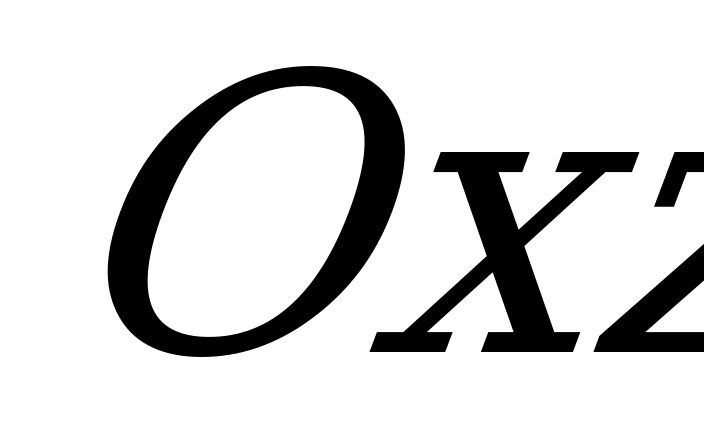 и проходит через начало координат).
и проходит через начало координат).
5.2 Прямая в пространстве
Для задания прямой в пространстве одного уравнения недостаточно. Это объясняется тем, что всякое уравнение 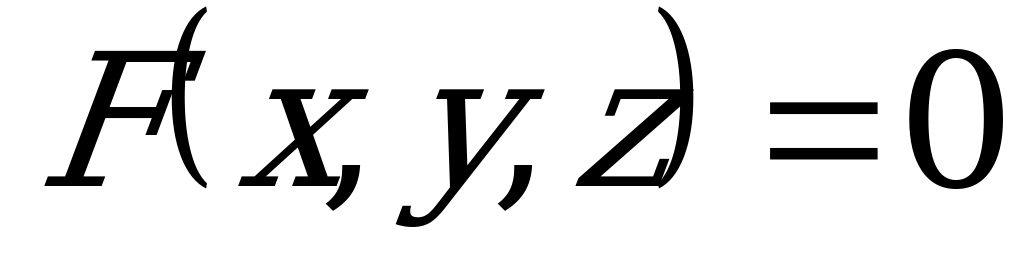 с тремя переменными
с тремя переменными 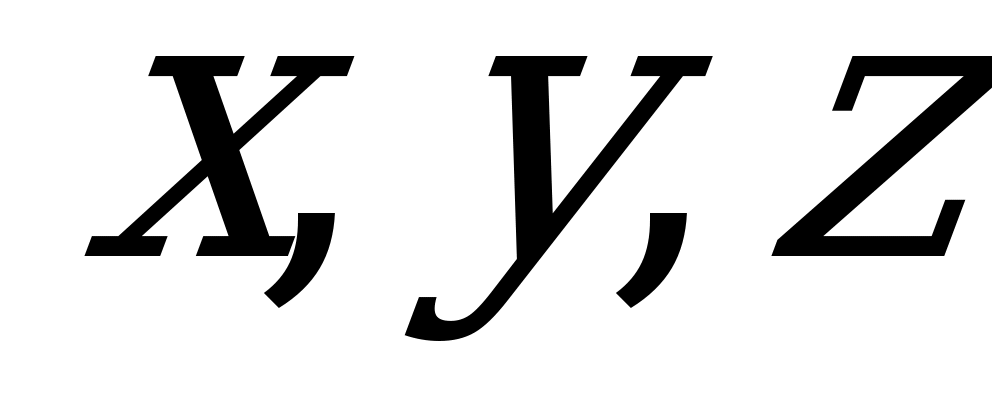 задает в пространстве некоторую поверхность
задает в пространстве некоторую поверхность  , а не линию.
, а не линию.
Рассмотрим различные виды уравнений прямой в пространстве.
1) Уравнения прямой, проходящей через точку  параллельно направляющему вектору
параллельно направляющему вектору 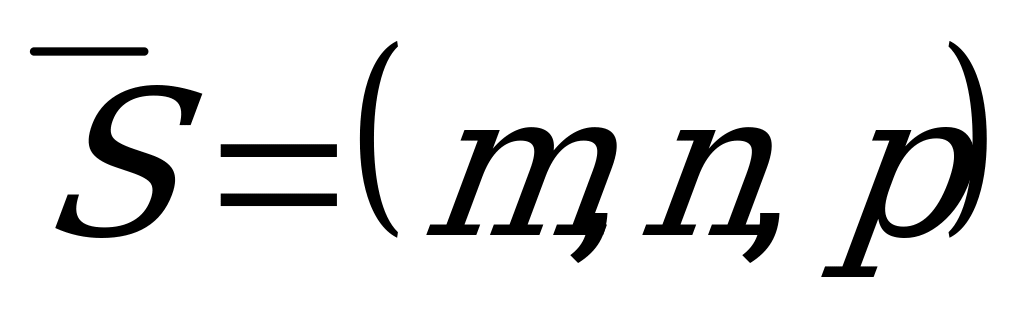
Уравнения (5.9) называются каноническими уравнениями прямой.
Уравнения (5.9) получены из следующих соображений.
Если 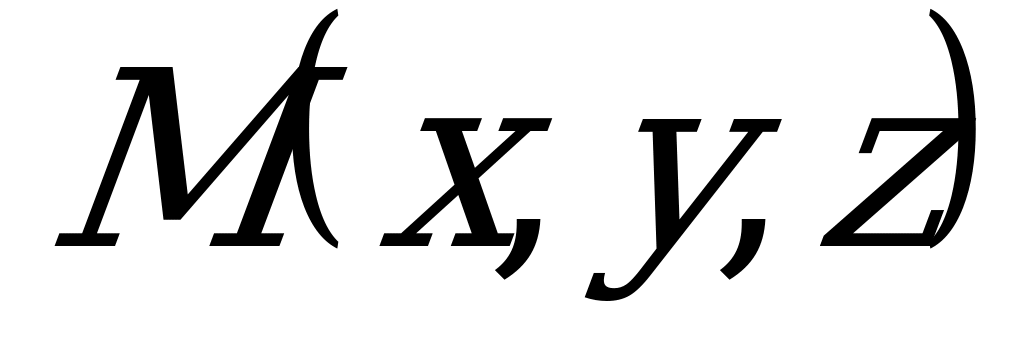 - произвольная точка прямой, то вектор
- произвольная точка прямой, то вектор 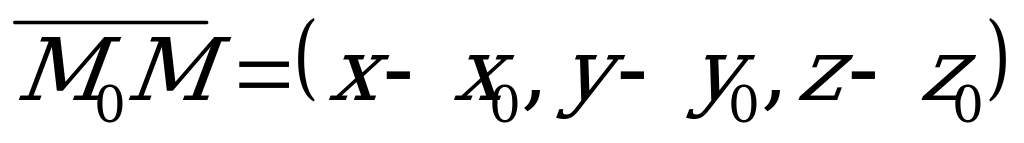 коллинеарен вектору
коллинеарен вектору 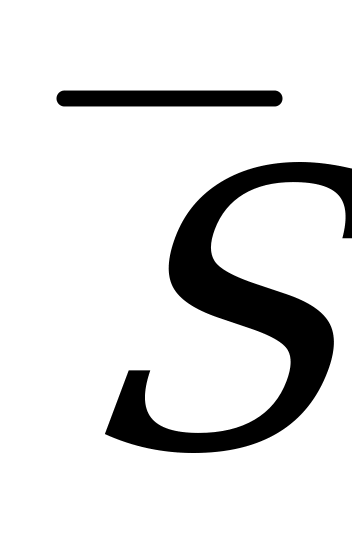 , а значит, их координаты пропорциональны, из чего и следуют уравнения (5.9).
, а значит, их координаты пропорциональны, из чего и следуют уравнения (5.9).
2) Уравнения прямой, проходящей через две точки 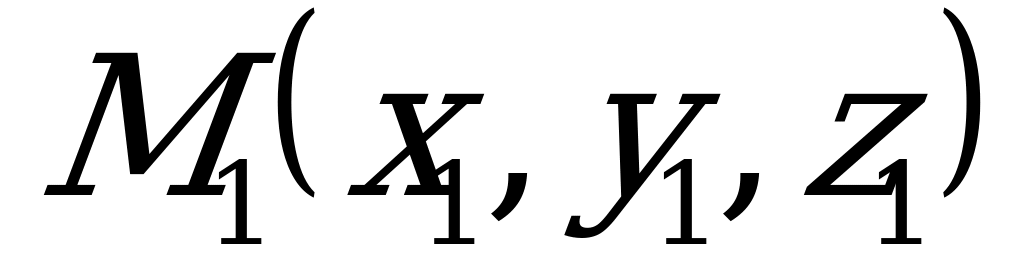 и
и 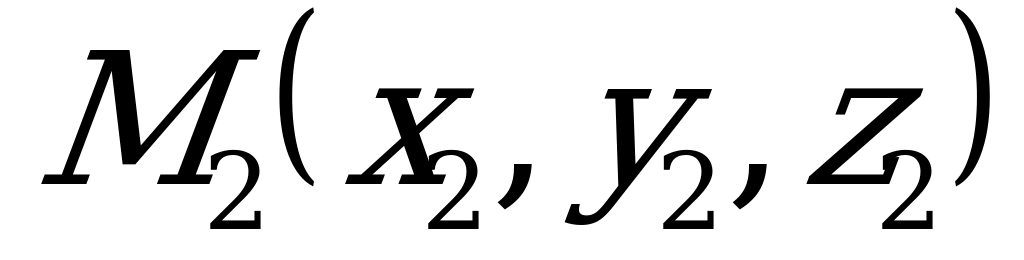 .
.
Уравнения (5.10) также являются каноническими уравнениями прямой, так как числа, стоящие в знаменателях, есть координаты вектора 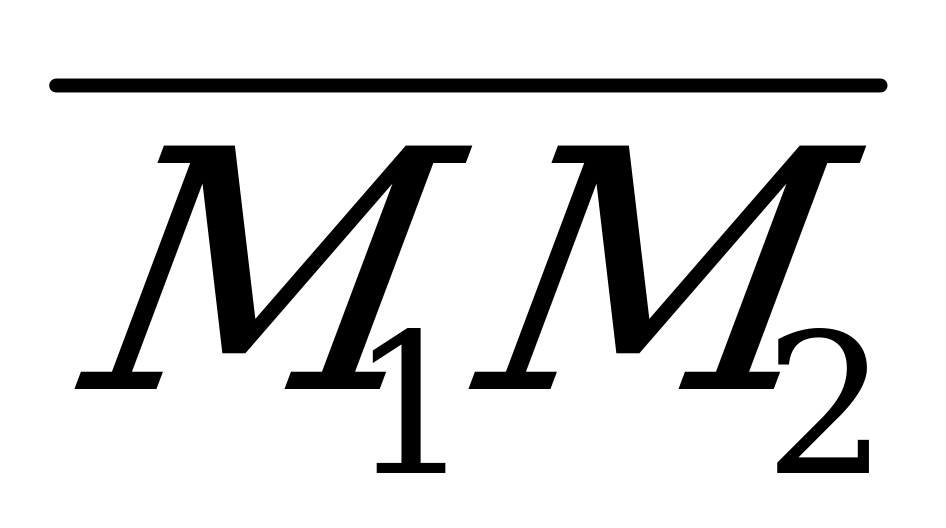 , являющегося направляющим для данной прямой.
, являющегося направляющим для данной прямой.
3) Параметрические уравнения прямой в пространстве:

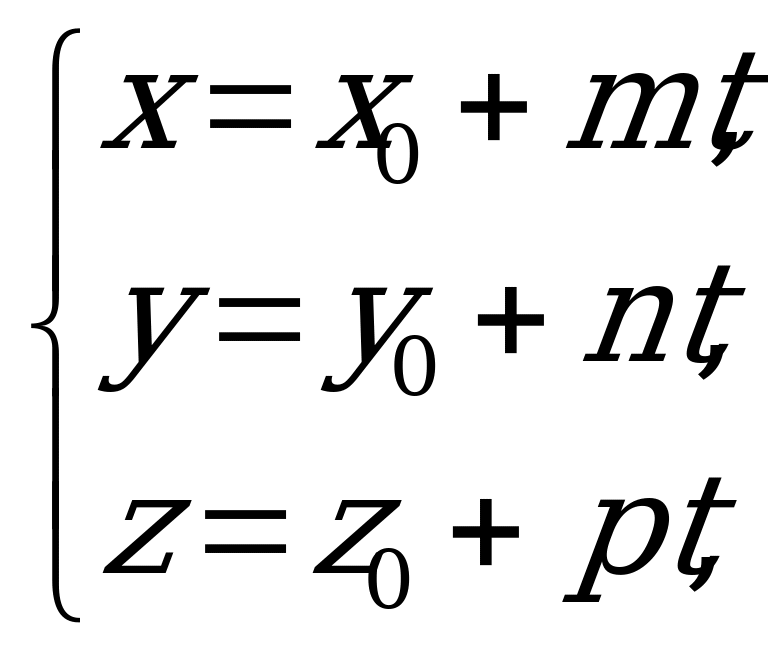 где
где 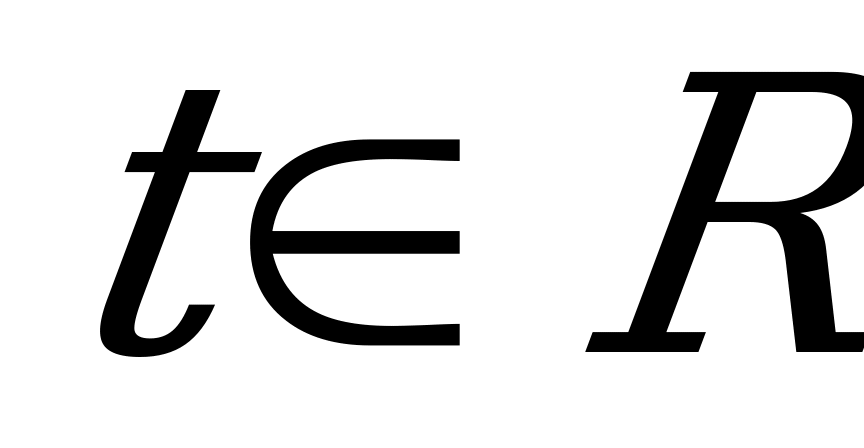 (5.11)
(5.11)
Уравнения (5.11) получаются из канонических уравнений (5.9), если все три отношения в них приравнять к некоторому параметру  , а затем выразить
, а затем выразить 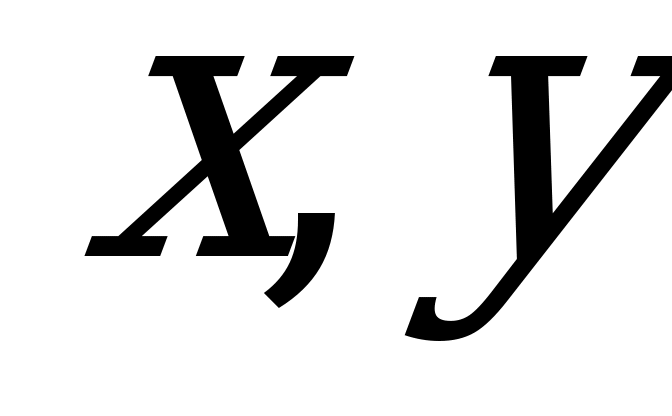 и
и через
через  .
.
При этом 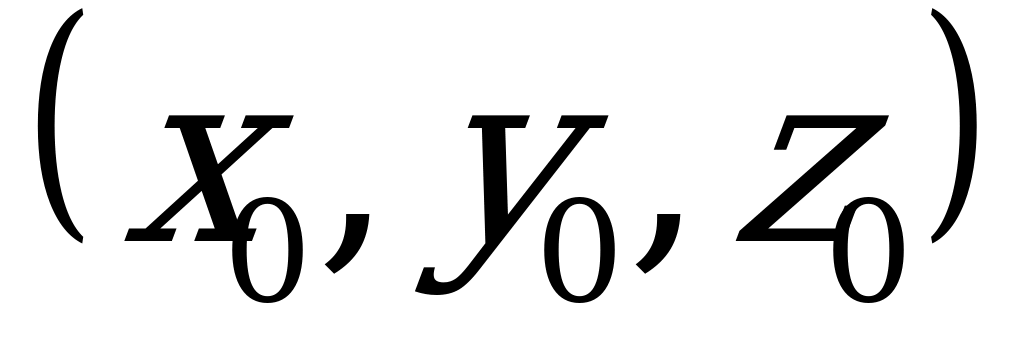 - координаты точки
- координаты точки 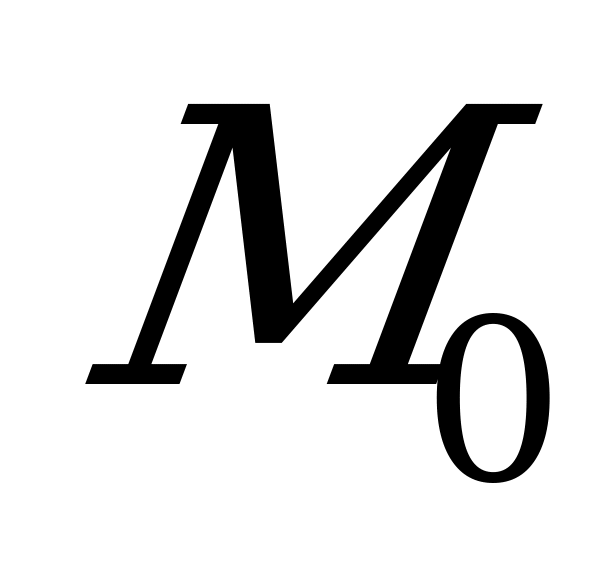 , через которую проходит прямая параллельно направляющему вектору
, через которую проходит прямая параллельно направляющему вектору  .
.
Замечание. Если какая–либо координата вектора 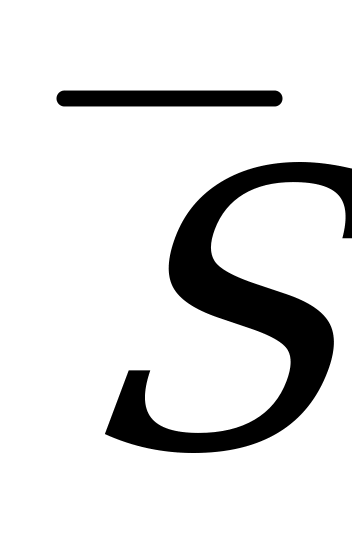 равна
равна 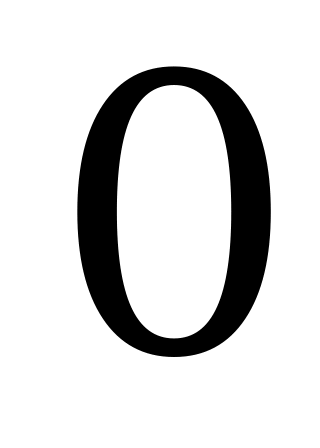 , то равен
, то равен 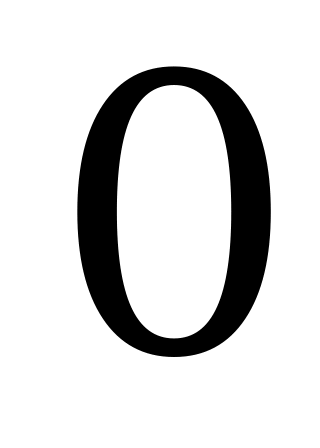 и знаменатель соответствующей дроби в уравнениях (5.9).
и знаменатель соответствующей дроби в уравнениях (5.9).
Не следует воспринимать такую дробь как деление на 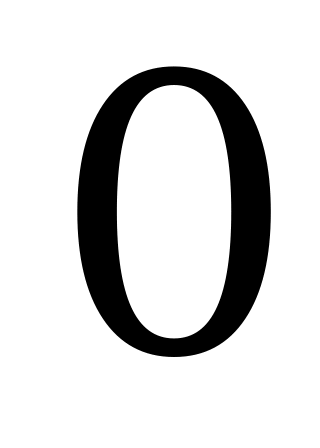 . Если, например,
. Если, например,  , то уравнения (5.9) примут вид:
, то уравнения (5.9) примут вид: 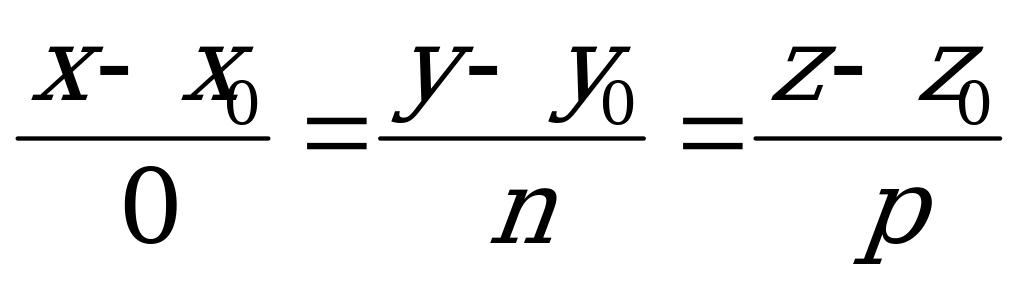 .
.
Перейдем к параметрическим уравнениям прямой. Получим
 где
где 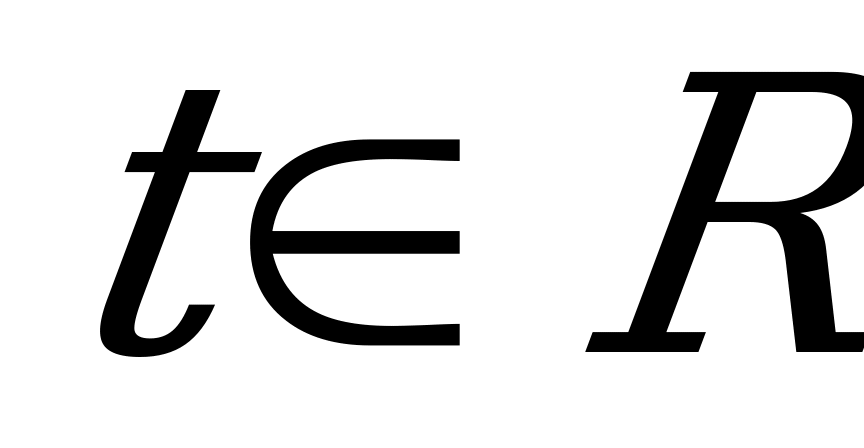 или
или 
Первое уравнение  , означает, что прямая лежит на плоскости
, означает, что прямая лежит на плоскости  , перпендикулярной оси
, перпендикулярной оси 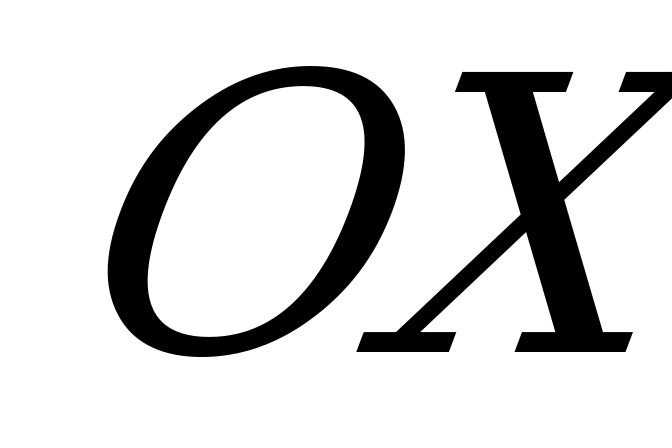 .
.
4) Общие уравнения прямой в пространстве
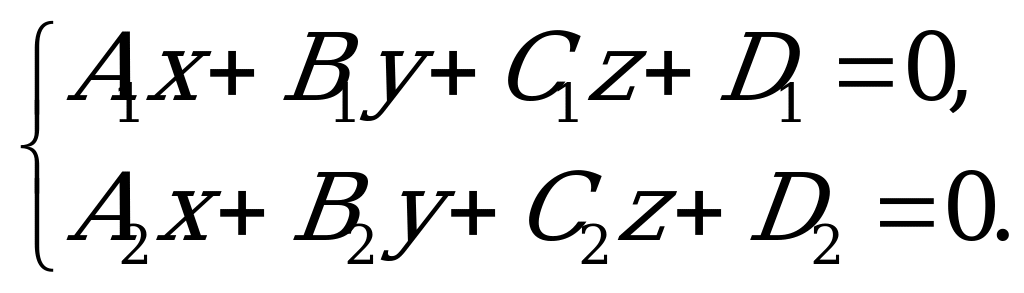 (5.12)
(5.12)
Уравнения (5.12) задают прямую, как линию пересечения двух плоскостей. Общие уравнения прямой могут быть преобразованы к каноническому или параметрическому виду.
5) Пусть даны две прямые, заданные каноническими уравнениями
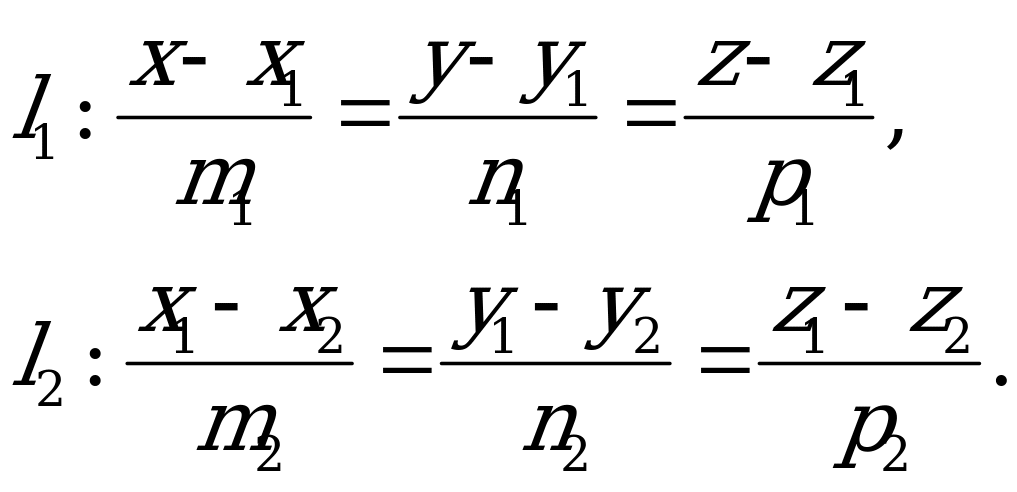
Угол 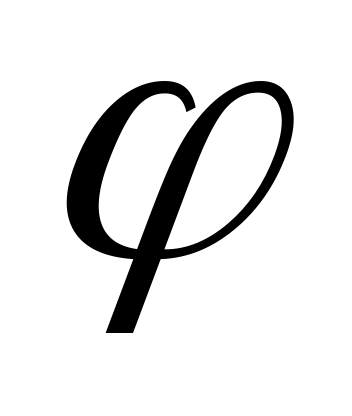 между прямыми
между прямыми  и
и 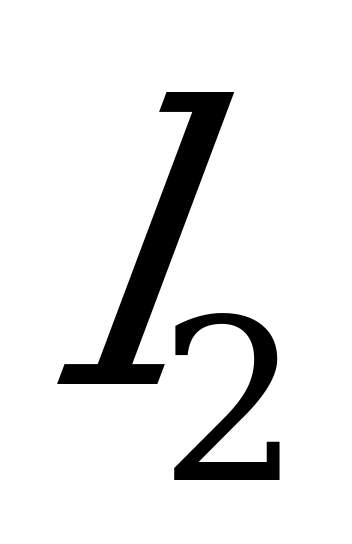 определяется, как угол между направляющими векторами данных прямых
определяется, как угол между направляющими векторами данных прямых 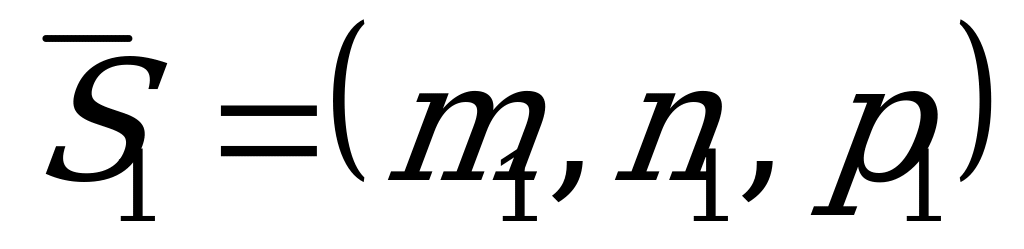 и
и 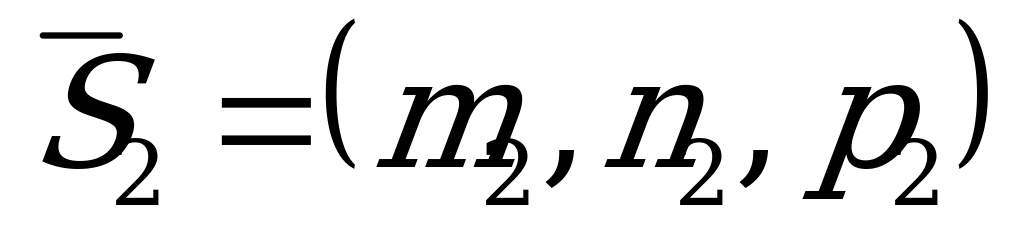 :
:
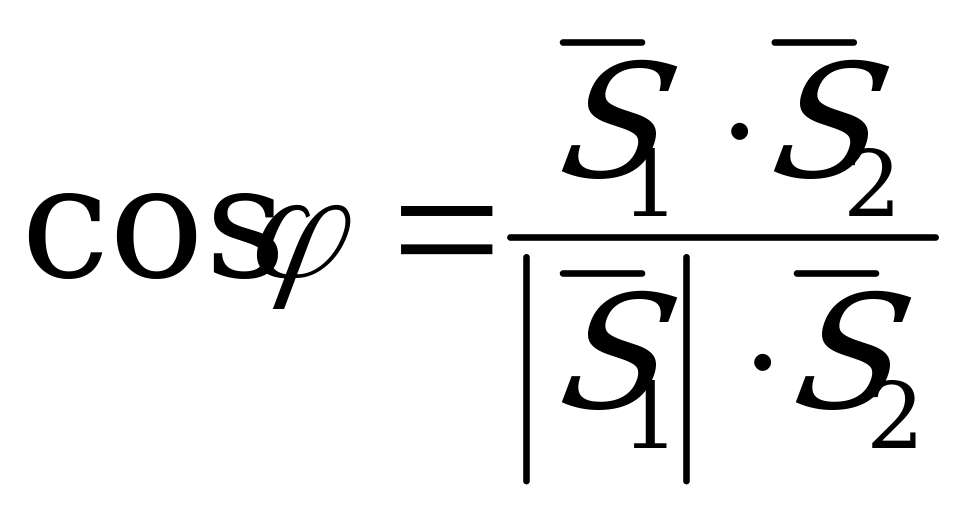 , или в координатной форме
, или в координатной форме
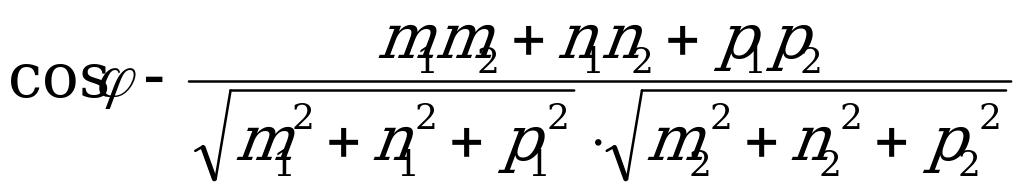 . (5.13)
. (5.13)
6) Условие параллельности двух прямых  и
и 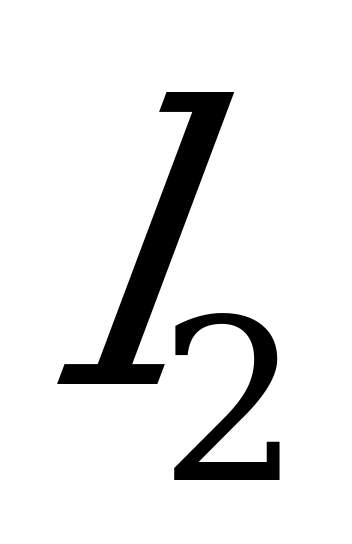 :
:
 или
или 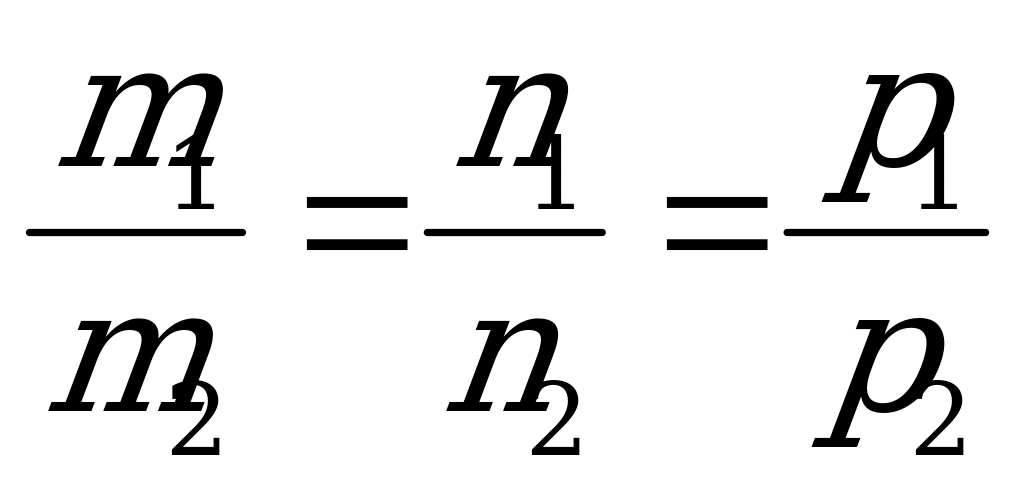 . (5.14)
. (5.14)
7) Условие перпендикулярности двух прямых  и
и 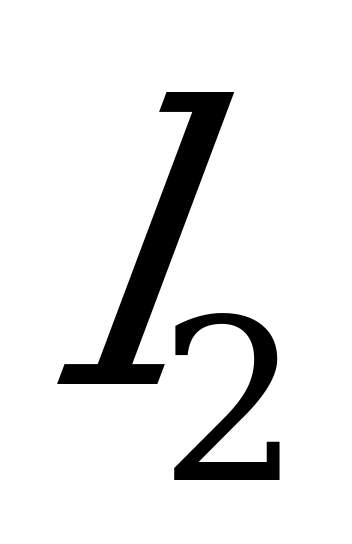 :
:
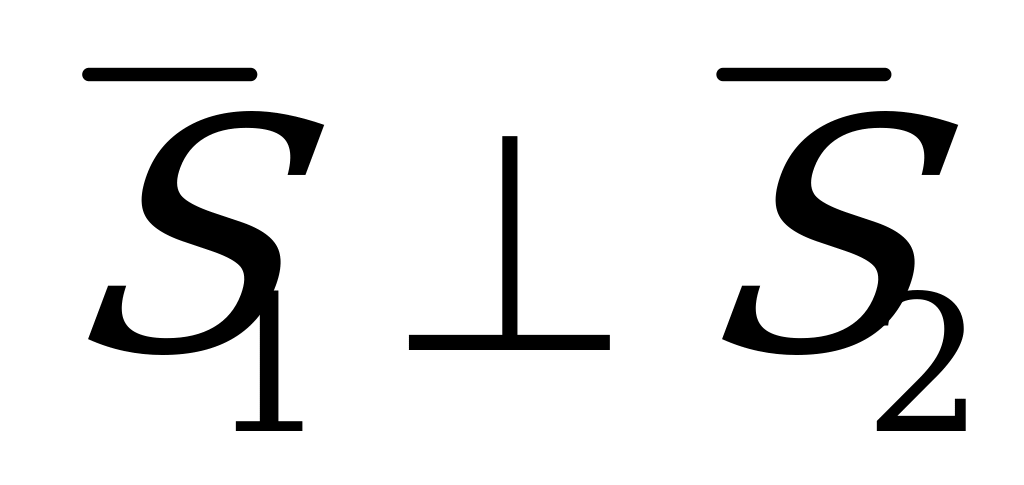 или
или 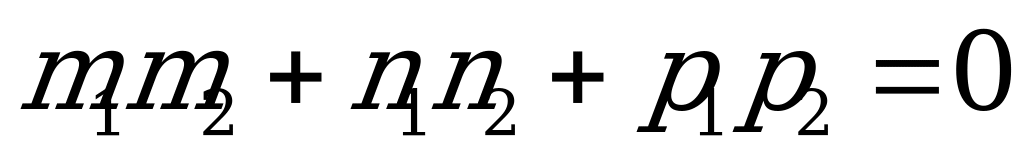 . (5.15)
. (5.15)
5.3 Прямая и плоскость в пространстве
Рассмотрим смешанные задачи на прямую и плоскость в пространстве.
Пусть дана прямая  с направляющим вектором
с направляющим вектором 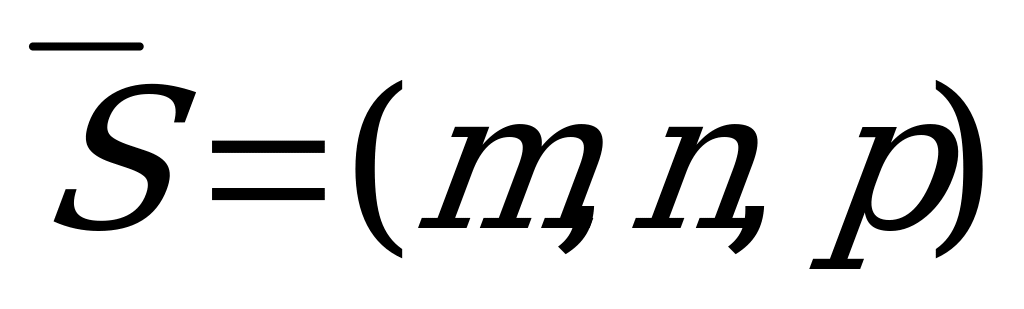 и плоскостью
и плоскостью  с нормалью
с нормалью 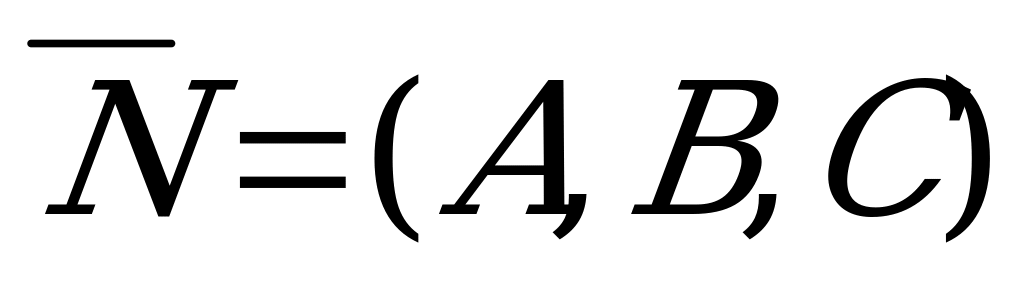 .
.
1) Угол 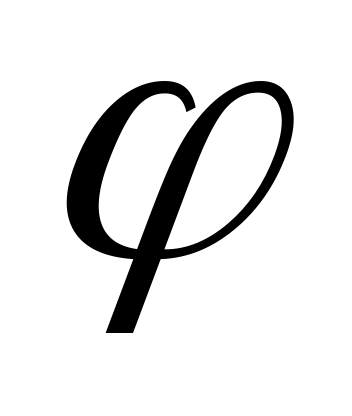 между прямой
между прямой  и плоскостью
и плоскостью  определяется формулой
определяется формулой
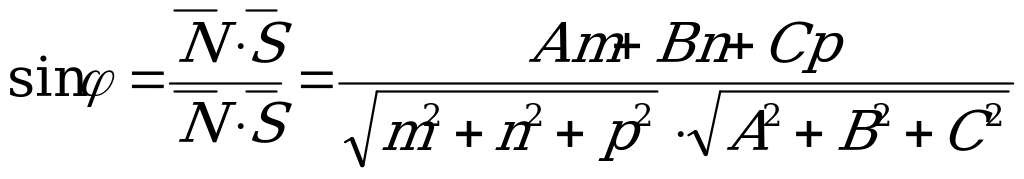 . (5.16)
. (5.16)
2) Условие параллельности прямой и плоскости:
3) Условие перпендикулярности прямой и плоскости:













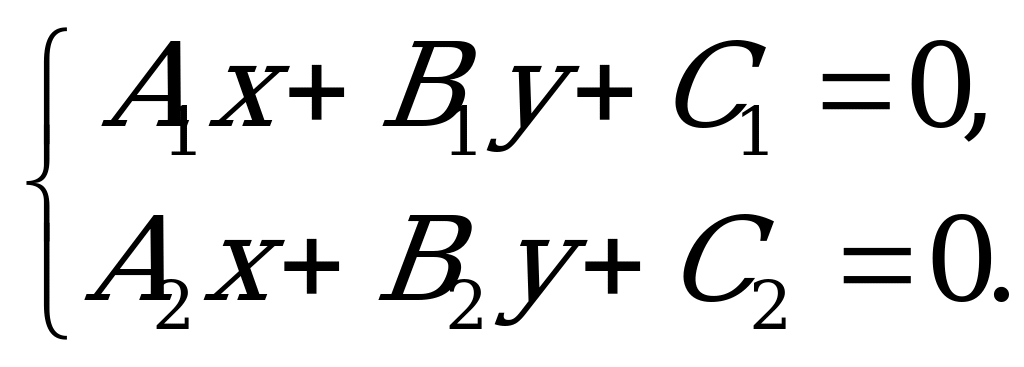 (4.10)
(4.10)


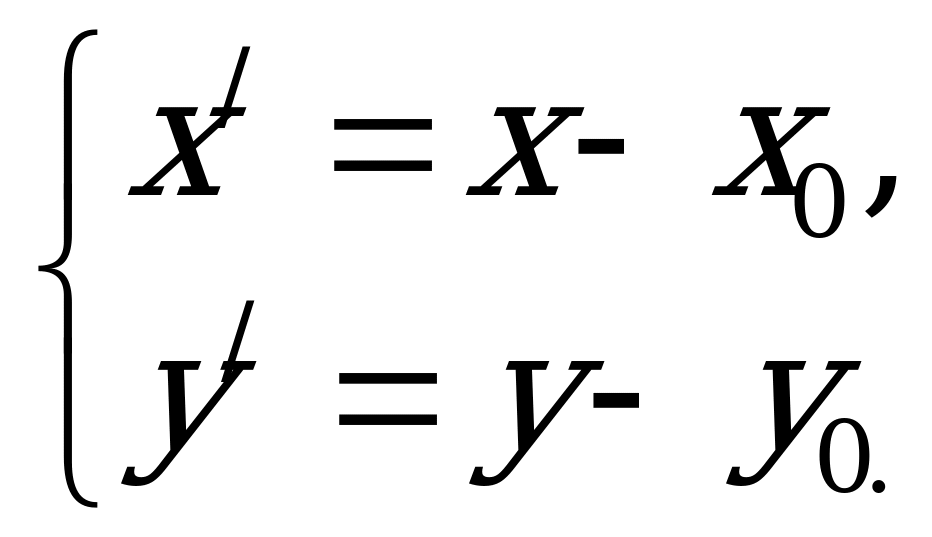 (4.17)
(4.17)







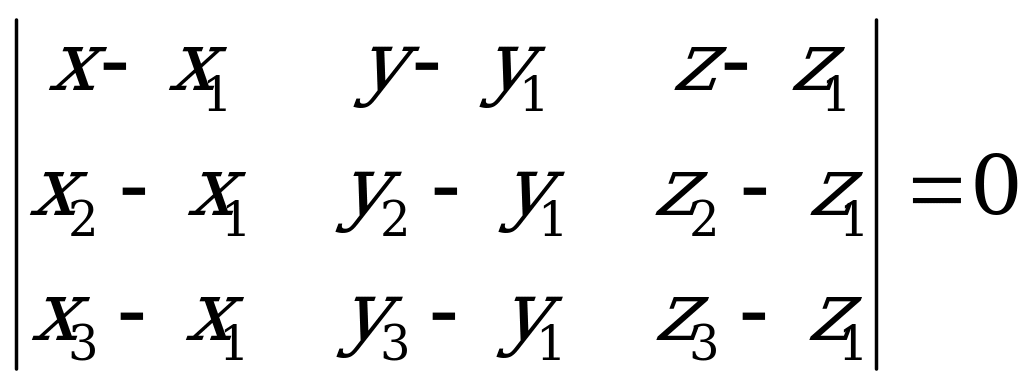 . (5.4)
. (5.4)



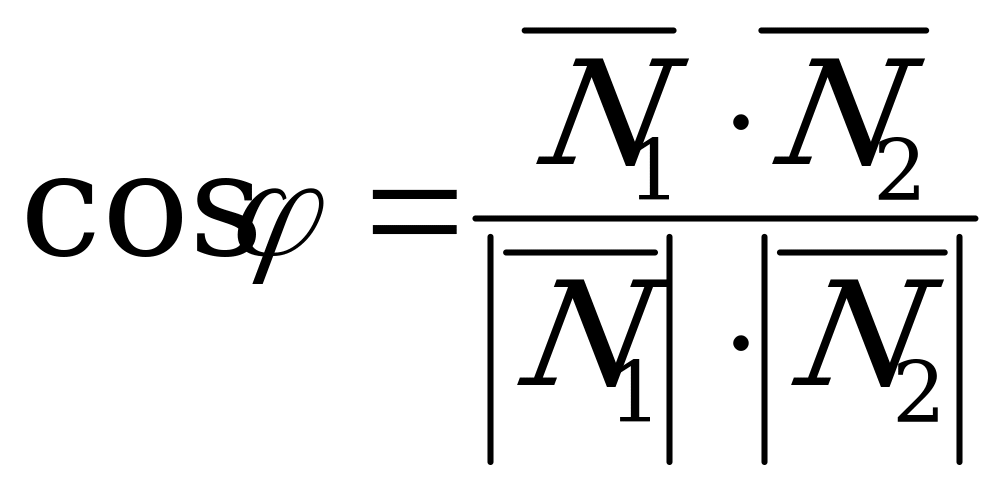 или в координатной форме
или в координатной форме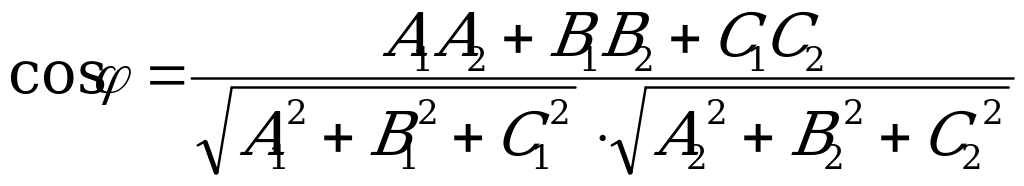 . (5.6)
. (5.6)



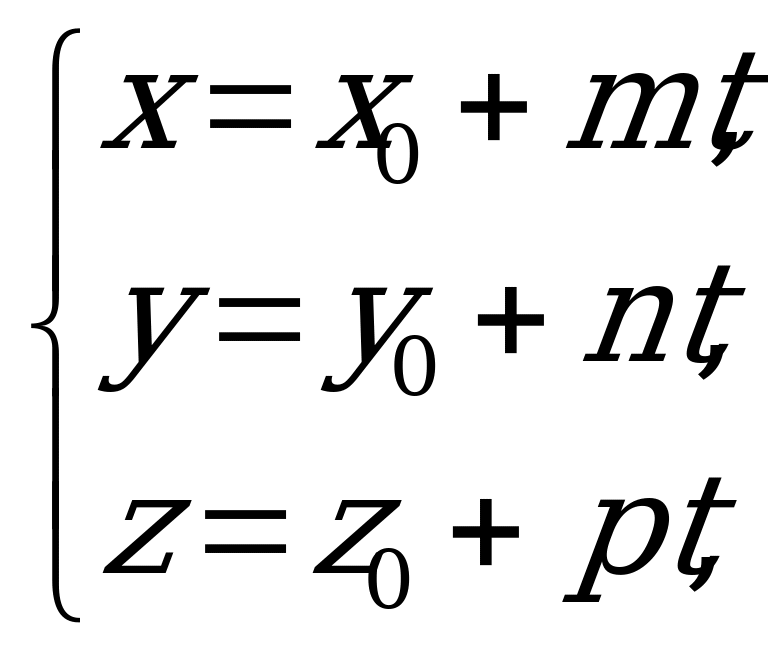 где
где  где
где 
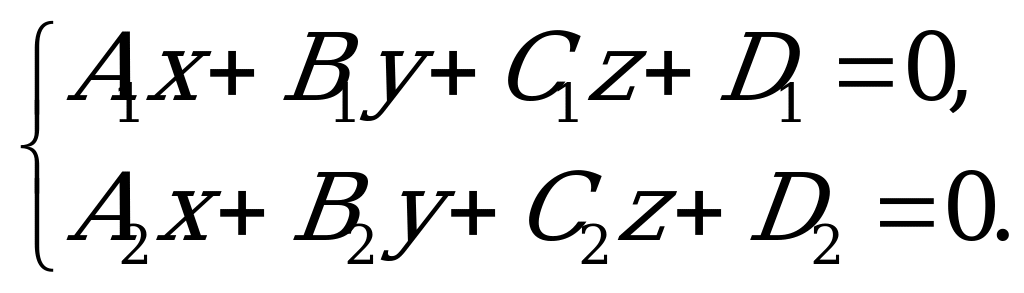 (5.12)
(5.12)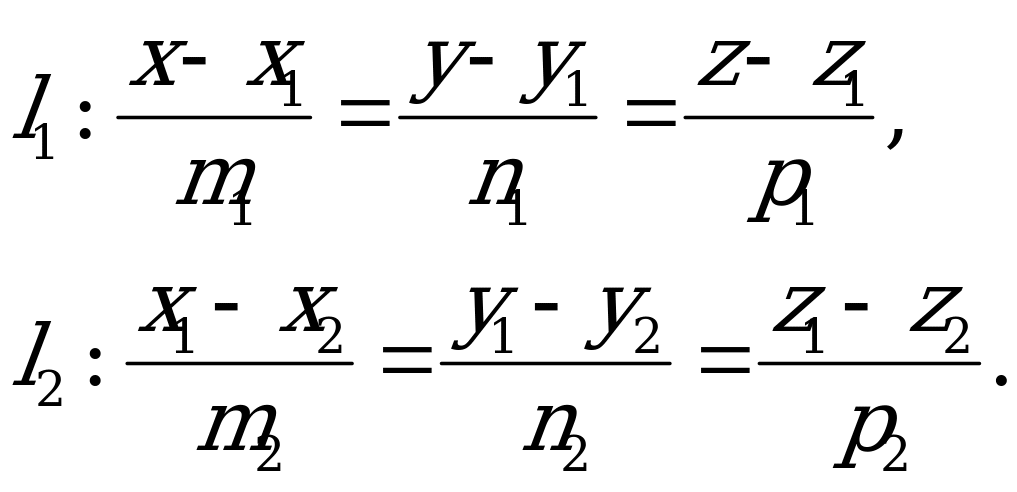
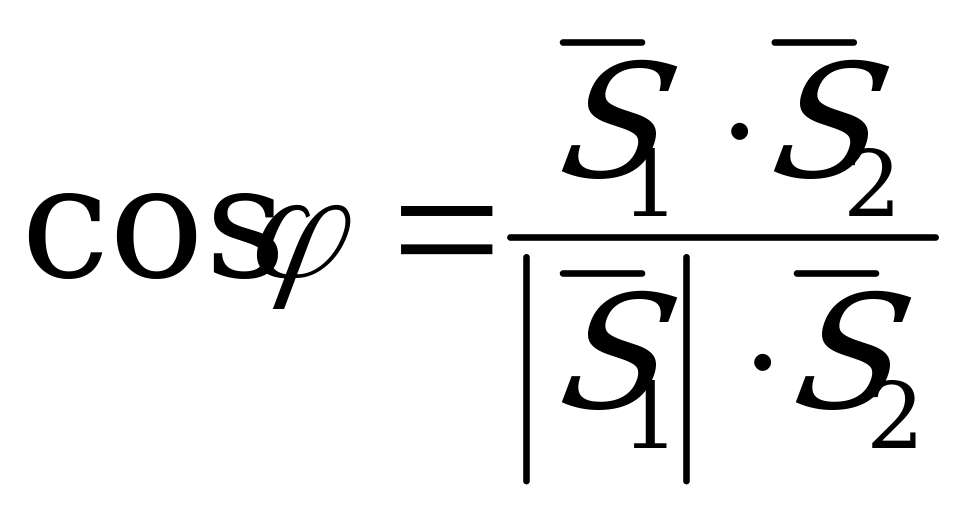 , или в координатной форме
, или в координатной форме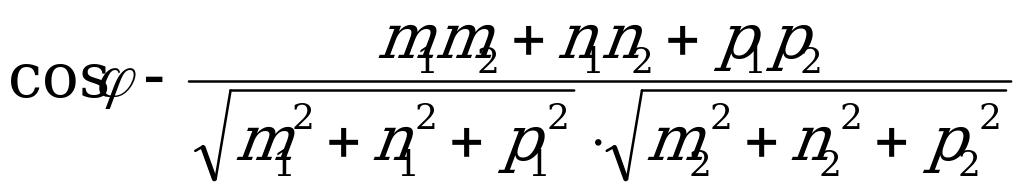 . (5.13)
. (5.13)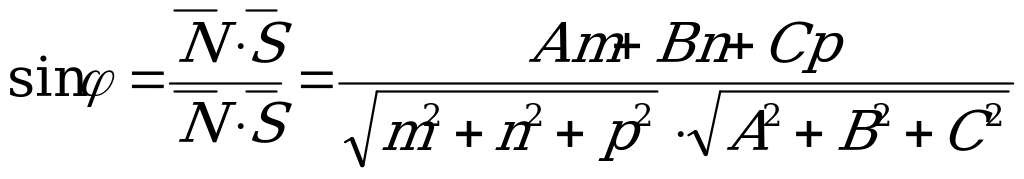 . (5.16)
. (5.16)