«Числа Фибоначчи»

Числа Фибоначчи

выполнила ученица

МБОУ «Лицей» 7 класса Б

Чиркова Екатерина

Учитель : Семёнова О.Е.

Расположение листьев растения – идеальная последовательность спиралей

Устройство мира описывается с помощью чисел Фибоначчи.

Расположение витков спирали ракушки – идеальная последовательность по теории Фибоначчи

Гипотеза:

Исчезновение и появление площадей фигур происходит только в случаи, если разрезание квадрата (прямоугольника) на части выполнить по закону ряда чисел Фибоначчи

Объект:

Числа Фибоначчи и математические геометрические задачи с исчезновением и появлением площадей фигур

Математическое геометрическое исчезновение и появление площадей фигур в задачах на разрезание квадрата (прямоугольника) на части по закону ряда чисел Фибоначчи. 

Предмет :

Цель:

Выявить связь геометрического исчезновения и появления площадей фигур на примере решения задач на разрезание квадрата (прямоугольника) на части с законом ряда чисел Фибоначчи.

Задачи:

• Изучить историю чисел Фибоначчи.

• Изучить формулу по которой составляется ряд Фибоначчи

• рассмотреть закономерность чисел Фибоначчи на примере решения задачи о кроликах.

• Изучить свойства чисел Фибоначчи

• Изучить использование чисел Фибоначчи в науке Геометрия.

• Провести эксперимент с делением сторон квадрата (прямоугольника) на части по закону чисел Фибоначчи (математические фокусы).

Методы исследования:

1.Изучение и анализ литературы, интернет источников по объекту исследования.

2.Практическое исследование (изучение чертежей, наблюдение, сравнение, математические расчеты).

Практическая значимость исследования

Результаты данного исследования помогут больше узнать о правилах использования и применения Законов ряда чисел Фибоначчи и разобраться в геометрических парадоксах.

Леонардо Пизанский (Фибоначчи)

«Книга абака» (1202 г.) - содержит почти все арифметические и алгебраические сведения того времени

«Практика геометрии» (1220 г.) - содержит теоремы, относящиеся к измерительным методам

( около 1170 – около 1250 гг .)

Родился в г.Пиза, в семье дипломата.

Первый крупный математик средневековой Европпы

Загадка итальянского математика

«Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения».

В итоге получается такая последовательность чисел:

1, 1, 2, 3, 5, 8, 13, 21,…

2 u n = u n -1 + u n -2 , и u 1 =1 и u 2 =1 Эта последовательность была известна ещё в древней Индии, где она применялась в метрических науках. " width="640"

Числа Фибоначчи

Числа Фибоначчи – элементы числовой последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 , …

в которой каждое последующее число, начиная с третьего, равно сумме двух предыдущих чисел, первые два числа считаются заданными - это числа 1 и 1. Т.е. при всяком n 2

u n = u n -1 + u n -2 , и u 1 =1 и u 2 =1

Эта последовательность была известна ещё в древней Индии, где она применялась в метрических науках.

Свойства последовательности Фибоначчи

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , …

Отношение какого-либо элемента последовательности к предшествующему ему колеблется около числа 1,618…, через раз то превосходя, то не достигая его:

- Отношение какого-либо элемента последовательности к последующему приближается к числу 0,618…- «Золотой пропорции», что обратно пропорционально числу 1,618…- «Золотому сечению»;

- Если делить элементы последовательности через один, то получим числа 2,618… и 0,382…, которые так же являются взаимно обратными числами;

- Каждое третье число чётное , каждое четвёртое делится на 3, каждое пятое - на 5, каждое пятнадцатое – на10;

- Невозможно построить треугольник, сторонами которого являются числа ряда Фибоначчи (никакое число ряда не может повторяться дважды)

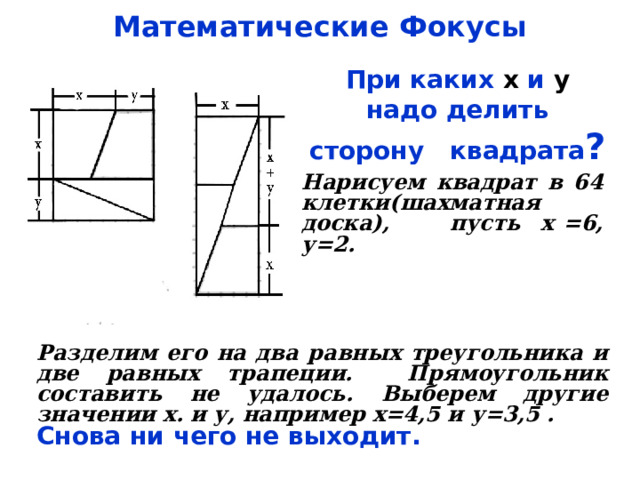
Математические Фокусы

При каких х и у надо делить сторону квадрата ?

Нарисуем квадрат в 64 клетки(шахматная доска), пусть х =6, у=2.

Разделим его на два равных треугольника и две равных трапеции. Прямоугольник составить не удалось. Выберем другие значении х. и у, например х=4,5 и у=3,5 .

Снова ни чего не выходит.

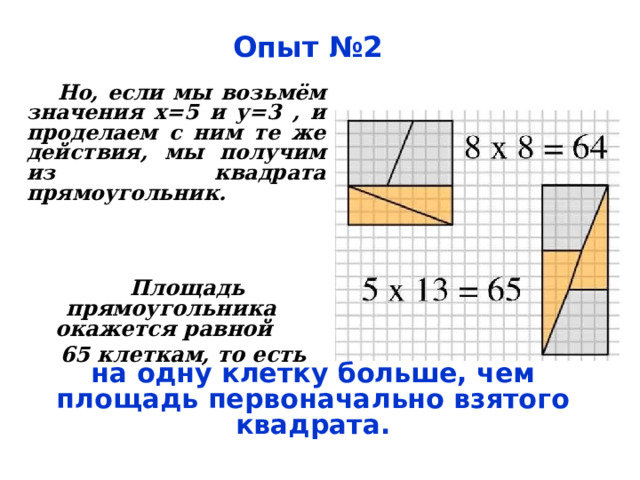
Опыт №2

Но, если мы возьмём значения х=5 и у=3 , и проделаем с ним те же действия, мы получим из квадрата прямоугольник.

Площадь прямоугольника окажется равной

65 клеткам, то есть

на одну клетку больше, чем площадь первоначально взятого квадрата.

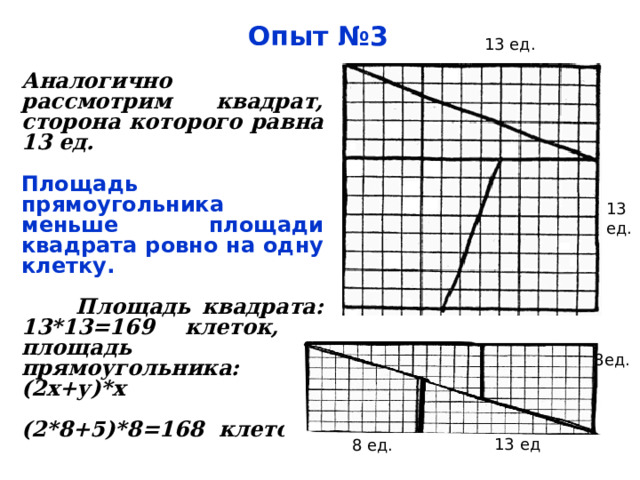
Опыт №3

13 ед.

Аналогично рассмотрим квадрат, сторона которого равна 13 ед.

Площадь прямоугольника меньше площади квадрата ровно на одну клетку.

Площадь квадрата: 13*13=169 клеток, а площадь прямоугольника: (2х+у)*х

(2*8+5)*8=168 клеток .

13 ед.

8ед.

13 ед

8 ед.

Опыт №4

Возьмем квадрат 5 на 5 единиц и три его стороны разделим на отрезки длиной в 2 и 3 единицы, а затем разрежем.

Составим прямоугольник.

Площадь квадрата равна 25 квадратным единицам.

Стороны прямоугольника, образованного частями квадратов, будут 8 ед. и 3 ед., что дает площадь в 24 квадратных единицы.

В данном эксперименте одна квадратная единица не прибавляется, а теряется .

Опыт № 5

Рассмотрим ряд 2,4,6,10,16,…

Возьмем квадрат со стороной 10 ед., тогда его площадь равна 100(кв.ед.).Стороны соответствующего прямоугольника будут равны: 10 + 6 = 16 (ед.) и 10 – 4 = 6 (ед.) S= 96 кв.ед., разность результатов в 4 кв. ед..

4 = 100 – 6 • 16 или

4 = | 36 – 40 |.

Аналогично в Опыте №6 я рассмотрела ряд 2,5,7, 12, 19, 31 …..и убедилась, что он дает прирост или потерю площади в 11 кв. ед.

например: а) 11 = 12 2 – 7 • 19

б) 11 = | 7 2 – 5 • 12|

Рассмотрим следующие две формулы:

А + В = С

В 2 = AC + Х.

Если подставить вместо Х желаемый прирост или потерю, а вместо В число, которое принято за длину стороны квадрата, то можно построить квадратное уравнение, из которого найдутся два других числа Фибоначчи.

Заключение:

• Впервые о числах Фибоначчи была рассказано в энциклопедии и «Книга абака» Леонардо Фибоначчи в 1202 году.

• Последовательность 1,1,2,3,5,8,13,21 …., была описана при решении задачи о размножении кроликов.

• Познакомилась с некоторыми свойствами последовательности Фибоначчи

• Основная закономерность этих чисел позволяет решать геометрические задачи - парадоксы с делением сторон квадрата на части по закону чисел Фибоначчи и составлением из них прямоугольника.

• Выяснила, какому закону подчиняются «приросты» или «недостатки» площадей для любого ряда чисел Фибоначчи.

• Вывод : Гипотеза, что «прирост» или «недостаток» для любого ряда чисел Фибоначчи равен разности между квадратом любого их числа и произведением соседни х, подтвердилась опытами № 5 и № 6.

Спасибо за внимание