| Какую тему вы изучили на прошлом уроке?
Есть ли связь между алфавитным подходом к измерению информации и содержанием информации? Почему?
Что такое бит с позиции алфавитного подхода к измерению информации?
Что называют информационным весом символа?
Из чего складывается информационный объём текста?
По какой формуле вычисляется информационный объём?
Какой информационный вес имеет каждая буква русского алфавита?
Какие ещё единицы измерения информации вы знаете?
Расположите в порядке убывания единицы измерения информации: байт, Мб, Тб, бит, Кб, Гб. Все вопросы выводятся на слайде по ходу устного опроса. | Алфавитный подход к измерению информации. Нет. Т. к. при алфавитном подходе для определения количества информации имеет значение лишь размер хранимого и передаваемого кода. Основная единица измерения информации. В двоичном коде каждая двоичная цифра несет одну единицу информации, которая называется 1 бит. Длину двоичного кода, с помощью которого кодируется символ алфавита. Информационный объём текста складывается из информационных весов всех составляющих текст символов. I = K ∙ i (битов), где i– информационный вес символа алфавита, а К– количество символов в тексте, записанном с помощью этого алфавита. В русском алфавите 33 буквы. Применим формулу 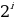 = N. Т. к. = N. Т. к. 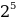 = 32; 32 = 32; 32 Байт, Кб, Мб, Гб, Тб. Тб, Гб, Мб, Кб, байт, бит. | Коммуникативные:
умение точно выражать свои мысли в соответствии с задачами коммуникации;
Познавательные:
построение логической цепи рассуждений; контроль и оценка процесса и результата товарищеской деятельности; структурирование знаний;
Регулятивные: выделение и осознание того, что уже пройдено. |
| Предварительно попросив трех учеников задать учителю один и тот же вопрос: «Сегодня у вас есть урок информатики?», первому ученику учитель отвечает «Да», второму — «Yes», а третьему просто кивает головой. При этом фиксируя свои ответы на доске. Получил ли каждый из вас (те, кто задавал вопрос) информацию? Сколько информации вы получили? Одинаковое ли количество в каждом случае?
Итак, вопрос: как измерить полученное количество информации? На прошлом уроке мы отметили, что есть несколько подходов к измерению информации. Мы рассмотрели один из них (алфавитный). Сегодня мы рассмотрим еще один подход к измерению информации. Это содержательный подход. Запишите число и тему урока «Содержательный подход к измерению информации». |
Да.
Варианты учеников. В результате приходят к выводу, что количество символов в ответах разное, но содержание ответов одинаково.
Записывают число, тему урока. | Регулятивные: планирование своих действий в соответствии с поставленной задачей; выдвижение гипотез; Коммуникативные:
умение точно выражать свои мысли в соответствии с задачами коммуникации;
Познавательные: построение логической цепи рассуждений;
Личностные: готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию. |
| Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе какого-то события, снимает неопределённость знания человека об этом событии. Чем больше первоначальная неопределённость знания, тем больше информации несёт сообщение, снимающее эту неопределённость. Рассмотрим примеры, иллюстрирующие данное утверждение: На слайде: Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина». Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаёте, что игра закончилась победой «Зенита». Ситуация 3. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин. Вопрос: в какой из трёх ситуаций полученное сообщение несёт больше информации? Неопределённость знания – это количество возможных вариантов ответа на интересующий вас вопрос. Ещё можно сказать: возможных исходов события. Здесь событие – например, выборы мэра; исход – выбор, например, Н. Н. Никитина. Тогда в первой ситуации сколько вариантов ответа? Какие? Во второй?
В третьей?
Согласно данному ранее определению, наибольшее количество информации несёт сообщение в третьей ситуации, поскольку неопределённость знания об исходе события в этом случае была наибольшей. В 40-х годах 20 в. Проблема измерения информации была решена американским ученым Клодом Шенноном – основателем теории информации. Согласно Шеннону, информация – это снятая неопределенность знания человека об исходе какого-то события. Сообщение, уменьшающее неопределённость знания об исходе некоторого события в два раза, несет 1 бит информации. Исходя из этого, сообщение, представленное в 1-й ситуации, несет 1 бит информации. Следовательно, количество информации, полученное во 2-й и 3-й ситуациях, больше, чем 1 бит. Но как измерить это количество? Рассмотрим ещё один пример. Вы написали контрольную по информатике и спрашиваете учителя о полученной оценке. Сколько вариантов оценок возможно? Я предлагаю вам угадать оценку за два вопроса, ответом на которые может быть «да» или «нет». Ваши варианты вопросов? Возможный вариант рассуждения: Ученик: Вопрос 1. Оценка выше тройки? Учитель: Да. Ученик: Вопрос 2. Это пятёрка? Учитель: Нет. Ученик понимает, что он получил четвёрку. Какая бы ни была оценка, таким способом она будет угадана! Первоначально неопределенность знания (количество возможных оценок) была равна, как вы правильно отметили, четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза, и, следовательно, передавался 1 бит информации. На слайде: Первоначальные варианты: Варианты, оставшиеся после 1-го вопроса (1 бит): Вариант, оставшийся после 2-го вопроса (+1 бит): Узнав оценку, ученик получил 2 бита информации. Рассмотрим ещё один пример. Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет». Аналогичные рассуждения при рассмотрении данного примера. Способ решения проблемы, примененный в данных двух примерах, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределённость знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несёт 1 бит информации. Сформулируем важное условие, относящееся к рассмотренным примерам, в т. ч. к трём рассмотренным ситуациям в начале урока. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Тогда полученные нами результаты описываются следующими формулировками: На слайде: -
сообщение об одном из двух равновероятных исходов некоторого события несет 1 бит информации; -
сообщение об одном из четырёх равновероятных исходов некоторого события несет 2 бита информации; -
сообщение об одном из восьми равновероятных исходов некоторого события несет 3 бита информации. Обозначим буквой N количество возможных исходов события, i- количество информации в сообщении об одном из N результатов. На слайде: В примете с учителем: N = 2, i = 1 бит; В примере с оценками: N = 4, i = 2 бита; В примере с вагонами: N = 8, i = 3 бита. Посмотрите внимательно на запись. Что заметили?
Верно. Есть вопросы по новому материалу? Всё объяснение учителя нового материала сопровождается презентацией. | Слушают рассказ учителя.
Слушают рассказ учителя.
Варианты учеников.
.
Два: мужчина, женщина. Три: выиграл «Зенит», ничья, выиграло «Динамо». Четыре. Четыре кандидата на пост мэра.
Слушают рассказ учителя.
Оценка может оказаться любой от 2 до 5, т. е. четыре варианта: 2, 3, 4, 5. Варианты учеников.
Вместе с учителем анализируют пример.
Опираясь на предыдущий пример, ученики совместно с учителем разбирают пример. В итоге приходят к выводу, что информация о номере вагона несет 3 бита информации.
Слушают рассказ учителя.
Связь между этими величинами выражается формулой 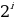 = N. = N. Если есть вопросы, задают. | Личностные: первичная сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками; развитие речевого аппарата; Познавательные: формирование умения обобщать, составлять алгоритм действий; Регулятивные: планирование, определение последовательности действий; Коммуникативные: формирование умения оформлять свои мысли в устной и письменной форме, слушать и понимать речь других, инициативное сотрудничество в группе. |
| Рассмотрим пример. Вернёмся к рассмотренному ранее примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Нужно узнать, какое количество информации содержится в сообщении о номере искомого вагона. Какую формулу будем использовать при решении задачи? Что нам известно из условия задачи? Верно. Подставляем данное значение в формулу и получаем 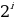 = 16. Для того чтобы найти i, нужно решить уравнение. Как такой вид уравнений называют в математике? = 16. Для того чтобы найти i, нужно решить уравнение. Как такой вид уравнений называют в математике? Тогда чему будет равно i? Верно. Запишите ответ. При решении задачи учитель делает записи на доске, а ученики фиксируют решение в тетрадях. Решим ещё одну задачу. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несёт сообщение о том, что вам купили билет на 12-й ряд, 10-е место? Прочитайте внимательно условие задачи. Данную задачу можно решить двумя способами.
Как ещё можно решить данную задачу?
Всё верно. Есть вопросы по решению задачи?
|
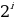 = N. = N.
N = 16.
Показательное.
i= 4 бита.
Записывают решение задачи в тетрадь.
К доске выходит ученик.
Можно найти сколько всего мест в кинозале. 16 ∙ 32 = 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Составим уравнение: 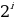 = 512. Отсюда i = 9 битов. = 512. Отсюда i = 9 битов. Можно найти сколько битов информации несёт сообщение о номере ряда (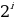 = 16, отсюда i = 4 бита), затем найти сколько битов информации несёт сообщение о номере места ( = 16, отсюда i = 4 бита), затем найти сколько битов информации несёт сообщение о номере места (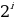 = 32, отсюда i = 5 битов). В целом сообщение про ряд и место несет 4 + 5 = 9 битов информации. = 32, отсюда i = 5 битов). В целом сообщение про ряд и место несет 4 + 5 = 9 битов информации. Ученики записывают оба способа решения задачи. Если есть вопросы по решению, задают. | Регулятивные: планирование, определение последовательности действий; работа по алгоритму; прогнозирование результата. |






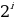 = N. Т. к.
= N. Т. к. 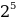 = 32; 32
= 32; 32
















