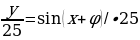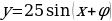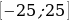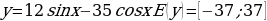Просмотр содержимого документа
«Использование пифагоровых троек при изучении математики»
Использование пифагоровых троек при изучении математики.
Использование рациональных вычислений является неотъемлемой частью урока математики. Это позволяет не только рационально использовать время урока, но и развивать у детей память, логическое мышление, способность видеть и развивать числовые закономерности.
Изучая в 8 классе теорему Пифагора, учитель знакомит учеников и с теоремой, обратной теореме Пифагора. В результате этого и вводится понятие «пифагоровых троек чисел». Работая в старших классах, я заметила, что их можно активно использовать не только при решении геометрических задач (нахождение катетов и гипотенузы в прямоугольном треугольнике, диагонали в прямоугольнике, расстояния от оси цилиндра до секущей плоскости, высоты в пирамиде и т.д.), но и в тригонометрии, после чего стала специально обучать учащихся применять их.
Пифагоровых троек существует бесконечное множество, но чаще всего используются следующие: 3,4,5 5,12,13 8,15,17 7,24,25 9,40,41 20,21,29 12,35,37. Общий вид пифагоровых троек чисел :
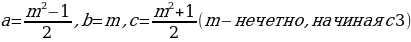
Рассмотрим некоторые примеры использования пифагоровых троек чисел при изучении тригонометрии.
Пример 1.
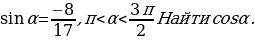
Используя тройку: 8,15,17, мы сразу находим 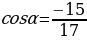 (ведь основное тригонометрическое тождество
(ведь основное тригонометрическое тождество 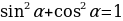 есть не что иное, как теорема Пифагора.
есть не что иное, как теорема Пифагора.
Пример 2.
Вычислить 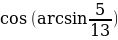
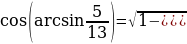 =
=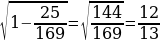
Можно заметить, что здесь снова «работает» пифагорова тройка чисел : 5,12,13, что позволяет устно выполнять такие задания:
Пример 3.
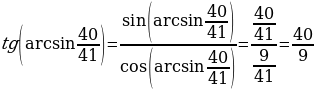
Пример 4.
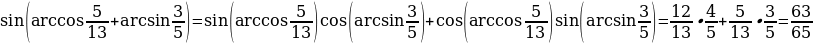
Пример 5.
Решить уравнение: 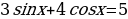
Это уравнение решается методом введения вспомогательного угла.
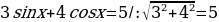
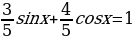
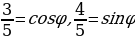
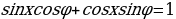
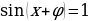
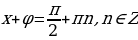
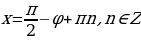
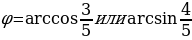
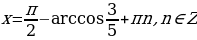
Решая это уравнение, мы делили на 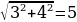 , а значит снова можно использовать пифагоровы тройки чисел и решать такие уравнения устно.
, а значит снова можно использовать пифагоровы тройки чисел и решать такие уравнения устно.
Например:
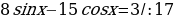 (тройка: 8, 15, 17)
(тройка: 8, 15, 17)
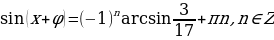
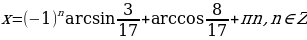
Или 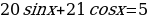
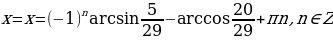 (тройка: 20, 21, 29)
(тройка: 20, 21, 29)
Пример 6.
Найти множество значений функции:
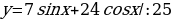
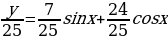 (тройка: 7, 24, 25)
(тройка: 7, 24, 25)
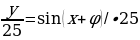
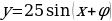
Таким образом множество значений функции будет равно 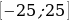
И для функции 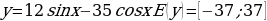
Своим исследованием я хотела показать, что использование пифагоровых троек позволяет устно решать некоторые типы геометрических задач, тригонометрических заданий, очень экономит время при решении подобных заданий, а значит позволит потратить время на экзамене, в том числе и ЕГЭ, на более сложные задания.
Буду рада, если мое исследование, которое я провела уже более 10 лет тому назад, будет полезно для работы коллег.






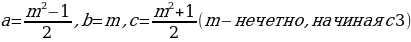
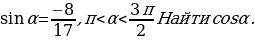
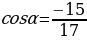 (ведь основное тригонометрическое тождество
(ведь основное тригонометрическое тождество 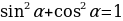 есть не что иное, как теорема Пифагора.
есть не что иное, как теорема Пифагора.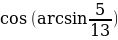
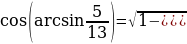 =
=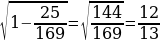
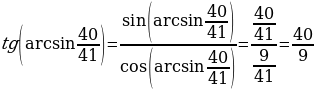
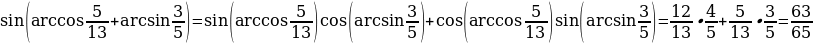
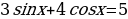
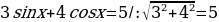
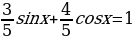
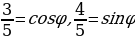
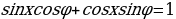
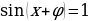
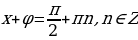
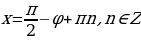
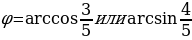
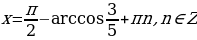
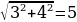 , а значит снова можно использовать пифагоровы тройки чисел и решать такие уравнения устно.
, а значит снова можно использовать пифагоровы тройки чисел и решать такие уравнения устно.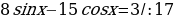 (тройка: 8, 15, 17)
(тройка: 8, 15, 17)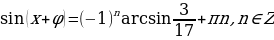
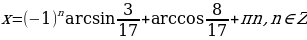
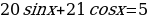
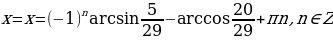 (тройка: 20, 21, 29)
(тройка: 20, 21, 29)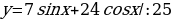
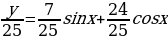 (тройка: 7, 24, 25)
(тройка: 7, 24, 25)