Использование практико-ориентированных задач на уроках физики

Использование практико-ориентированных задач на уроках физики

Александрова З.В., учитель физики и информатики

МБОУ СОШ №5 пгт Печенга Мурманской области

При преподавании физики очень большую роль играет эксперимент, посредством которого осуществляется более тесный контакт между учащимся и природой, являющейся объектом их изучения.

Но показ даже большого количества опытов на уроках физики сам по себе ещё не обеспечивает в нужной степени осуществления основных этапов процесса познания и тем самым недостаточно способствует приобретению осознанных и активных знаний, то есть таких знаний, которые могли бы быть самостоятельно использованы учеником для решения практических вопросов.

Постановка экспериментальных задач помогает вскрыть недопонятое, ошибочное представляемое учащимися, причем задача может быть очень простой, но заставляющей учащихся выявить их внутреннее понимание вопроса, а не формальное знание его.

Физика очень тесно связана с повседневной жизнью, поэтому подобрать задачу с практическим содержанием можно практически к любой теме. Рассмотрим варианты задач применительно к различным темам.

Задача 1

При изучении в 7 классе темы «Условия плавания тел» можно рассмотреть следующую задачу. Учитель перед началом урока наполняет ёмкость водой и рядом с ней ставит небольшую прямоугольную коробочку и гирьки по 5 грамм. Когда начинается урок, к доске вызывается ученик, который назначается ведущим инженером судостроительного завода. Ученику предлагается выяснить, сколько пассажиров может перевозить данный корабль (рисунок 1).

Рисунок 1 – Плавание коробочки с гирей

Задача поставлена, но никаких числовых данных для её решения нет. И вообще неизвестно, что надо знать для решения задачи, какие величины должны быть найдены путем непосредственных измерений. Поэтому решение начинается не с попыток производить различные математические операции над готовыми числами (этот путь для учащихся закрыт отсутствием готовых данных), но и не с попыток производить различные измерения, еще не зная, пригодятся они или нет (против этого должен протестовать учитель), а с продумывания физической сущности задачи, с представления того физического процесса, о котором идет речь в данной задаче.

Когда мы опустим наш коробок-«корабль» в воду, она будет погружаться в нее до тех пор, пока ее вес не будет уравновешиваться выталкивающей силой воды действующей на банку снизу, т. е. Р=F. Но выталкивающая сила F равна весу вытесненной жидкости

,

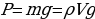где V объем погруженной части коробочки, а ρ – плотность воды. Объем погруженной части банки равен произведению площади основания на её высоту.

Ученик проводит измерения, заполняет дано и выполняет вычисления. После определения максимального числа пассажиров, он помещает коробочку в воду и ставит на неё гирьки, если в расчётах не было допущено ошибок, то коробочка остаётся на плаву, если же ошибка была, он идёт ко дну.

Чаще всего ошибкой допускаемой при решении данной задачи является не учёт массы самой коробочки, что ведёт к перегрузу и утоплению. Данная задача демонстрирует детям важность точности расчетов и применимость формул к решению практических задач.

Задача 2

После изучения в 7 классе темы «Масса» и проведения лабораторной работы по измерению массы тела на рычажных весах, полезно решить следующую задачу.

На стол ставится мензурка с водой и рядом с ней кладётся пробирка, вызванному к доске ученику предлагается определить вес пробирки, используя только мензурку.

Задача решается просто. Измерив уровень воды в мензурке, опускают в нее пробирку. Пробирка плавает (опрокинуться ей мешают стенки мензурки), вытесняя некоторое количество воды, в результате чего уровень воды в мензурке поднимается (рисунок 2).

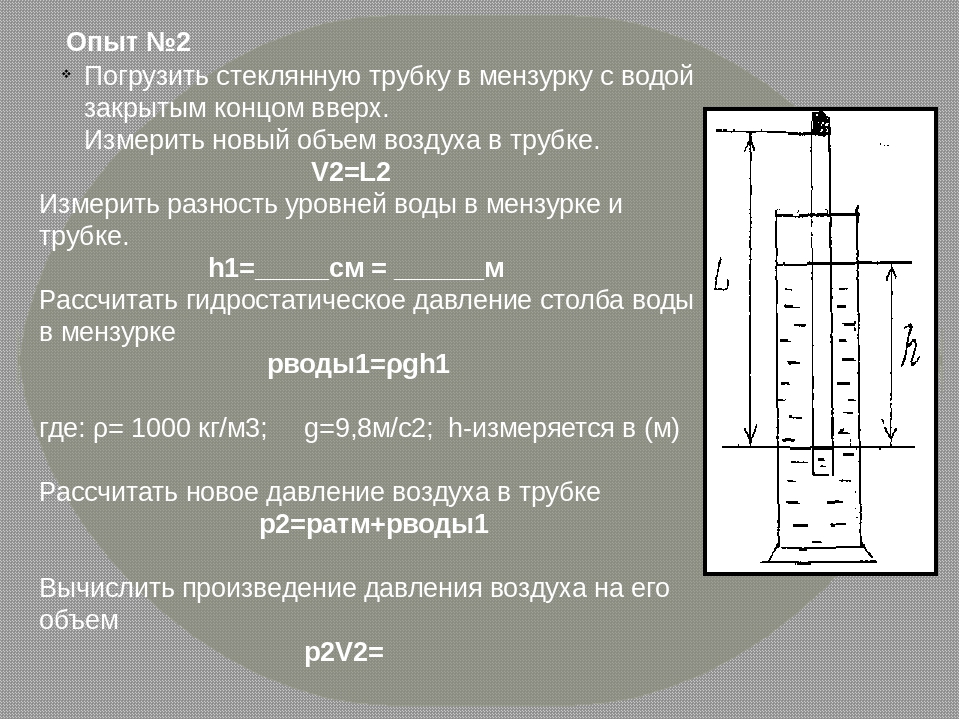
Рисунок 2 – Плавание пробирки в мензурке

Так как удельный вес воды равен единице, и следовательно, объем вытесненной воды численно равен весу плавающего тела, задача решается устно. Правильность решения проверяется на весах.

Разобранная задача является примером устной количественной экспериментальной задачи.

Решив задачу и опустив вновь пробирку в воду, обращаем внимание учащихся на то обстоятельство, что плавающее в воде тело как бы непрерывно находится на весах. Стоит пробирку немного нагрузить, и она глубже опускается, вытесняя большее количество воды, объем которой все время остается численно равным весу плавающего тела. В нашем случае объем вытесненной жидкости мы узнавали по шкале мензурки, но можно шкалу нанести непосредственно на пробирке, и тогда необходимость в мензурке отпадает.

В жизни так и поступают. На наружной обшивке корпуса корабля наносят шкалу, глядя на которую, можно определить вес корабля в данный момент и, следовательно, вес принятого на корабль или снятого с него груза.

Задача 3

Учитель ставит на стол брусок, имеющий форму прямоугольного параллелепипеда, и спрашивает, в каком положении будет плавать брусок, если его поместить в воду?

На тело, помещенное в жидкость, действуют две силы: вес тела Р и выталкивающая сила F. Для случая плавания эти силы равны и противоположны по направлению. Следовательно, брусок будет в равновесии в таких положениях, когда обе эти силы будут направлены по одной вертикали. Таких положений может быть три: 1) вертикальное, 2) горизонтальное (плашмя), одной из боковых сторон вниз и 3) горизонтальное, одним из ребер вниз. Положения равновесия могут быть устойчивыми и неустойчивыми. Очевидно, что брусок примет такое положение, при котором его равновесие будет устойчивым, поэтому для решения задачи надо установить, в каком случае брусок будет в положении устойчивого равновесия.

1) Пустим брусок плавать в вертикальном положении. Если бы удалось придать бруску строго вертикальное положение и оградить его от всяких сотрясений и движений окружающего воздуха, то брусок находился бы в равновесии. Но это равновесие не было бы устойчивым, так как при малейшем наклоне бруска точка приложения выталкивающей силы с, лежащая в центре тяжести подводной части тела, смещается с вертикали, опущенной из общего центра тяжести тела О, в результате чего тело под действием «пары сил» опрокинется (рисунок 3, а) и перейдет в горизонтальное положение. Это рассуждение справедливо для однородного бруска любой плотности, меньшей плотности жидкости. При одинаковых плотностях бруска и жидкости положение равновесия будет безразличным, так как брусок должен будет погрузиться в жидкость полностью, и следовательно, точка приложения силы тяжести и выталкивающей силы совместятся.

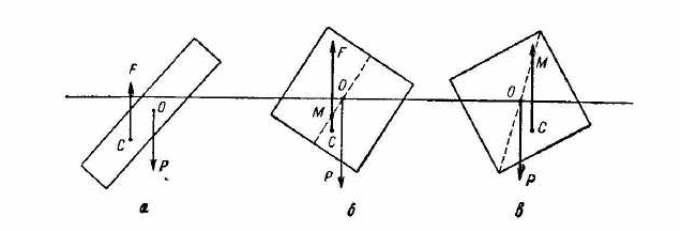
Рисунок 3 – Действие сил на брусок при различных положениях

2) При горизонтальном положении, лежа на одной из своих боковых поверхностей, брусок вновь будет находиться в неустойчивом равновесии. При малейшем отклонении бруска от положения равновесия точка приложения выталкивающей силы С будет смещаться в сторону от вертикали, опущенной из центра тяжести тела О, и опять появится «пара сил», поворачивающая брусок дальше в этом же направлении (рисунок 3, б).

Сущность решения заключается в определении стороны, в какую произойдет смещение точки приложения выталкивающей силы при наклоне бруска. Нахождение положения точки приложения выталкивающей силы, или «центра величины», как ее называют моряки, сводится к нахождению центра тяжести подводной части бруска. При любом положении бруска его подводный объем делится плоскостью, проведенной через вектор Р вдоль бруска, на две равные части. Центр тяжести той части подводного объема бруска, точки которого имеют большую удаленность от вектора Р, лежит от этого вектора на большем расстоянии, чем центр тяжести другой части подводного объема, поэтому их общий центр тяжести смещен в сторону центра тяжести, имеющего наибольшее удаление от вектора Р.

Получившаяся «пара сил» будет вращать брусок до тех пор, пока «центр величины» и центр тяжести тела вновь не попадут на одну вертикаль, а это произойдет при положении бруска ребром вниз, так как при этом положении все точки обеих половин подводной части объема бруска будут одинаково удалены от вертикали, вдоль которой направлен вектор Р и, следовательно, центр тяжести подводной части бруска будет лежать на этой вертикали.

3) Положение бруска ребром вниз является устойчивым. При отклонениях его от этого положения возникающая «пара сил» препятствует его повороту и возвращает в положение ребром вниз (рисунок 3, в). Используя данные чертежи, можно познакомить учащихся с морским техническим термином «метацентр». Метацентром (вне центра) называется точка пересечения направления выталкивающей силы с вертикальной плоскостью, идущей вдоль корабля по середине его ширины и разделяющей его на две симметричные части (на рисунке 3 точка М). Если метацентр лежит выше центра тяжести корабля, то корабль остойчив, т. е. при кренах он будет сам выпрямляться, если наоборот, то корабль при кренах будет опрокидываться, что и должно происходить с нашим бруском в первом и втором положениях.

Расстояние между метацентром и центром тяжести корабля называется метацентрической высотой. Чем больше метацентрическая высота, тем остойчивее корабль. Каждому классу корабля присуща своя метацентрическая высота: для линейных кораблей – 2 м, для крейсеров – 1,3 м, для миноносцев – 1 м, для товаро-пассажирских пароходов – 1,5 м.

Основываясь на приведенных выше рассуждениях, мы можем утверждать, что однородный деревянный брусок с поперечным сечением в форме квадрата будет плавать в воде в горизонтальном положении ребром вниз.

Правильность решения задачи проверяется опытом. Помещенный в вертикальном положении в воду брусок падает на бок, поворачивается ребром вниз и в этом положении остается на плаву.

Задача 4

После изучения темы «Работа» можно предложить ученикам следующую задачу. На столе мешочек с песком. Необходимо переместить данный груз из одной точки стола в другую, находящуюся от первой на расстоянии 1 м, так, чтобы при этом произвести наименьшую механическую работу (рисунок 4).

Рисунок 4 – Работа по перемещению груза

При перемещении груза волоком надо произвести работу A=μPs. Если приподнять груз над столом и перенести его по воздуху, то, пренебрегая сопротивлением воздуха, надо произвести механическую работу A = Ph. Во время перенесения груза над столом, параллельно его поверхности, работа против силы тяжести не производится, так как высота груза над столом не меняется.

Поскольку при перемещении груза волоком коэффициент трения μ выражается дробью порядка нескольких десятых долей, а высота подъема h может выражаться сотыми и менее долями метра, то величина механической работы во втором случае будет в десятки раз меньше, чем в первом.

Правильность решения может быть проверена измерением при помощи динамометра силы тяги и веса груза и подсчетом механической работы в том и в другом случае.

Решение этой задачи уточняет понятие механической работы и показывает, что в жизни часто предпочитают совершать большую работу, но зато при ее совершении прикладывать меньшую силу (использование простых механизмов).

Задача 5

После изучения законов сохранения в 9 классе целесообразно разобрать следующую задачу. На столе собрана установка, представляющая собой баллистический маятник (рисунок 5). А – деревянный цилиндр, подвешенный к раме на четырех нитях, В – картонный зажим, С – отверстие для пружинного пистолета, весы Беранже, разновес, пружинный пистолет и к нему «снаряд», имеющий форму шара, масштабная линейка.

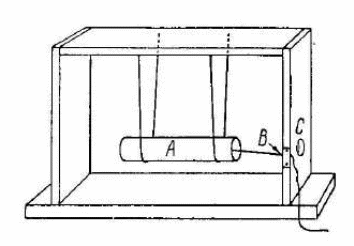
Рисунок 5 – Баллистический маятник

Если произвести выстрел из пистолета через отверстие С в деревянный цилиндр, то «снаряд» прилипнет к пластилину и цилиндр вместе со «снарядом» качнется назад и вверх. Нить, продернутая под картон зажима В, этому движению не помешает, но при обратном движении цилиндра под зажимом пройти не сможет.

«Снаряд», ударившись в деревянный цилиндр, передаст ему свой импульс, и за счет этого цилиндр, откачиваясь назад, поднимется на некоторую высоту.

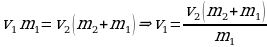
Масса снаряда» – m₁ и масса цилиндра – m₂ определяются путем взвешивания. Начальная скорость цилиндра v₂ может быть определена из выражения

,

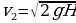где H – высота подъема цилиндра. Для определения высоты подъема производится измерение высоты цилиндра над основанием рамы до выстрела и в отклоненном положении, для чего цилиндр вновь отклоняется рукой до тех пор, пока позволяет это делать прикрепленная к нему нить. При отклонении цилиндра рукой надо следить, чтобы нить под зажимом В дополнительно не продергивалась. Окончательно получаем следующее выражение для нахождения скорости пули

.

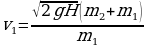Ученикам рассказывается, что до появления фотодатчиков именно этим способом пользовались инженеры при разработке огнестрельного оружия.
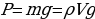
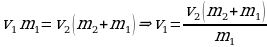
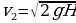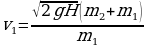