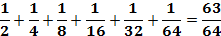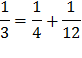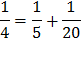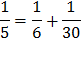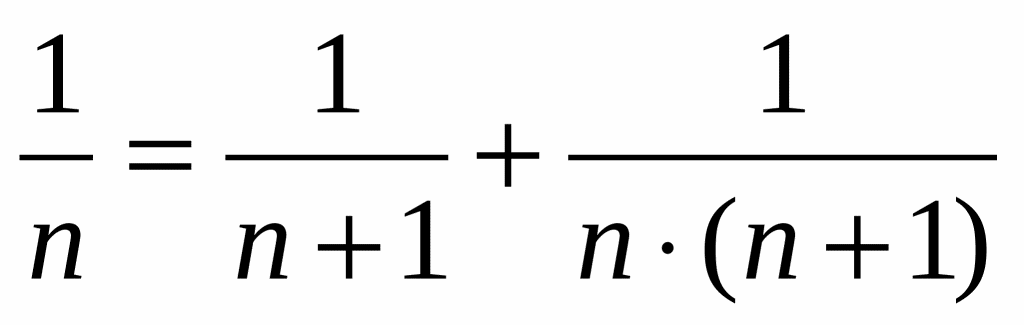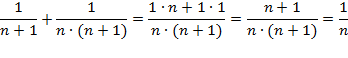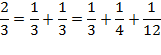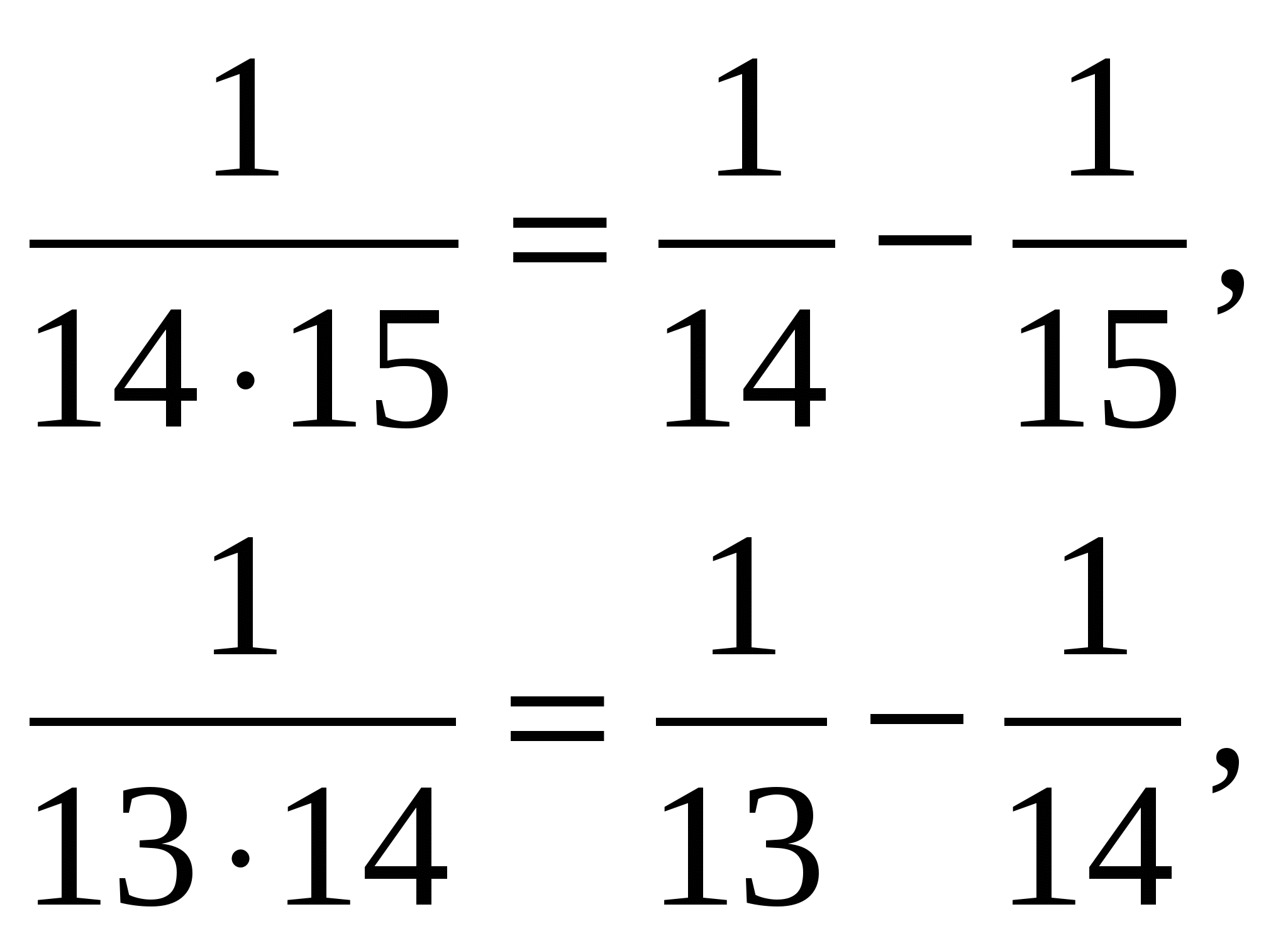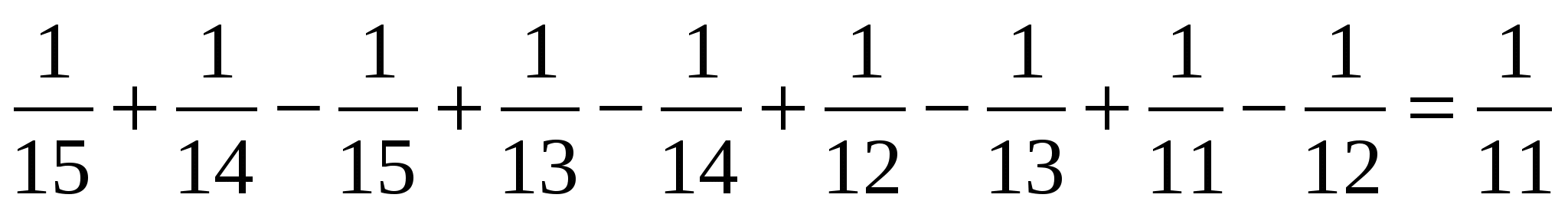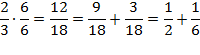Исследовательский проект "Аликвотные дроби"

Муниципальный этап Всероссийского конкурса

исследовательских работ учащихся «Шаги в науку»

СЕКЦИЯ МАТЕМАТИКА

Тема: «Аликвотные дроби»

Выполнена: 5 класс,

МБОУ «Львовская СОШ»,

Новооскольского Муниципального округа

Попова Карина Дмитриевна

Научный руководитель:

учитель,

Искендерова Надежда Герасимовна

2025

Введение

Мы начали изучение обыкновенных дробей. Я поняла как они записываются, что означают, как выполнять с ними действия. Меня заинтересовал вопрос о их происхождении, кто и когда обратил внимание на необходимость этих чисел и применение их в обыденной жизни. Я задалась целью узнать о происхождении обыкновенных дробей и всё, что связано с ними. Историко-математические материалы демонстрируют нам, что дробные числа возникли у разных народов в древние времена вскоре после натуральных чисел.

Наряду с необходимостью считать вещи, люди в древности испытывали потребность в измерении числовых величин, таких как длина, площадь, объем и время. Измерения не всегда выражаются в натуральных числах. Нужно учитывать и части употребляемой меры. Таким образом, во всех цивилизациях понятие дроби возникло из процесса дробления целого на равные части.

Однажды, готовясь к олимпиаде по математике, учительница мне предложила задание «Разделите 7 хлебов между 8 людьми так, чтобы всем досталось поровну, сделав как можно меньше разрезов».

Моё решение, конечно, было таким: надо разрезать каждый хлеб на 8 равных частей, то есть сделать 7 разрезов, дать каждому по кусочку из каждой буханки, тогда каждому достанется по 7/8 хлеба. Таким образом будет сделано 49 разрезов в этих 7 хлебах. Но была и вторая часть вопроса: «сделав как можно меньше разрезов». Значит 49 это правильный, но не окончательный ответ.

Каково же было удивление, что решить эту задачу можно с меньшим числом разрезов. Сделать всего 17 разрезов.

4 хлеба надо разрезать пополам, тогда каждый получит по половине буханки , а разрезов будет 4, 2 хлеба – на 4 равные части, каждый получит ещё по 1/4 буханки — 6 разрезов и только один хлеб – на 8 частей, каждый получит по 1/8 буханки — 7 разрезов. В итоге каждый получит 1/2 + 1/4 + 1/8 = 7/8 буханки за 17 разрезов. Оказалось, что древние египтяне решили эту задачу с помощью аликвотных дробей.

Вот так я столкнулась, с новым понятием – аликвотные дроби. Эта название меня очень заинтересовало, поэтому я решила познакомиться с историей аликвотных дробей и их применением.

Так, собирая информацию, я еще больше увлеклась обыкновенными дробями. Особое внимание привлекли аликвотные дроби. Это и определило цель и задачи моего исследования.

Цель работы: выяснить, какое значение имеют аликвотные дроби в нашей жизни и изучить практическую значимость применения этих дробей в современной математике и в других науках.

Задачи:

• Найти в различных источниках информацию об истории появления аликвотных добей.

• Изучить свойства аликвотных дробей.

• Рассмотреть основные операции с аликвотными дробями.

• Научиться использовать аликвотные дроби при решении задач.

Актуальность работы: данная тема, которая представлена в моей работе, помогает расширить знания по истории развития математики и решать сложные олимпиадные задачи по математике более рациональными способами.

Гипотеза: умение раскладывать дроби на две аликвотные, позволяет легко решать олимпиадные задачи по математике.

Практическая значимость: задачи с использованием аликвотных дробей составляют обширный класс нестандартных задач. Эта работа поможет им разобраться с этими задачами и научиться их решать.

Проблема: недостаток внимания к аликвотным дробям в школьной программе и отсутствие понимания их полезности.

Продукт: исследовательская работа с примерами применения аликвотных дробей, собранная в формате научного отчета.

1. История аликвотных дробей

1.1. Возникновение аликвотных дробей

Всем нам хорошо известно, что вначале появились натуральные числа, в области которых всегда были выполнимы два математических действия: это сложение и умножение. Но, к сожалению, деление не всегда было осуществимо. И возникновение данной проблемы, еще в древности (при решении практических задач: разделение участка на несколько частей, деление добычи и т.д.) привело к появлению дробных чисел. Результаты измерения не всегда получается выразить натуральным числом. Приходится учитывать и части употребляемой меры. Таким образом, во всех цивилизациях понятие дроби возникло из процесса дробления целого на равные части. Первой дробью, с которой познакомились люди, была половина.

В дальнейшем с помощью этих дробей составлялись дроби вида - рациональные числа. Однако этот путь был пройден не всеми цивилизациями: например, он так и не реализовался в древнеегипетской математике.

1.2. Аликвотные дроби в Древнем Египте

Система записи дробей, правила действий с ними заметно различались как у разных народов, так и в разные времена у одного и того же народа. Значительную роль играли также многочисленные заимствования идей при культурных контактах различных цивилизаций.

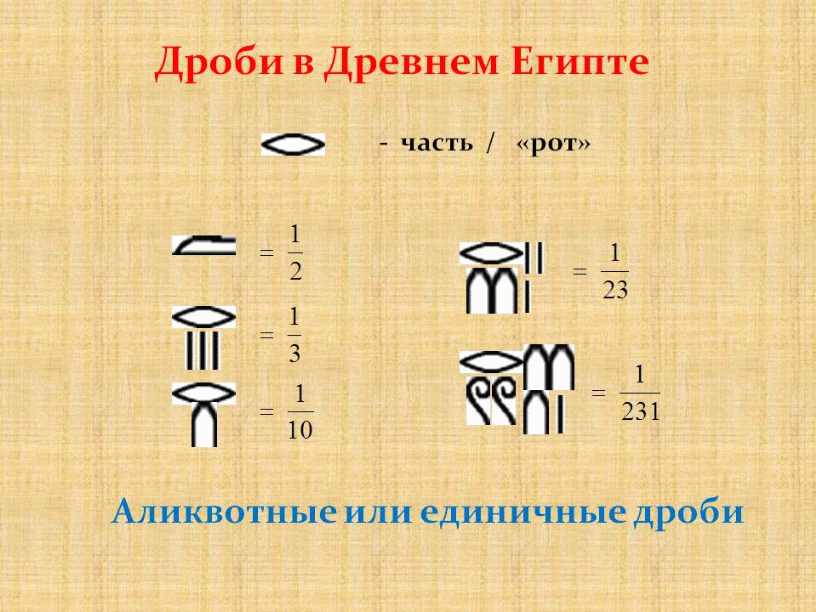
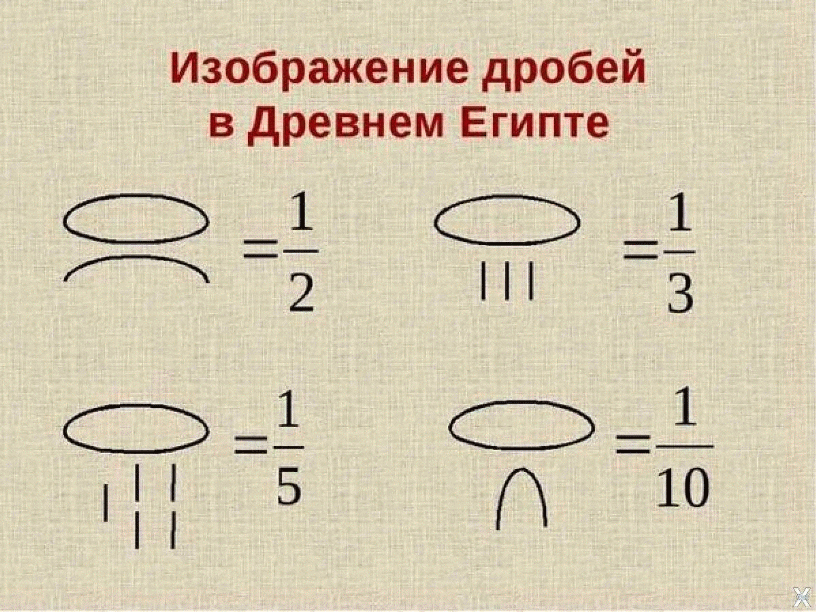
В древнем Египте пользовались лишь простейшими дробями, у которых числитель равен единице (те, которые мы называем «долями»).

Египтяне все дроби записывали как суммы долей. Дроби вида 1/n, где n - натуральные число, которым египтяне отдавали предпочтение, в современной математике именуются аликвотными ( от латинского aliguot- " несколько''). То есть аликвотными дробями называются дроби с числителем 1. И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Например,

1/2=1/3+1/6, 1/4=1/5+1/20

Так же используется название основные дроби или единичные дроби. Для обозначения единичной дроби египтяне над обычным числом ставили специальный иероглиф

- «рот» .

Например дроби 1/3 и 1/10 выглядели так:

и

Египтяне также использовали письменность, основанную на иероглифах "Ока Гора" (Уаджет).

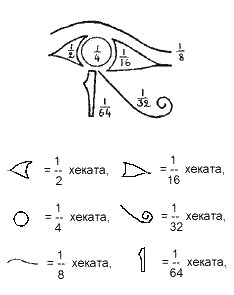
Ассоциация солнца с образом глаза характерна для древних. В египетской мифологии часто упоминается бог Гор, олицетворяющий крылатое солнце, который является одним из самых распространенных священных символов. В битве с врагами Солнца, воплощенными в образе Сета, Гор сначала терпит поражение. Сет вырывает у него Глаз — чудесное око — и разрывает его в клочья. Тот — бог учения, разума и правосудия — снова сложил части глаза в одно целое, создав "здоровый глаз Гора". Изображения частей разрубленного Ока использовались при письме в Древнем Египте для обозначения дробей от ½ до 1/64.

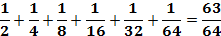
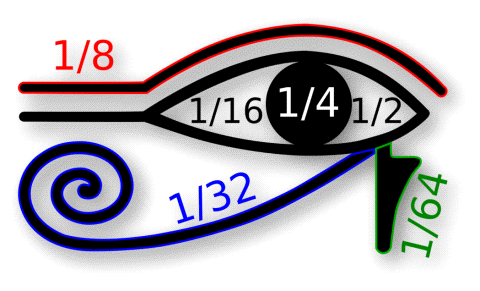
Сумма шести знаков, входящих в Уаджет, и приведенных к общему знаменателю: 32/64 + 16/64 + 8/64 + 4/64 + 2/64 + 1/64 = 63/64

Причиной появления этих дробей являлась необходимость разбить единицу на доли. Это нужно было для того, чтобы поделить добычу после охоты, ведь, нужно было знать, сколько частей составляет целое и кому какая часть добычи будет принадлежать, чтобы поделить основную меру объёма в Древнем Египте - «хекат».

Подобные дроби использовались совместно с другими формами записи египетских дробей для того, чтобы поделить хекат, основную меру объёма в Древнем Египте. Эта комбинированная запись также применялась для измерения объёма зерна, хлеба и пива. Если после записи количества в виде дроби Глаза Гора оставался какой-то остаток, его записывали в обычном виде кратно ро, единице измерения, равной 1/320 хеката. При этом «рот» помещался перед всеми иероглифами.

Хекат ячменя: 1/2+ 1/4 +1/32 (то есть 25/32 сосуда ячменя).

Хекат равнялся примерно 4,785 литрам

Сейчас сумма нескольких аликвотных дробей называется египетской дробью. Другими словами, любая дробь суммы имеет числитель, равный единице, и знаменатель, представляющий собой натуральное число.

Проводить всевозможные вычисления, выражая все дроби через единичные, было, конечно, очень трудно и отнимало немало времени. Поэтому египетские ученые позаботились о том, чтобы облегчить работу писцов. Они составили особые таблицы разложений дробей на простейшие. Математические документы древнего Египта это не научные трактаты по математике, а практические учебники с примерами, взятыми из жизни. Среди задач, которые должен был решать ученик школы писцов, - вычисления и вместимости амбаров, и объема корзины, и площади поля, и раздела имущества среди наследников, и другие. Писец должен был запомнить эти образцы и уметь быстро использовать их для расчетов.

Одним из первых известных упоминаний о египетских дробях является Математический папирус Ринда. Три более древних текста, в которых упоминаются египетские дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима.

Самый большой математический документ - папирус по руководству к вычислениям писца Ахмеса - найден в 1858 году английским коллекционером Райндом. Папирус составлен в XVII веке до нашей эры. Его длина 20 метров, ширина 30 сантиметров. Он содержит 84 математических задачи, их решения и ответы, записаны в виде египетских дробей.

1.3. Аликвотные дроби в Древней Греции

В Древней Греции арифметику – учение об общих свойствах чисел – отделяли от логистики – искусства исчисления. Греки считали, что дроби можно использовать только в логистике. Греки очень часто использовали все арифметические действия, производимые с дробями, но не считали их числами. В найденных источниках того времени понятие дроби не встречалось. Ученые в Греции считали, что в математике должны использоваться только целые числа. Они считали, что заниматься дробями могут купцы, ремесленники, астрономы, землемеры, механики и другой «черной люд». «Если ты захочешь делить единицу, математики высмеют тебя и не позволят это делать», – писал основатель афинской академии Платон.

Но в те времена с Платоном соглашались не все древнегреческие математики. Архимед, например, в трактате «Об измерении круга» использует дроби. Герон Александрийский тоже их использовал.

Пифагор, работая над теорией музыкальной шкалы, показал зависимость музыкальных интервалов с дробями, хотя с огромным трепетом относился к натуральным числам. Но если говорить точно, то определением или, скорее, понятием дроби ни Пифагор, ни его ученики не пользовались.

Для дробей вида 1/n использовалась запись: знаменатель дроби сопровождался штрихом справа, числитель не писали. Например, число 32 записывалось как λβ, а дробь 1/32 – λβ’.

«Число» в понимании греков – это набор единиц. Это было недостатком при написании дробного числа. Поэтому сейчас мы используем дробь как единое рациональное число, а греки – как отношение одного целого числа к другому. Вот почему обыкновенные, неединичные дроби практически не встречались в арифметике у греков. Дроби с числителем, равным 1 – именно им отдавалось предпочтение.

1.4. Аликвотные дроби на Руси

Русский термин «дробь»появилось в VIII веке, как и его аналоги в других языках, происходит от лат. fractura, который, в свою очередь, является переводом арабского термина с тем же значением: ломать, раздроблять. По одной из версий разбивали в Новгороде брусок серебра – гривну. Этот брусок рубили на четыре части. Каждая такая часть и назывался – рубль. Рубль, в свою очередь, также могли делить на части.

Всё это наши предки делали для удобства торговых расчётов. Как бы то ни было, нам понятно, что из хозяйственной деятельности появилась дробь.

Первый русский математик, известный нам по имени – монах Новгородского монастыря Кирик, занимался вопросами хронологии и календаря. В его рукописной книге «Учение им же ведати человеку числа всех лет» (1136 г.), т. е. «Наставление, как человеку познать счисление лет» применяется деление часа на пятые, двадцать пятые и т. д. доли, которые он называл «дробными часами» или «часцами».

В VII веке на Руси в писаниях о математике дроби сначала именовались как доли, а позже – «ломаными числами». Слово «дробь» в русском языке впервые упоминалось в VIII веке, это производное от «дробить» – разбивать на части или ломать. Числитель и знаменатель числа разделяла горизонтальная черта.

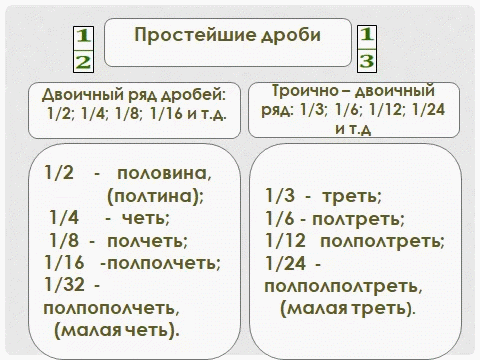
В старых руководствах есть следующие названия дробей на Руси:

1/2 - половина, полтина

1/3 – треть

1/4 – четь

1/6 – полтреть

1/8 - полчеть

1/12 –полполтреть

1/16 - полполчеть

1/24 – полполполтреть (малая треть)

1/32 – полполполчеть (малая четь)

1/5 – пятина

1/7 - седьмина

1/10 – десятина.

Это были аликвотные дроби и при помощи их могли представить другие дроби.

7/12 - четь да треть( 1/4 +1/3)

2/15- треть без пятины(1/3 - 1/5)

7/8 - един без полчети(1 - 1/8)

1.5. Аликвотные дроби в Древнем Китае

В Китае уже ко II в. до н. э. были описаны почти все известные арифметические операции с обыкновенными дробями. К примеру, в фундаментальном своде математических знаний древнего Китая – «Математике в девяти книгах», окончательная редакция которой принадлежит Чжан Цану. Выделяя наибольший общий делитель в числителе и знаменателе, аналогично тому, что делал Евклид, в Китае сокращали дроби.

Изначально китайцы работали с простейшими дробями, которые получили названия от иероглифа бань:

шао бань («малая половина») –1/3;

тай бань («большая половина») –2/3.

Издревле математики Китая пользовались смешанными числами. Самый ранний трактат о математике «Чжоу би суань цзин» («Канон расчета чжоуского гномона»/«Математический трактат о гномоне»), приводит вычисления возведения в степень различных чисел. Встречается даже 247933/1460.

В «Цзю чжан суань шу» («Правила счета в девяти разделах») дробь – это часть целого, и выражается в n-ном числе его долей – фэнь – m /n

2. Формулы аликвотных дробей

2.1. Основные операции над аликвотными дробями

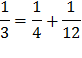
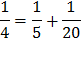
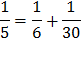
Закономерность :

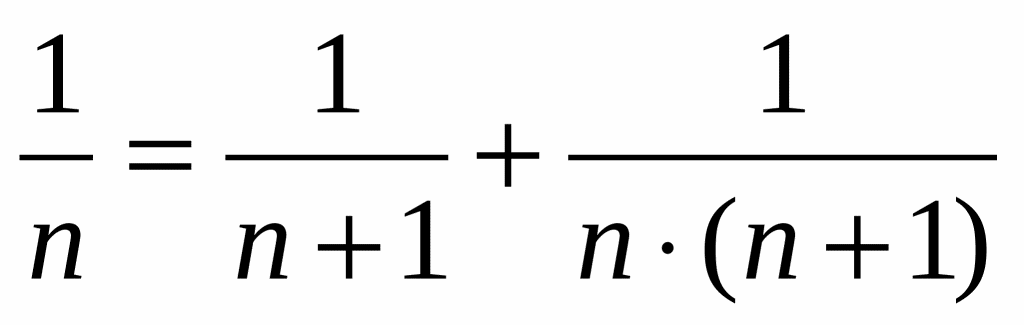
Доказательство:

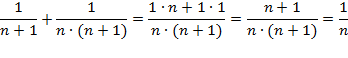
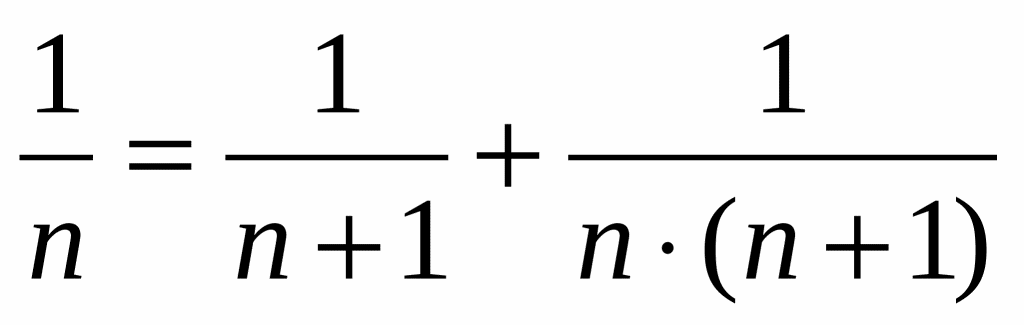
Если числитель дроби больше единицы, то можно поступить так:

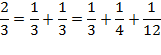
3. Аликвотные дроби на практике

3.1. Действия с аликвотными дробями

Аликвотные дроби можно:

складывать: 1/3+1/5=8/15,

вычитать: 1/2-1/3=1/6,

умножать: 1/5*1/3=1/15,

делить: 1/8:1/4=1/2.

Из этого можно сделать вывод: при выполнении действий с аликвотными дробями не всегда в ответе получается аликвотная дробь.

3.2. Природный звукоряд

Всем известно, что Пифагор был ученым и, в частности, автором знаменитой теоремы. Однако менее известно, что он также был блестящим музыкантом. Именно это сочетание талантов позволило ему первым додуматься о существовании природного звукоряда. Ему еще предстояло доказать это. Для своих опытов Пифагор соорудил полуинструмент-полуприбор под названием "монохорд". Это был продолговатый ящик с натянутой поверх него струной. Под струной, на верхней крышке ящика, Пифагор расчертил шкалу, чтобы легче было зрительно делить струну на части. Пифагор много экспериментировал с монохордом и, наконец, сумел математически описать действие звучащей струны.

Работа Пифагора легла в основу того, что сегодня известно как музыкальная акустика. Семь нот в октаве были признаны столь же естественными для музыки, как десять пальцев в арифметике. Уже тетива самого первого лука, колеблясь после выстрела, издавала тот готовый музыкальный звук, который мы используем почти без изменений по сей день.

С физической точки зрения тетива и струна - это одно и то же. Да, и люди создали струну, обратив внимание на особенностях тетивы. Звучащая струна колеблется не только целиком, но одновременно и половинками, третями, четвертями и т.д. Давайте теперь подойдем к этому явлению с арифметической точки зрения. Половинки колеблются вдвое чаще, чем целая струна, трети — втрое, четверти — вчетверо. Другими словами, во сколько раз меньше колеблющаяся часть струны, во столько же раз больше частота её колебаний. Предположим, что вся струна колеблется с частотой 24 Гц. Если посчитать дробные колебания до шестнадцатых, то получится последовательность чисел, показанная в таблице. Эта последовательность частот так и называется — натуральный, т.е природный, звукоряд.

3.3. Применение аликвотных дробей к решению задач

1.Найдите сумму:

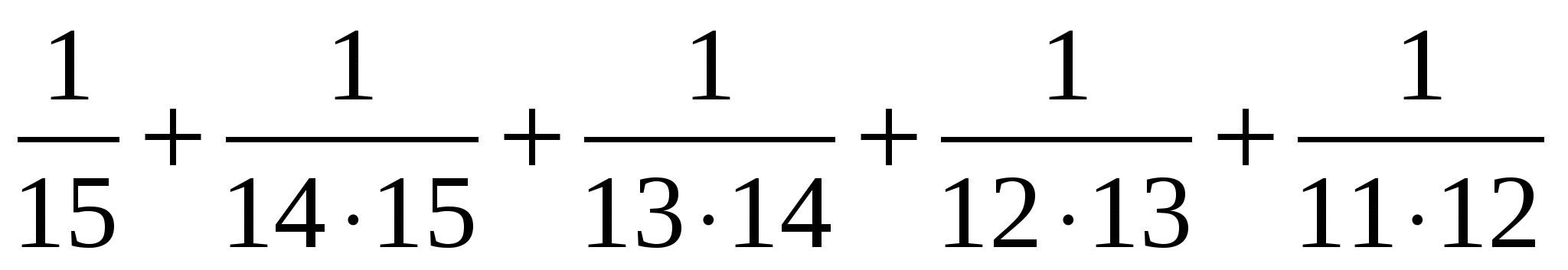
Решение:

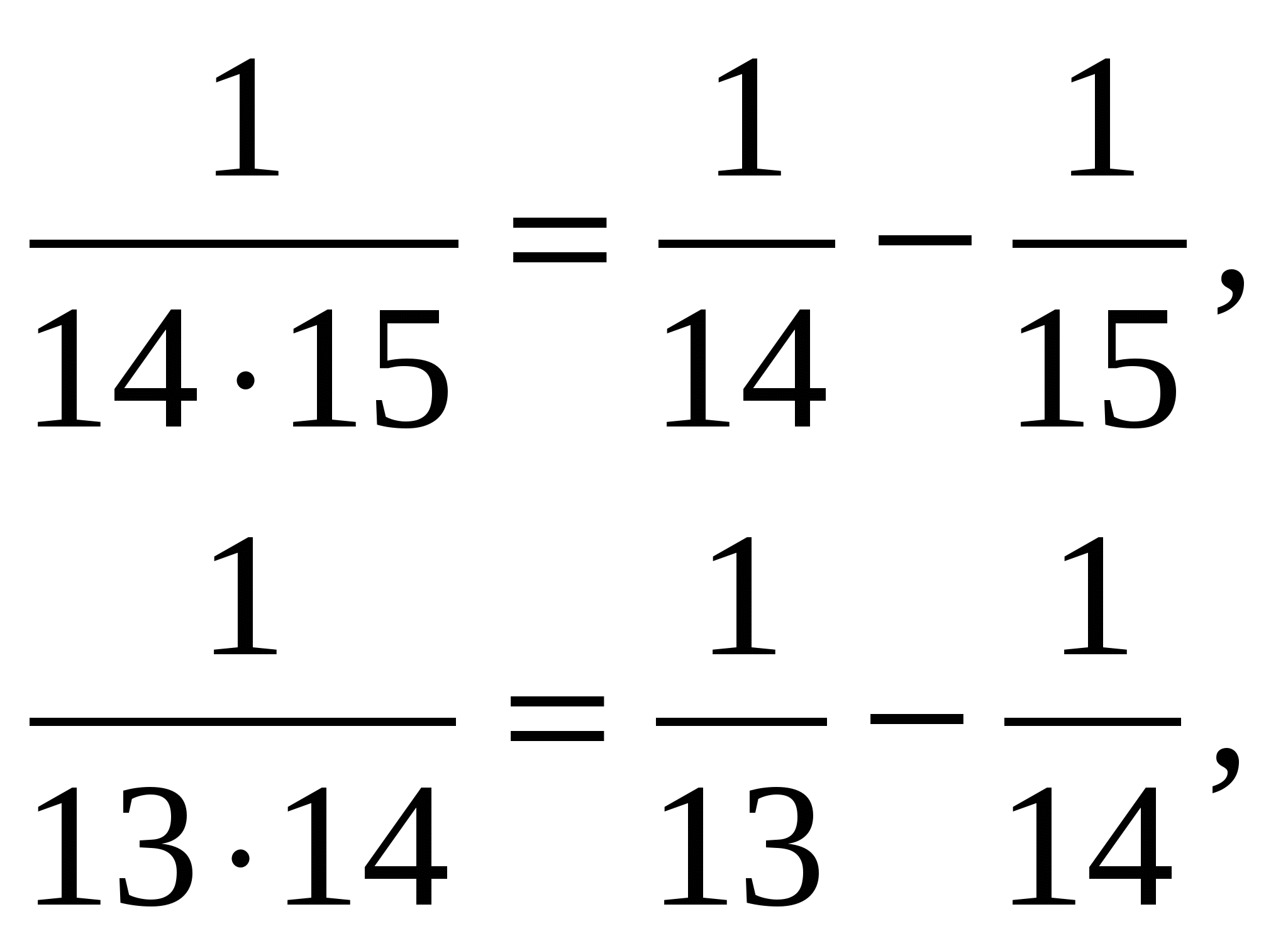
и т. д.

Таким образом получим

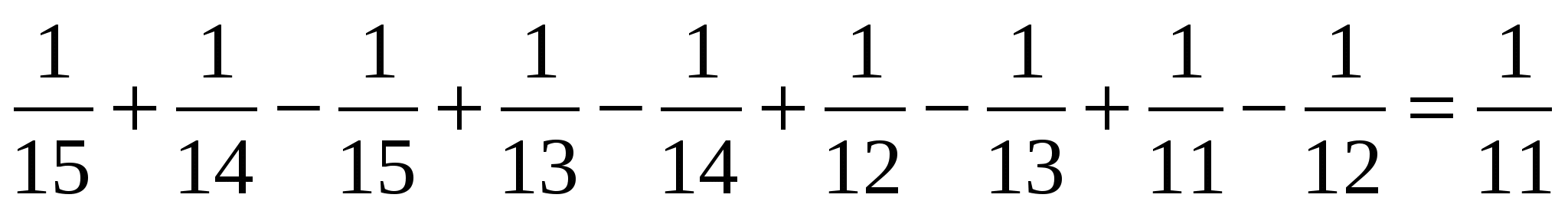
2. Найди сумму:

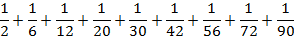
Можно подметить, что знаменатели дробей, можно представить в виде произведения двух последовательных натуральных чисел.

Таким образом:

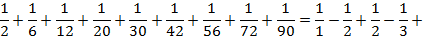
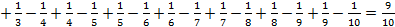
3. Стас принёс в школу 5 яблок. Как разделить их поровну между 12 мальчиками, не разрезая ни одного из них на 12 частей?

Решение:

Каждый должен получить по 5/12 яблока. Но для этого надо разрезать каждое яблоко на 12 частей, что нам не рекомендуют делать.

Поступим так: 5/12 = 3/12 + 2/12 = 1/4 + 1/6, значит, каждое из 3 яблок нужно разделить на 4 части и каждое из 2 яблок - на 6 частей.

4. Коля, Миша и Алик купили 2 дыни. Как, не разрезая каждую дыню на 3 доли, мальчики разделят их поровну?

Решение:

По условию задачи 2 дыни нужно разделить на 3 равные части.

Рассмотрим дробь 2/3

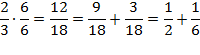
Значит каждому достанется по половине дыни и ещё по 1/6, то есть каждую дыню надо разрезать пополам, взять по половине дыни (3 половины) и четвёртую половину разрезать на 3 равные части.

5. Задача из сказки “1001ночь”:

В знаменитой книге «1001 ночь» мудрец задаёт юной деве следующую задачу:

Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину от того, сколько осталось. Так же она поступила и с третьим стражником, а когда она поделилась яблоками с четвёртым стражником, у неё осталось 10 яблок. Сколько яблок она собрала в саду?

Решение:

Половина всех яблок 1/2, половина половины — 1/4 и так далее, то есть

S = 1/2+1/4+1/8+1/16+1/16.

По условию задачи осталось 10 яблок, поэтому 1/16 = 10 яблокам,

1/8 = 20 яблокам, 1/4 = 40 яблокам, 1/2 = 80 яблокам

тогда S = 80+40+20+10+10= 160(яблок)

Всего было собрано 160 яблок.

Заключение

Изучив и исследовав аликвотные дроби, я узнала, что они являются началом обыкновенных дробей. Научилась складывать и вычитать эти дроби, решать задачи на аликвотные дроби.

Аликвотные дроби часто бывают более удобными при решении задач и используются в окружающем нас мире, в разных областях, не только в математике. В музыке есть понятие аликвотных струн. Аликвотные или резонансные струны – это дополнительные струны, не используемые непосредственно исполнителем, а самовозбуждающиеся от колебания игровых струн. Аликвотные струны служат для обогащения тембра и усиления звучания.

В физике, химии и фармацевтике используется понятие аликвотная доля или аликвота - это точно известная часть раствора.

Я узнала как и где употребляются аликвоты:

1)Аликвотная дробь(математика)

2)Аликвотная струна(музыка)

3)Аликвотная часть(физика и химия)

Моя гипотеза оказалась верной, дроби можно использовать для решения олимпиадных задач.

Список используемой литературы

Бородин А.И. Из истории арифметики. Головное издательство «Ваша школа» - К.,1986.

Гаврилова Т. Д. «Занимательная математика». 5-11 класс. Волгоград. Учитель, 2008 год.

Глейзер Г. И. История математики в школе: IV – VI кл. Пособие для учителей. — М.: Просвещение, 1981.

Материал из Википедии – свободной энциклопедии.

Фомин А. А., Кузнецова Г. М. «Международные математические олимпиады». Москва. ДРОФА, 2006 год.

Энциклопедический словарь юного математика для среднего и старшего школьного возраста. М.: Педагогика,1989

https://ru.wikipedia.org/wiki/Египетские_дроби