Вариант 1 8. Стереометрия
1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.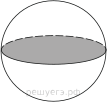
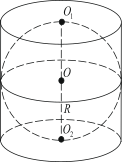
2. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
3. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.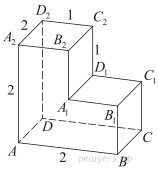
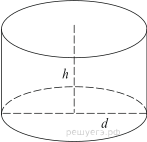
4. Площадь боковой поверхности цилиндра равна  , а диаметр основания — 8. Найдите высоту цилиндра.
, а диаметр основания — 8. Найдите высоту цилиндра.
5. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.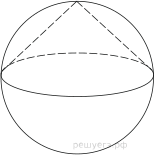
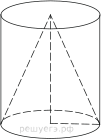
6. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.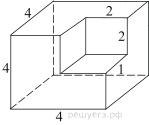
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
8. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?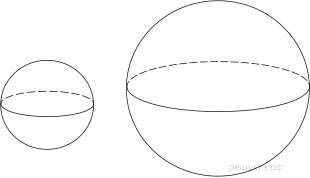
9. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Вариант 2 8. Стереометрия
1. Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.
2. Гранью параллелепипеда является ромб со стороной 4 и острым углом 30°. Одно из ребер параллелепипеда составляет с этой гранью угол в 30° и равно 6. Найдите объем параллелепипеда.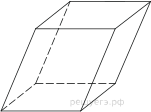
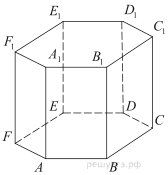
3. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 10.
4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.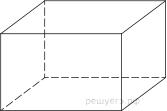
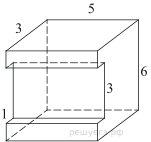
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
6. В правильной четырехугольной пирамиде 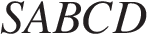 точка
точка  — центр основания,
— центр основания, 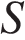 вершина,
вершина,  ,
, 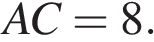 Найдите длину отрезка
Найдите длину отрезка 

7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из ребер параллелепипеда составляет с этой гранью угол в 45° и равно 5. Найдите объем параллелепипеда.

8. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.
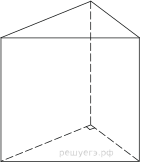
10.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Вариант 3 8. Стереометрия
1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C2C3B2.
2. Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Найдите угол  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

6. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 0,5 и 16. Найдите ребро равновеликого ему куба.
7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 24. Найдите объем пирамиды.
8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.
9. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
10. В прямоугольном параллелепипеде известно, что Найдите длину ребра 
Вариант 4 8. Стереометрия
1. Найдите квадрат расстояния между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. В прямоугольном параллелепипеде известно, что Найдите длину ребра 

3. Площадь боковой поверхности цилиндра равна 18 , а диаметр основания равен 9. Найдите высоту цилиндра.
, а диаметр основания равен 9. Найдите высоту цилиндра.
4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?
5. Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 9, а боковое ребро равно 8.
6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.

7. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.
правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.
8. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π.
9. Диагональ куба равна 13. Найдите площадь его поверхности.
10. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.
Вариант 5 8. Стереометрия
1. Диагональ куба равна 1. Найдите площадь его поверхности.
2. Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.
3. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1.
4. Найдите квадрат расстояния между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
5. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в  раза больше первого? Ответ выразите в см.
раза больше первого? Ответ выразите в см.
6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300  воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см3.
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см3.
7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
8. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны  Найдите объем цилиндра, описанного около этой призмы.
Найдите объем цилиндра, описанного около этой призмы.
9. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны  Найдите объем цилиндра, описанного около этой призмы
Найдите объем цилиндра, описанного около этой призмы
.
10.Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.
Вариант 6 8. Стереометрия
1. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.

2. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
3. Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?

4. Найдите объем многогранника, вершинами которого являются точки  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.
правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.

5. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.

6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
7. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

10. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Вариант 7 8. Стереометрия
1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
2. Найдите объем  части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите 
3. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны  Найдите объем цилиндра, описанного около этой призмы.
Найдите объем цилиндра, описанного около этой призмы.
4. Найдите объем  части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите 
5. Найдите объем  части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите 
6. Найдите объем  части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите 
7. Найдите объем  части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите 
8. Найдите объем  части цилиндра, изображенной на рисунке. В ответе укажите
части цилиндра, изображенной на рисунке. В ответе укажите 
9. Найдите объем  части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите 
10. Найдите объем  части конуса, изображенной на рисунке. В ответе укажите
части конуса, изображенной на рисунке. В ответе укажите 
Вариант 8 8. Стереометрия
1. Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
2. В правильной четырехугольной пирамиде 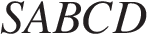 точка
точка  — центр основания,
— центр основания, 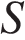 вершина, , Найдите длину отрезка
вершина, , Найдите длину отрезка 
3. В правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
4. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
7. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
8. В правильной треугольной пирамиде медианы основания пересекаются в точке  Объем пирамиды равен
Объем пирамиды равен  ,
,  Найдите площадь треугольника
Найдите площадь треугольника
9. В прямоугольном параллелепипеде известно, что , , Найдите длину ребра 
10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
Вариант 9 8. Стереометрия
1. Найдите расстояние между вершинами  и
и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
2. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
3. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на 
4. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

5. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

6. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

7. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
9. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
Вариант 10 8. Стереометрия
1. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмыABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
2.Высота конуса равна 12, образующая равна 15. Найдите его объем, деленный на 
3. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.
4. В правильной четырехугольной пирамиде 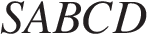 точка О - центр основания,
точка О - центр основания, 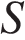 вершина, , Найдите длину отрезка
вершина, , Найдите длину отрезка 
5. В правильной четырехугольной пирамиде 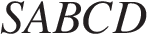 точка
точка  — центр основания,
— центр основания, 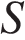 вершина, , Найдите длину отрезка
вершина, , Найдите длину отрезка 
6. ЗВ правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
7. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.
8. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
10. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
| 8. Стереометрия |
| Вариант 1 12 166,5 60 2 28 75 96 27 68 1,25 | Вариант 2 72 24 45 4 130 3 2,5 3 28 10 | Вариант 3 3 60 45 4 152 2 2304 48 29 4 | Вариант 4 29 5 2 27 24 6 4 19,5 338 4704 | Вариант 5 2 24 5 29 4 184 5 125 4 75 |
| Вариант 6 9 45 3375 8 6 1,5 22 110 94 36 | Вариант 7 340 216 4 3,75 144 937,5 14 105 87,75 243 | Вариант 8 81 6 3 2 1 1 1 3 1 5 | Вариант 9 3 30 144 60 3 9 10 1,5 2 28 | Вариант 10 6 324 5 4 6 3 2 1 1 1 |






























