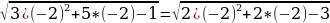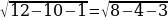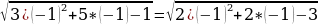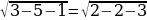МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ШКОЛА №48 ГОРОДА ДОНЕЦКА»

Конспект урока по предмету «Алгебра и начала математического анализа»
для 10 класса
углублённый уровень
Тема: Иррациональные уравнения.
Методы решения иррациональных уравнений.
Автор: учитель математики
Смолякова Юлия Леонидовна Класс:10 Дата: 17.11.2023 Предмет: Алгебра и начала математического анализа Тема: Иррациональные уравнения. Методы решения иррациональных уравнений.
Цели урока: ввести понятие «Иррациональное уравнение», изучить методы решения иррациональных уравнений.
Задачи урока:
Образовательные:
- ввести понятие иррациональных уравнений;
- открыть правило решения иррациональных уравнений;
- показать оформление решения;
- формирование умения решать иррациональные уравнения.
Развивающие:
- развитие умения правильно оперировать полученными знаниями, логически мыслить;
- развитие интеллектуальных умений и мыслительных операций – анализ, синтез, сравнение и обобщение;
- развитие инициативы, умение принимать решения, не останавливаться на достигнутом;
- развитие критического мышления;
- развитие навыков исследовательской деятельности.
Воспитательные:
- воспитание познавательного интереса к предмету;
- воспитание самостоятельности при решении учебных задач;
- воспитание воли и упорства для достижения конечных результатов.
Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.
Учебник: Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа, 10-11 классы/ Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и другие, Акционерное общество «Издательство «Просвещение»-2023
Оборудование: компьютер, графический планшет, презентация, учебник.
Продолжительность занятия: 45 минут.
Ход занятия
На доске написаны уравнения. Посмотрите на них внимательно. Распределите их на три группы и назовите каждую группу. Можно ли, не решая уравнения третьей группы, сделать вывод о неразрешимости предложенных уравнений.
2х-1=3 2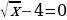 19х-3х+4х=80 х2+4х+4=0 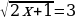 | (х-1)(х+1)=8 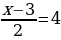 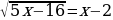 х2-2√3х+3=0 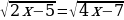 |
| I группа 2х-1=3 19х-3х+4х=80 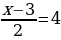 | II группа х2+4х+4=0 (х-1)(х+1)=8 х2-2√3х+3=0
| III группа 2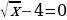 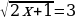 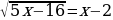 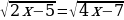 |
-Дайте название уравнениям I группы (линейные).
-Дайте название уравнениям II группы (квадратные).
-Дайте название уравнениям III группы (?).
-Что объединяет уравнения III группы? (Переменная содержится под знаком квадратного корня.)
Уравнения, в которых переменная содержится под знаком квадратного корня, называются иррациональными уравнениями.
- Как вы думаете, что мы будем изучать сегодня на уроке?
- Сформулируйте тему урока. (Иррациональные уравнения).
Повторение теоретического материала по теме.
Работа с презентацией к уроку. Обучающиеся дают ответы на вопросы, представленные на слайдах.
А сейчас мы повторим основной теоретический материал, который понадобится нам для изучения новой темы. Ответьте пожалуйста, на следующие вопросы:
Что такое уравнение? (равенство с переменной или переменными)
Что значит решить уравнение? (найти все его корни или убедиться, что их нет)
Что такое корень уравнения? (значение переменной, которое при подстановке его в исходное равенство обращает его в верное числовое равенство)
Дайте определение квадратного корня из неотрицательного числа. (квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а. на доске 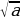 =b, b≥0 и b2=a)
=b, b≥0 и b2=a)
Укажите способ решения линейных уравнений. (все с неизвестными перенести в левую часть уравнения, все числа в правую. Привести подобные слагаемые. Найти неизвестный множитель)
Укажите способы решения квадратных уравнений. (выделение полного квадрата, по формулам, используя теорему, обратную т. Виета, графический)
Какие свойства используются при решении уравнений? (1. Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному; 2. Если обе части «*» или «:» на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.)
3) Объяснение нового материала.
Итак, мы все очень хорошо повторили, а теперь вернемся к теме урока.
-Сможете ли вы теперь из множества всех уравнений выделить иррациональные уравнения?
-Что будет отличать их от остальных уравнений?
-А зачем нам надо изучать иррациональные уравнения? Ведь жили мы без них спокойно.
- Иногда реальные ситуации представляют собой иррациональное уравнение, например, мы с ними встретились, когда находили длину стороны прямоугольного треугольника используя теорему Пифагора.
Я вам более того скажу, эта тема настолько важная, что ее изучают и в старшей школе, и иррациональные уравнения вынесены на ЕГЭ.
Слайд
Какие уравнения не являются иррациональными?(устно)
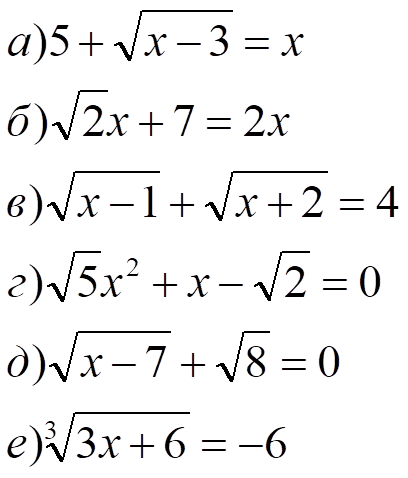
Решить в тетрадях и на доске уравнение № 1
2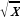 - 4=0,
- 4=0,
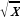 =2,
=2,
х=22 , (по определению квадратного корня)
х=4.
Ответ: 4
-Какое иррациональное уравнение можно попробовать решить, используя определение квадратного корня?
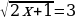 ,
,
2х+1=9,
х=4.
Ответ: 4.
-Давайте убедимся, что полученное число действий является корнем уравнения. Как это сделать? (выполнить проверку)
Проверка: 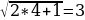 ,
,
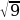 =3;
=3;
 3=3 – верно.
3=3 – верно.
Ответ: 4.
Теперь попытайтесь решить уравнение № 3.
| 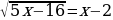 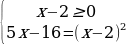 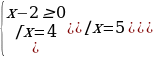 | 5х-16=(х-2)2 5х-16=х2-4х+4 х2-9х+20=0 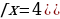 (по теореме обратной (по теореме обратной 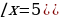 т. Виета) т. Виета)
|
-Можем ли мы дать ответ? В чем трудность?
-Проблема в том, что мы пока не умеем решать уравнения.
-А как убедиться, что найденные числа являются корнями?
-Сделать проверку. Сделайте проверку и запишите ответ.
Ответ: 4; 5.
Работа с презентацией. Разбор методов решения иррациональных уравнений.

-У нас остался не разобранным пример № 4.
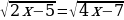
-Знает кто-нибудь способ решения?
Если учащиеся затрудняются, то спросить, как можно освободиться от знака квадратного корня? (возведением в квадрат)
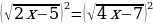
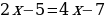
2х=2
х=1
Проверка: 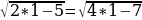
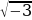 =
=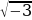 – не имеет смысла.
– не имеет смысла.
-В подобных случаях говорят, что х=1 – посторонний корень. Поэтому уравнение не имеет корней.
Ответ: корней нет.
Метод, который мы использовали, называется возведением в квадрат обеих частей уравнения. Это основной метод решения иррациональных уравнений. Он не сложен, но иногда приводит к неприятностям, как в предыдущем примере. Поэтому проверку выполнять обязательно.
Фактически решая примеры № 1- № 3 мы применяли этот метод.
Попробуйте сформулировать правило решения иррациональных уравнений, которые мы изучили сегодня на уроке.
С помощью учащихся составить алгоритм решения иррациональных уравнений.
Возведи обе части уравнения в нужную степень.
Решаем полученное уравнение
2.Сделай проверку.
Изучение дополнительных методов решения иррациональных уравнений 
Первичное осмысление нового материала.
Подробный разбор методов решения иррациональных уравнений, выводы о преимуществах и недостатках каждого из них.
Способ I. Метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой
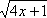
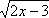 + =4,
+ =4,
возведем обе части уравнения в квадрат.
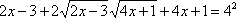 ,
,
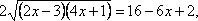
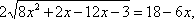
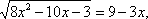
возведем обе части уравнения в квадрат.
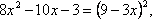
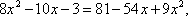
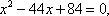
По теореме Виета:
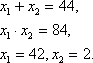
Проверка:
Если х=42, то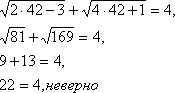
Значит, число 42 не является корнем уравнения.
Если х=2, то
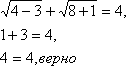
Значит, число 2 является корнем уравнения. Ответ: 2
| Достоинства | Недостатки |
| 1. Понятно | 1. Словесная запись |
| 2. Доступно | 2. Громоздкая проверка иногда занимает много времени и места |
Вывод: При решении иррациональных уравнений методом возведения обеих частей уравнения в одну и туже степень необходимо вести словесную запись, что делает решение понятным и доступным. Однако обязательная проверка иногда бывает громоздкой и занимает много времени. Этот метод можно использовать для несложных иррациональных уравнений, содержащих 1-2 радикала.

Способ III. Метод введения новых переменных
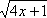
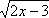 + =4.
+ =4.
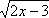
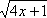 Введем новые переменные, обозначив =а, =b. Получим первое уравнение системы: a+b=4.
Введем новые переменные, обозначив =а, =b. Получим первое уравнение системы: a+b=4.
Составим второе уравнение системы: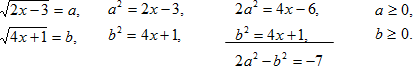
Получим систему двух рациональных уравнений, относительно а и b:
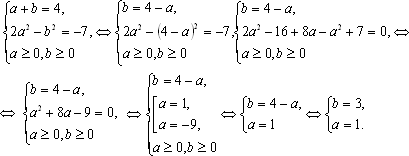
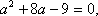
по теореме Виета: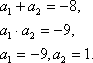
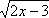
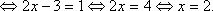 Вернемся к переменной х: =1 Ответ: 2.
Вернемся к переменной х: =1 Ответ: 2.
| Достоинства | Недостатки |
| 1. Этот метод для данного уравнения | 1.Словесное описание. |
| не рационален. | 2. Громоздкое решение. |
Вывод: Метод введения новых переменных и переход к системе рациональных уравнений для данного уравнения не рационален. Этот метод лучше применять для иррациональных уравнений, содержащих радикалы различных степеней, или одинаковые многочлены под знаком корня и за знаком корня, или взаимообратные выражения под знаками корня.
Способ II. Разложение на множители (метод равносильных преобразований)
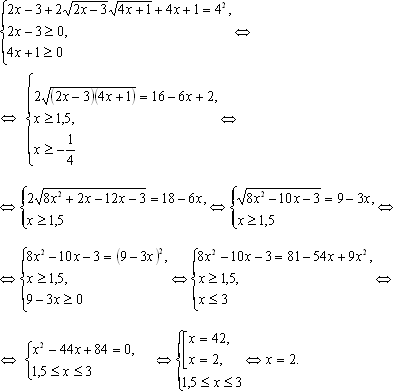
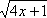
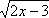 + =4
+ =4
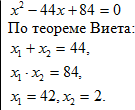
Ответ: 2.
| Достоинства | Недостатки |
| 1. Отсутствие словесного описания | 1. Громоздкая запись |
| 2. Нет проверки | 2. Можно ошибиться при комбинации знаков системы и совокупности и получить неверный ответ |
| 3. Четкая логическая запись |
| 4. Последовательность равносильных переходов |
|
Вывод: При решении иррациональных уравнений методом равносильных переходов нужно четко знать, когда ставить знак системы, а когда совокупности. Громоздкость записи, различные комбинации знаков системы и совокупности не редко приводят к ошибкам. Однако, последовательность равносильных переходов, четкая логическая запись без словесного описания, не требующая проверки, являются бесспорными плюсами данного способа.
Итоги: Для каждого иррационального уравнения необходимо выбирать наиболее рациональный способ решения: понятный, доступный, логически грамотно оформленный.
Самостоятельная работа:
Решить уравнения:
I вариант II вариант
Учащиеся выполняют самостоятельно. Затем самопроверка: ответы и решение записано на доске.
Сделайте задание другого варианта.
| I вариант | II вариант |
|
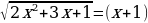 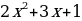 = = 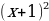 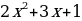 = х2+2х+1 = х2+2х+1 х2+х=0 х(х+1)=0 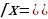 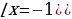 Проверка: 1) х = 0:
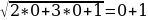 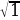 = 1 = 1
1 = 1 - верно. 2) х = -1: 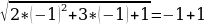
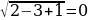
0 = 0 – верно. Ответ: -1; 0. |
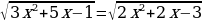 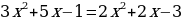 х2+3х+2=0 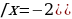 (по теореме обратной (по теореме обратной 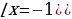 т. Виета) т. Виета) Проверка: 1) х = -2:
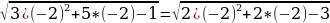 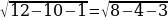
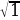 = = 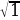 - верно. - верно.
2) х = -1: 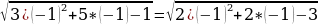
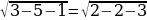
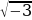 = =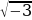 – не имеет смысла. – не имеет смысла. Ответ: -2. |
5. Рефлексия.
Обучающимся предлагается закончить одно из предложений на слайде: Мне сегодня удалось (понять, разобраться, уяснить, осознать)…
Теперь я умею…
Самым интересным было … Труднее всего было…
Домашнее задание.
1. Прочитать § 9 из учебника
2. Решить в тетрадях № 156,158(2-4)







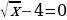
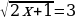
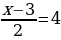
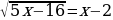
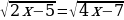
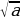 =b, b≥0 и b2=a)
=b, b≥0 и b2=a)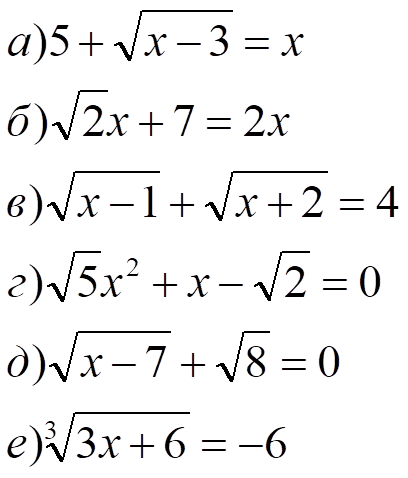
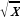 - 4=0,
- 4=0,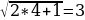 ,
,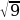 =3;
=3; 3=3 – верно.
3=3 – верно.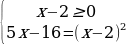
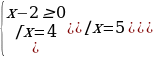
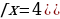 (по теореме обратной
(по теореме обратной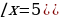 т. Виета)
т. Виета)
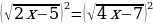
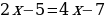
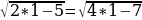
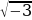 =
=
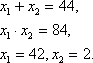
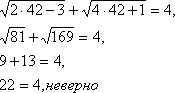
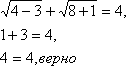
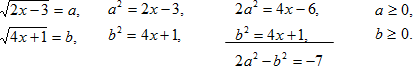
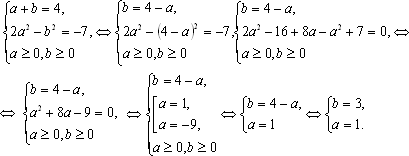
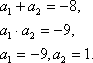
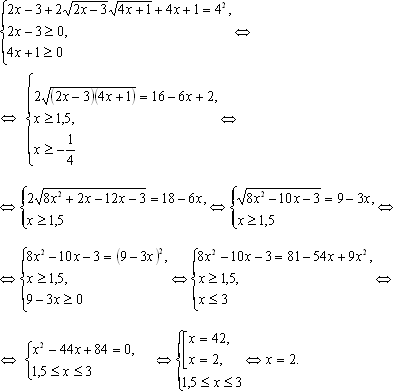
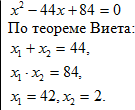
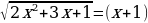
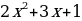 =
= 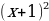
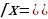
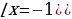
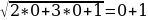
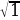 = 1
= 1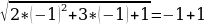
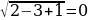
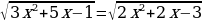
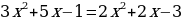
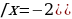 (по теореме обратной
(по теореме обратной