Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа – детский сад № 37 имени партизана-подпольщика И.Г. Генова» муниципального образования городской округ Симферополь Республики Крым
Методическая разработка урока
По алгебре в 10 классе на тему:
Решение упражнений по теме «Синус, косинус, тангенс, котангенс»
Подготовила и провела
учитель математики
Морозова В.А.
2022/2023 учебный год
Цели урока:
Образовательные: ввести понятие тригонометрических функций синуса, косинуса, тангенса и котангенса, как координат точки единичной окружности; определить множество значении этих функций; рассмотреть перевод градусной меры измерения улов в радианную меру и наоборот; сформировать умение определять знаки тригонометрических функций; рассмотреть зависимости между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента; научить находить значения тригонометрических функций по тригонометрической окружности выполнять действия с тригонометрическими функциями.
Развивающие: развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки.
Воспитательные: воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.
Тип урока: комбинированный.
Форма работы: фронтальная.
Методы обучения: диалогическое изложение материала с использованием ИКТ.
Оборудование: компьютер, мультимедийный проектор, раздаточный материал, презентация к уроку.
Ход урока
I. Организационный момент.
II. Активизация знаний.
С этим разделом математики вас познакомили учителя на уроках геометрии при изучении отношений между сторонами и углами в прямоугольном треугольнике.
Давайте вспомним: какие понятий связывают стороны и острые углы прямоугольного треугольника?
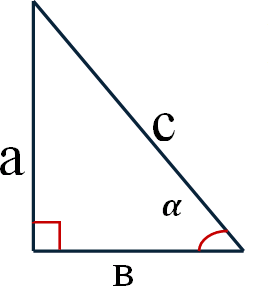
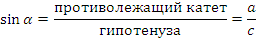
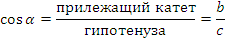
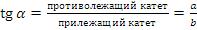
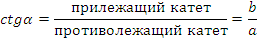
Итак, синус, косинус, тангенс и котангенс – это некоторые числа. Причем для каждого угла свои и их значение зависит только от величины угла.
Также вам уже известно, что синус, косинус, тангенс и котангенс называют тригонометрическими функциями, и мы можем их найти по величине угла или наоборот найти величину угла, если нам известно значение одной из этих функций. Для этого существуют специальные таблицы Брадиса. Правда, в настоящее время мы обращаемся к ним редко, а скажите почему?
III. Изложение нового материала.
Сегодня на уроке мы продолжим изучать эти тригонометрические функции, а также познакомимся с тригонометрической окружностью, рассмотрим понятие этих функций с помощью окружности, научимся находить по ней значения функций, их знаки, вспомним основные тригонометрические тождества и разберем, как их применять для решения задач.
Обратимся к нашему треугольнику и вспомним теорему Пифагора. Радиус единичной окружности - это гипотенуза треугольника, а ее катеты равны соответственно 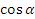 и
и 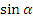 . Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством:
. Тогда применяя теорему Пифагора (квадрат гипотенузы прямоугольного треугольника равен сумме квадратов ее катетов) получаем равенство, называемое основным тригонометрическим тождеством: 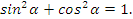
А сейчас давайте разберемся, как нам определять знаки тригонометрических функций. Это не сложно. Знаки тригонометрических функций соответствуют знакам координат точки единичной окружности. Координатные оси разбивают всю координатную плоскость и окружность на четыре координатные четверти. Нумерация четвертей совпадает с началом движения точки 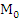 по окружности в положительном направлении, то есть против часовой стрелки. (далее указываем по рисунку номера четвертей). Границы наших четвертей: от точки
по окружности в положительном направлении, то есть против часовой стрелки. (далее указываем по рисунку номера четвертей). Границы наших четвертей: от точки 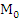 – это
– это 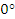 до
до 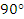 , от
, от 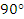 до
до 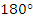 , от
, от 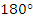 до
до 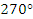 , от
, от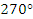 до
до 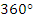 .
.
Определим знаки тригонометрических функций в каждой четверти, для этого заполним таблицу:
|
| I | II | III | IV |
| 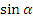
| + | + | - | - |
| 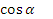
| + | - | - | + |
| 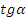
| + | - | + | - |
| 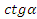
| + | - | + | - |
Вы уже знаете, что величины углов могут измеряться в радианной мере и градусной мере. А. А это означает, что вы должны уметь переходить от радианной меры измерения угла к градусной.
Углом в 1 радиан это центральный угол, который опирается на дугу, равную радиусу. Длина окружности равна: 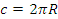 . То есть в нашей окружности помещается ровно два пи дуг длина которых равна радиусу и значит, во всей нашей окружности помещается два пи углов в один радиан. Вся окружность равна
. То есть в нашей окружности помещается ровно два пи дуг длина которых равна радиусу и значит, во всей нашей окружности помещается два пи углов в один радиан. Вся окружность равна  . Значит,
. Значит,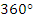 соответствует
соответствует 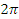 радианам, а
радианам, а 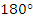 соответствует
соответствует 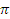 радиан.
радиан.
При переходе от радианной меры к градусной и наоборот проще всего использовать это соотношение: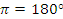 .
.
Вы должны находить значение тригонометрических функций по известному значению одной из них. Например, найти чему будет равен косинус, тангенс или котангенс какого-то угла, если синус этого же угла принимает такое-то значение. Для этого надо знать формулы, которые связывают известную и неизвестную величины. В тригонометрии их называют тригонометрические тождества.
Вот основные из них: это основное тригонометрическое тождество, мы его с вами вывели ранее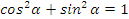 вместе с вот этим формулами:
вместе с вот этим формулами: 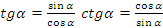 . А вот эти три тождества вытекают из предыдущих:
. А вот эти три тождества вытекают из предыдущих:
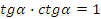
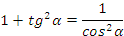
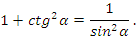
IV Первичное закрепление материала.
Мы рассмотрели тригонометрические функции, но еще Жан Жак Руссо говорил, что час работы научит больше, чем день объяснения. Значит, пора переходить к решению упражнений. Но перед этим давайте еще раз коротко обговорим, какие новые знания мы сегодня получили и должны запомнить. Проведем блиц опрос по рассмотренному материалу.
Устная работа (повторение теории). Вопросы для учащихся.
Какие тригонометрические функции мы рассматривали?
Как определяют функцию синус, косинус, тангенс, котангенс?
На какой оси находятся значения синуса, косинуса, тангенса котангенса?
В каких пределах может изменяться значение синуса, косинуса, тангенса и котангенса?
В какой четверти косинус больше 0, синус отрицателен, тангенс положителен, а котангенс меньше нуля?
Что необходимо знать, чтобы определить знак функции?
Какое направление считается положительным, а какое отрицательным?
В каких единицах может выражаться угол?
Как выполнить переход от радианной меры к градусной и наоборот?
V. Решение упражнений.
Работа по решению упражнений идет у доски с вызовом учащихся и на местах. Каждое задание отображено на слайде:
1 задание:
а) 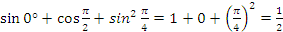
б) 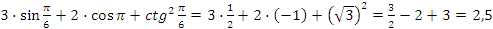 .
.
2 задание: текст задания дан на слайде презентации: найдите знак произведения:
а) 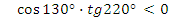
б) 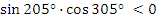
в) 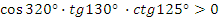
г) 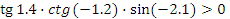
3 задание: № 8.21 (а) по учебнику.
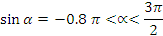
Найдите: 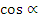 ,
, 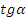 ,
, 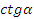 .
.
Решение.
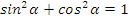
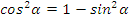
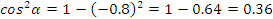
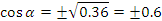
Так угол лежит в 3 четверти, то
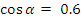
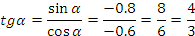
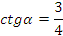
Ответ: 0,6 ; ;
;  .
.
VI. Домашнее задание. Задание на дом вывести на слайд презентации: по учебнику № 8.20 (а и в), № 8.22 (г), № 8.24 (в и г
VII. Рефлексия.
Подвести итоги урока, проведя беседу с учащимися по вопросам: что узнали, что решали?


















