Конспект урока по геометрии в 10 классе "Многогранники вокруг нас"

Урок-конференция

"Многогранники вокруг нас" (10-й класс)

Цели урока:

показать учащимся “мир в целом”, преодолев разобщенность научного знания по дисциплинам;

способствовать систематизации знаний об основных видах многогранников, показать их применение в других видах деятельности;

способствовать формированию и развитию эвристического мышления;

способствовать развитию самостоятельности и творчества, расширению кругозора, проявлению личностных качеств и способностей, обогащению межличностных отношений.

Методы обучения: словесный, наглядный, деятельностный

Средства обучения:

(в том числе технические средства обучения)

Компьютер, мультимедийный проектор, экран.

Для каждого ученика существенное значение имеют такие личностные качества и способности, как самостоятельность, практическая направленность и гибкость мышления, творческое решение практических задач, способность оперативно находить, подбирать и целенаправленно использовать необходимую информацию в практической работе.

Воспитанию и развитию таких качеств и способностей у учащихся в значительной мере содействует их участие в творческой деятельности.

Подготовка реферата способствует всестороннему знакомству с литературой по избранной теме, создает возможность комплексно использовать приобретенные навыки работы с источниками, развивает самостоятельность мышления, умение на научной основе анализировать явления деятельности и делать выводы. Реферат является одной из форм углубленного изучения первоисточников, применения полученных знаний к анализу.

Доклад позволяет приобщить учащихся к самостоятельной работе, учит его говорить перед аудиторией, что является полезным навыком для любого взрослого человека. Подготовка и чтение доклада ставят ученика на место преподавателя, наглядно демонстрируют некоторые особенности преподавательской работы.

Содержание урока:

I. Вступительное слово учителя.

Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. “Правильных многогранников так мало, - написал когда-то Л. Кэрролл, - но это весьма скромный по численности отряд сумел пробраться в самые глубины различных наук”.

Сегодня на уроке мы поговорим о многогранниках, а точнее о том какие многогранники называются правильными, где встречаются многогранники в природе. А так же услышим мнения ученых древности об использовании многогранников.

Урок помогли подготовить ученики 10 класса:

1 ученик- биолог

Два ученика- археологи

1 ученик- историк

1 ученик- математик

которые методом самостоятельного поиска материала по данной теме, фотографий с достопримечательностями города Саранска рассмотрели все виды многогранников, а также показали их применение в других видах деятельности.

Они не только сумели рассмотреть все виды многогранников, но и выполнили творческую работу – создали мультимедийную презентацию.

Учащиеся разбились на четыре группы: “историки”, “математики”, “биологи”, “архитекторы”.

“Математики” исследовали тему с математической точки зрения, “историки” связали тему с историей математики и сакральной геометрией, “биологи” нашли связь многогранников с природой, “архитекторы” подготовили фотовыставку с достопримечательностями города Саранска

II. Выступление группы “Математики”

Группа “математиков” вводит определение правильных многогранников,

Рассматривают признаки многогранников. Демонстрирует их модели, дают характеристику, каждого многогранника.

Многогранник называется правильным, если он выпуклый, все его грани равны друг другу и в вершине находится одинаковое количество ребер.

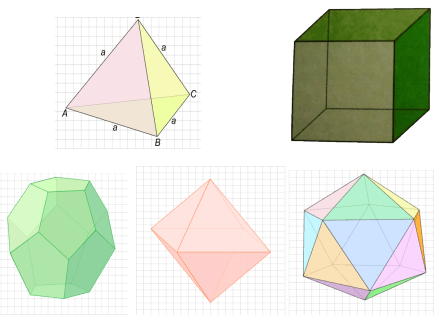
Мы уже знаем 5 примеров правильных многогранников:

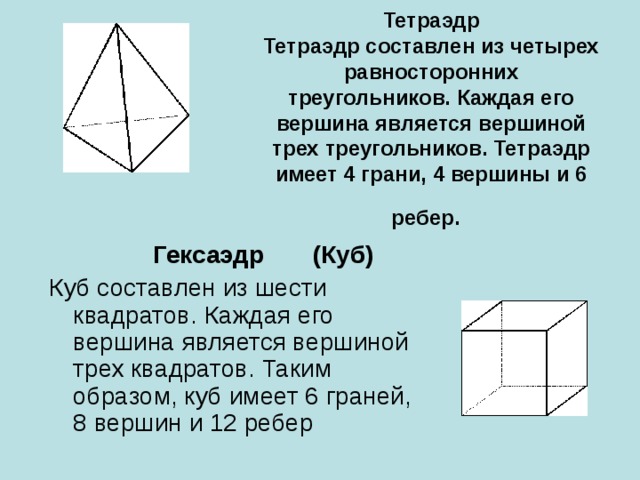
правильный тетраэдр;

куб или правильный гексаэдр;

правильный октаэдр;

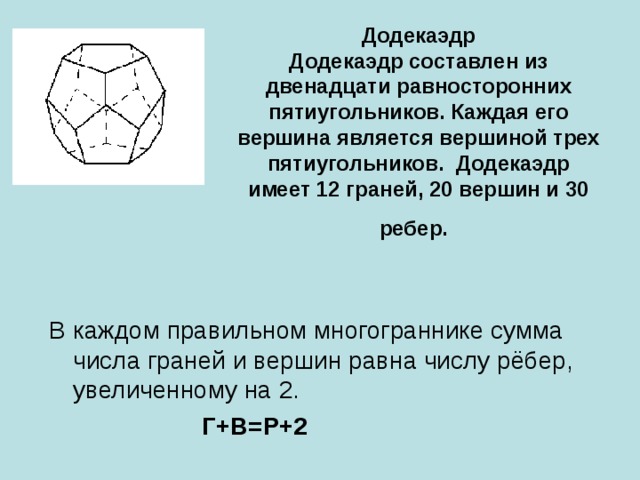
правильный додекаэдр;

правильный икосаэдр

Доказывают существование только пяти правильных многогранников, Cлайд№10

Каково же это вызывающе малое количество и почему их именно столько. А сколько? Оказывается, ровно пять - ни больше, ни меньше. Подтвердить это можно с помощью развертки выпуклого многогранного угла. В самом деле, для того чтобы получить какой-нибудь правильный многогранник согласно его определению, в каждой вершине должно сходиться одинаковое количество граней, каждая из которых является правильным многоугольником. Сумма плоских углов многогранного угла должна быть меньше 360, иначе никакой многогранной поверхности не получится. Перебирая возможные целые решения неравенств: 60к ̊, 90 ̊ ̊ и 108 ̊ ̊, можно доказать, что правильных многогранников ровно пять (к - число плоских углов, сходящихся в одной вершине многогранника)

Итак, было выяснено, что правильных многогранников ровно пять. А как определить в них количество ребер, граней, вершин? Это нетрудно сделать для многогранников с небольшим числом ребер, а как, например, получить такие сведения для икосаэдра? Знаменитый математик Л. Эйлер получил формулу В+Г-Р=2, которая связывает число вершин В, граней Г и ребер Р любого многогранника. Простота этой формулы заключается в том, что она не связана ни с расстоянием, ни с углами. Для того чтобы определить число ребер, вершин и граней правильного многогранника, найдем сначала число к=2у - ху+2х, где х - число ребер, принадлежащих одной грани, у - число граней, сходящихся в одной вершине. Для нахождения количества граней, вершин и ребер правильного многогранника используем формулы. После этого нетрудно заполнить таблицу, в которой приведены сведения об элементах правильных многогранников:

Рассматривают теорему Эйлера и заполняют таблицу свойств правильных многогранников. Cлайд№11-12

III. Выступление группы “Историки”

Названия правильных многогранников пришли из Греции. В дословном переводе с греческого "тетраэдр", "октаэдр", "гексаэдр", "додекаэдр", "икосаэдр" означают: "четырехгранник", "восьмигранник", "шестигранник". "двенадцатигранник", "двадцатигранник". Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии". Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх. Икосаэдр - воду, т.к. он самый "обтекаемый. Куб - землю, как самый "устойчивый. Октаэдр - воздух, как самый "воздушный". Пятый многогранник, додекаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным. Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы "стихий" настраивались Платоном в совершенных консонансах, как четыре струны лиры. Консонансом называется приятное созвучие. Надо сказать, что своеобразные музыкальные отношения в Платоновых телах являются чисто умозрительными и не имеют под собой никакой геометрической основы. Этими отношениями не связаны ни число вершин Платоновых тел, ни объемы правильных многогранников, ни число ребер или граней. В связи с этими телами уместно будет сказать, что первая система элементов, включавшая четыре элемента - землю, воду, воздух и огонь, - была канонизирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течение многих веков. Вполне возможно отождествить их, с известными нам, четырьмя состояниями вещества - твердым, жидким, газообразным и плазменным. Важное место занимали правильные многогранники в системе гармоничного устройства мира И. Кеплера. Все та же вера в гармонию, красоту и математически закономерное устройство мироздания привела И. Кеплера к мысли о том, что поскольку существует пять правильных многогранников, то им соответствуют только шесть планет. По его мнению, сферы планет связаны между собой вписанными в них Платоновыми телами. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором будет находиться Солнце. Проделав огромную вычислительную работу, в 1596 г. И. Кеплер в книге "Тайна мироздания" опубликовал результаты своего открытия. В сферу орбиты Сатурна он вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера Меркурия. Тайна мироздания кажется открытой. Сегодня можно с уверенностью сказать, что расстояния между планетами не связаны ни с какими многогранниками. Впрочем, возможно, что без "Тайны мироздания", "Гармонии мира" И. Кеплера, правильных многогранников не было бы трех знаменитых законов И. Кеплера, которые играют важную роль в описании движения планет.

IV. Выступление группы “Биологи”

Где еще можно увидеть эти удивительные тела? В очень красивой книге немецкого биолога начала нашего века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".

В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН4, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

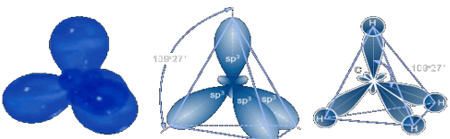
Задача.

Модель молекулы метана CH4 имеет форму правильного тетраэдра, в четырех вершинах которого находятся атомы водорода, а в центре - атом углерода. Определить угол связи между двумя СН связями.

Решение.

Так как правильный тетраэдр имеет шесть равных ребер, то можно подобрать такой куб, чтобы диагонали его граней были ребрами правильного тетраэдра (рис.2). Центр куба является и центром тетраэдра, ведь четыре вершины тетраэдра являются и вершинами куба, а описываемая около них сфера однозначно определяется четырьмя точками, не лежащими в одной плоскости. Искомый угол j между двумя СН связями равен углу АОС. Треугольник АОС- равнобедренный. Отсюда , где а - сторона куба, d- длина диагонали боковой грани или ребро тетраэдра. Итак, , откуда =54,73561О и j= 109,47О .

Создания природы, приведенные в этой книге, красивы и симметричны. Это неотделимое свойство природной гармонии. Но здесь видно и одноклеточные организмы - феодарии, форма которых точно передает икосаэдр. Чем же вызвана такая природная геометризация? Может быть, тем, что из всех многогранников с таким же количеством граней именно икосаэдр имеет наибольший обьем и наименьшую площадь поверхности. Это геометрическое свойство помогает морскому микроорганизму преодолевать давление водной толщи.

Интересно и то, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус.

Оказалось, что только один многогранник дает точно такую же тень - икосаэдр. Его геометрические свойства, о которых говорилось выше, позволяют экономить генетическую информацию.

Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли NaCl, монокристалл алюминиево-калиевых квасцов (KAlSO4)2 12Н2О имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьменистый сернокислый натрий - тетраэдра, бор - икосаэдра. Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.

Идеи Пифагора, Платона, И. Кеплера о связи правильных многогранников с гармоничным устройством мира уже в наше время нашли свое продолжение в интересной научной гипотезе, авторами которой (в начале 80-х годов) явились московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла,

оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли , проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Их 62 вершины и середины ребер, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления.

В трехмерном пространстве деления сферы ведут к созданию пяти правильных многогранников, так называемых пяти тел Платона. Формы Платона связаны с человеческим телом и природой сознания, раскрытие которой ведет не только к понимание интеллекта Вселенной, но и к эмпирическому восприятию Бога, даруя ощущение глубокой всеобщей взаимосвязи элементов бытия. Здесь особую роль играет число 5. Оно связано с зарождением жизни на земле и в то же время с бессмертием.

Первичные многоугольники и многогранники — фундаментальные образцы творения, представляющие творческие силы самоорганизации, которые формируют и определяют мир. Все в природе может быть описано в терминологии математических принципов, которые свойственны этим формам.

Какую форму могло бы иметь первое творение? Каковы изначально сотворенные объемные формы? Существует пять таких творений, которые являются наиболее существенными, потому что они — единственные тела, у которых все грани и все внутренние углы равны. Это тетраэдр, октаэдр, куб, додекаэдр и икосаэдр; производные от треугольника, квадрата и пятиугольника; воплощение чисел 3, 4 и 5. Все другие тела представляют собой только модификации эти пяти.

V. Выступление группы “Архитекторы”

Цели исследования Познакомиться с яркими примерами применения многогранников в архитектуре города Саранска.

Гипотеза исследования

Какую роль могут играть многогранники при проектировании и построении таких архитектурных сооружений как церкви и небоскребы?

Проблемные вопросы

Каким образом форма многогранника нашла приложение в архитектуре?

Многогранники вокруг нас или мы внутри многогранника? Группа “архитекторов” подготовила фотовыставку с достопримечательностями города Саранска.

Итог урока

Мы с вами рассмотрели: что называют правильными многогранниками и сколько их существует; где встречаются многогранники, для чего мы их изучаем. А также узнали исторические предположения о применении правильных многогранниках. Я думаю, каждый из вас для себя сделает выводы в области математики, насколько она близка с нами, как важно ее изучать.

МОУ»Зыковская общеобразовательная школа»

МНОГОГРАННИКИ ВОКРУГ НАС

Урок-конференция по геометрии в 10 классе

Подготовила учитель математики

Боронахина И.И.

2011-2012 у.г.

Многогранники в биологии

Выполнила: Балашова Ж.И.

Ученица 10 класса

Проверила: Боронахина И.И.

Многогранник  - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника

В очень красивой книге немецкого биолога начала нашего века Э. Геккеля "Красота форм в природе" можно прочитать такие строки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы". В молекуле метана, который удается очень точно измерить в эксперименте, а поскольку ни один атом водорода в молекуле СН4, очевидно, ничем не выделен, то разумно предположить, что эта молекула имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного микроскопа.

    Скелет одноклеточного организма  феодарии ( Circjgjnia icosahtdra ) по форме напоминает икосаэдр. Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. 

Водоросль вольвокс — один из простейших многоклеточных организмов — представляет собой сферическую оболочку, сложенную в основном семиугольными, шестиугольными и пятиугольными клетками (то есть клетками, имеющими семь, шесть или пять соседних; в каждой «вершине» сходятся три клетки). Бывают экземпляры, у которых есть и четырехугольные, и восьмиугольные клетки, но биологи заметили, что если таких «нестандартных» клеток (менее, чем с пятью и более, чем с семью)сторонами нет, то пятиугольных клеток всегда ровно на двенадцать больше, чем семиугольных (всего клеток может быть несколько сотен и даже тысяч). Это утверждение следует из известной формулы Эйлера.

Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на  правильный двадцатигранник, или  икосаэдр . Есть вирусы, размножающиеся в клетках животных (позвоночных и беспозвоночных), другие облюбовали растения, третьи (их называют бактериофагами или просто фагами) паразитируют в микробах, но  икосаэдрическая форма  встречается у вирусов всех этих трех групп.

Исторически  первой формой огранки , появившейся в середине  XIV  века, стал «октаэдр». Алмаз «Шах» почти сохранил свой  естественный вид. Он имеет форму вытянутого кристалла - октаэдра, массу 88,7 карата и цвет воды с желто-бурым    оттенком. В начале  XIX  века «Шах» оказался в Персии. В 1829 году в ходе беспорядков в Тегеране был убит русский посол, автор комедии «Горе от ума» А. С. Грибоедов, и персидское правительство для разрешения конфликта подарило алмаз Николаю  I . 

Благодаря правильным многогранникам открываются не только удивительные свойства геометрических фигур. Но и пути познания природной гармонии

Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книг о многогранниках. Некоторые из правильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов (которые можно рассмотреть с помощью электронного микроскопа). Пчелы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел (подобных пирамидам) наряду с другими видами пластических искусств уходит в глубь веков. Пять правильных тел изучали Теэтет, Платон, Евклид, Гипсикл и Папп.

СПАСИБО ЗА ВНИМАНИЕ!!!

Многогранники в архитектуре города Саранска

«Мордо́вский госуда́рственный национа́льный драмати́ческий теа́тр»

• «Мордо́вский госуда́рственный национа́льный драмати́ческий теа́тр» — театр в городе Саранск, столице Республики Мордовия. Здание национального драматического театра построено по проекту саранского архитектора С. О. Левкова. Оно примыкает к восточной стороне Выставочного зала Мордовского республиканского музея изобразительных искусств и соединено с ним одноэтажной вставкой. Отделка здания выполнена из тёмно-красного и сиреневого кирпича, светло-бежевой штукатурки, с использованием зеркального остекления и декоративных металлических вставок с мордовским орнаментом.

Кафедральный собор святого праведного воина Феодора Ушакова

• Кафедральный собор святого праведного воина Феодора Ушакова
• Решение о строительстве храма было принято в 2001 году после канонизации святого праведного воина Феодора Ушакова. 6 марта 2002 года был утверждён эскизный проект собора. 8 мая 2002 года был совершен молебен и освящено место под строительство собора. 9 сентября 2004 года состоялась церемония закладки капсулы с мощами в фундамент строящегося храма. Строительство собора было закончено к середине 2006 года. 5 августа 2006 года во время визита в Саранск Святейший Патриарх Московский и всея Руси Алексий II совершил освящение собора во имя святого праведного воина Феодора Ушакова. Кафедральный собор города Саранска является одним из самых больших храмов России и самым высоким в Поволжье. Его высота составляет 63 метра. Собор может вместить 3 тысячи молящихся (общая площадь — 900 кв. м.). На четырех звонницах размещены 12 колоколов, самый большой из которых весит 6 тонн. Одна из главных святынь собора — ковчег с частицами мощей святого праведного воина Феодора Ушакова.

Храм Казанской иконы Божией Матери

• Место под строительство храма было освящено 23 декабря 2000 года. Его возведение началось летом 2001 года и велось на средства, выделяемые из республиканского, городского и районного бюджета, пожертвования крупных промышленных предприятий республики и частных благотворителей. Имена жертвователей начертаны на кирпичах, из которых выложены стены храма. 13 марта 2005 года был совершен молебен и освящен цокольный этаж храма, где на следующий день состоялось первое богослужение. 12 июня 2010 года митрополит Саранский и Мордовский Варсонофий совершил чин освящения колоколов (самый большой из них весит около 4 тонн). 21 июля 2011 года Святейший Патриарх Московский и всея Руси Кирилл совершил чин великого освящения храма в честь Казанской иконы Божией Матери города Саранска и Божественную литургию в новоосвященном храме

Церковь Иоанна Богослова

• Церковь построена в 1693 году в Стрелецкой слободе Саранска на месте стоявшей там ранее деревянной церкви. Впоследствии перестраивалась в XVIII веке, в результате чего у церкви появились приделы. В 1810-х годах к церкви была пристроена колокольня. В течение короткого периода в 1930-е — 1940-е годы церковь была закрыта, затем вновь открыта в 1946 году, долгое время оставаясь единственным действующим православным храмом Саранска. Служила вторым кафедральным собором Пензенской и Саранской епархии (первый находился в Пензе). Является самым старым сохранившимся зданием Мордовии. С 1991 по 2006 год выполняла функции кафедрального собора Саранской и Мордовской епархии

Мордовский государственный университет имени Н. П. Огарёва

;

Спортивный комплекс «Олимп»;

Музей боевого и трудового подвига 1941—1945 гг.

А так же…

• Мордовский государственный педагогический институт имени М. Е. Евсевьева;
• Саранский кооперативный институт — филиал Российского университета кооперации;
• Мордовский гуманитарный институт;
• Саранский филиал Современной гуманитарной академии;
• Государственный музыкальный театр имени И. М. Яушева Республики Мордовия;
• Государственный русский драматический театр Республики Мордовия;
• Государственный театр кукол Республики Мордовия;
• Мордовский республиканский музей изобразительных искусств им. С. Д. Эрьзи;
• Мордовский республиканский объединенный краеведческий музей;
• Музей боевого и трудового подвига 1941—1945 гг
• Национальная библиотека им. А. С. Пушкина;
• Научная библиотека имени М. М. Бахтина Мордовского госуниверситета.
• Мордовская республиканская детская библиотека

Уважаемые ученики и учителя!!!

Определение: многогранник называется правильным, если все его грани правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число рёбер. Существует 5 видов правильных многогранников.

Названия многогранников пришли из Древней Греции и в них указывается число граней:

• «эдра» - грань
• «тетра» - 4
• «гекса» - 6
• «окта» - 8
• «икоса» - 20
• «дедека» - 12

Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Тетраэдр имеет 4 грани, 4 вершины и 6 ребер.

Гексаэдр (Куб)

Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер

Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Октаэдр имеет 8 граней, 6 вершин и 12 ребер.

Икосаэдр

Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Икосаэдр имеет 20 граней, 12 вершин и 30 ребер

Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер.

В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2.

Г+В=Р+2

Тела

Тела

Форма грани

тетраэдр

куб

Грани

Правильный треугольник

Квадрат

октаэдр

4

Вершины

4

икосаэдр

Правильный треугольник

6

Ребра

додекаэдр

8

8

6

Правильный пятиугольник

6

20

Правильный треугольник

12

12

12

12

30

20

30

Многогранники в исторических памятниках.

Египетские пирамиды

• Еги́петские пирами́ды  — величайшие архитектурные памятники Древнего Египта , среди которых одно из «семи чудес света»  — пирамида Хеопса и почётный кандидат «новых семи чудес света» — Пирамиды Гизы. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы, использовавшиеся в качестве гробниц для фараонов Древнего Египта. Слово «пирамида» — греческое. По мнению одних исследователей, большая куча пшеницы и стала прообразом пирамиды. По мнению других учёных, это слово произошло от названия поминального пирога пирамидальной формы. Всего в Египте было обнаружено 118 пирамид

Самые большие пирамиды Египта

• Пирамида Хеопса (IV династия): размер основания - 230 м (высота - 146,6 м);
• Пирамида Хефрена (IV династия): 215 м (143 м);
• Розовая пирамида , Снофру (IV династия): 219 м (105 м);
• Ломаная пирамида , Снофру (IV династия): 189 м (105 м);
• Пирамида в Мейдуме , Снофру (IV династия): 144 м (94 м);
• Пирамида Джосера (III династия): 121 × 109 м (62 м).

Ломаная пирамида

• Ломаная пирамида  — египетская пирамида в Дахшуре , возведение которой приписывается фараону Снофру (XXVI в. до н. э.)
• Для объяснения нестандартной формы пирамиды немецкий египтолог Людвиг Бурхардт (1863—1938) предложил свою «теорию приращивания». Согласно ей, царь умер неожиданно и угол наклона граней пирамиды был резко изменен с 54°31' до 43°21', чтобы быстро закончить работу. Курт Мендельсон предложил альтернативу: пирамида в Мейдуме и южная пирамида в Дахшуре были построены одновременно, но случилась авария в Мейдуме — возможно, после дождей облицовка обрушилась — и этот инцидент заставил спешно изменить угол наклона сторон пирамиды в Дахшуре, когда она была построена уже наполовину.

Пирамиды Хефрена и Микерина

• Пирамида Хефрена (точнее — Хафры ) — вторая по величине древнеегипетская пирамида . Расположена рядом с Великим Сфинксом , а также пирамидами Хеопса ( Хуфу ) и Микерина в Гизе . Построенное в сер. XXVI в. до н. э. сооружение (215,3 × 215,3 м и высота 143,5 м) получило название Урт-Хафра («Хафра Великий» или «Почитаемый Хафра»).

Пирамиды Греции

• На территории Греции обнаружены недавно фрагменты 26 сооружений, удивительно напоминающих известные всем древнеегипетские пирамиды. Наиболее сохранившейся является первая из них — Элленикоса. Она сложена из прямоугольных камней, обработанных снаружи. В легендах Древней Эллады сохранились сведения о происшедшей в этих местах битве между войсками двух братьев-близнецов, боровшихся за царский престол. В её память над могилой, где захоронили погибших, якобы было сооружено здание в форме пирамиды. Впрочем, раскопки пока не подтвердили древнее сказание, не удалось обнаружить и ничего, что смогло бы рассказать о строителях или об орудиях труда.

Пирамиды в Афинах

• Парфенон в Афинах был построен в V веке до нашей эры для защиты короля от его врагов. Кажется орды, наконец, преуспели в захвате. Во время недавнего ремонта южного и западного склонов были расширены подходы в храм, по которым орды туристов по-прежнему маршируют вверх, как муравьи в муравейнике, особенно в летнее время.

• Названия правильных многогранников пришли из Греции. В дословном переводе с греческого "тетраэдр", "октаэдр", "гексаэдр", "додекаэдр", "икосаэдр" означают: "четырехгранник", "восьмигранник", "шестигранник". "двенадцатигранник", "двадцатигранник". Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии". Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх. Икосаэдр - воду, т.к. он самый "обтекаемый. Куб -
• землю, как самый "устойчивый. Октаэдр - воздух, как самый "воздушный". Пятый многогранник, додекаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным. Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы "стихий" настраивались Платоном в совершенных консонансах, как четыре струны лиры. Консонансом называется приятное созвучие. Надо сказать, что своеобразные музыкальные отношения в Платоновых телах являются чисто умозрительными и не имеют под собой никакой геометрической основы. Этими отношениями не связаны ни число вершин Платоновых тел, ни объемы правильных многогранников, ни число ребер или граней. В связи с этими телами уместно будет сказать, что первая система элементов, включавшая четыре элемента - землю, воду, воздух и огонь, - была канонизирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течение многих веков. Вполне возможно отождествить их, с известными нам, четырьмя состояниями вещества - твердым, жидким, газообразным и плазменным