| Теорема. Объем шара радиуса R равен 
Итак, нам дан шар радиуса R. Нужно доказать формулу объема шара – объем шара радиуса R равен  Рассмотрим доказательство.
Для вычисления объема шара применим уже известную нам интегральную формулу:  , где S(x) – площадь сечения, перпендикулярного оси Ox и проходящего через точку с абсциссой x. , где S(x) – площадь сечения, перпендикулярного оси Ox и проходящего через точку с абсциссой x.
Введем координатную ось OX, проходящую через центр шара. Проведем сечение, проходящее через точку P перпендикулярно оси Ox. Найдем зависимость площади сечения S от значения x.
Сечением будет круг, с центром в точке P. Обозначим его радиус через r, а площадь через S(x).
Рассмотрим прямоугольный треугольник OPQ. Точка P в нашей системе координат имеет абсциссу x, поэтому OP = x; PQ – это радиус сечения r, OQ – радиусом шара R.
Найдем радиус сечения r: r малое = PQ = корню квадратному из  и равен корню квадратному из и равен корню квадратному из  Так как  . .
Осталось вычислить определенный интеграл. Объем шара = интегралу от –R до R умножить на разность 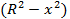 dx dx
Этот интеграл разбивается на разность двух интегралов  интеграл от –R до R dx минус интеграл от –R до R x2dx. интеграл от –R до R dx минус интеграл от –R до R x2dx.
Выполнив несложные вычисления, получим формулу объема шара: 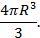 Теорема доказана.
| Теорема. Объем шара радиуса R равен  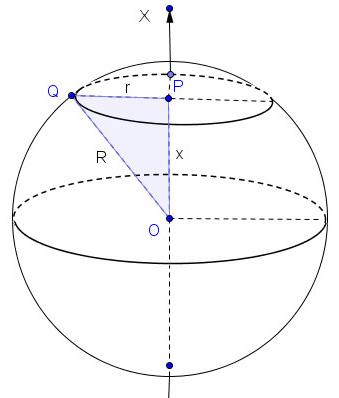
Доказательство. Дано: Шар R – радиус шара Доказать:V Доказательство. Проведем ось Ox через цент шара. Проведем сечение через и и  . . Найдем зависимость площади сечения Sот значения x.  
OP = x; PQ =r; OQ= R 
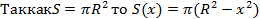 . .
Осталось вычислить определенный интеграл 

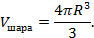
Ч.т.д. |
| Переходим к рассмотрению задач.
Задача 1. Пусть V – объем шара радиуса R, а S – площадь его поверхности, найдите R и V, если S = 64 см2. | Задача 1. Пусть V – объем шара радиуса R, а S – площадь его поверхности, найдите R и V, если S = 64 см2. 
|
| Дано: Шар радиуса R. Площадь поверхности шара S равна 64 квадратных сантиметров. Найти: радиус и объем шара. Решение. Для вычисления радиуса воспользуемся уже известной нам формулой площади поверхности сферы:

Выразим из этой формулы радиус. Радиус будет равен корню квадратному из дроби, в числителе которой S, в знаменателе 4.
Подставив в полученную формулу известное по условию задачи значение площади, S=64, найдем радиус.
Радиус будет равен корню квадратному из дроби, в числителе которой 64, в знаменателе 4, и равен 4 см.
Теперь, зная радиус сферы, мы можем вычислить ее объем.
Объем равен 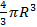 , и равен 4, умноженное на 4 в кубе, деленное на три, умноженное на , и равен 256 третьих кубических сантиметров. , и равен 4, умноженное на 4 в кубе, деленное на три, умноженное на , и равен 256 третьих кубических сантиметров.
Ответ: Радиус шара равен 4 сантиметра, Объём шара равен 256 третьих кубических сантиметров.
| Дано: Шар R – радиус шара S = 64 см2 Найти: Rи V Решение. Найдем радиус. 
 . .
Вычислим объем: см3 Ответ: 
|
| Задача 2. Дан шар. По одну сторону от центра проведены два параллельных сечения, радиусы которых равны 9 и 12. Найдите объем шара, если расстояние между плоскостями сечений равно 3.
| Задача 2. Дан шар. По одну сторону от центра проведены два параллельных сечения, радиусы которых равны 9 и 12. Найдите объем шара, если расстояние между плоскостями сечений равно 3.
|
| Дано: Шар r1,r2 – радиусы сечений r1 = 9 см r2 = 12 см O1O2 – расстояние между сечениями O1O2 = 3 см Найти:  Рассмотрим решение. Формула для нахождения объема шара: 
Найдем радиус шара R.
На чертеже мы видим два параллельных сечения (два круга), с центами в точках O1 и O2, радиусы которых обозначены через r1 и r2. Проведем ось Ox через центр шара, перпендикулярно плоскостям сечений, она пройдет через точки O1 , O2. (перпендикуляр, опущенный из центра шара на секущую плоскость, проходит через центр круга, лежащего в сечении).
Рассмотрим треугольники:  и и  . . Так как ось Ox проведена перпендикулярно плоскостям сечений, то эти треугольники прямоугольные.
Отрезок . Из  по теореме Пифагора находим: по теореме Пифагора находим:

В  
Так как OM = ON = R, то можно составить уравнение:  Решая уравнение, находим x.
  x = 9. Итак,
Из . Теперь, зная радиус шара, можно найти его объем. Ответ: 4500.
| Дано: Шар r1,r2 – радиусы сечений r1 = 9 см r2 = 12 см O1O2 – расстояние между сечениями O1O2 = 3 см Найти:  Решение. Найдем радиус шара. Проведем ось Ox  плоскостям сечений, она пройдет через точки O1 O2. плоскостям сечений, она пройдет через точки O1 O2.   и и  . –прямоугольные . –прямоугольные
Введем обозначение: 




Так как OM = ON = R , то  ; ;




Находим объем шара: Ответ: 4500.
|




















