Степени с рациональными показателями, их свойства
“Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь”.
М. В. Ломоносов
Цель урока: Повторить определение степени с рациональным показателем и свойства степени с рациональным показателем (2 часа)
Задачи урока:
Обобщить и систематизировать знания по теме «Степени и их свойства»
Продолжить отрабатывать:
а) вычислительные навыки;
б) умение устанавливать причинно-следственную связь, получая решение в общем виде;
в) рефлексивное умение оценивать полученные результаты решения и их достоверность;
г) рефлексивные навыки самоконтроля в режиме самостоятельной работы.
а) логическое мышление.
б) зрительную, слуховую и моторную память.
Способствовать развитию у обучающихся грамотной математической речи, мышления (умения обобщать и систематизировать, строить аналогии).
Воспитывать ответственность.
Форма урока: урок-практикум.
Методы: наглядно-иллюстративный; самостоятельная работа с последующей проверкой.
Средства: компьютер; презентация Power Point; интерактивная доска.
Используемые технологии:
- информационно-компьютерная технология.
План урока:
1. Организационный момент.
2. Актуализация целей урока.
3. Актуализация опорных знаний.
4. Тренировочные упражнения.
5. Дешифратор.
6. Лабиринт.
7. Задания для самостоятельной работы с последующей проверкой.
8. Подведение итогов урока.
9. Задание на дом.
Ход урока
1. Организационный момент.
2. Актуализация целей урока.
Цель нашего урока - повторить определение и свойства степени с рациональным показателем, применение свойств при решении упражнений.
3. Актуализация опорных знаний
Вспомним теорию. [Приложение 1]
1) Определение. Арифметическим корнем n-й степени (n 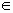 N, n
N, n  2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а.
2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а.



2) Определение. Степень с рациональным показателем
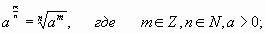
Если
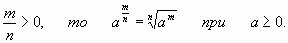
3) Свойства степени с рациональным показателем:
При a 0, b 0, p и q - рациональные числа:
а) 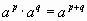
б )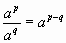
в) 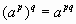
г) 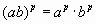
д) 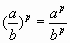
4) Вспомним теорию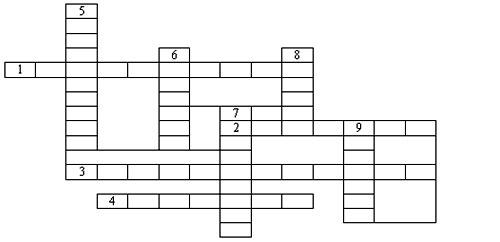
По горизонтали:
1.Действие, с помощью которого вычисляется значение степени
2. Произведение, состоящее из одинаковых множителей .
3. Действие показателей степеней при возведении степени в степень .
4. Действие степеней, при которых показатели степеней вычитаются .
По вертикали:
5. Число всех одинаковых множителей
6. Степень с нулевым показателем .
7. Повторяющийся множитель .
8. Значение 105 : ( 23 • 55 ) .
9. Показатель степени, который обычно не пишут .
4. Тренировочные упражнения.
1) Базовый уровень.
№1. Вычислить.

Ответ. -26,5.
№2. Найдите значение выражения.

Ответ. -2.
№3. Упростите выражение.

Ответ. 1.
№4. Найдите значение выражения.

Ответ. 4.
№5. Упростить выражение

Ответ.  .
.
2) Повышенный уровень.
№6. Упростить выражение

Ответ. 2.
Указание. Преобразовать подкоренные выражения, воспользоваться формулами сокращённого умножения (квадрат суммы и квадрат разности).
5. Дешифратор
Вычислить, сопоставить полученный результат с ключом
1) Фамилия немецкого математика, который ввел термин - “показатель степени”.
1) -81\3 2) 811\2 3) (3\5)-1 4) (5\7)0 5) 27-1\3 6) (2\3)-2 7) 161\2 . 1251\3
| Л | Т | Н | Р | Ш | О | Ь | И | Е | Ф | К | А | Д | Ю |
| 9\4 | 9 | 5 | 11 | -2 | 4\9 | 20 | 5\3 | 1\3 | 1 | 3 | 8 | 64 | 2 |
-
| -
| -
| -
| -
| -
| -
|
| -2 | 9 | 5/3 | 1 | 1/3 | 9/4 | 20 |
| Ш | Т | И | Ф | Е | Л | Ь |
Слово:

Михаэль Штифель - (около 1487, Эсслинген-на-Неккаре — 19 апреля 1567, Йена) — немецкий математик, один из изобретателей логарифмов, активный деятель протестантской Реформации.
2) Фамилия французского математика, который ввел современную запись степени.
1) х1\3=4 2) у-1= 3 3) ( х+6)1\2 = 3 4) у1\3 =2 5) (у-3)1\3=2 6) а1\2 : а = 1\3
| Л | Т | Н | Р | Ш | О | Ь | И | Е | Ф | К | А | Д | Ю |
| 9\4 | 9 | 5 | 11 | -2 | 4\9 | 20 | 5\3 | 1\3 | 1 | 3 | 8 | 64 | 2 |
-
| -
| -
| -
| -
| -
|
| 64 | 1/3 | 3 | 8 | 11 | 9 |
| Д | Е | К | А | Р | Т |
Слово:
Рене Декарт (31 марта 1596, Лаэ (провинция Турень), ныне Декарт (департамент Эндр и Луара) — 11 февраля 1650, Стокгольм) — французский философ, математик, механик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.

6. Лабиринт
I вариант II вариант
| 0,02 | умножить на 10 m-2 |
| -5 | умножить на 0,1 a-3 |
| 0,2m-2 | умножить на m-4 |
| -0,5a-3 | умножить на -0,5a9 |
| -0,008m-6n3 | извлечь корень кубический |
| 0,25a6b-2 | извлечь корень квадратный |
| -0б2m-2n | возвести в -4 степень |
| 0,5a3b-1 | возвести в -3 степень |
| 625m8n-4 | разделить на 625mknk-4,5 |
| 8a-9b3 | разделить на 8am-7,5bm |
| m8-kn0,5-k | вычислить при k=2, m=2, n=16 |
| a-1,5-mb3-m | вычислить при m=-1, a=4, b=-3 |
| Ответ: 1 |
| Ответ: 1 |
7. Задания для самостоятельной работы с последующей проверкой.
Вычислить:
1)  ;
;
2) ;
;
3)  ;
;
4) ;
;
5)  ;
;
Упростить:
6)  ;
;
7) .
Проверка.
1) 
 ;
;
2) 
3) 
4) 
5) 

Указание. Использовать формулу разности кубов
 ;
;
6) 
 ;
;
7)
8. Подведение итогов урока.
Повторение изученных свойств, выставление оценок.
9. Задание на дом.
1. п 34, № 437-440 абв
2. Софизм по теме урока:
сформулировать,
придумать доказательство
разбор софизма
Используемый учебно-методический комплект:
Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.
Москва. “Просвещение” 2010 г.
Журнал “Математика. Первое сентября” № 19 2008 г., “Подготовка к ЕГЭ”.
Сборники для подготовки к ЕГЭ по математике.
Интернет-ресурс. Сайт http://www.mathege.ru. Открытый банк задач по математике.
























