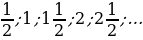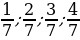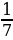КСП "Формула n-го члена арифметической прогрессии

Раздел долгосрочного планирования: 2. Алгебра (2.3 Последовательности и суммирование) Школа: КГУ «ШЛ №34» УО ВКО по г. Усть-каменогорску

Дата : ФИО учителя: Мусина Ю.Н.

класс: 9 Участвовали: Не участвовали:

Тема урока

Арифметическая прогрессия. Формула n-го члена арифметической прогрессии.

Цели обучения (из программы)

9.2.3.4 распознавать арифметическую и геометрическую прогрессии среди числовых последовательностей;

9.2.3.5 знать и применять формулы n-го члена, суммы n первых членов и характеристическое свойство арифметической прогрессии;

Цель урока

-распознавать арифметическую прогрессию среди числовых последовательностей.

-применять формулу n-го члена арифметической прогрессии при решении задач.

Критерии оценивания

Обучающийся:

- распознает арифметическую прогрессию среди числовых последовательностей

- применяет формулу n-го члена арифметической прогрессии при решении задач

Предыдущие знания

Возрастающие и убывающие числовые последовательности. Способы задания числовой последовательности.

Запланированные

этапы урока

Виды упражнений, запланированных на урок:

Ресурсы

Начало урока

1. Создание колаборативной среды

А) Построение по росту от самого высокого до самого низкого.

Б) по цвету глаз от самого светлого к самому темному.

1. Актуализация знаний.

Задание 1. Стратегия «Найди ошибку»

Последовательности заданы формулой n-го члена. Определите верно ли найдены первые четыре члена данных последовательностей.

1) a_n = n + 5; 2) a_n = 5n − 1.

а₁ = 1+5 =6 а₁ = 5·2-1 = 9

а₂ = 2-5 = -3 а₂ = 5·1 -1 = 4

а₃ = 3+5 =8 а₃ = 5·3 -1 = 7

а₄ = 4+5 = - 9 а₄ = 5·4 - 1 = 19

Ключ:

1) a_n = n + 5; 2) a_n = 5n − 1.

а₁ = 1+5 =6 а₁ = 5·1-1 = 4

а₂ = 2+5 =7 а₂ = 5·2 -1 = 9

а₃ = 3+5 =8 а₃ = 5·3 -1 = 14

а₄ = 4+5 =9 а₄ = 5·4 - 1 = 19

ФО: сравнение с образцом

Б) Метод «Парная беседа»

Учащиеся опрашивают друг друга в парах по вопросам, предложенным учителем.

Вопросы:

1) Каким способом заданы данные последовательности? /аналитическим/

2) Данные последовательности являются убывающими или возрастающими? Поясните ответ. /возрастающими, так как каждый член последовательности больше предыдущего/

3) Какие последовательности называются убывающими? /последовательность называется убывающей, если каждый её член меньше предыдущего/.

4) На какое число увеличился каждый последующий член последовательностей, начиная со второго?

/в первой последовательности увеличился на число 1

во второй последовательности увеличился на 5/

ФО «Уточняющие вопросы»

Задание 2. Индивидуальная работа

Стратегия «Собери слово»

Дифференциация по темпу

Выбери в таблице правильные ответы. Из букв, соответствующих правильным ответам, составь слово.

Таблица 1

ФО: Самооценивание «Сравнение с образцом»

Ответ

Определение темы урока и личностных целей учащихся с опорой на цели обучения учебной программы.

Середина урока

1. Изучение нового материала

Задание 3. Работа в парах. Стратегия «Классификационная таблица»

Дифференциация по заключению.

Каждая пара получает карточки с теоретическим материалом (Приложение 1) и таблицу.

Изучите теоретический материал индивидуально, затем обсудите его в паре и заполните таблицу.

Сделайте вывод, ответив на вопрос «Каким числом может быть разность арифметической прогрессии?»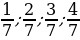

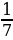
Вывод: разность арифметической прогрессии может быть любым числом – положительным, отрицательным и даже нулем. В зависимости от значения разности арифметическая прогрессия может быть возрастающей, убывающей или стационарной.

ФО: Взаимооценивание «Эксперты», «Устный комментарий»

Учитель проверяет работу учащихся выполнивших работу быстрее остальных, а затем данные учащиеся проверяют работу других учеников в роли экспертов.

Задание 3. Групповая работа. Метод «ДЖИГСО» (4 группы по 4 человека) Дифференциация по заданию. (№ 4 самые сильные ученики)

Задание для групп. (Приложение 2) Изучите теоретический материал в учебнике по теме . Запишите формулу n- го члена в тетрадь. Обсудите решение данной задачи, решите её и подготовьте объяснения решения этой задачи для других групп.

Задача 1. (уровень А)

Дана арифметическая прогрессия 216; 200; 184; 168; 152; … . Найдите 27 –й член данной прогрессии.

а₁ = 216, а₂ =200, n =27

а₂₇ - ?

Подсказки при необходимости:

1. Найдите разность d арифметической прогрессии.

2. Используйте формулу а_n =а₁ +(n-1)·d чтобы найти а₂₇.

Решение:

а₁ = 216, а₂ =200, n =27

а₂₇ - ?

d = 200 - 216 = -16

a_n = a₁ +(n-1)·d

a₂₇ = 216 +(27-1)·(-16)=216 +26·(-16) = 216 - 416= -200

Ответ: -200.

Критерий: - применяет формулу n-го члена арифметической прогрессии при решении задач.

Дескриптор:

-находит разность арифметической прогрессии

-записывает формулу n-го члена арифметической прогрессии

- Подставляет данные в формулу а_n

- находит значение а₂₇

Задача 2. (уровень А)

Найдите порядковый номер члена 887 арифметической прогрессии 7; 15; 23; 31; 39; ….

а₁ = 7, а₂ = 15, а_n =887

n-?

Подсказки при необходимости:

1. Найдите разность d арифметической прогрессии.

2. Используйте формулу а_n =а₁ +(n-1)·d чтобы составить уравнение и найти n_.

Решение:

а₁ = 7, а₂ = 15, а_n =887

n-?

d = 15-7=8

a_n = a₁ +(n-1)·d

7 + (n-1)·8 = 887

7+8n-8=887

8n=888

n =111

Ответ: 111.

Критерий: - применяет формулу n-го члена арифметической прогрессии при решении задач.

Дескриптор:

- находит разность арифметической прогрессии

-записывает формулу n-го члена арифметической прогрессии

- подставляет данные в формулу а_n

- решает полученное уравнение

-находит n =111.

Задача 3. (уровень А)

Найдите формулу n –го члена арифметической прогрессии 75; 64; 53; 42; 31; ….

а₁ =75, а₂ =64

а_n -?

Подсказки при необходимости:

1. Найдите разность d арифметической прогрессии.

2. Используйте формулу а_n =а₁ +(n-1)·d чтобы найти формулу n –го члена арифметической прогрессии.

Решение:

а₁ =75, а₂ =64

а_n -?

d =64 - 75= -11

a_n = a₁ +(n-1)·d

a_n = 75+(n-1)·(-11) = 75 -11n +11 = -11n +86

Ответ: a_n= -11n +86

Критерий: - применяет формулу n-го члена арифметической прогрессии при решении задач.

Дескриптор:

- находит разность арифметической прогрессии

-записывает формулу n-го члена арифметической прогрессии

- подставляет данные в формулу n –го члена.

- упрощает полученное выражение

- записывает формулу n –го члена -11n +86.

Задание группы № 4. Изучите теоретический материал в учебнике. Запишите формулу n- го члена в тетрадь. Обсудите решение данной задачи, решите её и подготовьте объяснения решения этой задачи для других групп.

Задача 4. (уровень В)

Является ли число 135 членом арифметической прогрессии 15; 21; 27; …?

Критерий: применяет формулу n-го члена арифметической прогрессии при решении задач.

Дескриптор:

- находит разность арифметической прогрессии

- записывает формулу n-го члена арифметической прогрессии

- подставляет данные в формулу а_n

- решает уравнение

-делает вывод, что число 135 является 21-м членом арифметической прогрессии.

ФО: «Измерение температуры», учащиеся осуществляют оценивание по разработанным к задачам критериям и дескрипторам.

«Две звезды и одно пожелание»

https://works.doklad.ru/view/eOrCLS2WSJo/all.html

Алгебра: учебник для 9 кл. общеобраз. шк. Часть 1. /Абылкасымова А.Е., Т.П. Кучер, В.Е. Корчевский, З.А. Жумагулова. –Алматы: Мектеп, 2019

Конец урока

4.Индивидуальная работа. Тест

Дифференциация по темпу

1. Из данных последовательностей выберите арифметическую прогрессию:

А) 17; 25; 35; 43; …

В) -10; -12; -14; -16; …

С) -5; 5; 16; 28; …

2.Найдите разность арифметической прогрессии 29; 22; 15; 8; 1; …

А) - 7

В) -9

С) -8

3. Выберите из данных формул, формулу n- го члена арифметической прогрессии:

А) а_n =а₁ - (n+1)·d

В) а_n =а₁ + (n-1)·d

С) а_n =(n-1)·а₁ +d

4.Найдите 10 –й член арифметической прогрессии 20; 23; 26; 29; …

А) 3

В) 30

С) 47

ФО Самопроверка по готовым ответам.

Ключ: 1-В, 2-А, 3-В, 4-С

Домашнее задание

Стр 111 -115 п13, выучить определение и формулы.

Разноуровневые задачи.

Уровень А обязательный для выполнения стр 117 №13.2 (1,3), № 13.3(3,4)

уровень В по желанию учащегося. стр 118 № 13.11(2)

Рефлексия учеников в конце урока:

Метод «Неоконченное предложение»

Я узнал (а) __________________________

Мне было трудно_____________________

Мне было легко______________________

Алгебра: учебник для 9 кл. общеобраз. шк. Часть 1. /Абылкасымова А.Е., Т.П. Кучер, В.Е. Корчевский, З.А. Жумагулова. –Алматы: Мектеп, 2019