Лекция 1.
Тема 1.1. Основы теории множеств
План:
Основные понятия.
Операции над множествами. Диаграммы Эйлера-Венна.
Основные числовые множества
Дискретная математика – область математики, занимающаяся изучением свойств структур конечного характера, которые возникают как внутри математики, так и в её приложениях.
Дискретная (конечная) математика – это раздел математики, не связанный с понятиями предела, непрерывности и бесконечности.
Логика- наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств
Математическая логика — раздел математики, посвящённый изучению математических доказательств и вопросов оснований математики.
1. Основные понятия.
Понятие "множество" является первичным и неопределяемым.
О.1. Множество – это совокупность некоторых объектов объединенных по какому либо признаку.
Объекты любой природы (числа, люди, вещи и т. д.), составляющие множество, называют его элементами.
Например, студент Иванов является элементом множества студентов IV курса, март – элементом множества месяцев в году и т.д.
Множества обозначаются прописными буквами латинского алфавита: A, B, X, Y, A1, A2, …, элементы множеств – строчными буквами: a, b, x, y, a1, a2, … .
Замечание. Элементы множество сами могут являться множествами.
Множество, элементами которого являются множества называют классом или семейством.
Множество групп студентов СРМК состоит из элементов (групп) которые в свою очередь состоят из студентов СРМК.
О.2. Множество состоящее из конечного (бесконечного) числа элементов называется конечными (бесконечными).
О.3. Множество которое не содержит ни одного элемента называется пустым и обозначается 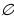 .
.
Например: 1) Множество дней недели – конечно.
2) Множество натуральных чисел – бесконечно.
3) Множество действительных корней уравнения 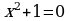 - пустое, т.к.
- пустое, т.к. 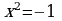 , корней не существует.
, корней не существует.
2. Способы задания множеств.
Существует 3 способа задания множеств:
1. Перечисления всех элементов множеств: 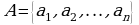 .
.
2. Указание правила перечисления элементов множества (записываются несколько первых элементов с «…»):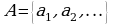 .
.
3. Указание характеристических свойств (свойства элементов множества): 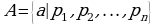 или
или 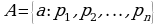 , где
, где 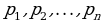 система характеристических свойств, элементы множества
система характеристических свойств, элементы множества 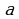 .
.
Например: 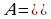 a – целое число,
a – целое число, 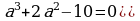 - это множество целых корней уравнения
- это множество целых корней уравнения 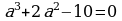 .
.
О.4. Множество А называется подмножеством множества В, если все элементы множество А входит во множество В. (Обозначается 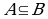 ).
).
Множество пустое 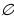 и В называют собственными подмножествами множества В.
и В называют собственными подмножествами множества В.
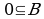 и
и 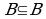 .
.
О.5. Множества А и В называются равными (совпадающими) если они состоят из одних и тех же элементов.
О.6. Если множество 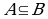 и
и 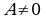 ,
, 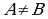 , то А называют собственным подмножеством множества В.
, то А называют собственным подмножеством множества В.
В этом случаи говорят, что В строго включает А.
О.7. Совокупность всех подмножеств множества А называется Булеаном множества А или множеством степени множества А.
Операции над множествами. Диаграммы Эйлера-Венна
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
1. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):
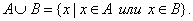
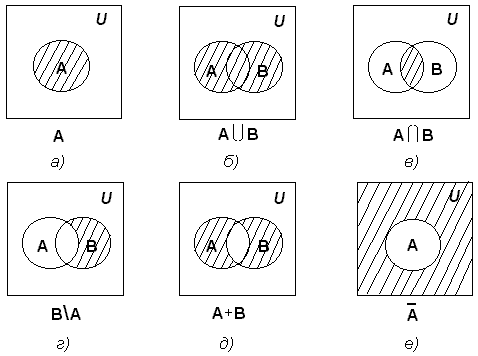
Рис. 1
2. Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):
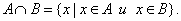

Рис. 2
3. Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):
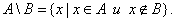

Рис. 3
4. Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):
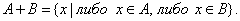

Рис. 4
5. Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):
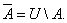

Рис. 5
3. Основные числовые множества.
N - множество всех натуральных чисел;
N0 - множество неотрицательных целых чисел
Z -множество целых чисел;
Q - множество рациональных чисел;
I - множество иррациональных чисел;
R - множество действительных чисел;
C - множество комплексных чисел;






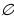 .
.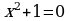 - пустое, т.к.
- пустое, т.к. 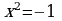 , корней не существует.
, корней не существует.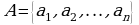 .
.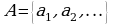 .
.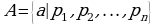 или
или 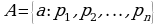 , где
, где 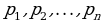 система характеристических свойств, элементы множества
система характеристических свойств, элементы множества 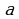 .
.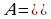 a – целое число,
a – целое число, 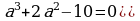 - это множество целых корней уравнения
- это множество целых корней уравнения 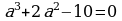 .
.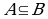 ).
).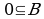 и
и 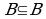 .
.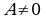 ,
, 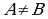 , то А называют собственным подмножеством множества В.
, то А называют собственным подмножеством множества В. 










