Якутская государственная сельскохозяйственная академия
Олекминский филиал
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНЫХ РАБОТ(ЗАДАНИЙ)
по теории вероятностей и математической статистике
Олекминск
2013
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Якутская государственная сельскохозяйственная академия»
Олекминский филиал
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ (УКАЗАНИЯ) ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНЫХ РАБОТ(ЗАДАНИЙ)
по теории вероятностей и математической статистике
Олекминск
2013
ББК 22.161.6
Теория вероятностей и математическая статистика: методические указания по выполнению контрольных работ по направлению 080100.62 «Экономика» ,
Олекминск, 2013
Составитель: Тирский А.С., старший преподаватель кафедры естественных и
технических наук.
Утверждена на заседании кафедры естественных и технических наук
Протокол заседания кафедры № ___от «__»_________2013г.
Утверждена и рекомендована к издаеию методическим советом олекмиского филиала ФГБОУ ВПО «Якутской ГСХА»
Протокол заседания МС №____от «___» ________2013г.
© Якутская ГСХА, 2013
© Олекминский филиал, 2013
Содержание:
Введение……………………………………………………………………………..4
Методические рекомендации по выполнению
контрольных заданий………………………………………………………………4
Описание контрольных заданий…………………………………………………...19
Введение
Роли и значение выполнения контрольных заданий в профессиональной подготовке студентов:
Выполнение контрольных заданий является важной частью изучения дисциплины, т.к. при самостоятельном выполнении контрольных работ студенты перерабатывают информацию ,получаемую на занятиях и при самостоятельном изучении дисциплины по учебникам, проверяют и демонстрируют преподавателю свой уровень подготовки по данной дисциплине.
Взаимосвязь контрольных заданий с различными формами организации учебного процесса:
При выполнении контрольных заданий студентами происходит автоматическая подготовка к экзаменам. Развивается логическое мышление, что несомненно важно для будущего экономиста.
Цели и задачи контрольных работ по «математике»:
Цель: Подготовка к экзамену
Задачи:
Отработка практической составляющей программы
Изучение теоретического материала, необходимого для решения задач
Развитие логического и оптимального мышления у студентов.
Требования к знаниям студентов, необходимым при выполнении контрольных заданий:
При выполнении контрольных заданий студенты должны
знать:
Основные формулы и понятия школьного курса математики, математического анализа
Теоретический материал дисциплины (определения, формулы, теоремы …)
Уметь:
Решать основные виды задач школьного курса математики, теории рядов дифференциального и интегрального исчисления
Применять теоретический материал курса для решения базовых задач
Методические рекомендации по выполнению контрольных заданий
К выполнению контрольной работы следует приступать только после изучения материала курса по учебнику и учебным пособиям. Далее следует внимательно разобрать все решенные задачи демонстрационного варианта. При выполнении работы следует руководствоваться следующими указаниями:
1. Контрольную работу следует выполнять в общей тетради, на внешней
обложке которой должны быть указаны фамилия и инициалы студентов,
полный шифр, номер варианта и дата ее отправки в академию. Решения
всех задач должны быть достаточно подробными. Все вычисления
необходимо делать полностью. Чертежи и графики должны быть
выполнены аккуратно, с указанием единиц масштаба, координатных осей
и других элементов чертежа. Для замечаний преподавателя необходимо
оставлять на каждой странице поля шириной 3-4 см и после каждой
задачи оставлять место 4-5 клеток.
2. Контрольная работа сдается как минимум за 10 дней до начала экзаменационной сессии на кафедру ( не преподавателю лично).
3) контрольная работа считается зачтенной,если в ней верно решено более 80% всех заданий
4. После получения незачтенной работы студент должен в короткий срок
исправить все ошибки в этой же тетради и сдать работу на проверку
повторно.
5. Контрольные работы должны выполняться самостоятельно. Не
самостоятельно выполненные работы автоматически считаются
незачтенными.
6. Студент выполняет тот вариант контрольной работы, который совпадает с
последней цифрой зачетной книжки (если шифр заканчивается цифрой 0,
то студент выполняет работу 10 варианта).
Вопросы, которые должны быть разобраны перед выполнением работы:
Тема 1 Основные понятия теории вероятностей
Предмет теории вероятностей. Случайные события и их классификация. Классическое определение вероятностей. Элементы комбинаторики. Геометрические вероятности.
Тема 2. Теоремы сложения
Понятие суммы событий. Противоположные события. Теорема сложения вероятностей совместных событий. Теорема сложения вероятностей несовместных событий.
Тема 3. Теоремы умножения.
Понятие зависимых событий. Теорема умножения двух независимых событий. Понятие условной вероятности. Теорема умножения двух зависимых событий.
Тема 4. Следствия из теорем сложения и умножения
Вероятность появления хотя бы одного события. Формула полной вероятности и формула Бейеса
Тема 5. Схема Бернулли
Независимые испытания. Схема Бернулли. Формула Бернулли. Теорема Пуассона. Локальная и интегральная теоремы Лапласа.
Тема 6 Виды случайных величин. Задание дискретной случайной величины (ДСВ).
Понятие случайной величины. Закон распределения случайной величины. ДСВ. Закон распределения ДСВ. Многоугольник распределения.
Тема 7. Математическое ожидание ДСВ.
Определение математического ожидания. Вероятностный смысл математического ожидания. Свойства математического ожидания
Тема 8. Дисперсия ДСВ
Определение дисперсии. Вычисление дисперсии. Свойства дисперсии. Среднее квадратическое отклонение.
Тема 9. Закон больших чисел
Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. Центральная предельная теорема. Интегральная теорема Муавра – Лапласа.
Тема 10. Функция распределения вероятностей НСВ
Функция распределения и ее свойства. Функция распределения ДСВ.
Тема 11. Плотность распределения вероятностей НСВ
Плотность распределения и ее свойства. Числовые характеристики НСВ. Вероятность попадания значения случайной величины в интервал. Условие нормировки. Производящая функция.
Тема 12 Нормальное распределение.
Определение нормального распределения. Числовые характеристики. Вероятность попадания в интервал нормально распределенной величины. Нормальная кривая и ее исследование. Правило трех сигм.
Тема 13. Показательная плотность
Определение показательного закона. Числовые характеристики. Вероятность попадания в интервал. Функция надежности и ее практическое применение.
Тема 14. Система двух случайных величин.
Понятие о системе случайных величин и законе распределения. Функция распределения двумерной случайной величины и ее свойства. Плотность распределения вероятностей двумерной случайной величины и ее свойства. Зависимость и независимость двух случайных величин. Условные законы распределения. Числовые характеристики двумерной случайной величины. Корреляционный момент, коэффициент корреляции. Двумерное нормальное распределение. Регрессия. Многомерная случайная величина. Характеристическая функция и ее свойства.
Тема 15 Выборочный метод
Распределение частот. Эмпирическая функция распределения. Полигон и гистограмма.
Тема 16. Статистические оценки параметров нормального распределения.
Оценка неизвестных параметров. Методы нахождения точечных оценок. Понятие интервального оценивания параметров. Доверительные интервалы
Тема 17 Проверка статистических гипотез
Понятие о проверке статистических гипотез. Сравнение выборочной средней с математическим ожиданием. Сравнение двух дисперсий. Сравнение двух математических ожиданий. Проверка гипотезы о распределении. Критерий Пирсона.
Тема 18. Регрессионный анализ
Линейная регрессия с несгруппированными данными.
Тема 19. Дисперсионный анализ
Понятие дисперсионного анализа. Алгоритм проведения дисперсионного анализа.
Рекомендуемая дитература
Данко П.Е.., Попов А.Г.., Кожевникова Т.Я., Высшая математика в упражнениях и задачах, в 2-х частях Ч-2.: Учебное пособие для ВУЗов - .М.: Высшая школа, 1999
Теория вероятностей и математическая статистика: Учебное пособие для ВУЗов/В.Е. Гмурман. – М.: Высшая школа., 2003г
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для студентов ВУЗов. – М.: высшая школа., 1999г.
Примеры выполнения контрольных заданий (образцы решения задач)
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
1. В урне находятся 12 белых и 8 черных шаров. Найти вероятность того,
что среди наугад вынутых 5 шаров 3 будут черными.
Решение:
Воспользуемся классическим определением вероятности: 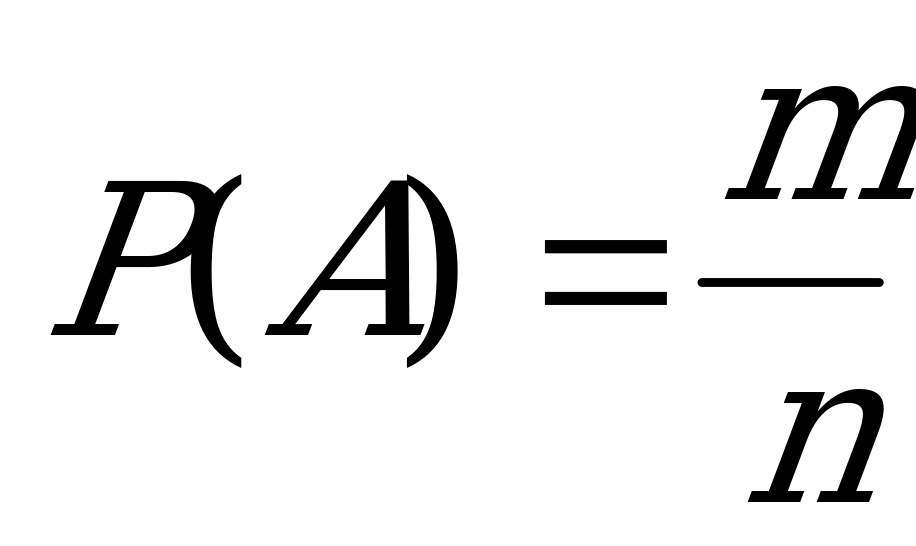
Испытание - выбор 5- ти шаров из 20.
Событие А – среди вынутых пяти шаров 3 оказались черными.(3 ч и 2 б)
Выбрать 5 шаров из 20 можно 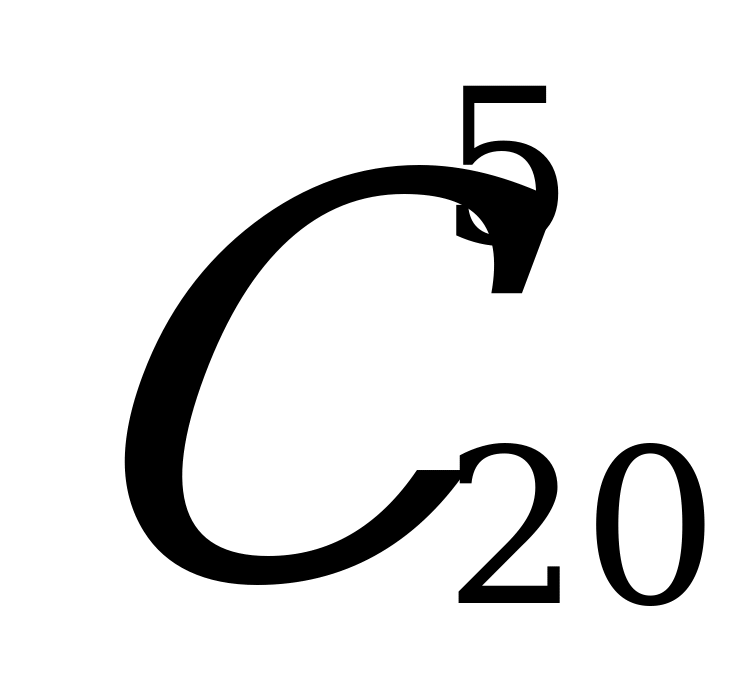 способами. Значит число всех элементарных исходов у данного испытания равно
способами. Значит число всех элементарных исходов у данного испытания равно 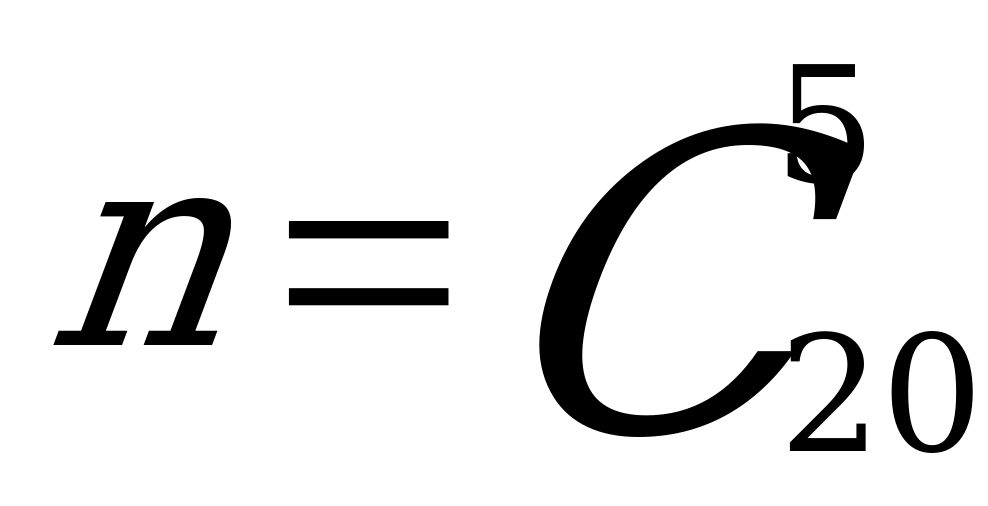 . Определим число исходов, благоприятствующих появлению события А. Число способов выбрать 3 черных шара из 8 равно
. Определим число исходов, благоприятствующих появлению события А. Число способов выбрать 3 черных шара из 8 равно 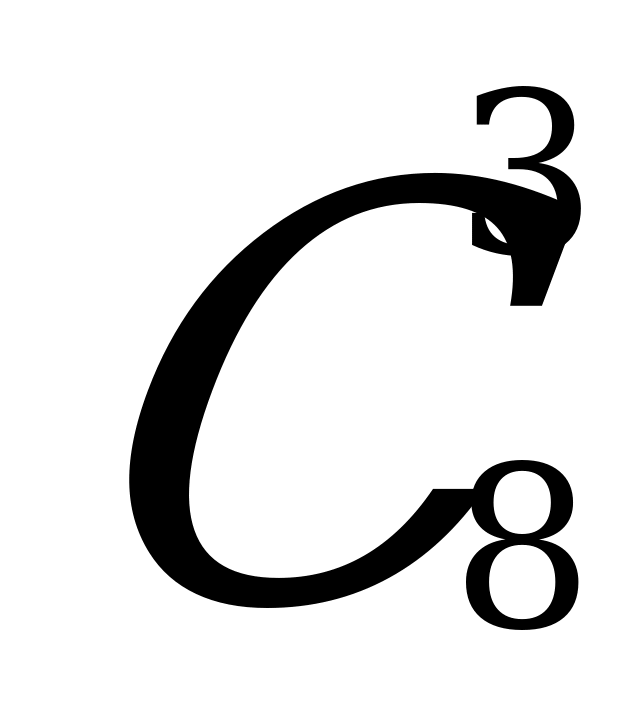 . Каждому такому выбору соответствует
. Каждому такому выбору соответствует 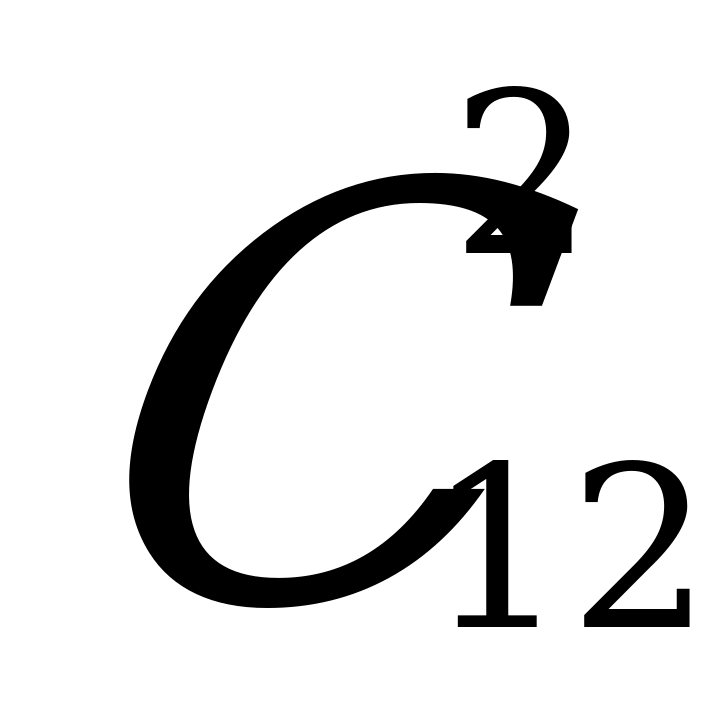 способов выбора 2-х белых шаров из 12 белых в урне. Следовательно, по правилу произведения, имеем
способов выбора 2-х белых шаров из 12 белых в урне. Следовательно, по правилу произведения, имеем 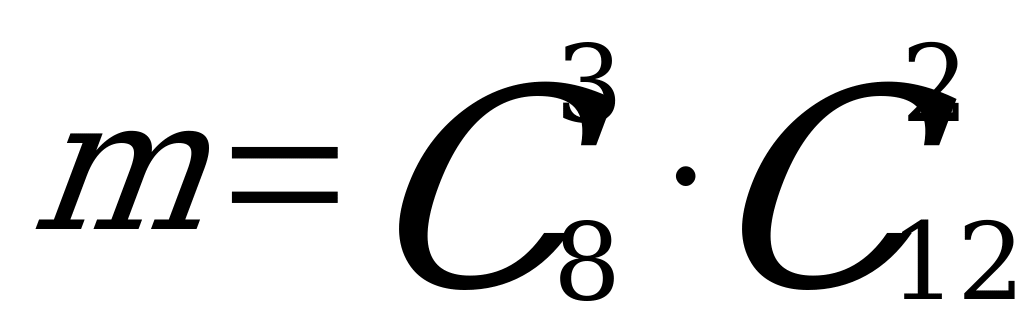 . Значит,
. Значит, 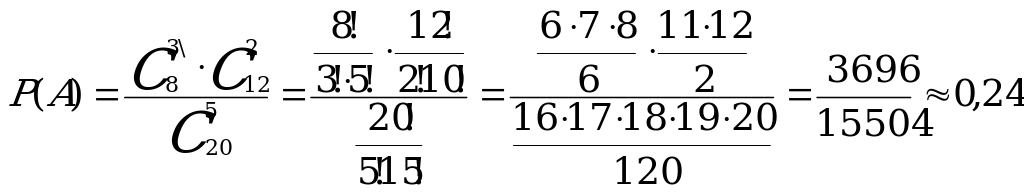
2. На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три – по математическому анализу и четыре по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность, сто он возьмет книгу по теории вероятностей или по линейной алгебре?
Решение:
Пусть А- студент взял книгу по теории вероятностей
В – студент взял книгу по линейной алгебре
С- студент взял книгу по теории вероятностей или по линейной
алгебре
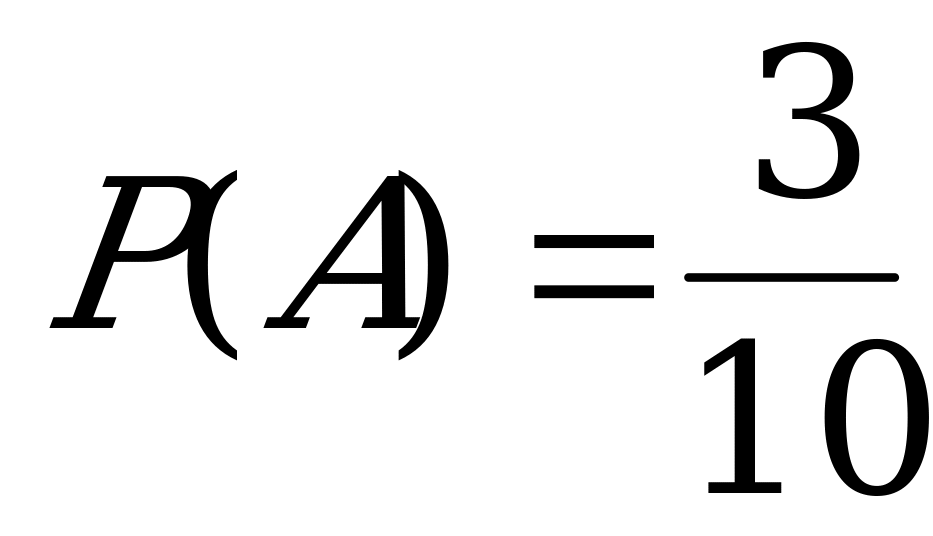
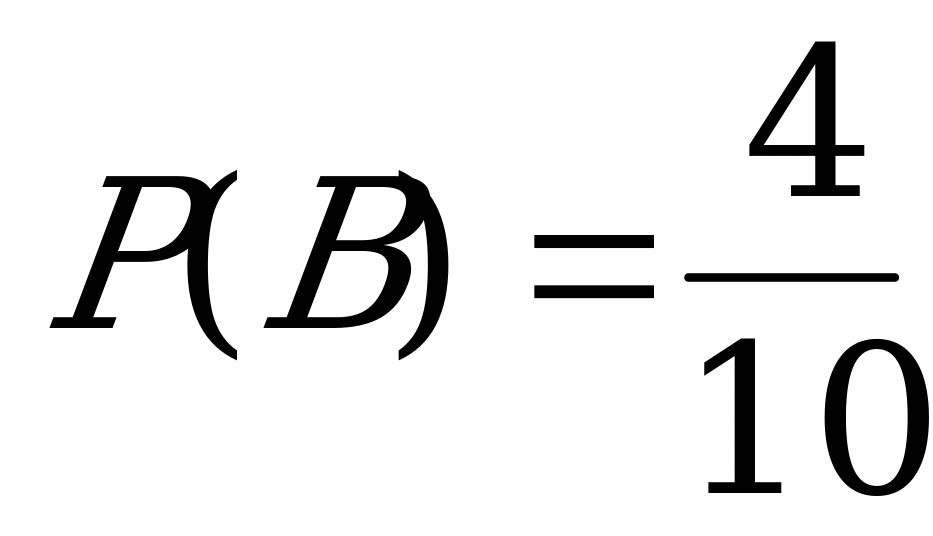 .
.
Так как событие С состоит в наступлении одного из событий А или В, то С=А+В. События А и В несовместны. По теореме сложения вероятностей несовместных событий, получаем: 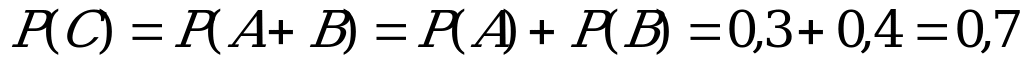 .
.
3.Контролер проверяет изделия на соответствие стандарту. Известно, что
вероятность соответствия стандарту изделий равна 0,9.
А) какова вероятность того, что из двух проверенных изделий оба будут
стандартными, если события появления стандартных изделий
независимы?
Б) какова вероятность того, что из двух проверенных изделий только
одно стандартное?
Решение:
а) Учитывая то, что события А (первое изделие стандартное) и В (второе
изделие стандартное) независимы, используем формулу:
Р(АВ)=Р(А)Р(В)=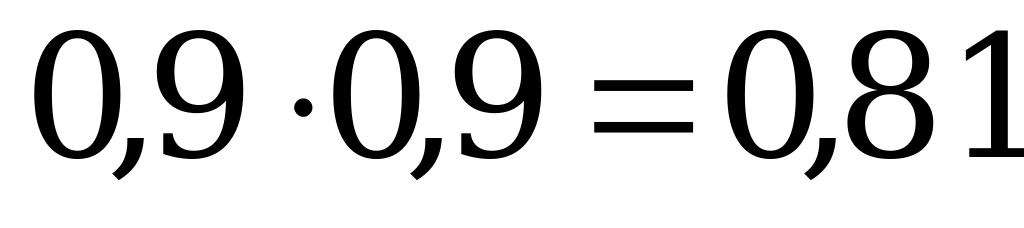 .
.
Б) Пусть 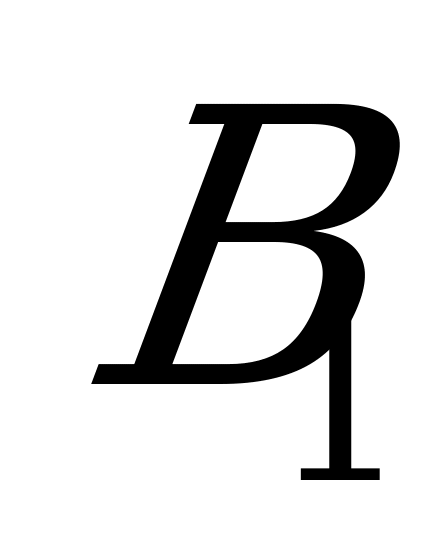 - событие, состоящее в том, что только первое событие стандартное,
- событие, состоящее в том, что только первое событие стандартное, 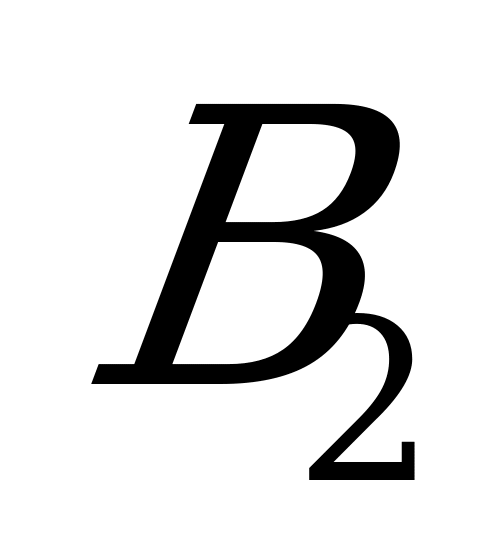 - только второе стандартное. Событие С-« из двух проверенных изделий только одно стандартное» состоит в наступлении одного из
- только второе стандартное. Событие С-« из двух проверенных изделий только одно стандартное» состоит в наступлении одного из 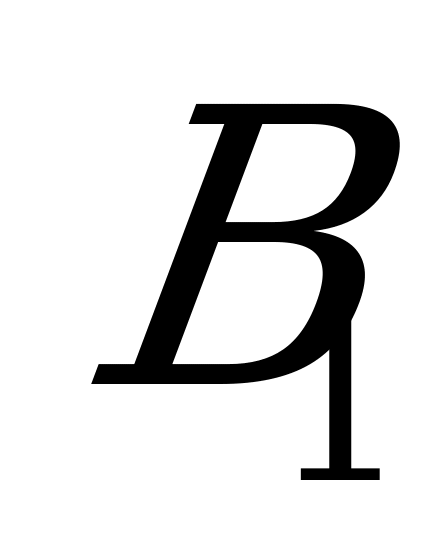 и
и 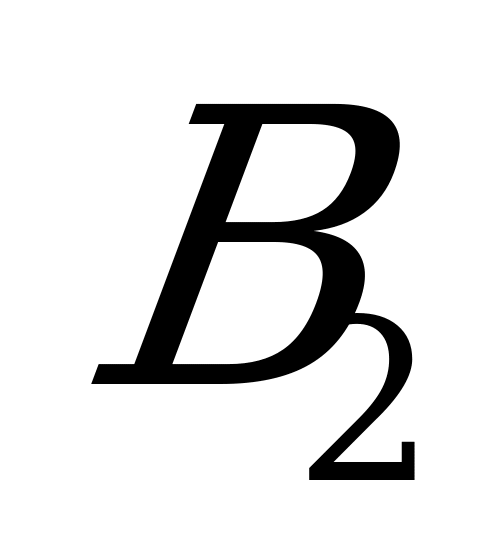 , поэтому С=
, поэтому С=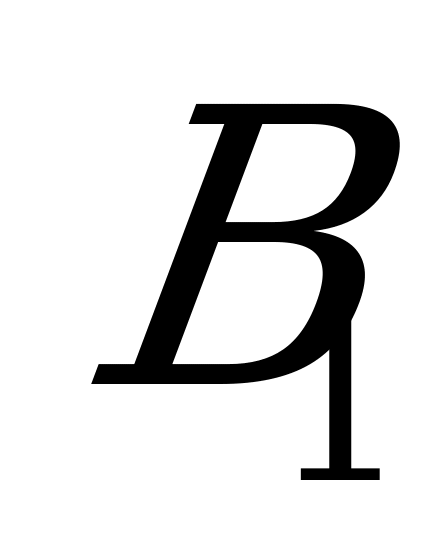 +
+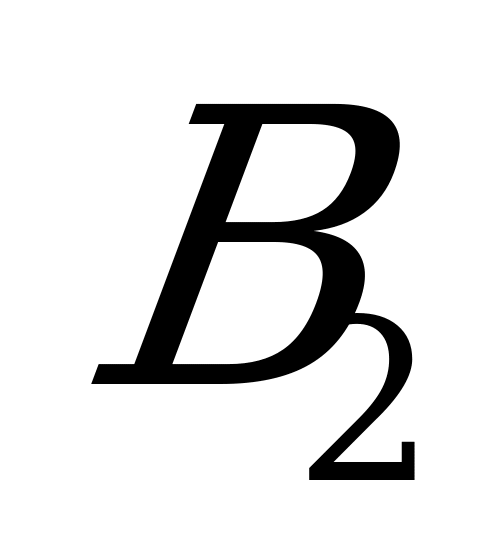 . Так как события
. Так как события 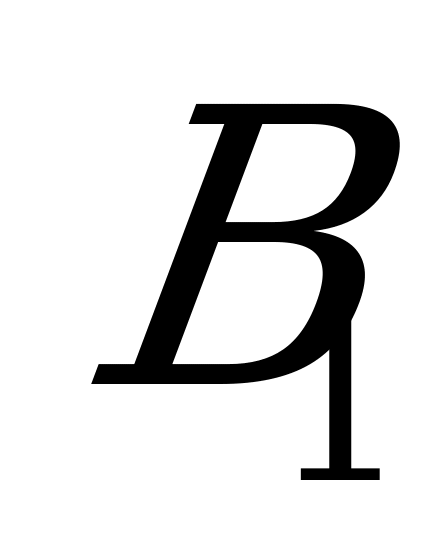 и
и 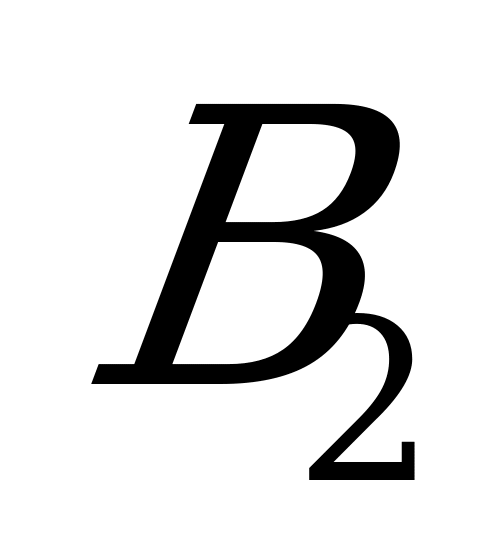 несовместны, то Р(С)=Р(
несовместны, то Р(С)=Р(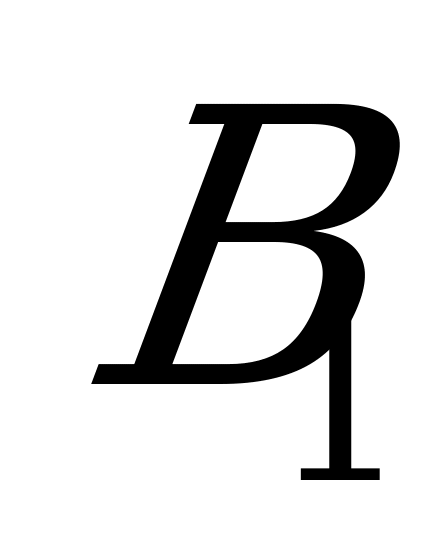 +
+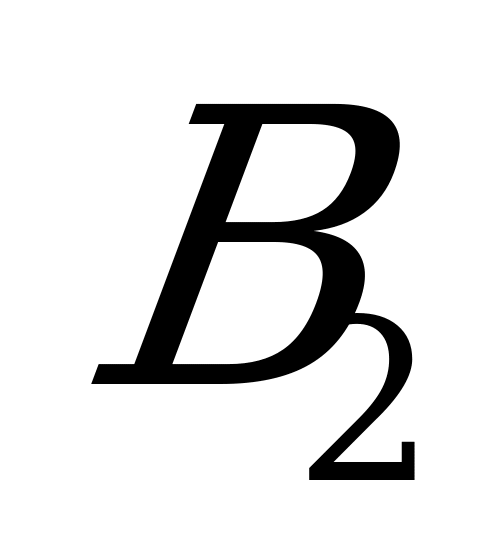 )=Р(
)=Р(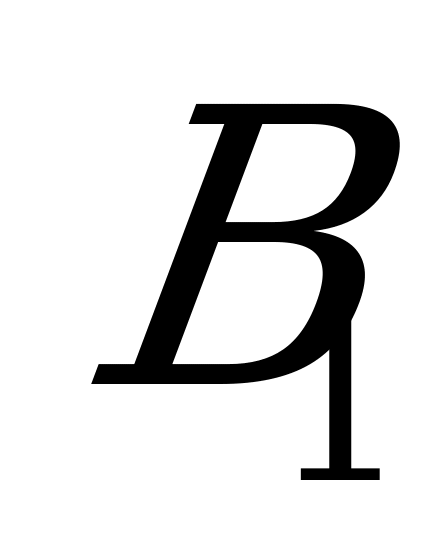 )+Р(
)+Р(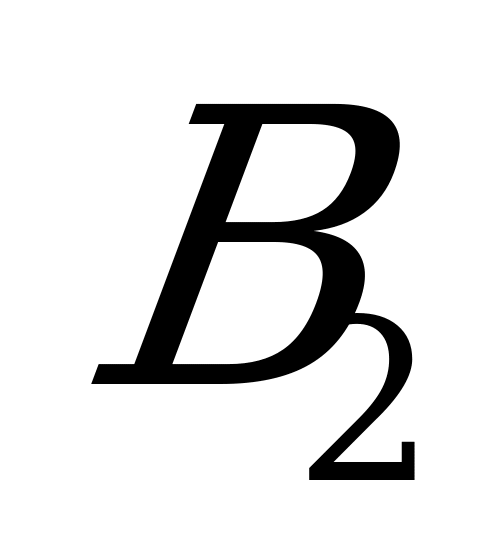 ).
).
Событие  можно рассматривать как произведение двух событий:
можно рассматривать как произведение двух событий: 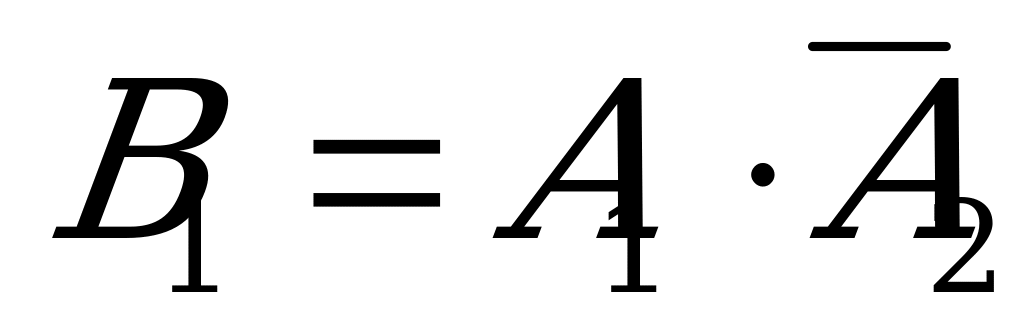 , т.е. появилось первое событие и не появилось второе. Аналогично,
, т.е. появилось первое событие и не появилось второе. Аналогично, 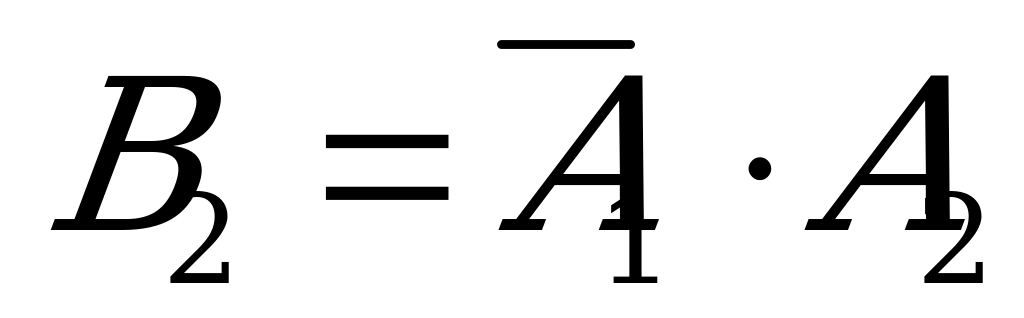 .
.
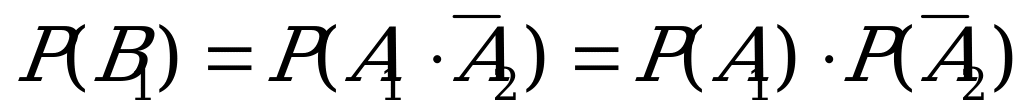 ,
, 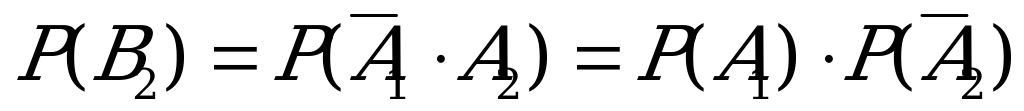 .
.
Если обозначить вероятность появления стандартного изделия через р, а вероятность противоположного события через 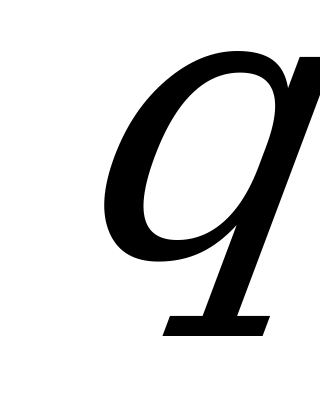 =1-р, то получим:
=1-р, то получим:
Р(С)=Р(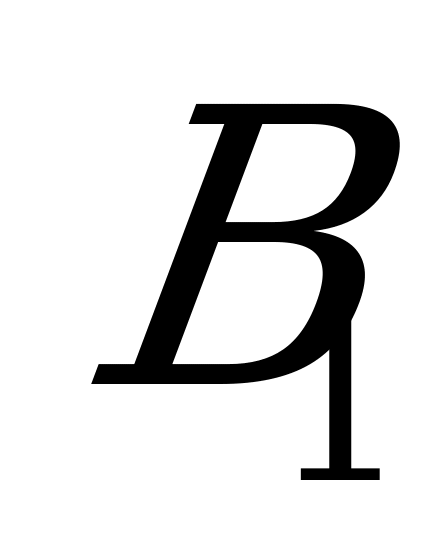 +
+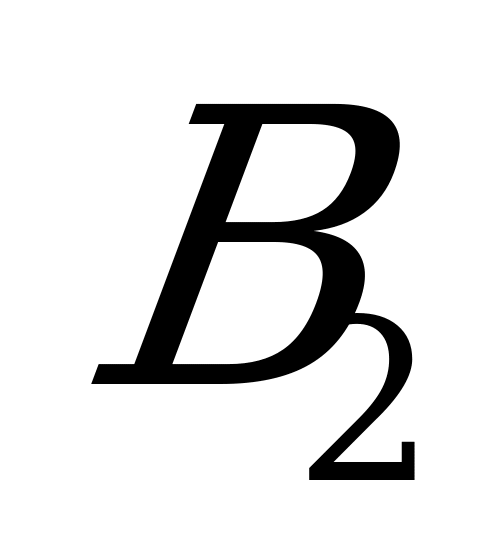 )=Р(
)=Р(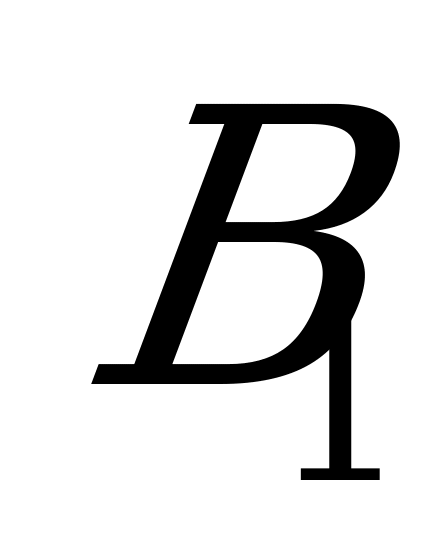 )+Р(
)+Р(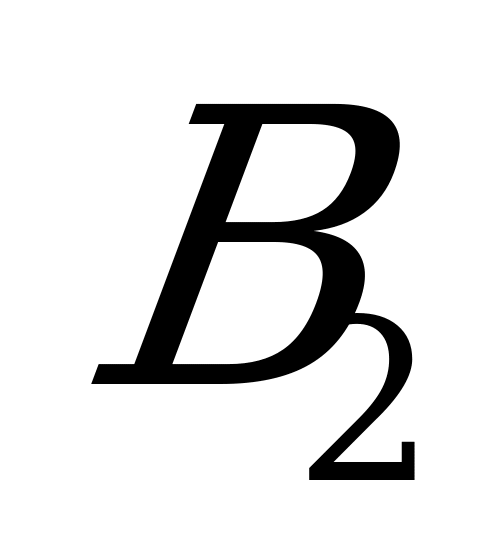 )
)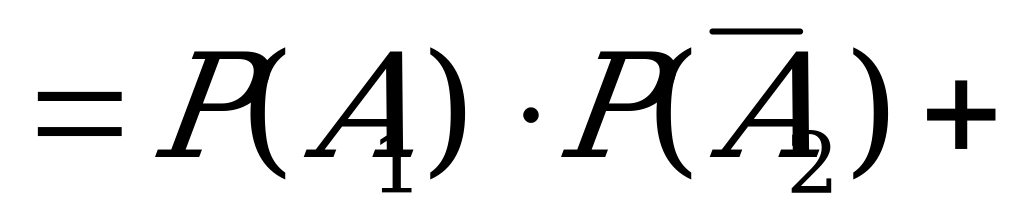
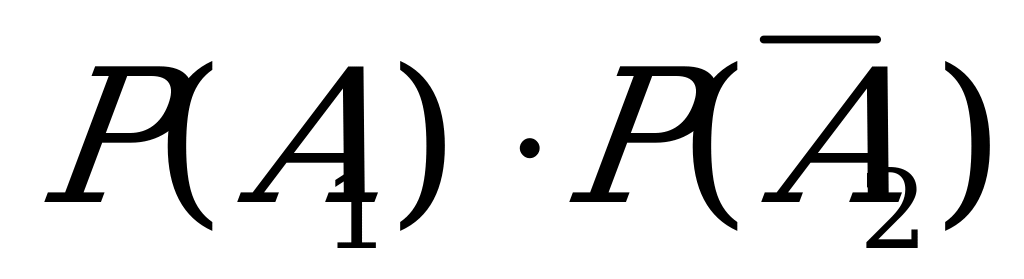 =
=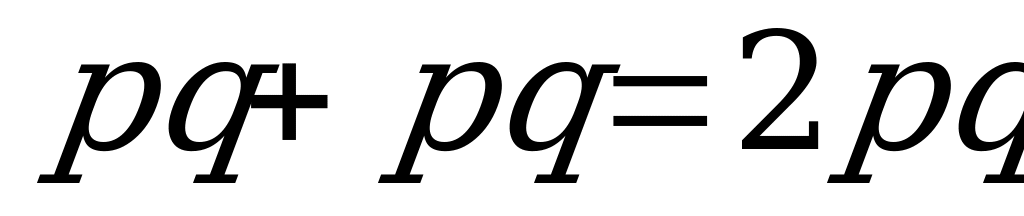
Так как р=0,9, то q=1-0,9=0,1 Значит 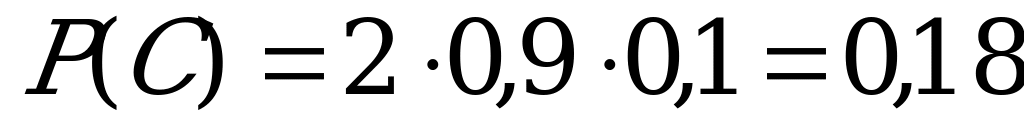 .
.
4. В районе 100 поселков. В пяти из них находятся пункты проката сельской
техники. Случайным образом отобраны 2 поселка. Найти вероятность
того, что в них окажутся пункты проката.
Решение:
Пусть А – событие, состоящее в том, что в первом выбранном поселке находится пункт проката, В – событие, состоящее в том, что во втором выбранном поселке находится пункт проката.
Вероятность события А равна 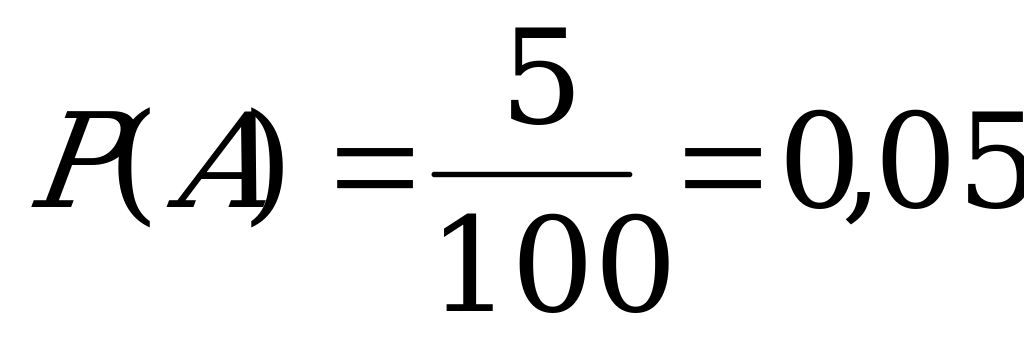 .
.
Рассмотрим событие В при условии, что событие А уже произошло. Найдем условную вероятность 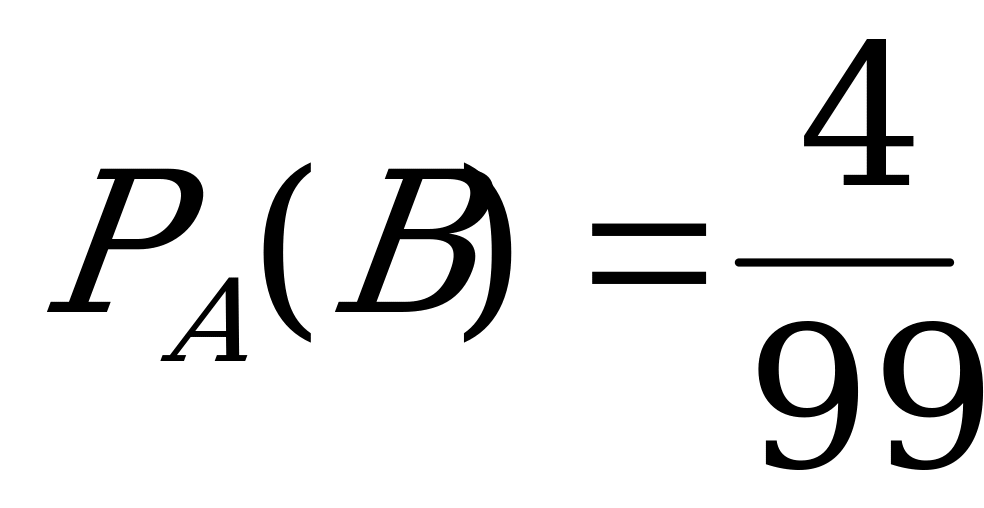 .
.
Искомая вероятность найдется как вероятность произведения двух событий:
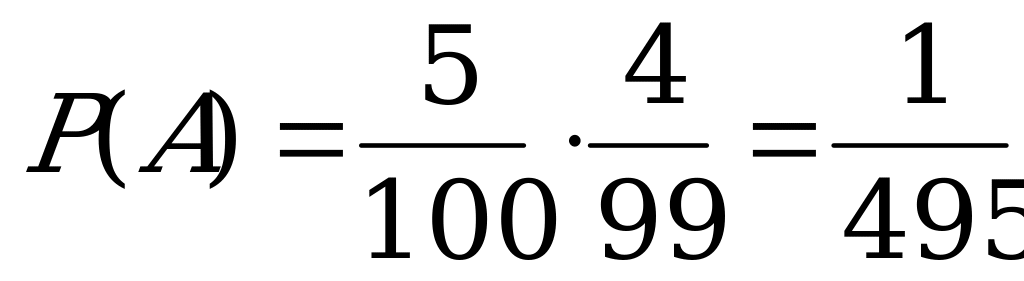 .
.
5. На автозавод поступили двигатели от трех моторных заводов. От
первого завода поступило 10 двигателей, от второго 6, и от третьего – 4
двигателя. Вероятности безотказной работы этих двигателей в течение
гарантийного срока соответственно равны 0,9;0,8;0,7.
Какова вероятность того, что:
А) установленный на машине двигатель будет работать без дефектов в
течение гарантийного срока.
Б) проработавший без дефекта двигатель изготовлен на первом заводе, на
втором заводе?
Решение:
Обозначим через 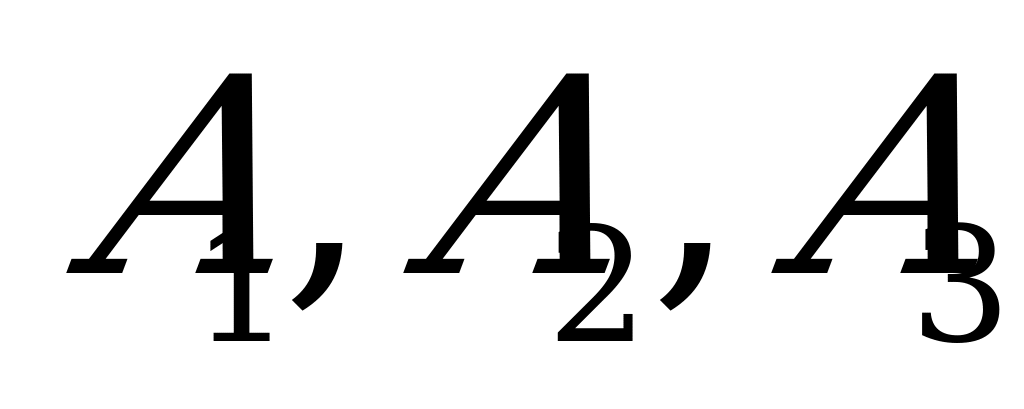 события установки на автомашину двигателей, изготовленных соответственно на первом, втором и третьем моторных заводах. Вероятности этих событий таковы:
события установки на автомашину двигателей, изготовленных соответственно на первом, втором и третьем моторных заводах. Вероятности этих событий таковы: 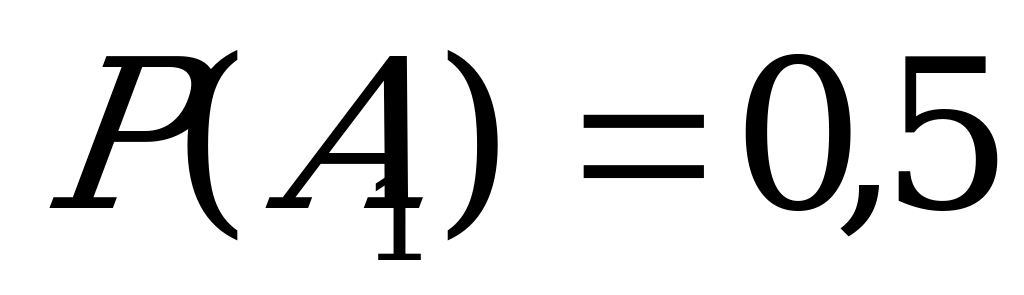 ,
, 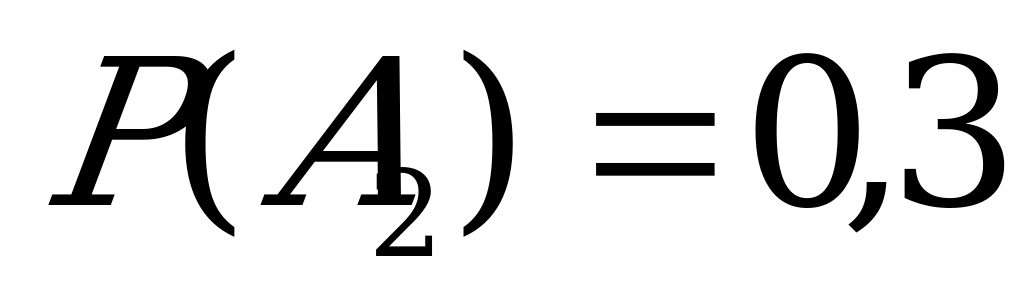 ,
, 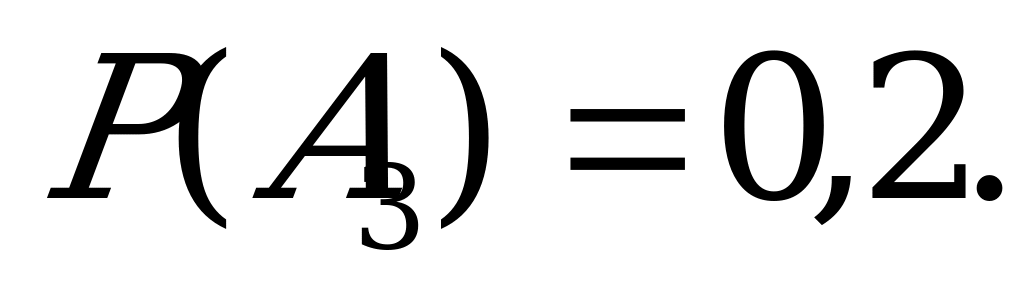
А)Вероятность того, что наугад взятый двигатель проработает без дефектов,
найдем по формуле полной вероятности:
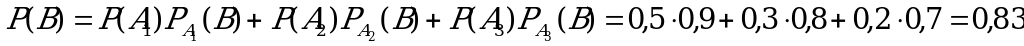
Б) Если двигатель проработал без дефектов гарантийный срок, то
вероятности того, что он изготовлен на первом, втором заводах, найдем
по формуле Байеса:
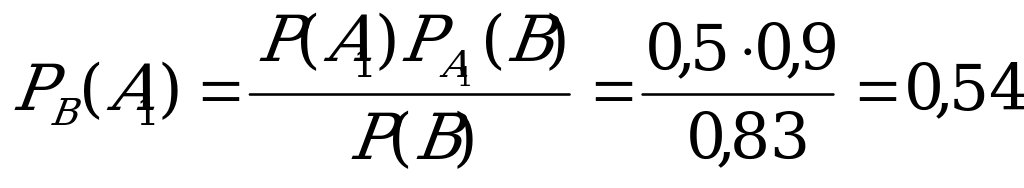

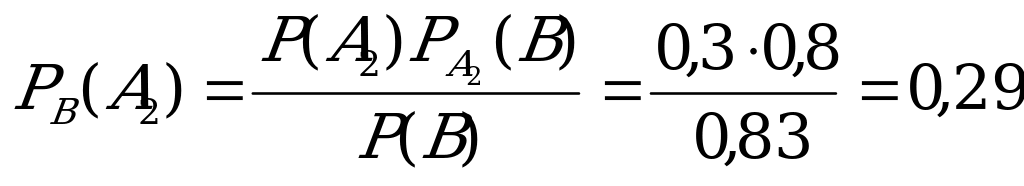
6. В результате обследования были выделены семьи, имеющие по 4 ребенка.
Считая вероятности появления мальчика и девочки в семье равными,
определить вероятности появления в ней:
А)одного мальчика
Б) двух мальчиков.
Решение:
Вероятность появления мальчика или девочки равна р=0,5. Вероятность появления мальчика в семье, имеющей четырех детей, находится по формуле Бернулли:
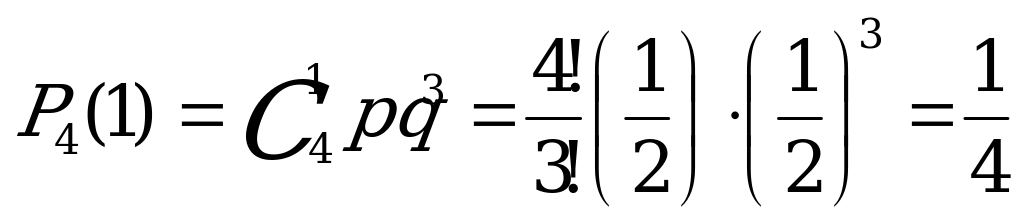 .
.
Вероятность появления в семье двух мальчиков равна
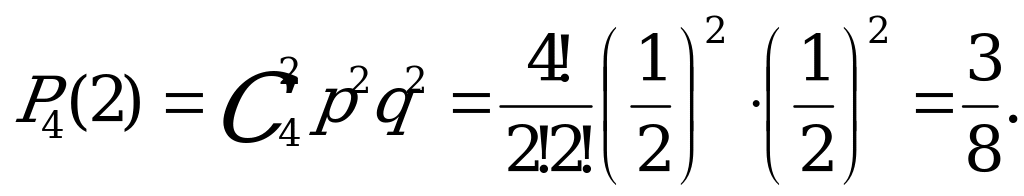
7. В новом микрорайоне поставлено 10000 кодовых замков на входных
дверях домов. Вероятность выхода из строя одного замка в течение
месяца равна 0,0002. Найти вероятность того, что за месяц откажут два,
три и пять замков.
Решение:
Используем формулу Пуассона: 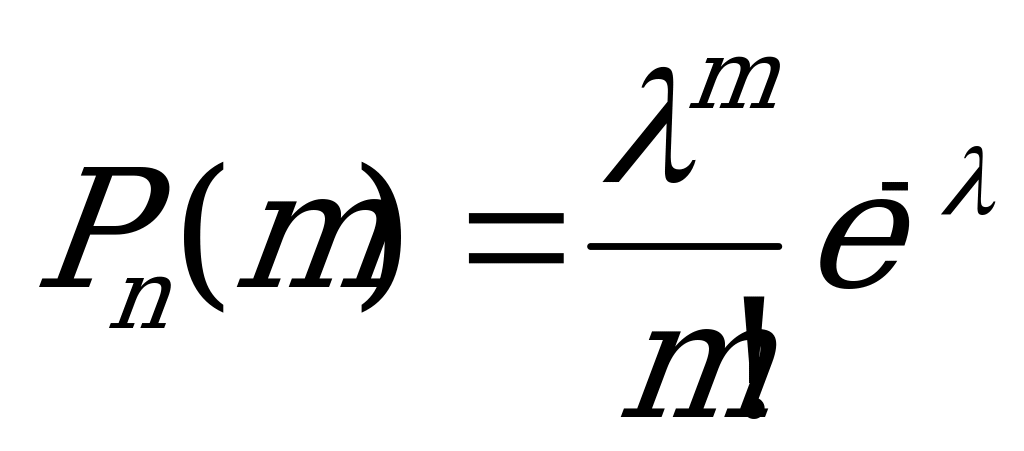 ,
, 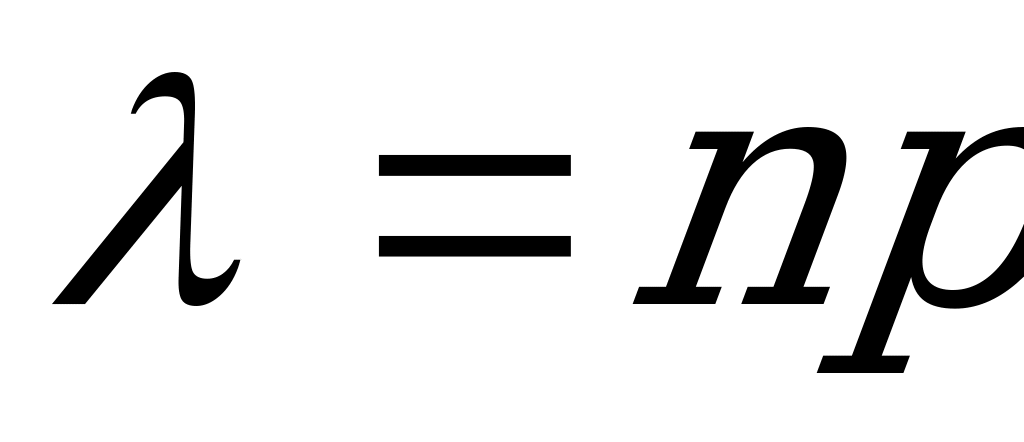 .
.
В нашем случае: 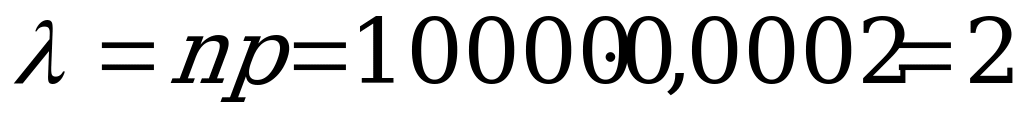 ,
,
тогда 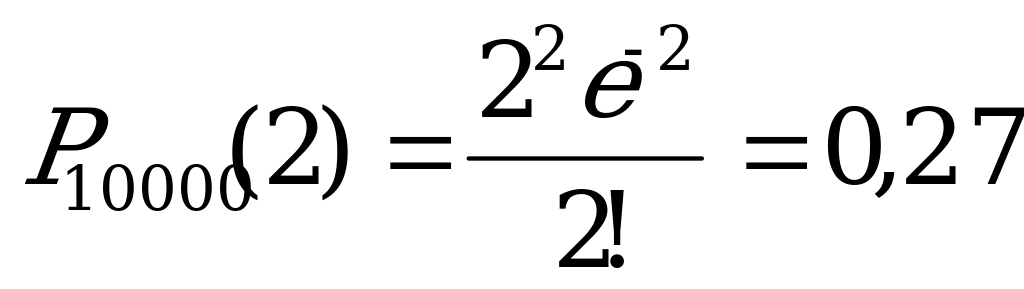 ,
, 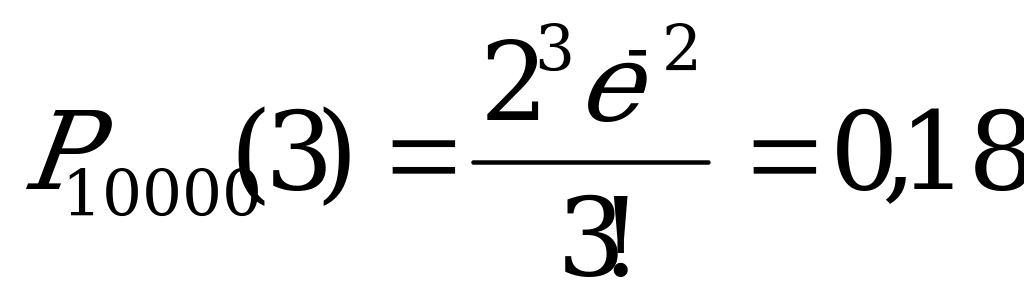 ,
, 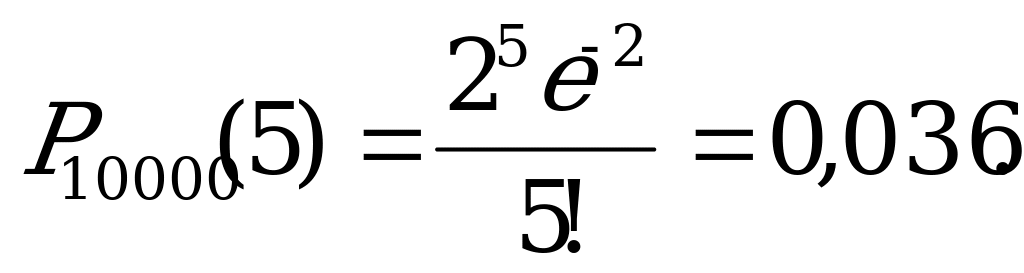
8. Среди 10 лотерейных билетов имеется 4 билета с выигрышем. Наудачу
покупают 2 билета. Написать закон распределения числа выигрышных
билетов среди купленных.
Решение:
Пусть Х – случайная величина числа выигрышных билетов среди 2 купленных билетов. Очевидно, что она может принимать значения: 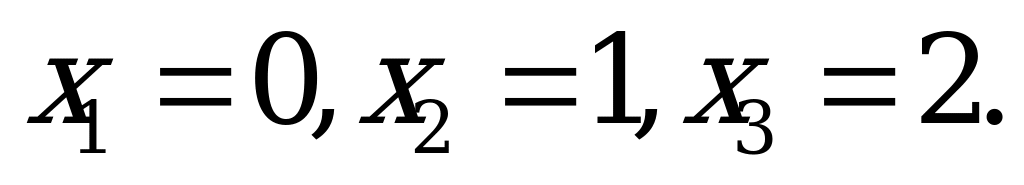 Для определения вероятности появления каждого из этих значений воспользуемся следующей формулой:
Для определения вероятности появления каждого из этих значений воспользуемся следующей формулой:
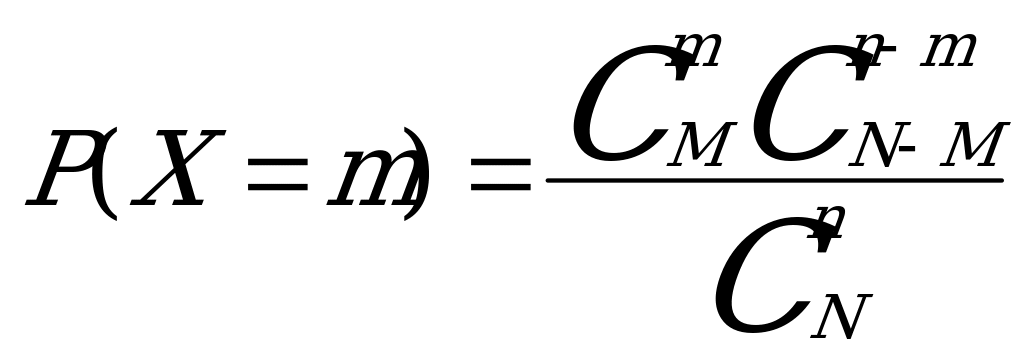 ,
,
где m=0,1,2 – число выигрышных билетов среди наудачу купленных n=2
билетов.
N=10 – всего имеющихся билетов
М=4 – число выигрышных среди всех 10 билетов.
Вычисляем соответствующие вероятности:
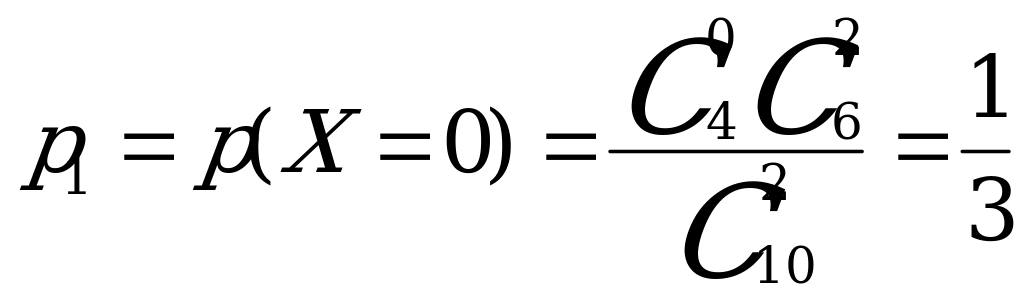 ,
, 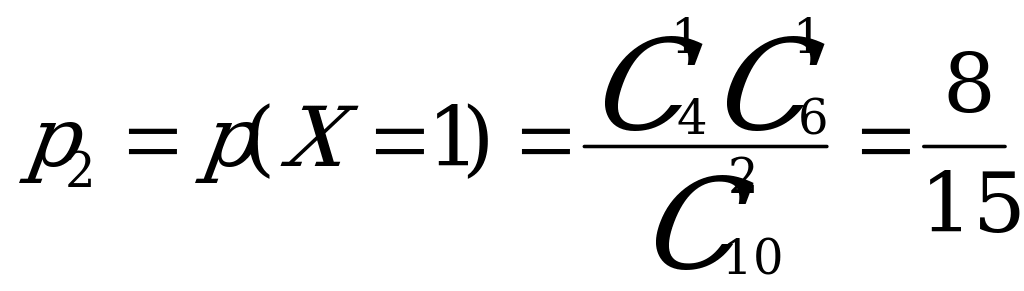
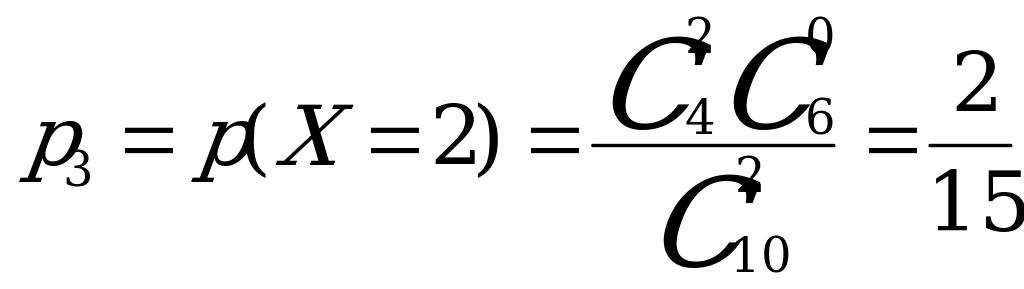 .
.
Для проверки вычислений сложим 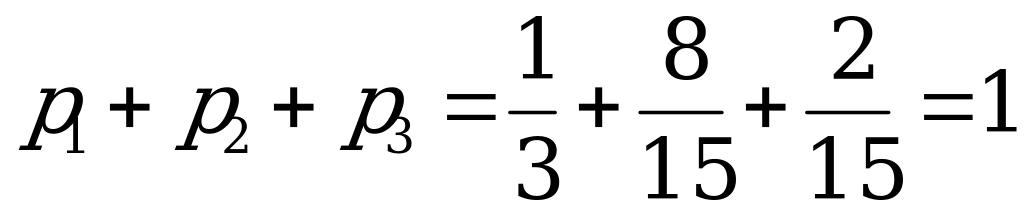 .
.
Следовательно, искомый закон распределения имеет вид:
9. Баскетболист делает три штрафных броска. Вероятность попадания при
каждом броске равна 0,7. Построить ряд распределения числа попаданий
мяча в корзину.
Решение:
Пусть Х – случайная величина числа попаданий мяча в корзину. Баскетболист может не попасть ни разу, один раз, два раза и все три раза, значит 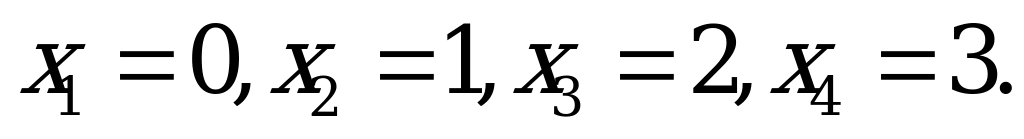 Вероятности вычисляем по формуле Бернулли, при этом
Вероятности вычисляем по формуле Бернулли, при этом 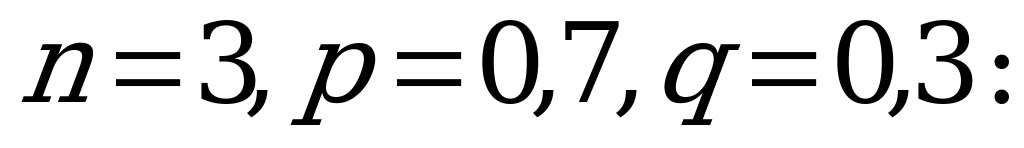
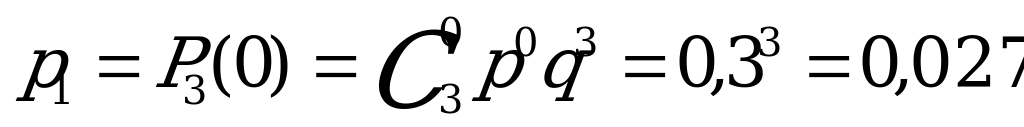
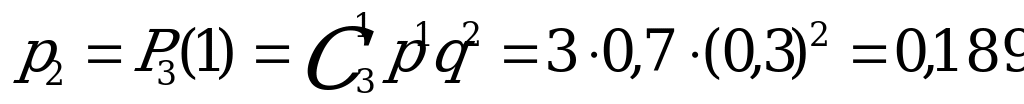
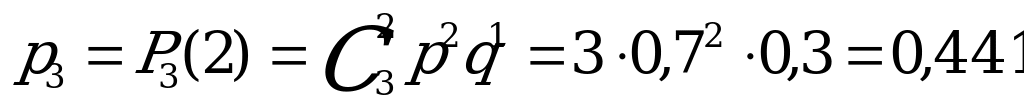 .
.
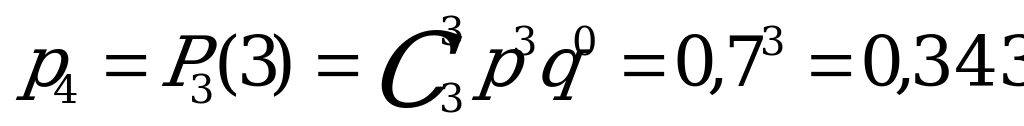
Для проверки вычислений сложим 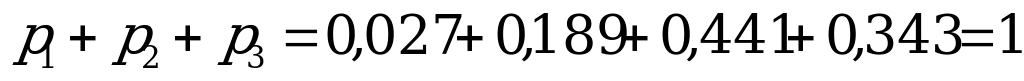 .
.
Тогда ряд распределения случайной величины числа попаданий мяча в корзину при трех бросках имеет вид:
| Х | 0 | 1 | 2 | 3 |
| р | 0,027 | 0,189 | 0,441 | 0,343 |
10. Даны законы распределения двух независимых случайных величин:
| Х | 2 | 4 | 6 | 8 |
| р | 0,4 | 0,2 | 0,1 | 0,3 |
Найти математическое ожидание и дисперсию случайной величины Z=2X+3Y.
Решение:
Используя свойства математического ожидания и дисперсии, а также учитывая, что X и Y независимые случайные величины, имеем:
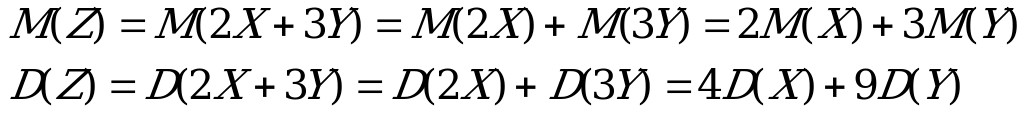
Используя определение математического ожидания и свойства дисперсии, получаем:
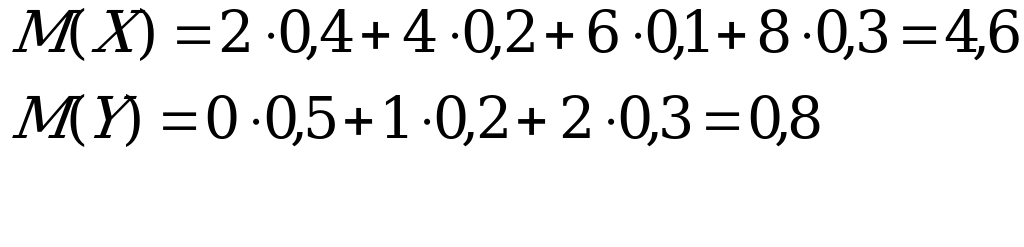
Тогда 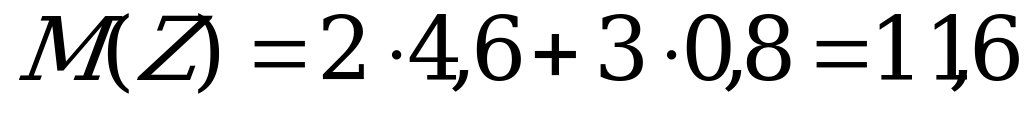
По формуле 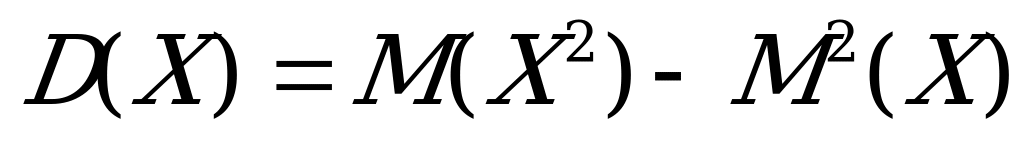
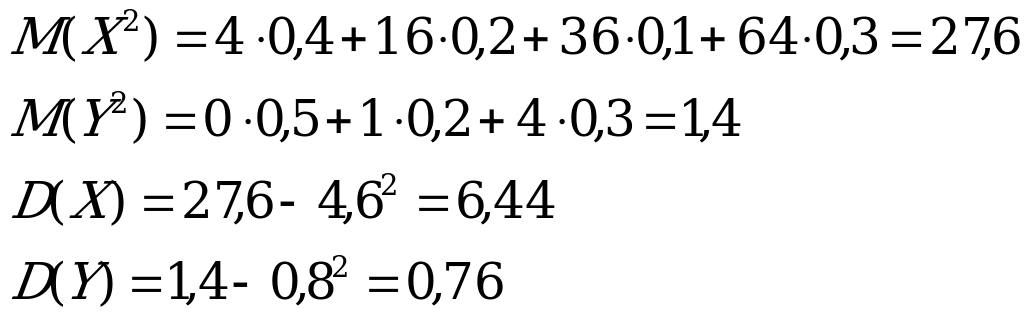
Тогда 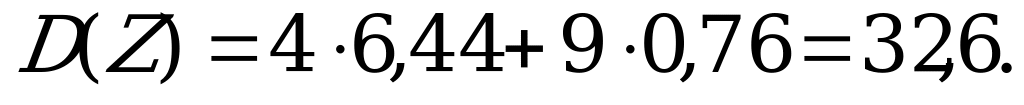
11. Два консервных завода оставляют продукцию в магазин в пропорции
2:3. Доля продукции высшего качества на первом заводе составляют
90%, на втором – 80%. В магазине куплено три банки консервов. Найти
математическое ожидание и среднее квадратичное отклонение числа
банок с продукцией высшего качества.
Решение:
Вначале составим закон распределения случайной величины Х – числа банок с продукцией высшего качества среди купленных трех банок. Вероятность появления события А - куплена банка с продукцией высшего качества – найдем по формуле полной вероятности:
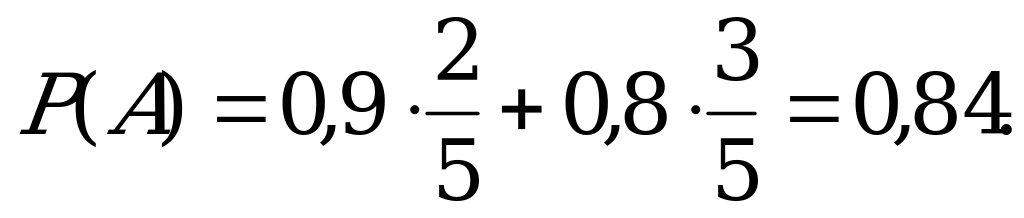
Закон распределения случайной величины Х можно определить, используя формулу Бернулли:
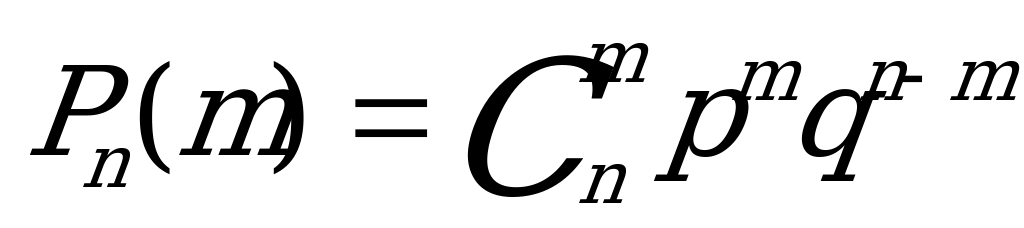
Случайная величина Х может принимать значения 0,1,2,3. Закон ее распределения ( с учетом того, что р=0,84, q=0,16) примет вид
| Х | 0 | 1 | 2 | 3 |
| р | 0,004 | 0,066 | 0,337 | 0,593 |
(Убедитесь самостоятельно)
Тогда,
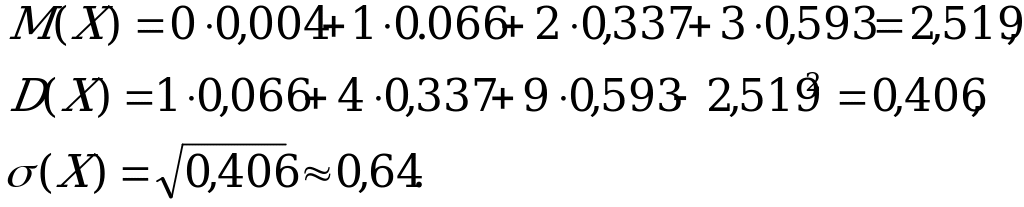
12. Случайная величина Х задана функцией распределения вероятностей

 если
если 
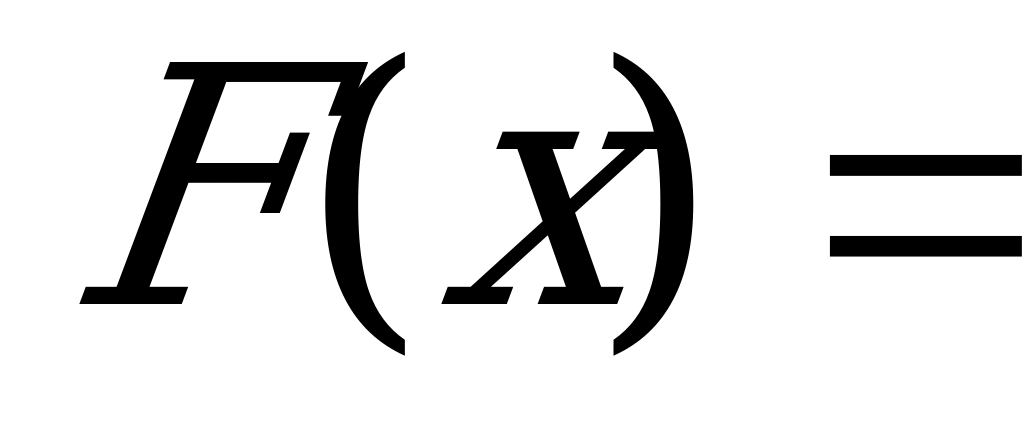
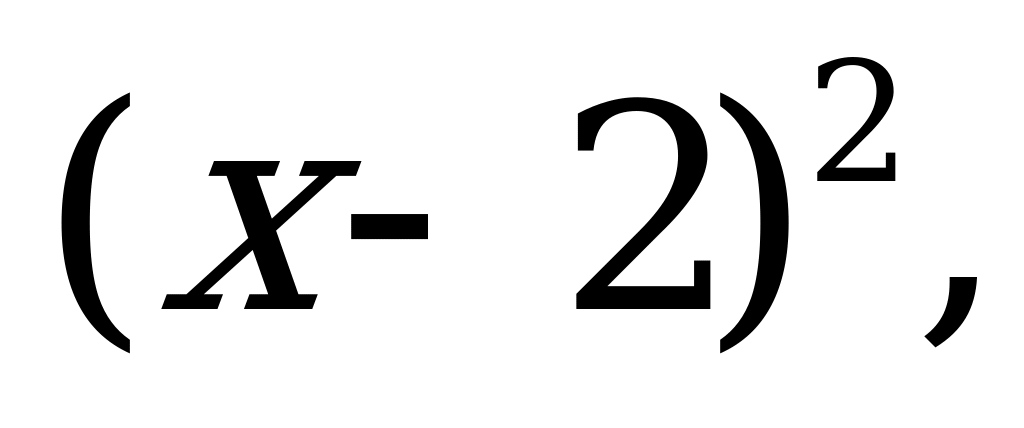 если
если 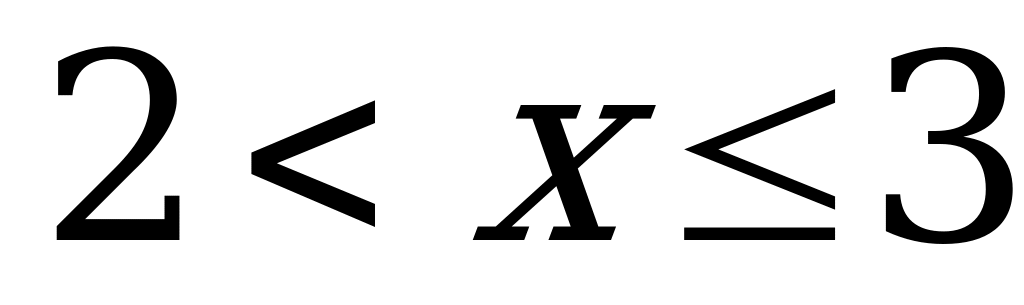
1, если 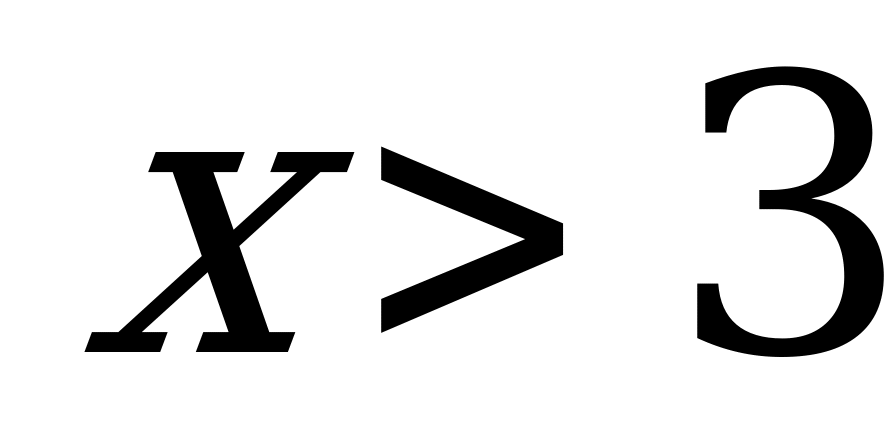
Найти плотность вероятности f(x) и вероятность попадания случайной величины Х в интервалы (1;2,5), (2,5;3,5).
Решение:
Плотность вероятности находим по формуле 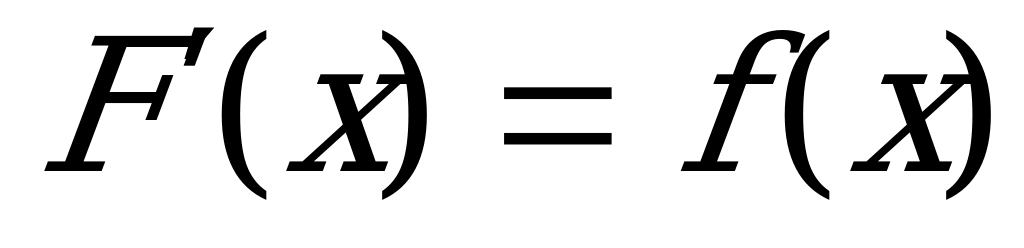 ;
;

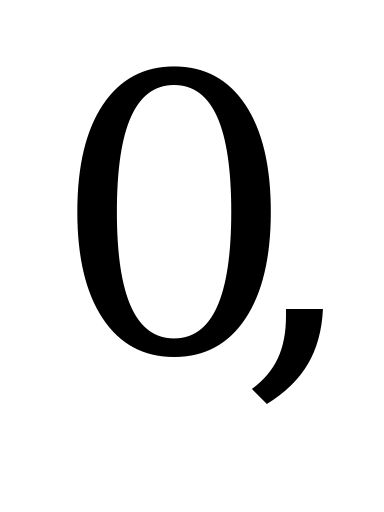 если
если 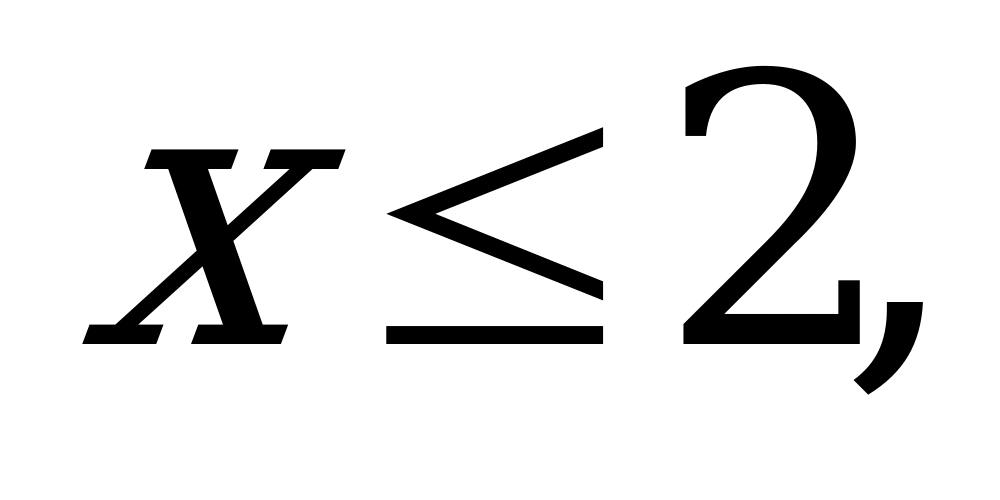
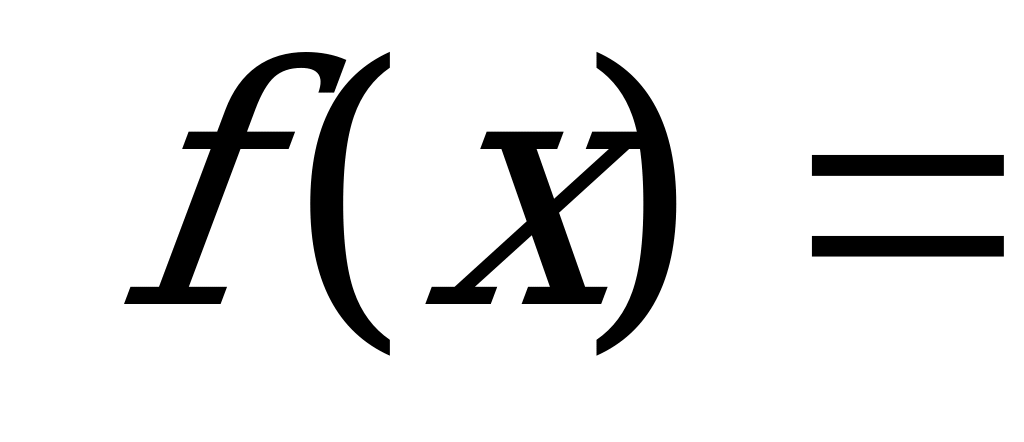
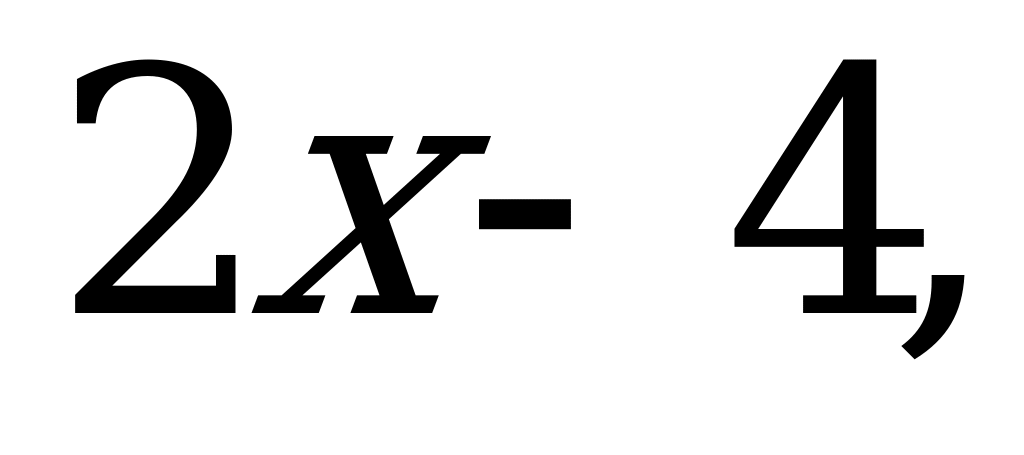 если
если 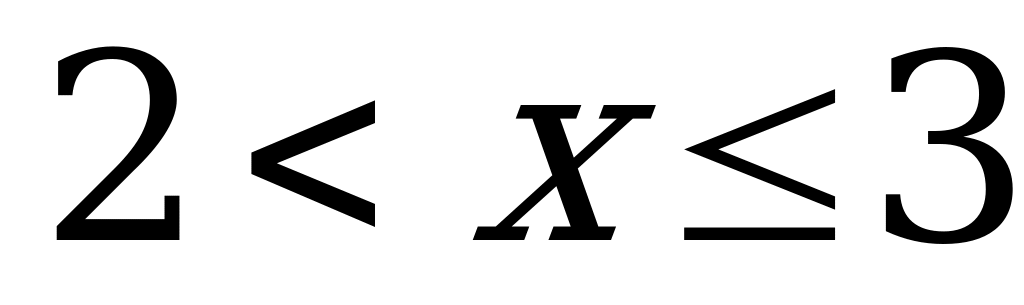
0, если 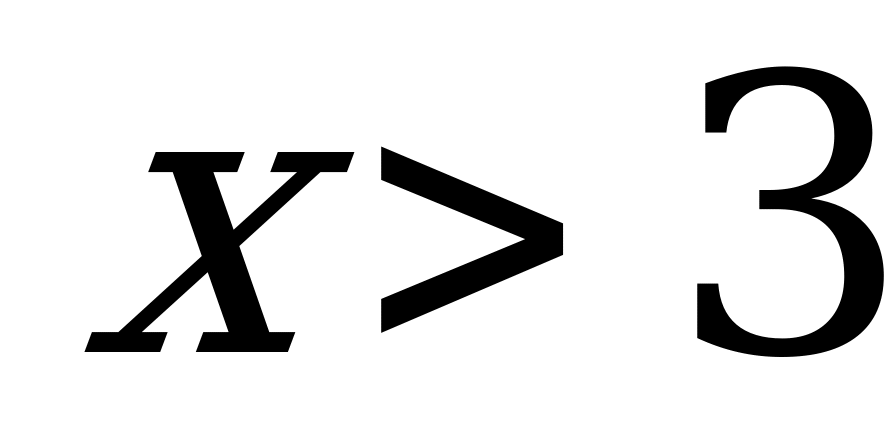
Находим вероятности попадания случайной величины Х в интервалы
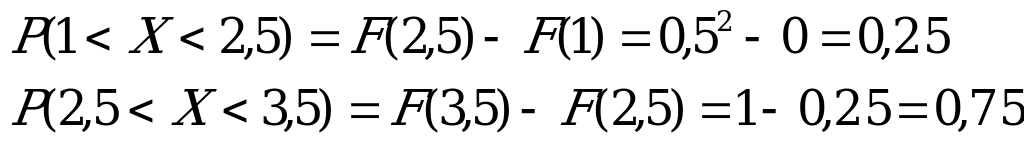
13. Плотность вероятности непрерывной случайной величины Х

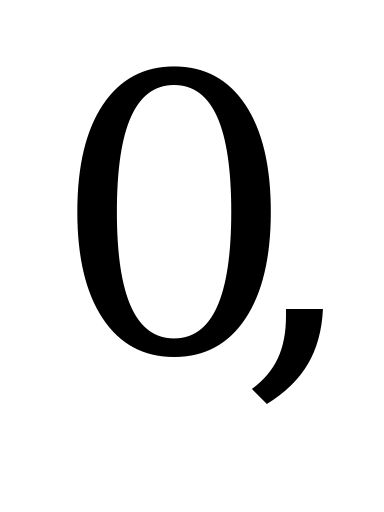 если
если 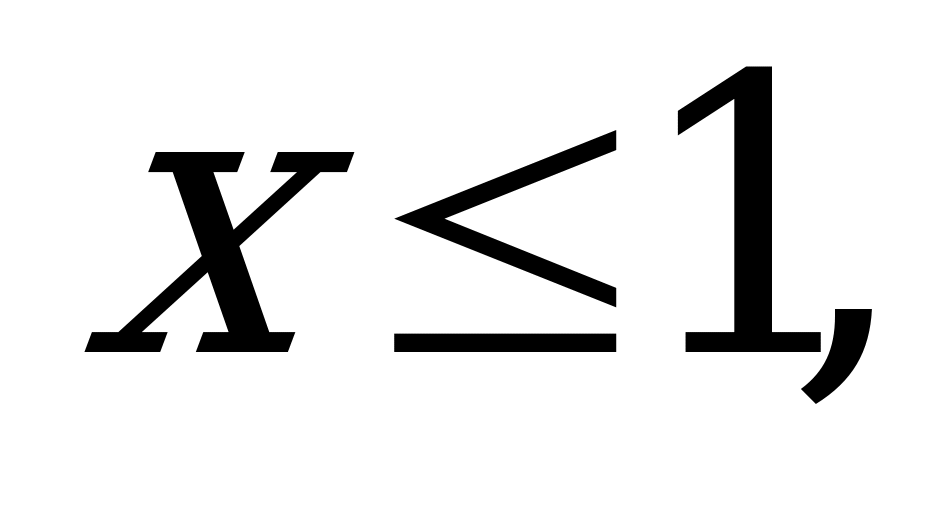
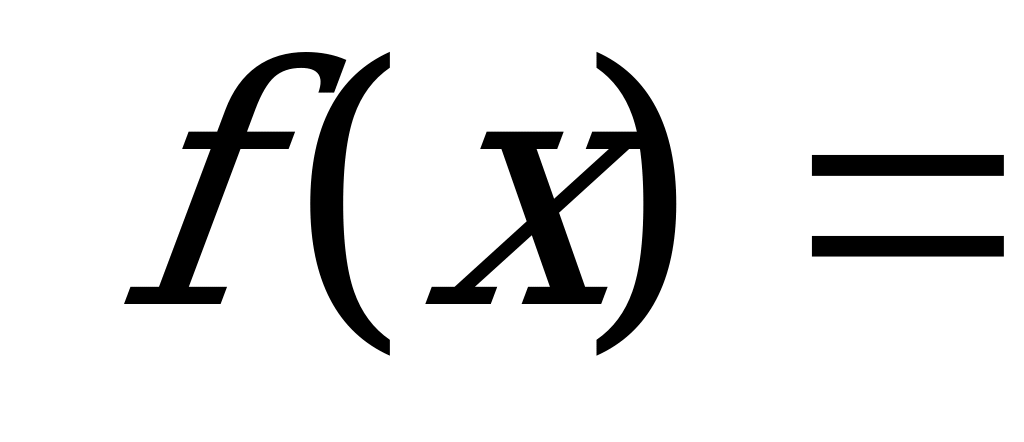
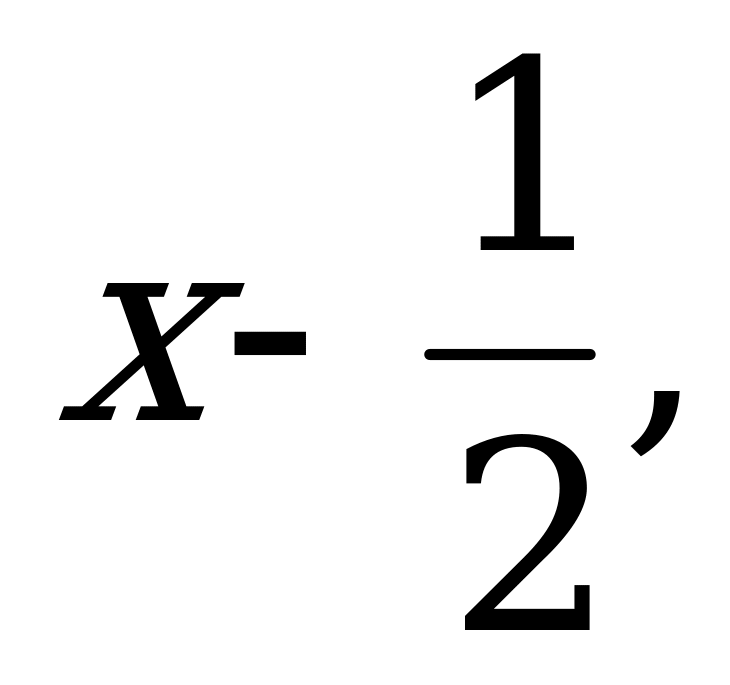 если
если 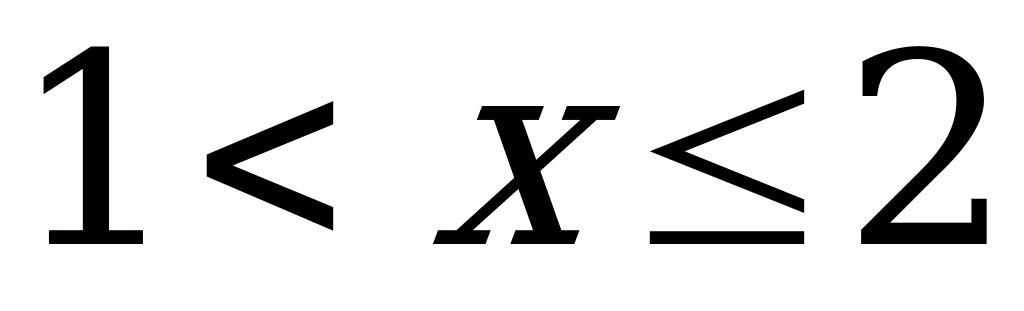
0, если 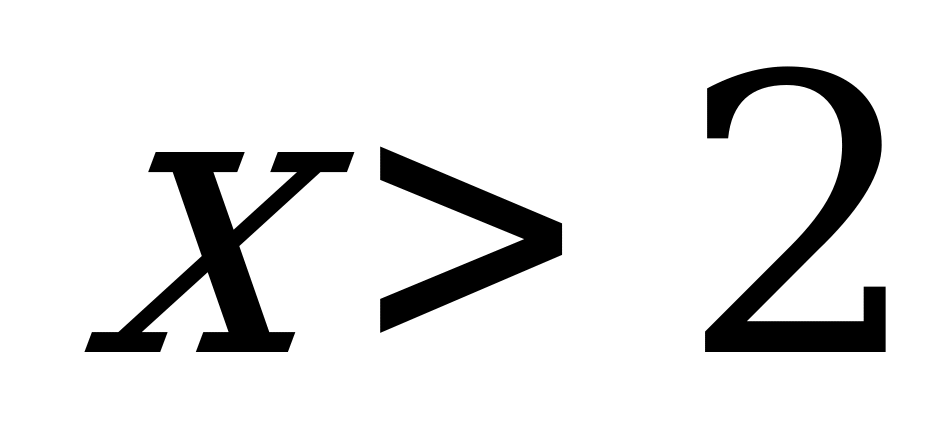
Найти функцию распределения F(x).
Решение:
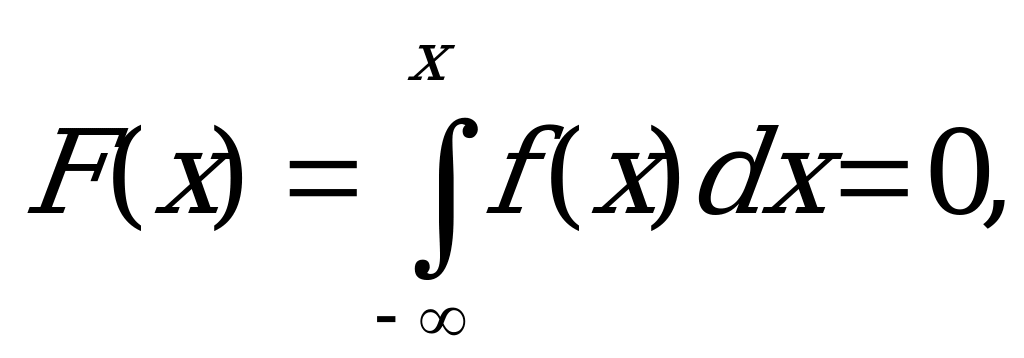 если
если 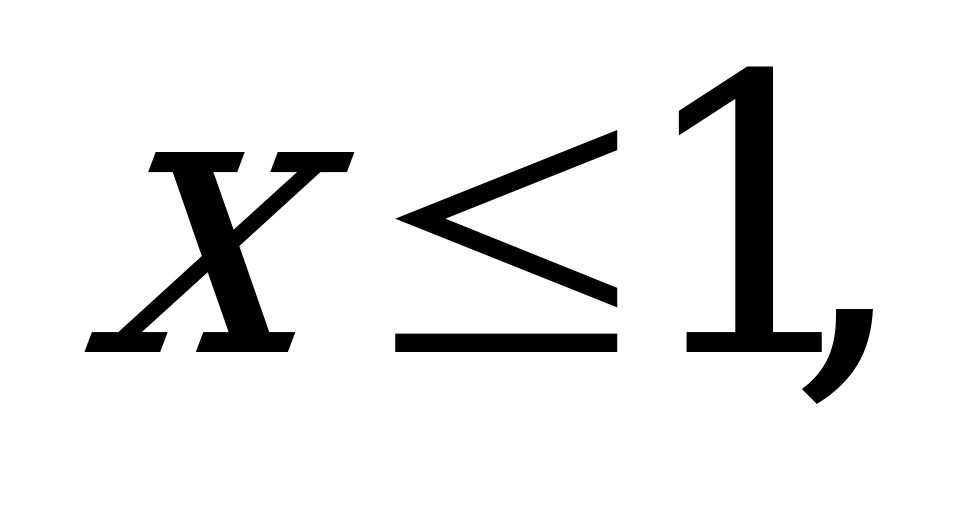
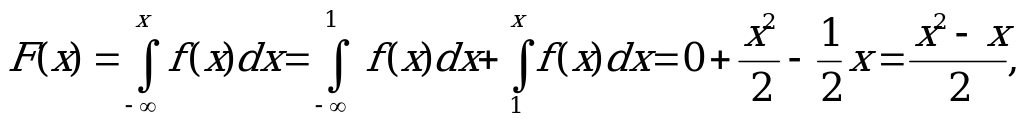 если
если 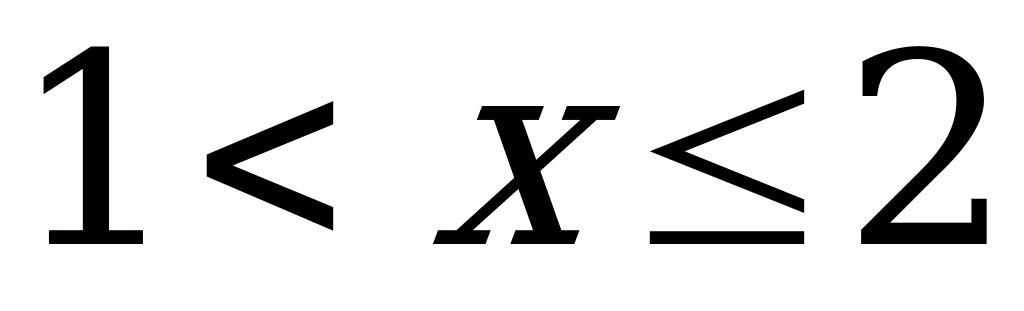
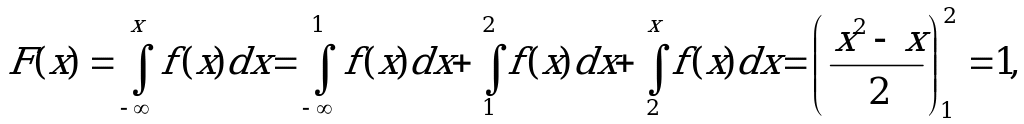 если х2.
если х2.
14. Плотность вероятности непрерывной случайной величины Х задана в
виде 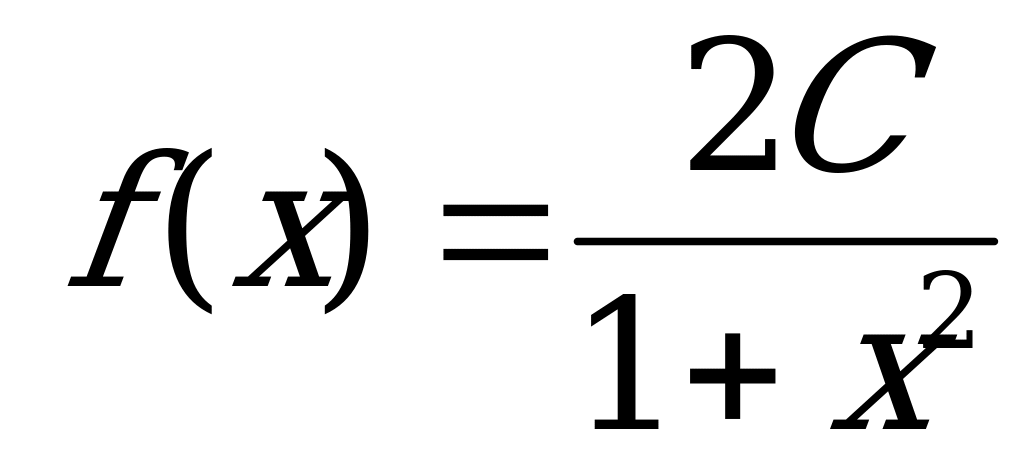 . Найти параметр С.
. Найти параметр С.
Решение:
На основании условия нормировки 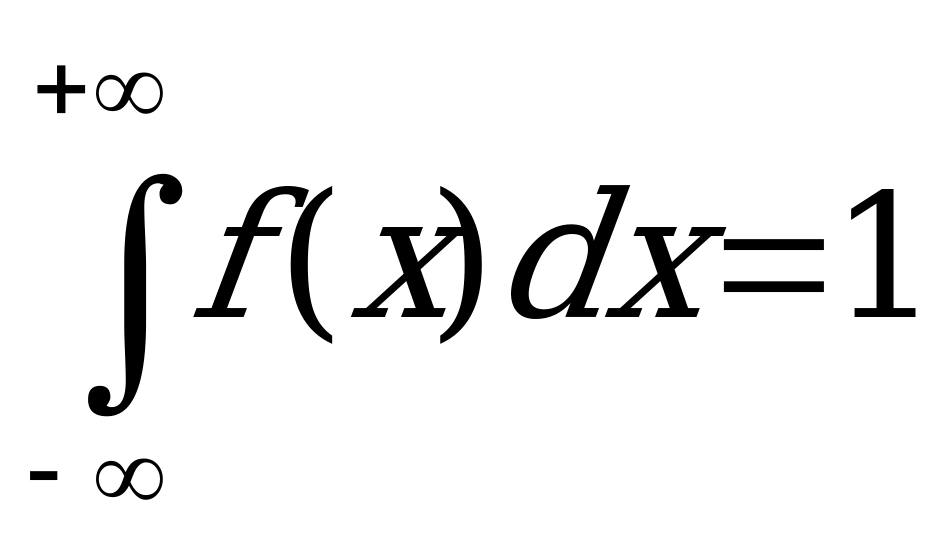
Имеем
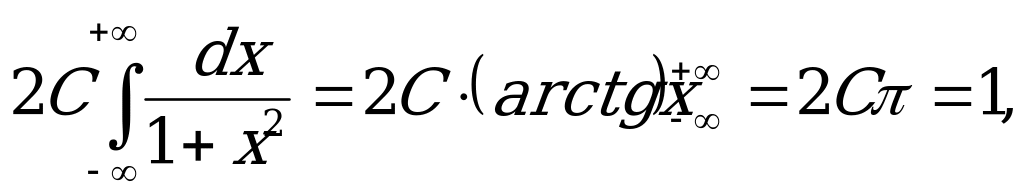 значит
значит 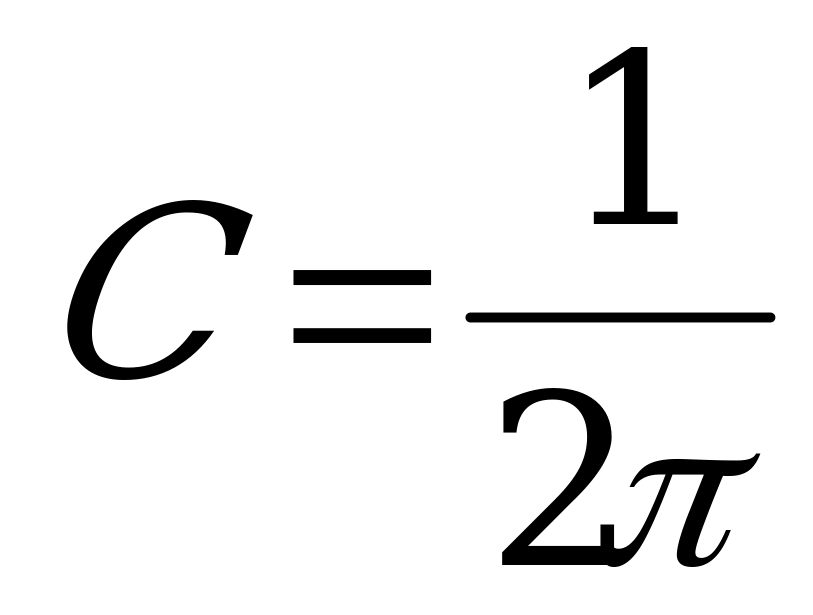
15. Случайная величина Х задана плотностью вероятности 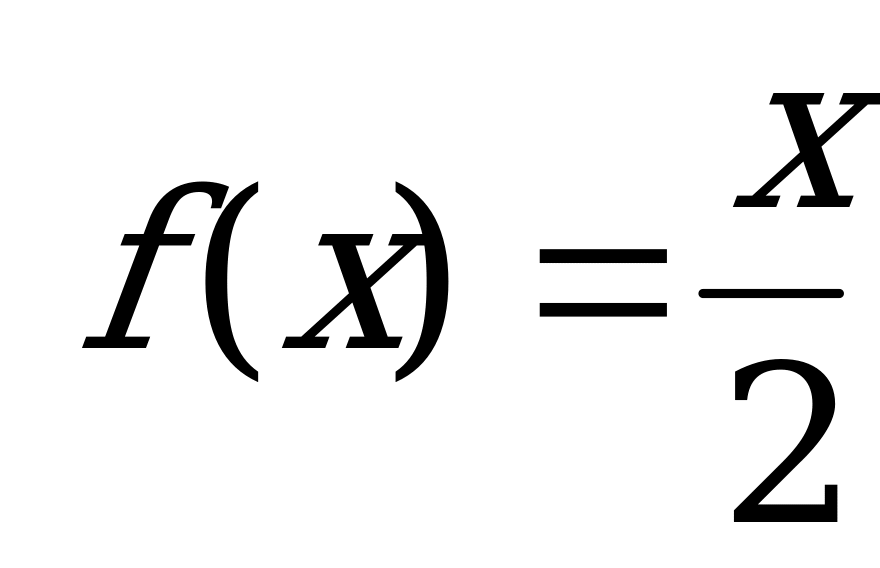 на
на
интервале (0;2), вне этого интервала f(x)=0. Найти математическое
ожидание величины Х.
Решение:
На основании формулы 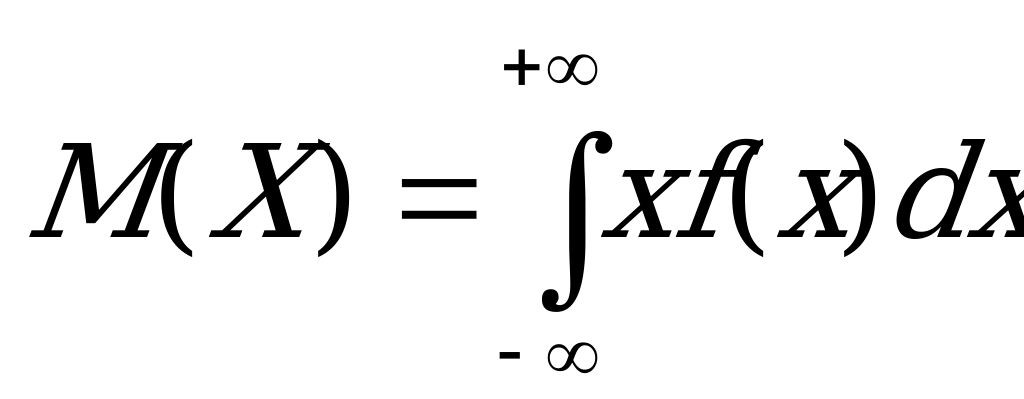 , имеем
, имеем
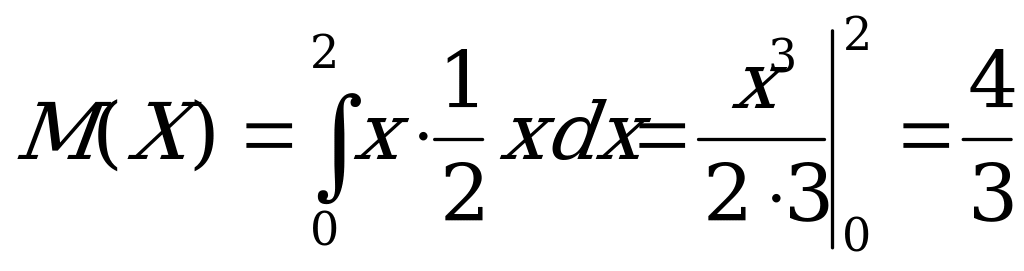 .
.
16. Случайная величина Х задана плотностью вероятности 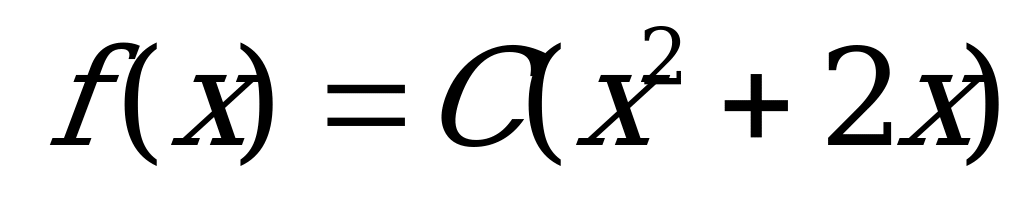
в интервале (0;1). Вне этого интервала f(x)=0. Найти параметр С.
Решение:
Так как 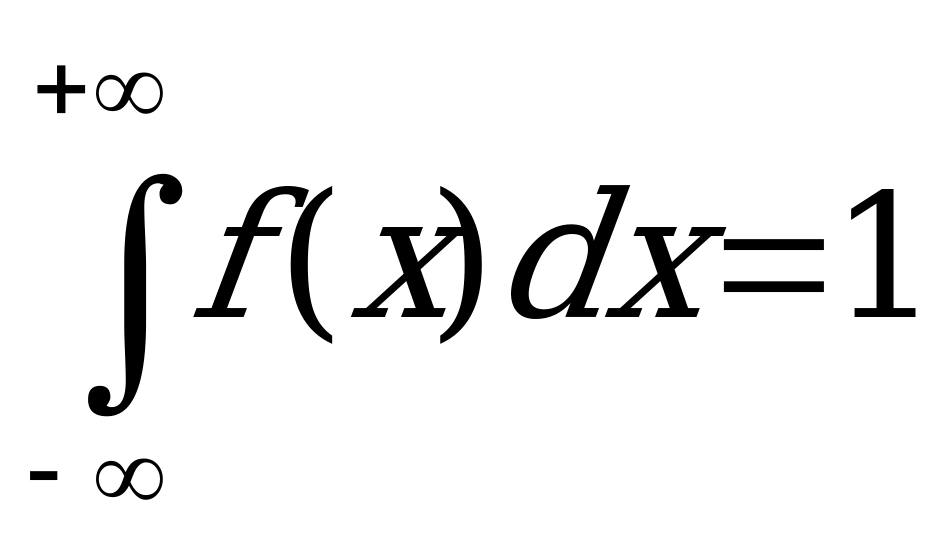 , то
, то 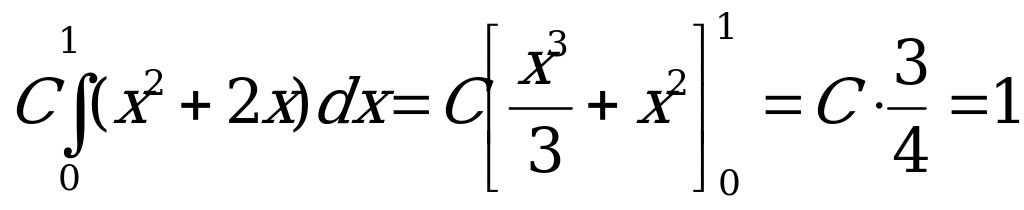 .
.
Откуда С=0,75.
17. Случайная величина Х задана в интервале (0; плотностью
плотностью
вероятности 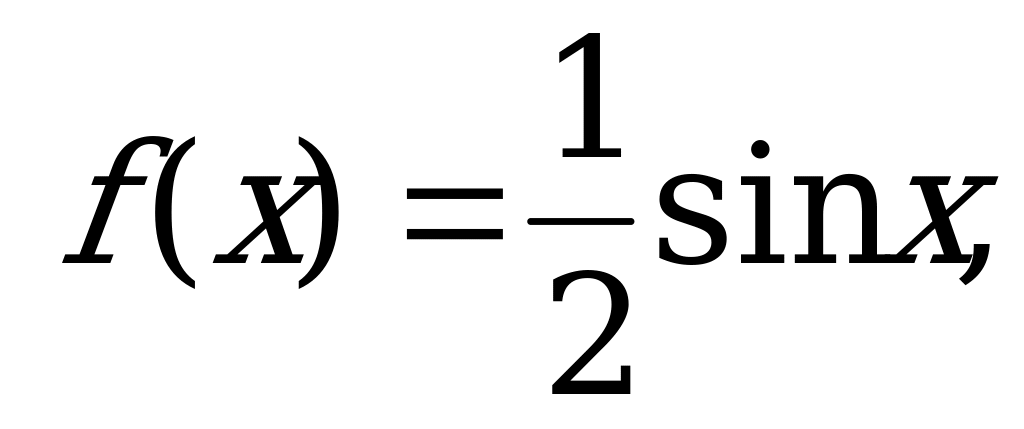 вне этого интервала f(x)=0. Найти дисперсию
вне этого интервала f(x)=0. Найти дисперсию
величины Х.
Решение:
Для нахождения дисперсии используем формулу
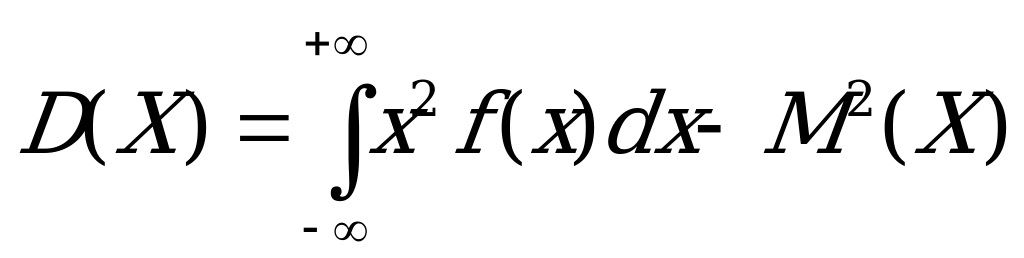
Математическое ожидание
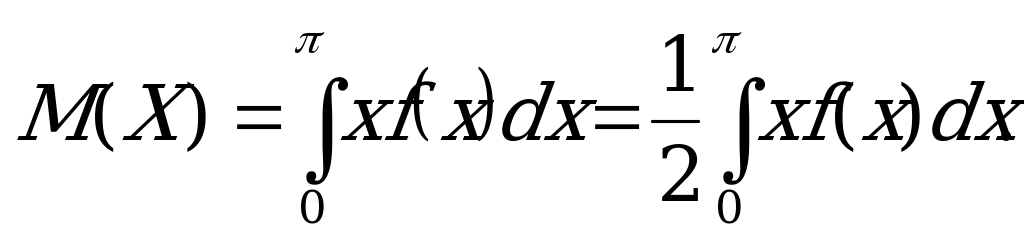
Интегрируя по частям, получаем 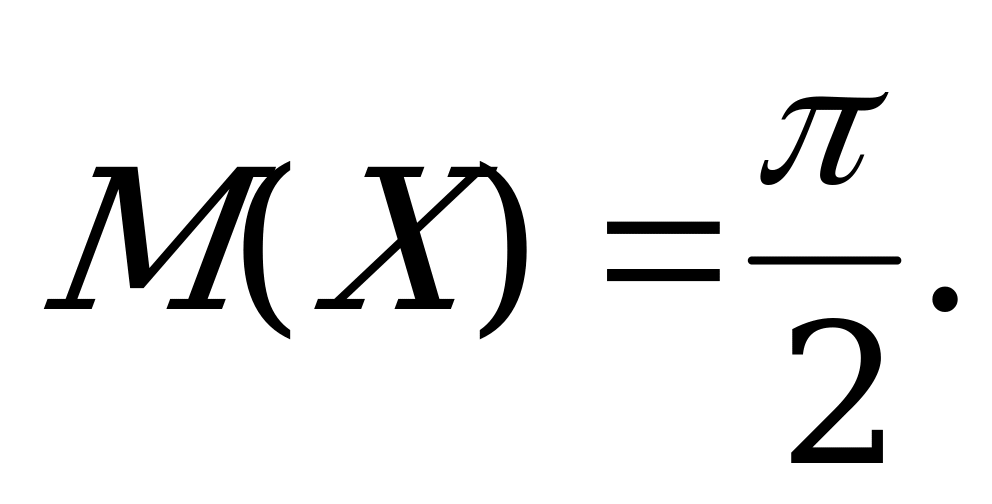 Находим значение первого слагаемого в выражении дисперсии:
Находим значение первого слагаемого в выражении дисперсии:
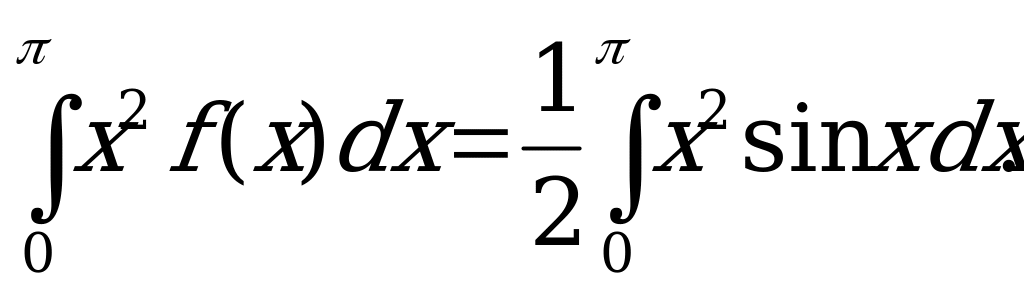
Интегрируя по частям дважды, получаем
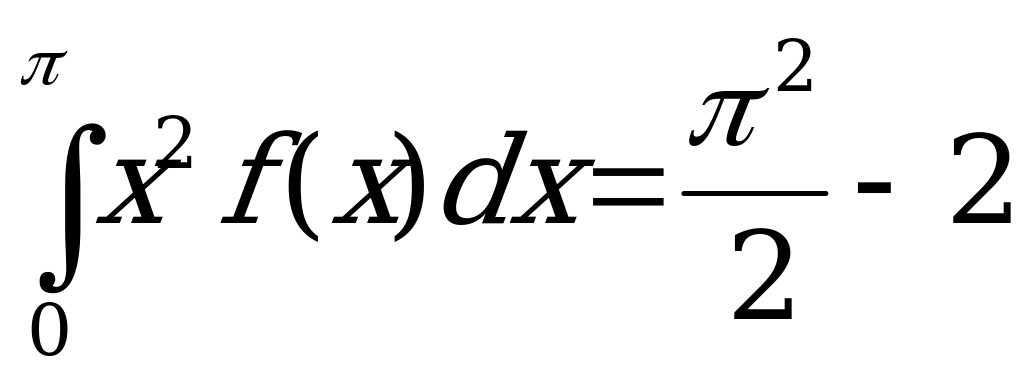
Подставляя в выражение дисперсии полученные значения, получаем
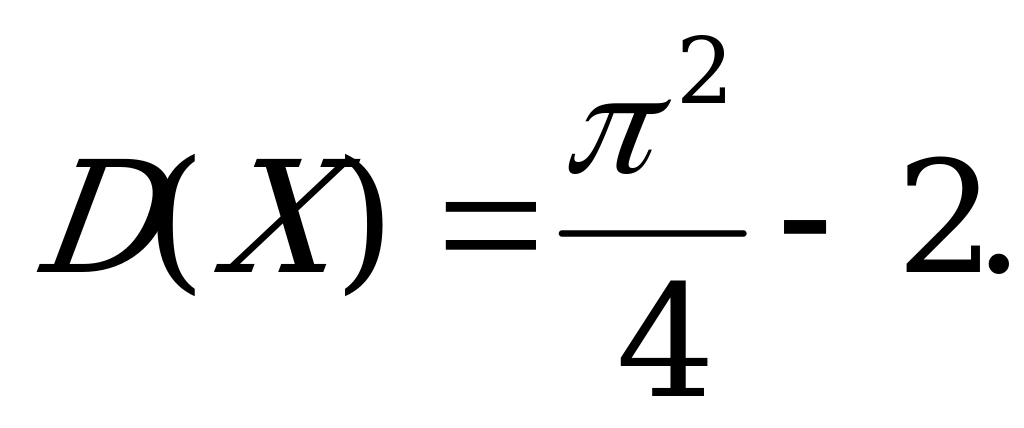
18. Случайная величина Х распределена равномерно на отрезке 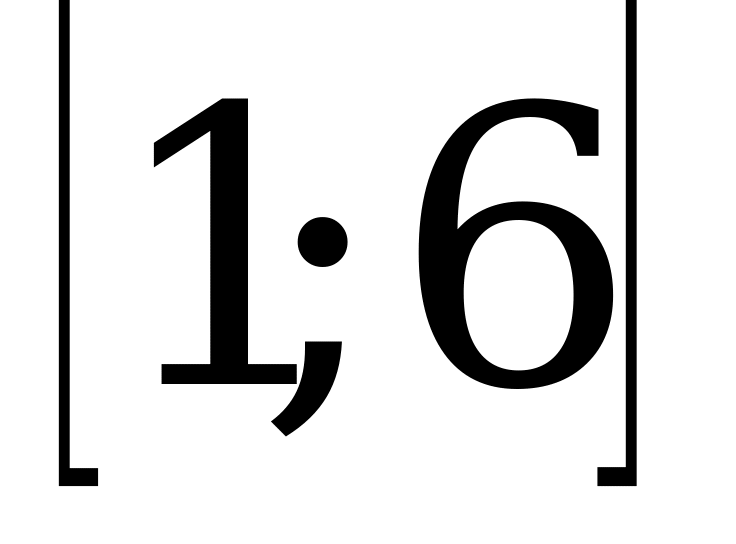 . Найти функцию распределения F(x), математическое ожидание, дисперсию и среднее квадратическое отклонение величины.
. Найти функцию распределения F(x), математическое ожидание, дисперсию и среднее квадратическое отклонение величины.
Решение: Плотность вероятности для величины Х прмет вид

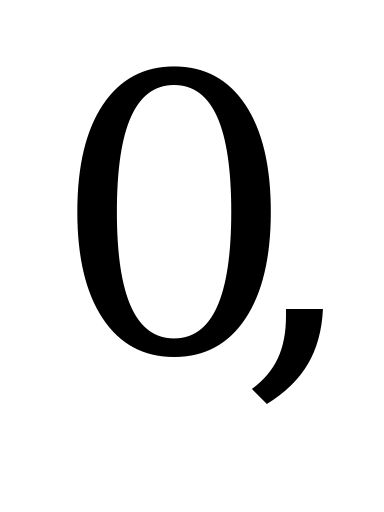 если
если 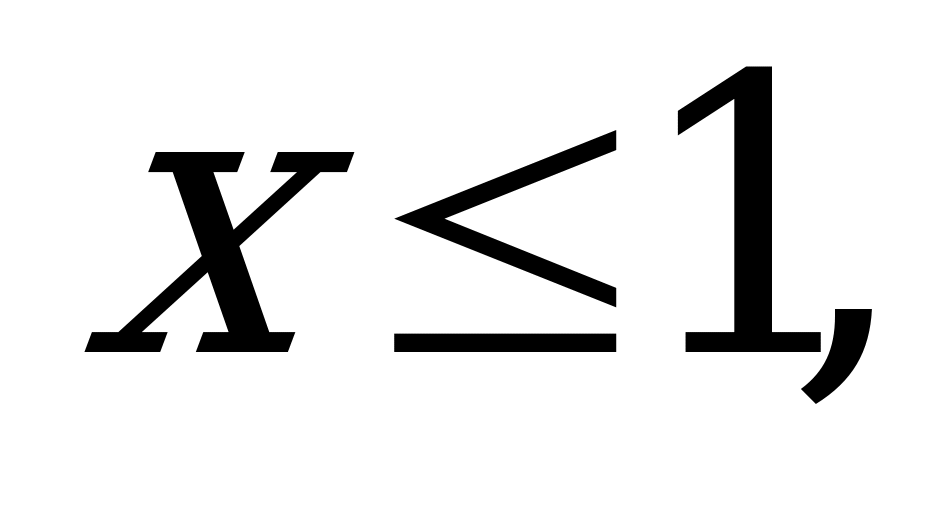
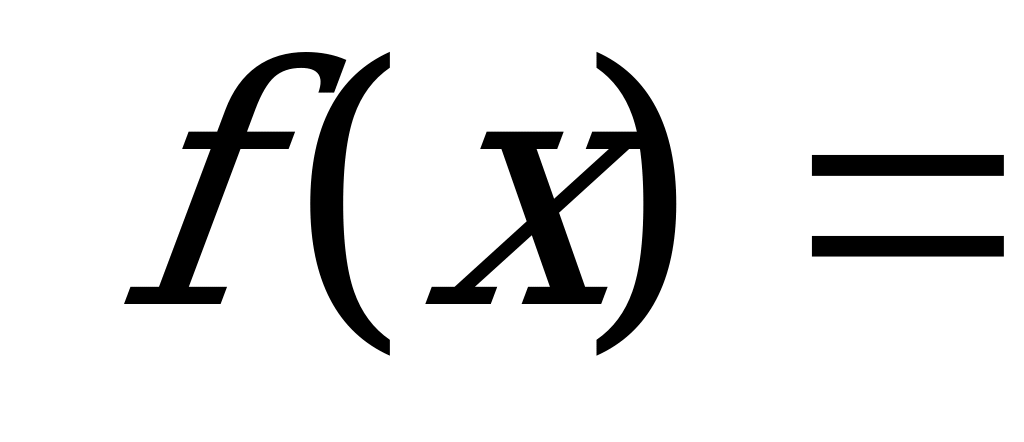
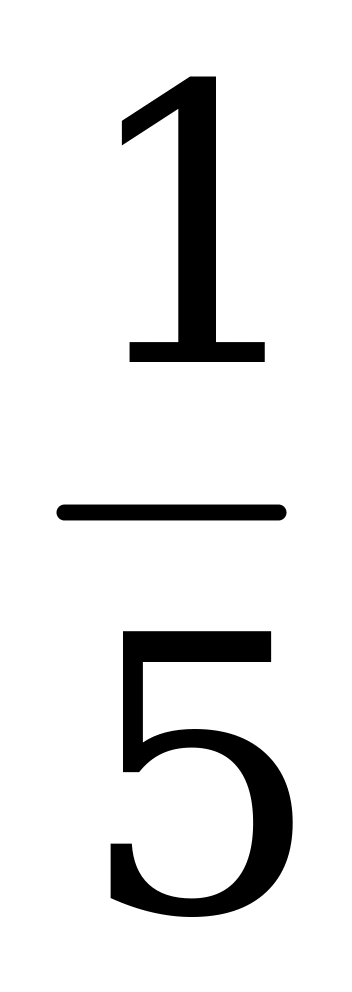 , если
, если 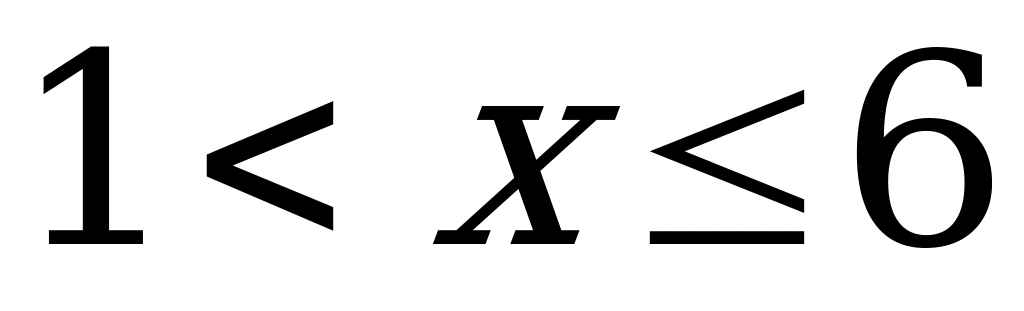
0, если 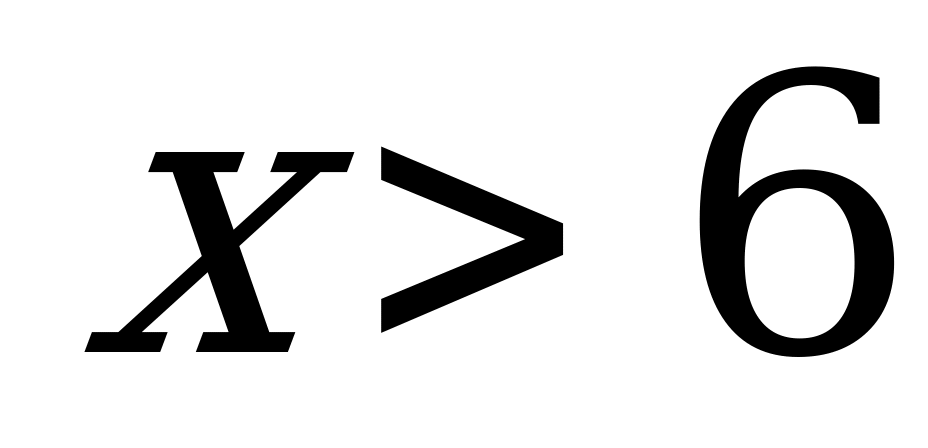
Следовательно, функция распределения, вычисляемая по формуле
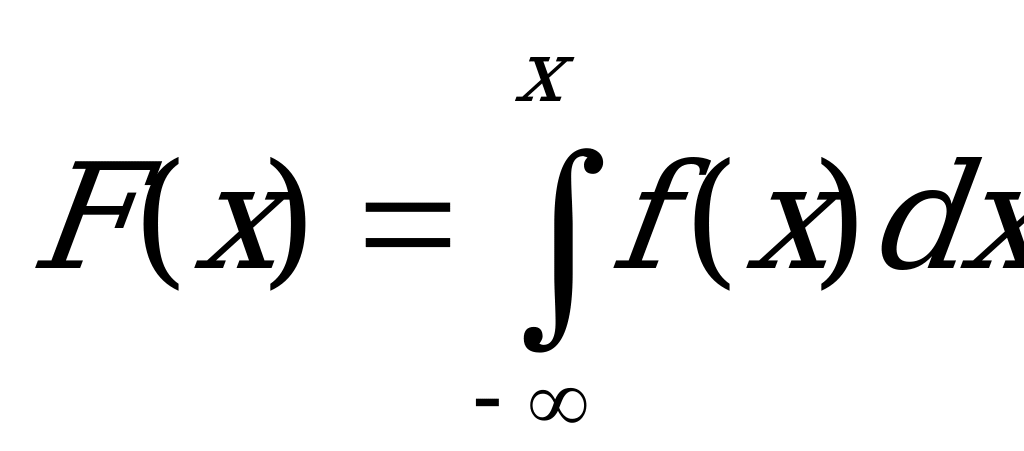 , запишется следующим образом
, запишется следующим образом

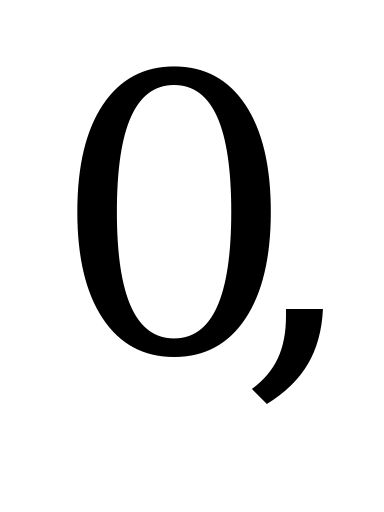 если
если 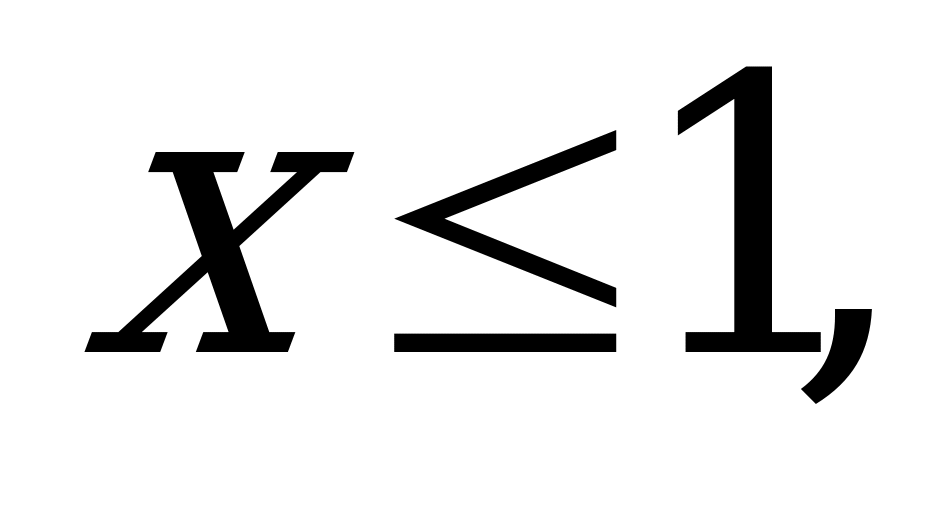
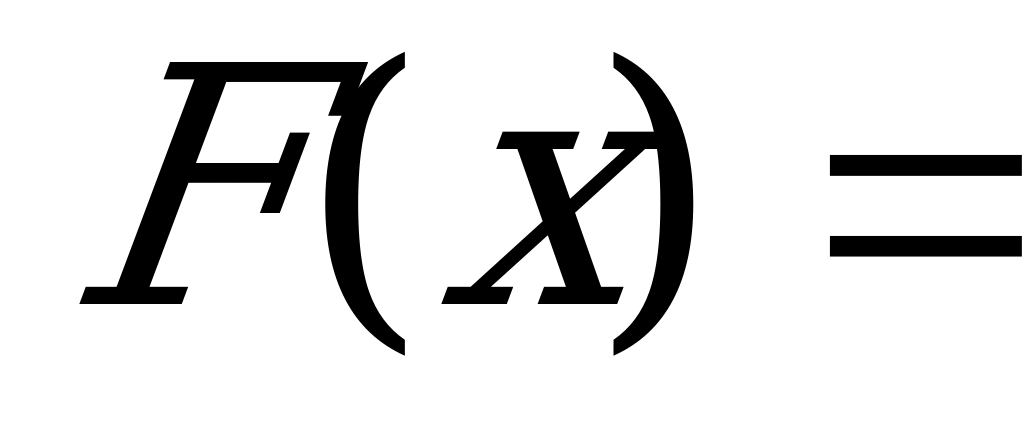
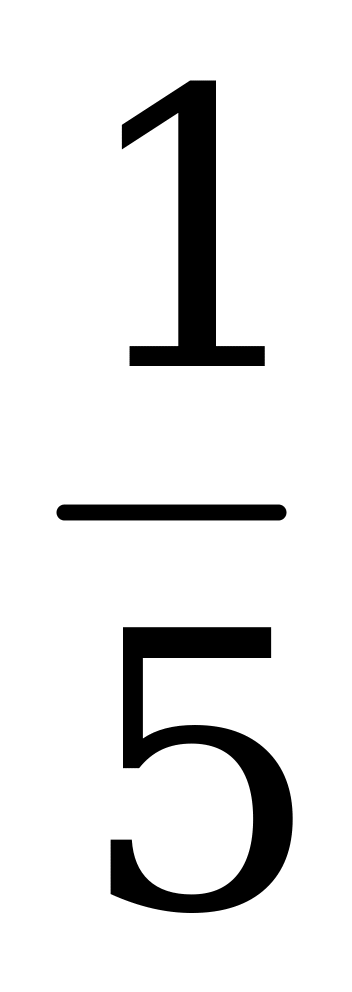
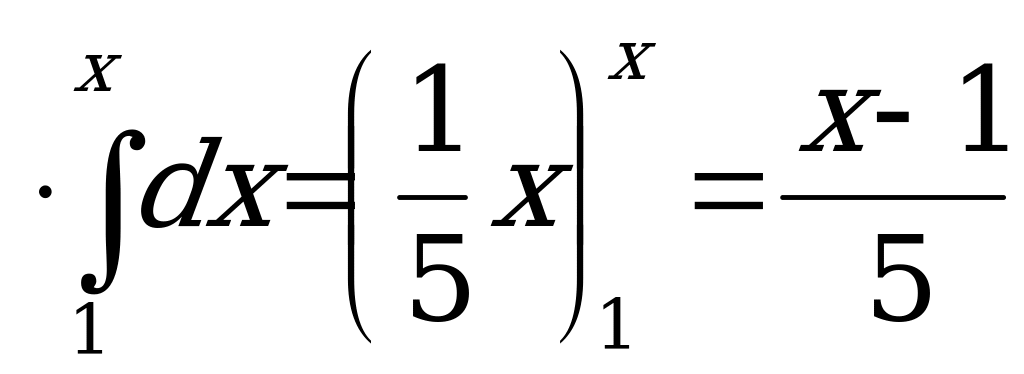 , если
, если 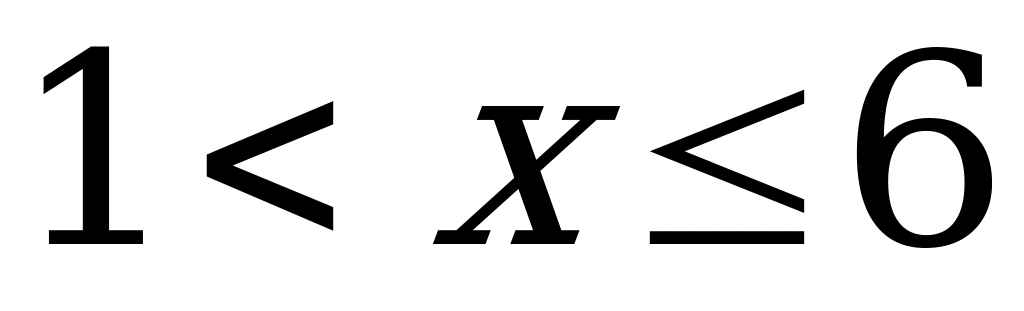
1, если 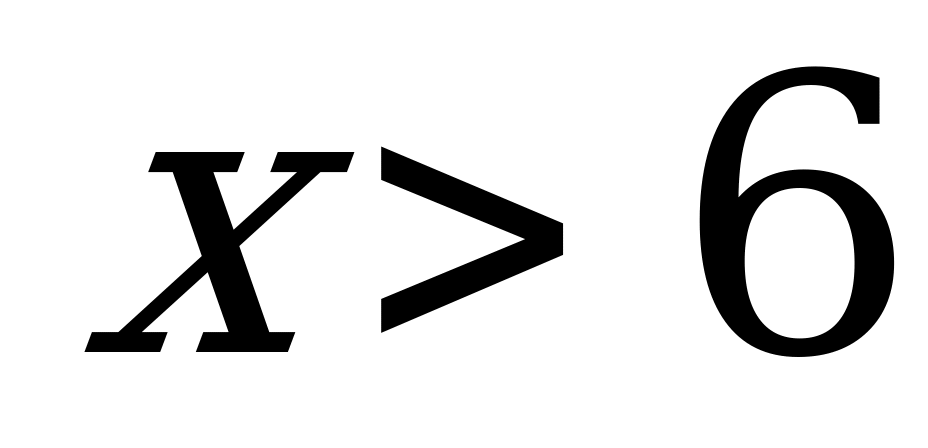
Математическое ожидание равно М(Х)=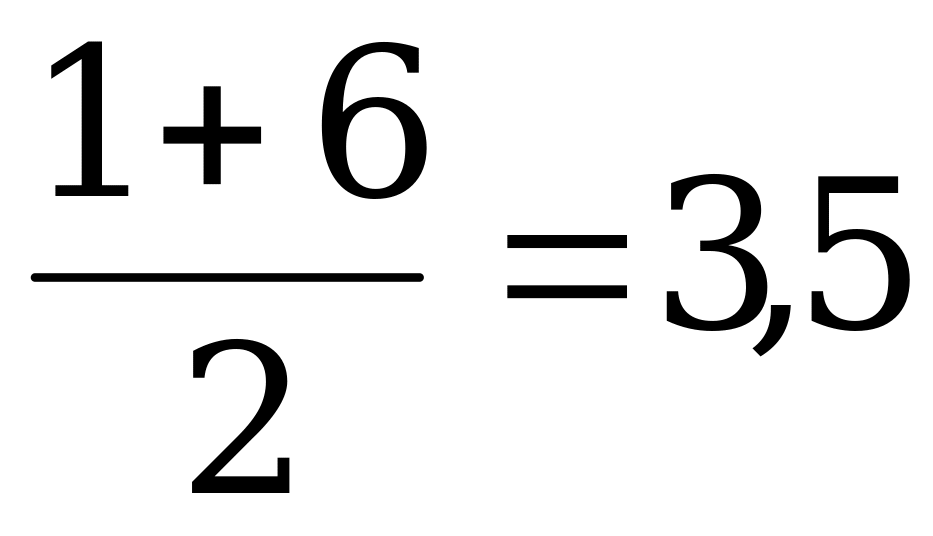 . Находим дисперсию и среднее квадратическое отклонение Д(Х)=
. Находим дисперсию и среднее квадратическое отклонение Д(Х)=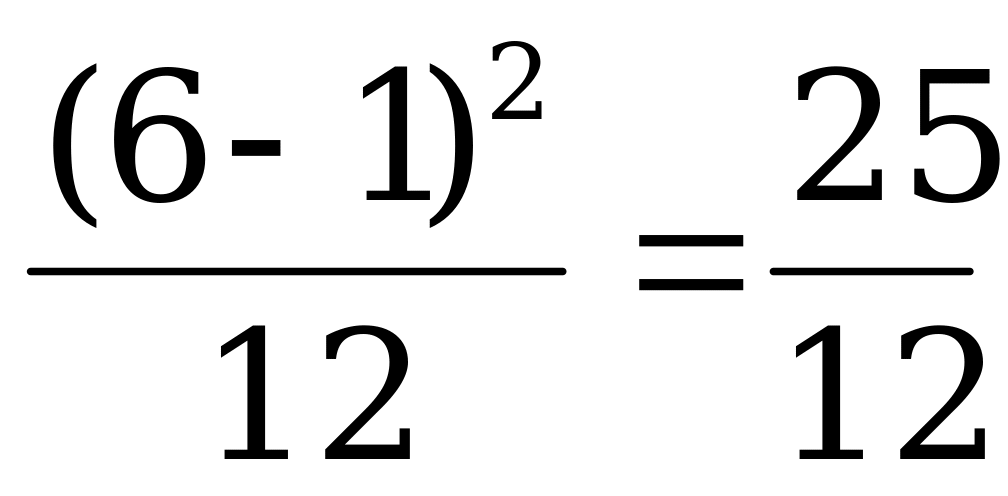 ,
, 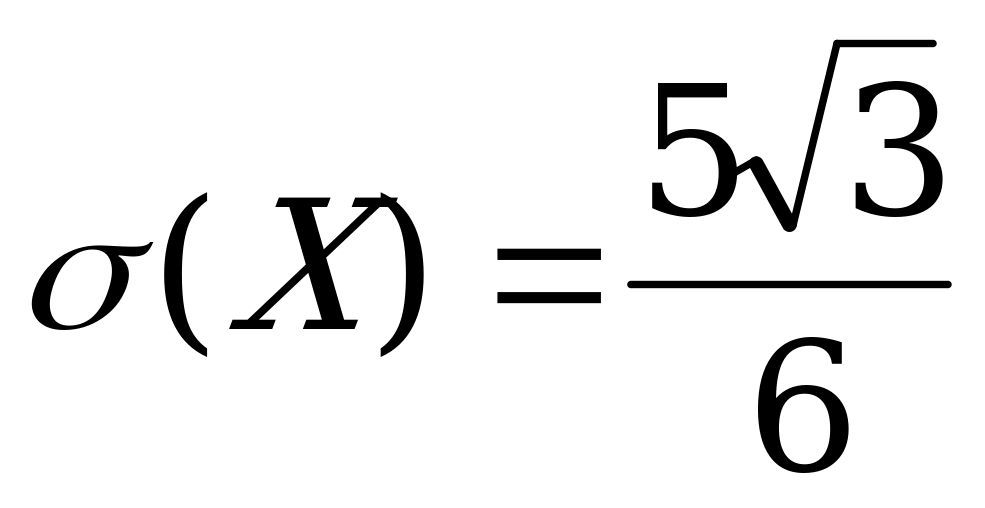 .
.
19. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 12 и 2. Найти вероятность того, что случайная величина примет значение, заключенное в интервале (14,16).
Решение:
Воспользуемся формулой:
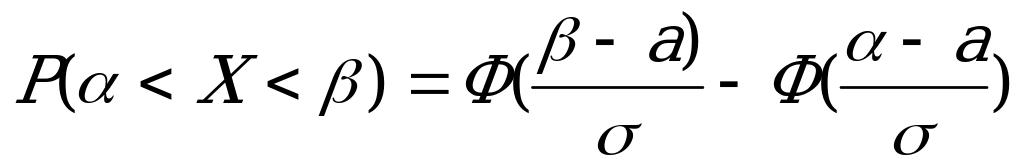 =
=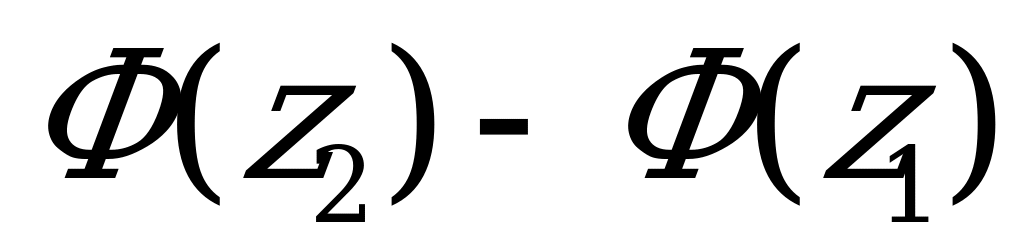 , где а – математическое ожидание величины Х, а
, где а – математическое ожидание величины Х, а  - ее среднее квадратическое отклонение.
- ее среднее квадратическое отклонение.
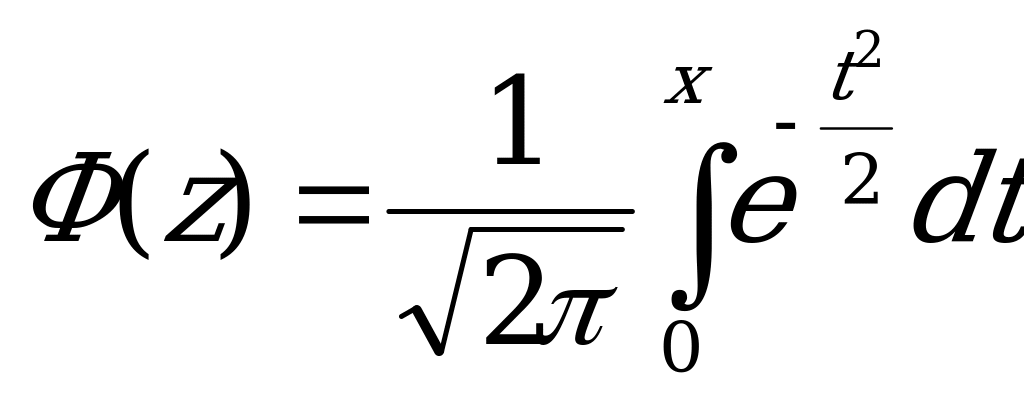 - функция Лапласа.
- функция Лапласа.
В нашем случае по этой формуле, получим:
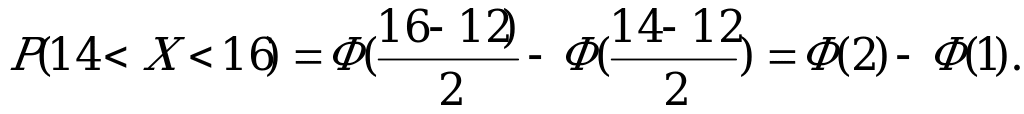
По таблице значений функции Лапласа находим: Ф(1)=0,3413
Ф(2)=0,4772. После подстановки получаем значение искомой вероятности:
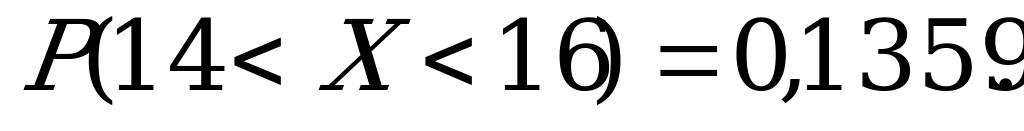
20. Случайная величина Х задана функцией распределения вероятностей

 если
если 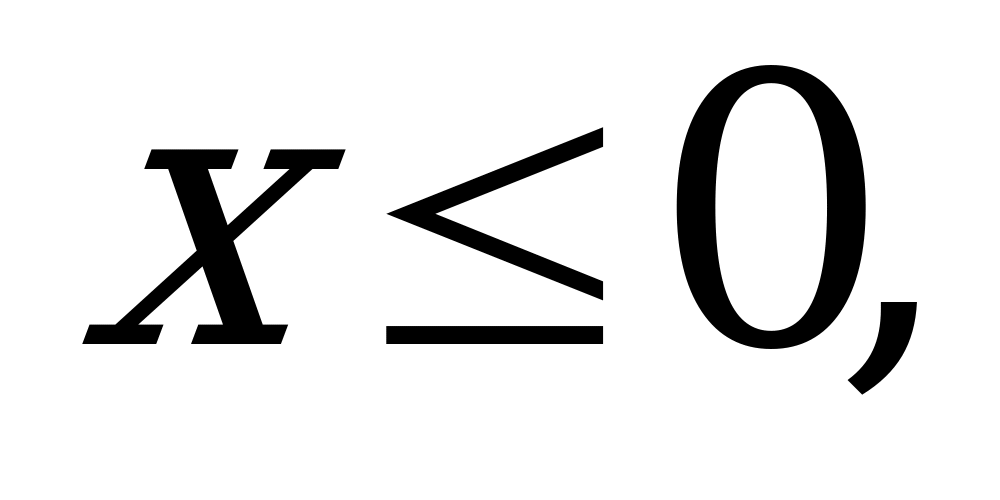
F(x)= 1-e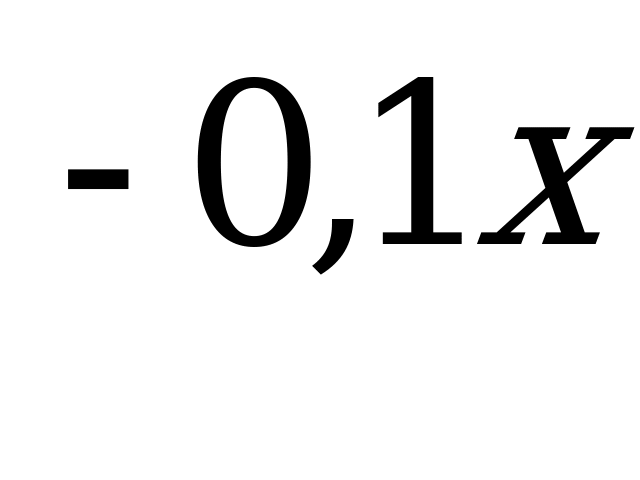 , если
, если 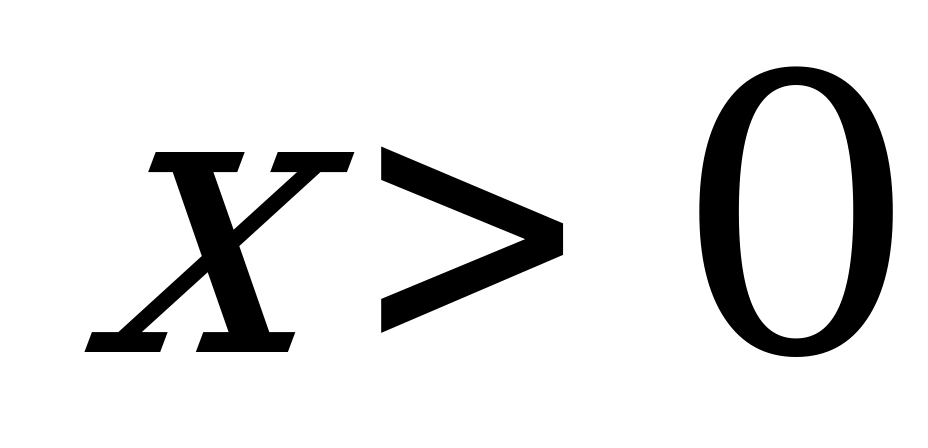
Найти математическое ожидание и дисперсию величины Х.
Решение:
Для решение задачи используем формулы математического ожидания и дисперсии непрерывной случайной величины:
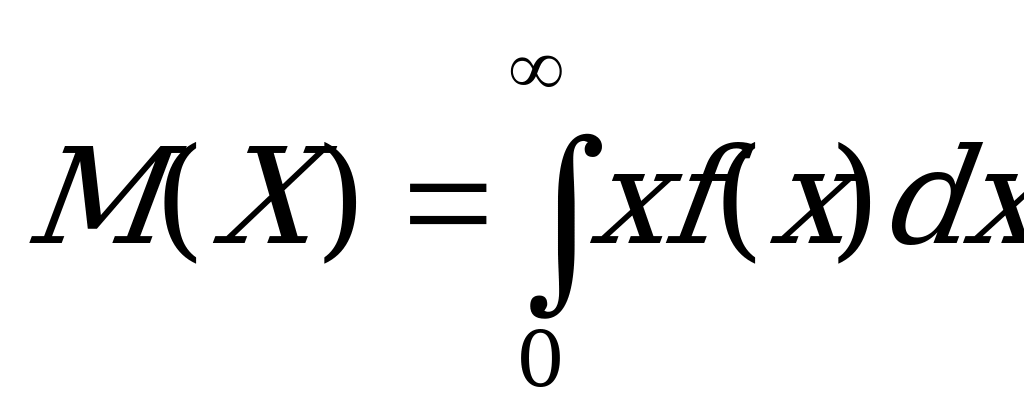 ,
, 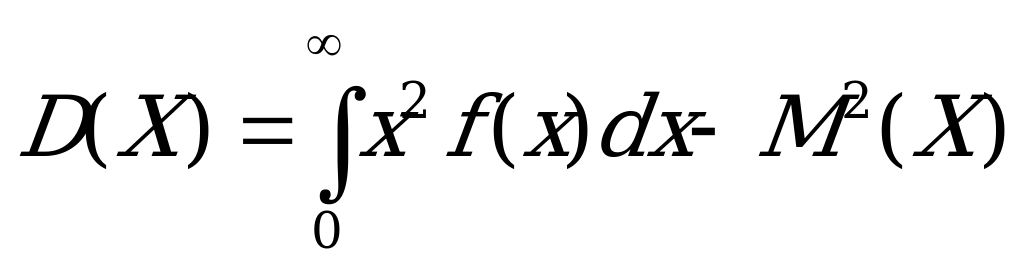
Учтем, что 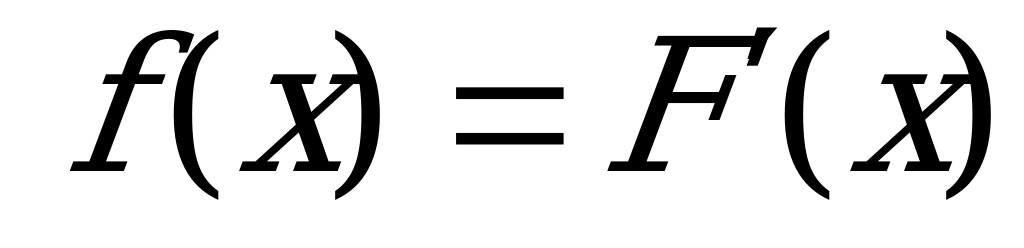 . Тогда получим:
. Тогда получим:

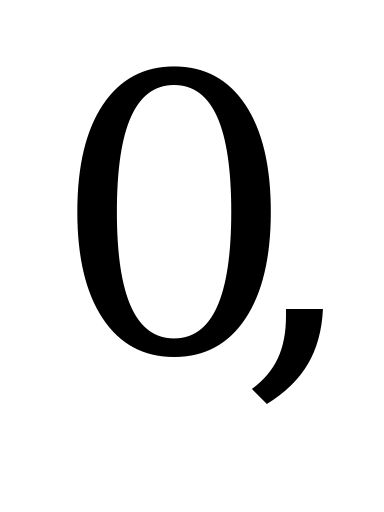 если
если 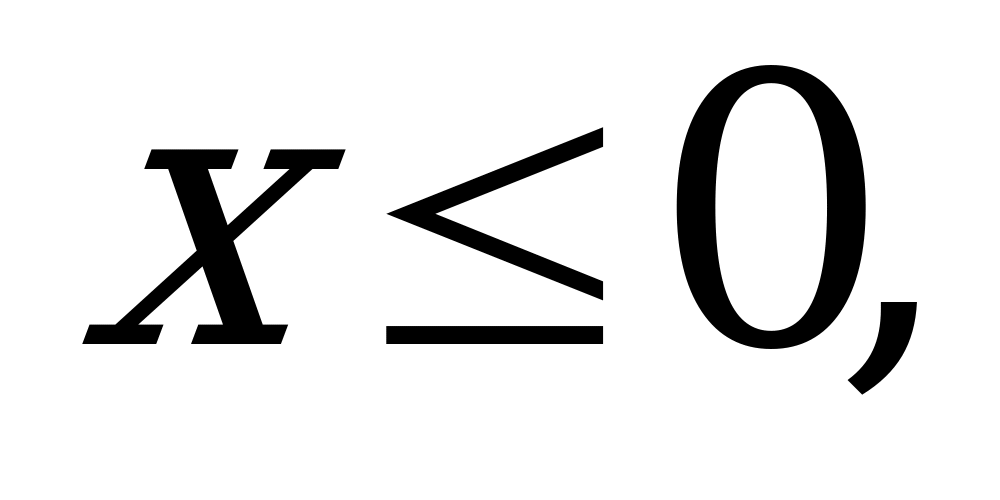
f(x)= 0,1e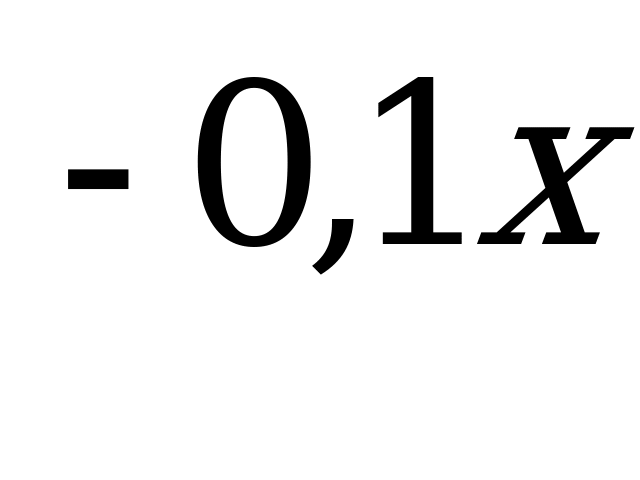 если
если 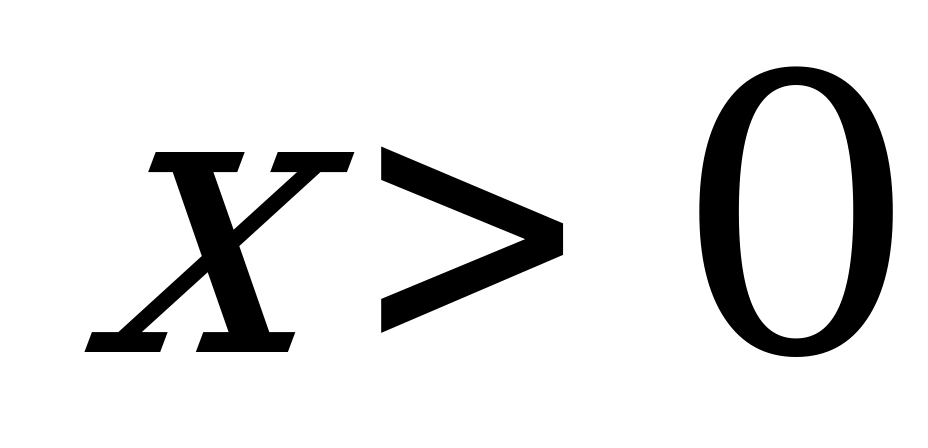
Подставим в выражение для математического ожидания
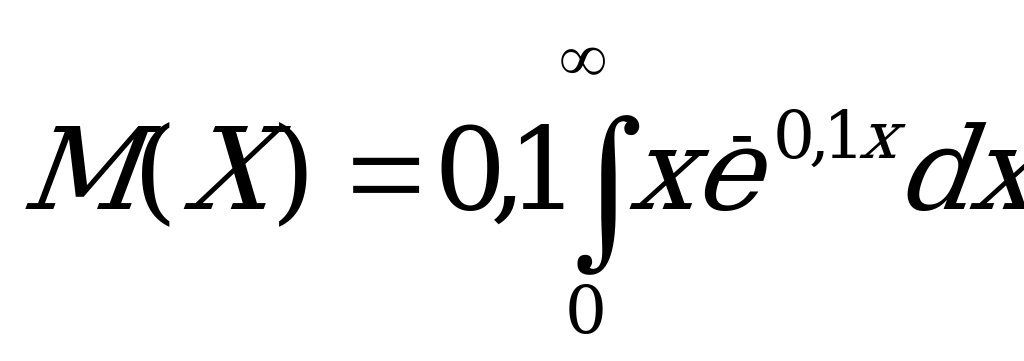
Интегрируя по частям, получаем М(Х)=10. Найдем дисперсию:
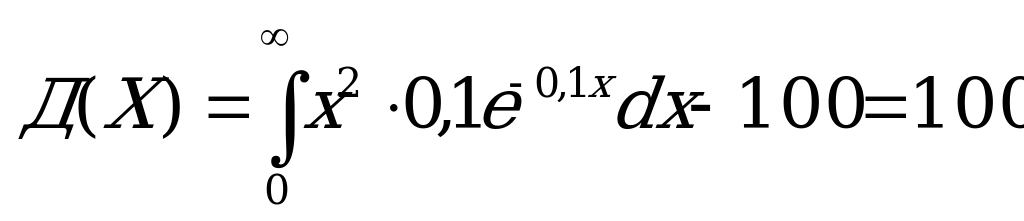 . Для вычисления записанного интеграла применяется формула интегрирования по частям два раза. Итак, М(Х)=10, Д(Х)=100.
. Для вычисления записанного интеграла применяется формула интегрирования по частям два раза. Итак, М(Х)=10, Д(Х)=100.
21. Фирма выпускает мини заводы по производству хлеба. На рекламу может быть израсходовано определенное количество средств. В таблице приведены возможное количество проданных в течение месяца заводов (Х) и объем средств, израсходованных на рекламу (У). Каждой паре 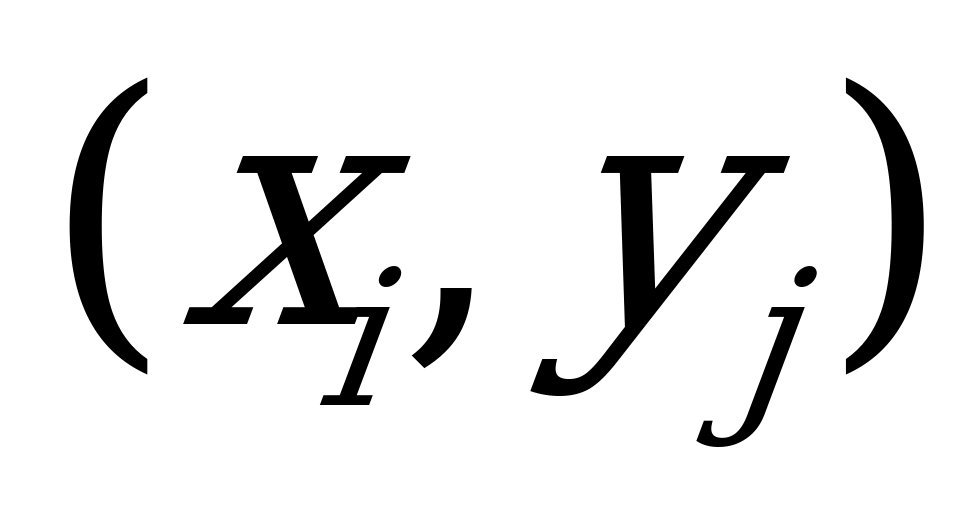 случайных величин (Х,У) поставлена в соответствие вероятность р
случайных величин (Х,У) поставлена в соответствие вероятность р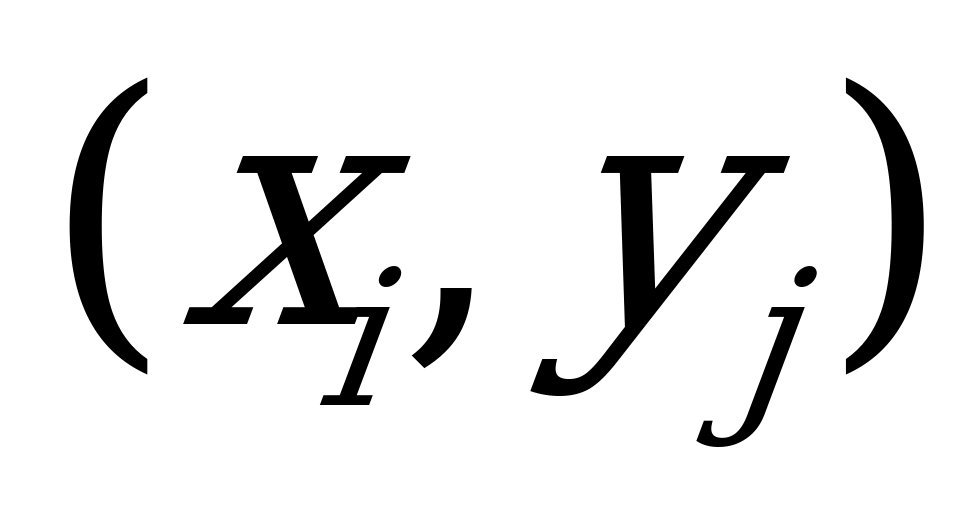 появления этой пары
появления этой пары

| Х У | 0 | 1 | 2 |
| 1 | 0,12 | 0,15 | 0,10 |
| 2 | 0,08 | 0,10 | 0,12 |
| 3 | 0,05 | 0,10 | 0,18 |
Требуется составить таблицы распределения вероятностей для каждой из величин Х и У и выразить условный закон распределения вероятностей величины У при Х=2.
Решение:
Так как с каждым значением  встречается ровно три значения
встречается ровно три значения  , т.е имеет место полная группа событий, сумма вероятностей которых равна 1, то
, т.е имеет место полная группа событий, сумма вероятностей которых равна 1, то
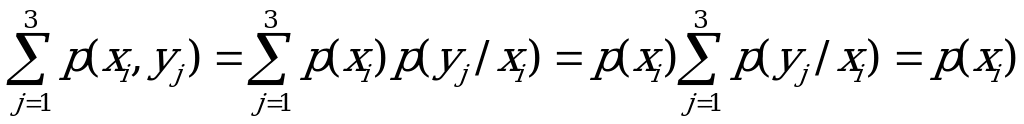
Таким образом, вероятность события 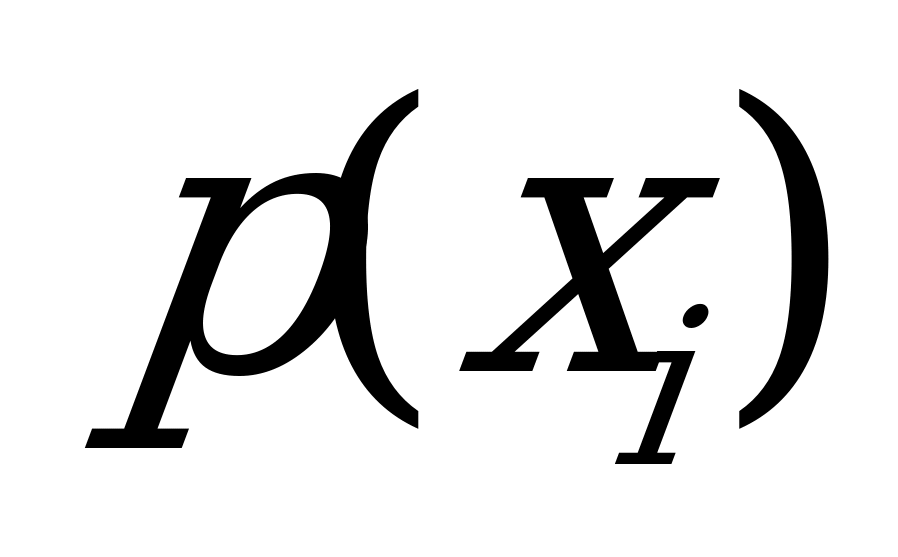 равна сумме вероятностей р
равна сумме вероятностей р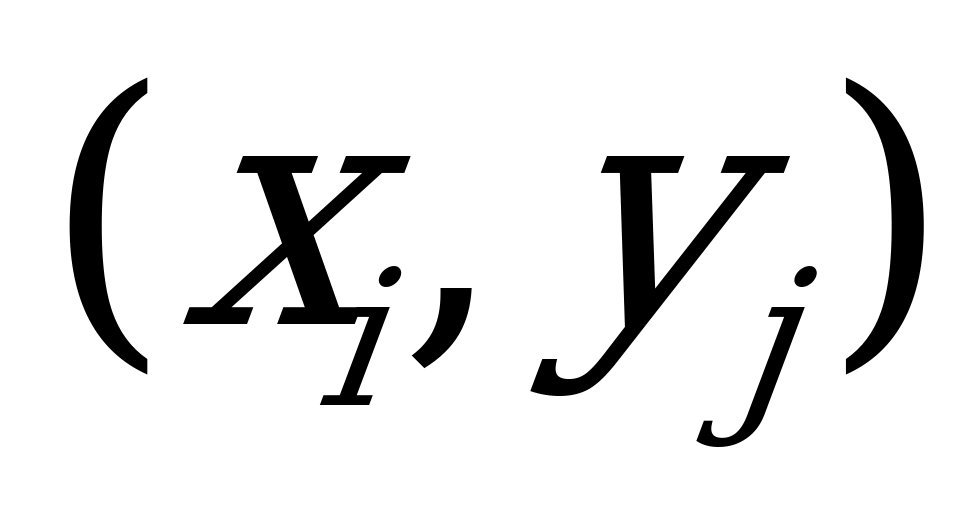 в каждой колонке.
в каждой колонке.
В результате получаем таблицу распределения вероятностей величины Х и по аналогии для У:
Сумма вероятностей для каждой из величин должна быть равна 1. Проведем проверку:
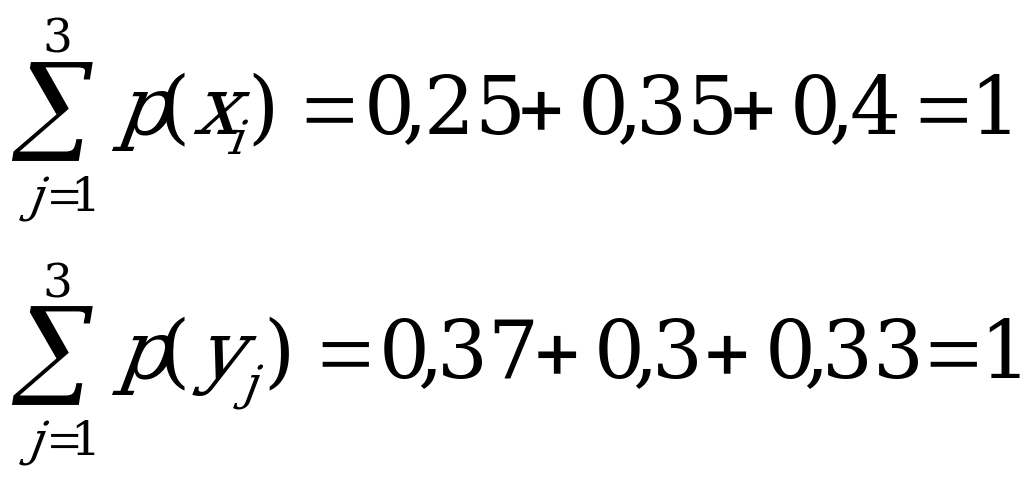
Находим условные вероятности для величины У при Х=2
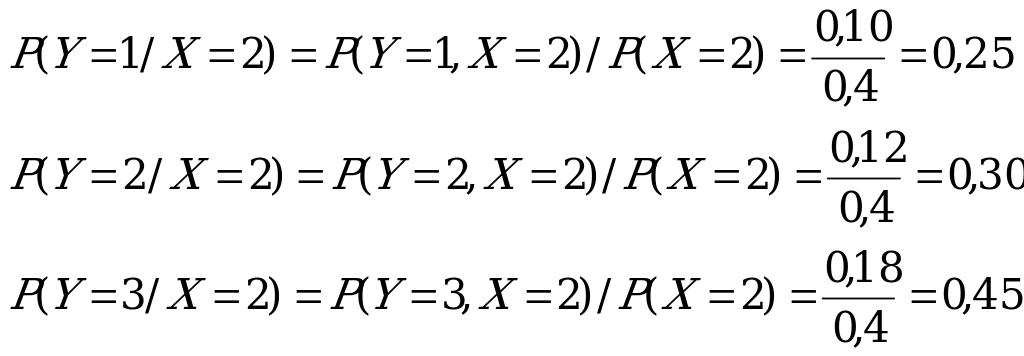
22. Найти регрессию величины У на Х для двух значений 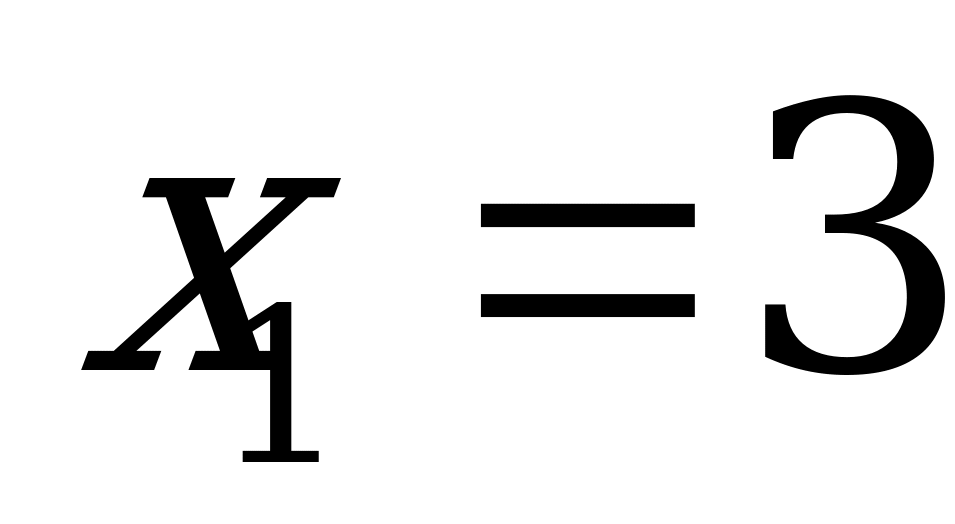 и
и 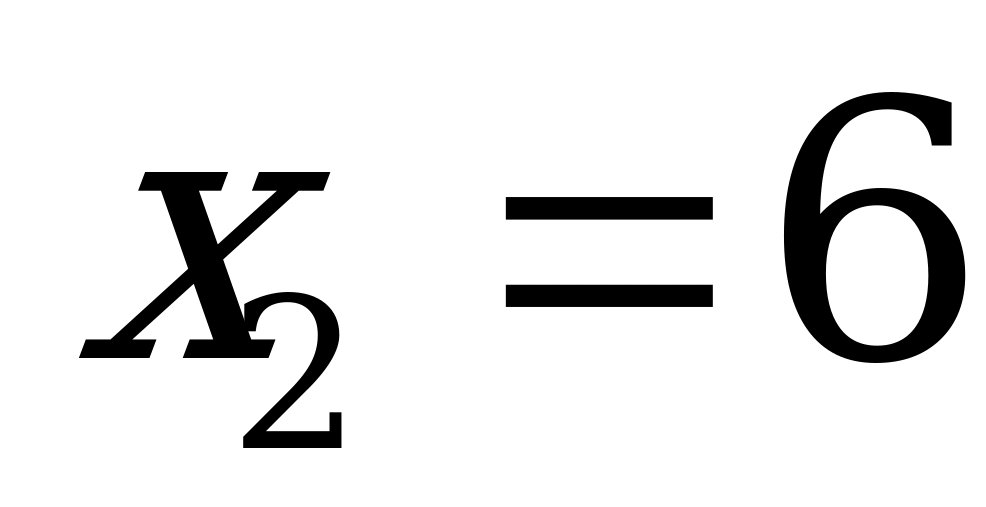 на основе заданной таблицы распределения двумерной случайной величины
на основе заданной таблицы распределения двумерной случайной величины
|  Х Х
 У У
| 3 | 6 |
| 10 | 0,25 | 0,10 |
| 14 | 0,15 | 0,05 |
| 18 | 0,32 | 0,13 |
Решение
Условное математическое ожидание, или регрессия, величины У на Х находится на основе соотношения
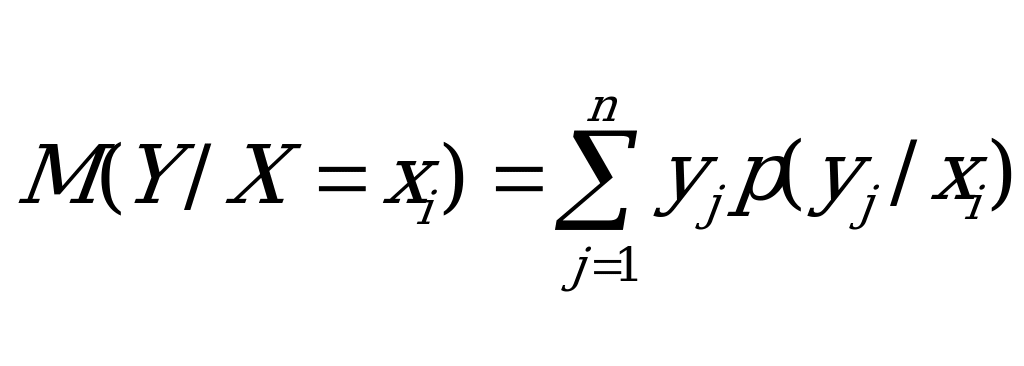
где 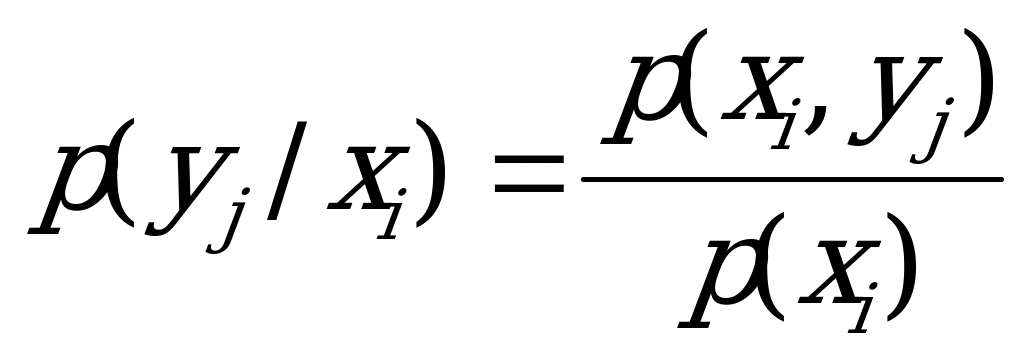
Определяем Р(Х=3) и Р(Х=6):
Р(Х=3)=0,25+0,15+0,32=0,72
Р(Х=6)=0,10+0,05+0,13=0,28
Вычисляем условные вероятности:
Р(У=10/Х=3)=0,25/0,72=0,35 Р(У=10/Х=6)=0,10/0,28=0,36
Р(У=14/Х=3)=0,15/0,72=0,21 Р(У=14/Х=6)=0,05/0,28=0,18
Р(У=18/Х=3)=0,32/0,72=0,44 Р(У=18/Х=6)=0,13/0,28=0,46
Находим условные математические ожидания:
М(У/Х=3)=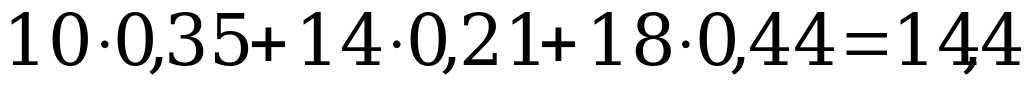
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1. В супермаркете проводились наблюдения над числом Х покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов дали следующие результаты:
70,75,100,120,75,60,100,120,70,60,65,100,65,100,70,75,60,100,100,120,70,75,70,120,65,70, 75,70,100,100 .
Число Х является дискретной случайной величиной, а полученные данные представляют собой выборку из n=30 наблюдений. Требуется составить вариационный ряд.
Решение:
Сначала составим ранжированный ряд:
60,60,60,65,65,65,70,70,70,70,70,70,70,75,75,75,75,75,100,100,100,100,100,100,100,100,120,120,120.120.
Получено 6 групп, т.е. 6 различных значений случайной величины
(6 вариант). Для каждой группы подсчитаем частоту значений варианты и соответствующую относительную частоту. Все результаты укажем в таблице, которая и будет представлять вариационный ряд.
| Номер группы | 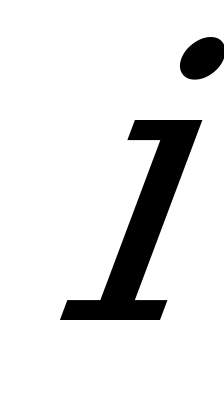
| 1 | 2 | 3 | 4 | 5 | 6 |
| Число обращений покупателей в кассу | 
| 60 | 65 | 70 | 75 | 100 | 120 |
| Частота | 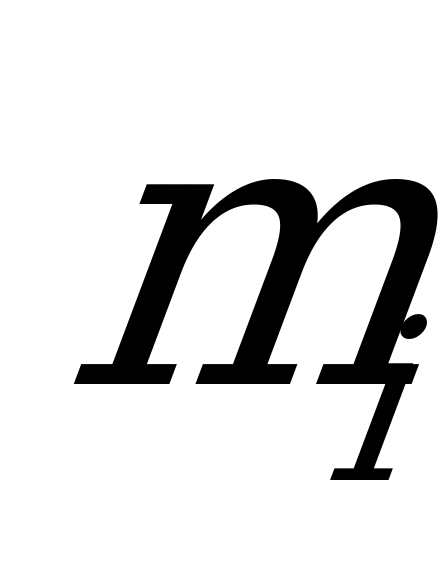
| 3 | 3 | 7 | 5 | 8 | 4 |
| Относительная частота | 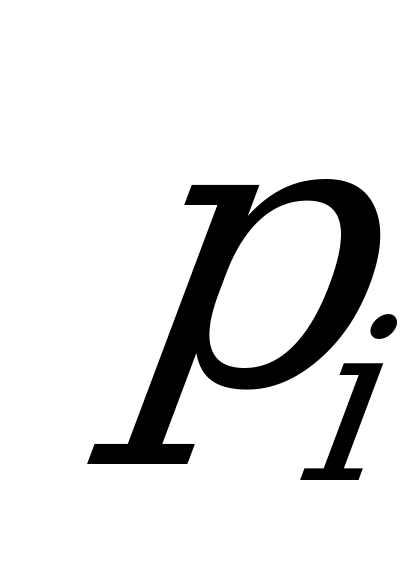
| 3/30 | 3/30 | 7/30 | 5/30 | 8/30 | 4/30 |
2. В таблице приведена выборка результатов измерения поста 105 студентов. Измерения проводились с точностью до 1 см.
| 155 | 170 | 185 | 180 | 188 | 152 | 173 | 178 | 178 | 168 | 185 |
| 173 | 170 | 183 | 175 | 173 | 170 | 183 | 175 | 180 | 175 | 193 |
| 178 | 183 | 180 | 197 | 178 | 181 | 187 | 168 | 174 | 179 | 184 |
| 183 | 178 | 180 | 178 | 163 | 166 | 178 | 175 | 182 | 190 | 167 |
| 170 | 178 | 183 | 170 | 178 | 181 | 173 | 168 | 185 | 175 | 170 |
| 155 | 169 | 186 | 179 | 189 | 155 | 174 | 179 | 179 | 169 | 186 |
| 174 | 171 | 184 | 175 | 193 | 178 | 184 | 180 | 196 | 175 | 181 |
| 188 | 168 | 179 | 178 | 183 | 184 | 178 | 181 | 177 | 163 | 166 |
| 178 | 17 5 5 | 183 | 190 | 167 | 170 | 178 | 183 | 170 | 178 | 182 |
| 173 | 168 | 186 | 176 | 171 | 188 |
|
|
|
|
|
Требуется составить интервальный вариационный ряд.
Решение:
Очевидно, что рост студентов есть случайная непрерывная величина. Найдем сначала минимальное и максимальное значения случайной величины: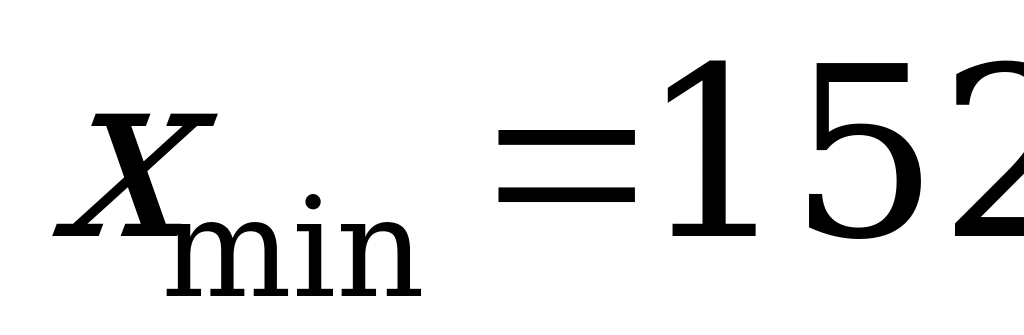 см,
см, 
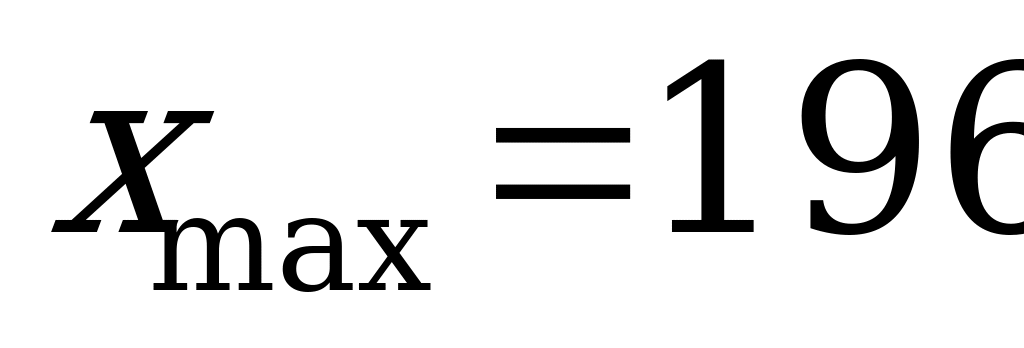 см. Тогда интервал варьирования R равен R=196-152=44см.
см. Тогда интервал варьирования R равен R=196-152=44см.
На практике обычно считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов, однако фактическое число частичных интервалов, а следовательно и размер интервала определяется условиями конкретной задачи.
В нашем случае удобно выбирать длину частичного интервала равной 5 см, тогда число частичных интервалов, начиная со 150 см и кончая 200 см, будет равно 10. Соответствующий интервальный вариационный ряд приведен в таблице
| Индекс интервала i | Рост студентов (интервалы) 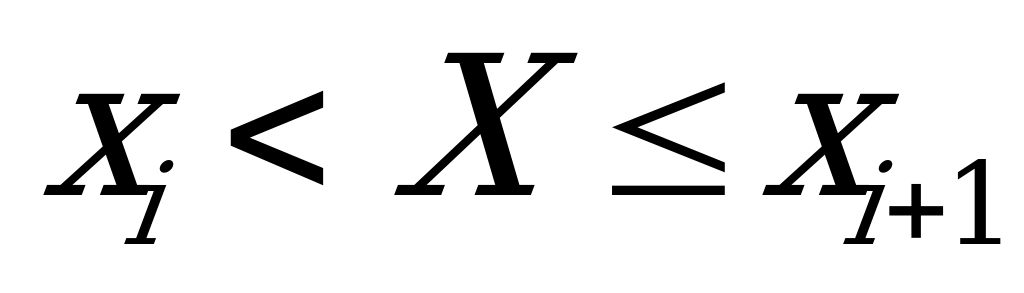 | Частота 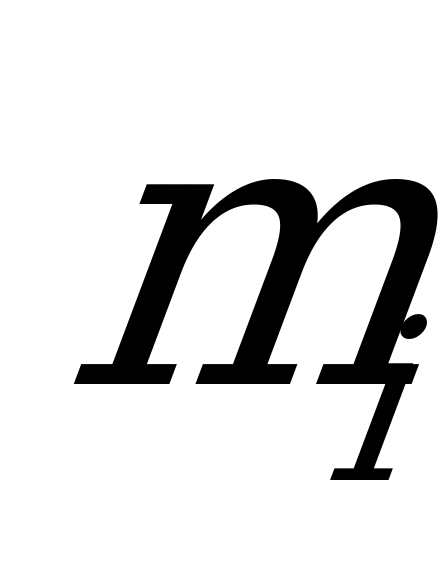 | Относительная Частота 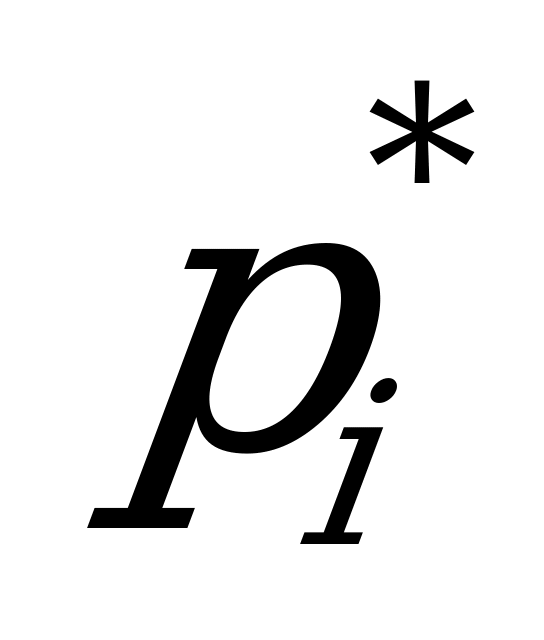 |
| 1 | 150-155 | 4 | 0,0381 |
| 2 | 155-160 | - | - |
| 3 | 160-165 | 2 | 0,0190 |
| 4 | 165-170 | 19 | 0,1810 |
| 5 | 170-175 | 19 | 0,1810 |
| 6 | 175-180 | 26 | 0,2476 |
| 7 | 180-185 | 21 | 0,2000 |
| 8 | 185-190 | 10 | 0,0953 |
| 9 | 190-195 | 2 | 0,0190 |
| 10 | 195-200 | 2 | 0,0190 |
3. Найти выборочную среднюю по данному распределению выборки:
| 
| 1450 | 1480 | 1490 |
| 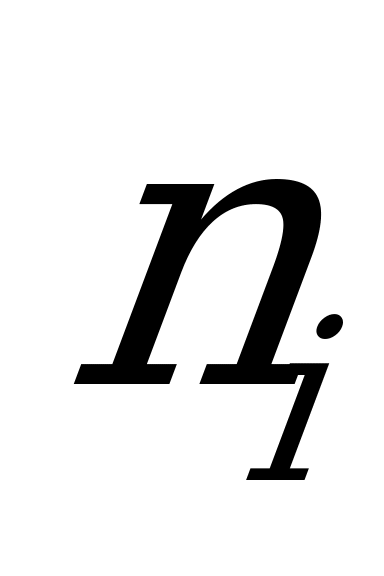
| 3 | 5 | 2 |
Решение:
Так как выборочные значения – большие числа, то целесообразно ввести условные варианты. В качестве ложного нуля выбираем С=1470 и рассчитываем 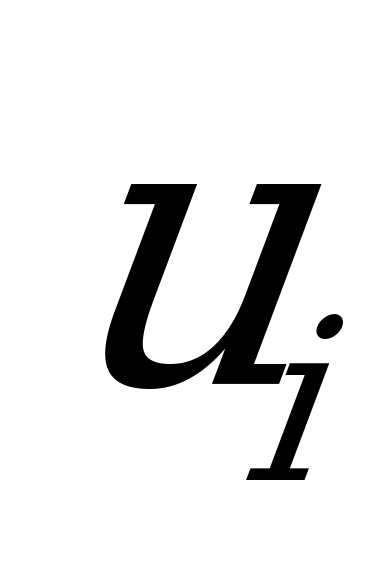 по формуле
по формуле 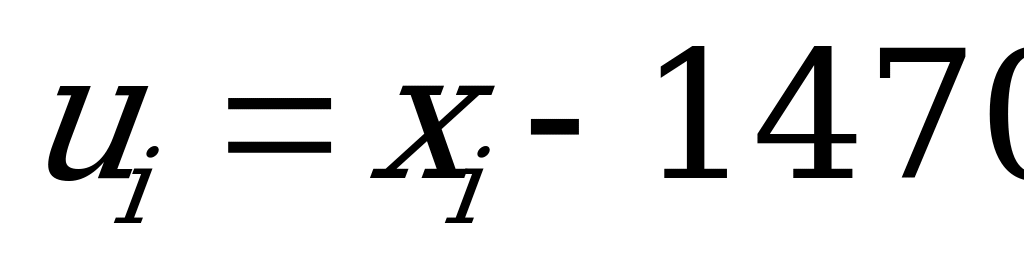
| 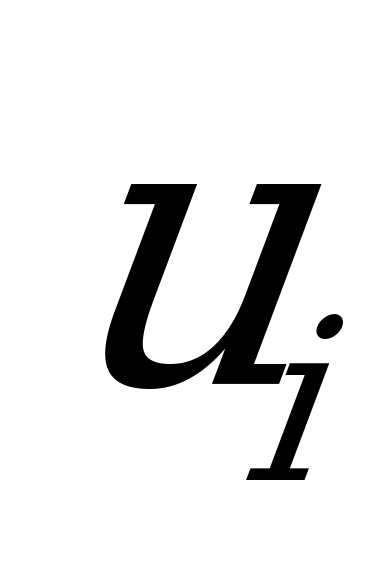
| -20 | 10 | 20 |
| 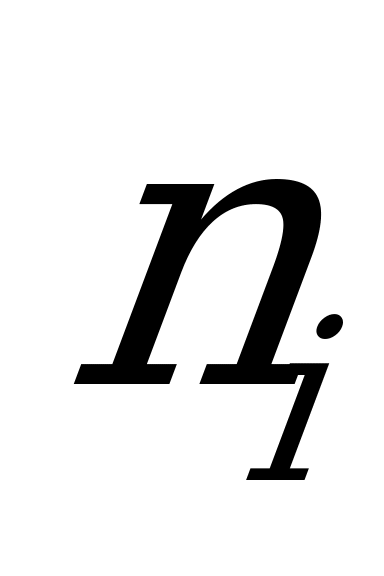
| 3 | 5 | 2 |
Определяем выборочную среднюю 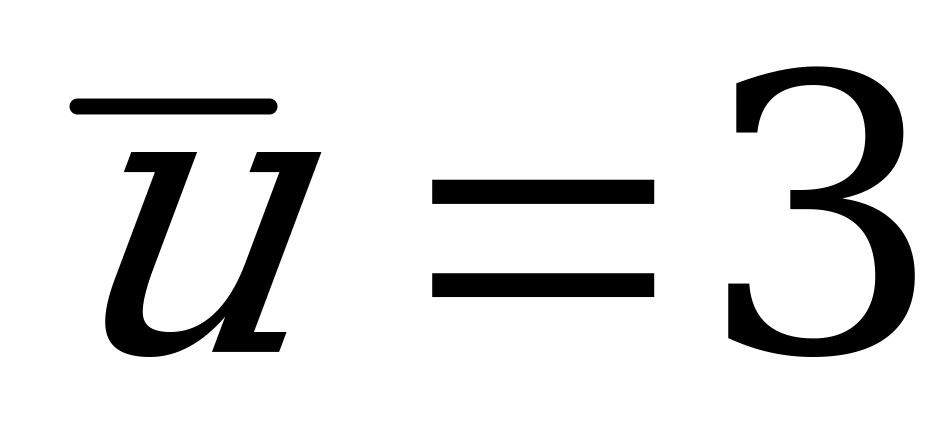 .
.
После этого находим 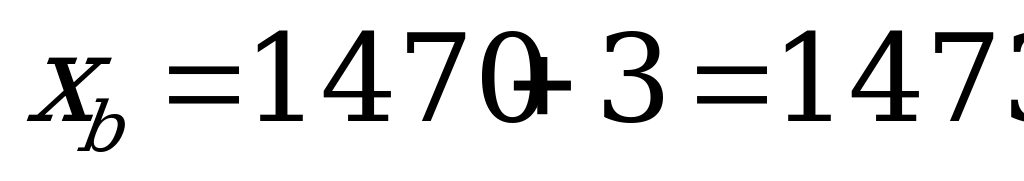
4. Найти несмещенную оценку дисперсии случайной величины Х на основании данного распределения выборки
| 
| 2 | 7 | 9 | 10 |
| 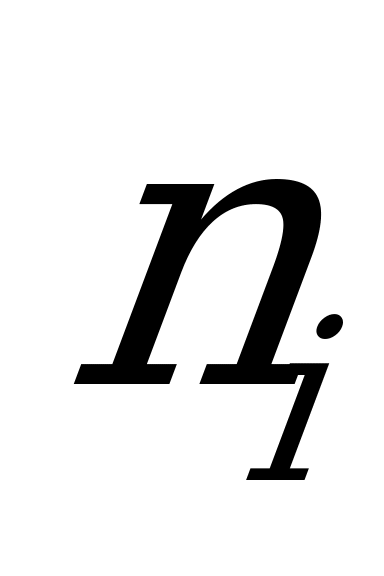
| 8 | 14 | 10 | 18 |
Решение:
Находим выборочную среднюю

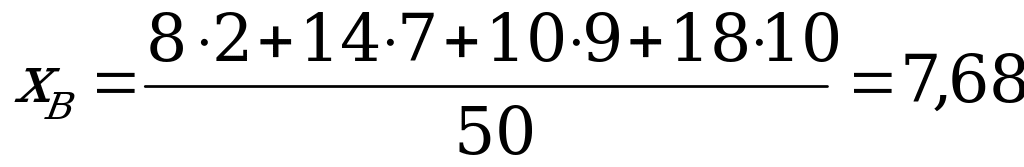
Для вычисления выборочной дисперсии используем формулу:
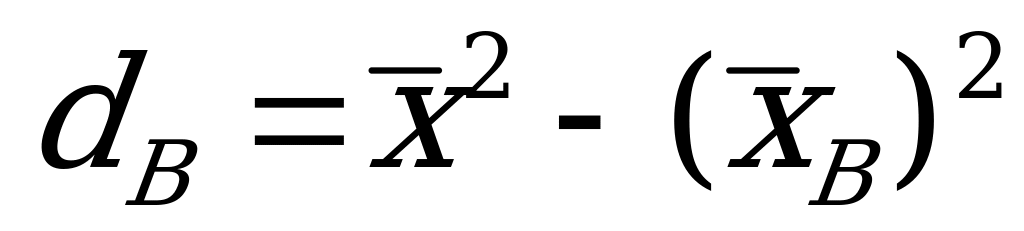
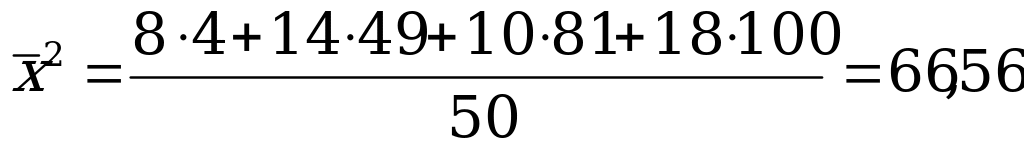
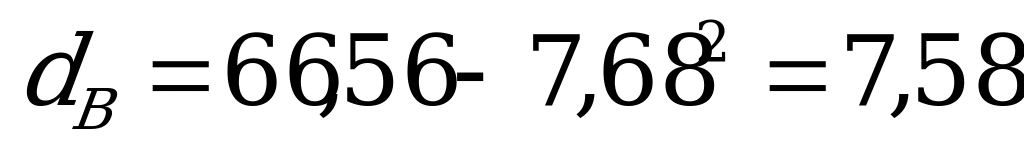 . Теперь находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию):
. Теперь находим несмещенную оценку дисперсии («исправленную» выборочную дисперсию):
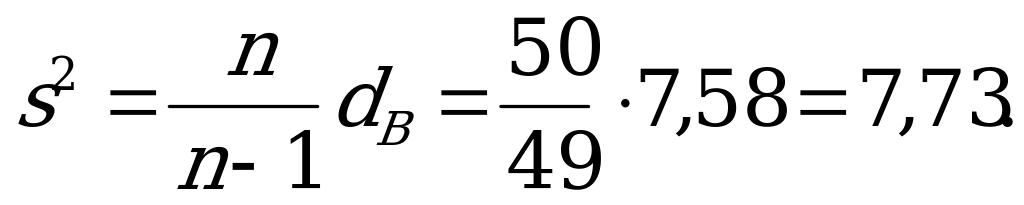
5. Найти выборочную дисперсию по данному распределению выборки:
| 
| 0,02 | 0,05 | 0,08 |
| 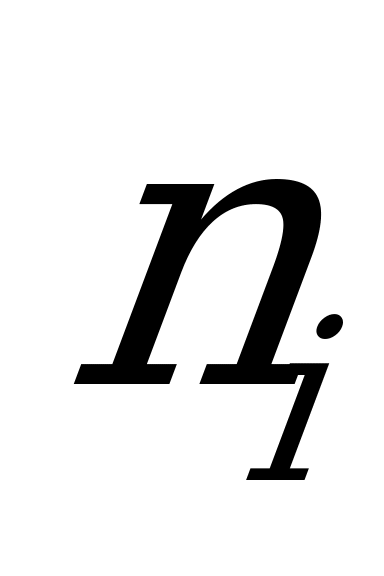
| 3 | 2 | 5 |
Решение:
В целях упрощения расчетов целесообразно перейти к условным вариантам
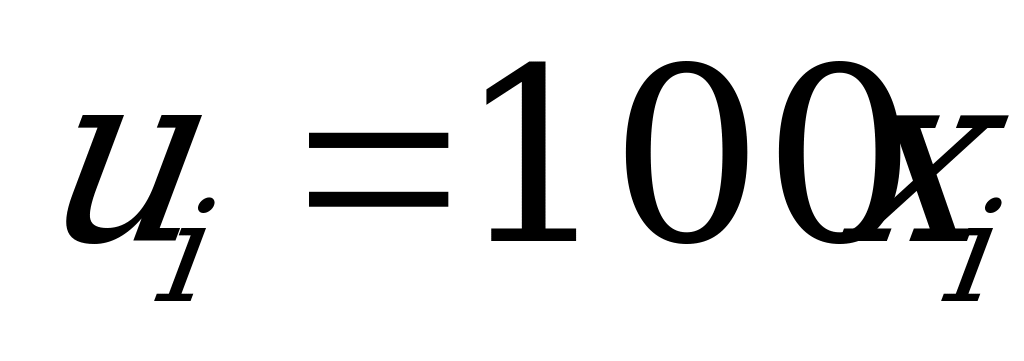 :
:
| 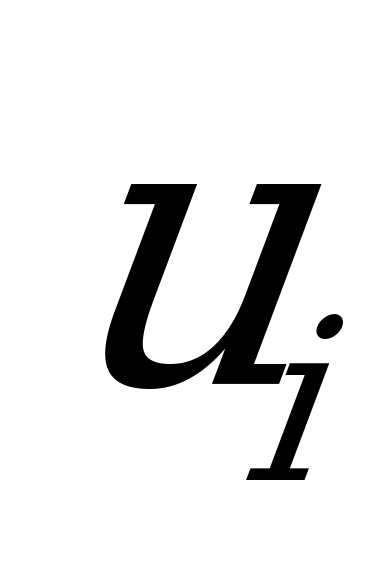
| 2 | 5 | 8 |
| 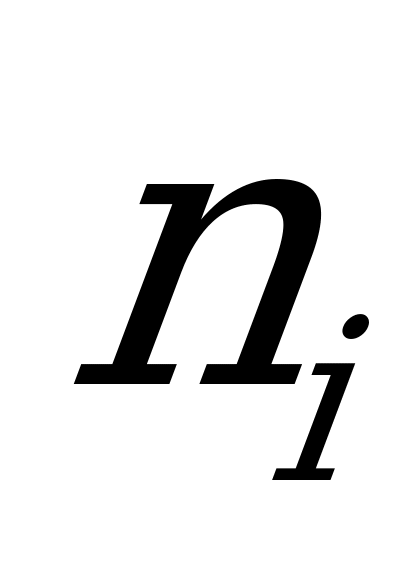
| 3 | 2 | 5 |
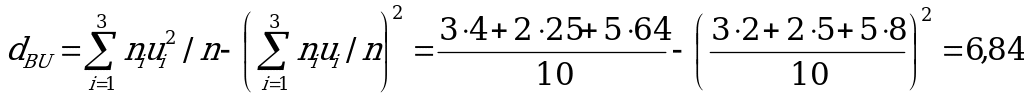
Выборочная дисперсия данного распределения вариант  находится на основе выражения:
находится на основе выражения:
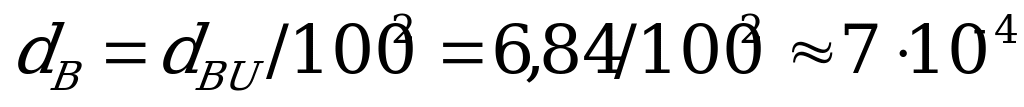 .
.
6. На предприятии изготавливается определенный вид продукции. Ежемесячный объем выпуска этой продукции является случайной величиной, для характеристики которой принят показательный закон распределения
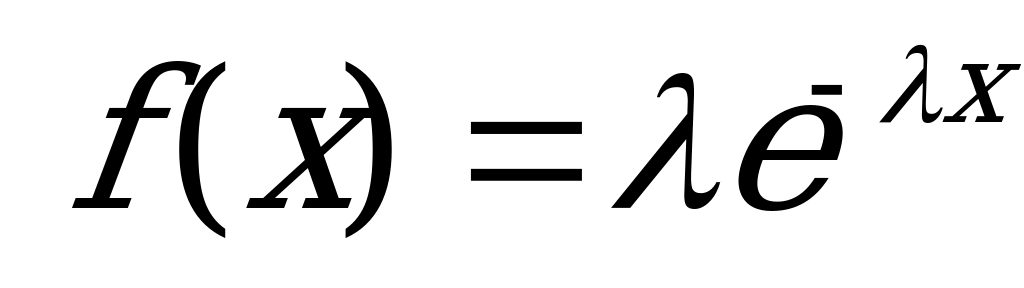 (
(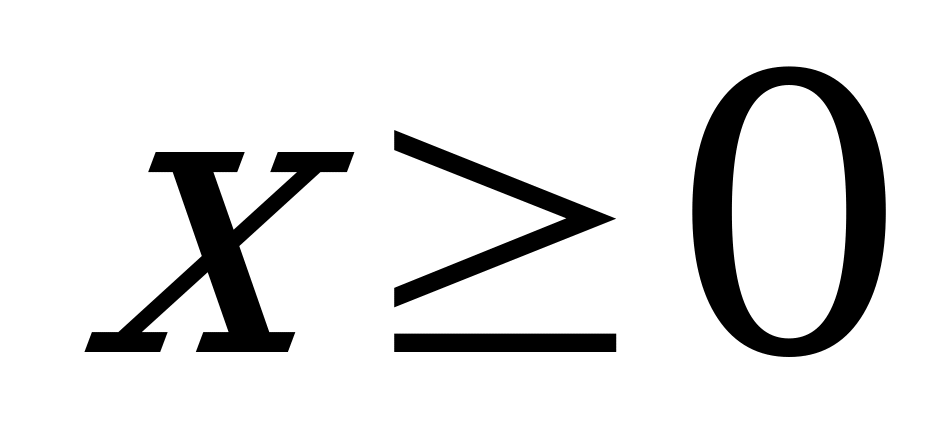 )
)
В течении шести месяцев проводится замер объемов выпусков продукции, получены следующие данные:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 |
| Объем выпуска | 20 | 24 | 25 | 28 | 27 | 32 |
Найти оценку параметра 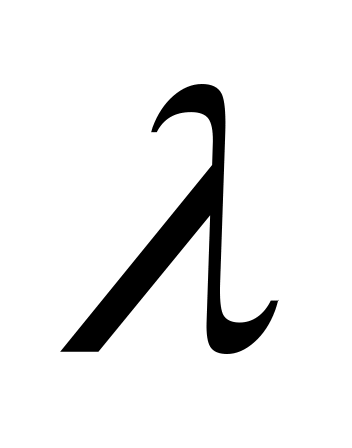 .
.
Решение:
Так как закон распределения содержит только один параметр, то для его оценки требуется составить одно уравнение.
Находим выборочную среднюю:
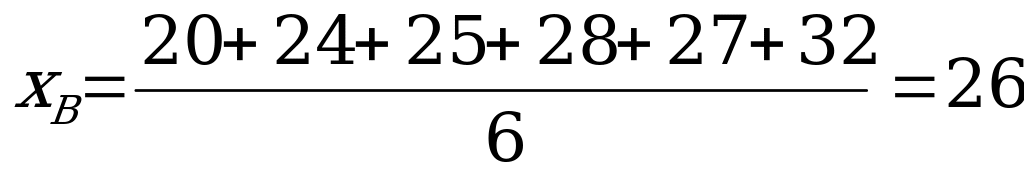
Определяем математическое ожидание:
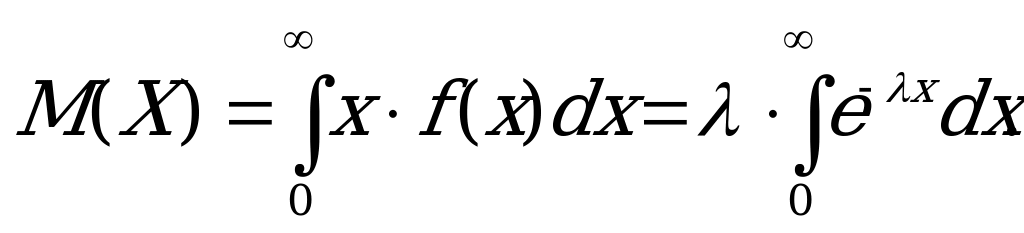
Интегрируя по частям, получаем 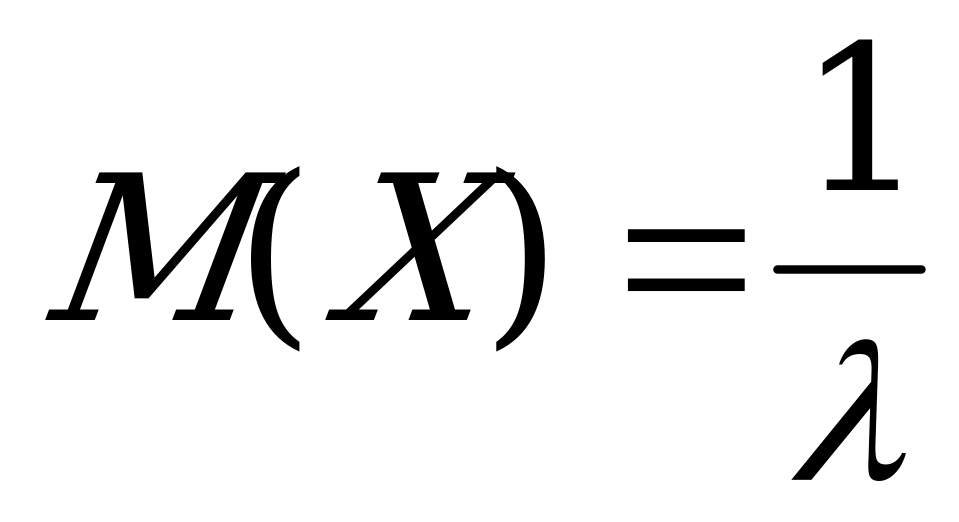 . А так как
. А так как 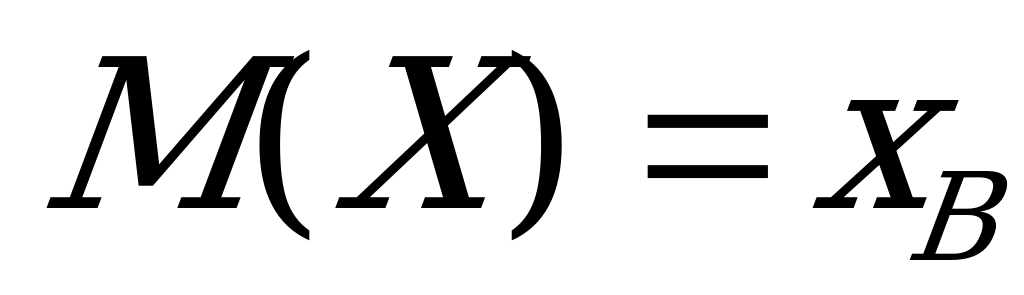 , то имеем
, то имеем
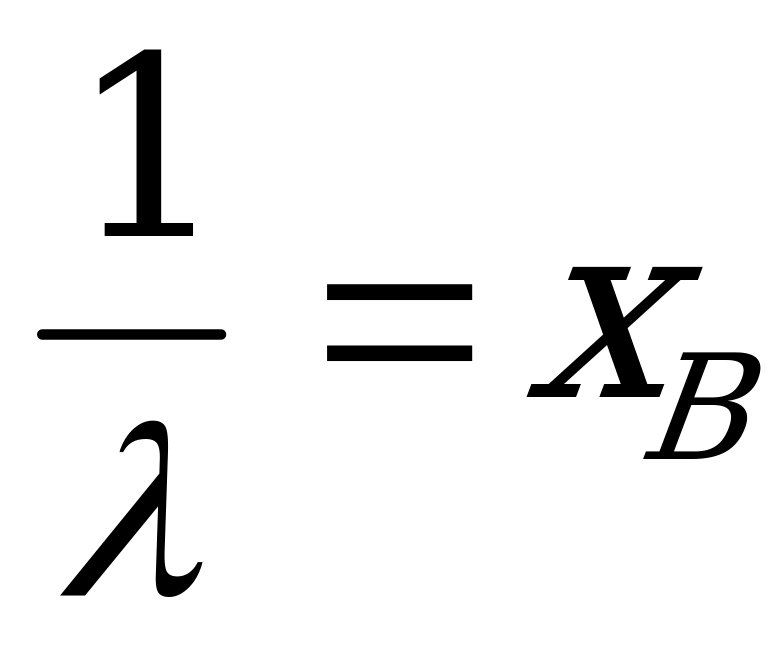 . Это равенство является приближенным, так как правая его часть является случайной величиной. Таким образом, из последнего уравнения получается не точное значение
. Это равенство является приближенным, так как правая его часть является случайной величиной. Таким образом, из последнего уравнения получается не точное значение  , а его оценка
, а его оценка 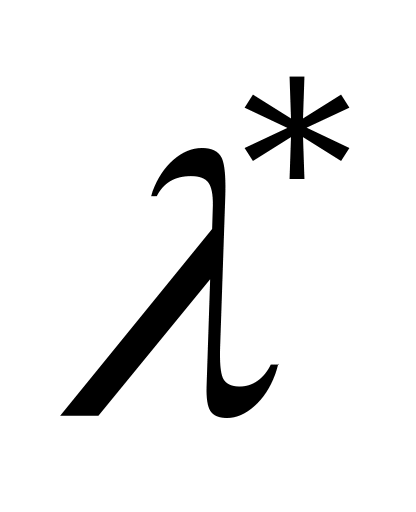 :
:
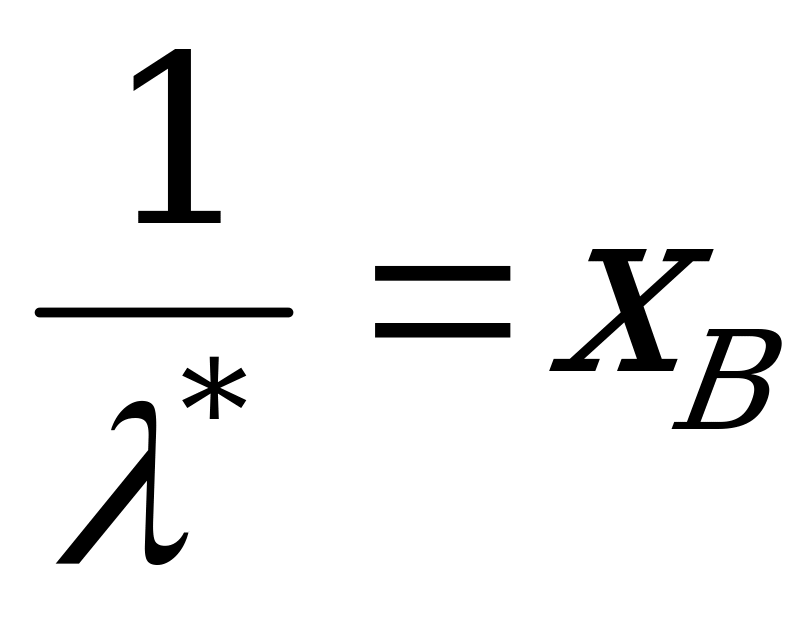 . Итак,
. Итак, 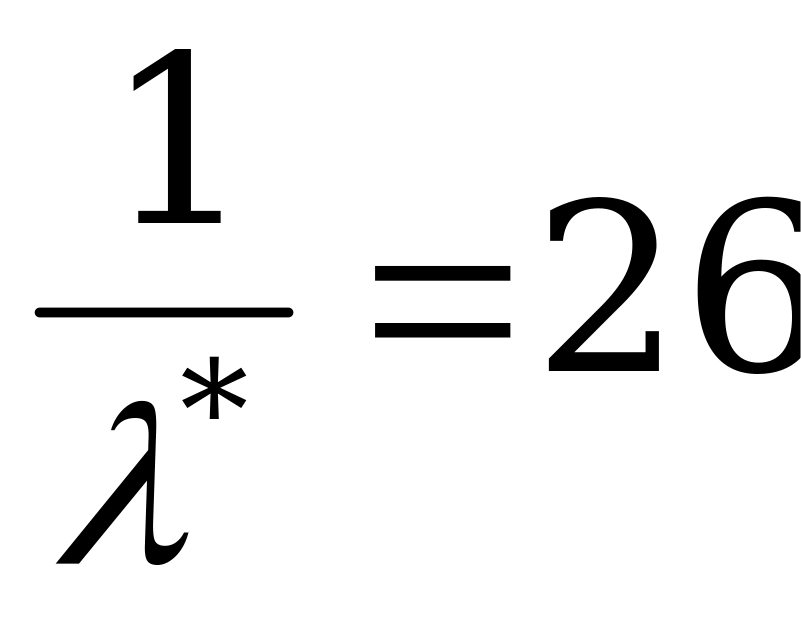 , откуда
, откуда 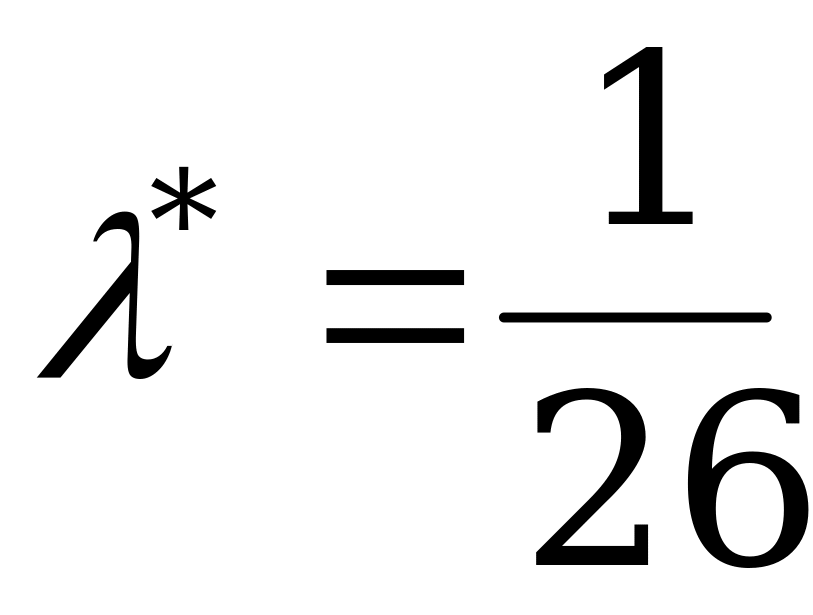 .
.
Найти доверительный интервал с надежностью 0,95 для оценки
математического ожидания нормально распределенной случайной
величины, если известны ее среднее квадратическое отклонение 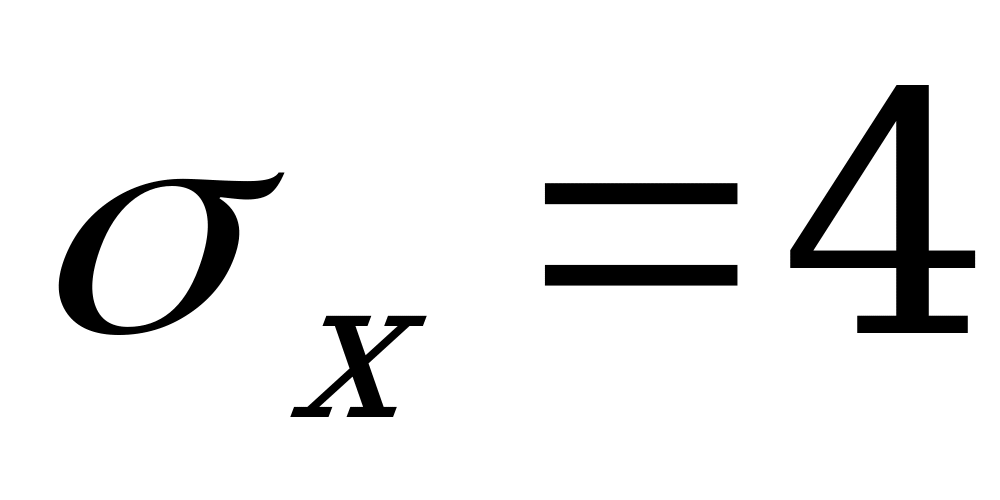 ,
,
выборочная средняя 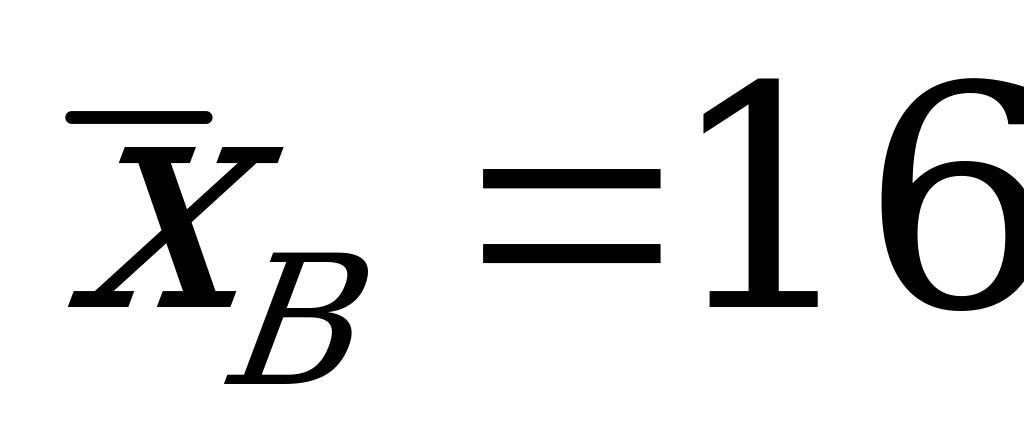 и объем выборки n=16.
и объем выборки n=16.
Решение:
По надежности 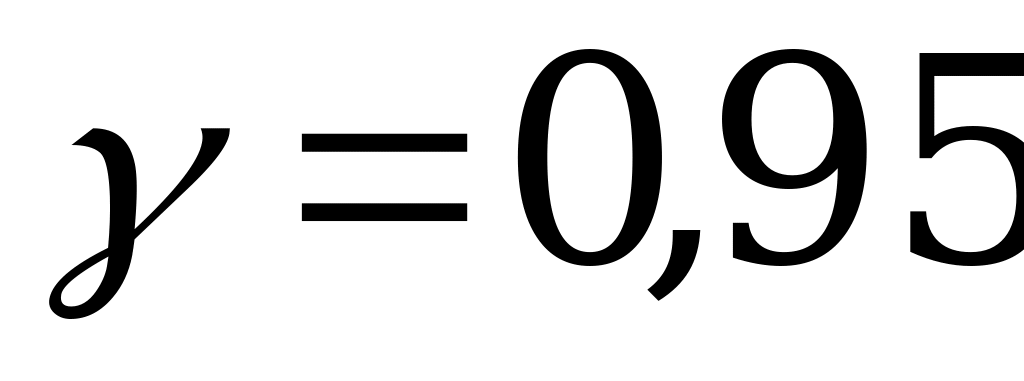 из соотношения
из соотношения 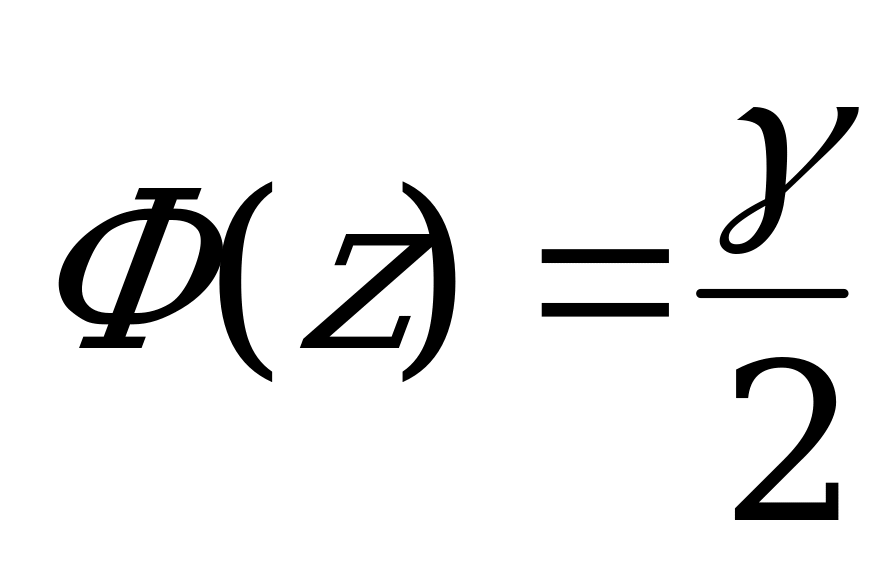 находим значение функции Лапласа Ф(z)=0,475
находим значение функции Лапласа Ф(z)=0,475
По таблице значений функции Лапласа (см. Приложение 2) находим z=1,96. Используя неравенства для интервальной оценки математического ожидания, получаем:
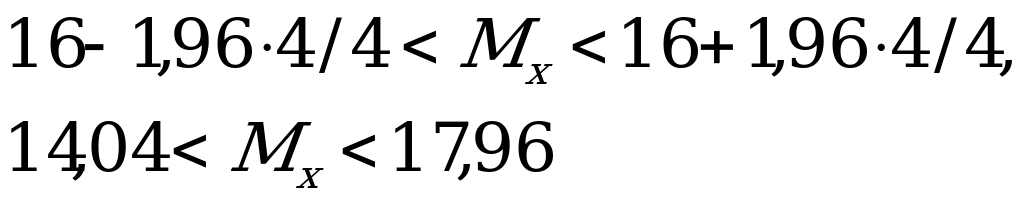
Описания контрольных заданий
Теория вероятностей
ЗАДАНИЯ
1. В партии из N изделий n изделий имеют скрытый дефект. Какова
вероятность того, что из взятых наугад m изделий k изделий являются
дефектными? (таблица 1)
2. В магазине выставлены для продажи n изделий, среди которых k
изделий некачественные. Какова вероятность того, что взятые
случайным образом m изделий будут некачественными. ( таблица 2)
3. На сборочное предприятие поступили однотипные комплектующие с трех
заводов в количестве: 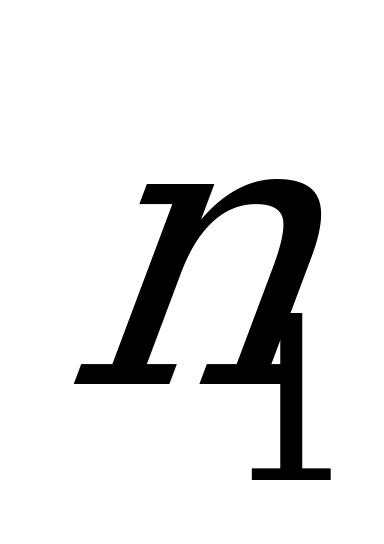 с первого завода,
с первого завода, 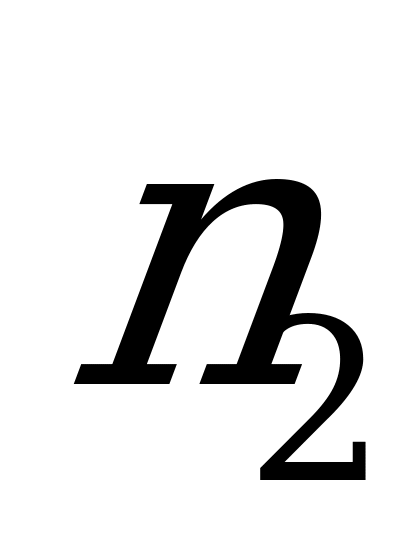 со второго,
со второго, 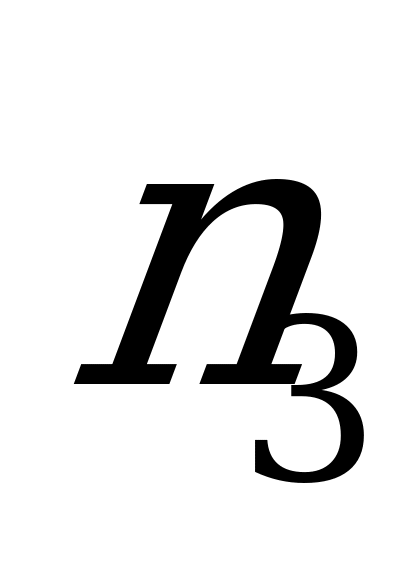 с третьего.
с третьего.
Вероятность качественного изготовления изделий на первом заводе - 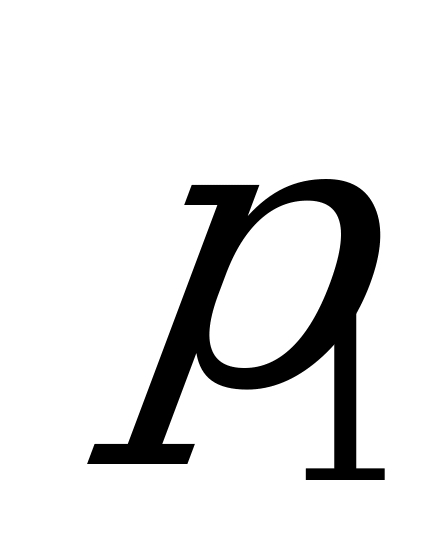 ,
,
на втором - 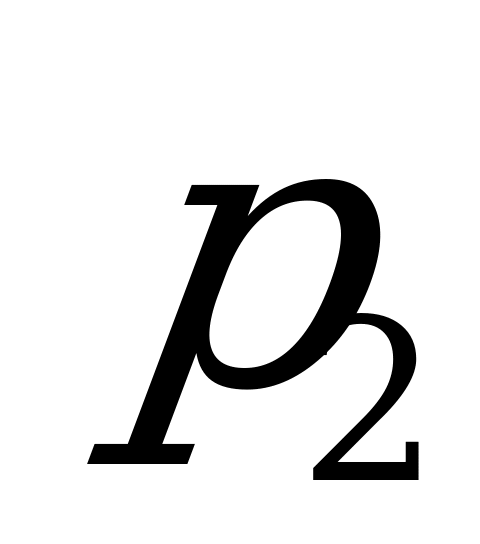 , на третьем
, на третьем 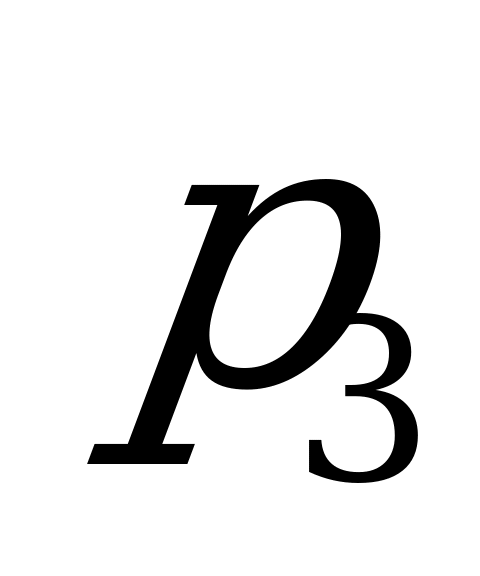 . Какова вероятность того, что взятое
. Какова вероятность того, что взятое
случайным образом изделие будет качественным? (таблица 3)
4. Дано распределение дискретной случайной величины Х ( таблица 4).
Найти математическое ожидание и среднее квадратическое отклонение.
5. В городе имеется N оптовых баз. Вероятность того, что требуемого сорта
товар отсутствует на этих базах одинакова и равна р. Составить закон
распределения числа баз, на которых искомый товар отсутствует в данный
момент.(таблица 5)
6. Непрерывная случайная величина имеет нормальное распределение. Ее
математическое ожидание равно 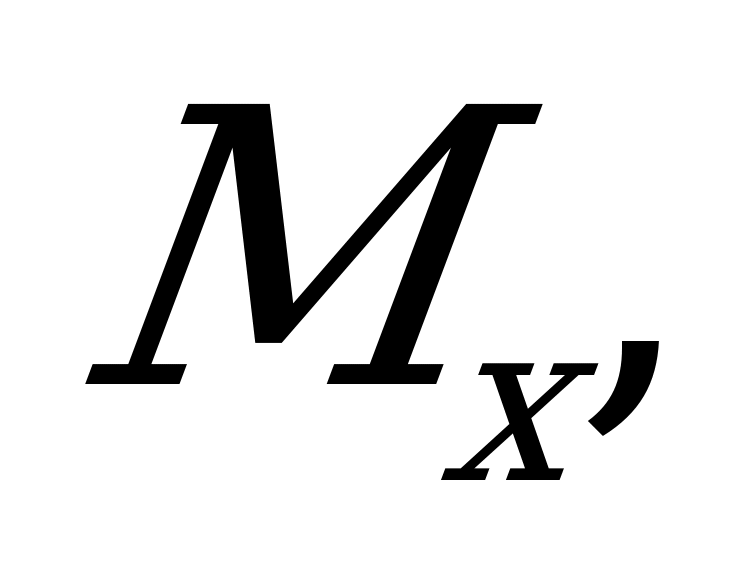 дисперсия -
дисперсия - 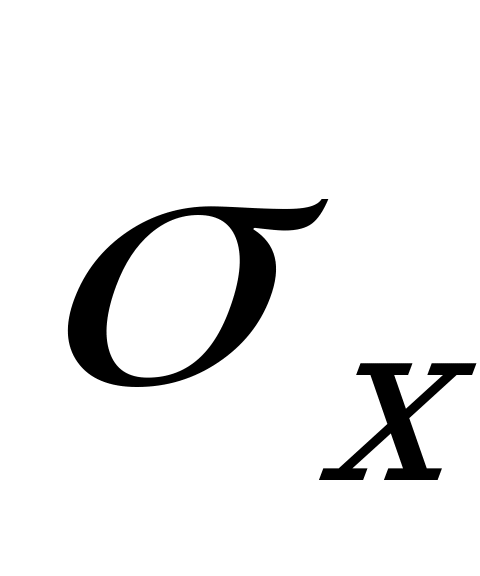 . Найти
. Найти
вероятность того, что в результате испытания случайная величина примет
значение в интервале  ( таблица 6).
( таблица 6).
7. Найти линейную среднюю квадратическую регрессию случайной
величины Y на случайную величину Х на основе заданного закона
распределения двумерной случайной величины. (таблица 7)
Математическая статистика
ЗАДАНИЯ
1. Рассчитать и построить гистограмму относительных частот по
сгруппированным данным ( таблица 8), где  - частота попадания
- частота попадания
вариант в промежуток 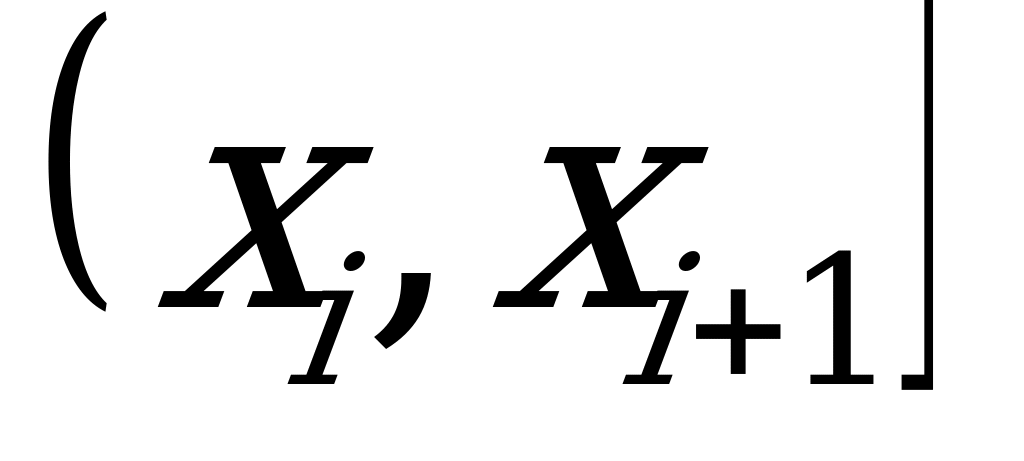 .
.
2. Найти несмещенную выборочную дисперсию на основании данного
распределения выборки ( таблица 9).
3. Проверить нулевую гипотезу о том, что заданное значение 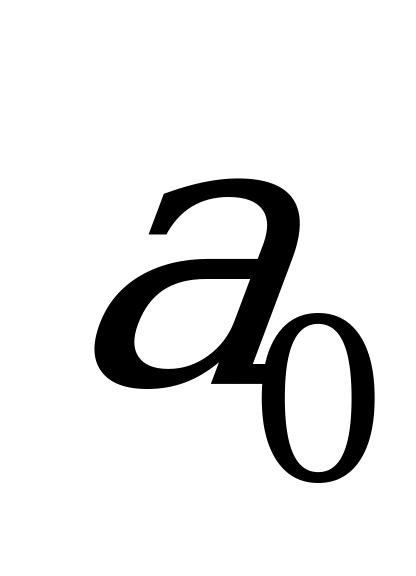 является
является
математическим ожиданием нормально распределенной случайной
величины при 5%-м уровне значимости для двусторонней критической
области, если в результаты обработки выборки объема n=10 получено
выборочное среднее 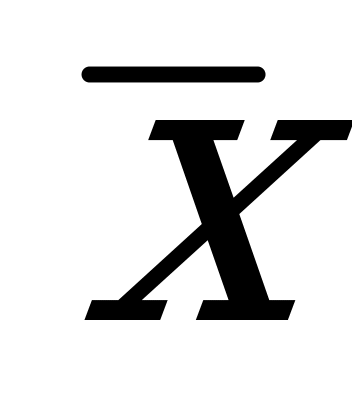 , а выборочное среднее квадратичное отклонение
, а выборочное среднее квадратичное отклонение
равно 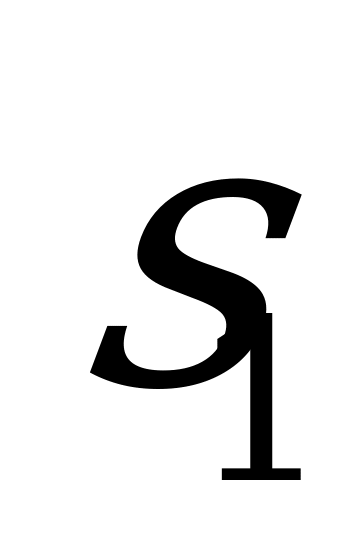 ( таблица 10)
( таблица 10)
4. При уровне значимости 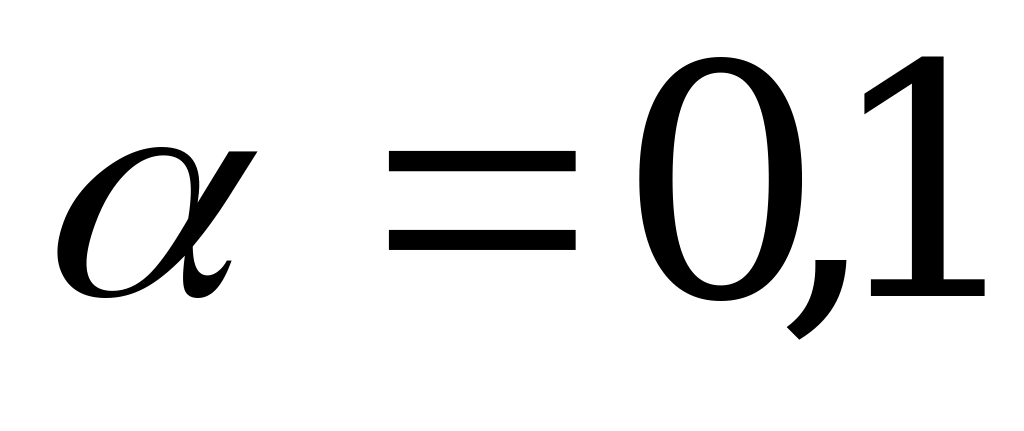 проверить гипотезу о равенстве дисперсий
проверить гипотезу о равенстве дисперсий
двух нормально распределенных случайных величин X и Y на основе
выборочных данных ( таблица 11) при альтернативной гипотезе
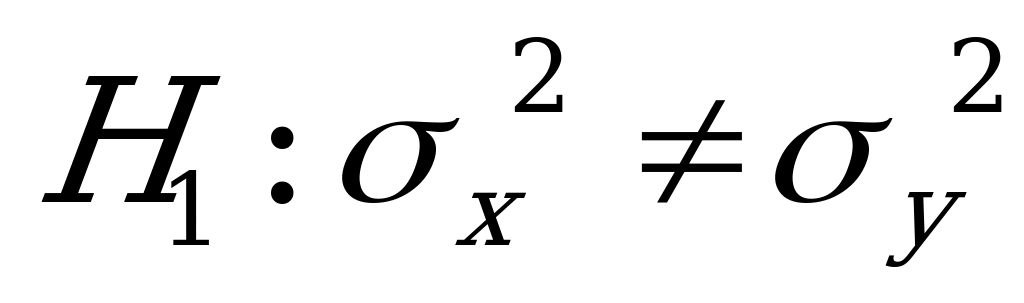 .
.
5. Найти выборочное уравнение линейной регрессии Y на Х на основании
корреляционной таблицы (таблица 12)
6. При уровне значимости 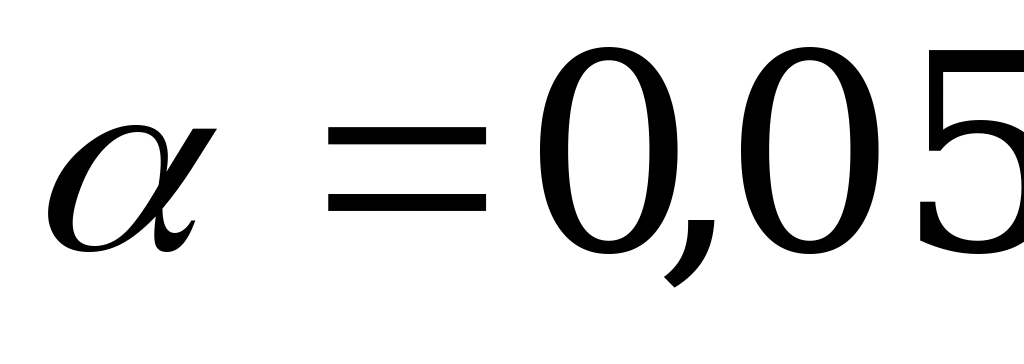 методом дисперсионного анализа
методом дисперсионного анализа
проверить нулевую гипотезу о влиянии фактора на качество объекта на
основании пяти измерений для трех уровней фактора ( таблица 13)
| вариант | n | k | m |
| 1 | 20 | 6 | 2 |
| 2 | 18 | 8 | 3 |
| 3 | 16 | 6 | 2 |
| 4 | 14 | 5 | 3 |
| 5 | 15 | 5 | 2 |
| 6 | 17 | 6 | 3 |
| 7 | 18 | 8 | 4 |
| 8 | 20 | 7 | 2 |
| 9 | 12 | 4 | 3 |
| 10 | 10 | 4 | 2 |
Таблица 1 Таблица 2
| Вариант | N | n | m | k |
| 1 | 20 | 4 | 5 | 2 |
| 2 | 30 | 5 | 5 | 3 |
| 3 | 20 | 5 | 4 | 2 |
| 4 | 25 | 6 | 5 | 3 |
| 5 | 15 | 4 | 3 | 2 |
| 6 | 20 | 6 | 4 | 1 |
| 7 | 30 | 4 | 3 | 2 |
| 8 | 16 | 4 | 3 | 2 |
| 9 | 18 | 6 | 5 | 3 |
| 10 | 12 | 5 | 4 | 2 |
Таблица 3
| вариант | 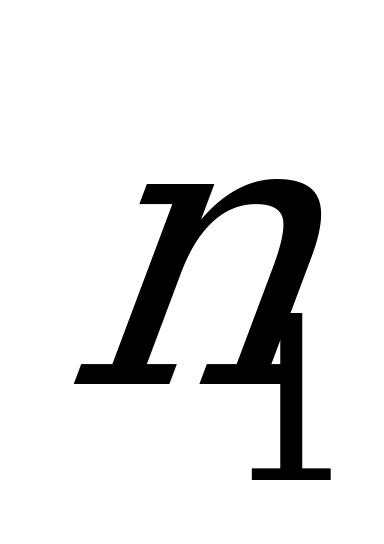
| 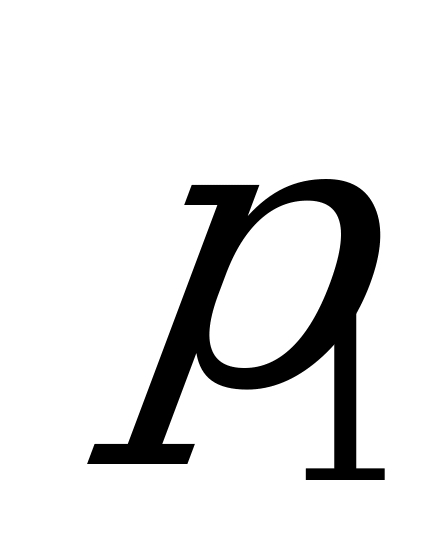
| 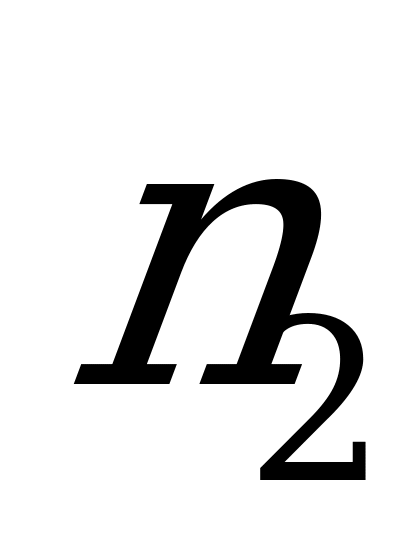
| 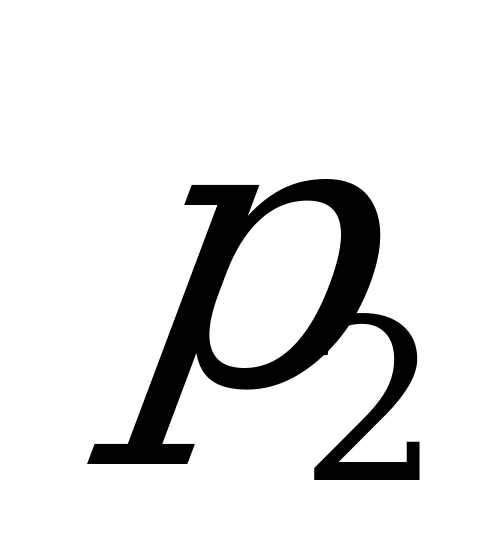
| 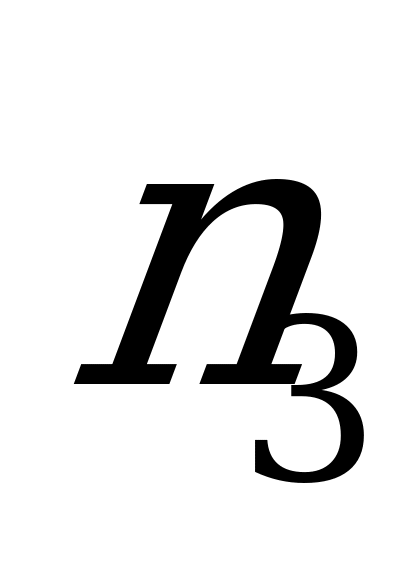
| 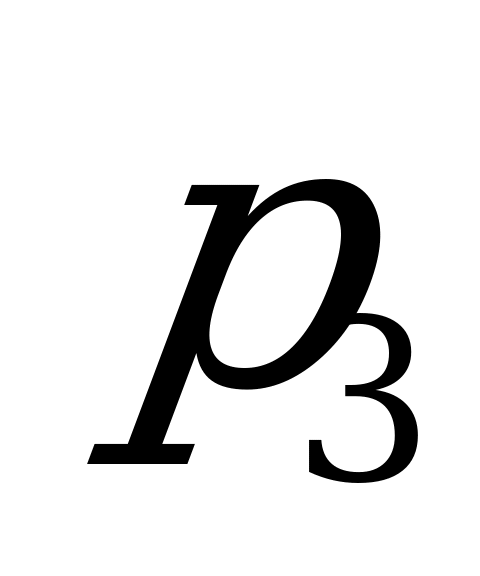
|
| 1 | 25 | 0,9 | 35 | 0,8 | 40 | 0,7 |
| 2 | 15 | 0,8 | 25 | 0,7 | 10 | 0,7 |
| 3 | 40 | 0,9 | 35 | 0,7 | 25 | 0,9 |
| 4 | 25 | 0,7 | 10 | 0,9 | 15 | 0,8 |
| 5 | 10 | 0,9 | 20 | 0,8 | 20 | 0,6 |
| 6 | 40 | 0,8 | 30 | 0,8 | 30 | 0,9 |
| 7 | 20 | 0,8 | 50 | 0,9 | 30 | 0,8 |
| 8 | 35 | 0,7 | 35 | 0,8 | 30 | 0,9 |
| 9 | 15 | 0,9 | 45 | 0,8 | 40 | 0,9 |
| 10 | 40 | 0,8 | 15 | 0,7 | 45 | 0,8 |
Таблица 4
| вариант | Числовые данные | вариант | Числовые данные |
| 1 | | 
| -5 | 2 | 3 | 4 | | 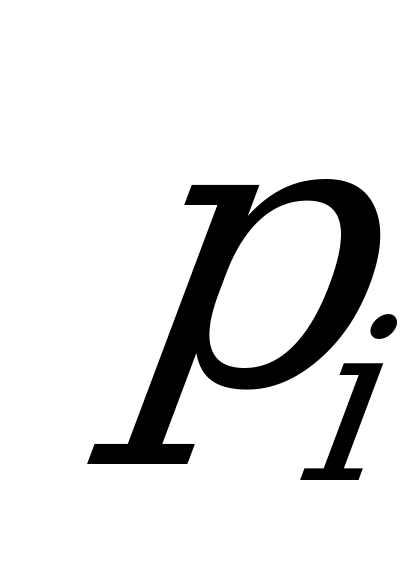
| 0,4 | 0,3 | 0,1 | 0,2 |
| 6 | | 
| -3 | 2 | 3 | 5 | | 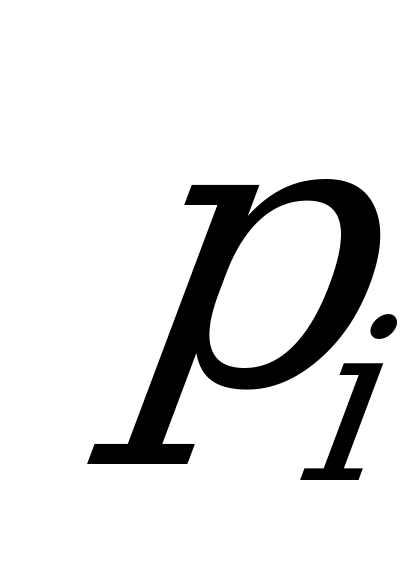
| 0,3 | 0,4 | 0,1 | 0,2 |
|
| 2 | | 
| -6 | -2 | 1 | 4 | | 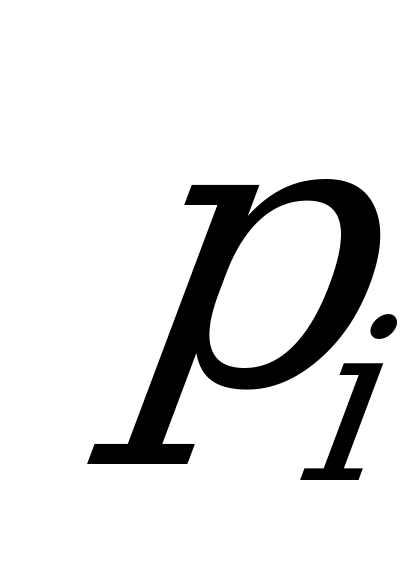
| 0,1 | 0,3 | 0,4 | 0,2 |
| 7 | | 
| 2 | 3 | 10 | | 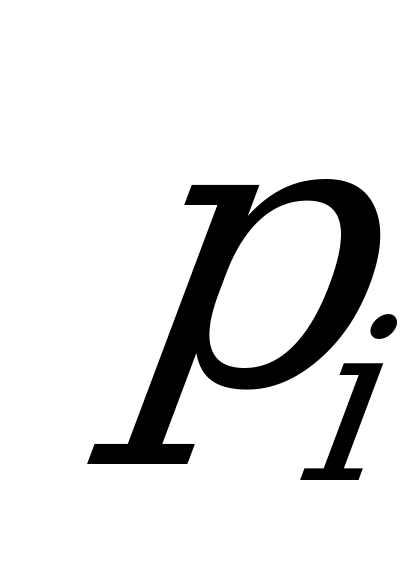
| 0,1 | 0,4 | 0,5 |
|
| 3 |
| 8 | | 
| -4 | -1 | 2 | 3 | | 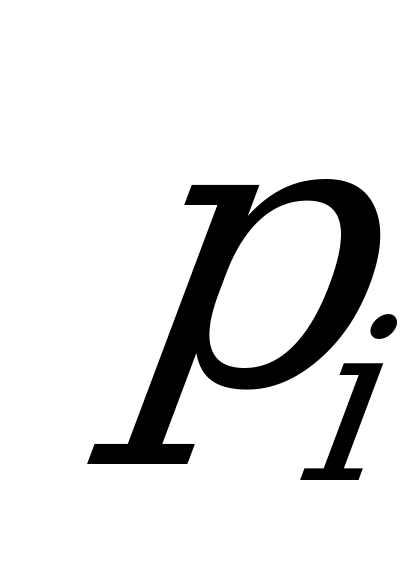
| 0,3 | 0,1 | 0,4 | 0,2 |
|
| 4 | | 
| -8 | -2 | 1 | 3 | | 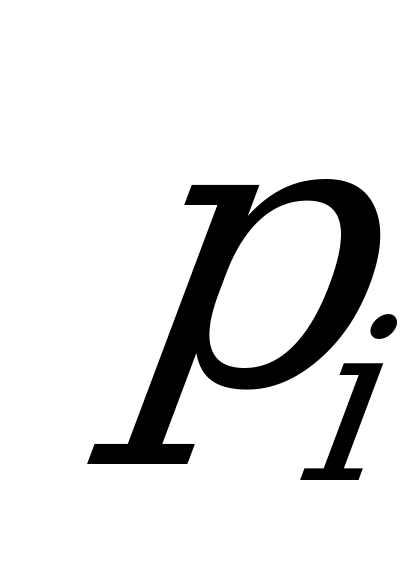
| 0,1 | 0,3 | 0,4 | 0,2 |
| 9 | | 
| 4 | 6 | 9 | | 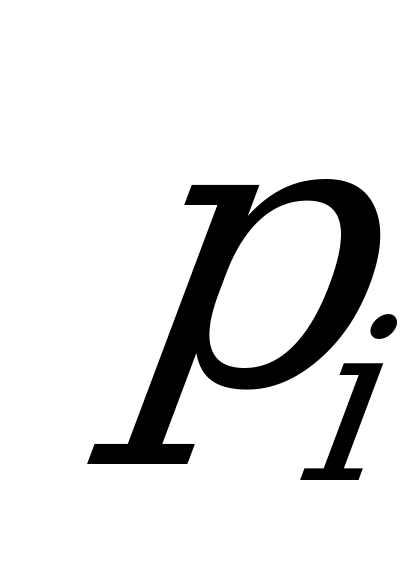
| 0,4 | 0,3 | 0,3 |
|
| 5 | | 
| -2 | 1 | 3 | 5 | | 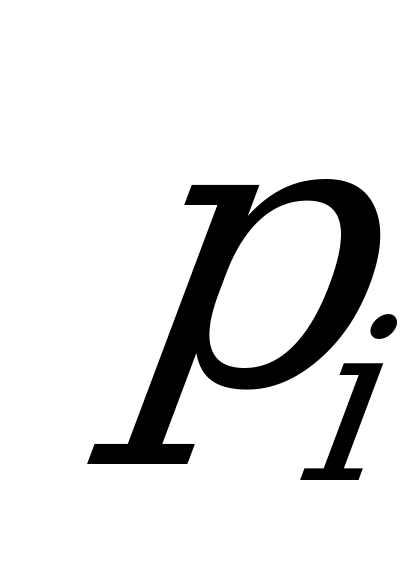
| 0,1 | 0,3 | 0,4 | 0,2 |
| 10 | | 
| 6 | 8 | 12 | 16 | | 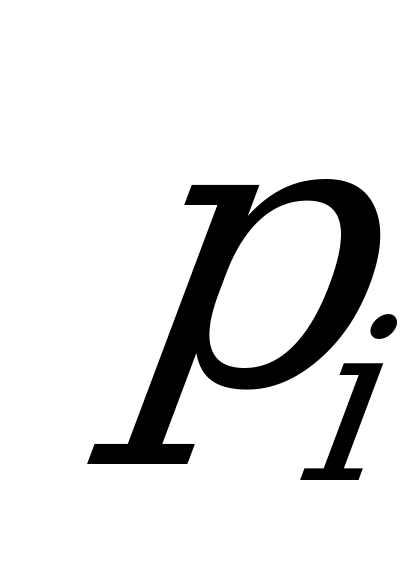
| 0,2 | 0,3 | 0,1 | 0,4 |
|
Таблица 5 Таблица 6
| вариант | 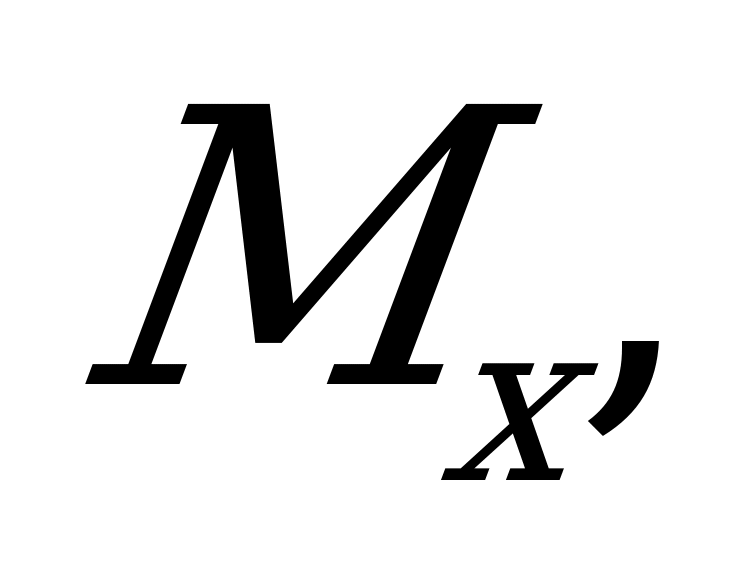
| 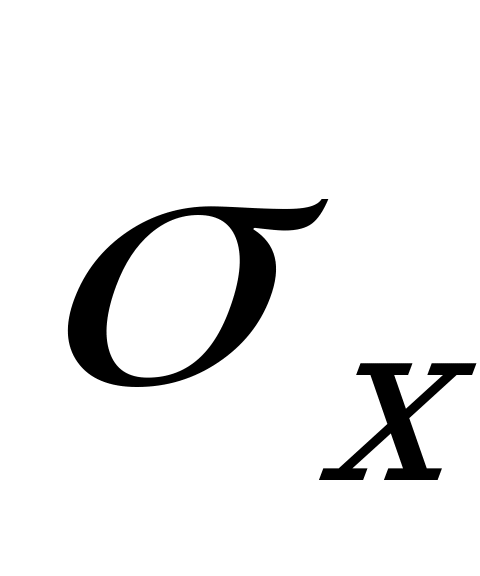
| a | b |
| 1 | 10 | 1 | 8 | 14 |
| 2 | 12 | 2 | 8 | 14 |
| 3 | 14 | 3 | 10 | 15 |
| 4 | 16 | 2 | 15 | 18 |
| 5 | 18 | 1 | 16 | 21 |
| 6 | 20 | 2 | 17 | 22 |
| 7 | 24 | 1 | 20 | 26 |
| 8 | 26 | 3 | 23 | 27 |
| 9 | 28 | 2 | 24 | 30 |
| 10 | 30 | 1 | 27 | 32 |
| вариант | N | p |
| 1 | 3 | 0,2 |
| 2 | 4 | 0,25 |
| 3 | 3 | 0,1 |
| 4 | 2 | 0,2 |
| 5 | 4 | 0,1 |
| 6 | 3 | 0,2 |
| 7 | 4 | 0,3 |
| 8 | 3 | 0,1 |
| 9 | 3 | 0,12 |
| 10 | 4 | 0,3 |
Таблица 7
| вариант | Числовые данные
|
| 1 | У Х | 1 | 3 | 4 |
| 2 3 | 0,16 0,14 | 0,10 0,20 | 0,28 0,12 |
| 2 | У Х | 2 | 3 | 5 |
| 1 4 | 0,06 0,12 | 0,18 0,13 | 0,24 0,27 |
| 3 | Х У | 2 | 3 | 4 |
| 1 3 | 0,16 0,14 | 0,10 0,20 | 0,28 0,12 |
| 4 | У Х | 1 | 2 | 4 |
| 3 4 | 0,12 0,20 | 0,24 0,15 | 0,22 0,07 |
| 5 | Х У | 2 | 3 | 5 |
| 4 6 | 0,06 0,12 | 0,18 0,13 | 0,24 0,27 |
| Вариант | Числовые данные |
| 6 | Х У | 2
| 3
| 4
|
| 1 3 | 0,16 0,14 | 0,10 0,20 | 0,28 0,12 |
| 7 | Х У | 2 | 4 | 5 |
| 1 3 | 0,12 0,18 | 0,13 0,06 | 0,24 0,27 |
| 8 | У Х | 4 | 5 | 6 |
| 2 3 | 0,06 0,12 | 0,18 0,13 | 0,24 0,27 |
| 9 | У Х | 2 | 4 | 5 |
| 1 3 | 0,12 0,18 | 0,13 0,06 | 0,24 0,27 |
| 10 | У Х | 1 | 3 | 4 |
| 3 6 | 0,13 0,18 | 0,24 0,06 | 0,12 0,27 |
Таблица 8
| вариант | 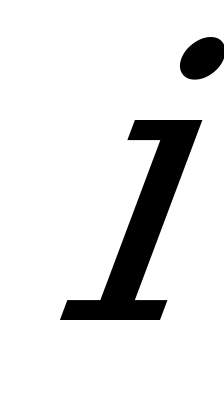
| 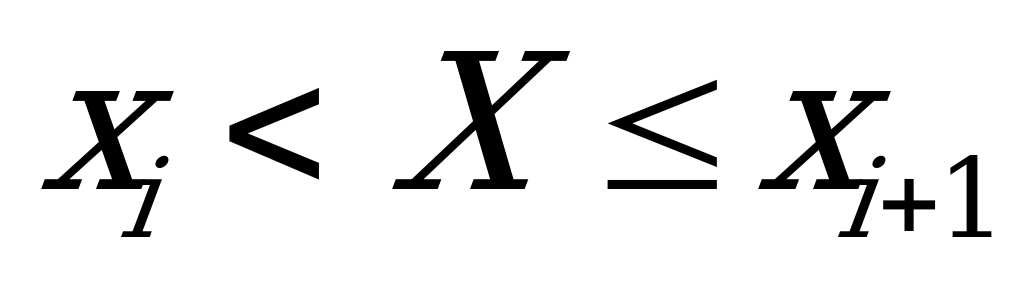
| 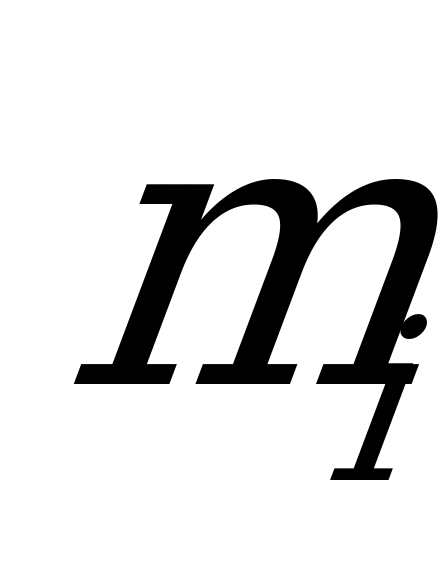
| вариант | 
| 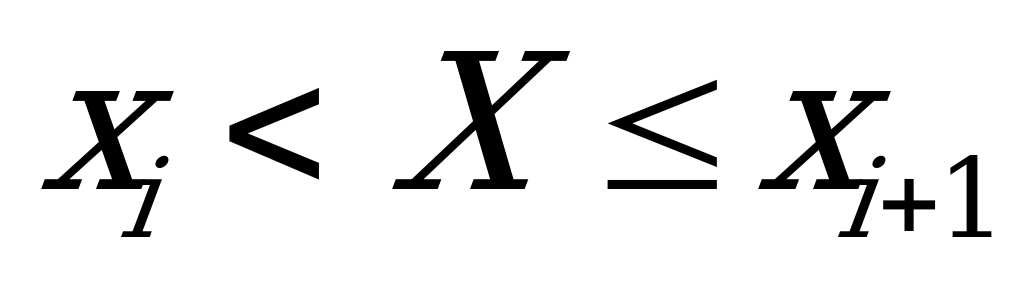
| 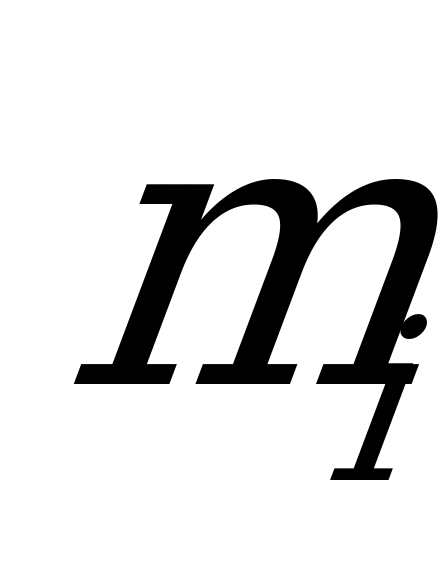
|
| 1 | 1 2 3 4 5 | 2 – 4 4 – 6 6 – 8 8 – 10 10 – 12 | 5 8 16 12 9 | 6 | 1 2 3 4 5 | 10 – 12 12 – 14 14 – 16 16 – 18 18 – 20 | 4 12 8 8 18 |
| 2 | 1 2 3 4 5 | 3 – 7 7 – 11 11 – 15 15 – 19 19 – 23 | 4 6 9 10 11 | 7 | 1 2 3 4 5 | 3 – 7 7 – 11 11 – 15 15 – 19 19 - 23 | 6 8 10 12 4 |
| 3 | 1 2 3 4 5 | 4 – 8 8 – 12 12 – 16 16 – 20 20 – 24 | 5 7 10 12 6 | 8 | 1 2 3 4 5 | 5 – 7 7 – 9 9 – 11 11 – 13 13 - 15 | 4 14 12 8 2 |
| 4 | 1 2 3 4 5 | 7 – 9 9 – 11 11 – 13 13 – 15 15 – 17 | 5 4 8 12 11 | 9 | 1 2 3 4 5 | 2 – 5 5 – 8 8 – 11 11 – 14 14 – 17 | 6 24 13 1 6 |
| 5 | 1 2 3 4 5 | 5 – 8 8 – 11 11 – 14 14 – 17 17 – 20 | 5 7 4 1 3 | 10 | 1 2 3 4 5 | 10 – 14 14 – 18 18 – 22 22 – 26 26 – 30 | 5 14 26 9 6 |
Таблица 9
| вариант | Числовые данные | вариант | Числовые данные |
| 1 | | 
| -6 | -2 | 3 | 6 | | 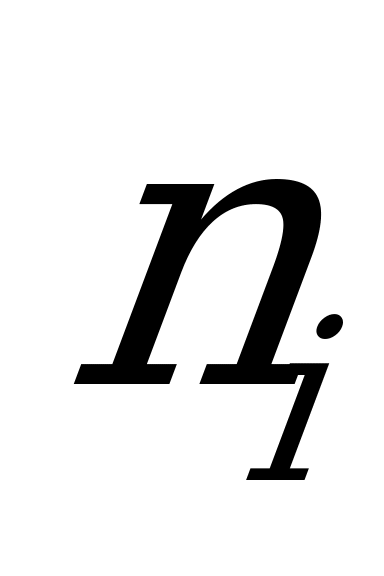
| 12 | 14 | 16 | 8 |
| 6 | | 
| -3 | 1 | 4 | 8 | | 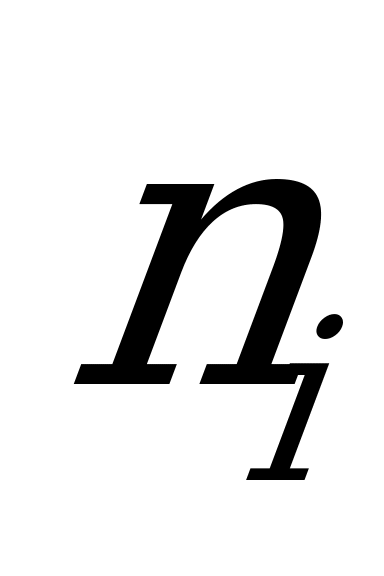
| 2 | 3 | 1 | 4 |
|
| 2 | | 
| -10 | -5 | -1 | 4 | | 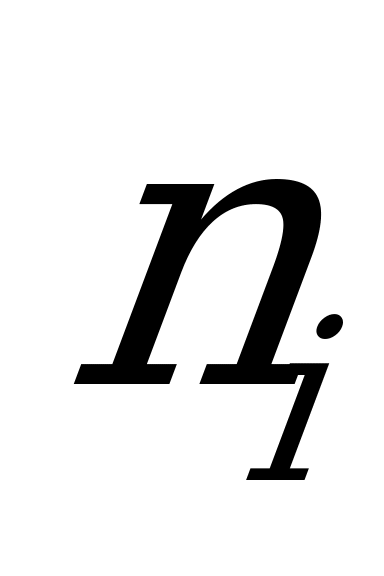
| 25 | 44 | 16 | 15 |
| 7 | | 
| 38 | 42 | 46 | | 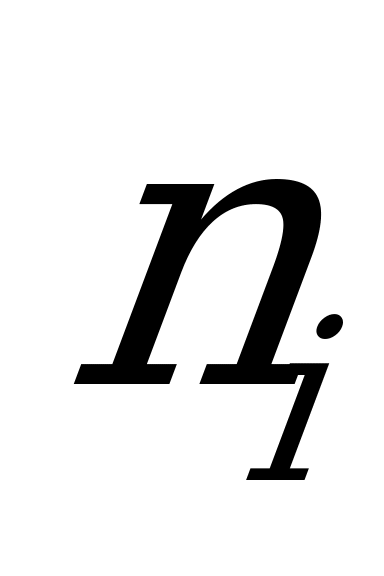
| 52 | 36 | 12 |
|
| 3 |
| 8 | | 
| 16 | 20 | 22 | 30 | | 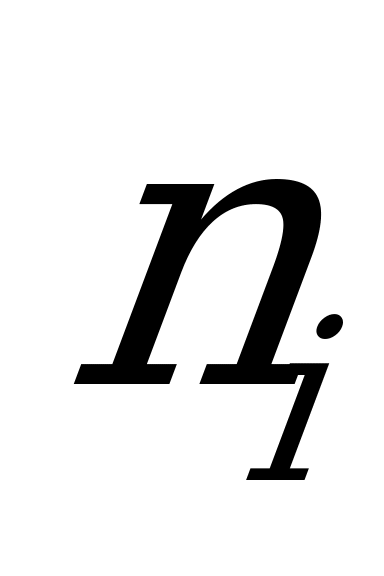
| 14 | 26 | 17 | 3 |
|
| 4 | | 
| 4 | 8 | 16 | 24 | | 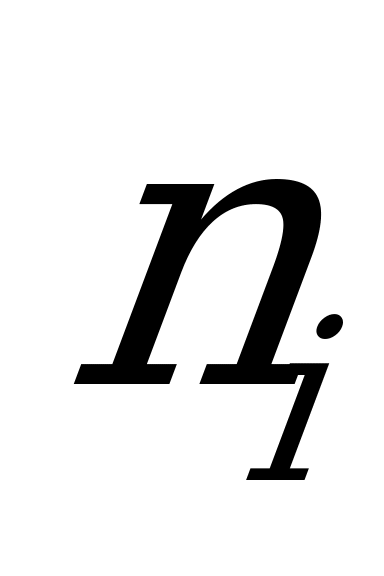
| 31 | 14 | 28 | 27 |
| 9 | | 
| 15 | 26 | 31 | | 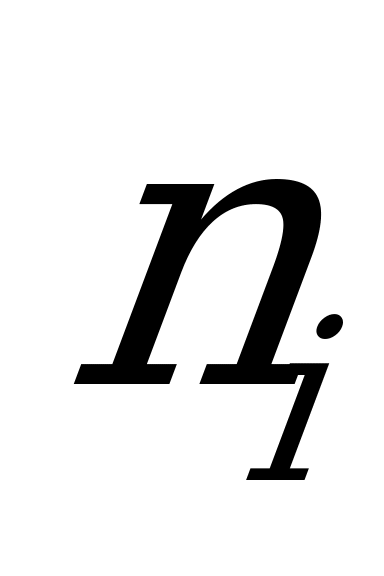
| 426 | 318 | 256 |
|
| 5 | | 
| 0,01 | 0,04 | 0,08 | 0,14 | | 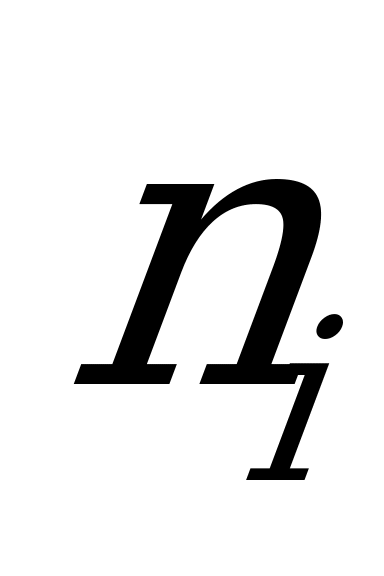
| 19 | 28 | 31 | 22 |
| 10 | | 
| 4 | 8 | 10 | 14 | | 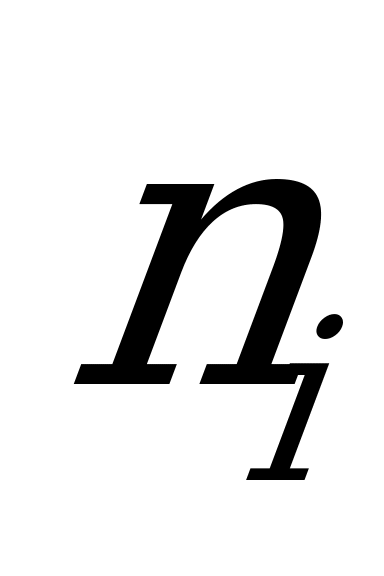
| 12 | 24 | 38 | 26 |
|
Таблица 10
| вариант | 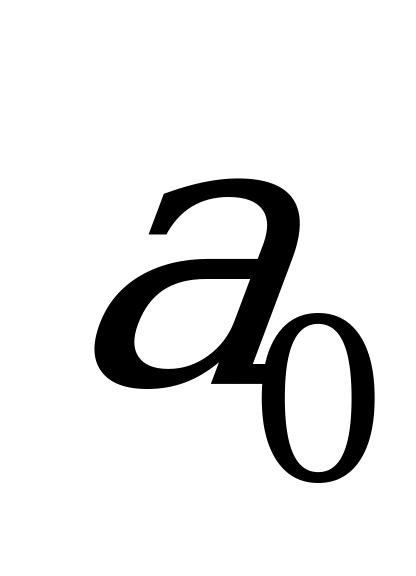
| 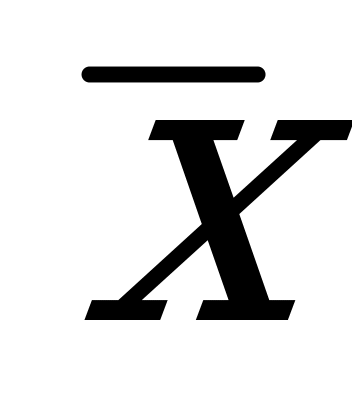
| 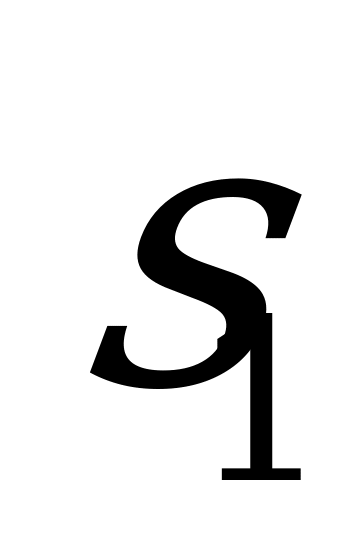
|
| 1 | 10 | 12 | 1 |
| 2 | 20 | 22 | 4 |
| 3 | 20 | 18 | 2 |
| 4 | 40 | 44 | 3 |
| 5 | 58 | 56 | 4 |
| 6 | 60 | 64 | 6 |
| 7 | 70 | 66 | 8 |
| 8 | 70 | 72 | 5 |
| 9 | 50 | 48 | 2 |
| 10 | 30 | 34 | 4 |
Таблица 11
| вариант | Х
| У | вариант | Х | У |
| 
| 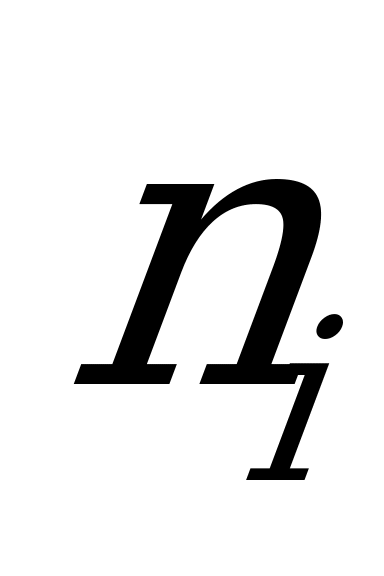
| 
| 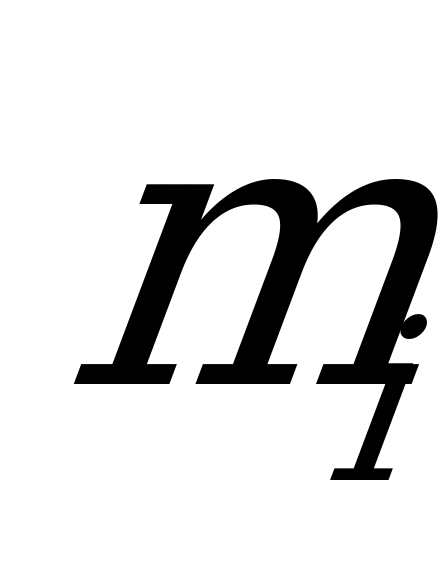
| 
| 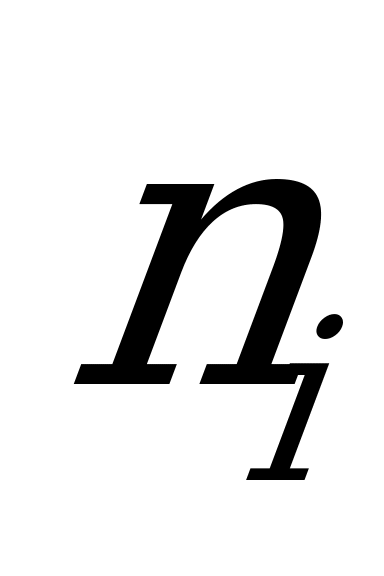
| 
| 
|
| 1 | 142 145 146 148 | 3 1 2 4 | 140 146 147 151 | 5 3 2 2 | 6 | 42 45 46 50 | 15 17 12 16 | 84 87 92 96 | 3 2 4 1 |
| 2 | 37 38 40 41 42 | 2 1 4 3 6 | 38 39 40 41 43 | 4 3 2 2 3 | 7 | 30 32 33 34 36 | 4 5 8 1 2 | 30 31 32 34 35 | 6 4 3 5 2 |
| 3 | 39 43 45 47 51 | 4 2 3 4 2 | 75 80 84 91 94 | 4 2 3 4 2 | 8 | 42 44 48 50 53 | 4 8 3 5 10 | 44 45 46 51 55 | 16 12 11 6 5 |
| 4 | 3,5 3,7 3,9 4,0 4,1 | 1 3 5 4 4 | 3,6 3,7 3,8 4,4 4,2 | 3 5 2 1 4 | 9 | 31 35 40 42 44 | 7 3 4 2 4 | 29 32 33 35 39 | 8 9 12 10 11 |
| 5 | 9 10 11 12 14 | 4 5 3 2 1 | 9 10 11 13 14 | 5 6 4 8 3 | 10 | 61 62 64 67 68 | 5 4 6 2 3 | 60 63 64 68 70 | 4 3 2 6 5 |
Таблица 12
| вариант | таблица |
| 1 | Х У |
10 |
15 |
20 |
25 |
30 |
35 |
| 15 25 35 45 55 | 6
| 4 6 |
8
|
21 4 |
2 12 1 |
5 6 5 |
| 2 | Х У | 20 | 25 | 30 | 35 | 40 | 45 |
| 10 20 30 40
|
2 | 4
4
| 8 4 10 |
8 10 |
2
4
| 4 |
| 3 | Х У | 5 | 10 | 15 | 20 | 25 | 30 |
| 14 24 34 44
| 4
| 6 8 |
10 32 4 | 8
12 |
6
6 | 4 |
| 4 | Х У | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 120 140 160 | 2 4 | 1
5 |
2
3 | 7
10 1 |
5 2 |
3 2 3 |
| 5 | Х У | 20 | 25 | 30 | 35 | 40 | 45 |
| 105 115 125 135 145 |
2
3 1 |
1 4 2 3 | 4
2 10 | 2 3 1
8 | 1 8
3 |
5 3 2 2 |
| 6 | Х У | 10 | 15 | 20 | 25 | 30 | 35 |
| 15 25 35 45 55 | 6 | 4 6 |
8 |
20 5 |
2 12 1 |
5 6 5 |
| 7 | Х У | 5 | 10 | 15 | 20 | 25 | 30 |
| 15 25 35 45 55
|
4
5 9 | 6 2
3 5 | 4 8
8 | 2 1 10
4 |
5 7 6 | 2
1 7 1 |
| 8 | Х У | 20 | 25 | 30 | 35 | 40 | 45 |
| 30 40 50 60 70
|
4 3 5 | 6 1
3 2 |
5 4
3 | 4
5 10 |
7
2 3 | 2
6
5 |
| 9 | Х У | 10 | 15 | 20 | 25 | 30 | 35 |
| 36 46 56 66 76
|
2 3
1 | 4 3
2 |
1 5 | 3
1 8 |
10
2 |
4 1 |
| 10 | Х У | 42 | 46 | 50 | 54 | 58 | 62 |
| 15 25 35 45 55
|
2
3 1 |
1 4 2 3 | 4
2 10 | 2 3 1
9 | 1 8
3 |
5 3 2 1 |
Таблица 13
| Вариант | Номер измерения | 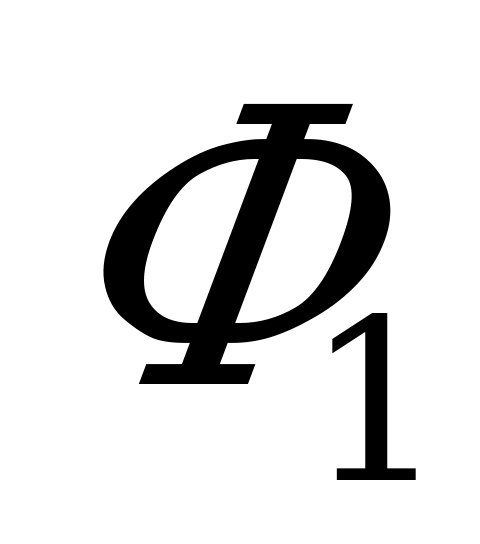
| 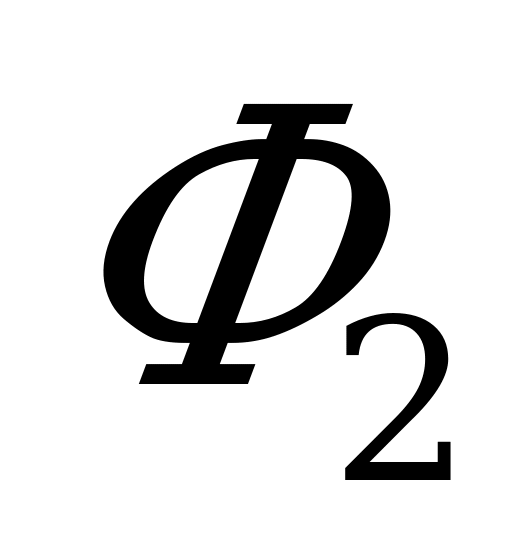
| 
|
| 1 | 1 2 3 4 5 | 24 16 12 5 6 | 18 14 10 4 16 | 22 15 16 12 8 |
| 2 | 1 2 3 4 5 | 10 8 7 18 6 | 14 5 14 4 12 | 12 9 10 7 8 |
| 3 | 1 2 3 4 5 | 16 10 20 25 24 | 9 8 9 7 5 | 14 16 12 16 14 |
| 4 | 1 2 3 4 5 | 34 36 26 25 30 | 38 30 34 36 38 | 28 24 22 20 23 |
| 5 | 1 2 3 4 5 | 48 38 30 40 36 | 40 42 37 33 39 | 34 38 44 41 45 |
| 6 | 1 2 3 4 5 | 12 16 15 17 14 | 10 8 7 5 9 | 20 26 28 24 27 |
| 7 | 1 2 3 4 5 | 44 45 48 45 40 | 40 36 32 35 30 | 38 28 30 32 26 |
| 8 | 1 2 3 4 5 | 16 12 10 11 10 | 18 20 22 25 24 | 26 15 28 30 26 |
| 9 | 1 2 3 4 5 | 9 11 10 12 9 | 4 6 5 6 5 | 12 18 24 20 23 |
| 10 | 1 2 3 4 5 | 54 50 43 47 36 | 32 46 28 37 28 | 16 36 30 25 17 |
34







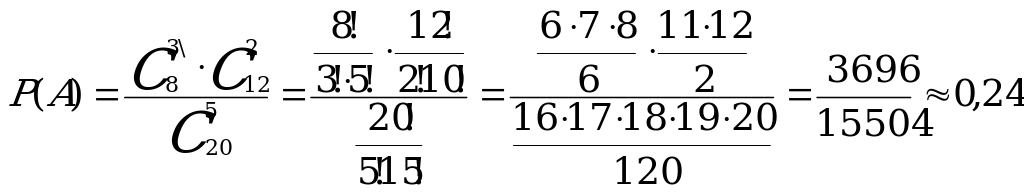
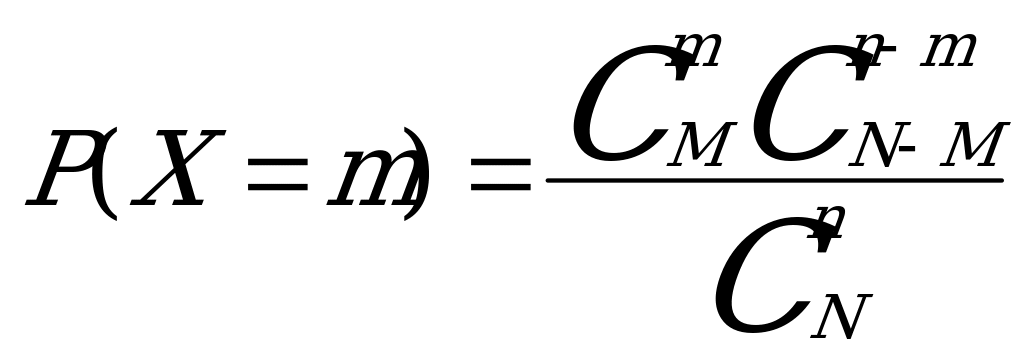 ,
,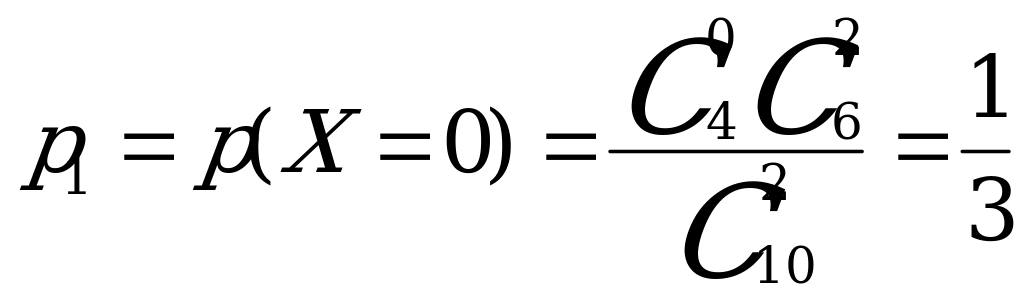 ,
, 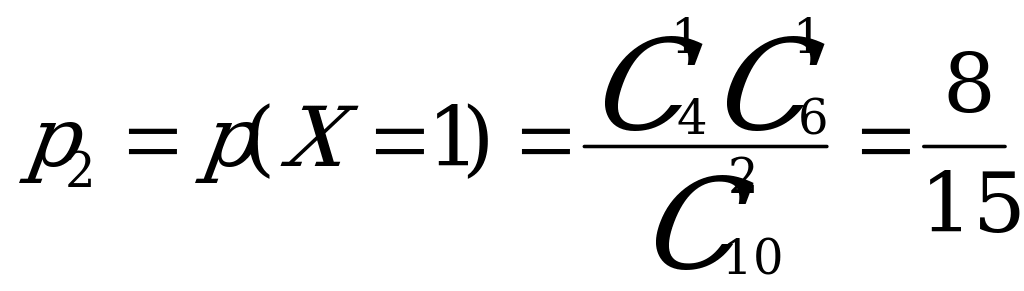
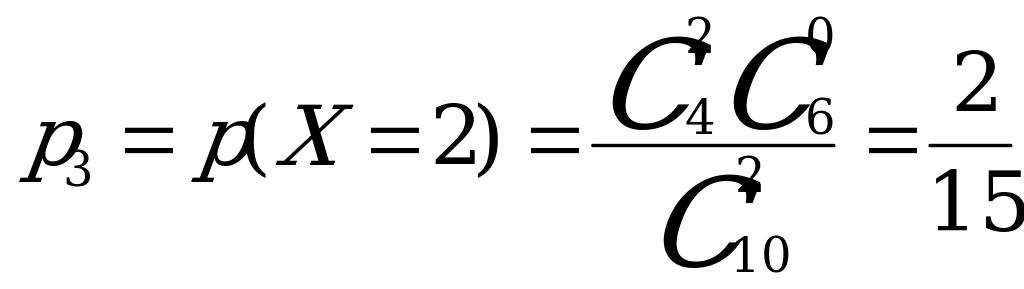 .
.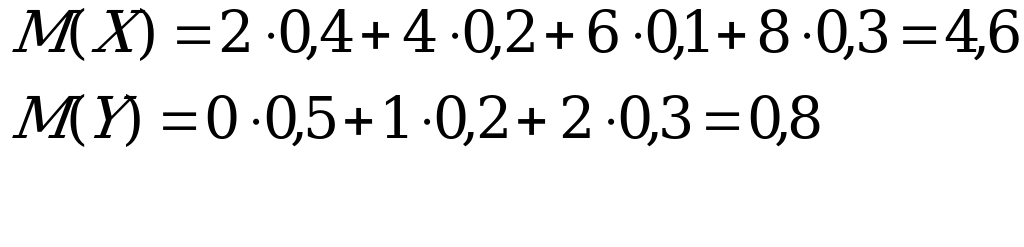
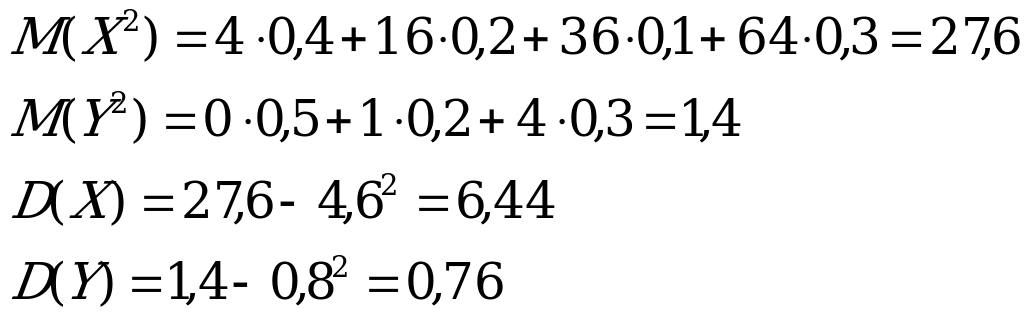
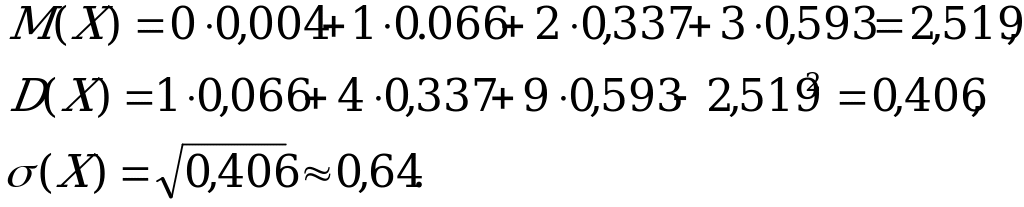

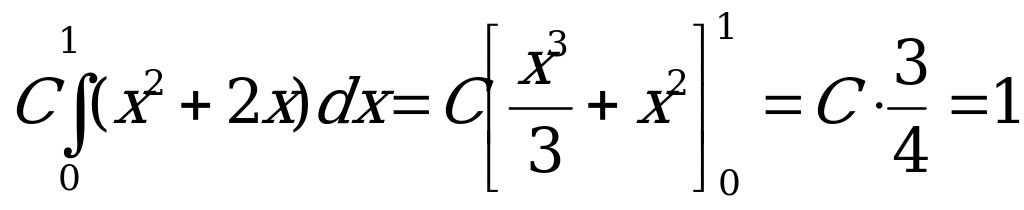 .
.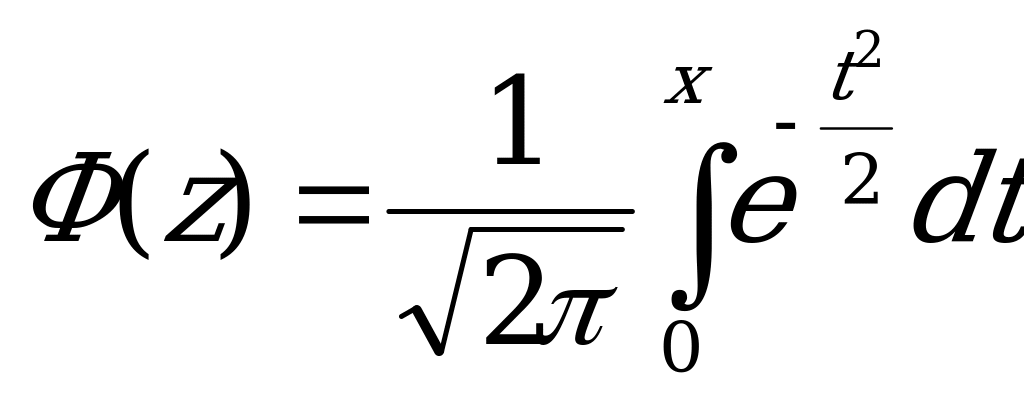 - функция Лапласа.
- функция Лапласа.

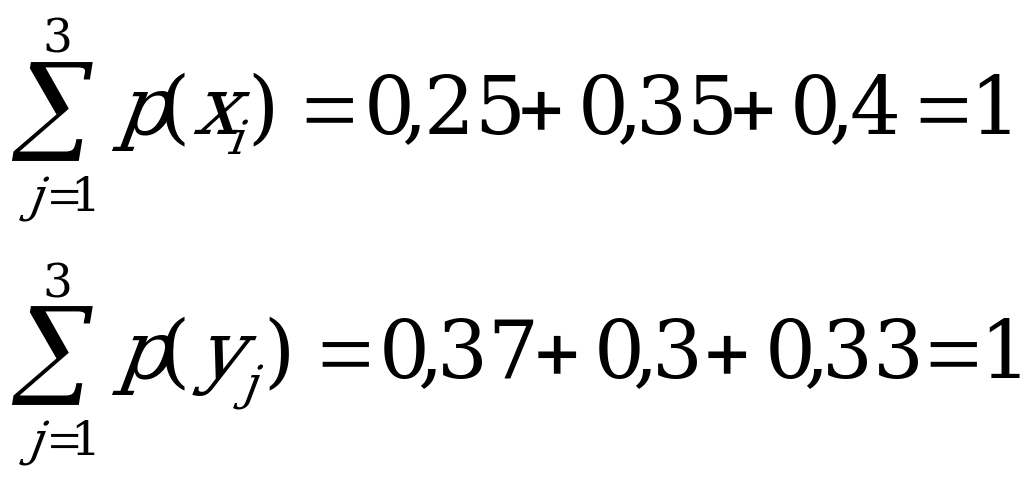
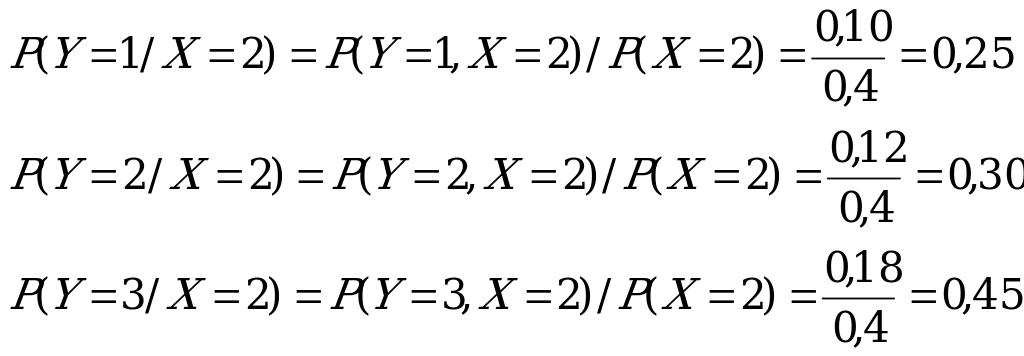
 Х
Х У
У