Методическое пособие на тему: "Алгебраические уравнения и неравенства высших степеней"

Методические рекомендации.

Алгебра и начало анализа в классах профильного обучения или на занятиях факультатива

10 класс

Первые уроки по теме

«Алгебраические уравнения и неравенства высших степеней»

Урок № 1, № 2

(Рассчитано на два спаренных урока)

Тема урока: Многочлен и его корни

Цель урока: Повторить основные сведения о многочлене, действия над многочленами (сложение, вычитание и умножение).

Ввести понятие корня многочлена, ознакомить с теоремой Безу, и обратной и обобщенной теоремой Безу; теоремой Виета для многочленов третьей и четвертой степеней, и последствий из теоремы Виета; развивать познавательную активность учащихся; воспитывать культуру устной и письменной речи.

Тип урока: урок усвоения новых знаний

Оборудование урока: цветные мелки, графопроектор, кодопозитивы.

Ход урока

1. Организационный этап (2 мин.)

II. Актуализация опорных знаний.

* Фронтальный опрос

1. Что такое многочлен?

(Сумма нескольких одночленов)

2. Что значит записать многочлен в стандартном виде?

(Многочлен записано в стандартном виде, если все его члены - одночлены стандартного вида, и среди них нет подобных)

3. Как называется многочлен, содержащий два или три слагаемых?

(Двучлен и трехчлен)

4. Какие действия вы умеете выполнять с многочленами? (Сложение, вычитание, умножение)

5. Как добавить или вычесть два многочлена? (Поставить между многочленами знак «плюс» или «минус» и открыть скобки, учитывая правило открытия скобок перед которыми стоит знак «плюс» или «минус»).

6. Как умножить многочлен на многочлен?

(Чтобы умножить многочлен на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена и полученные произведения добавить).

7. Как в общем виде записывается квадратный трехчлен? (aх2 + bх + с)

8. Что называется корнем квадратного трехчлена?

(Число, которое превращает квадратный трехчлен в равенство, равное нулю)

9. Как разложить квадратный трехчлен ах2 + bх + с на множители? (aх2 + bх + с = а (х - х1) (х - х2), где х1 и х2 - корни трехчлена).

10. Какое уравнение называется квадратным? (Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где а ≠ 0, b и с - любые числа, х - переменная).

11. Записать алгоритм нахождения решений квадратного уравнения, и сводного квадратного уравнения.

(Ответ на кодопозитиве № 1)

12. Теорема Виета для полного и приведенного квадратного уравнения.

(Ответ на кодопозитиве № 2)

Кодопозитив №1

ах² + вх + с = 0

D = в² – 4ас;

а) D₁₌

б) D=0,

в) D0,

Кодопозитив № 2

ах² + вх + с = 0 х² + рх + q = 0

х₁ + х₂ = - в/а х₁ + х₂ = -р

х₁* х₂ = с/а х₁*х₂ = q

III. Сообщение темы, цели урока, места урока в теме.

IV. Мотивация учебной деятельности учащихся.

Учитель: Алгебра долго раскрывалась как наука о решения уравнений, прежде всего уравнений вида:

а₀хⁿ + а₁ х^n-1 + ...а _n-1х + х_n = 0

Мы повторили формулы решений квадратных уравнений.

В XVI - XVII возрасте были получены аналогичные, но более громоздкие формулы для уравнений третьей и четвертой степени.

Вот как выглядит, например знаменитая формула Кардано для решения уравнения у³ + ру + q = 0.

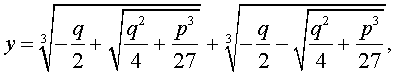
Корни многочленов степени выше четвертой, как правило, не могут быть выражены формулами, в которые входят такие операции над коэффициентами многочлена, как сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Это было доказано в 1823 году норвежским математиком Галуа (1811 - 1832.) И положило конец многократным попыткам решить в общем виде уравнения пятой степени.

V. Восприятие и осознание учениками нового материала.

Учитель: Основными способами решения уравнений высших степеней два: разложение на множители и введения новой переменной.

Сначала рассмотрим произвольный многочлен n-ной степени в стандартной форме

Р(х) = а₀хⁿ + а₁ х^n-1 + ...а _n-1х + а_n а₀ - старший коэффициент, а_n - свободный член. Важно знать, что многочлен от одной переменной с коэффициентом, равным единице, называется нормированным. Произведение нормированных многочленов является нормированным многочленом.

Запишем в тетрадях:

Определение 1. Число а называют корнем многочлена Р (х), если Р (а) = 0

Теорема Безу. Остаток от деления многочлена Р (х) на двучлен х - а равно Р (а), то есть Р(х) = (х – а)Q (х) + r

Обратная теорема Безу. Если число а является корнем многочлена Р (х), то этот многочлен делится на х - а без остатка.

Обобщенная теорема Безу. Если многочлен Р (х) имеет попарно различные корни а₁ , а₂, ...а_n , то он делится без остатка на произведение (х - а₁)(х - а₂) ... (х – а_n)

Последствия. Многочлен степени n имеет не более n различных корней.

Теорема Виета для трехчлена и многочлена четвертой степени.

Используются таблицы и кодопозитивы.

Кодопозитив № 3

а₀х³ + а₁ х² + а ₂х + а₃=0. х₁, х₂, х₃ – корни уравнения

х₁+х₂+х₃= - а₁/а₀

х₁ х₂+ х₁ х₃ +х₁ х₂ = а₂/а₀

х₁х₂х₃=- а₃/а₀

Кодопозитив № 4

а₀х⁴ + а₁ х³ + а ₂х² + а₁х + а₀ =0. х₁, х₂, х_3, х₄ – корни уравнения

х₁+х₂+х₃+х₄= - а₁/а₀

х₁ х₂+ х₁ х₃ +х₂ х₃ + х₁ х₄+ х₂ х₄ +х₃ х₄ = а₂/а₀

х₁х₂х₃ + х₁х₂х₄ + х₁х₃х₄ + х₂х₃х₃₄=- а₃/а₀

х₁ х₂ х₃ х₄ = а₄/а₀

Нужно помнить, что, если многочлен Р (х) делится без остатка на (х – а)^к, но не делится без остатка на (х – а)^к+1, то говорят, что число а - корень кратности для Р (х). Например: (х +4)³(х – 5)²(х + 1)(х + 2) получили многочлен Р (х), для которых число - 4 корень кратности три, число 5 - корень кратности два, а - 1 и -2 - корни кратности один.

VI. Закрепление и осмысление изученного материала.

Учитель рассматривает у доски пример №1 на деления многочлена на многочлен, подчеркивая, что это можно выполнить «углом», как это выполняется для целых чисел.

Разделить многочлен Р(х) = 2х⁴ - 2 х³ + х² + 4х + 5 на тричлен х² + х +2

2х⁴ - 2 х³ + х² + 4х + 5∟ х² + х +2

2х⁴ + 2 х³ +4 х² 2 х² – 4х + 1

-4х³ -3 х² + 4х

-4х³ -4 х² - 8х

х² + 12х + 5

х² + х +2

11х +3 – остаток.

Значит, 2х⁴ - 2 х³ + х² + 4х + 5 = (х² + х +2)( 2 х² – 4х + 1) +11х +3

Ученик у доски выполняет пример № 2.

Разделить Р(х) = х⁴ - 4х³ + 6х² - 7х + 2 на тричлен х² - х - 2

х⁴ - 4х³ +6 х² - 7х + 2∟ х² - х - 2

х⁴ - х³ + 2х² х² – 3х + 1

-3х³ +4 х² -7х

-3х³ +3 х² - 6х

х² - х + 2

х² - х +2

0 – остаток

х⁴ - 4х³ +6 х² - 7х + 2 = (х² - х – 2)( х² – 3х + 1)

VII. Итог урока.

Обсуждаем, что нового учащиеся узнали на уроке.

VIII. Задачи урока: составить план к материалу, записанному на уроке.

Разделить многочлен Р(х)=х⁴ -2х³+х²-3х+5 на двочлен х² – 3х

(два ученика воспроизводят решение на прозрачной пленке)

Самостоятельная работа выполняется на отдельных листочках.

Каждому ученику раздается карточка с одним из вариантов.

Учащимся с высоким уровнем достижений -вариант №1 и №2. Работа проверяется учителем после уроков (каждый учащийся работает в индивидуальном режиме).

Вариант № 1. Выполнить деление многочлена на многочлен:

7х⁴ - 4х³ +3 х² - 10х + 4 на х- 5

Вариант № 2. Выполнить деление многочлена на многочлен:

3х⁴ - 5х³ +2х² + 7х - 1 на х + 2

Вариант № 3. Выполнить деление многочлена на многочлен:

2х⁴ - 7х³ +10х - 8 на х - 4

Вариант № 4. Выполнить деление многочлена на многочлен:

х⁴ - 4х³ +7х - 9 на х + 1

Подготовить рефераты на тему:

1. Прямая и обратная теорема Виета и ее применение.

2. Теорема Безу и ее следствия.

3. Многочлены и их свойства.

4. Нестандартные методы решения некоторых типов уравнений и неравенств.

Литература:

1. И. Глейзер «История математики в школе»

2. М. Л. Галицкий «Углубленное изучение алгебры и математического анализа»

3. И. В. Виленкин «Алгебра и математический анализ. 10 класс»

4. И. Ф. Шарыгин «Факультативный курс по математике. 10 класс». (Решение задач)

5. М. И. Сканави «Сборник задач по математике»

Урок № 3, № 4 (рассчитано на два спаренные уроки)

Тема урока: Разложение многочлена на множители. Самостоятельная робота

Цель урока: 1) формировать умения и навыки при нахождении корней многочленов различными способами: используя практические выводы из теоремы Виета и обратную теорему Безу, схему Горнера и метод неопределенных коефициентов. усовершенствовать деления многочлена на многочлен «углом».

2) развивать в учащихся такие качества, как самостоятельность, творчество и инициативу, формирование у учащихся адекватной самооценки;

3) воспитывать настойчивость и усердие в работе.

Тип урока: урок формирования умений и навыков учащихся.

Оборудование урока: цветные мелки, комплект индивидуальных досок, графопроектор.

План урока.

I. Организационный момент

II. Проверка домашнего задания.

III. Актуализация опорных знаний

IV. Анализ самостоятельной работы, проведенной на предыдущем уроке.

V. Сообщение темы, цели урока, места урока в теми.

VI. Мотивация учебной деятельности учащихся.

VII. Восприятие и осознание учениками нового материалу.VИИИ. Закрепление нового материала.

IХ. Самостоятельная робота.

Х. Итог урока. Сообщение домашнего завдання.

Ход урока:

I. Организационный момент (2 мин.)

II. Проверка домашнего задания. 1. Верность выполнения домашних упражнений проверяется с помощью графопроектора. На прозрачной пленке записан пример, выполненный двумя учащимися.

Кодопозитив № 1

Разделить многочлен х⁴ - 2х³ + х² - 3х + 5 на х² - 3х

х⁴ - 2х³ + х² - 3х + 5∟ х² -3 х

х⁴ - 3х³ х² + х +4

х³ + х²

х³ - 3 х²

4 х² - 3х

4 х² - 12х

9х+5- остаток

Имеем х⁴ - 2х³ + х² - 3х + 5 = ( х² - 3х)( х² + х +4) +9х +5

Зачитать план теоретического материала, записанный на предыдущем уроке. Образец плана может быть таким:

а) Как записывается произвольный многочлен n-й степени в стандартной форме?

б) Какой многочлен называется нормированным?

в) Дать определение корня многочлена.

г) Сформулировать теорему Безу, обратную теорему Безу и обобщенную теорему Безу

д) Последствия теоремы Безу и теоремы Виета (Ученики обсуждают ответ на вопрос плана, образовав «карусель», объединившись в группы по четыре ученика)

III. Актуализация опорных знань.

Тренировочные упражнения. (Тренировочные упражнения подготовлены учителем перед уроком на обратной части доски.

Ответ ученики записывают на индивидуальных досочках) .

Дан многочлен Р(х) =3 х⁶ - 2х⁵ + х³ - 2х + 7

1. Записать:

а) старший коэффициент (3)

б) свободный член (7)

в) степень многочлена (6)

г) делители свободного члена (+ 1; + 7)

д) делители старшего коэффициента (+ 1; + 3)

ж) возможные рациональные корни многочлена (+ 1; + 7/3)

Разложить квадратный трехчлен на множители, используя теорему Виета

х² -7 х + 12 = (х+3)(х+4)

х² - х – 12 = (х+4)(х – 3)

х² + х – 12 = (х – 4)(х + 3)

х² + 7 х +12 = (х – 3)(х – 4)

IV. Анализ самостоятельной работы, проведенной на предыдущем уроке.

Учитель демонстрирует кодопозитивы, на которых показано деления многочлена на многочлен «углом» .

Вариант №1.

7х⁴ - 4х³ + 3х² - 10х + 4∟ х – 5

7х⁴ - 35х³ 7х³ + 31х² + 158 х + 780

31х³ + 3х²

31х³ - 155 х²

158х² - 10х

158х² - 790х

780х +4

780х – 3900

3904 - остаток

Значит, 7х⁴ - 4х³ + 3х² - 10х + 4 = (х – 5)( 7х³ + 31х² + 158 х + 780) + 3904

Имеет смысл подчеркнуть, что если верно выполнено деления, то остаток от делений равно Р (5).

Проверим: Р (5) = 7 ∙ 625 - 4 ∙ 125 + 3 ∙ 25 - 10 ∙ 5 + 4 = 3904

Аналогично

Вариант № 2 .

3х⁴ - 5х³ + 2х² + 7х - 1 ∟ х + 2

3х⁴ + 6х³ 3х³ - 11х² + 24х - 41

- 11х³ + 2х²

-11х³ - 22 х²

24х² +7х

24х² + 48х

- 41х - 1

- 41х – 82

81 - остаток

Значит, 3х⁴ - 5х³ + 2х² + 7х - 1 = (х + 2)( 3х³ - 11х² + 24х - 41) + 81

Проверка остатка Р (-2) = 3 ∙ 16 + 5 ∙ 8 + 2 ∙ 4 – 7 ∙ 2 – 1 = 81

Вариант № 3

2х⁴ - 7х³ + 10х - 8 ∟ х - 4

2х⁴ - 8х³ 2х³ + х² + 4х + 26

х³ + 0х²

х³ - 4х²

4х² +10х

4х² - 16х

26х - 8

26х – 104

96- остаток

2х⁴ - 7х³ + 10х - 8 = (х – 4)( 2х³ + х² + 4х + 26) + 96

Проверка остатка Р(4) = 2 ∙ 256 – 7 ∙ 64 + 10 ∙ 4 – 8 = 96

Вариант № 4

х⁴ - 4х³ + 7х - 9 ∟ х +1

х⁴ + х³ х³ - 5х² + 5х + 2

-5х³ + 0х²

5х³ - 5х²

5х² +7х

5х² +5х

2х - 9

2х + 2

• 11- остаток

х⁴ - 4х³ + 7х - 9 = (х + 1)( х³ - 5х² + 5х + 2) – 11

Проверка остатка Р( - 1) = 1+4 – 7 – 9 = - 11

V. Сообщение темы, цели урока, места урока в теми

VI. Мотивация учебной деятельности учащихся.

Одним из способов решения уравнений высших степеней - способ разложения на множители многочлена, стоящего в левой части уравнения.

VII. Восприятие и осознание учениками нового материалу.

Учитель: Как разложить квадратный трехчлен на множители, мы уже изучили. Пусть требуется разложить на множители с целыми коэффициентами многочлен

Р(х) =2х⁴ - 7х³ - 3х² + 5х – 1

Напомним выводы из теоремы Виета:

а) корни многочлена с первым коэффициентом, равным единице, являются делителями свободного члена

б) корни многочлена общего вида могут быть дробными: числитель является делителем свободного члена, а знаменатель - первого коефициента

Значит: ищем цели корни среди делителей свободного члена: + 1.

Подходит - 1 Р (1) = 2 - 7 - 3 + 5 - 1 = - 4 Р (1) = 2 + 7 - 3 - 5 - 1 = 0

Учитель: обратите внимание, что число 1 является корнем многочлена, тогда и только тогда, когда сумма его коэффициентов равна нулю. Если число - 1 является корнем многочлена необходимо и достаточно, чтобы сумма его коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах.

Первый способ, деление многочлена на многочлен «углом» .

Таким образом, делим

Р(х)= 2х⁴ - 7х³ - 3х² + 5х - 1 на х + 1

2х⁴ - 7х³ - 3х² + 5х - 1 ∟ х + 1

2х⁴ + 2х³ 2х³ - 9х² + 6х - 1

- 9х³ - 3х²

-9х³ - 9х²

6х² +5х

6х² + 6х

- х - 1

- х - 1

0

Р(х) = (х + 1)( 2х³ - 9х² + 6х - 1)

Ищем целые корни кубического многочлена среди делителей его свободного члена: + 1.2 - 9 + 6 - 1 ≠ 0 - 2 - 9 - 6 - 1 = - 18 ≠ 0

Вычисления показали, что целых корней нет. Так как старший коэффициент многочлена не равен 1, то многочлен может иметь дробные рациональные корни. Дробными корнями могут быть только числа - ½; ½.

Подходит ½ ; 2 ∙ 1/8 – 9 ∙ ¼ + 6 ∙ ½ - 1 = ¼ - 9/4 + 3 – 1 = -2 + 3 – 1 = 0

Значит,

_

2х³ - 9х² + 6х - 1 ∟ х + 1

2х³ - х² 2х² - 8х+2

_ - 8х² +6х

-8х² + 4х

_2х - 1

2х - 1

0

Таким образом, имеем:

Р(х) = (х + 1)(х – ½ )( 2х² - 8х+2) = (х + 1)(2х – 1)(х² - 4х+1)

трехчлен х² - 4х+1 на множители с целыми коэффициентами НЕ разлаживается.

Ответ: Р(х) = (х + 1)(2х – 1)(х² - 4х+1)

Второй способ-по схеме Горнера.

Пример 2. Разложить многочлен Р (х) на множители по схеме Горнера

Р(х) =х⁴ - 2х³ - 13х² + 14х + 24

Алгоритм нахождения корней многочлена:

а) записать делители свободного члена + 1; + 2; + 3; + 4; + 6; + 12; + 24

б) записать делители первого коэффициента + 1

в) записать возможные рациональные корни + 1; + 2; + 3; + 4; + 6; + 12; + 24.

г) способом подстановки найдем два корня, этого достаточно, чтобы получить в остатка квадратный тричлен.

Р(1) = 1 – 2 – 13 + 14 + 24 ≠ 0

Р( - 1) = 1+2 – 13 – 14 + 24 = 0

Р(2) = 16 – 2 ∙ 8 – 13 ∙ 4 + 14 ∙ 2 + 24 = 0

Составляем схему. В первой строчке этой таблицы записаны коэффициенты многочлена Р (х). Во второй строчке получаются коэффициенты доли и остаток. Старший коэффициент части равен старшему коэффициенту делимого. Если заполнено несколько ячеек второй строчки, то следующая пустая ячейка заполняется так: берут то число, стоящее над ним первой строчки и добавляют к нему произведение корня и предыдущего элемента второй строчки. В последний ячейке второй строки под свободным членом получается остаток от деления.

Для нашего примера имеем:

	1	- 2	- 13	14	24
х=- 1	1	-1 ∙ 1 – 2 =- 3	- 1 ∙ ( - 3) – 13=-10	-10 ∙ (-1)+14=24	24∙(-1)+24=0
х = 2	1	2 ∙ 1 – 3 = - 1	2 ∙(-1) – 10= - 12	2∙(-12)+24 = 0

Таким образом, имеем

х⁴ - 2х³ - 13х² + 14х + 24= (х+1)(х – 2) (х² –х-12) = (х +1)(х – 2)(х – 3)(х + 4)

Третий способ- метод неопределенных коэффициентов состоит вот в чем:

х⁴ - 2х³ - 13х² + 14х + 24 = (х+1)(х – 2) (ах² + вх + с)

х⁴ - 2х³ - 13х² + 14х + 24 = (х² - х – 12) (ах² + вх + с) = ах⁴ + вх³ + сх² - ах³ - вх² – сх – 2ах² - 2вх – 2с = ах⁴ + х³ (в – а) + х² (с – в – 2а) + х(- с – 2в) – 2с.

Приравниваем соответствующие коэффициенты, имеем а = 1, в – а = - 2; с – в – 2а = - 13.

Или : а= 1, в = - 1; с = - 12

Значит , аналогично:

х⁴ - 2х³ - 13х² + 14х + 24 = (х+1)(х – 2) (х² - х -12) = (х +1)(х – 2)(х – 3)(х + 4)

VIII. Закрепление нового материала.

Возле доски по очереди трое учеников раскладывают на множители многочлен

Р(х) = х³ - 6х² + 15х – 14различными способами.

1 способ.

а) делители свободного члена + 1; + 2; + 7; + 14

б) делители первого коэффициента + 1;

в) возможно рациональные корни + 1; + 2; + 7; + 14.

Способом подстановки находим, что подходит х = 2.

Делим многочлен на двучлен «углом» ._

_х³ - 6х² + 15х - 14 ∟ х + 1

х³ - 2х² х² - 4х+7

_ - 4х² +15х

-4х² + 8х

_ 7х - 14

7х - 14

0

Квадратний тричлен х² - 4х+7 действительных корней не имеет, так как D = 16 - 28 = -12

Таким образом, х³ - 6х² + 15х - 14 = (х - 2) (х² - 4х+7)

2 способ

По схеме Горнера

	1	- 6	15	14
х=2	1	2 ∙ 1 – 6 =- 3	2 ∙ ( - 4) + 15=-10	2 ∙ 7 - 14=24

Р(х) = х³ - 6х² + 15х - 14 = (х – 2) (х² - 4х + 7)

3 способ

Метод неопределенных коэффициентов

х³ - 6х² + 15х - 14 = (х – 2) (ах² + вх + с) = ах³ + вх² + сх – 2ах² - 2вх – 2с = ах³ + х² (в –2а) + х (с –2в ) – 2с.

а = 1, в – 2а = - 6; с – 2в = 15, - 2с = - 14

в = - 4, с = 7.

Таким образом, х³ - 6х² + 15х - 14 = (х – 2) (х² - 4х + 7).

IХ. Самостоятельная работа.

(Класс делится на группы по четыре учащихся)

Выполняют работу в тетрадях.

Если возникают вопросы, обращаются к учителю.

Карточка № 1

Разложить многочлен Р(х) = х³ + 6х² - х - 4 на множители:

1) делением многочлена на многочлен «углом» (самостоятельное выполнение)

2) по схеме Горнера (коллективное исполнение)

3) методом неопределенных коэффициентов (коллективное исполнение)

4) замечания по поводу нарушения дисциплины

5) самооценка деятельности ученика на уроке

6) оценка вчителя.

Карточка №2

Разложить многочлен Р(х) = х⁴ - 4х³ - 7х² + 22х + 24

на множители:

1) делением многочлена на многочлен «углом» (самостоятельное выполнение)

2) по схеме Горнера (коллективное исполнение)

3) методом неопределенных коэффициентов (коллективное исполнение)

4) замечания по поводу нарушения дисциплины

5) самооценка деятельности ученика на уроке

6) оценка учителя.

Карточка № 3

Разложить многочлен Р(х)= х⁴ + 4х³ - 18х² - 12х + 9 на множители:

1. делением многочлена на многочлен «углом» (самостоятельное выполнение)

2. по схеме Горнера (коллективное исполнение)

3) методом неопределенных коэффициентов (коллективное исполнение) 4) замечания по поводу нарушения дисциплины

5) самооценка деятельности ученика на уроке

6) оценка учителя.

Карточка № 4

Разложить многочлен Р(х)= х⁴ + 4х³ + 3х² - 2х - 2 на множители:

1. делением многочлена на многочлен «углом» (самостоятельное выполнение)

2. по схеме Горнера (коллективное исполнение)

3) методом неопределенных коэффициентов (коллективное исполнение) 4) замечания по поводу нарушения дисциплины

5) самооценка деятельности ученика на уроке

6) оценка учителя.

Х. Итог урока:

Что нового учащиеся узнали на уроке?

Домашнее задание.

Разложить многочлен Р(х) = х⁴ - 4х³ + 8х² - 16х + 16 на множители тремя способами. Составить многочлен четвертой степени

Самостоятельная работа проверяется после уроков учителем.

Решение упражнений с карточек.

Карточка № 1

Р (х) = х3 + 6х2 - х – 4

Делители свободного члена + 1; + 2; + 4.

Так как старший коэффициент равен единице, то возможные корни находим среди чисел + 1; + 2; + 4.

Имеем Р (1) = 1 + 4 - 1 - 4 = 0

а) делением многочлена на многочлен:

_х³ +4х² - х - 4 ∟ х - 1

х³ - х² х² + 5х+4

_ - 5х² - х

-5х² -5х

_ 4х - 4

4х - 4

0

х² + 5х+4 = ( х + 1)(х + 4)

Значит, х³ + 4х² - х - 4 = (х – 1)( х + 1)(х + 4)

б) По схеме Горнера

	1	4	- 1	- 4
х=1	1	5	4	0

х³ + 4х² - х - 4 = (х – 1)( х² + 5х+4) =(х – 1)( х + 1)(х + 4)

в) Метод неопределенных коэффициентов

х³ + 4х² -х - 4 = (х – 1) (ах² + вх + с) = (х – 1) (х³ + вх + с) так як а = 1

(х – 1) (х³ + вх + с) = х³ + вх² + сх – х² - вх – с = х³ + х² (в – 1) + х (с –в ) – с = (х – 1)( х² + 5х+4) =(х – 1)( х + 1)(х + 4)

Для карточки № 2

Р(х)= х⁴ - 4х³ - 7х² + 22х + 24

Р (1) = 1 – 4 – 7 – 22 + 24 ≠ 0

Р ( - 1) = 1 + 4 – 7 – 22 + 24 = 0

Р ( 2 ) = 16 – 16 – 28 + 44 + 24 ≠ 0

Р ( - 2 ) = 16 + 32 – 28 – 44 + 24 = 0

а) Делением многочлена на многочлен:

х⁴ - 4х³ - 3х² + 22х +24 ∟ (х + 1)(х + 2) = (х² + 3х + 2 )

х⁴ + 3х³ + 2х² х² - 7 х + 12

- 7х³ - 9х² + 22х

-7х³ - 21х² – 14х

12х² + 36х +24

12х² +36х + 24

0

х² - 7 х + 12 = (х + 3)(х + 4)

х⁴ - 4х³ - 3х² + 22х +24 = (х + 1)(х + 2) (х + 3)(х + 4)

б) По схеме Горнера.

	1	- 4	- 7	22	24
х = - 1	1	- 5	- 2	24	0
х = -2	1	- 7	12	0

х² - 7 х + 12 = (х + 3)(х + 4)

х⁴ - 4х³ - 3х² + 22х +24 = (х + 1)(х + 2) (х + 3)(х + 4)

в) Метод неопределенных коэффициентов

х⁴ - 4х³ - 3х² + 22х +24 = (х² + 3х + 2 ) (х³ + вх + с) = х⁴ + вх³ + сх² +3вх² +3х³+3хс + 2х² +2вх + 2с = х⁴ + х³ (в + 3) + х² (с + 3в + 2) + х(3с +2в) +2с.

Значит, в + 3 = - 4

с + 3в + 2 = - 7

3с + 2в = 22

2с = 24

Имем х⁴ - 4х³ - 3х² + 22х +24 = (х + 1)(х + 2) (х² - 7 х + 12) = (х + 1)(х + 2) (х + 3)(х + 4)

Для карточки № 3

Р(х)= х⁴ + 4х³ - 18х² - 12х + 9

Р (1) = 1+4+3 – 2 – 2 ≠ 0

Р( - 1) = 1 – 4+3+2 = 0

а) Делением многочлена на многочлен:

х⁴ + 4х³ + 3х² - 2х - 2 ∟ х + 1

х⁴ + х³ х³ + 3х² + 0х - 2

3х³ + 3х²

3х³ +3х²

- 2 х - 2

- 2х - 2

0

Q (х) = х³ + 3х² - 2

Q (1) = 1 + 3 – 2 ≠ 0

Q (-1) = -1 + 3 – 2 = 0

_х³ + 3х² - 2 ∟ х + 1 х= - 1 – двократный корень

х³ + х² х² + 2х -2

_ 2х² - 2

2х² +2х

_ -2х - 2

-2х - 2

0

х² + 2х -2 – квадратный тричлен рациональних корней не имеет,

поскольку D = 4+8 = 12

Значит, х⁴ + 4х³ + 3х² - 2х - 2 = (х + 1)²(х² + 2х -2)

б) Схема Горнера

	1	4	3	- 2	-2
х = - 1	1	3	0	- 2	0
х = - 1	1	2	-2	0

х⁴ + 4х³ + 3х² - 2х - 2 = (х + 1)²(х² + 2х -2)

в) Метод неопределенных коэффициентов

х⁴ + 4х³ + 3х² - 2х - 2 =(х +1 )² (х³ + вх + с) = (х² + 2х + 1 ) (х³ + вх + с) = х⁴ + вх³ + сх² +2вх²+2хс + х² +вх + с = х⁴ + х³ (в + 2) + х² (с + 2в + 1) + х(2с +в) + с.

Итак, в + 2 = 4 в = 2

с + 2в + 1 = 3 с = - 2

2с + в = - 2

с = - 2

х⁴ + 4х³ + 3х² - 2х - 2 = (х + 1)²(х² + 2х -2)

Для карточки № 4

Р(х)= х⁴ + 4х³ + 3х² - 2х-2.

Р (1) = 1 + 4 – 18 – 12 + 9 ≠ 0

Р ( - 1) = 1 - 4 – 18 + 12 + 9 = 0

Р ( 3) = 81 + 4∙ 27 – 18 ∙ 9 – 12 ∙ 3 + 9 = 81 + 108 – 162 – 36 + 9 = - 198 + 198 = 0

Итак, х₁ = - 1, х₂ = 3

(х+ 1)(х – 3) = х² - 2х - 3

а) делением многочлена на многочлен:

х⁴ + 4х³ - 18х² - 12х + 9 ∟ х² - 2х - 3

х⁴ - 2х³ - 3х² х² +6 х - 3

6х³ - 15х² - 12х

6х³ - 12х² - 18х

- 3х² + 6х + 9

- 3х² +6х + 9

0

Тричлен х² +6 х - 3 не имеет рациональних корней, так як D = 36 + 4∙ 3 = 36 + 12 = 48

х⁴ + 4х³ - 18х² - 12х + 9 =(х+ 1)(х – 3)( х² +6х – 3)

б) Схема Горнера

	1	4	- 18	- 12	9
х = - 1	1	3	-21	9	0
х = 3	1	6	-3	0

х⁴ + 4х³ - 18х² - 12х + 9 =(х + 1)(х – 3)( х² +6х – 3)

в) метод неопределенных коэффициентов

х⁴ + 4х³ - 18х² - 12х +9 = (х² - 2х - 3 ) (х² + вх + с) = х⁴ + вх³ + сх² - 2вх² - 2х³ - 2хс - 3х² - 3вх - 3с = х⁴ + х³ (в - 3) + х² (с - 2в -3) + х(-2с -3в) -3с.

Отже, - 3с =9, с = -3 с – 2в – 3 = - 18

в – 2 = 4, в = 6 - 2с – 3в = - 12

Таким образом, имеем:

х⁴ + 4х³ - 18х² - 12х + 9 =(х + 1)(х – 3)( х² +6х – 3).

Урок №5.

Тема урока: Разложение многочленов на множители различными способами.

Цель урока: 1) Повторить, обобщить и систематизировать знания учащихся по теме «Разложение многочленов на множители»:

а) повторить алгоритмы нахождения корней многочленов;

б) разложения многочлена на множители делением многочлена на многочлен «углом»;

в) разложение многочлена на множители, используя схему Горнера;

г) разложение многочлена на множители методом неопределенных коэффициентов.

2) Развивать умение оценивать учебную деятельность (свою и товарищей) по образцу оценки учителя.

3) Воспитывать любовь и устойчивый интерес к предмету.

Тип урока: урок обобщения и систематизации знаний и умений учащихся.

Оборудование урока: цветные мелки, кодоскоп, раздаточный материал

План урока.

I. Организационный момент

II. Проверка домашнего задания. Наличие домашнего задания проверено «экспертной группой» до начала урока.

Правильность выполнения проверяется с помощью графопроектора.

Кодопозитив № 1

Р(х) = х⁴ - 4х³ + 8х² - 16х + 16

Делители свободного члена + 1; + 2; + 4; + 4+ 16;

Р(1) = 1 – 4 + 8 – 16 + 16 ≠ 0

Р( - 1) = 1 + 4 + 8 + 16 +16 ≠ 0

Р(2) = 16 – 32 + 32 - 32 + 16 = 0
х = 2

Разделим многочлен на многочлен

_х⁴ - 4х³ + 8х² - 16х + 16 ∟ х - 2

х⁴ - 2х³ х³ - 2х² + 4х - 8

_- 2х³ + 8х²

-2х³ + 4х²

_ 4х² - 16х

4х² - 8х

_ - 8х + 16

- 8х + 16

0

Отметим, что

Р₁(х) = х³ – 2х² + 4х – 8

Р₁(2) = 8 – 8 + 8 – 8 = 0

Значит, _х³ - 2х² + 4х – 8 ∟ х – 2

х³ -2 х² х² + 4

_ 4х – 8

4х – 8

0

х² + 4

х⁴ - 4х³ + 8х² - 16х + 16 = (х – 2)²(х² + 4)

Кодопозитив № 2

б ) Схема Горнера

	1	- 4	8	- 16	16
х = 2	1	-2	4	-8	0
х = 2	1	0	4	0

х⁴ - 4х³ + 8х² - 16х + 16 = (х – 2)²(х² + 4)

Кодопозитив № 3 Метод неопределенных коэффициентов.

х⁴ - 4х³ + 8х² - 16х + 16 = (х – 2)²(х³ + вх + с) = (х² - 4х + 4 ) (х² + вх + с) = х⁴ + вх³ + сх² - 4х³ - 4вх² - 4хс + 4х² + 4вх + 4с = х⁴ + х³ (в - 4) + х² (с - 4в + 4) + х(- 4с +4в) + 4с.

Так как в – 4 = - 4; с – 4в + 4 = 8; - 4с + 4в = - 16

4с = 16, то в = 0; с = 4

х⁴ - 4х³ + 8х² - 16х + 16 = (х – 2)²(х² + 4)

Вторая задача домашней работы (составить многочлен четвертой степени) проверяется так: Ученики, сидящие за одной партой, меняются тетрадями и проверяют работы своих соседей, выставляя им оценку 5 баллов, если многочлен составлен верно. Верно составлены многочлены ученики одного ряда выписывают в отдельную карточку.

ІІІ. Повторение, обобщение и систематизация учебного материала проводится в виде математического турнира.

1. Подготовительный этап.

Клас делится на три команды. Команды выбирают капитана и «экспертную группу» - в составе двух учеников с высоким уровнем достижений.

Каждой команде ставится задача: Составить карточку задач, используя в домашней работе верно составленые многочлены.

Образец карточки:

1. Разложить на множители многочлен делением многочлена на многочлен

Р(х) = х⁴ - 5х³ - х² + 17х + 12

Ответ: х⁴ - 5х³ - х² + 17х + 12 = (х + 1)²(х – 3)(х – 4)

2)разложить на множители с помощью схемы Горнера

Р(х) = х⁴ - 3х³ - 9х² + 23х - 12

Ответ: х⁴ - 3х³ - 9х² + 23х - 12 = (х - 1)²(х + 3)(х – 4)

1. разложить на множители методом неопределенных коэффициентов

Р(х) = х⁴ - 4х³ + 3х² + 4х - 4

1. Составить многочлен пятой степени, который имеет один двукратный корень и три простых корня.

2) Начало игры

а) Конкурс капитанов

Капитан каждой команды дает по одному вопросу капитанам двух других команд. Вопросы могут быть такими:

• Как записывается произвольный многочлен n-й степени в стандартной форме?

• Какой многочлен называется нормированным?

• Дать определение корня многочлена.

• Как формулируется теорема Безу?

• Что значит многочлен кратности два?

• Какие вы знаете практические последствия из теоремы Виета?

• Алгоритм нахождения корней многочлена.

б) Каждая команда обменивается картами заданий. Члены одной команды распределяют между собой упражнения. Работают 15 минут. Решения записывают в тетради. Членам «экспертной группы» разрешаются консультации среди членов своей команды. Капитаны каждой команды выбирают учеников для участия в турнире. Ученики по очереди записывают свои решения у доски. Выигрывает та команда, которая правильно и быстрее решит все завдання.

IV Итог урока-игры. Подводятся итоги математического турнира. Учитывается количество баллов за правильно выполненное домашнее задание каждым рядом (составить многочлен четвертой степени). Выставляются оценки капитанам за конкурс капитанов; ученикам, которые решали задачи у доски.

V Домашнее задание.

Подготовиться к тематической контрольной работы, составить многочлен четвертой степени с одним трехкратным корнем и разложить его на множители тремя способами.

Например, Р(х) = (х – 1)³(х + 4)и т. д.

Урок №6.

Тема урока: Тематическая контрольная работа по теме: «Разложение квадратного многочлена на множители»

Цель урока: 1) Проверить качество усвоения учащимися материала по теме, уровень сформированности раскладывать многочлены на множители различными способами.

Тип урока:

Ход урока:

I. Организационный этап (2 мин.)

II. Выполнение контрольной работы.

Левая сторона.

1. Разложить многочлен на множители делением многочлена на многочлен:

Р(х)= х⁴ + 12х³ +49х² +78х + 40 .

1. Разложить многочлен на множители по схеме Горнера:

Р(х)= х⁴ -4х³ - 31х² +46х + 168.

1. Разложить многочлен на множители методом неопределенных коэффициентов:

Р(х)=х⁴ -3х³ - 12х² +20х + 48.

Правая сторона.

1. Разложить многочлен на множители делением многочлена

на многочлен: Р(х)= х⁴ -х³ -16х² +4х + 48.

1. Разложить многочлен на множители по схеме Горнера:

Р(х)= х⁴ -12х³ +47х² -72х + 36.

1. Разложить многочлен на множители методом неопределенных коэффициентов:

Р(х)=х⁴ -4х³ - 7х² +22х +24.

Критерии оценивания учебных достижений учеников: верно выполнено одно задание оценивается четырьмя баллами. Максимальная оценка за контрольную работу-пять балов. Задание домой: подготовить презентацию на тему: Различные способы решения уравнений высших степенем.

Образец оформления контрольной работы:

Левая сторона.1) Разложить многочлен на множители делением многочлена на многочлен: Р(х)= х⁴ + 12х³ +49х² +78х + 40 .

Делители свободного члена

+ 1; + 2; ; + 4; + 5; + 8; + 20; + 40.

Р(1)≠0, Р(-1)=1-12+49-78+40=0, Р(2) )≠0, Р(-2)=16-96+196-156+40=0

Корни многочлена х=-1, х=-2. (х+1)(х+2)=х²+3х+2

_ х⁴ + 12х³ +49х² +78х + 40 ∟ х² +3х +2

х⁴ + 3х³ + 2х² х² +9х + 20

_ 9х³ + 47х² +78х

9х³ + 27х² +18х

_ 20х² + 60х + 40

20х² + 60х + 40

0

Разложим на множители квадратный трехчлен по формуле Виета: х² +9х + 20=(х+4)(х+5).

Итак, имеем: х⁴ + 12х³ +49х² +78х + 40 = (х+1)(х+2)(х+4)(х+5).

Ответ: х⁴ + 12х³ +49х² +78х + 40 = (х+1)(х+2)(х+4)(х+5).

1. Разложить многочлен на множители по схеме Горнера:

Р(х)= х⁴ -4х³ - 31х² +46х + 168.

Делители свободного члена: + 1; + 2; + 3; + 4; + 6; + 8; + 12; + 14; + 21 и т. д.

Р (1) ≠ 0; Р (-1) ≠ 0; Р (2) = 16-32-124 + 92 + 168 ≠ 0; Р (-2) = 16 + 32-124-92 + 168 = 0. Р (3) = 81-108-279 + 138 + 168 = 387-387 = 0.

Схема Горнера:

	1	- 4	-31	46	168
х = - 2	1	-6	-19	84	0
х = 3	1	-3	-28	0

Трехчлен х²-3х-28=(х-7)(х+4), по теореме Виета.

Итак, имеем: Р(х)= х⁴ -4х³ - 31х² +46х + 168=(х-7)(х-3)(х+2)(х+4).

Ответ: х⁴ -4х³ - 31х² +46х + 168=(х-7)(х-3)(х+2)(х+4).

3)Разложить многочлен на множители методом неопределенных коэффициентов: Р(х)=х⁴ -3х³ - 12х² +20х + 48.

Делители свободного члена: + 1; + 2; + 3; + 4; + 6; + 8; + 12; + 24; +48.

Р(1)≠0; Р(-1)=1+3-12-20+48≠0; Р(2)≠0; Р(-2)=16+24-48-40+48=0;

Р(3)=81-81-108+60+48=0. (х-3)(х+2)=х²-х-6

х⁴ -3х³ - 12х² +20х + 48=( х²-х-6)( х²+рх+q)=х⁴+ рх³+ qх²-х³- рх²-qх-

-6х² -6 рх-6 q=х⁴+х³(р-1)+х²(q-6-р)+х(-q-6р)-6q.

Таким образом: р-1 = 3; q-6-р = -12; q-6р = 20; - 6q = 48, откуда: р = 2,; q = 8.

По теореме Виета х2-2х-8 = (х-4) (х + 2).

Итак, имеем: х²-2х-8=(х-4)(х+2).

Р(х)=х⁴ -3х³ - 12х² +20х + 48=(х-4)(х-3)(х+2)(х+2)= (х+2)²(х-3)(х-4).

Ответ : х⁴ -3х³ - 12х² +20х + 48= (х+2)²(х-3)(х-4).

Правая сторона.

1. Разложить многочлен на множители делением многочлена на многочлен: Р(х)= х⁴ -х³ -16х² +4х + 48.

Делители свободного члена: + 1; + 2; + 3; + 4; + 6; + 8; + 12; + 24; +48.

Р(1)≠0; Р(-1)≠0; Р(2)=16-8-64+8+48=0; Р(-2)=16+8-64-8+48=0.

(х-2)(х+2)=х²-4.

_ х⁴ -х³ -16х² +4х + 48 ∟ х² -4

х⁴ +0х³ -4х² х² -х -12

_ -х³ -12х²

-х³ +0х² +4х

-12х²+ 0х + 48

-12х² +0х + 48

0

Разложим на множители квадратный трехчлен по формуле Виета:

х² -х -12 =(х-4)(х+3).

Итак, имеем: Р(х)= х⁴ -х³ -16х² +4х + 48= (х-2)(х+2)(х-4)(х+3).

Ответ: х⁴ -х³ -16х² +4х + 48 = (х-4)(х-2)(х+2)(х+3).

1. Разложить многочлен на множители по схеме Горнера:

Р (х) = х⁴ -12х³ +47х² -72х + 36

Делители свободного члена: + 1; + 2; + 3; + 4; + 6; + 12; + 18; + 36;

Р(1)=1-12+47-72+36=0; Р(-1)≠0; Р(2)=16-96+188-144+36=240-240=0;

х=1; х=2.

Схема Горнера:

	1	- 12	+47	-72	36
х = 1	1	-11	+36	-36	0
х = 2	1	-9	+18	0

Трехчлен х²-9х+18=(х-3)(х-6), по теореме Виета .

Итак, имеем: Р(х)= х⁴ -12х³ +47х² -72х + 36=(х-6)(х-3)(х-2)(х-1).

Ответ: х⁴ -12х³ +47х² -72х + 36=(х-6)(х-3)(х-2)(х-1).

1. Разложить многочлен на множители методом неопределенных коэффициентов: х⁴ -х³ -19х² +49х - 30.

Делители свободного члена: + 1; + 2; + 3; + 5; + 6; + 15; + 30.

Р (1) = 1-1-19 + 49-30 = 0; Р (-1) ≠ 0; Р (2) = 16-8-19 ∙ 4 + 49 ∙ 2-30 = = 16-8-76 + 98-30 = 0.

Корни многочлена х=1, х=2. (х-1)(х-2)=х²-3х+2

х⁴ -х³ - 19х² +49х -30=( х²3х+2)( х²+рх+q)=х⁴+ рх³+ qх²-3х³-

-3 рх²-3qх +2х² +2 рх+2 q=х⁴+х³(р-3)+х²(q+2-3р)+х(-3q+2р)+2q.

Таким образом: р-3 = 1; q + 2-3р = -19; -3q + 2р = 49; 2q = 30, откуда: р = 2; q = 15.

По теореме Виета х²+2х-15=(х-3)(х+5).

Итак, имеем: Р(х)=х⁴ -х³ - 19х² +49х -30=(х-3)(х-2)(х-1)(х+5).

Ответ: х⁴ -х³ - 19х² +49х -30=(х-3)(х-2)(х-1)(х+5).